 Open Access
Open Access
ARTICLE
Conjugate Usage of Experimental for and Theoretical Models Aqua Carboxymethyl Cellulose Nanofluid Flow in Convergent-Divergent Shaped Microchannel
1 Department of Mechanical Engineering, Science and Research Branch, Islamic Azad University, Tehran, 1477893855, Iran
2 Department of Mechanical Engineering, Central Tehran Branch, Islamic Azad University, Tehran, 1469669191, Iran
3 Department of Petroleum Engineering, Chemistry and Chemical Engineering Research Center of Iran, Tehran, 1497716320, Iran
* Corresponding Authors: Saeed Dinarvand. Email: ,
(This article belongs to the Special Issue: Advances in Computational Thermo-Fluids and Nanofluids)
Frontiers in Heat and Mass Transfer 2025, 23(2), 663-684. https://doi.org/10.32604/fhmt.2025.060559
Received 04 November 2024; Accepted 02 February 2025; Issue published 25 April 2025
Abstract
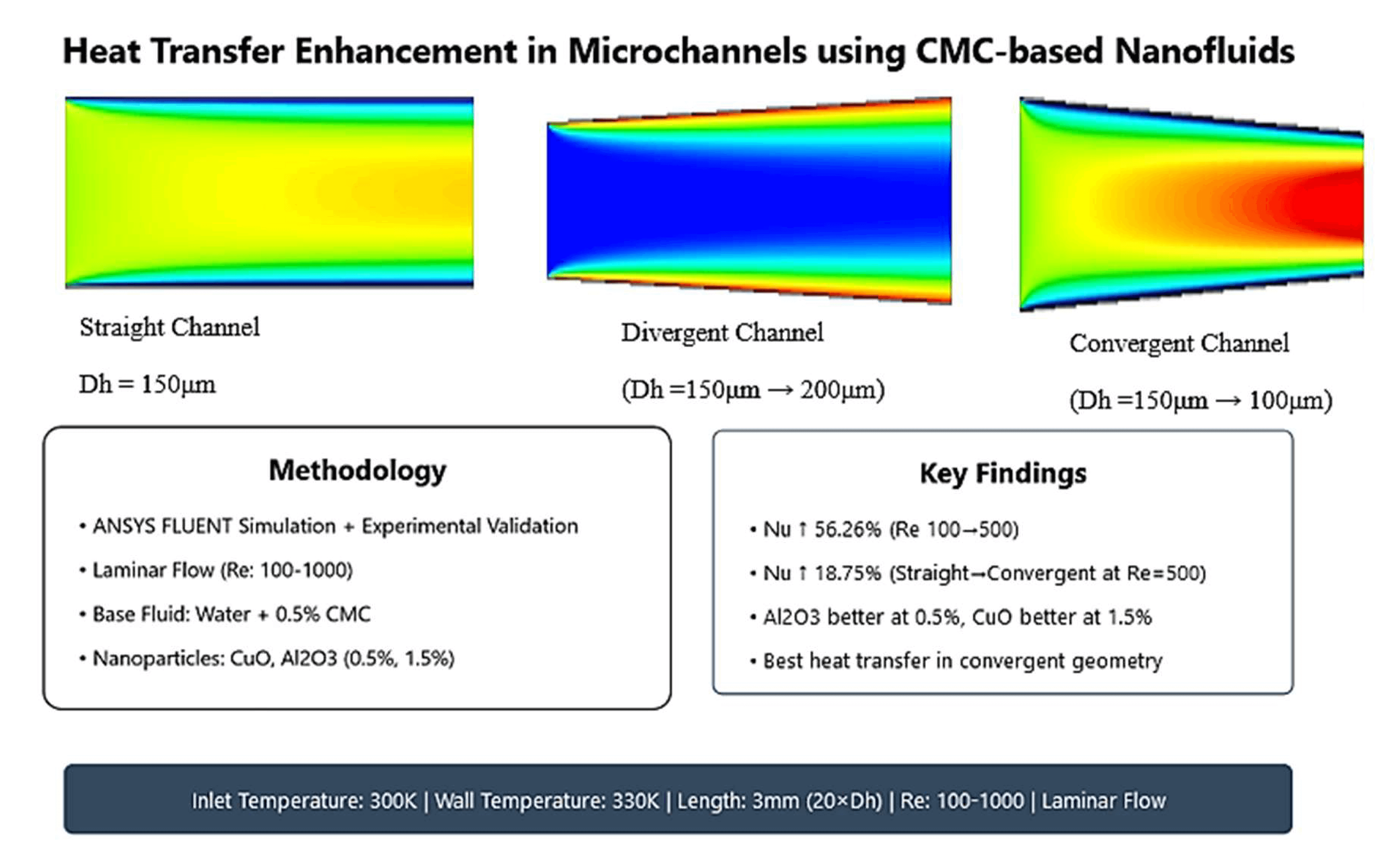
This article aims to model and analyze the heat and fluid flow characteristics of a carboxymethyl cellulose (CMC) nanofluid within a convergent-divergent shaped microchannel (Two-dimensional). The base fluid, water + CMC (0.5%), is mixed with CuO and Al2O3 nanoparticles at volume fractions of 0.5% and 1.5%, respectively. The research is conducted through the conjugate usage of experimental and theoretical models to represent more realistic properties of the non-Newtonian nanofluid. Three types of microchannels including straight, divergent, and convergent are considered, all having the same length and identical inlet cross-sectional area. Using ANSYS FLUENT software, Navier-Stokes equations are solved for the laminar flow of the non-Newtonian nanofluid. The study examines the effects of Reynolds number, nanoparticle concentration and type, and microchannel geometry on flow and heat transfer. The results prove that the alumina nanoparticles outperform copper oxide in increasing the Nusselt number at a 0.5% volume fraction, while copper oxide nanoparticles excel at a 1.5% volume fraction. Moreover, in the selected case study, as the Reynolds number increases from 100 to 500, the Nusselt number rises by 56.26% in straight geometry, 52.93% in divergent geometry, and 59.10% in convergent geometry. Besides, the Nusselt number enhances by 18.75% when transitioning from straight to convergent geometry at a Reynolds number of 500, and by 19.81% at a Reynolds number of 1000. Finally, the results of the research depict that the use of thermophysical properties derived from the experimental achievements, despite creating complexity in the modeling and the solution method, leads to more accurate and realistic outputs.Graphic Abstract
Keywords
Nomenclature
| Cp | Specific heat, J/kg K |
| D | Diameter, m |
| K | Thermal conductivity, W/m K |
| Kn | Knudsen number |
| Nu | Total Nusselt number |
| P | Pressure, N/m² |
| Q | Volumetric flow rate |
| Re | Reynolds number |
| T | Temperature, K |
| u, v | Components of velocity, m/s |
| Velocity vector, m/s | |
| x, y | Cartesian coordinates, m |
| Greek Symbols | |
| ∅ | Volume fraction of nanoparticles |
| μ | Dynamic viscosity, N s/m² |
| θ | Dimensionless temperature |
| ρ | Density, kg/m³ |
| Superscripts and Subscripts | |
| in | Inlet of microchannel |
| p | Particles |
| bf | Base fluid |
| nf | Nanofluid |
| eff | Properties effective |
| * | Dimensionless |
In recent decades, significant efforts have been undertaken to create highly efficient heat exchange devices that focus on energy conservation and the optimization of raw materials, all while addressing economic and environmental concerns [1,2]. The primary goal is to reduce the size of the heat exchanger required for a given thermal load and to increase the capacity of existing heat exchangers [3]. The worldwide need for high-performance and cost-effective heat exchange systems continues to grow significantly, especially in industrial processes, power plants, HVAC applications, and automotive sectors. Heat transfer enhancement can be achieved through various approaches, which are primarily classified into passive and active techniques. Passive methods do not require external force and include the use of extended surfaces [4], compact heat exchangers [5], non-circular cross-section channels, vortex-enhanced heat transfer, altering the rheological properties of fluids, microchannels, surface coating and finishing, using moving devices within the fluid channel, flow rotating devices, creating interruptions and breaks in flow [6], helical tubes, and additives to liquids and gases. Active methods require external power and include mechanical stirring, surface scraping, rotating surfaces [7], surface oscillation, fluid oscillation, using electric fields, injection, and suction [8].
Microchannels [9,10] are increasingly recognized as an effective passive method for enhancing heat transfer in various applications, including cooling systems, power generation, and electronic devices. These channels characterized by their small hydraulic diameters [11]. The enhanced thermal performance is attributed to the increased surface contact between the fluid and the channel walls, as well as the higher heat transfer coefficients achievable in micro-scale flows [12]. Microchannels facilitate rapid heat dissipation, making them ideal for applications where space is limited and high heat fluxes are encountered, such as in microprocessors and compact heat exchangers. Additionally, the use of microchannels can lead to a reduction in the overall size and weight of thermal management systems, contributing to energy and material savings. The manufacturing of microchannels involves advanced techniques such as micro-milling, photolithography, and etching, which allow for precise control over the channel dimensions and surface characteristics. Incorporating microchannels into heat exchange devices can lead to substantial improvements in thermal performance and energy efficiency, aligning with the growing demand for reliable, economical, and environmentally friendly thermal management solutions.
Nanofluids, which are engineered colloidal suspensions containing either a single type of nanoparticle (conventional nanofluids) or multiple types of nanoparticles (hybrid nanofluids, e.g., Fe2O4-TiO2-Ag/H2O) in a base fluids, represent a promising advancement in the field of heat transfer enhancement [13–15]. These fluids show interesting properties in the thermal framework [16–19]. The high thermal conductivity of nanoparticles significantly enhances the thermal conductivity of the base fluid [20–23]. This enhancement leads to more efficient heat transfer, which is crucial for applications requiring high thermal performance, such as electronic device cooling. The preparation of nanofluids involves techniques such as two-step methods, where nanoparticles are first produced and then dispersed into the base fluid, and one-step methods, where nanoparticles are synthesized and dispersed simultaneously. Stabilizing agents or surfactants are often added to prevent particle agglomeration and ensure uniform dispersion, maintaining the stability and performance of the nanofluid. Despite their potential, the application of nanofluids faces challenges such as high production costs, potential long-term stability issues, and the need for extensive research to fully understand their thermal behavior and interactions with various materials. However, ongoing advancements in nanotechnology and material science continue to address these challenges, paving the way for broader adoption of nanofluids in enhancing heat transfer efficiency. The integration of nanofluids into thermal management systems aligns with the global demand for innovative, energy-efficient, and environmentally friendly solutions, contributing to advancements in various industrial sectors.
The increasing demand for efficient cooling systems in various industries has served as the primary motivation for this research. This study deals with the behavior and performance of nanofluids within microchannels, as microchannels, owing to their high surface-to-volume ratio, and nanofluids, due to their superior thermal properties, hold significant potential for enhanced heat transfer. In addition, the unique properties of non-Newtonian nanofluids, combined with the characteristics of microchannels, hold immense potential for enhancement in heat exchanger performance. These findings emphasize how important the optimal selection of channel geometry, base fluid, and volume fraction of nanoparticles is in order to obtain superior heat transfer rates with minimum pressure drop.
The objective of the present study is to model and analyze the flow and heat transfer characteristics of non-Newtonian nanofluids within microchannels of different geometries. Various geometries, namely straight, diverging, and converging microchannels, will be used and compared for their efficiency in heat transfer and pressure drop. Moreover, the influence of various parameters, such as the Reynolds number and nanoparticle concentration, on the performance will be studied in detail. To improve the accuracy in numerical models, experimental data should be included. Some of the important parameters tested in this study, which probably affect the thermal and hydrodynamic performance of non-Newtonian fluids, include the channel geometry, the type of nanoparticle, and the nanoparticle concentration. Two types of nanoparticles, copper and alumina, dispersed in a CMC-based fluid at 0.5% and 1.5% concentrations are considered, while Reynolds numbers in a wide range, between 100 and 1000, characterizing the laminar flow regime, are tested. These results could, therefore, lead to ways to optimize the cooling systems widely used in electronics, automobiles, medical equipment, and harnessing solar energy. The unique feature of this study lies in the creative combination of different parameters, various microchannel geometries, different nanoparticles, and a comprehensive analysis of their mutual effects on the behavior of non-Newtonian nanofluid flow.
2 Geometry, Flow Characteristics and Modeling
This involves the use of three microchannels with the same length but different geometries: a straight microchannel (Case 1), a divergent microchannel (Case 2), and a convergent microchannel (Case 3). Considering the hydraulic diameter formula
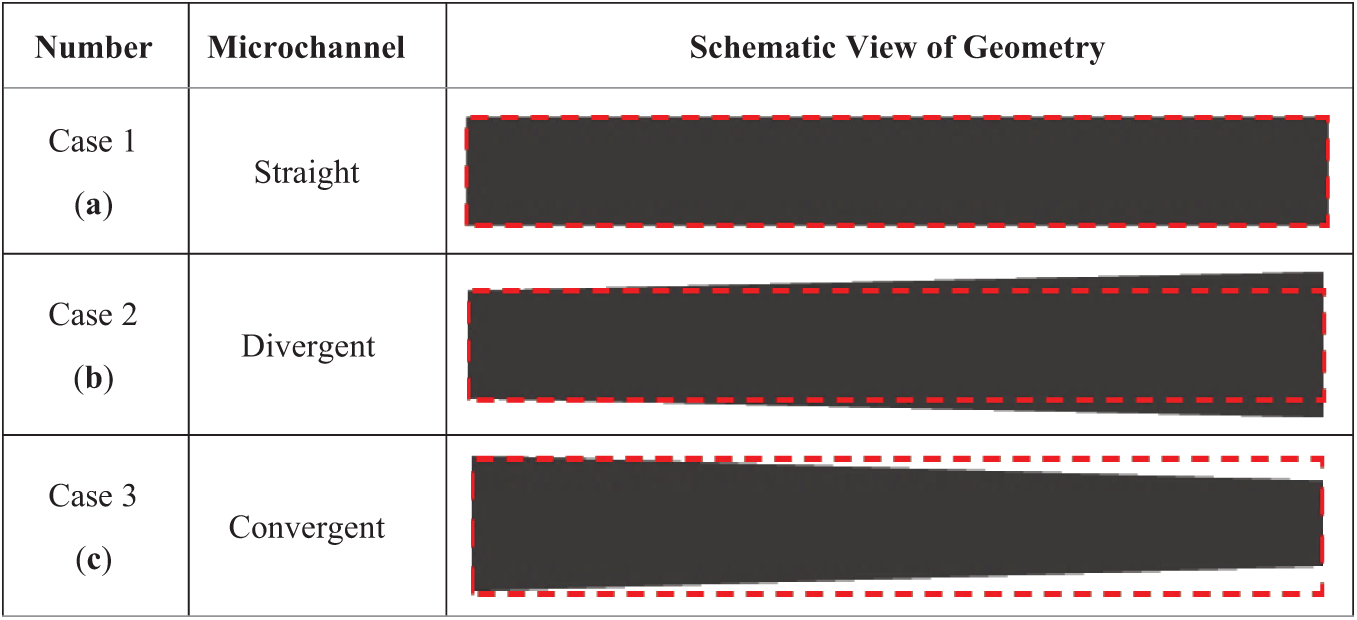
Figure 1: Schematic of two-dimensional geometries used in this study: (a) straight (Case 1); (b) divergent (Case 2); (c) converging (Case 3)

Figure 2: Schematic of a straight microchannel with a constant cross-section (Case 1) and coordinate axes
In this study, given the hydraulic diameter of the microchannel and the mean free path of water, the Knudsen number is very small (
In the steady state, assuming constant properties and laminar flow, equations for a single-phase non-Newtonian nanofluid are as follows:
In the above equations, P and T are the pressure and temperature of the nanofluid, respectively.

Using the above-mentioned formulas, the first step is to calculate the effective properties at the average temperature (315 K). To do so, Table 1 is made based on the mentioned references that includes the utilized formula. Then, using the formulas provided in Table 1, the thermophysical properties required for nanofluids simulation are derived as presented by Table 2.

In this study, the microchannel walls are subject to a constant temperature boundary condition. The fluid enters the microchannel with a constant inlet velocity (determined based on the specified Reynolds number) and a uniform temperature profile. The inlet temperature is 300 K, and the outlet boundary condition is an outlet pressure of 0 Pa. The no-slip boundary condition is imposed at the walls, which are maintained at a constant temperature of 330 K. These boundary conditions provide a realistic basis for accurate flow and heat transfer simulations in the microchannel, enabling the study of fluid behavior and thermal characteristics along the flow path. The dimensionless parameters are defined as follows:
here,
Alumina and copper oxide nanoparticles are used in the present study owing to their proven thermophysical superiority, exceptional thermal properties, strong chemical stability, and low cost. Besides that, nanoparticles of such types are also commonly used in the previous studies on nanofluids, which therefore justifies their applicability here. For the low concentrations of nanoparticles (0.5% and 1.5%), a single-phase homogeneous model is used, in which good agreements with experimental data are obtained. The combination of experimental methods with numerical techniques provides more accurate results that better reflect reality. This approach helps us reduce the complexity of non-Newtonian nanofluid simulations and lower computational costs. Consequently, we can solve the problem using a single-phase homogeneous approach without the need for two-phase analysis, while the obtained results will be very close to those of the two-phase model. After determining the thermophysical properties, the next step is to select the problem-solving method. The power law model is chosen based on the provided references, and the rheological properties are extracted from it (Table 3). Here, the shear stress relationship in the non-Newtonian fluid (power law) is as follows [28]:

In the above relation, K,
The rheological properties of the non-Newtonian nanofluids with aluminum oxide and copper nanoparticles at different volume fractions used in this study are shown in Table 3 [24,29].
In this research, the Nusselt number is calculated using the following relation:
The pumping power (PP) for circulating the nanofluid is as follows:
Additionally, to obtain the volumetric flow rate, we use the following equation:
where A represents the cross-sectional area of the inlet and
Calculation of the pressure drop in microchannels becomes important because it directly gives the level of consumption of the pump’s power and hence the system’s operating costs. Besides, pressure drop analysis enables the designer to obtain an optimal balance between enhanced heat transfer and the consumption of increased pump power.
The computational grid for simulating heat transfer and flow of non-Newtonian nanofluids in straight (Case 1), divergent (Case 2), and convergent (Case 3) two-dimensional microchannels were selected as 9 × 300, 18 × 300, 27 × 300, 36 × 300, and 36 × 600. We then analyzed the output for every microchannel. Table 4 shows the values of the global Nusselt number and the dimensionless total pressure drop for each of the grids investigated, calculated from the simulation of pure water flow at Reynolds Number of 500 (Table 4). Looking at the results per geometry, it can be seen that the results from the 27 × 300 and 36 × 300 grids are very close and differ slightly from one another (less than 2%). In addition, the distribution of the selected grid elements throughout each straight, divergent, and convergent geometries are provided respectively in Fig. 3. It can be seen from Fig. 3 that, in order to appropriately calculate the heat flux and shear rate in the flow of the non-Newtonian fluid, the smallest elements were distributed near the transverse boundaries and the largest elements were distributed in the central region.


Figure 3: Distribution of selected mesh elements in each of the straight, divergent, and convergent microchannel geometries: (a) straight; (b) divergent; (c) convergent
3 Numerical Method for Flow and Heat Transfer in Micro Dimensions and Validation
A combination of experimental and numerical methods plays a pivotal role in this research to comprehensively investigate heat transfer and nanofluid flow in microchannels. The experimental approach provides real-world data on the thermophysical properties of fluids, enabling the validation of numerical models and the discovery of novel phenomena. In this investigation, the governing equations for the problem were solved and the flow and heat transfer of a non-Newtonian nanofluid in a two-dimensional microchannel were simulated using the finite volume method and the commercial software ANSYS FLUENT. A coupled method was used to relate the velocity and pressure, and for the discretization of the momentum and energy equations, and the pressure equation, a second-order upwind scheme was utilized. The convergence criterion to ensure the accuracy of the results was the reduction of the maximum residual of the mass, momentum, and energy conservation equations to less than
To validate the method used for solving flow and heat transfer fields in micro dimensions, the study by Hajialigol et al. [30], which has conditions somewhat similar to the problem under study, was selected and simulated, and its results were compared. Hajialigol et al. numerically studied combined heat transfer and laminar flow of pure water in a three-dimensional straight microchannel with different aspect ratios and with a constant wall heat flux boundary condition in the Reynolds number range

Figure 4: Comparison of the results of present simulation and the research of Hajialigol et al. [30]: (a) schematic representation of Hajialigol et al.’s geometry [30]; (b) comparison of simulation results in the present study with those of Hajialigol et al. [30] regarding total pressure drop
Albojamal et al. [31] simulated the laminar flow of pure water and water-alumina nanofluid in a 1-m-long pipe with a constant circular cross-section of 1 cm in diameter and a constant wall heat flux boundary condition in two dimensions, using the ANSYS FLUENT software with an axial symmetry boundary condition. Table 5 shows that, in the Reynolds number range of 250 and nanoparticle volume fractions from 0 to 4 percent, the simulation results have a small discrepancy with the results obtained from the homogeneous single-phase nanofluid simulation method in the Albojamal et al. paper. The differences in the results obtained from the simulation are a maximum of 3.11 percent for the Nusselt number and 2.38 percent for the heat transfer coefficient compared to their results. As a result, by comparing the results in the Albojamal et al. paper and the simulation results, the accuracy of the chosen method for modeling the nanofluid as a homogeneous single-phase can be assured.

4.1 Analysis of Cross-Sectional Effect on Micro-Channel Flow
In this part, the influence of choosing microchannel geometry on heat transfer and non-Newtonian base fluid flow of 0.5 wt% carboxymethyl cellulose solution in water, at Reynolds numbers 100, 500, and 1000, is studied on straight, divergent and convergent microchannels. The non-Newtonian base fluid flow enters the straight, diverging, and converging microchannel with a constant and uniform velocity. Eq. (6) is used to calculate the input velocity. The non-Newtonian base fluid temperature at the entrance of each of the microchannels is 300 K and the wall temperature is 330 K. In the following, the results obtained from the simulation of the flow and heat transfer of the non-Newtonian base fluid in each of the microchannels are described. Fig. 5 shows the Nusselt number values of the total non-Newtonian base fluid flow at Reynolds numbers 100, 500 and 1000 obtained from straight (Case 1), divergent (Case 2) and convergent (Case 3) microchannels.

Figure 5: The Nusselt number values of the non-Newtonian base fluid flow at Reynolds numbers 100, 500, and 1000 obtained from straight (Case 1), divergent (Case 2) and convergent (Case 3) microchannels
Fig. 5 illustrates that in each of the studied microchannels, the Nusselt number is enhanced with the increase of the Reynolds number. This augmentation can be due to the increase in flow velocity and therefore the enhancement in velocity near the microchannel wall and the increase in convective heat transfer. In addition, Fig. 5 depicts that the values of the total Reynolds number obtained from the convergent microchannel are higher than the straight microchannel and the straight microchannel is higher than the divergent microchannel. The increase in the value of the Reynolds number in the convergent geometry and its decrease in the divergent geometry according to the law of conservation of mass can be due to the increase in the flow velocity due to the decrease in the cross-sectional area in the convergent geometry and the reduction in the flow velocity due to the increase in the cross-section area in the divergent geometry.
Fig. 6 shows the influence of increasing the Reynolds number on the dimensionless total pressure drop values of the non-Newtonian base fluid flow. In each geometry, the total pressure drop values are dimensionless with the total pressure drop value at Reynolds number 100. Fig. 6 shows that the dimensionless total pressure drop usually increases with the enhancement of Reynolds number. The increase in the dimensionless total pressure drop with the enhancement in the Reynolds number can be due to the increase in velocity near the surface and therefore the enhancement in friction. The augmentation in the value of the dimensionless total pressure drop in the convergent geometry and its decrease in the divergent geometry according to law of conservation of mass can be due to the changes in the cross-section area.

Figure 6: The dimensionless total pressure drop of the non-Newtonian base fluid flow obtained from straight (Case 1), divergent (Case 2) and convergent (Case 3) microchannel compared with total pressure drop value at Reynolds number 100
Table 6 also demonstrates the values of the Nusselt number at Reynolds numbers 100, 500 and 1000 and the percentage change of the Nusselt number values with the enhancement of the Reynolds number in each of the microchannels. For example, in straight geometry, as the Reynolds number increases from 100 to 500, the Nusselt number increases by 56.26%. This enhancement is 52.93% in divergent geometry and 59.10% in convergent geometry. Examining the results of Table 6 shows that the enhancement of the Nusselt number with the enhancement of the Reynolds number is more in convergent geometry than in straight and divergent geometry. Further, by examining the results of Table 6, it can be seen that at a Reynolds number of 100, by changing the geometry from straight geometry to divergent geometry, the Nusselt number decreases by 11.01%, and by changing the geometry from straight geometry to convergent geometry, the Nusselt number enhances by 16.64%. The reduction of the Nusselt number by changing the geometry from straight geometry to divergent geometry is 12.91% at Reynolds number 500% and 14.05% at Reynolds number 1000. In contrast, the increase in the value of the Nusselt number by changing the geometry from straight geometry to convergent geometry is 18.75% at Reynolds number 500% and 19.81% at Reynolds number 1000. In summary, the results show that the selection of convergent geometry improves the transmission compared to direct geometry. On the other hand, choosing divergent geometry reduces heat transfer compared to straight geometry.

To study the effect of choosing the geometry and increasing the Reynolds number on the flow field and temperature, the contours of velocity and temperature are presented in Figs. 7 and 8. Fig. 7 shows the velocity contours obtained from straight (Case 1), divergent (Case 2) and convergent (Case 3) geometries at Reynolds numbers 100 and 500. The study of the velocity contours in Fig. 7 depicts that in each of the Reynolds numbers, by choosing the divergent geometry, the velocity in the central part along the length of the microchannel decreases and tends to the green color. On the other hand, by choosing the convergent geometry, the velocity increases in the central part along the microchannel and tends to the red color. The reduction of the velocity in the central part in the converging microchannel and its increase in the converging microchannel is justified according to the law of conservation of mass. According to the assumption of continuity of the base fluid and the boundary condition of non-slip on the surface of the microchannel, the velocity on the surface of the microchannel is 0 m/s. Therefore, the velocity of the central part should decrease as it approaches the surface. The speed reduction rate in the divergent microchannel is lower than the straight microchannel due to the smaller velocity in the central part and the larger distance between the central part and the boundary surface. On the other hand, the velocity reduction rate in the convergent microchannel is higher due to the greater velocity in the central part and the smaller distance between the central part and the boundary surface compared to the straight microchannel. By choosing the convergent microchannel and as a result increasing the velocity reduction rate, it can be expected that the shear stress on the surface and as a result the pressure drop along the convergent microchannel will increase compared to the straight microchannels.

Figure 7: Velocity contours in Re = 100, and Re = 500 obtained from: (a) straight (Case 1); (b) divergent (Case 2); (c) convergent (Case 3) microchannels at Reynolds numbers 100 and 500
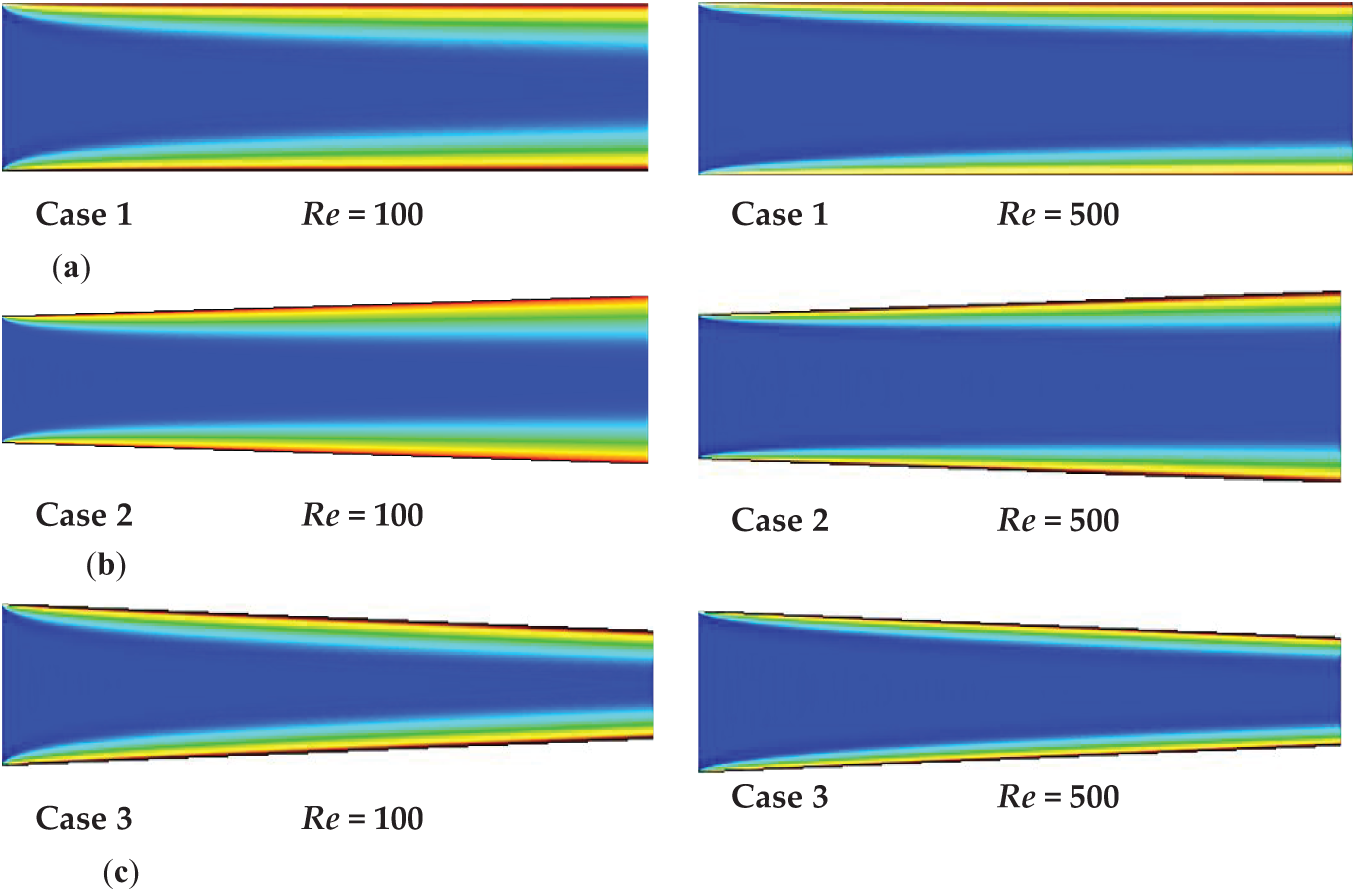
Figure 8: Temperature contours in Re = 100, and Re = 500 obtained from: (a) straight (Case 1); (b) divergent (Case 2); (c) convergent (Case 3) microchannels at Reynolds numbers 100 and 500
Fig. 8 depicts the temperature contours obtained from straight (Case 1), divergent (Case 2) and convergent (Case 3) geometries at Reynolds numbers 100 and 500. The study of the temperature contours in Fig. 8 shows that in each of the Reynolds numbers along each of the straight, divergent and convergent geometries, the thickness of the thermal boundary layer increases and a larger part of the cross-sectional area is placed under the effect of microchannel wall. By comparing the temperature contour obtained from straight, divergent and converging microchannels, it is observed that in each of the Reynolds numbers 100 and 500, the temperature changes from 300 K in the central part to 330 K on the boundary surface in the divergent microchannel due to the greater distance of the central part. It happens with the boundary surface in a longer length than the straight and converging microchannel. On the other hand, these changes occur in the convergent microchannel in a shorter length than the straight microchannel. Therefore, the rate of temperature change in the width and, as a result, the rate of heat transfer from the surface is higher in the converging microchannel than in the straight microchannel and in the straight microchannel than in the divergent microchannel. As a result, it is expected that the total heat transfer and Nusselt number will increase by choosing convergent geometry compared to straight geometry and decrease by choosing divergent geometry compared to straight geometry.
4.2 Analysis of Nanoparticle Effect on Micro-Channel Flow
To investigate the effect of increasing the Reynolds number on the variations in the Nusselt number and the influence of different nanoparticles at various volume fractions, Fig. 9 is plotted and examined. Fig. 9 shows the changes in the Nusselt number for the base fluid flow and non-Newtonian nanofluid in straight (Case 1), divergent (Case 2), and convergent (Case 3) microchannels as the Reynolds number increases from 100 to 1000 with volume fractions of 0.5% and 1.5% of alumina and copper oxide nanoparticles. The results indicate that, in general, increasing the Reynolds number leads to an increase in the Nusselt number across different geometries and nanoparticle volume fractions. This is because an increase in the Reynolds number, and consequently the flow velocity, while keeping the geometry and fluid properties constant, can increase the velocity near the microchannel surface. This increased velocity near the surface can enhance the convective heat transfer coefficient, thereby increasing the overall heat transfer in the microchannel.

Figure 9: The Nusselt number of base fluid and non-Newtonian nanofluid in the microchannel with increasing Reynolds number for various geometry of microchannels: (a) Straight Microchannel; (b) Divergent microchannel; (c) Convergent microchannel
Fig. 9 shows that adding nanoparticles improves the thermophysical properties of the non-Newtonian nanofluid mixture, resulting in increased heat transfer and consequently higher Nusselt numbers compared to the base fluid across all Reynolds numbers and geometries. For example, in the straight geometry (Case 1), the Nusselt number for the base fluid in a straight microchannel increase by 96.5%, from 7.21 to 14.17, as the Reynolds number increases from 100 to 1000. With the addition of 0.5% and 1.5% volume fractions of alumina nanoparticles to the non-Newtonian base fluid, the Nusselt number increases by 94.1%, from 7.89 to 15.31, and by 94.5%, from 8.03 to 15.62, respectively. Similarly, with the addition of 0.5% and 1.5% volume fractions of copper oxide nanoparticles to the non-Newtonian base fluid, the Nusselt number increases by 95.2%, from 7.82 to 15.27, and by 97.5%, from 8.01 to 15.82, respectively.
Moreover, the results show that at a 0.5% volume fraction, alumina nanoparticles perform better than copper oxide in increasing the Nusselt number, whereas at a 1.5% volume fraction, copper oxide nanoparticles show better performance. This trend is also observed in divergent (Case 2) and convergent (Case 3) microchannels. For instance, the Nusselt number in the divergent microchannel increases by 89.81%, from 6.42 to 12.18, for the non-Newtonian base fluid, by 88.02%, from 7.14 to 13.43, with the addition of 1.5% alumina nanoparticles, and by 91.25%, from 7.13 to 13.64, with the addition of 1.5% copper oxide nanoparticles as the Reynolds number increases from 100 to 1000. Similarly, in the convergent microchannel, the Nusselt number increases by 101.88%, from 8.41 to 16.98, for the non-Newtonian base fluid, by 99.45%, from 9.38 to 18.71, with the addition of 1.5% alumina nanoparticles, and by 102.34%, from 9.34 to 18.89, with the addition of 1.5% copper oxide nanoparticles, as the Reynolds number increases from 100 to 1000.
Table 7 presents the Nusselt number for the base fluid and non-Newtonian nanofluid with 0.5% and 1.5% volume fractions of alumina and copper oxide nanoparticles at Reynolds numbers of 100, 500, and 1000, across straight (Case 1), divergent (Case 2), and convergent (Case 3) geometries. Examining the results at these Reynolds numbers reveals that the highest increase in the Nusselt number compared to the base fluid flow in a straight microchannel is observed with a 33.3% increase for the 1.5% volume fraction of copper oxide nanofluid in the convergent microchannel. Conversely, the greatest decrease in the Nusselt number compared to the base fluid flow in a straight microchannel is observed with a 14.1% decrease for the base fluid flow in the divergent microchannel.

Figs. 10 and 11 illustrate, respectively, the dimensionless velocity profile normalized by the inlet velocity in each of the studied cases and the dimensionless temperature profile for pure water flow, the base fluid, and non-Newtonian nanofluid at a Reynolds number of 500. Comparing the velocity and temperature profiles in each of the different cases reveals that using a non-Newtonian fluid increases the rate of change of velocity and consequently the velocity near the microchannel surface. According to the law of mass conservation, this results in a decreased velocity in the central part of the microchannel compared to the flow of pure Newtonian water. The increased velocity near the microchannel surface leads to higher rates of temperature change and surface heat transfer, resulting in an increased convective heat transfer coefficient and Nusselt number compared to the pure Newtonian water flow. These changes follow a similar pattern across straight, divergent, and convergent geometries. The inlet velocity of the microchannel has a direct impact on the flow and heat transfer within the microchannel. At a constant Reynolds number, adding copper oxide and alumina nanoparticles at various volume fractions can alter the inlet velocity profile, which in turn can affect the velocity profile and changes near the surface, influencing the heat transfer in the microchannel. Besides, the comparison of the dimensionless velocity and temperature profiles shows that in pure Newtonian water and non-Newtonian nanofluid, the rate of change of velocity and temperature near the wall increases in convergent geometry compared to straight geometry, and in straight geometry compared to divergent geometry. This results in enhanced heat transfer and increased total pressure drop in the microchannel. Using non-Newtonian nanofluids not only improves the fluid properties but also increases the rates of temperature and velocity changes, thereby improving heat transfer and increasing the total pressure drop.

Figure 10: Dimensionless velocity for pure water, base fluid and non-Newtonian nanofluid at Reynolds number 500 and geometries of: (a) straight (Case 1); (b) divergent (Case 2) (c) convergent (Case 3)

Figure 11: Dimensionless temperature for pure water, base fluid and non-Newtonian nanofluid at Reynolds number 500 and geometries of: (a) straight (Case 1); (b) divergent (Case 2); (c) convergent (Case 3)
4.3 Geometry and Nanoparticles Effects on Pressure Drop and Pumping Power
Table 8 presents a detailed analysis of the influence of geometry and nanoparticles on pressure drop and pumping power. Results evidence that due to changes in geometry and the addition of nanoparticles, significant changes occur in the hydrodynamic performance compared to a straight microchannel (Case 1). During a base fluid Reynolds number of 500, the convergent geometry of Case 3 presents an increase in friction factor of about 188%, starting from that with the straight geometry at a value of 8694.30 to 25,036.90 (Pa), while the geometry of Case 2, having a diverging shape, gave a reduction in friction factor of about 70.7%, starting from a value of 8694.30 to 2545.38 (Pa). This becomes even more pronounced when the Reynolds number is increased to 1000: convergent geometry shows a pressure drop increase of 259% while the divergent geometry presents a reduction of 93.8% in respect to the straight channel. A peculiar feature of the divergent geometry is that both pressure drop and pumping power take negative values for higher Reynolds numbers, precisely Re = 1000, explained by the flow reversal occurring in this geometry.

This flow reversal, because of flow separation in divergent geometry, brings about a change in pressure gradient direction. Similarly, variations are observed in pumping power, with the Reynolds number 1000 recording a 259% increase from 15.554 to 55.81257 (W) in convergent geometry and a 93.8% decrease from 15.554 to 0.9642 (W) in divergent geometry compared to straight geometry.
The incorporation of copper oxide and alumina nanoparticles manifests the irregular features appearing in pressure drop and, hence, the pumping power, too. It has been inferred that adding 1.5% CuO nanoparticles to this base fluid caused approximately a pressure raise of about 37% as compared with the original value in the case of a straight microchannel at Re = 500 (8694.30 to 11,913.73 Pa). For horizontal microchannel, the pressure drop shows more decrement at an additive of 0.5% (Al2O3) NPs added to water, which has evidenced a pressure drop reduction from 8694.30 to 7233 Pa (−16.8%). This trend changes with an increase in Reynolds number to 1000, where in straight geometry, 1.5% CuO nanofluid shows an increase of 43.8%, and 0.5% Al2O3 nanofluid shows a decrease of 20.2%, as compared to the base fluid in pressure drop.
The combination of convergent geometry with 1.5% CuO nanofluid gives the highest increase in pressure drop and pumping power. These create a pressure drop enhancement of 394% at Reynolds number 1000 as compared with that obtained by the base fluid in the straight channel. But the combination of divergent geometry with 0.5% Al2O3 nanofluid has the least pressure drop in all, creating a pressure drop fall about 99.6% below the pressure drops exhibited by the base fluid in a straight channel when the Reynolds number is 1000 from 14,792.33 down to 61.89 (Pa).
These results suggest that microchannel geometry plays a much stronger role than nanoparticle addition in influencing pressure drop and pumping power. In addition, an increase in Reynolds number enhances these effects. These findings are useful in the optimal design of microchannels, as this involves consideration of a trade-off between thermal and hydrodynamic performance.
This study presents a comprehensive analysis and modeling of heat and fluid flow characteristics of a carboxymethyl cellulose (CMC) nanofluid in microchannels with varying geometries. The base fluid, composed of water and 0.5% CMC, is infused with CuO and Al2O3. Utilizing both experimental and theoretical approaches, the research aims to accurately depict the non-Newtonian nanofluid behavior. The governing equations for mass, momentum, and energy conservation were solved using ANSYS FLUENT. Main results are as follows:
(1) the research demonstrates the importance of using experimentally derived thermophysical properties for accurate modeling, despite the added complexity.
(2) in the selected case study, when the Reynolds number rises from 100 to 500, the Nusselt number increases by 56.26% in straight geometry, 52.93% in divergent geometry, and 59.10% in convergent geometry.
(3) in the selected case study, the Nusselt number increases by 18.75% when shifting from straight to convergent geometry at a Reynolds number of 500, and by 19.81% at a Reynolds number of 1000.
(4) along each of the straight, divergent and convergent geometries, the thickness of the thermal boundary layer increases and a larger part of the cross-sectional area is placed under the effect of microchannel wall.
(5) at a 0.5% volume fraction, alumina nanoparticles perform better than copper oxide in increasing the Nusselt number, whereas at a 1.5% volume fraction, copper oxide nanoparticles show better performance.
(6) In the final analyses, for microchannel, geometric effect prevails over nanoparticle addition at larger pressure drops and pumping powers. At 1000 Reynolds numbers, flow is characterized to enhance the geometry: convergent shows increases of about 259%, and divergent shows about a 93.8% decline in wall pressure drop concerning that of straight-channel geometry. Flow reversal also justifies the attainment of negative value with high Reynolds number geometries related to diverging microchannel geometry wall pressure drop and pumping power.
(7) The convergent geometry with the 1.5% CuO nanofluid combination exerts the maximum increase in pressure drop and pumping power, which is 394% of the base fluid in a straight channel with a Reynolds number of 1000. At the same time, the divergent geometry combined with 0.5% Al2O3 nanofluid exerts the least value in pressure drop by 99.6%.
Although the current study has produced significant findings on the flow and heat transfer characteristics of non-Newtonian nanofluids in microchannels, there are many limitations and opportunities for future research. The main challenges include long-term nanofluid stability, high production costs, corrosion and wear effects, microchannel clogging, manufacturing complexity, and non-uniform heat transfer in real applications. Future studies should focus on investigating various types of nanoparticles and hybrid composites at higher concentrations, while assessing their long-term stability. To address these challenges, research efforts should be directed toward developing cost-effective production methods, improving manufacturing techniques for complex microchannel geometries, and implementing advanced two-phase models that consider surface effects and magnetic forces. The scalability of laboratory results to industrial applications requires particular attention, especially regarding system performance in larger dimensions and under actual operating conditions.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization: Shervin Fateh Khanshir; Data curation: Shervin Fateh Khanshir, Saeed Dinarvand; Methodology: Shervin Fateh Khanshir; Software: Shervin Fateh Khanshir; Validation: Shervin Fateh Khanshir; Analysis and interpretation of results: Saeed Dinarvand, Shervin Fateh Khanshir, Ramtin Fateh Khanshir; Writing–original draft: Shervin Fateh Khanshir, Saeed Dinarvand; Project supervisor: Saeed Dinarvand; Editing and revising the manuscript: Ramtin Fateh Khanshir. Writing–review & finalization of manuscript: Ramtin Fateh Khanshir. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data can be provided on request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Hasan MM, Rahman MM, Islam MS, Chan WH, Alginahi YM, Kabir MN, et al. Artificial neural network modeling for predicting thermal conductivity of EG/water-based CNC nanofluid for engine cooling using different activation functions. Front Heat Mass Transf. 2024;22(2):537–56. doi:10.32604/fhmt.2024.047428. [Google Scholar] [CrossRef]
2. Tang S, Ding L, Wu X, Zhou J, Wang L, Yu Y. Numerical investigation of thermal-hydraulic characteristics in cross-flow heat exchangers with different twisted oval tubes. Case Stud Therm Eng. 2024;54:104063. doi:10.1016/j.csite.2024.104063. [Google Scholar] [CrossRef]
3. Cao Y, Meng X. A novel numerical method for simulating boiling heat transfer of nanofluids. Front Heat Mass Transf. 2024;22(2):583–95. doi:10.32604/fhmt.2024.049111. [Google Scholar] [CrossRef]
4. Hasan HA, Sherzaa JS, Abd LA, Ameena KA, Abed AM, hatem Arif A, et al. Study the effect of flow water/Al2O3 nanofluid inside mini-channel for cooling concentrated multi-junction solar cell. Front Heat Mass Transf. 2022;18(1):1–8. doi:10.5098/hmt.18.45. [Google Scholar] [CrossRef]
5. Dolui SK, Veeresh Babu A, Srinivas Reddy T. Experimental studies on the effect of Al2O3 + water nanofluid concentrations on dimensionless heat transfer parameters in a cleanroom air handling unit. Proc Inst Mech Eng Part E J Process Mech Eng. 2024:09544089241248150. doi:10.1177/09544089241248150. [Google Scholar] [CrossRef]
6. Dhumal GS, Havaldar SN. Enhancing heat transfer performance in a double tube heat exchanger: experimental study with twisted and helical tapes. Case Stud Therm Eng. 2023;51(5):103613. doi:10.1016/j.csite.2023.103613. [Google Scholar] [CrossRef]
7. Ghoben ZK, Hussein AK. Natural convection in a partially heated parallelogrammical cavity with v-shaped baffle and filled with various nanofluids. Front Heat Mass Transf. 2022;18(1):1–11. doi:10.5098/hmt.18.6. [Google Scholar] [CrossRef]
8. Mondal P, Maiti DK, Shit GC, Ibáñez G. Heat transfer and entropy generation in a MHD Couette-Poiseuille flow through a microchannel with slip, suction-injection and radiation. J Therm Anal Calorim. 2022;147(6):4253–73. doi:10.1007/s10973-021-10731-4. [Google Scholar] [CrossRef]
9. Paramanandam K, Venkatachalapathy S, Srinivasan B, PVR NK. Thermal performance improvement in wavy microchannels using secondary channels. Int J Numer Meth Heat Fluid Flow. 2024;34(4):1811–31. doi:10.1108/HFF-07-2023-0417. [Google Scholar] [CrossRef]
10. Ashok Kumar R, Patel VK. Review on nanofluid preparation, stability analysis, and heat enhancement by nanofluids in pipe with passive elements. Proc Inst Mech Eng Part E J Process Mech Eng. 2023;8:09544089231218125. doi:10.1177/09544089231218125. [Google Scholar] [CrossRef]
11. Das UJ, Majumdar NM. Bioconvective magnetohydrodynamic flow of tangent hyperbolic nanofluid across a stretched surface, with Arrhenius activation and convective heat and slip conditions. Proc Inst Mech Eng Part E J Process Mech Eng. 2024;10:09544089241289018. doi:10.1177/09544089241289018. [Google Scholar] [CrossRef]
12. Zhang H, Liu X. Numerical analysis of the flow and heat transfer characteristics in serpentine microchannel with variable bend amplitude. Int J Numer Meth Heat Fluid Flow. 2021;31(6):2022–41. doi:10.1108/hff-06-2020-0334. [Google Scholar] [CrossRef]
13. Mohana Ramana R, Maheswari C, Shaw SM, Dharmaiah G, Fernandez-Gamiz U, Noeiaghdam S. Numerical investigation of 3-D rotating hybrid nanofluid Forchheimer flow with radiation absorption over a stretching sheet. Results Eng. 2024;22:102019. doi:10.1016/j.rineng.2024.102019. [Google Scholar] [CrossRef]
14. Sharma BK, Sharma P, Mishra NK, Noeiaghdam S, Fernandez-Gamiz U. Bayesian regularization networks for micropolar ternary hybrid nanofluid flow of blood with homogeneous and heterogeneous reactions: entropy generation optimization. Alex Eng J. 2023;77:127–48. doi:10.1016/j.aej.2023.06.080. [Google Scholar] [CrossRef]
15. Ramesh GK, Madhukesh JK, Aly EH, Gireesha BJ. Endothermic and exothermic chemical reaction on MHD ternary (Fe2O4–TiO2–Ag/H2O) nanofluid flow over a variable thickness surface. J Therm Anal Calorim. 2024;149(12):6503–15. doi:10.1007/s10973-024-13013-x. [Google Scholar] [CrossRef]
16. Liu S, Liu Y, Gu H, Tian R, Huang H, Yu T. Experimental study of the cooling performance of γ-Al2O3/heat transfer fluid nanofluid for power batteries. J Energy Storage. 2023;72:108476. doi:10.1016/j.est.2023.108476. [Google Scholar] [CrossRef]
17. Sharma M, Sharma BK, Khanduri U, Mishra NK, Noeiaghdam S, Fernandez-Gamiz U. Optimization of heat transfer nanofluid blood flow through a stenosed artery in the presence of Hall effect and hematocrit dependent viscosity. Case Stud Therm Eng. 2023;47:103075. doi:10.1016/j.csite.2023.103075. [Google Scholar] [CrossRef]
18. Wilken N, Sharifpur M, Atofarati EO, Meyer JP. Experimental study on transient and steady-state impinging jet cooling condition with TiO2-water nanofluids. Case Stud Therm Eng. 2024;57:104301. doi:10.1016/j.csite.2024.104301. [Google Scholar] [CrossRef]
19. Ramana RM, Dharmaiah G, Kumar MS, Fernandez-Gamiz U, Noeiaghdam S. Numerical performance of Hall current and Darcy-forchheimer influences on dissipative Newtonian fluid flow over a thinner surface. Case Stud Therm Eng. 2024;60:104687. doi:10.1016/j.csite.2024.104687. [Google Scholar] [CrossRef]
20. Hameed N, Noeiaghdam S, Khan W, Pimpunchat B, Fernandez-Gamiz U, Khan MS, et al. Analytical analysis of the magnetic field, heat generation and absorption, viscous dissipation on couple stress casson hybrid nano fluid over a nonlinear stretching surface. Results Eng. 2022;16:100601. doi:10.1016/j.rineng.2022.100601. [Google Scholar] [CrossRef]
21. Behrouz M, Dinarvand S, Yazdi ME, Tamim H, Pop I, Chamkha AJ. Mass-based hybridity model for thermomicropolar binary nanofluid flow: first derivation of angular momentum equation. Chin J Phys. 2023;83(11):165–84. doi:10.1016/j.cjph.2023.03.006. [Google Scholar] [CrossRef]
22. Berrehal H, Karami R, Dinarvand S, Pop I, Chamkha A. Entropy generation analysis for convective flow of aqua Ag-CuO hybrid nanofluid adjacent to a warmed down-pointing rotating vertical cone. Int J Numer Meth Heat Fluid Flow. 2024;34(2):878–900. doi:10.1108/HFF-05-2023-0236. [Google Scholar] [CrossRef]
23. Dinarvand S, Berrehal H, Pop I, Chamkha AJ. Blood-based hybrid nanofluid flow through converging/diverging channel with multiple slips effect: a development of Jeffery-Hamel problem. Int J Numer Methods Heat Fluid Flow. 2023;33(3):1144–60. doi:10.1108/HFF-08-2022-0489. [Google Scholar] [CrossRef]
24. Ali Akbari O, Toghraie D, Karimipour A, Marzban A, Ahmadi GR. The effect of velocity and dimension of solid nanoparticles on heat transfer in non-Newtonian nanofluid. Phys E Low Dimension Syst Nanostruct. 2017;86(4):68–75. doi:10.1016/j.physe.2016.10.013. [Google Scholar] [CrossRef]
25. Vajjha RS, Das DK. Experimental determination of thermal conductivity of three nanofluids and development of new correlations. Int J Heat Mass Transf. 2009;52(21–22):4675–82. doi:10.1016/j.ijheatmasstransfer.2009.06.027. [Google Scholar] [CrossRef]
26. Sohankar A, Gharehkhani M. The effects of external magnetic fields on the flow and heat transfer in a three-dimensional microchannel. Numer Heat Transf Part A Appl. 2023:1–25. doi:10.1080/10407782.2023.2251081. [Google Scholar] [CrossRef]
27. Mahmoodi M, Sohankar A, Joulaei A. Investigations of nanofluid flow and heat transfer in a rotating microchannel using single- and two-phase approaches. Numer Heat Transf Part A Appl. 2023;83(2):80–115. doi:10.1080/10407782.2022.2083886. [Google Scholar] [CrossRef]
28. Hojjat M, Etemad SG, Bagheri R, Thibault J. Convective heat transfer of non-Newtonian nanofluids through a uniformly heated circular tube. Int J Therm Sci. 2011;50(4):525–31. doi:10.1016/j.ijthermalsci.2010.11.006. [Google Scholar] [CrossRef]
29. Hojjat M, Etemad SG, Bagheri R, Thibault J. Rheological characteristics of non-Newtonian nanofluids: experimental investigation. Int Commun Heat Mass Transf. 2011;38(2):144–8. doi:10.1016/j.icheatmasstransfer.2010.11.019. [Google Scholar] [CrossRef]
30. Hajialigol N, Fattahi A, Ahmadi MH, Qomi ME, Kakoli E. MHD mixed convection and entropy generation in a 3-D microchannel using Al2O3–water nanofluid. J Taiwan Inst Chem Eng. 2015;46:30–42. doi:10.1016/j.jtice.2014.09.002. [Google Scholar] [CrossRef]
31. Albojamal A, Vafai K. Analysis of single phase, discrete and mixture models, in predicting nanofluid transport. Int J Heat Mass Transf. 2017;114:225–37. doi:10.1016/j.ijheatmasstransfer.2017.06.030. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools