Spectral Quasi-Linearization Study of Variable Viscosity Casson Nanofluid Flow under Buoyancy and Magnetic Fields

1  Introduction

The flow within the boundary layer that is generated by stretching a sheet is a significant engineering challenge that has a wide range of industrial applications, including plastic extrusion, melting and spinning, rolling and hot, drawing wire, producing glass fiber, manufacturing polymer and rubber sheets, and improved petroleum resource recovery. In stretching sheet problems, the heat transfer mechanism plays a pivotal role, as it shapes the thermal environment that ultimately governs the quality and consistency of the final product [1–3]. In light of these applications, Crane [4] pioneered the analysis of the Newtonian boundary layer in the sheet, stretched with a linear velocity. Subsequently, flow over a sheet stretched along the surface has emerged as a topic of intensive interest, prompting substantial research in this field [5–8]. Since Newtonian fluid viscosity is not dependent on external factors, the non-Newtonian fluids receive much attention because they can change their flow behavior in response to applied stress or shear rate [9–12]. Non-Newtonian fluids are categorized by their rheological behavior into shear-thinning and shear-thickening types. Among them, Casson fluids show a distinctive non-linear correlation between shear stress and shear rate. Examples include concentrated fruit liquids, coal tar, sauces, honey, jelly, and human blood. Several industrial and engineering sectors, such as the pharmaceutical, cosmetic, and textile industries, as well as food processing facilities, utilize Casson fluid, which can either be shear-thinning or shear-thickening depending on the shear stress [13–15].

Non-Newtonian fluids are integrated with nanoparticles to create nanofluids, which possess exceptional thermal, electrical, and magnetic properties, hence enhancing reliability. These qualities serve a variety of industries, including energy, engineering, and technology, by producing enhanced heat transfer efficiency, improved fluid behavior, and superior control [16,17]. The numerical study, namely, the Runge-Kutta-Fehlberg method, was utilized to analyze the boundary layer flow of Casson nanofluid across a stretching sheet by Nadeem et al. [18] shows that the Casson parameter raises the fluid’s temperature and decreases the fluid’s velocity. Sulochana et al. [19] investigated the heat and flow of the fluid over a stretching sheet of Casson nanofluid using the Runge-Kutta based shooting numerical method and showed that the magnetic field parameter governs the flow, reducing friction; hence, the heat and mass transfer rate are comparatively high in non-Newtonian fluids. Vajravelu et al. [20] analyzed the impacts of thermal conductivity on Casson nanofluid flow over a stretching sheet, which shows that the thermal transmission and thickness of the thermal boundary layer enhance for the rise in thermal radiation parameter.

In addition to this, the interesting components that can be added to study the heat transmission or control of the nanofluid boundary layer are the MHD, ohmic, and viscous dissipation effects. Ohm’s law regulates kinetic dissipation in electrical flows by turning electrical energy into heat through resistance and exploring the effects of electrical currents on other substances. Viscous dissipation occurs when the kinetic energy in a fluid is transformed into heat energy due to the viscous effect of the fluid. This phenomenon is used in various industrial processes, including electronic cooling systems, gas and oil transportation, and polymer processing [21–25]. Pal et al. [26] observed the impacts of ohmic heating and heat radiation in Casson nanofluid along a sheet stretched vertically, noting that suction reduces thermal boundary layer thickness and fluid temperature with increasing Eckert number. Ghadikolaei et al. [27] studied the impacts of viscous and joule’s heating on Casson nanofluid across an inclined stretching sheet and observed that the radiation effect reduces the buoyancy and thermal boundary layer thickness. Khader et al. [28] revealed the effects of joule’s and viscous dissipations on the Casson fluid flow. Wang et al. [29] investigated the magnetohydrodynamic flow of a Casson-type sodium alginate nanofluid across a radiatively heated stretching sheet, revealing that thermal radiation enhances heat energy within the fluid, thereby increasing both temperature and thermal boundary layer thickness. Additionally, the Casson parameter and nanoparticle volume fraction also improve entropy generation.

Magnetic field-dependent (MFD) viscosity refers to changes in a fluid’s viscosity due to interactions between the magnetic field and charged particles or magnetic domains, affecting its flow behavior. This peculiar characteristic allows for dynamic changes in fluid viscosity in response to magnetic field changes, enhancing its worth across multiple industries, including automotive, aeronautical engineering, and medical applications [30]. Vaidyanathan et al. [31] noted that MFD viscosity increases resistance, delaying the onset of convection in ferrofluids and making it more difficult for thermal gradients to induce convection using the Brickman analytical method. An analytical study by Ramanathan et al. [32] looked into the effects of MFD viscosity in porous medium for ferro convection via the Darcy model. They found that MFD viscosity helps keep things stable by changing its thickness in response to the magnetic field. Sheikholeslami et al. [33,34] used the finite element method to analyze the impacts of MFD viscosity on the velocity of the flow and temperature within the boundary layer of MHD nanofluids and found that MFD viscosity dominated significantly. Molana et al. [35] revealed the hydrothermal characteristics of a water-based nanofluid-filled cavity under the effect of MFD viscosity using the finite element method and discovered that increasing the Hartmann number, which is controlled by a magnetic field, slows down the heat transfer.

It is clear from the existing literature remains limited in exploring the impacts of MFD viscosity, and no study has examined the combined dynamics of mixed convection and MFD viscosity. In this work, we conduct a SQLM analysis to investigate the mixed convection and MFD viscosity impact on a sodium alginate-based Casson nanofluid containing Fe3O4 nanoparticles as it flows across a sheet stretched vertically under the impacts of both ohmic and viscous dissipations. It focused on the variations in the temperature characteristics of sodium alginate-based Fe3O4 nanofluid across a sheet stretched vertically. To approach the problem, lie group transformations were applied to non-dimensionalize the governing equations, and the non-linear coupled equations were solved using the implicit method, specifically the SQLM. Numerical results are obtained for specific parameters, and graphical representations were generated to facilitate deeper understanding of the outcomes.

2  Formulation of the Problem

The physical model involves a 2-D incompressible and steady flow of sodium alginate-based Fe3O4 nanofluid occurring across a sheet stretched vertically in an impermeable surface with the velocity Uw∗=x∗/a−1 (see Fig. 1) is oriented transversely to the sheet in the existence of magnetic field of strength B0. The surface stretches from a slit, with coordinates x* and y* indicating directions on and perpendicular to the surface. The model assumes, that nanoparticles are thermally stable with the base fluid and have zero relative velocity. Impacts of thermal radiation, viscous, and ohmic dissipations are incorporated. Tw∗ denotes the temperature at the surface and T∞∗ the temperature at the free-stream.

Figure 1: Physical configuration of the model

The Lorentz force governs the fluid flow under the influence of a uniform transverse magnetic field (B0=B0xex+B0yey) with the magnitude B02=B0x2+B0y2 and is represented as [36]:

F=σnf(V×B0+E)×B0,(1)

where σnf and V×B0+E represent the electric conductivity, ex and ey are the unit vector along the Cartesian coordinates and the total current density with negligible magnetic Reynolds number.

The Lorentz force is defined under E = 0 as:

F=σnf(V×B0+E)×B0=−σnf[B0(V⋅B0)−V(B0⋅B0)]=−σnf(u∗B02)(2)

Nanofluid velocity, influenced by the magnetic field, is defined as [35]:

ηnf=(1+δ∗)μnf,(3)

where δ∗=δxex+δyey with δx=δy=δ represents the variation in the viscosity due to the applied magnetic field B0.

The problem governing the equations of mass, momentum and energy of a Casson based Fe3O4 nanofluid can be derived, with respect to the influence of MFD viscosity, thermal radiation, viscous and ohmic dissipations given as [19]:

Ux∗∗+Vy∗∗=0,(4)

U∗Ux∗∗+σnfB02U∗ρnf+V∗Vy∗∗=(1+β−1)ηnfρnfUy∗y∗∗+gβnf(T∗−T∗∞)ρnf,(5)

U∗Tx∗∗+V∗Ty∗∗=αnfTy∗y∗∗+σnfB02U∗2(ρCP)nf+(1+β−1)ηnf(ρCP)nfUy∗∗2−1(ρCP)nfqry∗,(6)

where the velocities U* along x* direction, and V* in y* directions, respectively, and T* is the fluid’s local temperature. Here, Ux∗∗ represents the differentiation of U* under x* and Vy∗∗ represents the differentiation of V* under y*. The following represents boundary conditions for subsequent Eqs. (4)–(6):

U∗+ax∗=Uw∗(x∗)+ax∗=2ax∗,V∗=0,T∗−Tw∗=0,at y∗=0,(7)

U∗→0, T∗−T∞∗→0, as y∗→∞.

The radiative heat flux qr is evaluated using Rosseland diffusion approximation [19] to be:

qr=−4σ∗3k∗T∗y4,(8)

where σ∗ is the Stephan-Boltzmann constant and k∗ is the Rosseland mean absorption coefficient, respectively. Small temperature gradients are assumed within the flow so that T∗4 can be represented as a linear relation of T. Using Taylor series, T4 is expanded in terms of T∗∞, ignoring higher power terms, the following is obtained:

T∗4≅4T∗T∗∞3−3T∗∞4.(9)

Applying the expressions in (8) and (9), Eq. (6) becomes:

UT∗x+VT∗y=αnfT∗yy+σnfB02U∗2(ρCP)nf+(1+β−1)ηnf(ρCP)nfU∗y2+1(ρCP)nf16σ∗T∗∞33k∗T∗yy,(10)

the physical and thermal quantities in Eqs. (4) and (10) are expressed in Tables 1 and 2.

3  Non Dimensionalization and Lie Group Transformation

The non-dimensional variables utilized in the study are:

x=x∗(vf/a)−0.5;y=y∗(vf/a)−0.5;U=U∗(vfa)−0.5;V=V∗(vfa)−0.5;θ(Tw∗−T∞∗)=T∗−T∞∗.(11)

Using the foremost equations, Eqs. (4), (5), and (10) transform into the following:

Ux+Vy=0,(12)

UUx+VVy=(1+β−1)(1+δ∗)μnfρnfUyy−σnfB02Uρnf+gβnf(Tw∗−T∞∗)ρnfθ,(13)

Vθy+Uθx=αnfθyy+σnfB02U2(ρCP)nf+(1+β−1)(1+δ∗)μnf(ρCP)nfUy2+1(ρCP)nf16σ∗T∞∗33k∗θyy,(14)

along the boundary constraints,

U/x=1,V=0,θ=0,at y=0,U→0,θ→0,as y→∞.(15)

Eq. (12) is verified using ψ, the stream function as:

V+ψx=0,and U−ψy=0.(16)

Using the Eq. (16), the Eqs. (13) and (14) are expressed as follows:

ψyψxy−ψxψyy=(1+β−1)(1+δ∗)μnfρnfψyyy−σnfB02ψyρnf+gβnf(Tw∗−T∞∗)(ρCP)nfθ,(17)

ψyθx−ψxθy=αnfθyy+σnfB02ψy2(ρCP)nf+(1+β−1)(1+δ∗)ηnf(ρCP)nfψyy2+1(ρCP)nf16σ∗T∞∗33k∗θyy,(18)

Eq. (15) is derived as follows:

ψy/x=1,ψx=0,θ=0,aty=0,ψy→0,θ→0,asy→∞.(19)

Employing the following Lie-group transforms [37]:

y=η, ψ=xf(η), θ=θ(η).

In Eqs. (17)–(19), we have:

(1+β−1)(1+δ∗)(1−ϕ)−5/2f′′′+((1−ϕ)+ϕρsρf−1)(ff′′−f′2)−[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]Mf′+((1−ϕ)+ϕβsβf−1)λθ=0,(20)

(knfkf+43R)1Prθ″+((1−ϕ)+ϕ(ρCp)s(ρCp)f−1)fθ′+[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]MEcf′2+(1+β−1)(1+δ∗)(1−ϕ)−5/−522Ecf″2=0.(21)

Here, the dimensionless constants Pr, M, λ, R and Ec denote the Prandtl number, magnetic parameter, mixed convection parameter, radiation parameter and Eckert number which are all expressed as:

Pr=vfαf, M=B02σf(ρfa)−1, λ=gβf(Tw∗−T∞∗)aUw∗, R=4σ∗T∞∗3kfk∗, and Ec=vfUw∗2a2(Cp)f(Tw−T∞).

The pertinent boundary conditions are listed below:

f(η)=0,f′(η)−1=0,θ(η)−1=0, at η=0,f′(η)→0,θ(η)→0, as η→∞(22)

4  Essential Quantities in the Physical Study

The LSF coefficient Cf and the RNN Nux∗ are the interested essential physical quantities along with velocity and temperature profiles, the surface drag of the nanofluid and wall heat transfer rate are studied from these parameters (Table 3).

4.1 Local Skin Friction Coefficient

The LSF coefficient is expressed as:

Cf=τwlρf−1U−2.(23)

The wall shear stress τwl flow is expressed as:

τwl=−(1+β−1)ηnf(Uy∗∗)y∗=0.(24)

The following relation is obtained from the Eqs. (23) and (24), and Table 2.

Cf(1−ϕ)2.5Rex∗0.5(1+β−1)(1+δ∗)=−f′′(0).(25)

4.2 Reduced Nusselt Number

The RNN is expressed as:

Nux∗=x∗qwkf−1(Tw−T∞)−1,(26)

where the surface heat transfer rate is represented as:

qw=−(knf+16σ∗T∞33knf∗)(Ty∗∗)y∗=0.(27)

Thus, the dimensionless relation between wall heat transfer rates is obtained as follows, by using the Eqs. (26) and (27),

Nux∗Rex∗−0.5=−(knfkf+43R)θ′(0),(28)

where Rex∗=x∗Uw(x∗)(vf)−1 is the local Reynolds number and CfRex∗0.5 is the LSF coefficient, Nux∗Rex∗−0.5 is the RNN.

5  Computational Solution Using SQLM

System of non-linear differential Eqs. (20) and (21) with pertaining conditions in Eq. (22) is computed using SQLM [38,39]. We linearize the nonlinear components using the Taylor series expansion. Thus, the method converges rapidly if the differences between the consecutive iterations are minimal. For simplification, let us denote F and θ for the following expressions:

F=(1+β−1)(1+δ∗)(1−ϕ)−5/2f′′′+((1−ϕ)+ϕρsρf−1)(ff′′−f′2)−[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]Mf′+((1−ϕ)+ϕβsβf−1)λθ,(29)

Θ=(knfkf+43R)1Prθ″+((1−ϕ)+ϕ(ρCp)s(ρCp)f−1)fθ′+[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]MEcf′2+(1+β−1)(1+δ∗)(1−ϕ)−5/−522Ecf″2.(30)

An iterative procedure for the error function is constructed below:

Rf=A3,rfr′′′+A2,rfr′′+A1,rfr′+A0,rfr+A0,r∗θr−Fr,Rθ=B2,rθr′′+B1,rθr′+B0,rθr+B2,r∗fr′′+B1,r∗fr′+B0,r∗fr−Θr,(31)

with the relevant conditions,

fr+1(η)=0,fr+1′(η)=1,θr+1(η)=1, at η=0,fr+1′(η)→0,θr+1(η)→0, as η→∞.(32)

Expansions of the abbreviation used in Eq. (31) are as follows:

A0,r=(1−ϕ)5/2((1−ϕ)+ϕρsρf−1)fr′′,A0,r∗=(1−ϕ)5/2((1−ϕ)+ϕβsβf−1)λ,

A1,r=−2(1−ϕ)5/2((1−ϕ)+ϕρsρf−1)fr′−(1−ϕ)5/2[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]M,

A2,r=(1−ϕ)5/2((1−ϕ)+ϕσsσf−1)fr,

A3,r=(1+δ∗)(1+β−1),

B0,r=0,B0,r∗=((1−ϕ)+ϕ(ρCP)s(ρCP)f−1)θr′,

B1,r=((1−ϕ)+ϕ(ρCP)s(ρCP)f−1)fr,B1,r∗=2[1+3(σs−σf)ϕσs+2σf−(σs−σf)ϕ]MEcfr′,

B2,r=(knfkf+43R)1Pr,B2,r∗=2(1+β−1)(1+δ∗)(1−ϕ)−5/2Ecfr′′.

The initial guesses taken for the numerical procedure is:

f0(η)=1−e−η,and θ0(η)=e−η.

The spectral collocation method is used in Eqs. (20) and (21) to obtain the approximate solutions, change the flow domain η to [0,J] with the conversion mapping η=J(χ¯+1)2 to the domain [−1,1], where J∈Z∗. Chebyshev interpolating polynomials approximate the unknown functions fr+1 and θr+1, and the Gauss-Lobatto collocation (N) points are used to evaluate the derivatives as follows:

χ¯i=cos⁡(πiN),−1≤χ¯≤1,0≤i≤N,(33)

The matrix D is expressed as:

dnfr+1(χ¯i)dχ¯=∑k=0NDiknfr+1(χ¯i)=DnF,dnθr+1(χ¯i)dχ¯=∑k=0NDiknθr+1(χ¯i)=Dnθ,(34)

where D=2DJ−1, F=[fr+1(χ¯0),fr+1(χ¯1),fr+1(χ¯2),…,fr+1(χ¯N)]T, and θ=[θr+1(χ¯0),θr+1(χ¯1),θr+1(χ¯2),.....,θr+1(χ¯N)]T.

Using the fore-mentioned results from Eqs. (29), (30), (33) and (34), the following system of simultaneous equations are,

C11Fr+1+C12θr+1=Rf,C21Fr+1+C22θr+1=Rθ.(35)

Therefore, the matrix transformation of simultaneous equations in Eq. (35) are as follows:

[C11C12C21C22][Fr+1θr+1]=[RfRθ],(36)

where

C11=diag[A3,r]D3+diag[A2,r]D2+diag[A1,r]D+diag[A0,r]I,C12=A0,r∗,C21=diag[B2,r∗]D2+diag[B1,r∗]D+diag[B0,r∗]I,C22=diag[B2,r]D2+diag[B1,r]D.

where the diag[ ] is the diagonal matrix, and I is the identity matrix, respectively. To derive the solution, the matrix system provided in Eq. (36) is solved in conjunction with the boundary conditions specified in Eq. (32).

The practical challenges in fluid dynamics often involve complex, multi-order nonlinear differential equations due to their association with various physical processes. Solving these equations can be time-consuming, with traditional methods sometimes showing slow convergence or failure to yield results. The Spectral Quasi Linearization Method (SQLM) offers a notable improvement, providing faster convergence and simpler iterative steps. Its ability to break down complex systems into smaller, more manageable subsystems makes it a widely accepted and efficient numerical technique.

The following relation gives the residue errors as follows:

Res(f)=‖Δf[Fr,θr]‖∞,Res(θ)=‖Δθ[Fr,θr]‖∞,(37)

where Δf and Δθ denote the Eqs. (29) and (30), Fr and θr indicates the solution of nodes using the SQLM. In addition to this, Fig. 2 shows the residue errors in Eq. (37). It is observed that the associated error becomes constant after the fifth or sixth iteration, and the rate of rapid convergence falls at that point.

Figure 2: The residues of velocity profile and temperature profile

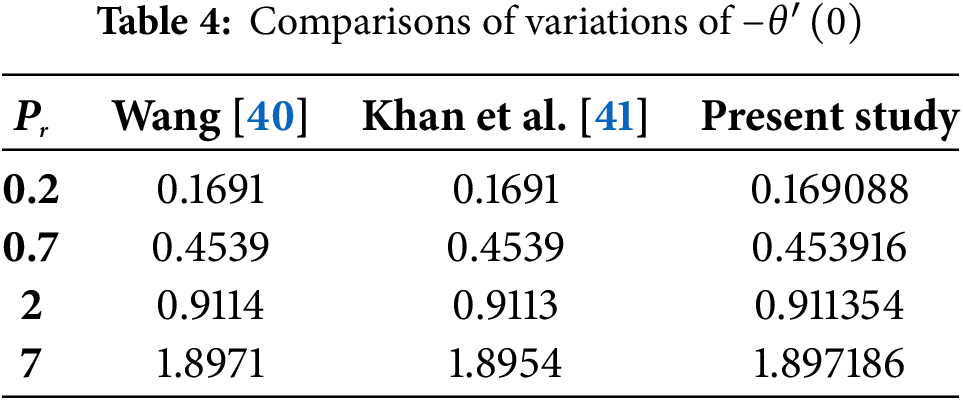
6  Validation of Numerical Solution

The governing equations of a non-Newtonian (Casson)-based Fe3O4 nanofluid was solved using the SQLM. The results showed excellent consistency with benchmark results from Wang [40] and Khan et al. [41], without the existence of MFD viscosity, Eckert number, and Hartmann number, which are listed in Table 4. Numerical outcomes for LSF and RNN are tabulated in Table 3. In this observation, the tolerance error was set to 10−7, and the residuals used to access accuracy had errors value for momentum and energy are 1/1010 and 1/1012, as shown in Fig. 2. Due to the limited availability of experimental data on magnetic field-dependent viscosity in nanofluids, direct validation remains a challenge. However, the present results offer a theoretical basis for future experimental investigations to enhance practical relevance.

7  Results and Discussion

Computational outcomes obtained from the system of equations for momentum and energy using the SQLM are interpreted through graphical representation. These graphs are analysed to know the relevance of key parameters on the buoyancy-driven boundary layer flow of sodium alginate-based Fe3O4 nanofluid over an impermeable moving surface. The parameters considered include the nanoparticle volume fraction (ϕ), magnetic parameter (M), isotropic MFD viscosity (δ*) parameter, Casson parameter (β), Eckert number (Ec), mixed convection parameter (λ), and thermal radiation parameter (R). Individual effects of each parameter are examined by holding certain parameters constant throughout the study. Initially, the collocation points are fixed at N = 80, and the constant values are fixed for the other parameters: Pr = 6.45, M = 0.5, ϕ = 0.1, Ec = 0.1, β = 0.1, λ = 1, and δ* = 0.1. The thermophysical properties of the nanoparticles are assumed to be constant for numerical simplicity, as is commonly done in nanofluid modeling. However, it is acknowledged that these properties may vary with temperature and magnetic field strength, which could slightly affect the quantitative accuracy of the results under extreme conditions.

The combined impacts of δ* and ϕ on the velocity f′(η) and temperature θ(η) profiles of the sodium alginate-based Fe3O4 nanofluid are shown in Fig. 3. Fig. 3a specifically displays the impacts of the δ* and ϕ on the f′(η). As δ* increases, the fluid’s viscosity becomes more responsive to changes in the magnetic field, leading to a reduction in shear viscosity near the wall. Hence the velocity profile accelerates and enhances momentum transfer within the boundary layer. As ϕ increases, more solid particles are suspended within the base fluid. These nanoparticles interact with fluid molecules and enhance internal momentum exchange due to increased collisions and particle-fluid interactions. This leads to improved momentum transfer within the fluid, effectively reducing flow resistance and enabling a more efficient transport of energy. As a result, the nanofluid exhibits a higher velocity profile as ϕ increases. Fig. 3b displays the temperature profile variation of the nanofluid for both the δ* and ϕ. An increase in the value of δ* intensifies the effect of the magnetic field on the fluid’s viscosity, which alters the flow dynamics and facilitates the generation of convection currents. These magnetically driven currents improve thermal interaction between the fluid and its environment. Consequently, the heat transfer rate is enhanced, leading to a rise in fluid temperature as δ* increases. As ϕ increases, more thermally conductive nanoparticles are suspended in the base fluid. These nanoparticles typically have much higher thermal conductivity than the base fluid, which enhances the overall thermal conductivity of the nanofluid and allows heat transfer more efficiently. As a result, heat diffuses more effectively into the fluid away from the surface, leading to a thicker thermal boundary layer and an increase in the temperature profile.

Figure 3: Impacts of MFD viscosity and volume fraction of nanoparticle with Pr = 6.45, M = 0.5, Ec = 0.1, R = 1, β = 0.1, and λ = 1, (δ* variation with ϕ = 0.1, & ϕ variation with δ* = 0.1) on (a) velocity profile (b) temperature profile

Fig. 4 displays the combined impacts of M and β on thef′(η) and θ(η) profiles. When an electrically conducting nanofluid is exposed to a magnetic field, the interaction between the fluid’s motion and the magnetic field generates a Lorentz force. This force opposes the direction of flow, acting as a resistive mechanism that suppresses fluid motion. As the magnetic parameter M increases, the Lorentz force intensifies, leading to greater resistance. Consequently, the nanofluid’s velocity profile diminishes due to the enhanced magnetic damping effect. As the Casson parameter β increases, it reflects a stronger yield stress behaviour in the nanofluid. At higher β values, the fluid exhibits more solid-like characteristics and resists motion until a critical shear stress is exceeded. This behavior increases resistance to deformation and flow, thereby reducing the fluid’s overall velocity. When combined with MFD viscosity, which introduces magnetic damping and viscous dissipation effects represented by the Eckert number, the resistance to flow becomes even more significant. Thus, an increase in the Casson parameter leads to a decrease in the fluid velocity as illustrated in Fig. 4a. The impacts of the M and β of the temperature profile are represented in Fig. 4b. With increasing M, the magnetic field enhances the Lorentz force, which not only resists fluid motion but also increases viscous dissipation—a mechanism that converts kinetic energy into thermal energy. Additionally, Joule heating, resulting from induced electric currents within the conducting fluid, contributes further to heat generation. These combined energy losses due to viscous and electrical effects elevate the fluid temperature. In contrast, an increase in β results in a slight decline in temperature, as the reduced velocity limits convective heat transport within the fluid.

Figure 4: Impacts of Magnetic parameter and Casson parameter with Pr = 6.45, ϕ = 0.1, Ec = 0.1, R = 1, δ* = 0.1, and λ = 1, (β variation with M = 0.5, & M variation with β = 0.1) on (a) velocity profile (b) temperature profile

The variations in λ and Ec are observed in Fig. 5 for the f′(η) and θ(η) profiles. When λ increases, it indicates that buoyancy forces are becoming more dominant compared to viscous forces. Buoyancy acts as a driving mechanism in convection, accelerating the fluid away from the heated surface. As a result, the momentum boundary layer becomes thicker, and the velocity profile rises. The Ec measures the ratio of kinetic energy to the enthalpy difference in the fluid. As Ec increases, it implies greater viscous dissipation, which converts mechanical energy into thermal energy, thereby elevating the fluid temperature. This increased thermal energy near the wall intensifies convective heat transfer. Consequently, to transport this additional heat, the fluid requires greater momentum, which enhances the flow near the wall and increases the velocity profile, as observed in Fig. 5a. The temperature increases for both the λ and Ec, as depicted in Fig. 5b. An increase in the value of λ enhances convection, promoting heat transfer from the surface to the fluid and thereby increasing the temperature profile. Additionally, a rise in the value of Ec signifies greater viscous dissipation, where kinetic energy is converted into thermal energy, further elevating the fluid temperature and enriching the thermal profile.

Figure 5: Impacts of Eckert number and mixed convection parameter with Pr = 6.45, ϕ = 0.1, M = 0.5, R = 1, δ* = 0.1, and β = 0.1, (λ variation with Ec = 0.1, & Ec variation with λ = 1) on (a) velocity profile (b) temperature profile

The R and Ec variations are observed in Fig. 6 for the f′(η) and θ(η) profiles. A marginal increase in fluid velocity is observed with an increasing thermal radiation parameter R, as radiation enhances the heat transfer rate and elevates the thermal energy in the fluid. This can slightly reduce viscous resistance near the wall, resulting in a marginal rise in the velocity profile, as depicted in Fig. 6a. An increase in R leads to a higher radiative heat flux from the surface, indicating more energy is being transferred into the fluid. This enhances the overall heat transfer rate, causing the fluid to absorb more thermal energy, which results in a higher temperature distribution throughout the boundary layer. This effect is evident in the substantial increase in the temperature profile depicted in Fig. 6b.

Figure 6: Impacts of Eckert number and Radiation parameter with Pr = 6.45, ϕ = 0.1, M = 0.5, δ* = 0.1, λ = 1 and β = 0.1, (R variation with Ec = 0.1, & Ec variation with R = 1) on (a) velocity profile (b) temperature profile

Figs. 7 and 8 show the impacts of δ* and λ on important physical quantities like RNN and LSF. For further reference, Table 4 displays the numerical results of the LSF and the RNN. As the δ* increases, the surface drag or LSF decreases due to reduced shear stress caused by δ*. A similar argument is observed with increasing λ, where stronger buoyancy forces reduce the wall shear stress, leading to a decrease in LSF, as shown in Fig. 7. The RNN decreases with increasing δ*, indicating a decline in convective heat transfer efficiency and increased thermal resistance. In contrast, the RNN increases with higher λ, reflecting enhanced heat transfer due to intensified buoyancy-driven convection. Based on the above findings, it is clear that both the δ* and λ are inversely proportional for local skin friction. Additionally, the δ* is inversely proportional to RNN, while the λ is directly proportional to RNN.

Figure 7: Impacts of MFD viscosity parameter and mixed convection parameter with Pr = 6.45, M = 0.5, Ec = 0.1, R = 1, β = 0.1, and ϕ = 0.1, (δ* variation with λ = 1, & λ variation with δ* = 0.1) on skin friction

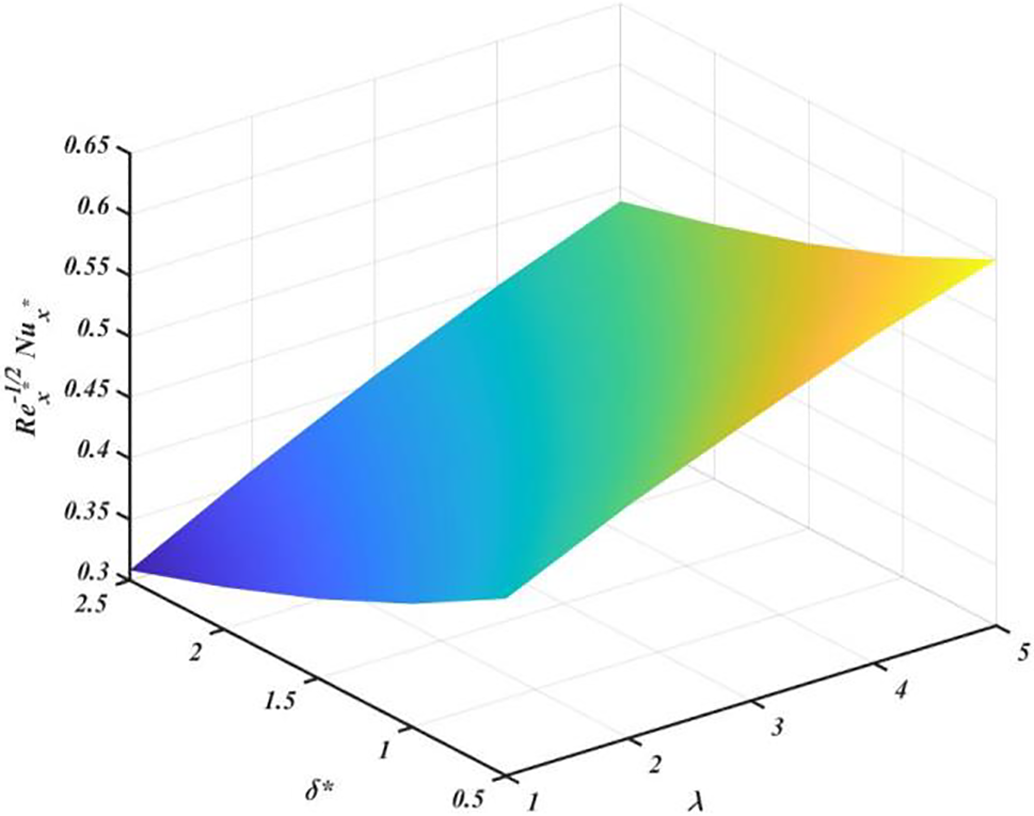
Figure 8: Impacts of MFD viscosity parameter and mixed convection parameter with Pr = 6.45, M = 0.5, Ec = 0.1, R = 1, β = 0.1, and ϕ = 0.1, (δ* variation with λ = 1, & λ variation with δ* = 0.1) on Nusselt number

8  Conclusion

Impacts of MFD viscosity, mixed convection, and radiation effects on nanofluid flow across a sheet which is stretched in the existence of viscous and ohmic dissipation, utilizing Casson-based sodium alginate and Fe3O4 nanoparticles to stimulate the flow and heat transfer rate. Governing dimensionless system of equations is solved using a SQLM scheme, and relevant graphs and computational results are explored to elucidate the parametric impacts on the flow and heat transfer. Key outcomes include:

•   MFD viscosity parameter rises the f′(η) profile and the boundary layer thickness, with only a marginal variation observed in temperature profiles as it increases.

•   As the mixed convection parameter and the Eckert number increases, the velocity and momentum boundary layer expand, with a slight temperature variation for the former and a significant one for the latter.

•   The temperature of the fluid rises due to more efficient heat distribution within the fluid if the radiation parameter enhances.

•   MFD viscosity parameter decreases both the LSF and the RNN as it increases, whereas a rise in the mixed convection parameter reduces the LSF but raises the RNN.

•   This work can be extended to three-dimensional flow problems and to different sheet orientations, providing engineers and researchers with insights to optimize industrial processes for improved control and efficiency.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection, analysis and interpretation of results, draft manuscript preparation: B. Rajesh, Fateh Mebarek-Oudina, N. Vishnu Ganesh, Qasem M. Al-Mdallal, Sami Ullah Khan, Murali Gundagnai, Hillary Muzara. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is available on request.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Sakiadis BC. Boundary-layer behavior on continuous solid surfaces: II. the boundary layer on a continuous flat surface. AlChE J. 1961;7(2):221–5. doi:10.1002/aic.690070211. [Google Scholar] [CrossRef]

2. Sakiadis BC. Equilibrium flow of a general fluid through a cylindrical tube. AlChE J. 1962;8(3):317–21. doi:10.1002/aic.690080311. [Google Scholar] [CrossRef]

3. Raza J, Mebarek-Oudina F, Ali H, Sarris IE. Slip effects on Casson nanofluid over a stretching sheet with activation energy: RSM analysis. Front Heat Mass Transf. 2024;22(4):1017–41. doi:10.32604/fhmt.2024.052749. [Google Scholar] [CrossRef]

4. Crane LJ. Flow past a stretching plate. J Appl Math Phys. 1970;21(4):645–7. doi:10.1007/bf01587695. [Google Scholar] [CrossRef]

5. Wang CY. The three-dimensional flow due to a stretching flat surface. Phys Fluids. 1984;27(8):1915–7. doi:10.1063/1.864868. [Google Scholar] [CrossRef]

6. Lakshmisha KN, Venkateswaran S, Nath G. Three-dimensional unsteady flow with heat and mass transfer over a continuous stretching surface. J Heat Transf. 1988;110(3):590–5. doi:10.1115/1.3250533. [Google Scholar] [CrossRef]

7. Mahanta G, Shaw S. 3D Casson fluid flow past a porous linearly stretching sheet with convective boundary condition. Alex Eng J. 2015;54(3):653–9. doi:10.1016/j.aej.2015.04.014. [Google Scholar] [CrossRef]

8. Arruna Nandhini C, Jothimani S, Chamkha AJ. Combined effect of radiation absorption and exponential parameter on chemically reactive Casson fluid over an exponentially stretching sheet. Partial Differ Equ Appl Math. 2023;8(5):100534. doi:10.1016/j.padiff.2023.100534. [Google Scholar] [CrossRef]

9. Mustafa M, Hayat T, Ioan P, Hendi A. Stagnation-point flow and heat transfer of a Casson fluid towards a stretching sheet. Z Für Naturforschung A. 2012;67(1–2):70–6. doi:10.5560/zna.2011-0057. [Google Scholar] [CrossRef]

10. Sobamowo MG. Combined effects of thermal radiation and nanoparticles on free convection flow and heat transfer of Casson fluid over a vertical plate. Int J Chem Eng. 2018;2018(339):7305973–25. doi:10.1155/2018/7305973. [Google Scholar] [CrossRef]

11. Kumar MA, Mebarek-Oudina F, Mangathai P, Shah NA, Vijayabhaskar C, Venkatesh N, et al. The impact of Soret Dufour and radiation on the laminar flow of a rotating liquid past a porous plate via chemical reaction. Mod Phys Lett B. 2025;39(10):2450458. doi:10.1142/s021798492450458x. [Google Scholar] [CrossRef]

12. Mebarek-Oudina F, Dharmaiah G, Rama Prasad JL, Vaidya H, Kumari MA. Thermal and flow dynamics of magnetohydrodynamic Burgers’ fluid induced by a stretching cylinder with internal heat generation and absorption. Int J Thermofluids. 2025;25(3):100986. doi:10.1016/j.ijft.2024.100986. [Google Scholar] [CrossRef]

13. Narsimha Reddy B, Maddileti P. Casson nanofluid and Joule parameter effects on variable radiative flow of MHD stretching sheet. Partial Differ Equ Appl Math. 2023;7(2):100487. doi:10.1016/j.padiff.2022.100487. [Google Scholar] [CrossRef]

14. Ali MY, Reza-E-Rabbi S, Ahmmed SF, Nabi MN, Azad AK, Muyeen SM. Hydromagnetic flow of Casson nano-fluid across a stretched sheet in the presence of thermoelectric and radiation. Int J Thermofluids. 2024;21(4):100484. doi:10.1016/j.ijft.2023.100484. [Google Scholar] [CrossRef]

15. Ramesh K, Mebarek-Oudina F, Souayeh B. Mathematical modelling of fluid dynamics and nanofluids. 1st ed. Boca Raton, FL, USA: CRC Press; 2023. 556 p. doi:10.1201/9781003299608. [Google Scholar] [CrossRef]

16. Sahoo B. Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partial slip. Commun Nonlinear Sci Numer Simul. 2010;15(3):602–15. doi:10.1016/j.cnsns.2009.04.032. [Google Scholar] [CrossRef]

17. Gopal D, Kishan N, Raju CSK. Viscous and Joule’s dissipation on Casson fluid over a chemically reacting stretching sheet with inclined magnetic field and multiple slips. Inform Med Unlocked. 2017;9(4):154–60. doi:10.1016/j.imu.2017.08.003. [Google Scholar] [CrossRef]

18. Nadeem S, Haq RU, Akbar NS. MHD three-dimensional boundary layer flow of Casson nanofluid past a linearly stretching sheet with convective boundary condition. IEEE Trans Nanotechnol. 2014;13(1):109–15. doi:10.1109/TNANO.2013.2293735. [Google Scholar] [CrossRef]

19. Sulochana C, Ashwinkumar GP, Sandeep N. Similarity solution of 3D Casson nanofluid flow over a stretching sheet with convective boundary conditions. J Niger Math Soc. 2016;35(1):128–41. doi:10.1016/j.jnnms.2016.01.001. [Google Scholar] [CrossRef]

20. Vajravelu K, Prasad KV, Vaidya H, Basha NZ, Ng CO. Mixed convective flow of a Casson fluid over a vertical stretching sheet. Int J Appl Comput Math. 2017;3(3):1619–38. doi:10.1007/s40819-016-0203-6. [Google Scholar] [CrossRef]

21. Ibrahim SM, Lorenzini G, Vijaya Kumar P, Raju CSK. Influence of chemical reaction and heat source on dissipative MHD mixed convection flow of a Casson nanofluid over a nonlinear permeable stretching sheet. Int J Heat Mass Transf. 2017;111:346–55. doi:10.1016/j.ijheatmasstransfer.2017.03.097. [Google Scholar] [CrossRef]

22. Baithalu R, Mishra SR, Pattnaik PK, Panda S. Analysis of heat and mass transfer rates in conducting Casson fluid flow over an expanding surface considering Ohmic heating and Darcy dissipation effects. Partial Differ Equ Appl Math. 2024;12(2):100972. doi:10.1016/j.padiff.2024.100972. [Google Scholar] [CrossRef]

23. Hussain M, Fatima S, Qayyum M. Radiative mixed convection flow of Casson nanofluid through exponentially permeable stretching sheet with internal heat generation. J Math. 2024;2024(4):9038635–12. doi:10.1155/2024/9038635. [Google Scholar] [CrossRef]

24. Mebarek-Oudina F, Bouselsal M, Biswas N, Vaidya H, Ramesh K. Thermal performance of MgO-SWCNT/water hybrid nanofluids in a zigzag walled cavity with differently shaped obstacles. Mod Phys Lett B. 2025;39(29):2550163. doi:10.1142/S0217984925501635. [Google Scholar] [CrossRef]

25. Alomari MA, Hassan AM, Alajmi A, Salho AK, Sadeq AM, Alqurashi F, et al. Analysis of double-diffusive transport and entropy generation in a wavy cylindrical enclosure with inner heated core: effects of MHD and radiation on Casson Cu-H2O nanofluid. Energy Sci Eng. 2025;13(6):2810–41. doi:10.1002/ese3.70069. [Google Scholar] [CrossRef]

26. Pal D, Roy N, Vajravelu K. Effects of thermal radiation and Ohmic dissipation on MHD Casson nanofluid flow over a vertical non-linear stretching surface using scaling group transformation. Int J Mech Sci. 2016;114(2):257–67. doi:10.1016/j.ijmecsci.2016.06.002. [Google Scholar] [CrossRef]

27. Ghadikolaei SS, Hosseinzadeh K, Ganji DD, Jafari B. Nonlinear thermal radiation effect on magneto Casson nanofluid flow with Joule heating effect over an inclined porous stretching sheet. Case Stud Therm Eng. 2018;12(12):176–87. doi:10.1016/j.csite.2018.04.009. [Google Scholar] [CrossRef]

28. Khader MM, Babatin MM, Megahed AM. On the numerical evaluation for studying Ohmic dissipation and thermal conductivity impacts on the flow of Casson fluid. Case Stud Therm Eng. 2023;49(335):103192. doi:10.1016/j.csite.2023.103192. [Google Scholar] [CrossRef]

29. Wang J, Farooq U, Waqas H, Muhammad T, Khan SA, Hendy AS, et al. Numerical solution of entropy generation in nanofluid flow through a surface with thermal radiation applications. Case Stud Therm Eng. 2024;54(1):103967. doi:10.1016/j.csite.2023.103967. [Google Scholar] [CrossRef]

30. Said BO, Mebarek-Oudina F, Medebber MA. Magneto-hydro-convective nanofluid flow in porous square enclosure. Front Heat Mass Transf. 2024;22(5):1343–60. doi:10.32604/fhmt.2024.054164. [Google Scholar] [CrossRef]

31. Vaidyanathan G, Sekar R, Vasanthakumari R, Ramanathan A. The effect of magnetic field dependent viscosity on ferroconvection in a rotating sparsely distributed porous medium. J Magn Magn Mater. 2002;250(2):65–76. doi:10.1016/S0304-8853(02)00355-4. [Google Scholar] [CrossRef]

32. Ramanathan A, Suresh G. Effect of magnetic field dependent viscosity and anisotropy of porous medium on ferroconvection. Int J Eng Sci. 2004;42(3–4):411–25. doi:10.1016/S0020-7225(02)00273-2. [Google Scholar] [CrossRef]

33. Sheikholeslami M, Rashidi MM, Hayat T, Ganji DD. Free convection of magnetic nanofluid considering MFD viscosity effect. J Mol Liq. 2016;218(8):393–9. doi:10.1016/j.molliq.2016.02.093. [Google Scholar] [CrossRef]

34. Sheikholeslami M, Sadoughi MK. Numerical modeling for Fe3O4-water nanofluid flow in porous medium considering MFD viscosity. J Mol Liq. 2017;242(9):255–64. doi:10.1016/j.molliq.2017.07.004. [Google Scholar] [CrossRef]

35. Molana M, Dogonchi AS, Armaghani T, Chamkha AJ, Ganji DD, Tlili I. Investigation of hydrothermal behavior of Fe3O4-H2O nanofluid natural convection in a novel shape of porous cavity subjected to magnetic field dependent (MFD) viscosity. J Energy Storage. 2020;30(3):101395. doi:10.1016/j.est.2020.101395. [Google Scholar] [CrossRef]

36. Hamid M, Usman M, Khan ZH, Ahmad R, Wang W. Dual solutions and stability analysis of flow and heat transfer of Casson fluid over a stretching sheet. Phys Lett A. 2019;383(20):2400–8. doi:10.1016/j.physleta.2019.04.050. [Google Scholar] [CrossRef]

37. Metri PG, Guariglia E, Silvestrov S. Lie group analysis for MHD boundary layer flow and heat transfer over stretching sheet in presence of viscous dissipation and uniform heat source/sink. AIP Conf Proc. 2017;1798(1):020096. doi:10.1063/1.4972688. [Google Scholar] [CrossRef]

38. Muzara H. Recent numerical techniques for differential equations arising in fluid flow problems [dissertation]. Thohoyandou, South Africa: University of Venda; 2019. [Google Scholar]

39. Akolade MT, Tijani YO. A comparative study of three dimensional flow of Casson-Williamson nanofluids past a Riga plate: spectral quasi-linearization approach. Partial Differ Equ Appl Math. 2021;4(3):100108. doi:10.1016/j.padiff.2021.100108. [Google Scholar] [CrossRef]

40. Wang CY. Free convection on a vertical stretching surface. J Appl Math Mech. 1989;69(11):418–20. [Google Scholar]

41. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transf. 2010;53(11–12):2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032. [Google Scholar] [CrossRef]