Experimental Method for Studying the Effect of Dissolved Substances on the Evaporation Rate of Watwer Droplets Suspended in Air

1  Introduction

The effect of dissolved substances on the evaporation rate of small airborne droplets of aqueous solutions is of interest for studying some natural phenomena in nature and solving various industrial problems in quite different applications. Among others, we should mention the drying of droplets in the pharmaceutical industry to obtain solid drugs in the form of powders or tablets [1–3] and some processes in food production [4]. The application in agriculture, which was the main motivation for this work, is to control the spraying of crop protection products [5–10]. The transfer of aqueous solution droplets and watered aerosols in the atmosphere, which is important for meteorology and possible pathogen transfer, should also be mentioned [11–13].

The research efforts have been focused mainly on pharmaceutical applications where water evaporation causes a non-volatile dissolved substance to form a solid crust on the droplet surface. Subsequent water evaporation from the droplet center usually results in the breakdown of the solid shell. As for the droplets of a salt solution, this often leads to the appearance of hollow particles with orifices through which the vapor and concentrated solution escape to the outside, forming small solid particles. This interesting phenomenon and related effects are discussed in papers [14–20].

The present work is oriented mainly towards agricultural problems related to the drip irrigation of plants. Therefore, only low-concentration solutions of dissolved substances are considered, and the main issue concerns the reduction of the droplet evaporation rate due to the dissolved substances. The influence of the same additives to water droplets on the balance between evaporation and condensation in the conditions of an equilibrium cluster of levitating small droplets was studied by the authors in papers [21–23]. The experiments showed a significant effect of even small concentrations of some non-volatile substances dissolved in water on the increase of the equilibrium droplet size, which is associated with the hindered evaporation of water at increasing concentrations of these substances near the surface of the evaporating droplet.

To the above-mentioned applied problem, one has to deal not with equilibrium droplets, as in the droplet cluster, when evaporation is compensated by condensation from the surrounding humid air. Therefore, one should consider a physically simpler process when the condensation of water vapor is negligible. We can focus on the motion and evaporation of the droplets suspended in atmospheric air. Unfortunately, the physical simplicity of the process (in comparison with the equilibrium droplet cluster) is combined with new difficulties of measurements, since one has to track the droplets travelling in the gas. As a result, it was necessary to create a fundamentally new laboratory setup and to develop a special measurement technique.

2  Laboratory Setup and Experimental Procedure

It is impossible to measure the size and velocity of individual evaporating droplets in the original droplet jet of a complex structure. The experimental technique used in this work eliminates the need to study the sprayed droplet stream. The basic idea of the present paper was to convert the complex droplet stream generated by the dispenser into a directed flow of evaporating droplets falling in an air-filled vertical tube. This can be done using a design shown in Fig. 1, where “1” is the plastic protective casing, inside which there is an ultrasonic dispenser (Altrasonic, China), the horizontal axis of which coincides with the axis of the protective casing. The cylindrical part of the casing (inner diameter of 38 mm) ends with a vertical channel “2” of square cross section of 17 × 17 mm. Only those droplets whose horizontal motion has completely ceased due to the viscosity of the gas remain in the vertical channel. These droplets fall vertically downward under the action of gravity. Of course, the viscosity of the gas leads to a stabilization of the droplets’ falling velocity, which changes only as a result of the gradual evaporation of the droplets. The distance of the vertical channel from the dispenser was chosen to observe a sufficient number of droplets falling in the channel. The corresponding calculations will be considered below. Two opposite rectangular windows “ww” (17 mm width and 19 mm height) were closed with a transparent film. The falling droplets are illuminated and observed through these windows. The vertical position of the windows was chosen to exclude the effects of the flow disturbances at the lower and upper ends of the channel. The LED light source BM-50 V 3200/5600 (Logocam, Israel) and a high-speed camera FASTCAM Nova (Photron, Japan) with a lens AF-S VR Micro-Nikkor 105 mm f/2.8 G (Nikon, Japan) are used.

Figure 1: The image of the experimental setup

Distilled water and solutions of fungicide “Therapist Pro” and KCl with a mass concentration of Csol=0.25% for the fungicide and Csol=0.1% for KCl were sprayed. The dispenser generates droplets that vary considerably in size, but only droplets with a radius of 30<a<40 μm were suitable for analyzing droplet images. Smaller droplets are difficult to distinguish, and larger droplets fly too quickly through the camera’s field of view. All experiments were performed at air temperature Tair=30±0.5°C and the air relative humidity φair=20±1%.

The natural uncertainty of the initial velocity of droplets generated by the dispenser and the complex interaction of evaporating polydisperse droplets at the initial part of the droplet jet [24–32] does not require theoretical analysis for the problem being solved. To clarify the droplets’ motion from the dispenser to the top of the vertical channel, it is sufficient to consider a single-droplet model, neglecting the droplets’ evaporation in this part of their trajectories. The velocity components of a droplet of radius a, which flies out of the dispenser horizontally with initial horizontal velocity u0 and zero vertical velocity, change with time according to the equations:

duddt=−3CD8aρairρwud2,ud(0)=u0(1)

dvddt=g−3CD8aρairρwvd2,vd(0)=0(2)

where ρw and ρair are the densities of water and air, g=9.81 m/s2 is the acceleration of gravity, and CD is the drag coefficient, which can be calculated from the Reynolds number of the droplet Red=2ρairuda/ηair using one of the approximate relations [33–37]. The known formula CD=24/Red is applicable only at Red<0.5, when the Stokes approximation can be used to streamline the droplet with air. At a=50 μm, substituting the density of air ρair=1.184 kg/m3 and its dynamic viscosity ηair=1.85×10−5 Pa s, we obtain Red=0.64 for u0=0.1 m/s and Red=0.96 for u0=0.15 m/s. At these values of Reynolds number, the Stokes formula slightly underestimates the drag coefficient. Nevertheless, the systematic error is small and the Stokes approximation can be used for calculating the droplet motion. In the adopted model, it is convenient to introduce the droplet dynamic relaxation time.

τrel=29ρwa2ηair,(3)

and rewrite Eqs. (1) and (2) as follows:

u˙d=−ud/τrel,ud(0)=u0,(4)

v˙d=g−vd/τrel,vd(0)=0.(5)

The trajectories of water droplets obtained by solving these equations for typical values of the droplet radius and its initial velocity are shown in Fig. 2, where y and z are the horizontal and vertical coordinates, respectively. The calculations allowed us to choose a horizontal distance of 35 mm from the dispenser to the axis of the vertical channel. Subsequent experiments confirmed the correctness of this choice. Fig. 2 shows that the droplets moving above the entrance to the vertical channel move almost vertically. The fall of slowly evaporating droplets continues in the channel.

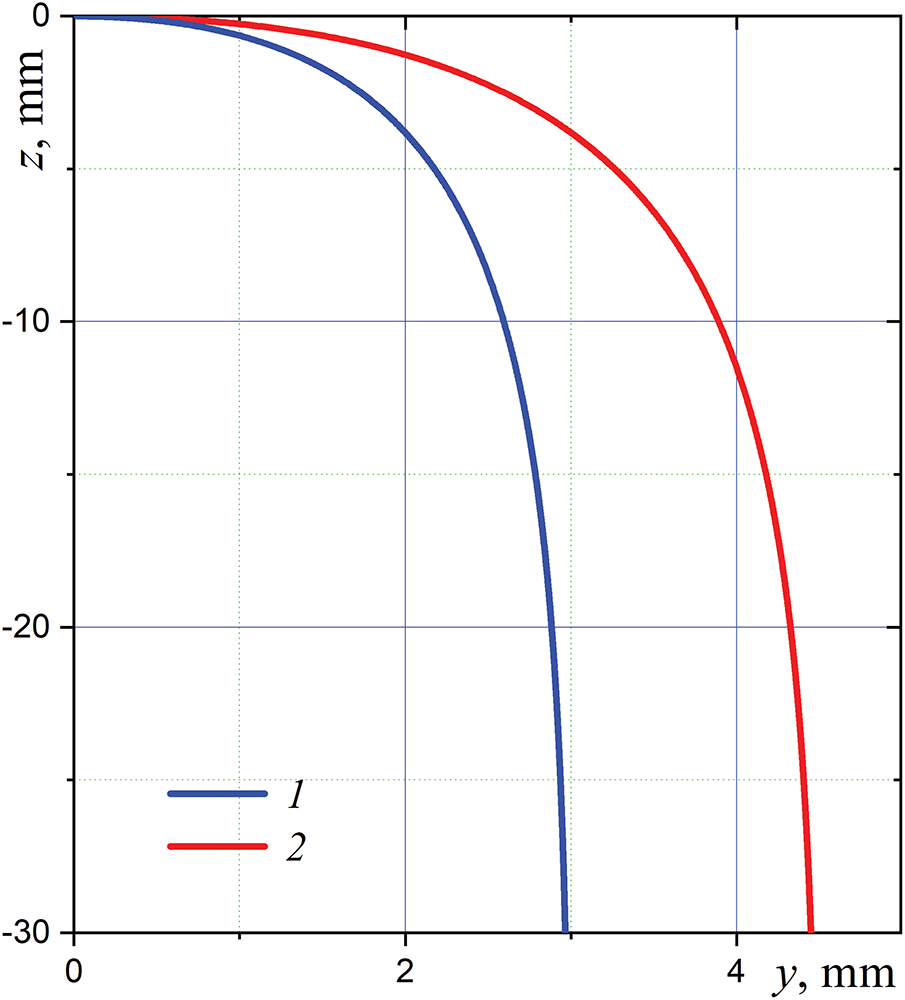
Figure 2: Calculated initial parts of trajectories for a droplet of radius a=50 μm: 1—u0=0.1 m/s, 2—u0=0.15 m/s

Note that the dynamic relaxation time of a water droplet in immovable air does not depend on the droplet velocity, and it is equal to τrel=0.03 s at a=50 μm. Such a small relaxation time means droplets fall in the vertical channel in a quasi-steady regime. In other words, the registered droplet velocity at each moment corresponds to the equilibrium of the forces acting on the droplet. At the equilibrium condition v˙d=0, the current radius of a falling droplet can be calculated as:

a=92ηairρwgvd(6)

For convenience of calculations, this equation can be written as follows:

a[µm]=2.91vd[mm/s].(7)

It should be noted that Eq. (7) is based on the Stokes approximation, which is applicable at a small Reynolds number. We will check below if this approach is sufficiently accurate for our laboratory experiments.

3  Experimental Results

Fig. 3 shows an example of a series of frames with an interval of δt=0.02 s (recording frequency 5000 fps). Water droplets A and B are selected for the analysis. The distances between the vertical positions of the droplet A at different time moments are designated as Hi, i=1,…,4. The camera resolution provides Hi measurement with an accuracy of ±20 μm. The ability to observe the trajectory of an individual droplet is necessary, since it is not the absolute value of the velocity that is important, but its change as the evaporating droplet falls. The recorded droplets were tracked along their entire trajectory. Only droplets with a radius of 30 to 40 μm were observed. The image of smaller droplets was blurred, and larger ones fell too quickly, making it difficult to determine their size change. Of course, the conclusion about the effect of impurities on the evaporation rate of droplets was made after averaging the measurements for several dozen similar droplets.

Figure 3: Typical images depicting falling droplets of pure water

The results for two initial and two final time intervals shown in Fig. 3 are presented in Fig. 4. The four points on each of the colored lines in Fig. 4 do not lie on straight lines. In other words, the line segments connecting the first two points and the last two points are not parallel. The tangent of the angle of inclination of these lines is the average droplet falling velocity at the considered part of the trajectory. For example, the velocity of droplet A decreases from about vd=161 to vd=159 mm/s, and the velocity of droplet B decreases from about vd=179 to vd=177 mm/s. Calculations according to Formula (7) show that the named values of the droplet velocity correspond to a decrease in the radius of droplet A from a=36.9 to a=36.7 μm, and of droplet B from a=38.9 to a=38.7 μm during the time Δt=0.08 s. Interestingly, the decrease in the droplet size is the same for both droplets. It will be shown below that this result agrees well with the evaporation theory.

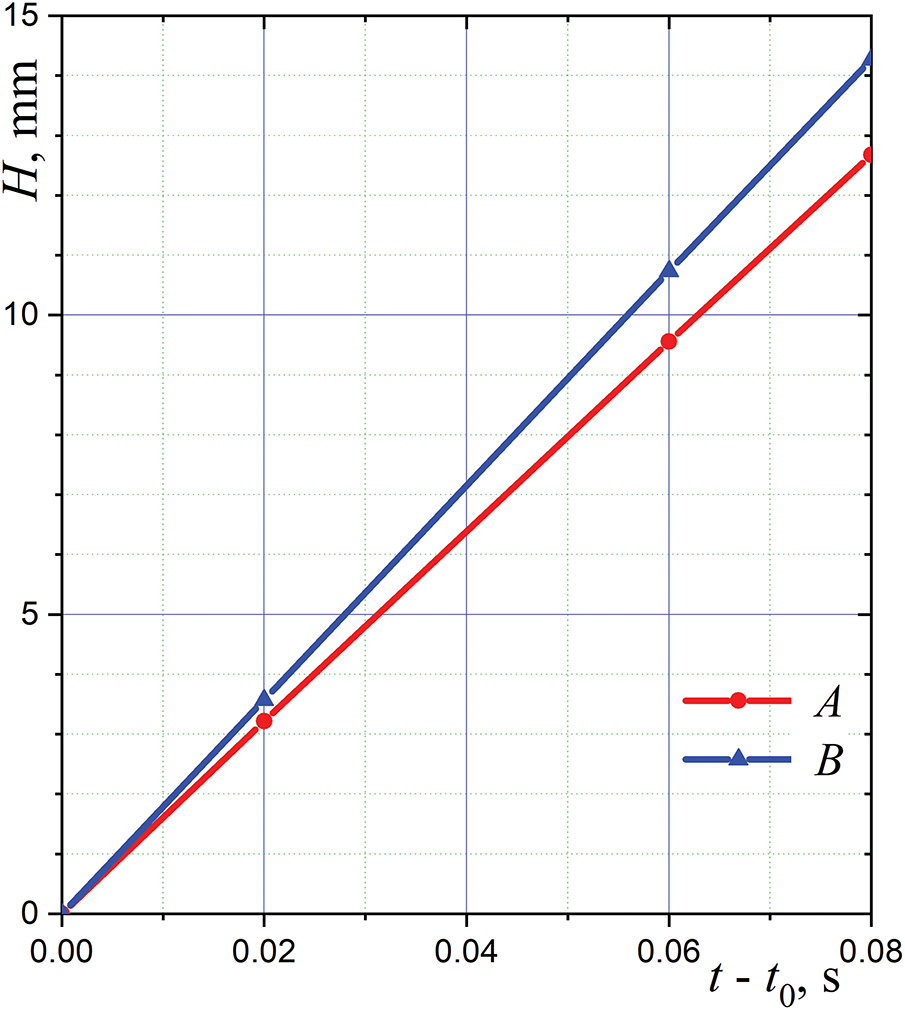
Figure 4: The distance travelled by the droplets of pure water

In addition to the unavoidable measurement error, there is a systematic error due to the Stokes approximation. To estimate this physical error, it is necessary to determine the Reynolds number of the observed droplets. Using the above-specified values of a and vd gives the following range of Reynolds number variation: 0.68<Red<0.83. It turns out that we are beyond the applicability range for the Stokes approximation. The associated error can be estimated by comparing the Stokes formula CD=24/Red and more accurate Oseen’s relation CD=24/Red+4.5 applicable when Red<5 [38]. Having substituted the values of Red=0.68 and Red=0.83 to the above relations, we find that Stokes’ formula underestimates the drag coefficient for water droplets A and B by 11–13%. As a result, Eq. (7) overestimates the equilibrium droplet radius by about 6%. This systematic error is the same for pure water and aqueous solution droplets. Therefore, this error doesn’t affect the relative change in the evaporation rate of water droplets with dissolved substances. So, the further processing of experimental data on the droplet falling velocity is carried out by the simplest Eq. (7). For pure water, the average rate of droplet radius decrease is about Δa/Δt=2.5 μm/s.

To obtain more accurate results, measurements were taken of the fall velocity of 90 droplets (thirty droplets of pure water and thirty droplets of fungicide and KCl solutions). The average values of the rate of decrease in the radius of the drops were found to be 2.7 μm/s for water, 2.4 μm/s for the selected fungicide solution at Csol=0.25%, and 1.5 μm/s for the KCl solution at a concentration of Csol=0.1%. The first of these three values can be compared with the theoretical prediction for pure water droplets. The results for the two solutions will be used to make the corrections to the droplet evaporation model.

4  Computational Model for Falling Droplets of Water Solutions

The problem statement for an isothermal droplet falling in immovable air is as follows:

ρwcwdTddt=−3a(m˙L−kairTd−Taira),T(0)=T0,(8)

ρwdadt=m˙,a(0)=a0(9)

where cw is the specific capacity of water, Td is the droplet temperature, m˙ is the mass rate of vapor flow from the droplet, L is the latent heat of evaporation, and kair is the thermal conductivity of air. As we assumed the Stokes flow around the droplet, the value of Nu=2 was used in the energy equation as was done in papers [19,21]. Eq. (8) is simpler than a similar equation in the mentioned papers due to the absence of the external thermal radiation absorbed partially by the droplets.

It is assumed that the values of ρw, cw, and L for the low-concentration aqueous solutions are the same as those for pure water. At the same time, the value of m˙ depends on a dissolved substance. Therefore, the resulting time dependences of Td and a are different for various solutions. The coupled Eqs. (8) and (9) should be completed by the evaporation model, which takes into account the rarefied gas flow in the Knudsen layer at the droplet surface [38,39]. The kinetic theory of gases describes the free-molecular flow in the Knudsen layer [40,41]. The diffusion equation for a continuous medium can be used outside this layer.

In the case of pure water, the mass flow rate of water vapor is determined as follows [42,43]:

m˙=DpairaRair(Tair,φair)Tairln1−ψ(Td,φK)φK1−ψ(Tair,φair)φair,ψ(T,φ)=psat(T)pairMvapMair(T,φ)(10)

where D is the diffusion coefficient of water vapor in air, Rair is the gas constant for humid air, pair is the atmospheric pressure, psat is the saturation pressure of water vapor [44], Mvap and Mair are the molecular masses of water vapor and humid air, and the value of φK at the boundary of the Knudsen layer is determined from the mass balance:

fevpsat(Td)2πRvapTd(φK−1)=DpairaRair(Tair,φair)Tairln1−ψ(Td,φK)φK1−ψ(Tair,φair)φair(11)

The molecular mass and gas constant of humid air are:

Mair(T,φ)=RRair(T,φ),Rair(T,φ)=Rair,01−φ(1−MvapMair,0)psat(T)pair,(12)

where Rair,0 and Mair,0 are calculated for the dry air and R=8314 J/(kmol K) is the universal gas constant. The coefficient fev=0.0024 in Eq. (11) was suggested in [43,45] to avoid time-consuming numerical solutions. The above model has been validated by comparing calculations and the experimental data of [46].

Calculations for the conditions of the laboratory experiment show that the mass rate of evaporation of pure water droplets is equal to m˙=2.926 g/(m2 s) and is constant during the droplets’ falling in the vertical channel. According to Eq. (9), we obtain the linear decrease of the droplet radius over time at a rate a˙≈2.93 μm/s. The latter value practically does not depend on the initial radius a0 (see Fig. 5a). The resulting equilibrium velocities of water droplets calculated using Eq. (7) are shown in Fig. 5b.

Figure 5: (a) decrease in the radius of evaporating water droplets over time, (b) decreasing the equilibrium droplet fall velocity: 1—a0=45 μm, 2—a0=50 μm, 3—a0=55 μm

The theoretically predicted value of a˙ for pure water droplets is close to the average experimental value a˙expav=2.7 μm/s obtained in Section 4. The ratio of ψ=a˙expav/a˙=0.92 will be used below to derive an approximate equation for the mass evaporation rate for droplets of various aqueous solutions.

This means that laboratory methodology is sufficiently accurate and applicable for comparative experiments with aqueous solutions of various substances at their small concentrations. Of course, the mass rate of evaporation, m˙, is also a constant value that does not depend on the droplet velocity. The effect of dissolved substances on the mass evaporation rate of droplets can be accounted for using the following exponential approximation for the correction factor:

m˙(Cs)=ψm˙(0)×(1−exp⁡(−ξCsol/Csol,1))(13)

where Csol,1 is the concentration of a solute in the above laboratory experiments and the correction coefficient ξ can be obtained from these experiments. Approximation (13) is physically correct in both limiting cases: m˙(Cs)≈ψm˙(0)×ξCsol/Csol,1 at ξCsol/Csol,1≪1 and m˙(Csol)≈ψm˙(0) at 1≪ξCsol/Csol,1 and Csol<Csolmax. For a solution of a typical fungicide ξ=0.356, and an aqueous solution of KCl is characterized by the correction coefficient of ξ=0.556. Based on recent studies [22,23], the relatively strong effect of NaCl and KCl salts on water droplet evaporation is explained by the very low diffusion coefficient of these salts in water. As a result, a thin layer with an increased concentration of dissolved salt forms on the surface of the evaporating droplet, which reduces the mass evaporation rate of water.

According to the authors, the same laboratory setup and similar procedure (with possible additional infrared heating) can be used to study specific effects (up to the formation of hollow solid particles) observed in droplets of aqueous solutions with a high concentration of non-volatile substances.

5  Conclusions

A new experimental method and laboratory setup were developed to investigate the effect of low-concentration dissolved substances on the evaporation rate of small water droplets suspended in the atmosphere. The main idea of this method is based on converting a complex droplet jet produced by an ultrasound dispenser into a directed flow of evaporating droplets falling in a vertical tube. The computational modeling of droplet motion was used to choose the setup geometrical parameters. Images of droplets with radii from 30 to 40 μm captured by a high-speed camera of 5000 fps were used to determine the velocities and sizes of individual falling droplets. The calculations using the previously developed evaporation model for pure water droplets agree well with the measurements. The new experimental data for low-concentration aqueous solutions of various substances were used to modify this evaporation model for these solutions. It was confirmed that the correction factor for droplets of aqueous solution of a typical fungicide is insignificant for agricultural applications. At the same time, the modified evaporation model for the sea salt components gives a realistically lower evaporation rate. The suggested approximate exponential variation of the correction factor is convenient for estimations at not small concentrations of dissolved substances. The latter is expected to be important for some industrial and geophysical applications.

Acknowledgement: The authors are grateful to the financial support for the work by the Russian Science Foundation.

Funding Statement: This study was financially supported by the Russian Science Foundation (project No. 24-29-00303: https://rscf.ru/project/24-29-00303/, accessed on 01 July 2025). The grant was received by the first author.

Author Contributions: The authors confirm contribution to the paper as follows: Study conception, Alexander A. Fedorets, Leonid A. Dombrovsky; Experimental design and procedure, Alexander A. Fedorets, Anna V. Nasyrova, Vyacheslav O. Mayorov; Computer processing of the experimental data, Eduard E. Kolmakov, Dmitry N. Medvedev, Anna V. Nasyrova; Physical analysis of experimental data, Alexander A. Fedorets, Vladimir Yu. Levashov, Leonid A. Dombrovsky; Computational model and calculations, Leonid A. Dombrovsky, Vladimir Yu. Levashov; Draft manuscript preparation, Alexander A. Fedorets, Leonid A. Dombrovsky. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Ethics Approval: Not applicable.

Conflicts of Interests: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Ziaee A, Albadarin AB, Padrela L, Femmer T, O’Reilly E, Walker G. Spray drying of pharmaceuticals and biopharmaceuticals: critical parameters and experimental process optimization approaches. Eur J Pharm Sci. 2019;127:300–18. doi:10.1016/j.ejps.2018.10.026. [Google Scholar] [PubMed] [CrossRef]

2. Baumann JM, Adam MS, Wood JD. Engineering advances in spray drying for pharmaceuticals. Annu Rev Chem Biomol Eng. 2021;12(1):217–40. doi:10.1146/annurev-chembioeng-091720-034106. [Google Scholar] [PubMed] [CrossRef]

3. Partheniadis I, Al-Zoubi N, Nikolakakis I. Pharmaceutical spray drying. In: Lamprou D, editor. Nano- and microfabrication techniques in drug delivery. Cham, Switzerland: Springer International Publishing; 2023. p. 71–97. doi:10.1007/978-3-031-26908-0_4. [Google Scholar] [CrossRef]

4. O’Sullivan JJ, Norwood EA, O’Mahony JA, Kelly AL. Atomisation technologies used in spray drying in the dairy industry: a review. J Food Eng. 2019;243(B):57–69. doi:10.1016/j.jfoodeng.2018.08.027. [Google Scholar] [CrossRef]

5. Li H, Cryer S, Raymond J, Acharya L. Interpreting atomization of agricultural spray image patterns using latent Dirichlet allocation techniques. Artif Intell Agric. 2020;4(8):253–61. doi:10.1016/j.aiia.2020.10.004. [Google Scholar] [CrossRef]

6. Jiang Y, Yang Z, Xu X, Shen D, Jiang T, Xie B, et al. Wetting and deposition characteristics of air-assisted spray droplet on large broad-leaved crop canopy. Front Plant Sci. 2023;14:1079703. doi:10.3389/fpls.2023.1079703. [Google Scholar] [PubMed] [CrossRef]

7. Wang B, Wang J, Yu C, Luo S, Peng J, Li N, et al. Sustained agricultural spraying: from leaf wettability to dynamic droplet impact behavior. Glob Chall. 2023;7(9):2300007. doi:10.1002/gch2.202300007. [Google Scholar] [PubMed] [CrossRef]

8. Aminpour Y, Dehghan D, Playán E, Maroufpoor E. Estimation of wind drift and evaporation losses of sprinkler irrigation systems using dimensional analysis. Agric Water Manag. 2023;289:108518. doi:10.1016/j.agwat.2023.108518. [Google Scholar] [CrossRef]

9. Spaska OA, Daszykowski M, Bushuev YG. Evaluation of evaporation fluxes for pesticides and low volatile hazardous materials based on evaporation kinetics of net liquids. ACS Omega. 2024;9(16):18617–23. doi:10.1021/acsomega.4c01405. [Google Scholar] [PubMed] [CrossRef]

10. Lankinen Å, Witzell J, Aleklett K, Furenhed S, Karlsson Green K, Latz M, et al. Challenges and opportunities for increasing the use of low-risk plant protection products in sustainable production. A review. Agron Sustain Dev. 2024;44(2):21. doi:10.1007/s13593-024-00957-5. [Google Scholar] [CrossRef]

11. Karset IHH, Gettelman A, Storelvmo T, Alterskjær K, Berntsen TK. Exploring impacts of size-dependent evaporation and entrainment in a global model. J Geophys Res Atmos. 2020;125(4):e2019JD031817. doi:10.1029/2019JD031817. [Google Scholar] [CrossRef]

12. Huynh E, Olinger A, Woolley D, Kohli RK, Choczynski JM, Davies JF, et al. Evidence for a semisolid phase state of aerosols and droplets relevant to the airborne and surface survival of pathogens. Proc Natl Acad Sci U S A. 2022;119(4):e2109750119. doi:10.1073/pnas.2109750119. [Google Scholar] [PubMed] [CrossRef]

13. Leung GR, Saleeby SM, Sokolowsky GA, Freeman SW, van den Heever SC. Aerosol-cloud impacts on aerosol detrainment and rainout in shallow maritime tropical clouds. Atmos Chem Phys. 2023;23(9):5263–78. doi:10.5194/acp-23-5263-2023. [Google Scholar] [CrossRef]

14. Charlesworth DH, Marshall Jr WRJr. Evaporation from drops containing dissolved solids. AIChE J. 1960;6(1):9–23. doi:10.1002/aic.690060104. [Google Scholar] [CrossRef]

15. Cheng RJ, Blanchard DC, Cipriano RJ. The formation of hollow sea-salt particles from the evaporation of drops of seawater. Atmos Res. 1988;22(1):15–25. doi:10.1016/0169-8095(88)90009-9. [Google Scholar] [CrossRef]

16. Vehring R, Foss WR, Lechuga-Ballesteros D. Particle formation in spray drying. J Aerosol Sci. 2007;38(7):728–46. doi:10.1016/j.jaerosci.2007.04.005. [Google Scholar] [CrossRef]

17. Vehring R. Pharmaceutical particle engineering via spray drying. Pharm Res. 2008;25(5):999–1022. doi:10.1007/s11095-007-9475-1. [Google Scholar] [PubMed] [CrossRef]

18. Fairhurst D. Droplets of ionic solutions. In: Brutin D, editor. Droplet wetting and evaporation. New York, NY, USA: Academic Press; 2015. p. 295–313. doi:10.1016/B978-0-12-800722-8.00020-5. [Google Scholar] [CrossRef]

19. Dombrovsky LA, Levashov VY, Kryukov AP, Dembele S, Wen JX. A comparative analysis of shielding of thermal radiation of fires using mist curtains containing droplets of pure water or sea water. Int J Therm Sci. 2020;152(1–3):106299. doi:10.1016/j.ijthermalsci.2020.106299. [Google Scholar] [CrossRef]

20. Miles BEA, Winter E, Mirembe S, Hardy D, Mahato LK, Miles REH, et al. Evaporation kinetics and final particle morphology of multicomponent salt solution droplets. J Phys Chem A. 2025;129(3):762–73. doi:10.1021/acs.jpca.4c07439. [Google Scholar] [PubMed] [CrossRef]

21. Dombrovsky LA, Fedorets AA, Levashov VY, Kryukov AP, Bormashenko E, Nosonovsky M. Stable cluster of identical water droplets formed under the infrared irradiation: experimental study and theoretical modeling. Int J Heat Mass Transf. 2020;161(8):120255. doi:10.1016/j.ijheatmasstransfer.2020.120255. [Google Scholar] [CrossRef]

22. Fedorets AA, Shcherbakov DV, Levashov VY, Dombrovsky LA. Self-stabilization of droplet clusters levitating over heated salt water. Int J Therm Sci. 2022;182(5):107822. doi:10.1016/j.ijthermalsci.2022.107822. [Google Scholar] [CrossRef]

23. Fedorets AA, Kolmakov EE, Dombrovsky LA. Experimental study of the effect of water salinity on the parameters of an equilibrium droplet cluster levitating over a water layer. Front Heat Mass Transf. 2024;22(1):1–14. doi:10.32604/fhmt.2024.049335. [Google Scholar] [CrossRef]

24. Bellan J, Cuffel R. A theory of nondilute spray evaporation based upon multiple drop interactions. Combust Flame. 1983;51(37):55–67. doi:10.1016/0010-2180(83)90083-4. [Google Scholar] [CrossRef]

25. Castanet G, Perrin L, Caballina O, Lemoine F. Evaporation of closely-spaced interacting droplets arranged in a single row. Int J Heat Mass Transf. 2016;93(5–6):788–802. doi:10.1016/j.ijheatmasstransfer.2015.09.064. [Google Scholar] [CrossRef]

26. de Rivas A, Villermaux E. Dense spray evaporation as a mixing process. Phys Rev Fluids. 2016;1(1):014201. doi:10.1103/physrevfluids.1.014201. [Google Scholar] [CrossRef]

27. Markadeh RS, Arabkhalaj A, Ghassemi H, Azimi A. Droplet evaporation under spray-like conditions. Int J Heat Mass Transf. 2020;148(17–18):119049. doi:10.1016/j.ijheatmasstransfer.2019.119049. [Google Scholar] [CrossRef]

28. Lupo G, Gruber A, Brandt L, Duwig C. Direct numerical simulation of spray droplet evaporation in hot turbulent channel flow. Int J Heat Mass Transf. 2020;160(1):120184. doi:10.1016/j.ijheatmasstransfer.2020.120184. [Google Scholar] [CrossRef]

29. Zamani S, Morris A. Effect of droplet collisions on evaporation in spray-drying. Dry Technol. 2022;40(7):1292–306. doi:10.1080/07373937.2020.1866006. [Google Scholar] [CrossRef]

30. Liu Q, Lu R, Qiao Y, Zhao F, Tan S. Analysis of the correction factors and coupling characteristics of multi-droplet evaporation. Int J Heat Mass Transf. 2022;195(4):123138. doi:10.1016/j.ijheatmasstransfer.2022.123138. [Google Scholar] [CrossRef]

31. Najafian M, Mortazavi S. Simulation of group of droplets evaporation. Eur J Mech B/Fluids. 2024;107(5):95–111. doi:10.1016/j.euromechflu.2024.06.005. [Google Scholar] [CrossRef]

32. Pandurangan N, Sahu S. Analysis of group evaporation characteristics of droplet clusters in an evaporating spray. J Fluid Mech. 2024;998:A26. doi:10.1017/jfm.2024.669. [Google Scholar] [CrossRef]

33. Johnson TA, Patel VC. Flow past a sphere up to a Reynolds number of 300. J Fluid Mech. 1999;378:19–70. doi:10.1017/s0022112098003206. [Google Scholar] [CrossRef]

34. Duan Z, He B, Duan Y. Sphere drag and heat transfer. Sci Rep. 2015;5(1):12304. doi:10.1038/srep12304. [Google Scholar] [PubMed] [CrossRef]

35. Goossens WRA. Review of the empirical correlations for the drag coefficient of rigid spheres. Powder Technol. 2019;352(5):350–9. doi:10.1016/j.powtec.2019.04.075. [Google Scholar] [CrossRef]

36. Singh N, Kroells M, Li C, Ching E, Ihme M, Hogan CJ, et al. General drag coefficient for flow over spherical particles. AIAA J. 2022;60(2):587–97. doi:10.2514/1.j060648. [Google Scholar] [CrossRef]

37. Michaelides EE, Sommerfeld M, van Wachem B. Multiphase flows with droplets and particles. 3rd ed. New York, NY, USA: CRC Press; 2022. 478 p. [Google Scholar]

38. Fuchs NA. Evaporation and droplet growth in gaseous media. London, UK: Pergamon Press; 1959. 72 p. [Google Scholar]

39. Labuntsov DA, Kryukov AP. Analysis of intensive evaporation and condensation. Int J Heat Mass Transf. 1979;22(7):989–1002. doi:10.1016/0017-9310(79)90172-8. [Google Scholar] [CrossRef]

40. Chambre PA, Schaaf SA. Flow of rarefied gases. New York NY, USA: Princeton University Press; 2017. 66 p. [Google Scholar]

41. Wu L. Rarefied gas dynamics: kinetic modeling and multi-scale simulation. New York NY USA: Springer; 2022. 460 p. [Google Scholar]

42. Levashov VY, Kryukov AP. Numerical simulation of water droplet evaporation into vapor-gas medium. Colloid J. 2017;79(5):647–53. doi:10.1134/s1061933x1705009x. [Google Scholar] [CrossRef]

43. Levashov VY, Kryukov AP, Shishkova IN. Influence of the noncondensable component on the characteristics of temperature change and the intensity of water droplet evaporation. Int J Heat Mass Transf. 2018;127(5):115–22. doi:10.1016/j.ijheatmasstransfer.2018.07.069. [Google Scholar] [CrossRef]

44. Stull DR. Vapor pressure of pure substances. Organic and inorganic compounds. Ind Eng Chem. 1947;39(4):517–50. doi:10.1021/ie50448a022. [Google Scholar] [CrossRef]

45. Kryukov AP, Levashov VY, Shishkova IN. Evaporation in mixture of vapor and gas mixture. Int J Heat Mass Transf. 2009;52(23–24):5585–90. doi:10.1016/j.ijheatmasstransfer.2009.06.021. [Google Scholar] [CrossRef]

46. Borodulin VY, Letushko VN, Nizovtsev MI, Sterlyagov AN. Determination of parameters of heat and mass transfer in evaporating drops. Int J Heat Mass Transf. 2017;109(4):609–18. doi:10.1016/j.ijheatmasstransfer.2017.02.042. [Google Scholar] [CrossRef]