 Open Access
Open Access
ARTICLE
Analysis of Heat Transfer inside Rectangular Micro-Channel with Wavy Surface and Hybrid Nanofluids
1 Engineering Technical College of Mosul, Northern Technical University, Cultural Group Street, Mosul, 41001, Iraq
2 Department of Construction Engineering & Project Management, AlNoor University College, Mosul, 41001, Iraq
* Corresponding Author: Omar Rafae Alomar. Email:
Frontiers in Heat and Mass Transfer 2025, 23(5), 1681-1700. https://doi.org/10.32604/fhmt.2025.066814
Received 18 April 2025; Accepted 08 September 2025; Issue published 31 October 2025
Abstract
The current work aims to numerically investigate the impact of using (50% ZnO and 50% Al2O3) hybrid nanofluid (HNf) on the performance of convective heat transfer inside a horizontal wavy micro-channel. This issue represents a novel approach that has not been extensively covered in previous research and provides more valuable insights into the performance of HNfs in complex flow geometries. The conjugate heat transfer approach is used to demonstrate the influence of adding hybrid nanoparticles (50% Al2O3 and 50% ZnO) to pure water on the rate of heat transfer. The governing equations are numerically solved by using ANSYS FLUENT (2021 R2). The behaviors of convective heat transfer coefficient (HTC), Nusselt number (Nu) and pressure drop are presented under various volume concentrations of (1%, 2% and 3%) and Reynolds numbers (Re = 600, 1200 and 1800). The numerical results are validated against the experimental one, where the validation test shows a good agreement between them. The findings display that the highest HTC enhancement is reached at 59.5% when using a volume concentration of 3% and Re = 1800. The Nusselt number is increased with the rise in volume concentration of nanoparticles, where the value of the Nusselt number is improved by 42.25% at 3% volume concentration. The reduction in pressure is raised with an increase in volume concentration and . The results also show that the combination of dispersion characteristics, Brownian movement and nanoparticles leads to an improvement in the rate of heat transfer. It is concluded that and the behavior of heat transfer are considerably enhanced when using a hybrid nanofluid inside a wavy micro-channel.Keywords
The rapid miniaturization of electronic devices and the continuous increase in their power densities have raised significant challenges in thermal management. Traditional cooling methods often fall short in meeting the stringent space and performance requirements of modern micro-electronic, photonic, and biomedical systems. As a result, Micro-channel Cooling Systems have become a promising solution due to their superior heat removal capability, high surface area-to-volume ratio, and potential for integration with compact devices [1]. The foundational work of Tuckerman and Pease [2] demonstrated the viability of silicon micro-channels for dissipating high heat fluxes exceeding 700 W/cm², sparking extensive research on optimizing micro-channel geometries, flow conditions, and working fluids. In parallel with experimental and numerical investigations, analytical modeling has played a crucial role in understanding and predicting the thermal and hydrodynamic behavior within micro-channels, offering simplified yet insightful solutions for design optimization. Conjugate heat transfer (CHT) is a procedure that explains the mechanisms for transferring heat between fluids and solid materials. Heat transfer is the study of thermal energy transmission between two physical entities. The rate of heat transmission between bodies is dependent on the temperature differential between them. The heat transfers in solids and fluids are combined in most applications. Because CHT has numerous practical uses, such as fins, heat exchangers, and electronic devices, CHT within micro-channels represents a prominent study area [3]. Corrugated surfaces of the micro-channel, which are the engineering adjustments or additions to the internal surface of the flow channel, are considered one way to improve heat transfer because it is a disturbance in the flow behavior, and their change leads to enhanced surface contact area [4]. In addition, nanofluid is an advanced high-conductivity synthetic fluid with enhanced physical-thermal properties, and has been proposed as a new way of heat transfer improvement, due to the increase in the molecule’s surface area, which enhances the stability of nanofluids compared to ordinary fluids [5].
In nanofluid systems, thermophoresis refers to the phenomenon where nanoparticles migrate from regions of higher temperature to regions of lower temperature under the influence of a thermal gradient. This effect becomes significant at the microscale or nanoscale, where temperature differences induce non-uniform particle distributions, directly affecting the thermal conductivity and heat transfer characteristics of the fluid. Diffusion effects, primarily driven by Brownian motion, describe the random movement of nanoparticles resulting from collisions with base fluid molecules. Brownian diffusion enhances the effective thermal conductivity and promotes uniform particle dispersion, which can improve the convective heat transfer performance of the nanofluid. The combined influence of thermophoresis and Brownian diffusion governs nanoparticle transport dynamics, impacting both heat and mass transfer within nanofluid flows. An accurate representation of these effects is crucial for predicting thermal performance, especially under non-uniform temperature fields or in microchannel and boundary layer applications [6].
Hybrid nanofluids (HNf) are created when more than one material is mixed to generate a homogenous stage with excellent dispersion. HNfs outperform unitary nanofluids in terms of heat transmission, rheology, and thermo-physical properties [7]. Recently, literature has explored the implementation of nanofluid and channels to improve the transfer of thermal energy. Singh et al. [8] employed the CFD approach to study numerically the heat rate of forced convection to augment heat transfer in a microtube and a wavy microchannel by utilizing HNf. It was observed that the heat transfer was enhanced by 21% compared to the base fluid. Rabiei et al. [9] inspect the effect of a volume fraction of hydraulic and thermal properties of an HNf including graphene sheets adorned with platinum through a wavy cylindrical microchannel. It was concluded that heat transfer was enhanced with increasing nanofluid volume fractions, but only a slight increase in friction factor was observed, which caused no penalty in pumping power. The impact of geometries and shapes of micro-channel heat sink (MCHS) on properties of heat transfer was numerically checked by Ghachem et al. [10] and Khan et al. [11]. Farsad et al. [12] studied numerically the effects of different volume fractions and three types of nanoparticles (Al2O3-H2O, CuO-H2O, and Cu-H2O) nanofluids on the MCHS performance. Ho and Chen [13], Saeed and Kim [14], and Kahani [15] experimentally and numerically, respectively, studied the thermal performance of (Al2O3-H2O) nanofluids, which is a coolant fluid within a square mini-channel for a thermal sink. Sivakumar et al. [16] investigated experimentally the forced convective heat transfer of (Al2O3-H2O and CuO-H2O) nanofluids flow in a serpentine MCHS. Liu and Yu [17] studied numerically the effects of non-uniform mini baffles inlets on the performance of mini-channel heat sinks.
Abdollahi et al. [18] studied numerically the fluid and heat transmission characteristics of a nanofluid flow in a V-type intake or outlet configuration of MCHS. The impact of nanoparticle type (Al2O3, CuO, SiO2, and ZnO) distributed in only water, volume fraction (1%, 1.5%, and 2%), as well as nanoparticle sizes (30, 40, and 60 nm) was examined. Feng et al. [19] examined numerically laminar liquid flows and heat transfer performance in a square MCHS having a wiring coil added. Khodabandeh and Abbassi [20] evaluated numerically the performance of the trapezoidal MCHS and optimum lateral angles (75°, 60°, 45°, and 30°) with a nanofluid of (Al2O3-H2O) of 1% as a coolant. Ambreen et al. [21] calculated numerically the thermal fluid characteristics for a heat source with 72 fins having a circular section and (Al2O3-H2O) nanofluid as a coolant. Kumar and Sarkar [22] analyzed experimentally and numerically the heat transition and pressure drop properties of a rectangular mini-channel for a heat-sink having nine parallel, using (Al2O3-TiO2) HNf with various nanoparticle mixture ratios as a coolant. Sajid et al. [23] investigated experimentally the influence of channel configurations and nanofluid concentrations on the performance of (TiO2-H2O) nanofluid in the wavy mini channel heat sink. Ataei et al. [24] experimentally inspected the thermal efficiency of square MCHS using (Al2O3/TiO2-H2O) HNf as a coolant. Sadegh Moghanlou et al. [25] evaluated the Al2O3 and TiO2 nanoparticles’ thermal behavior in water that circulated in an MCHS. Ali et al. [26] investigated experimentally the HTC and friction factor of the tube in a tube heat exchanger using Al2O3 nanoparticles dispersed in ethylene glycol with a diameter of 50 nm and a weight concentration of (0.1%, 0.3%, 0.5%, 0.7% and 1%). Numerical analysis was conducted by Saadoon et al. [27] to compare the enhancement in the HTC for straight as well as converge-diverge MCHSs. There are two kinds of (Fe3O4-H2O and Ag-H2O) nanofluids that are used as a coolant fluid. Soheel et al. [28] investigated numerically the HTC, pressure fall, and thermal conductivity of Al2O3 Nanoparticles dispersed in R134a with volume fractions of (0.015 and 0.03) flowing through the circular MCHS. Waqas et al. [29] examined the thermal transfer properties of micro-electronic chips in circular MCHS. (TiO2-H2O) nanofluid at (1%, 2% and 3%) volume concentrations is employed as a coolant. Saadoon et al. [30] investigated numerically straight and wavy channel configurations using different types of (CuO, Al2O3, Fe3O4, TiO2 and Ag) nanofluids with volume concentration varieties from 0 to 0.075. Lalagi et al. [31] studied the influence of various nanofluids, such as (Al2O3-H2O, CuO-H2O, and carbon Nanotube CNT-H2O), and their weight concentration percentage of (0.01, 0.03, and 0.05) on pressure drop and heat transition within micro-channel heat exchangers. Kamsuwan et al. [32] evaluated the effectiveness of a micro-channel heat exchanger using various nanofluids (Al2O3-H2O, CuO-H2O, and TiO2-H2O) with concentrations (0%, 3%, 5% and 7%). Elbadawy et al. [33] enhanced the flow of fluid and heat transition properties of various MCHS configurations (rectangular, triangular, trapezoidal, and circular). Various nanofluids (SiO2-H2O, Al2O3-H2O, and TiO2-H2O) with different concentrations ranging from 1% to 7% have been used as coolant fluid. Wang et al. [34] performed a numerical analysis to calculate the ideal operating parameters to prevent nanofluid deposition within a micro-channel cooled system.
Ahmad et al. [35] examined the coefficients affecting the heat transfer on the effectiveness of several electronic types, e.g., light-emitting diode, by adopting double diffusion and conjugate heat transfer. The non-linear rheology of Bingham fluid, utilizing the Papanastasiou model to manage yield stress discontinuities, is investigated inside a cubical enclosure. A solid vertical plate with slab fins is considered to be heated externally, playing the role of an LED base plate. The results indicated that the mass and heat fluxes are decreased with yield number when using non-Newtonian flow, where the maximum value is obtained when using Newtonian materials. Ahmed et al. [36] investigated the improvement of the heat transfer rate of peristalsis of hybrid nanofluid inside a curved duct by including the influences of thermal radiation and viscous dissipation. Impacts of several factors on heat transfer are presented. The findings displayed that the cooling process is improved and the flow rate is perturbed when adding nanomaterials to the liquid. The results confirmed that the rate of heat transfer using copper nanomaterial is 4% higher than the iron oxide nano-material case. Kumar et al. [37] numerically simulated the behaviours of flow and heat transfer of nanofluid flowing through a non-Darcy vertical porous sheet. The flow control conditions, e.g., uniform magnetic field and viscous dissipation, are also considered. The findings showed that the velocity profile is reduced when the velocity ratio is more than 1 and with increasing magnetic parameter. Nahlia et al. [38] numerically analyzed the advantages of magneto-hydrodynamic Maxwell fluid flow over an inclined exponential stretching surface. The actions of the internal heat source and mixed convection are also considered. The findings indicated that the thermal boundary layer and fluid velocity are diminished with an increase in the magnetic field parameter. Moreover, the inclination angle of the stretched surface and mixed convection have major effects on heat transfer features. Several recent studies have contributed to the analytical modeling of heat transfer in micro-channels. Morini [39] provided analytical correlations for convective heat transfer in rectangular and trapezoidal micro-channels under laminar flow conditions. Marzban et al. [40] investigated the conjugate heat transfer and the changes in the hydraulic and thermal terms of laminar flow (300 ł Re ł 800) in a 3-D wavy microchannel heat sink. Hussain et al. [41] investigated natural convection heat transport in micropolar fluids within an incinerator-shaped cavity, employing a mathematical model and numerical simulations. Turker et al. [42] investigated the flow and thermal characteristics of Al2O3-CuO, H2O within a microchannel with varying geometries and boundary conditions. Lalagi et al. [43] used CFD simulations and experimental methods to investigate the impact of channel geometry and nanofluid concentration on heat transfer performance in microchannel heat exchangers.
A thorough review of the literature and previous studies reveals that there are several numerical and experimental investigations have been conducted to display the performance of forced convection heat transfer under laminar fluid flow of nanofluids inside micro-channels. In these studies, the impacts of micro-channel shapes, nanofluid types and their volume concentrations on the heat transfer characteristics are studied. The previous literature review indicated that the conjugate heat transfer inside a wavy micro-channel filled with nanofluid under laminar flow is not adequately addressed. According to our knowledge, there is no study available in the open literature that has considered the conjugate heat transfer inside a wavy micro-channel filled with hybrid nanofluids (HNf) with water under laminar forced convection. The HNf is used as a coolant fluid, where it impacts each other on the fluid flow and heat transfer characteristics. Therefore, this study goals to numerically investigate the impacts of adding (50% ZnO/50%Al2O3 and H2O) nanofluids on the characteristics of conjugate heat transfer inside a wavy micro-channel. This work represents a novel study that is not extensively covered in previous research, where the outcomes from this work will contribute valuable insights into the performance of HNfs in complex flow geometries and filling a gap in the existing literature, and providing valuable insights for future research in this field. Furthermore, the current work offers a comprehensive understanding of how the combination of nanoparticles and channel configurations influences heat transfer characteristics. The governing equations, including the CHT approach, are numerically solved using ANSYS FLUENT (2021 R2). The impacts of volume concentrations of HNfs on heat transfer coefficient (HTC), Nusselt number (Nu), and pressure drop are displayed under different values of Reynolds numbers (Re). The results are obtained for different values of volume concentration of HNf (1%, 2% and 3%) and Re (600, 1200 and 1800). The results obtained with HNf are compared with those obtained using pure water.
2.1 Thermal and Physical Properties of Hybrid Nanofluid
The nanoparticles ZnO + Al2O3 dispersed in water were studied as a single-phase flow, a very viscous Newtonian, and an isotropic. The nanoparticles of ZnO and Al2O3 are used with a diameter of 20 nm. The HNf thermal characteristics, such as nanoparticle volume fraction (
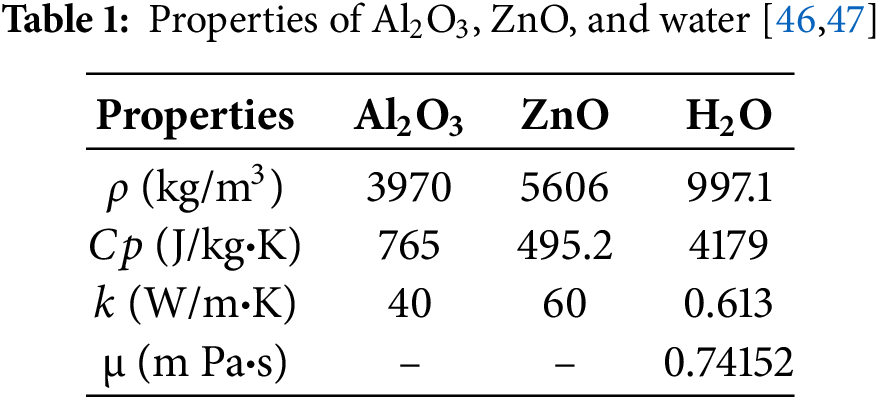
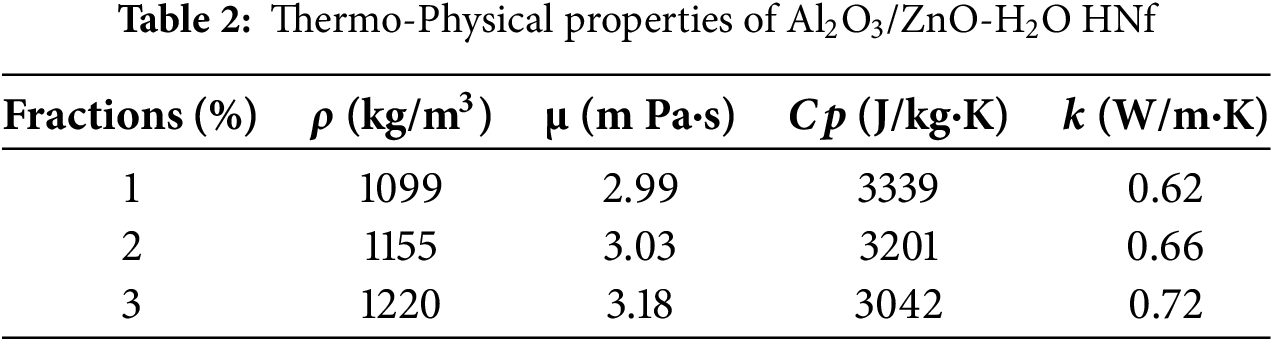
where np and bf refer to nanoparticles and base fluid, respectively. The physical properties of each particle of zinc oxide, alumina, and water are presented in Table 1 at the entry temperature 300 K [46,47]. The physical properties of Al2O3/ZnO-H2O HNf are computed and shown in Table 2. It can be noted here that the ZnO nanoparticles have superior thermal conductivity compared to CuO, TiO2, and SiO2. The ZnO-water nanofluid has the most substantial increase in the Nusselt number compared to CuO, TiO2, and SiO2 due to its superior thermal conductivity and effective boundary layer disruption. ZnO nanoparticles are more cost-effective than noble metals and carbon-based nanomaterials, while offering enhanced stability compared to SiO2, which sometimes requires surfactants to prevent aggregation.
2.2 Geometric Description of Wavy Micro Channel
A sinusoidal shape micro-wavy channel is used in this work with a fully developed flow through the entire channel length. For the case study, the temperature profiles of the fluid through the microchannel are provided in several parts. The flow of HNf inside the channel is deemed to be steady, laminar flow and 2D. The height of the micro channel (Hch) is equal to 12 mm, whereas the length (Lch) is equal to 50 mm. The bottom section of the sinusoidal-shaped solid conductive wall made of silicon material with a thickness (Hw) of 2 mm (calculated from the wave peak to the solid wall base), whereas the wavelength (WL) is 5 mm and the amplitude (WH) is 1 mm. The bottom straight base maintains a constant and uniform heat flux of 1000 W/m2. The top wall is solid, straight, and insulated, and hence, it is kept at a constant minimum temperature. The micro-channel geometry is depicted in Fig. 1.
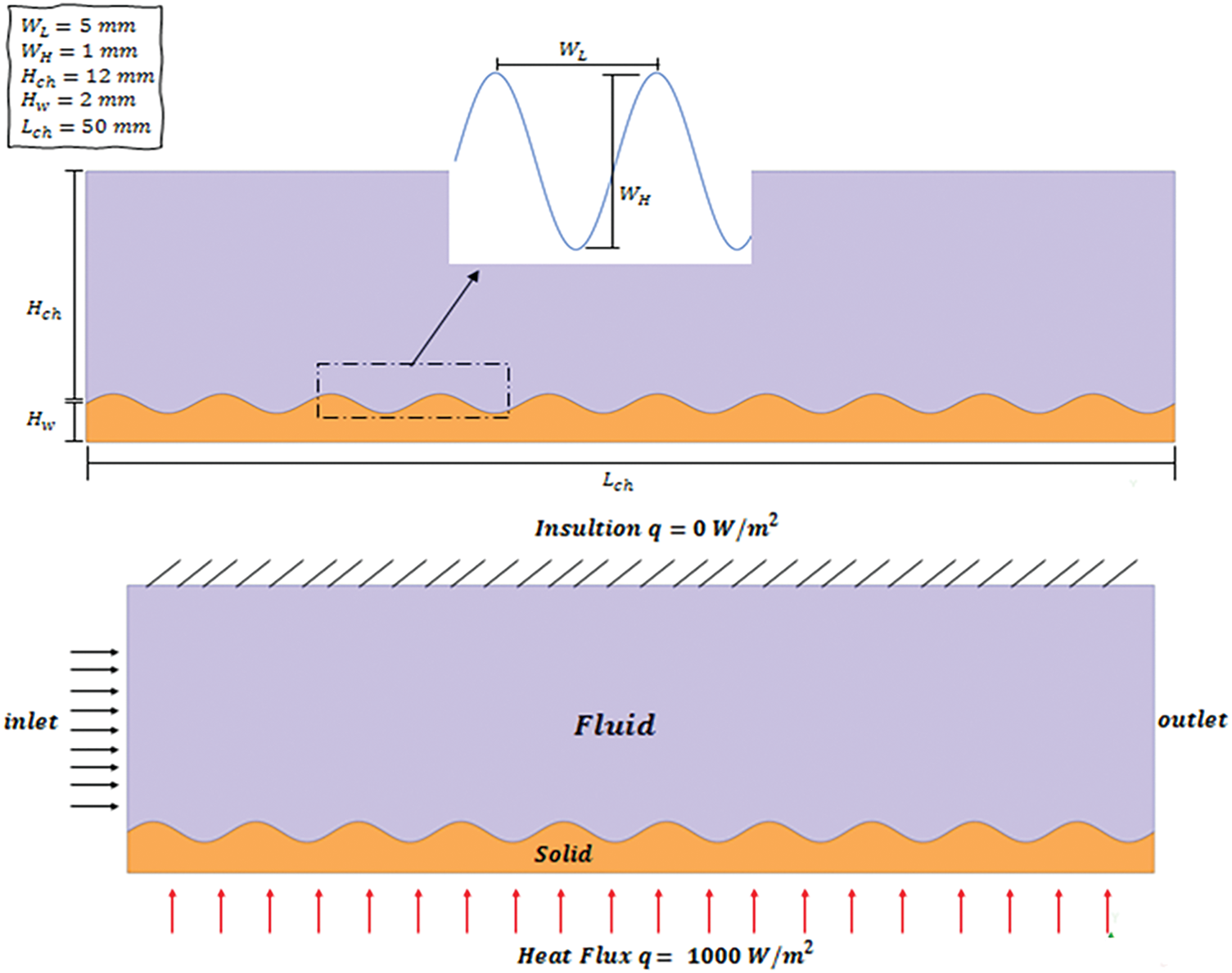
Figure 1: The wavy micro-channel geometry with boundary condition
The following assumptions were made in this study:
1. The HNf represents a single-phase flow containing water and hybrid Al2O3/ZnO nanoparticles as a homogeneous mixture.
2. The flow conditions are 2D, steady, fully developed, laminar, and incompressible.
3. Heat transfer by radiation, external body forces, and viscous dissipation is neglected.
4. Since the flow is Laminar, the values of Reynolds number (Re) are considered as (600, 1200, and 1800), whereas the heat flux and inlet temperature are taken as 1000 W/m2 and 300 K, respectively.
5. Neglecting the interfacial thermal resistance across the interface between the wall and fluid.
The mass, momentum, and energy conservation equations are expressed in the physical model, which is based on the previously mentioned assumptions. It is solved in the discipline of fluid mechanics and heat transfer. Thus, these equations are formed as follows [48]:
Mass equation:
Momentum equation:
Energy equation:
A. Reynolds number (Re)
The Re of HNf for laminar flow along the micro-channel can be estimated as follows [43,49]:
B. Brownian velocity
The Brownian velocity of HNfs can be computed as follows [43,49]:
where
C. Nusselt number
The Nu can be defined as follows [50,51]:
where
D. Pressure drop (
The pressure fall can be calculated using the following formula [52]:
The friction factor for laminar flow can be calculated as follows [52]:
The following conditions are taken into consideration to solve the differential equations.
i) The inlet temperature of an HNf is 300 K.
ii) The velocity of HNf, u = U, v = 0 (0 ≤
iii) The top and side walls are adiabatic and have no slip condition.
iv) The bottom surface provides a uniform and constant heat flux of 1000 W/m2.
v) The energy balance for the interface between both areas can be represented as:
The mesh-independent testing is achieved before obtaining the results. The micro-channel is discretized into a number of elements. The appropriate node number can be achieved by raising the number of nodes till the mesh becomes fine. The number of elements and nodes is chosen to be 114,625 and 116,114, respectively, where the convergence state is reached. In order to know its quality, the orthogonally of the mesh is measured at the best acceptable value of 0.05. Fig. 2 shows the mesh of the wavy channel, where the simulation becomes convergent when the error of equations is equal to 10−6.
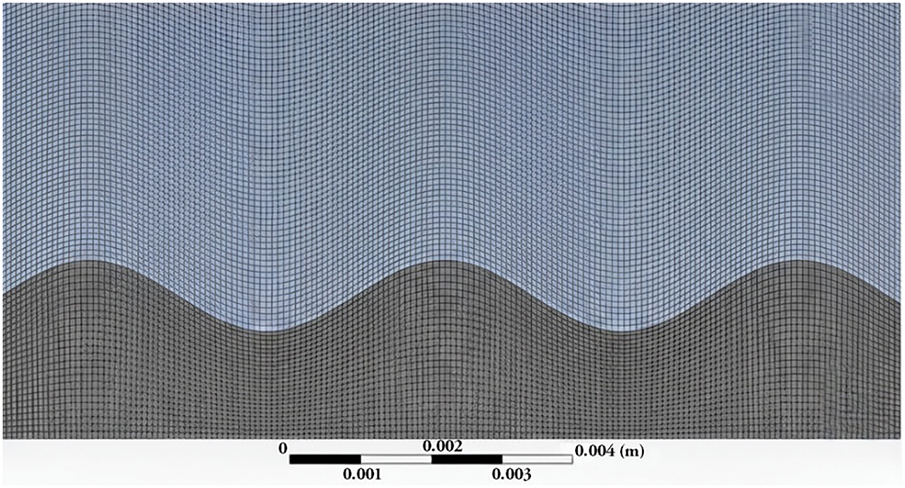
Figure 2: Mesh configuration for the wavy channel
The change of Nu against the number of grid cells for the lowest tested value of Re, that equal to 600, with 0.3% volume concentration of HNf, is presented in Fig. 3. It is depicted that the increment in the number of cells raised the temperature until it attained an almost fixed value.
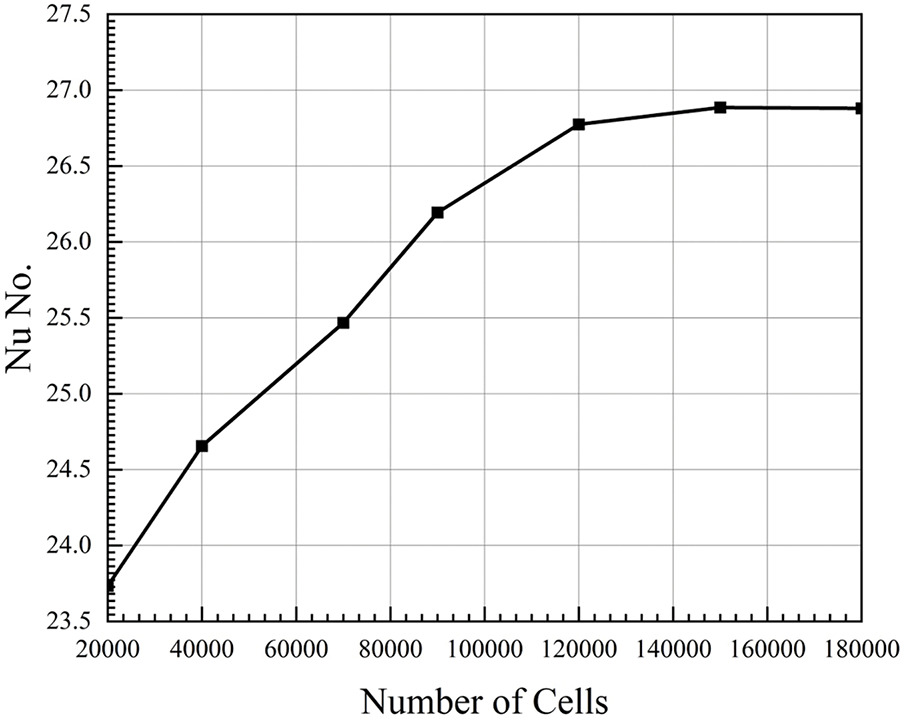
Figure 3: Mesh independent test
The finite volume approach is employed to solve the governing equations by using ANSYS FLUENT 2021 R2 software. The momentum, energy, and mass equations are solved numerically using the second-order upwind method. The SIMPLE technique is used to solve the pressure-velocity coupling equation [53,54]. For all variables, the convergence criteria for stopping the computation are equal to 10−6.
To confirm the accuracy of the current numerical model, the findings of this work are compared against the experimental results obtained by Ho and Chen [13]. The problem under validation is convective heat transfer inside a rectangular wavy channel using Al2O3-H2O nanofluid. The channel is 50 mm long. The validation test is performed under various values of
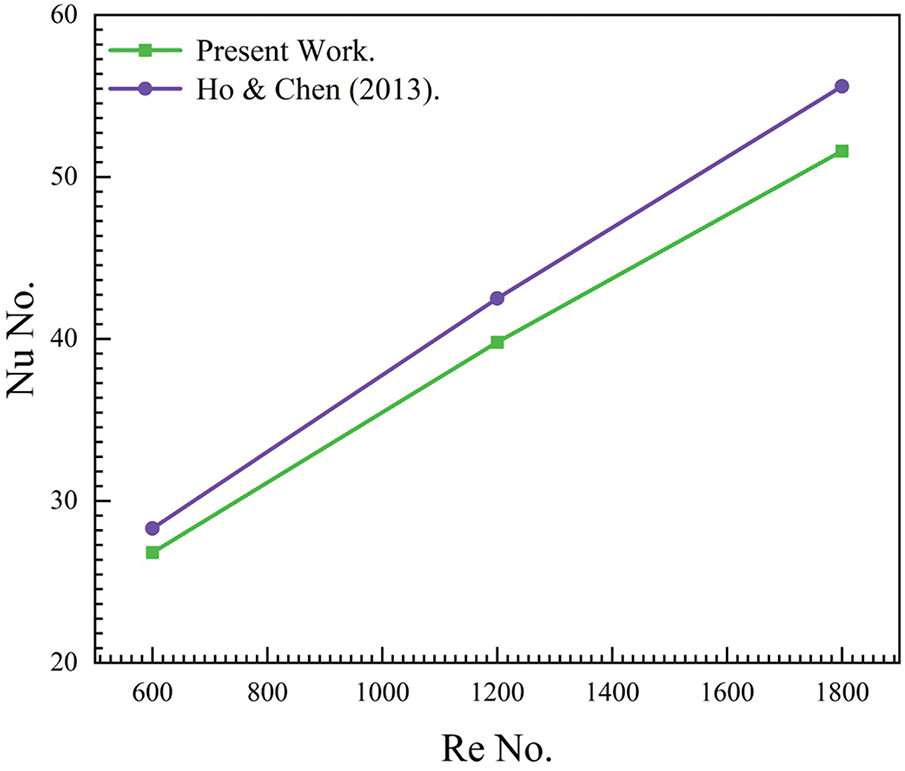
Figure 4: Comparison of the Nu No. for HNf at (1% volume concentration), for a range of Re No., between simulation results against Ho and Chen (2013) [13] experimental results
4.1 Hydrodynamics Characteristics and Velocity Distributions
Velocity distributions of a HNf in a wavy micro-channel for heat sinks were simulated. The Nu, HTC, and pressure fall were calculated for the pure and nanofluid with the boundary conditions that were stated in the assumption section. Figs. 5 and 6 show the velocity contours for pure water and 3% HNf flowing through the wavy channel at Re = 1800. It was noticed that the change in velocity distribution occurred in the wavy configuration because the velocity of the nanofluid will rise where the waveform adds activity and energy. The maximum velocity for the vertical direction is transferred downward from the center line towards the curved peaks, and the flow close to the curvy peaks was enhanced. As a result, both hydrodynamic and thermal boundary layers become thinner. Furthermore, it was observed that the velocity decreased when adding hybrid nanoparticles to the pure water due to the change in physical properties (density and viscosity).

Figure 5: Velocity contour for pure water within the wavy micro-channel at

Figure 6: Velocity contour for a 3% HNf within the wavy micro channel at
The pressure reduction variation of the MCHS for various hybrid nanoparticle volume fractions vs. Re is shown in Fig. 7. It is clear that the pressure fall rises slightly as the volume fraction of Al2O3/ZnO-H2O HNf rises from 1% to 3% because of nanoparticle deposition, which increases the roughness of the wall [12]. There can also be a significant difference in the pressure fall between pure water and Al2O3/ZnO-H2O HNf due to the viscosity of HNf being larger than pure water. The greater pressure drop is linked to the increase in thermal transfer efficiency for heat sinks attained by utilizing HNfs over the base liquid [8]. Fig. 7 also depicts the relation between pressure loss and Re. It was noticed that as the Re rose, the pressure fall rose also. The wavy micro-channel has a higher pressure loss than a simple straight micro-channel because of flow disruptions as a result of differences in micro-channel orientation and the flow’s secondary in a corrugated micro-channel formed. The contact between vortices and micro-channel walls frequently raises heat sink pressure losses of the heat sink [34].
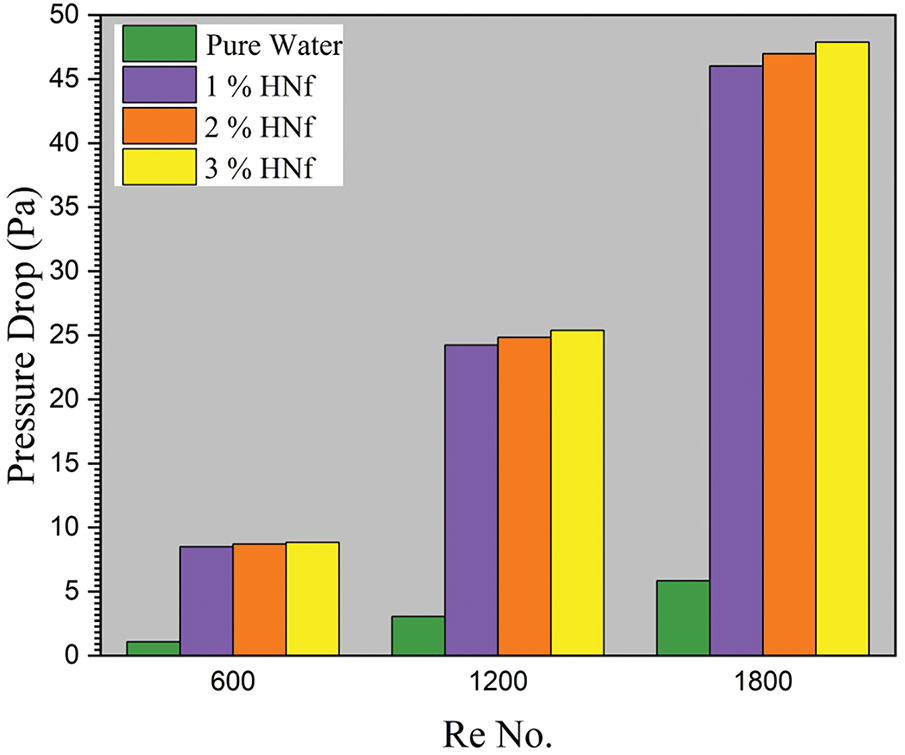
Figure 7: Pressure drop for different HNf volume fractions at different
4.3 Effect of Thermal Characteristics
A. Temperature distributions
The temperature increased from the inlet to the outlet with the direction of y-axis for the wavy channel, across the contact surfaces that exist between HNf and wall. The largest amount of heat dissipation generated by the micro-channel for the heat sink occurs at the intake due to the temperature of the nanofluid is small and the maximum difference in temperature between the channel and the input fluid. Heat transition happens via convection between a micro-channel’s walls and the HNf moving through it. As a result, the temperature variation is large, which enhances the heat transition between the surface and the cooling fluid, raising its temperature throughout its passage in the micro-channel.
Consequently, when the flow is exhausted, the temperature differential lowers, and heat transfer decreases, as shown in Figs. 8 and 9. It can be noted that the temperature contours for pure water and 3% HNf within the wavy channel at Re = 1800. The figures depicted the temperature raised when adding hybrid nanoparticles to the pure water due to improvement in physical properties when adding HNf led to an improvement in heat transition between HNf and the wavy channel.

Figure 8: Temperature contour for pure water within the wavy channel at

Figure 9: Temperature contour for a 3% HNf within the wavy micro channel at
B. Heat transfer coefficient (HTC)
Fig. 10 describes the variation of HTC vs. volume fraction of HNf along the wavy micro-channel at
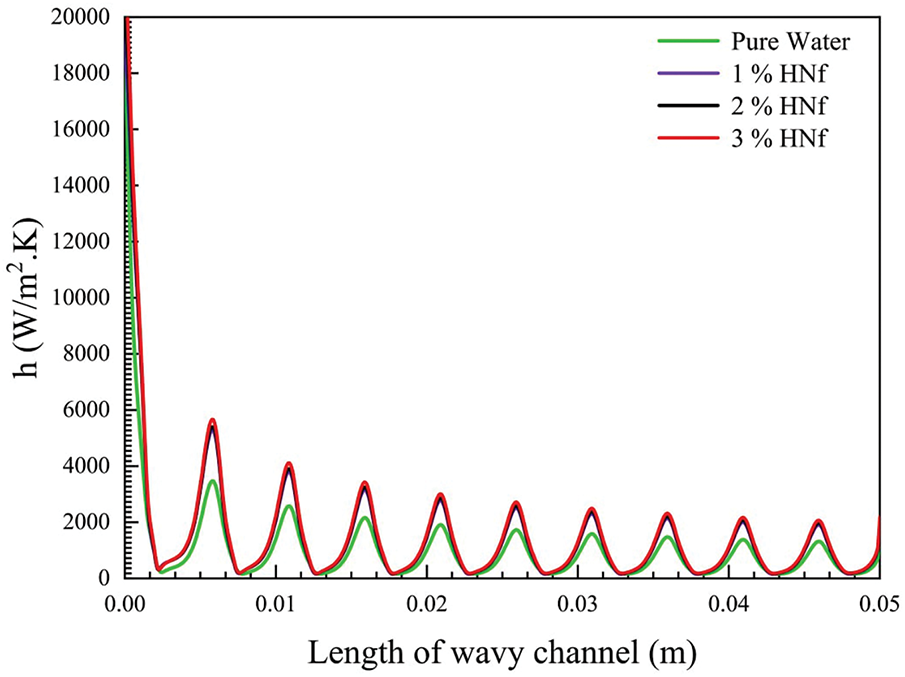
Figure 10: Variations of HTC vs. volume fraction of HNf along the micro-wavy micro-channel at
The heat transition is improved with an increase in HNf concentration, and this is a result of the hybrid nanoparticle’s thermal conductivity increasing, which leads to a rise in the HTC as seen in Fig. 11. The coefficient of heat transfer increased by 59.56% when adding a 3% volume concentration of hybrid nanoparticles to the pure water. Fig. 11 demonstrates the HTC for different HNf volume fractions at different
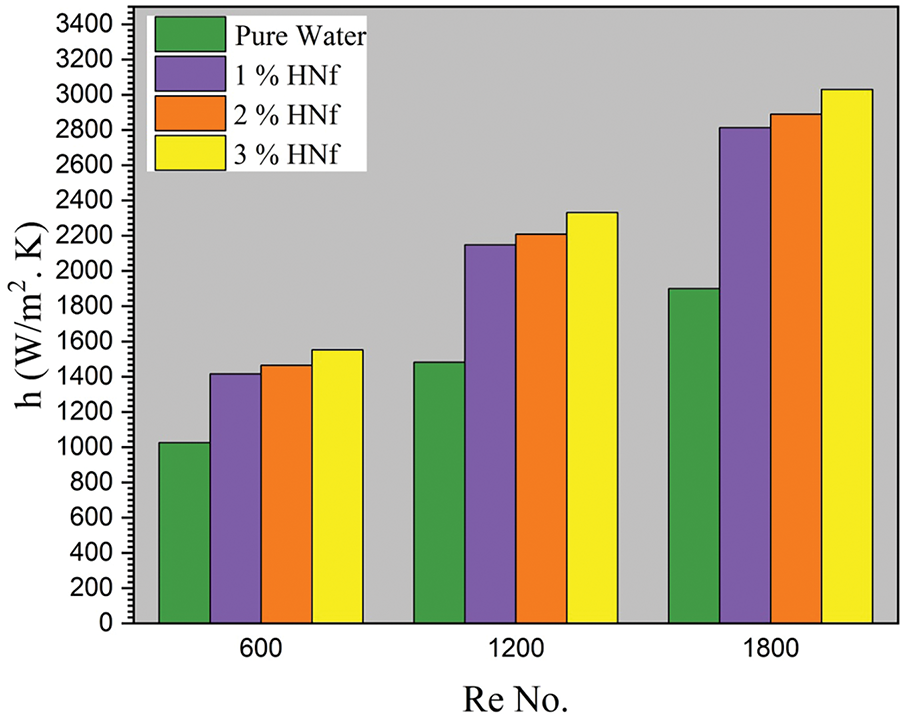
Figure 11: HTC for different HNf volume fractions at different
C. Nusselt number
An increase in the volume percentage of hybrid nanoparticles leads to an increase in Nu. The reduction and negative slope of
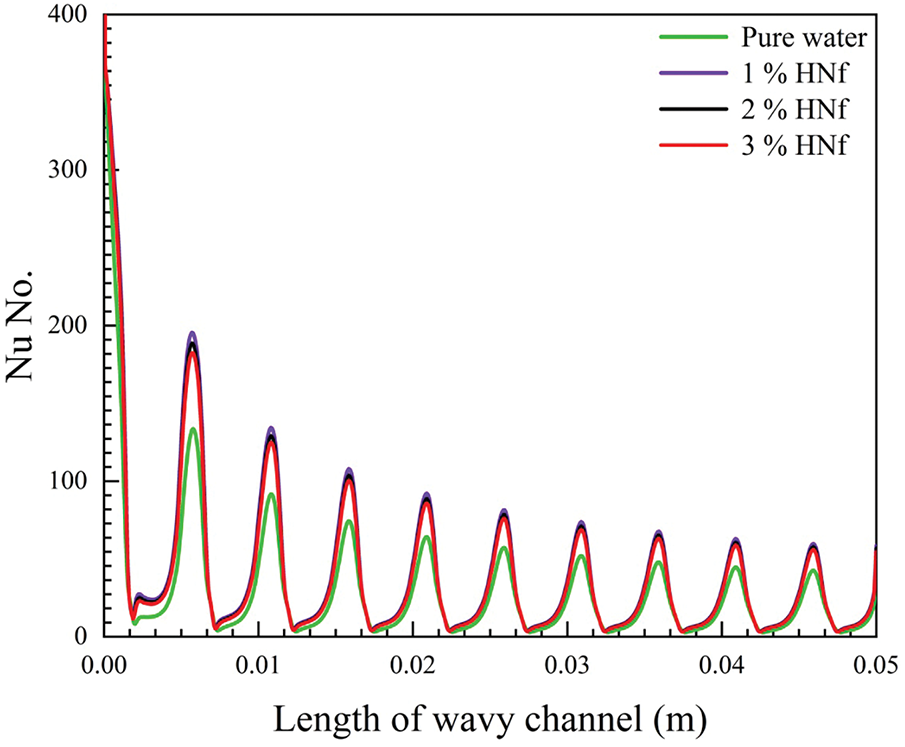
Figure 12: Variation of
The heat transfer characteristic quantity by using Nu results in Fig. 13, which presents the variation Nu vs. different HNf volume fractions at different Re. It is noticed from the figure the Nu increase occurred when adding Al2O3/ZnO hybrid nanoparticles to pure water. This is due to the impact of improved heat transfer caused by the solid hybrid nanoparticles’ higher thermal conductivity. Fig. 13 demonstrated that at a 3% volume concentration of Al2O3/ZnO-H2O HNf, the Nu. It was increased by 42.2% when compared with pure water. Also, the Nu raised slightly when the Al2O3/ZnO-H2O HNf volume fraction changed from 1% to 3%. Heat transfer increased as well, but at a slower rate due to Brownian motion. When the nanofluid has a higher concentration, the nanofluid’s kinetic energy increases due to rising collisions within nanoparticles as well as thermal transfer, resulting in considerable thermal conductivity [58]. Generally, in fluids, the
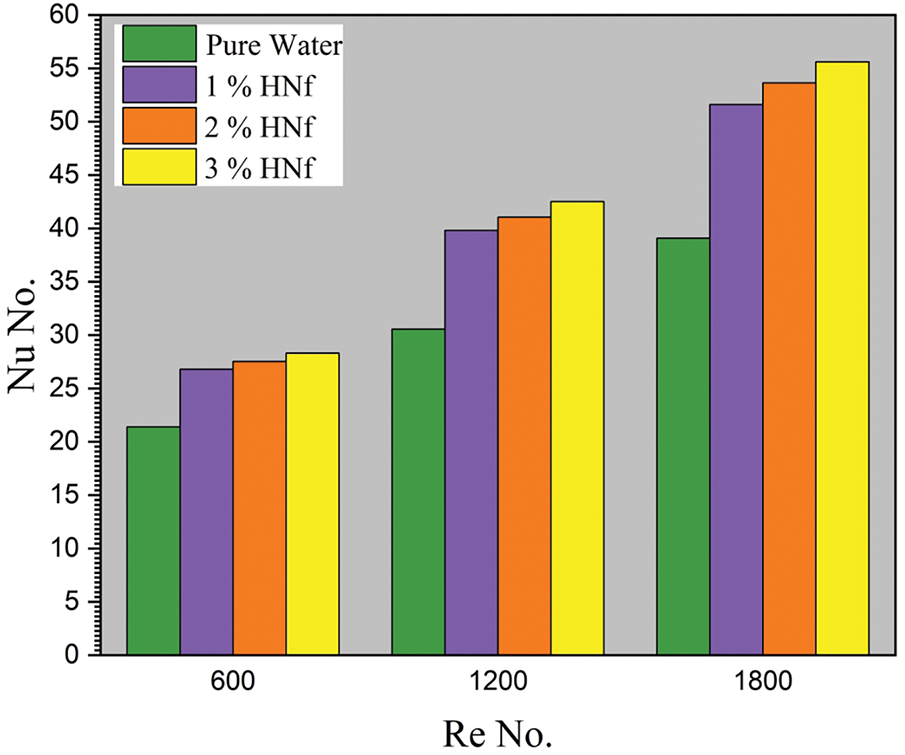
Figure 13: variations of
This work involves a numerical study on the performance of forced convection inside a horizontal wavy micro-channel by using a hybrid nanofluid. A conjugate heat transfer approach is used to confirm the impacts of adding (50% Al2O3 and 50% ZnO) hybrid nanoparticles to the pure water under various volume concentrations of (1%, 2% and 3%) and Reynolds number (Re = 600, 1200 and 1800). The governing equations are numerically solved by using ANSYS FLUENT (2021 R2). The numerical results are validated against the experimental results, where the validation test shows a good agreement between them. The following outcomes are drawn as conclusions:
(1) The comparison between numerical and experimental data shows that the Mean Absolute Percentage Error (MAPE) is 6.71% which represents a small error and hence, the current numerical solutions can be adopted.
(2) The findings showed that the use of hybrid nanoparticles with a high value of fraction leads to an enhancement the Nusselt number, resulting from an increase in the heat transfer coefficient (HTC). The peak value of HTC is obtained equal to 3030 W/m2·K, where the highest percentage enhancement is reached to 59.56% at
(3) The findings confirmed that the Nusselt number is slightly increased with an increase in volume fraction of nanoparticles from 1% to 3%. It has been found that the Nusselt number is improved by 42.25% at 3% volume fraction of nanoparticles.
(4) The outcomes indicated that the reduction in pressure is increased with the rise in the volume fraction of nanoparticles and
(5) The findings indicated that the wavy micro-channel has a high-pressure loss as compared to a simple straight micro-channel due to the flow disruptions resulting from differences in micro-channel orientation and the flow’s secondary in a corrugated micro-channel formed.
More work can be suggested to further progress this work as:
(1) Conducting a new numerical study by considering the problem of flow inside the wavy micro-channel as a 3D transient flow or a turbulent regime. This kind of problem can be solved by using ANSYS FLUENT 2021 R2 software.
(2) Performing a new numerical investigation by adding a bank of pipes inside the wavy micro-channel filled by porous medium and nanofluid.
(3) Performing a new numerical work by adding a porous structure inside the wavy micro-channel filled by nano-water under similar test conditions.
(4) Including the actions of adding the effect of surface radiation of the cannel wall on the performance of forced convection.
A final remark, several investigations have been numerically carried out on the problem of forced convection induced inside a duct. However, the experimental investigations related to this topic with integrated nanofluids and porous media available in the literature are too limited. Thus, to further improve this work, an experimental investigation shall be conducted on forced convection flow inside a porous wavy micro-channel filled with nanofluid. This investigation will be considered in the future as a separate work.
Acknowledgement: We would humbly like to express our appreciation to the Northern Technical University for their laboratories support for this study.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Banan Najim Abdullah, Karam Hashim Mohammed and Ammar Hassan Soheel; data collection: Bashar Mahmood Ali and Karam Hashim Mohammed; analysis and interpretation of results: Omar Rafae Alomar; draft manuscript preparation: Omar Rafae Alomar. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Data available on request from the authors.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Ag | Silver |
| Al2O3 | Alumina oxide |
| CFD | Computational-fluid dynamics |
| CHT | Conjugate-heat transfer |
| CuO | Copper oxide |
| Fe3O4 | Iron oxide |
| H2O | Water |
| HNf | Hybrid Nanofluid |
| HTC | Heat transfer coefficient |
| MAPE | Mean absolute percent error |
| MCHS | Micro channel heat sink |
| Nu | Nusselt number |
| Re | Reynolds number |
| SiO2 | Silicon oxide |
| TiO2 | Titanium oxide |
| ZnO | Zinc oxide |
| List of Symbols | |
| Specific heat capacity, J/kg·K | |
| dp | Nanoparticle diameter, mm |
| f | Darcy friction factor |
| Hch | Height of the channel above the wavy bottom solid wall, mm |
| Hw | Wavy bottom solid wall height, mm |
| h | Heat transfer coefficient, W/m2·K |
| k | Thermal conductivity, W/m·K |
| kb | Boltzmann constant, J/K |
| L | Length of channel, mm |
| Lch | Total channel length, mm |
| P | Pressure, Pa |
| q | Heat flux, W/m2 |
| T | Temperature, K |
| t | Time, s |
| V | Velocity vector, m/s |
| Y-axis velocity component, m/s | |
| WL | Wave length of one wavy channel, mm |
| WH | Distance from top to bottom one wave, mm |
| u | X-axis velocity component, m/s |
| Brownian speed, m/s | |
| Greek Symbols | |
| Nanoparticles volume fraction, % | |
| ρ | Density, kg/m3 |
| ∑ | Summation |
| μ | Dynamic viscosity, kg/m·s |
| Pi | |
| Time required to cover the movement, s | |
| Kinematic viscosity, m2/s | |
| Thermal diffusivity, m2/s | |
| Partial derivative | |
| Subscripts | |
| bf | Base fluid |
| h | Hydraulic |
| hnf | Hybrid Nanofluid |
| m | Mean |
| np | Nanoparticle |
| p | Particle |
| s | Silicon |
References
1. Kandlikar SG. Heat transfer and fluid flow in minichannels and microchannels. Boca Raton, FL, USA: CRC Press; 2012. [Google Scholar]
2. Tuckerman DB, Pease RFW. High-performance heat sinking for VLSI. IEEE Electron Device Lett. 1981;2(5):126–9. doi:10.1109/EDL.1981.25367. [Google Scholar] [CrossRef]
3. Hussein AM, Sharma KV, Bakar RA, Kadirgama K. Heat transfer enhancement with nanofluids—a review. J Mech Eng Sci. 2013;4:452–61. doi:10.15282/jmes.4.2013.9.0042. [Google Scholar] [CrossRef]
4. Azeez K, Ibrahim ZA, Hussein AM. Thermal conductivity and viscosity measurement of ZnO nanoparticles dispersing in various base fluids. J Adv Res Fluid Mech Therm Sci. 2020;66(2):1–10. [Google Scholar]
5. Hussein AM, Bakar RA, Kadirgama K, Sharma KV. Experimental measurements of nanofluids thermal properties. Int J Automot Mech Eng. 2013;7:850–63. doi:10.15282/ijame.7.2012.5.0070. [Google Scholar] [CrossRef]
6. Buongiorno J. Convective transport in nanofluids. J Heat Transf. 2006;128(3):240–50. doi:10.1115/1.2150834. [Google Scholar] [CrossRef]
7. Kaska SA, Khalefa RA, Hussein AM. Hybrid nanofluid to enhance heat transfer under turbulent flow in a flat tube. Case Stud Therm Eng. 2019;13:100398. doi:10.1016/j.csite.2019.100398. [Google Scholar] [CrossRef]
8. Singh SK, Bhattacharyya S, Paul AR, Sharifpur M, Meyer JP. Augmentation of heat transfer in a microtube and a wavy microchannel using hybrid nanofluid: a numerical investigation. Math Meth Appl Sci. 2020;66(1):99. doi:10.1002/mma.6849. [Google Scholar] [CrossRef]
9. Rabiei S, Khosravi R, Bahiraei M, Raziei M, Ahmadian Hosseini A. Thermal and hydraulic characteristics of a hybrid nanofluid containing graphene sheets decorated with platinum through a new wavy cylindrical microchannel. Appl Therm Eng. 2020;181:115981. doi:10.1016/j.applthermaleng.2020.115981. [Google Scholar] [CrossRef]
10. Ghachem K, Aich W, Kolsi L. Computational analysis of hybrid nanofluid enhanced heat transfer in cross flow micro heat exchanger with rectangular wavy channels. Case Stud Therm Eng. 2021;24:100822. doi:10.1016/j.csite.2020.100822. [Google Scholar] [CrossRef]
11. Khan MZU, Younis MY, Akram N, Akbar B, Rajput UA, Ahmad Bhutta R, et al. Investigation of heat transfer in wavy and dual wavy micro-channel heat sink using alumina nanoparticles. Case Stud Therm Eng. 2021;28(2):101515. doi:10.1016/j.csite.2021.101515. [Google Scholar] [CrossRef]
12. Farsad E, Abbasi SP, Zabihi MS, Sabbaghzadeh J. Numerical simulation of heat transfer in a micro channel heat sinks using nanofluids. Heat Mass Transf. 2011;47(4):479–90. doi:10.1007/s00231-010-0735-y. [Google Scholar] [CrossRef]
13. Ho CJ, Chen WC. An experimental study on thermal performance of Al2O3/water nanofluid in a minichannel heat sink. Appl Therm Eng. 2013;50:516–22. doi:10.1016/j.applthermaleng.2012.07.037. [Google Scholar] [CrossRef]
14. Saeed M, Kim MH. Heat transfer enhancement using nanofluids (Al2O3-H2O) in mini-channel heatsinks. Int J Heat Mass Transf. 2018;120:671–82. doi:10.1016/j.ijheatmasstransfer.2017.12.075. [Google Scholar] [CrossRef]
15. Kahani M. Simulation of nanofluid flow through rectangular microchannel by modified thermal dispersion model. Heat Transf Eng. 2020;41(4):377–92. doi:10.1080/01457632.2018.1540464. [Google Scholar] [CrossRef]
16. Sivakumar A, Alagumurthi N, Senthilvelan T. Experimental investigation of forced convective heat transfer performance in nanofluids of Al2O3/water and CuO/water in a serpentine shaped micro channel heat sink. Heat Mass Transf. 2016;52(7):1265–74. doi:10.1007/s00231-015-1649-5. [Google Scholar] [CrossRef]
17. Liu X, Yu J. Numerical study on performances of mini-channel heat sinks with non-uniform inlets. Appl Therm Eng. 2016;93:856–64. doi:10.1016/j.applthermaleng.2015.09.032. [Google Scholar] [CrossRef]
18. Abdollahi A, Mohammed HA, Vanaki SM, Osia A, Golbahar Haghighi MR. Fluid flow and heat transfer of nanofluids in microchannel heat sink with V-type inlet/outlet arrangement. Alex Eng J. 2017;56(1):161–70. doi:10.1016/j.aej.2016.09.019. [Google Scholar] [CrossRef]
19. Feng Z, Luo X, Guo F, Li H, Zhang J. Numerical investigation on laminar flow and heat transfer in rectangular microchannel heat sink with wire coil inserts. Appl Therm Eng. 2017;116:597–609. doi:10.1016/j.applthermaleng.2017.01.091. [Google Scholar] [CrossRef]
20. Khodabandeh E, Abbassi A. Performance optimization of water-Al2O3 nanofluid flow and heat transfer in trapezoidal cooling microchannel using constructal theory and two phase Eulerian-Lagrangian approach. Powder Technol. 2018;323:103–14. doi:10.1016/j.powtec.2017.09.046. [Google Scholar] [CrossRef]
21. Ambreen T, Saleem A, Park CW. Numerical analysis of the heat transfer and fluid flow characteristics of a nanofluid-cooled micropin-fin heat sink using the Eulerian-Lagrangian approach. Powder Technol. 2019;345:509–20. doi:10.1016/j.powtec.2019.01.042. [Google Scholar] [CrossRef]
22. Kumar V, Sarkar J. Numerical and experimental investigations on heat transfer and pressure drop characteristics of Al2O3-TiO2 hybrid nanofluid in minichannel heat sink with different mixture ratio. Powder Technol. 2019;345:717–27. doi:10.1016/j.powtec.2019.01.061. [Google Scholar] [CrossRef]
23. Sajid MU, Ali HM, Sufyan A, Rashid D, Zahid SU, Rehman WU. Experimental investigation of TiO2–water nanofluid flow and heat transfer inside wavy mini-channel heat sinks. J Therm Anal Calorim. 2019;137(4):1279–94. doi:10.1007/s10973-019-08043-9. [Google Scholar] [CrossRef]
24. Ataei M, Sadegh Moghanlou F, Noorzadeh S, Vajdi M, Shahedi Asl M. Heat transfer and flow characteristics of hybrid Al2O3/TiO2-water nanofluid in a minichannel heat sink. Heat Mass Transf. 2020;56(9):2757–67. doi:10.1007/s00231-020-02896-9. [Google Scholar] [CrossRef]
25. Sadegh Moghanlou F, Noorzadeh S, Ataei M, Vajdi M, Shahedi Asl M, Esmaeilzadeh E. Experimental investigation of heat transfer and pressure drop in a minichannel heat sink using Al2O3 and TiO2–water nanofluids. J Braz Soc Mech Sci Eng. 2020;42(6):315. doi:10.1007/s40430-020-02403-5. [Google Scholar] [CrossRef]
26. Ali FA, Alsaffawi AM, Mohammed KH. The impact of alumina nanoparticles suspended in ethylene glycol on the performance efficiency of a double pipe heat exchanger. Front Heat Mass Transf. 2020;15:1–7. doi:10.5098/hmt.15.21. [Google Scholar] [CrossRef]
27. Saadoon ZH, Ali FH, Sheikholeslami M. Numerical investigation of heat transfer enhancement using (Fe3O4 and Ag-H2O) nanofluids in (converge-diverge) mini-channel heat sinks. Mater Today Proc. 2023;80:2983–96. doi:10.1016/j.matpr.2021.07.091. [Google Scholar] [CrossRef]
28. Saleem AM, Saleem AH, Jumaah OM. Simulation and investigation of nano-refrigerant fluid characteristics with the two-phase flow in microchannel. Front Heat Mass Transf. 2021;17:1–7. doi:10.5098/hmt.17.21. [Google Scholar] [CrossRef]
29. Waqas H, Ali Khan S, Farooq U, Muhammad T, Alshehri A, Yasmin S. Thermal transport analysis of six circular microchannel heat sink using nanofluid. Sci Rep. 2022;12(1):8035. doi:10.1038/s41598-022-11121-y. [Google Scholar] [PubMed] [CrossRef]
30. Saadoon ZH, Ali FH, Hamzah HK, Abed AM, Hatami M. Improving the performance of mini-channel heat sink by using wavy channel and different types of nanofluids. Sci Rep. 2022;12(1):9402. doi:10.1038/s41598-022-13519-0. [Google Scholar] [PubMed] [CrossRef]
31. Lalagi G, Nagaraj PB, Talugeri V, Bidari MV. Study on heat transfer and pressure drop characteristics for nanofluids in microchannel heat exchangers. Phys Fluids. 2023;35(10):102015. doi:10.1063/5.0169130. [Google Scholar] [CrossRef]
32. Kamsuwan C, Wang X, Seng LP, Xian CK, Piemjaiswang R, Piumsomboon P, et al. Simulation of nanofluid micro-channel heat exchanger using computational fluid dynamics integrated with artificial neural network. Energy Rep. 2023;9:239–47. doi:10.1016/j.egyr.2022.10.412. [Google Scholar] [CrossRef]
33. Elbadawy I, Alhajri A, Doust M, Almulla Y, Fayed M, Dinc A, et al. Reliability of different nanofluids and different micro-channel configurations on the heat transfer augmentation. Processes. 2023;11(3):652. doi:10.3390/pr11030652. [Google Scholar] [CrossRef]
34. Wang M, Dobson PS, Paul MC. Numerical investigation of nanofluid deposition in a microchannel cooling system. Powder Technol. 2023;425:118582. doi:10.1016/j.powtec.2023.118582. [Google Scholar] [CrossRef]
35. Ahmad S, Liu D, Cham BM, Yang S, Sun SL. Exploring conjugate heat transfer in Bingham fluid flow: a 3D computational approach incorporating double diffusion and the Papanastasiou model. Appl Therm Eng. 2025;273:126500. doi:10.1016/j.applthermaleng.2025.126500. [Google Scholar] [CrossRef]
36. Ahmed B, Liu D, Hayat T, Nisar Z, Abdelmohimen MA. Thermal performance of radiative hydromagnetic peristaltic pumping of hybrid nanofluid through curved duct with industrial applications. Case Stud Therm Eng. 2024;64:105498. doi:10.1016/j.csite.2024.105498. [Google Scholar] [CrossRef]
37. Kumar S, Choudhary S, Kumari K, Sharma A, Choudhary P. MHD darcy-forchheimer flow of SWCNT-H2O nanofluid over a porous stretching sheet. Int J Thermofluids. 2025;26:101064. doi:10.1016/j.ijft.2025.101064. [Google Scholar] [CrossRef]
38. Nahlia MK, Sinha S, Loganathan K, Jat K, Choudhary P. Numerical Computation of Magnetohydrodynamic Maxwell fluid flow with mixed convection and heat source effects across an inclined exponential stretching surface. Partial Differ Equ Appl Math. 2025;14:101169. doi:10.1016/j.padiff.2025.101169. [Google Scholar] [CrossRef]
39. Morini L. Single-phase convective heat transfer in micro-channels: a review of experimental results. Int J Therm Sci. 2004;43(7):631–51. [Google Scholar]
40. Marzban F, Marzban M, Mohammadzadeh K, Davoodabadi Farahani S. Comparative study of two-phase flow approaches for modeling conjugate heat transfer in a three-dimensional wavy microchannel-heat sink with CuO-water nanofluid. Adv Mech Eng. 2024;16(8):16878132241273517. doi:10.1177/16878132241273517. [Google Scholar] [CrossRef]
41. Hussain S, Jayavel P, Almutairi B, Ramesh K. Enhanced heat transfer analysis of micropolar hybrid-nanofluids in an incinerator-shaped cavity. Therm Sci Eng Prog. 2025;60:103471. doi:10.1016/j.tsep.2025.103471. [Google Scholar] [CrossRef]
42. Türker H, Öğüt EB, Aslan E. Analysis of flow and thermal characteristics of hybrid nanofluids within a microchannel under magnetic field. Prog Comput Fluid Dyn Int J. 2025;25(1):31–43. doi:10.1504/pcfd.2025.143736. [Google Scholar] [CrossRef]
43. Lalagi G, Nagaraj PB, Omkaresh BR, Sharief HR. Optimizing heat transfer in microchannel heat ex-changers: a comparative analysis of channel geometry and nanofluids through CFD and experimental approaches. Eng Res Express. 2025;7(1):015562. doi:10.1088/2631-8695/adb665. [Google Scholar] [CrossRef]
44. Azeez K, Hameed AF, Hussein AM. Nanofluid heat transfer augmentation in a double pipe heat exchanger. In: AIP Conference Proceedings. Baghdad, Iraq: AIP Publishing; 2020. doi:10.1063/5.0000243. [Google Scholar] [CrossRef]
45. Hussein AM, Sharma KV, Bakar RA, Kadirgama K. A review of forced convection heat transfer enhancement and hydrodynamic characteristics of a nanofluid. Renew Sustain Energy Rev. 2014;29:734–43. doi:10.1016/j.rser.2013.08.014. [Google Scholar] [CrossRef]
46. Ahmed SE. Caputo fractional convective flow in an inclined wavy vented cavity filled with a porous medium using Al2O3-Cu hybrid nanofluids. Int Commun Heat Mass Transf. 2020;116:104690. doi:10.1016/j.icheatmasstransfer.2020.104690. [Google Scholar] [CrossRef]
47. Rahmati M. Effects of ZnO/water nanofluid on the thermal performance of wet cooling towers. Int J Refrig. 2021;131:526–34. doi:10.1016/j.ijrefrig.2021.03.017. [Google Scholar] [CrossRef]
48. Jiji LM. Heat convection. 2nd ed. Berlin/Heidelberg, Germany: Springer; 2009. [Google Scholar]
49. Corcione M. Empirical correlating equations for predicting the effective thermal conductivity and dynamic viscosity of nanofluids. Energy Convers Manag. 2011;52(1):789–93. doi:10.1016/j.enconman.2010.06.072. [Google Scholar] [CrossRef]
50. Yousif AA, Alomar OR, Hussein AT. Impact of using triple adiabatic obstacles on natural convection inside porous cavity under non-darcy flow and local thermal non-equilibrium model. Int Commun Heat Mass Transf. 2022;130:105760. doi:10.1016/j.icheatmasstransfer.2021.105760. [Google Scholar] [CrossRef]
51. Bejan A. Convection heat transfer. 4th ed. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2013. [Google Scholar]
52. Pritchard PJ. Fox and McDonald’s introduction to fluid mechanics. 8th ed. Hoboken, NJ, USA: John Wiley & Sons, Inc.; 2011. [Google Scholar]
53. Alomar OR. Numerical investigation of two-phase flow in a horizontal porous evaporator with localised heating using non-Darcian flow and two equations model. Heat Mass Transf. 2020;56(4):1203–21. doi:10.1007/s00231-019-02784-x. [Google Scholar] [CrossRef]
54. Basher NM, Alomar OR, Mohamed IA. Impact of using single heated obstacle on natural convection inside porous cavity under non-Darcy flow and thermal non-equilibrium model: a comparison between horizontal and vertical heated obstacle arrangements. Int Commun Heat Mass Transf. 2022;133:105925. doi:10.1016/j.icheatmasstransfer.2022.105925. [Google Scholar] [CrossRef]
55. He Y, Jin Y, Chen H, Ding Y, Cang D, Lu H. Heat transfer and flow behaviour of aqueous suspensions of TiO2 nanoparticles (nanofluids) flowing upward through a vertical pipe. Int J Heat Mass Transf. 2007;50(11–12):2272–81. doi:10.1016/j.ijheatmasstransfer.2006.10.024. [Google Scholar] [CrossRef]
56. Hussain S, Jamal M, Maatki C, Ghachem K, Kolsi L. MHD mixed convection of Al2O3-Cu-water hybrid nanofluid in a wavy channel with incorporated fixed cylinder. J Therm Anal Calorim. 2021;144(6):2219–33. doi:10.1007/s10973-020-10260-6. [Google Scholar] [CrossRef]
57. Elsafy KM, Saghir MZ. Forced convection in wavy microchannels porous media using TiO2 and Al2O3-Cu nanoparticles in water base fluids: numerical results. Micromachines. 2021;12(6):654. doi:10.3390/mi12060654. [Google Scholar] [PubMed] [CrossRef]
58. Apmann K, Fulmer R, Soto A, Vafaei S. Thermal conductivity and viscosity: review and optimization of effects of nanoparticles. Materials. 2021;14(5):1291. doi:10.3390/ma14051291. [Google Scholar] [PubMed] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools