Hybrid Optimized PI Controller Design for Grid Tied PV Based Electric Vehicle

1  Introduction

Electric Vehicles (EVs) have gained significant interest in many countries due to the growing demand of clean energy and the need to overcome the limitations of fossil fuels. The primary goals of EVs are to reduce air pollution, reduce reliance on fossil fuels and improve energy security. The aforementioned criteria are only met when EVs are integrated with Renewable Energy Sources (RESs) [1,2]. Among different RESs, solar PV based EV charging systems are highly preferred because of the abundant availability in nature with zero carbon emissions [3,4].

The low voltage of PV is insufficient to meet the demand and hence the inclusion of high gain dc–dc converters is preferred for maximizing the output voltage in a wider range [5]. Boost [6], buck-boost [7], Cuk [8], SEPIC [9] and Zeta [10] are some of the most widely used converters in PV applications. A boost converter is also termed as a step up converter as it maximizes its input voltage in a wider range. It is simple in structure with less number of converter components. The efficiency of this converter is reduced during high voltage applications due to the high voltage stress and the occurrence of reverse recovery issues. Both buck-boost and Cuk converter possess the capability to yield an inverted voltage output that is either greater or lesser than the input voltage. The buck-boost converter has pulsating input current whereas the Cuk converter has non-pulsating input current. The output current is discontinuous in both converters and these converters are operated at high duty cycle for obtaining maximum voltage gain. SEPIC converter has continuous input currents along with the ability to carry out both voltage step-down and step-up operation but the high ripple content in the input current minimizes the maximum power extraction capability of PV in a wider range. Luo converters are indeed the best choice for enhanced Power Quality (PQ)-based EV charging systems as these converters possess inherent voltage boosting features and the capability of handling high power ratings. Unlike other converters, Luo converters provide minimum current ripples and maximum output voltage. However, this converter encounters the drawback of pulsating current at converter input, which affects the battery life [11–15]. The Z-source inverter (ZSI) acquires buck and boost features from an impedance network on the DC side. The traditional ZSI suffers from certain drawbacks like high voltage spikes on capacitors, large initial inrush current and irregular input current. Thus, the quasi ZSI is introduced to subdue the limitations of conventional ZSI. The qZSI is employed to obtain lower voltage stress of the capacitor, minimum voltage overshoot on the bridge switches and continuous input current [16,17].

The PV system’s output voltage varies over time with environmental factors like temperature, solar insolation and so on. Hence, the power generation from the PV system is not consistent and a proper control strategy has to be implemented for enhancing the performance of the converter by minimizing the THD, obtaining near unity power factor, lowering steady state error and solving peak overshoot issues. The conventional PI controller is the most simple and feasible controller that has always been used for controlling the operation of the converters in PV grid tied systems. This controller when operated in the specified range regulates the DC link voltage more effectively with minimum THD. However, the process of estimating the appropriate PI controller values is considered to be a hard process owing to the intermittency associated with the PV system. Trial and error technique, which is adopted for tuning the PI controller is a time consuming and error prone process. The issues faced by conventional PI controllers are solved and the performance is enhanced by using metaheuristic algorithms, which are simple, robust and easy to implement [18–21]. Some of the metaheuristic algorithms that are adopted to tune the PI parameters more accurately are Grey Wolf Optimization (GWO) [22], Whale Optimization Algorithm (WOA) [23], Ant Colony Optimization (ACO) [24], Coot Bird Metaheuristic Optimizer (CBMO) [25], etc. For increasing the optimization efficiency in a wider range the hybrid algorithms are introduced by combining different algorithms. The inverter, which generates AC voltage by converting DC voltage is required to be included to the network along with a low pass filter for lessening the current harmonics injection into the grid. L, LC, and LCL filters are some of the most frequently used filter topologies in grid tied PV systems [26,27].

In this paper, Trans Z-source Based Luo converter (TZSBLC) is designed for enhancing the unregulated DC voltage output obtained from the PV. LGWO-PI controller is implemented for enhancing the output derived from the converter. The PV generated power is then supplied to the single phase grid and three phase BLDC motor. The control over the BLDC motor speed is ensured using a PI controller.

2  Proposed System Description

The concept of PV based EV, which supports decarbonized energy generation and transportation is acquiring massive attention in recent times due to the exhaustion of fossil fuel and need to curtail carbon emission for minimizing global warming. BLDC motors are the most commonly used motor in EVs due to the advantageous elements like simple design, high efficiency, excellent speed regulation capability, low losses and low maintenance. A PV fed BLDC motor drive for EV is designed with LGWO-PI controller in this work as illustrated in Fig. 1.

Figure 1: Proposed system

The PV system based power generation is not constant as it varies with temperature and solar irradiance. The unstable solar module output voltage is regulated as a stable DC output of desired voltage using LGWO-PI controller based DC-DC TZSBLC. The output voltage is fed to the 3 φ VSI for converting it to the AC voltage, which is then provided to the motor of the EV. The major objective of controlling the motor speed is attained through a PI controller. The error speed that is obtained after comparing the actual ( Nact ) and reference ( Nref) speeds of the motor is fed as the PI controller input. For controlling the switching operation of VSI, the controller output is injected to the PWM generator, which involves in producing the necessary pulses. The converter voltage is converted to AC voltage and fed to the 1 φ grid by using a 1 φ VSI. The grid voltage synchronization is achieved by using PI controller. The grid power is used for driving the BLDC motor in the absence of PV during the night time.

3  Proposed System Modelling

3.1 PV Fed TZSBLC

The photovoltaic principle is used to convert the solar irradiance into photo-generated power in a PV system. The PV output is maximized with the implementation of TZSBLC. The TZSBLC is a hybrid converter that combines the features of both Trans Z-source converter and Luo converter. This proposed converter comprises of a power switch S1 , four diodes ( D1 , D2 , D3andD4 ), five capacitors ( C1 , C2 , C3 , C4andCo ), three inductors ( L1 , L2 , and L3 ) and a load resistor R as shown in Fig. 2. The converter functions in Continuous Conduction Mode (CCM). Two working modes of the converter are illustrated in the Fig. 3.

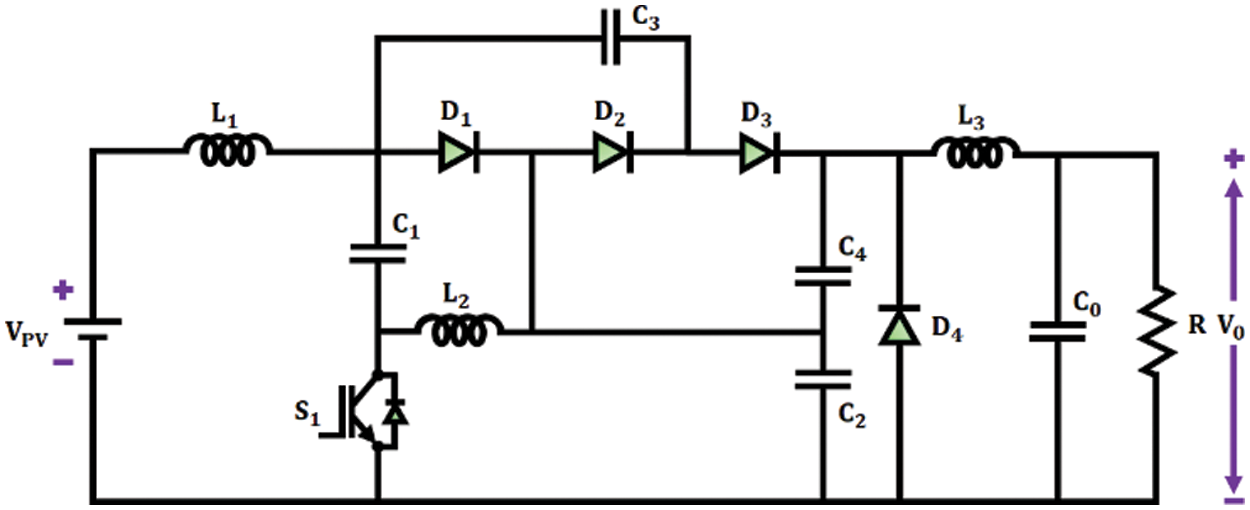
Figure 2: TZSBLC circuit diagram

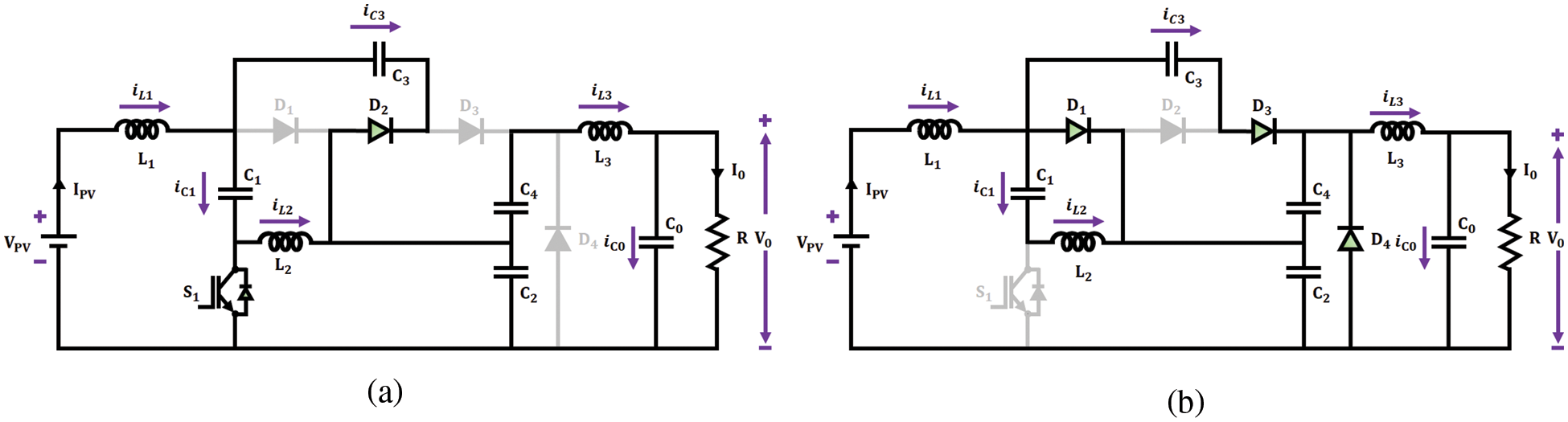
Figure 3: Circuit diagrams of (a) Mode 1 and (b) Mode 2 operation

3.1.1 Mode 1

The power switch S1 remains in ON state during this mode of operation. The diodes D1 , D3 and D4 stop conducting as these are reverse biased. The diode D2 is in forward biased condition. The inductor L1 begins to store energy via the source voltage VPV and capacitor C3 . As the stored energy from the inductor L2 gets discharged, the capacitor C1 begins to charge.

3.1.2 Mode 2

The power switch S1 remains in OFF state during this mode of operation. The diodes D1 , D3 and D4 are forward biased and begin to conduct. The diode D2 stops conducting as it is reverse biased whereas the load is energized by the input DC source through inductor L1 . The current and voltage waveforms of TZSBLC is illustrated in Fig. 4. The output voltage obtained from TZSBLC is,

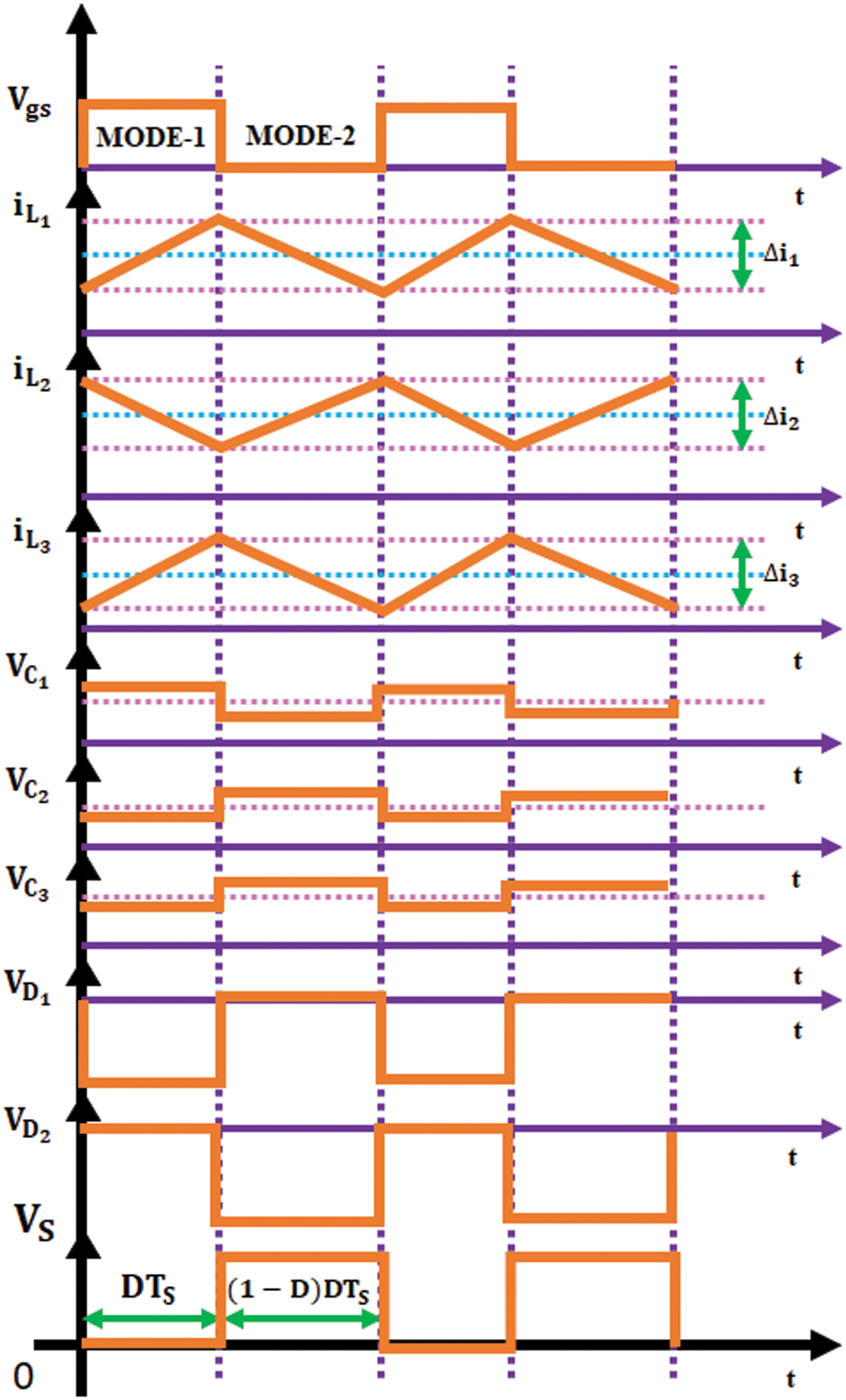
Figure 4: Current and voltage waveforms of TZSBLC

VO=(2−D1−2D)VPV (1)

The value of the inductors L1 , L2 , and L3 are given as,

L1=D(1−D)VPVΔiL1fs(1−2D) (2)

L2=D(1−D)VPVΔiL2fs(1−2D) (3)

L3=DVPVΔiL3fs (4)

The C1 , C2 , C3andC4 values are computed as,

C1=(1−D)IL2ΔVC1fs (5)

C2=(1−D)IL2ΔVC2fs (6)

C3=DIoΔVC3fs(1−D) (7)

C4=DIoΔVC4fs (8)

The value of the output capacitor is,

Co=DVPV8ΔVoL3fs2 (9)

The unstable DC output voltage obtained from the converter is optimized and made stable with the assistance of LGWO-PI controller.

3.2 Lion Grey Wolf Optimized PI Controller

LGWO algorithm is a hybrid optimization algorithm that is designed by combining both Lion Swarm Optimization (LSO) and GWO algorithm. The proposed LGWO approach incorporates the hunting behaviour of lions and encircling behaviour of grey wolves in order to estimate the values of KP and KI of the PI controller. The terms KP and KI stand for proportional and integral gain, respectively. Alpha, beta, delta and omega are the four groups of wolves in the GWO algorithm, whereas lion king, lioness and lion cubs are the three groups of lions in the LSO algorithm. The classification of these groups are done on the basis of the fitness value. The grey wolves in the alpha group and the lion king have the highest fitness value. The value of β lies between 0 and 1, which is a positive random number that represents the adult lions’ proportion factor. The β value is set below 0.5 for ensuring faster convergence speed of LGWO. The number of adult lions has a significant influence on the final optimization result. The total number of adult lions and lion cubs are inversely proportional since the number of lion cubs decreases when the number of adult lions gets increased. Fig. 5 depicts the flow chart for the LGWO algorithm.

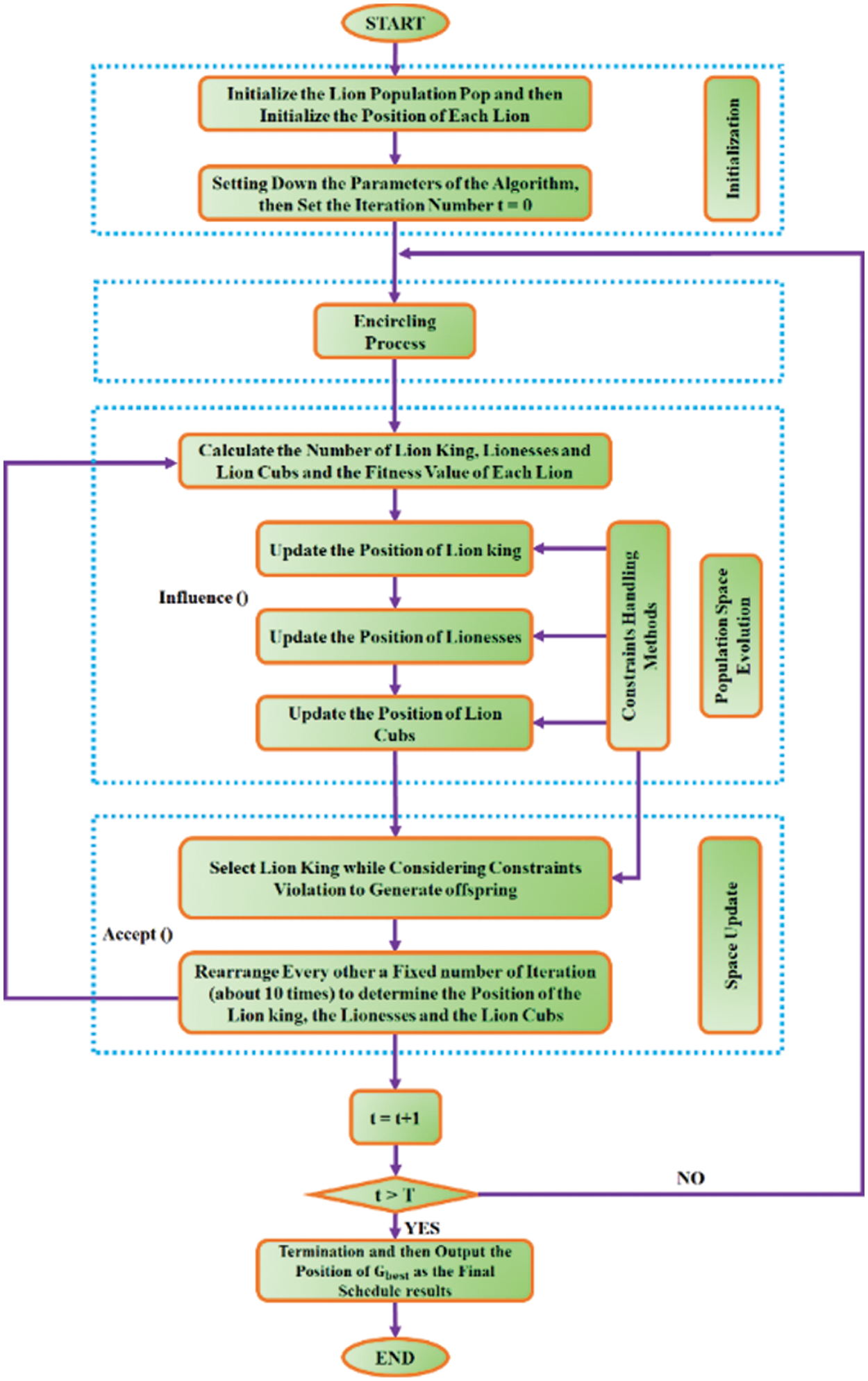
Figure 5: LGWO flowchart

The disturbance factor of lionesses αf , which is used to aid the lionesses in exploring the prey is given by the following expression as,

αf=Step1.exp(−30.tT)10 (10)

Here, T stands for maximum iterations and t represents the t -th current iteration. The value of the step in the activity range of lionesses is given as,

Step1=a1.(xmax¯−xmin¯) (11)

Here, xmax¯ and xmin¯ denote the maximum and minimum mean value for every single dimension, respectively. The term a1 , which is regarded as the lioness’ step control factor is a random number between 0 and 1.The disturbance factor of the lion cubs αc is given as,

αc=Step2.T−tT (12)

The value of the step in the activity range of lion cubs is specified as,

Step2=a2.(xmax¯−xmin¯) (13)

The term 2 , which is regarded as the lion cubs’ step control factor is a random number between 0 and 1.

3.2.1 Random Initialization

The position of each lion in this algorithm signifies a feasible solution to the problem that has to be evaluated. The nature of prey relies on the quality (fitness) of the related solution. In the case of a D-dimensional GOP, an initial population P with n solutions are generated in a random manner in search space ∏j=1D⁡[xmin,j,xmax,j] . The matrix equation given below represents the position of all lions.

x=[x1,1x1,2LLx1,Dx2,1x2,2LLx2,DMMMMMMMMMMxn,1xn,2LLxn,D] (14)

Here, the j-th dimension of i-th lion is specified by xi,j . The following equation is used to generate each D-dimensional vector xi=(xi,1,xi,2,Kxi,D) , which indicates the position of the i-th lion:

xi,j=xmin,j+rand(0,1).(xmax,j−xmin,j) (15)

The equation given below specifies the number of adult lions i.e., nLeader, which includes the lion king and lioness:

nLeader=⌈n⋅β⌉ (16)

n-nLeader gives the number of lion cubs and the value of nLeader ranges from 2 to n/2.

3.2.2 Encircling Process

The way the grey wolves encircles the prey is mathematically expressed as,

D→=|C→∗XP→(t)−X→(t)| (17)

X→(t+1)=|XP→(t)−A→D→| (18)

Here, XP→ and X→ represent the location of prey and wolf, t signifies the current iteration and D→ refers to the distance of the prey from the wolf.

The values of coefficient vectors A→andC→ are estimated by the equations given below,

A→=2a→r1→−a→ (19)

C→=2r2→ (20)

Here, a→ undergoes linear reduction from 2 to 0. Values of random vectors r1→ and r2→ lie in between 0 and 1.

3.2.3 Fitness Evaluation

When the user-defined fitness functions are substituted with the decision variable value i.e., solution vector, the fitness value of the position of every single lion is obtained as,

f=[f1([x1,1,x1,2,L,x1,D])f2([x2,1,x2,2,L,x2,D])MMfn([xn,1,xn,2,L,xn,D])] (21)

Little prey, normal prey and optimal prey are the quality of prey searched by the lion cubs, lioness and lion king, respectively. The f value indicates the quality of prey targeted by each lion.

3.2.4 Hunting Nature of Lions

Based on the experience of each lion and its neighbours, the location of each lion is adjusted. The lions follow different hunting methods to hunt the prey.

3.2.5 Lion King

The lion king starts moving towards the location with the least fitness value (best food) to make sure that it has a higher priority for prey. The following equation specifies the lion king’s new position,

xi(t+1)=gbest(t)⋅(1+γ⋅||pbesti(t)−gbest(t)||) (22)

Here, t denotes the current iteration value, gbest(t) and pbesti(t) represent the pride’s global best position and i-th lion’s historically best position in the present iteration and the term γ specifies a random number among 0 and 1.

3.2.6 Lionesses

The typical hunting behaviour of lioness is to locate the prey, encircle it and then attack the prey. The lioness hunts its prey in cooperation with another lioness. The lionesses’ new position is expressed as,

xi(t+1)=pbesti(t)+pbestc(t)2⋅(1+αf⋅γ) (23)

At current iteration, pbestc(t) specifies the best position of the cooperated lioness.

3.2.7 Lion Cubs

There are three possibilities during the vibrant hunting of lion cubs and the following equation specifies the lion cubs’ new position as,

xi(t+1)={gbest(t)+pbesti(t)2⋅(1+αc⋅γ),q≤13pbestm(t)+pbesti(t)2⋅(1+αc⋅γ),13<q<23gbest¯(t)+pbesti(t)2⋅(1+αc⋅γ),23≤q≤1 (24)

Here, q specifies a random number among 0 and 1. The position, in which ith lion cub is pushed out from the purview of hunting is specified as gbest¯(t) , which it is calculated by,

gbest¯(t)=xmax¯+xmin¯−gbest(t) (25)

The LGWO parameters are clearly listed out in Tab. 1.

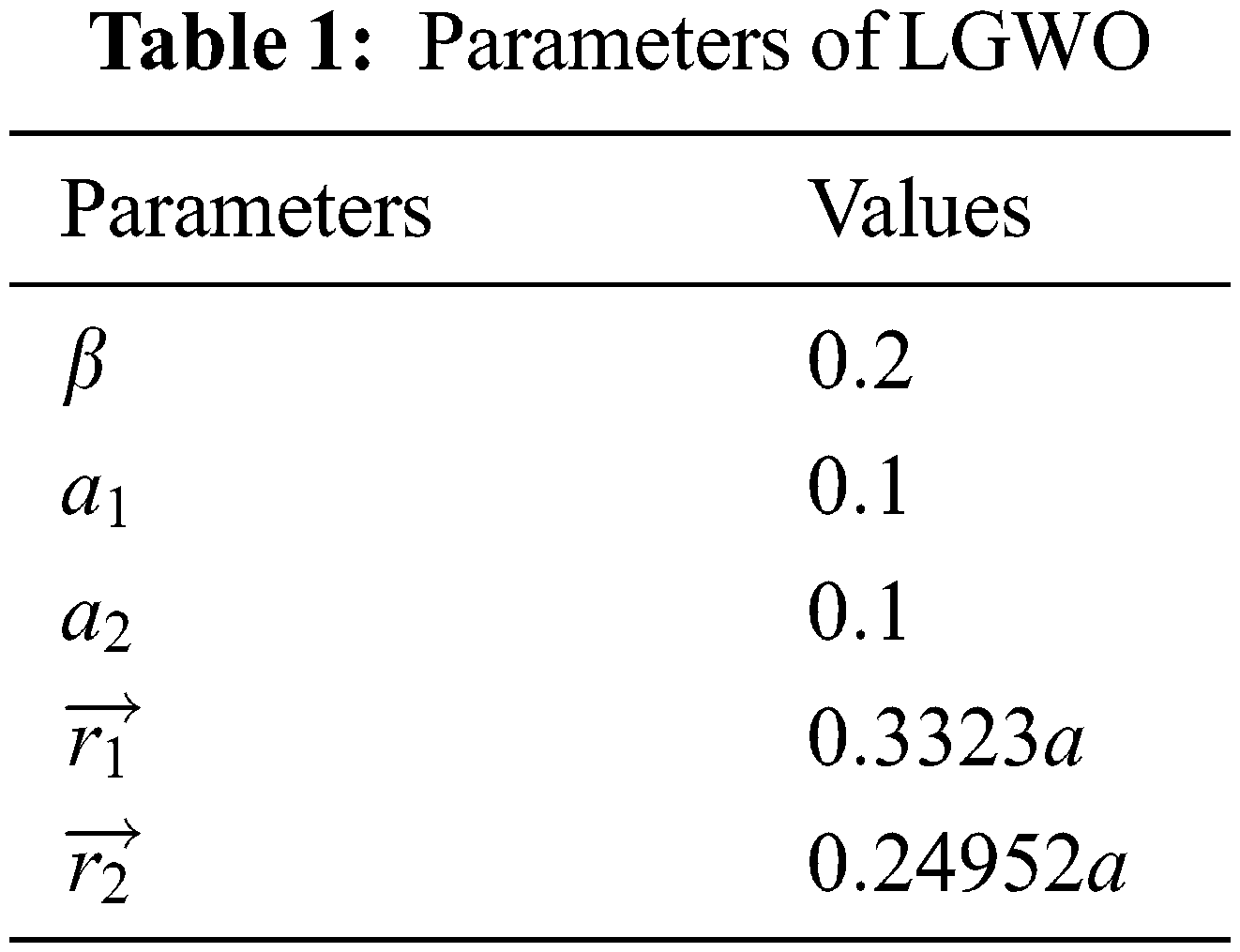
The pseudo code of this LGWO is evidently explained in the subsequent section in an efficient manner.

3.3 Mathematical Model of BLDC Motor

The stable and distortion free DC output voltage obtained from TZSBLC with the assistance of LGWO-PI controller is given to the 3φ VSI. The circuit and model of 3 φ BLDC motor are represented in Fig. 6.

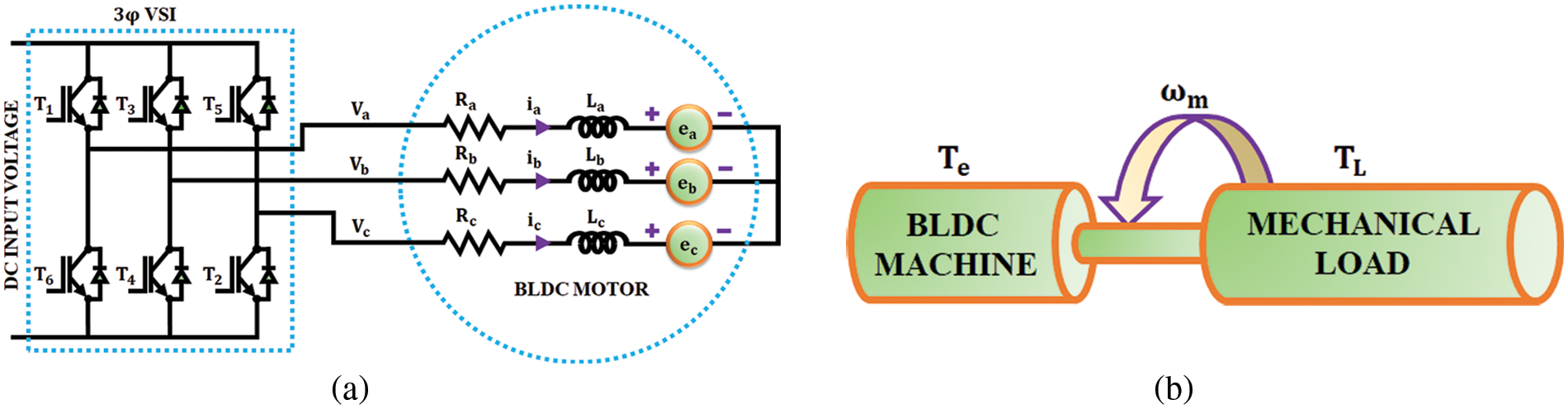
Figure 6: (a) Equivalent circuit (b) mechanical model

The 3φ star connected BLDC motor is represented using the subsequent equations,

vab=R(ia−ib)+Lddt(ia−ib)+ea−eb (26)

vbc=R(ib−ic)+Lddt(ib−ic)+eb−ec (27)

vca=R(ic−ia)+Lddt(ic−ia)+ec−ea (28)

Te=kfωm+Jdωmdt+TL (29)

The phase back emf, phase currents and phase-to-phase voltages are denoted by e, i and v respectively. The load torque and electrical torque are represented by t TL and Te . R and L are per phase values that represent the resistance and inductance respectively. The rotor inertia is J, the rotor speed is ωm and the friction constant is kf . The back emf equations for the three phases are specified as,

ea=ke2ωmF(θe) (30)

eb=ke2ωmF(θe−2π3) (31)

ec=ke2ωmF(θe−4π3) (32)

The electrical torque is given as,

Te=kt2[F(θe)ia+F(θe−2π3)ib+F(θe−4π3)ic] (33)

Here, kt specifies torque constant and ke specifies back emf constant. The electrical angle is given as,

θe=P2θm (34)

Here, θm→ mechanical angle and P2→ no. of pole pairs

The trapezoidal waveform of the back emf is given by the function F(θe) as specified below,

F(θe)={1,0≤θe<2π31−6π(θe−2π3)−1−1+6π(θe−5π3)2π3≤θe<ππ≤θe<5π35π3≤θe<2π (35)

By using the current Eq. (36), voltages specified in Eqs. (37) and (38) are obtained,

ia+ib+ic=0 (36)

vab=R(ia−ib)+Lddt(ia−ib)+ea−eb (37)

vbc=R(ia+2ib)+Lddt(ia+2ib)+eb−ec (38)

The entire model becomes,

(ia′ib′ωm′θm′)=(−RL0000−RL0000−kfJ00010)(iaibωmθm)+(23L13L0−13L13L0001J000)(vab−eabvbc−ebcTe−TL) (39)

(iaibicωmθm)=(10000100−1−10000100001)(iaibωmθm) (40)

To simplify and achieve better computational efficiency, the machine model is generally converted to a rotating reference frame.

4  Results and Discussions

The performance of the proposed PV based BLDC motor with TZSBLC and LGWO-PI controller is examined using MATLAB simulation and the outcomes are evidently discussed in this section. The solar panel, TZSBLC and BLDC motor parameters are specified in Tab. 2 whereas the gain values of PI controller are specified in Tab. 3.

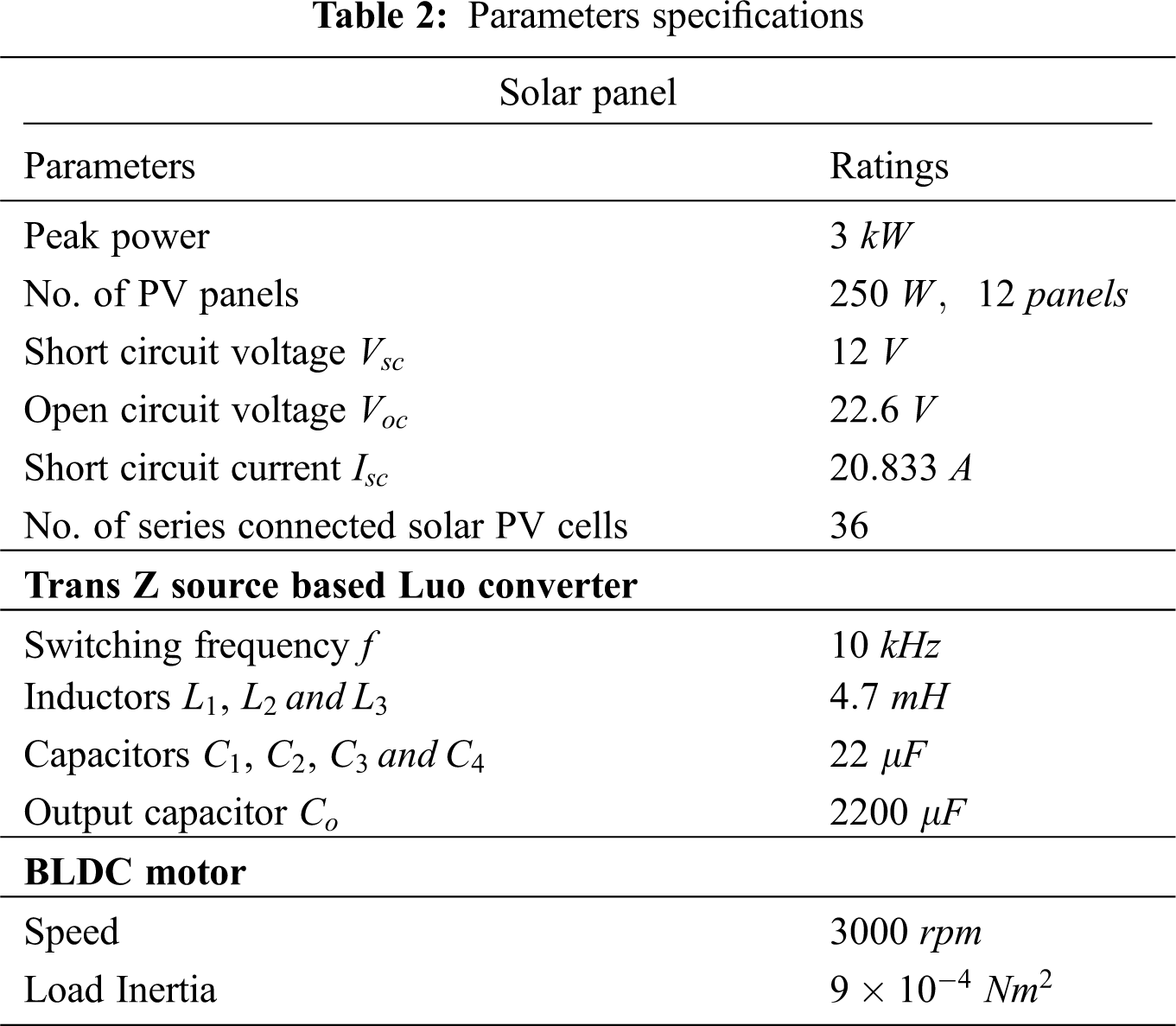
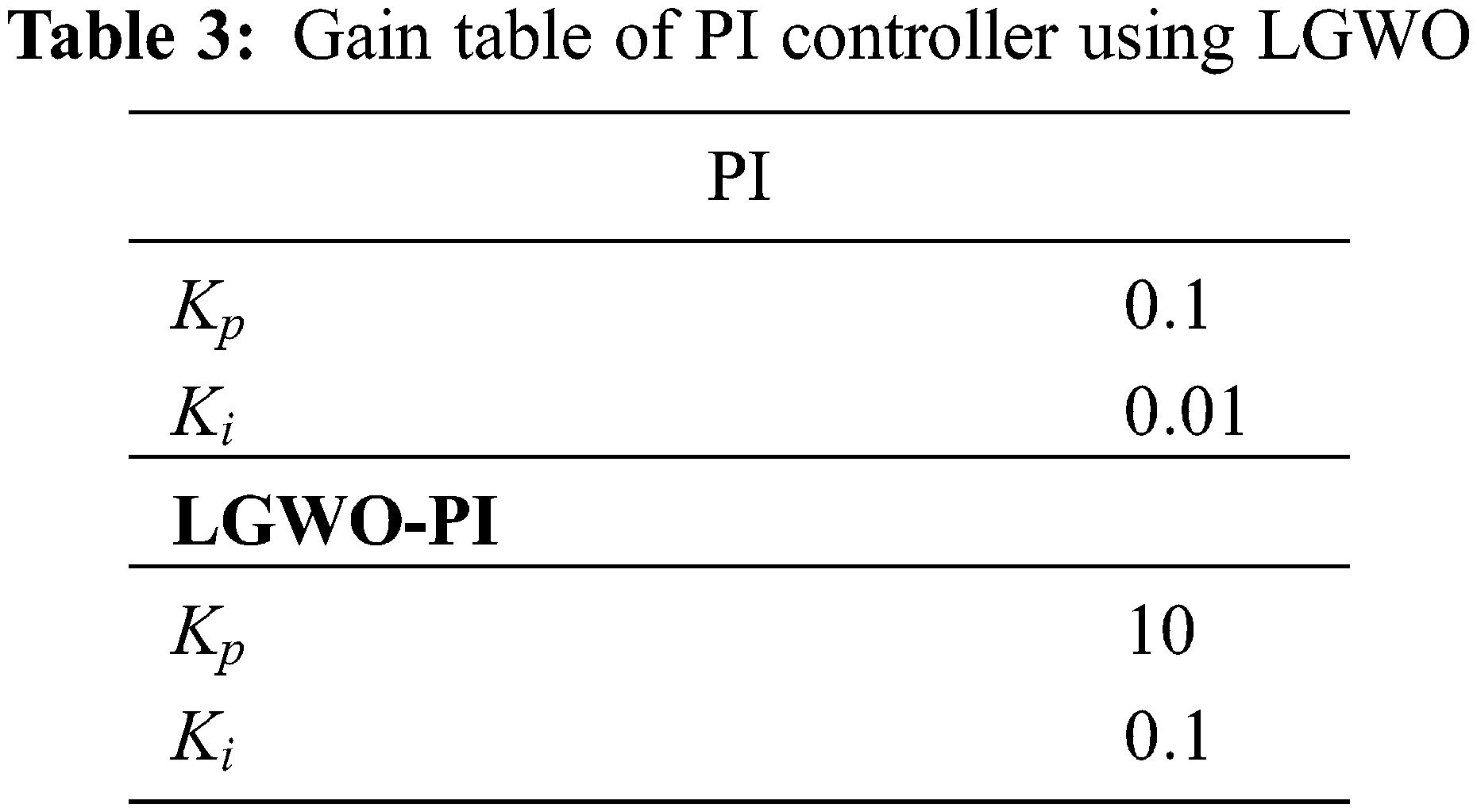
Fig. 7 illustrates the solar PV panel temperature, voltage, current and power waveforms. For analyzing the effectiveness of the introduced methodology in overcoming the non-linearity of PV system, the operating condition is altered in the form of temperature variation. The temperature is constantly maintained at 25∘C up to 0.25s and after that the temperature is increased to 30∘C . The impact of variation in temperature is seen in waveforms. The PV voltage, which is initially at a magnitude of 160 V rises to a magnitude of 165.6 V with respect to the change in temperature. Similarly, the PV current varies from 19 A to 26 A at 0.25 s, while the PV power alters from 3000 to 4300 W at 0.25 s.

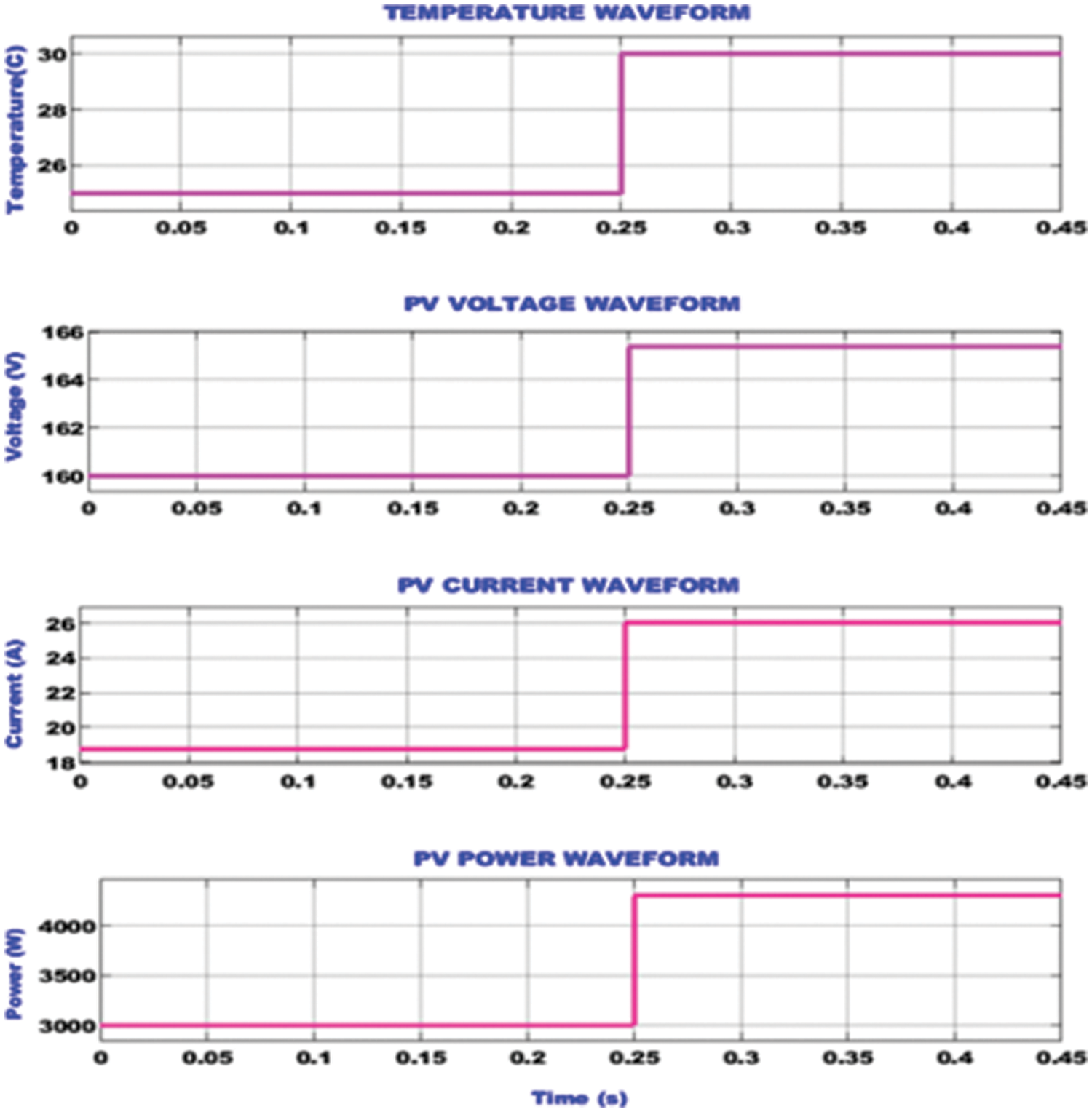
Figure 7: Waveforms of solar PV panel input and output variables

The simulation waveforms used to ascertain the performance of the proposed TZSBLC, which comprises of its input voltage, output voltage using PI controller and output voltage using optimized PI is illustrated in Fig. 8. The PV output is provided as input to the TZSBLC. Due to influence of change in temperature, the PV voltage increases from 160 to 165.6 V at 0.25 s. The PI controller is not effective in enhancing the operation of the TZSBLC since the converter output voltage is not constant. However, the proposed hybrid LGWO based PI controller displays remarkable performance in stabilizing the TZSBLC output by providing a constant voltage of 340 V from 0.05 s. The proposed hybrid optimization technique also significantly overcomes the impact of change in temperature.

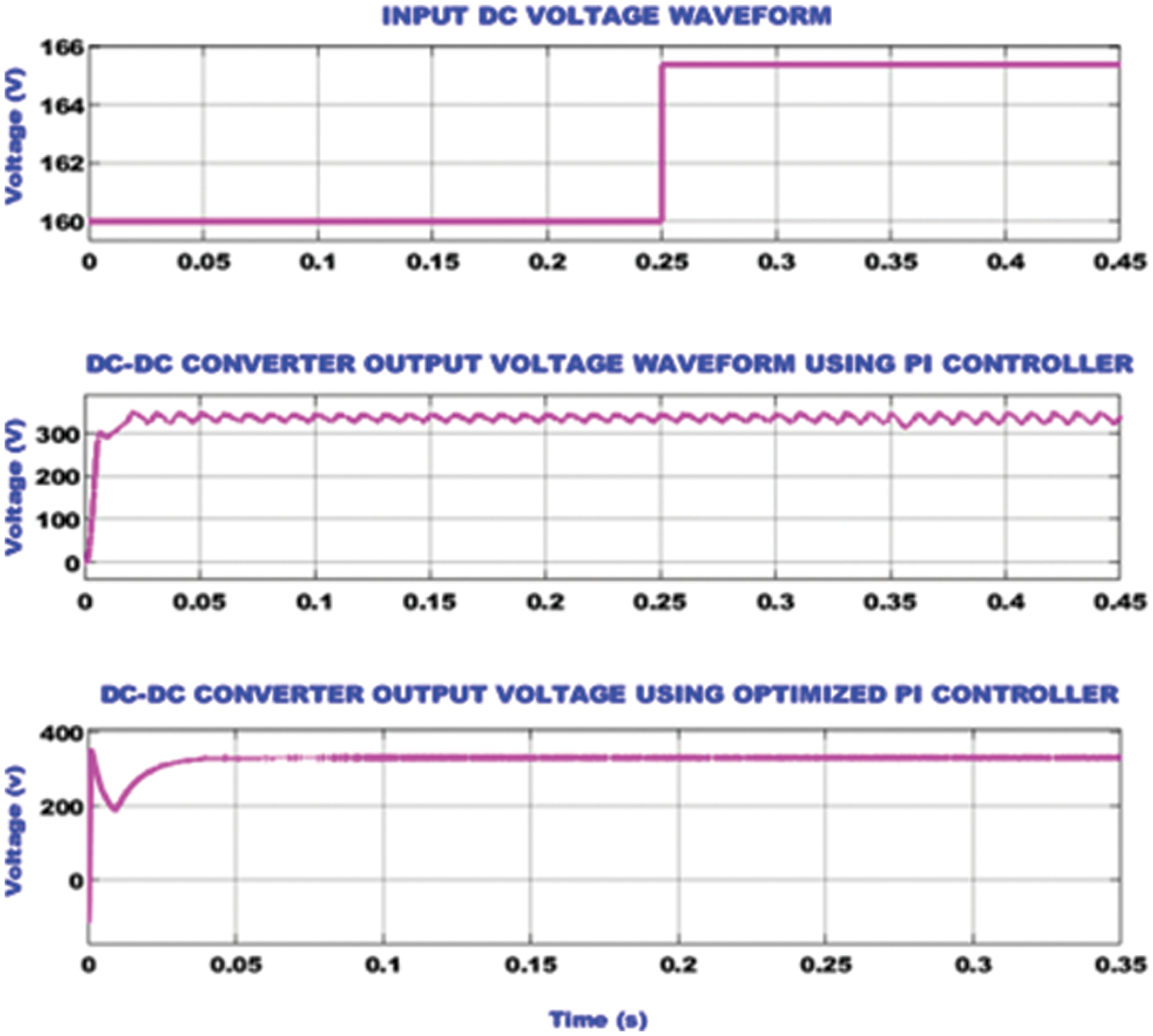
Figure 8: TZSBLC waveforms representing the input voltage, output voltage using PI controller and output voltage using optimized PI controller

The grid side waveforms for the developed EV charging system is portrayed in Fig. 9. The constant AC voltage and current of magnitude 230 V and current 10 A, respectively are maintained in the grid. After the disturbances at initial stage, the value of real power increases to reach a steady value of 1000 W from 0.1 s. The reactive power magnitude reaches a peak value of 2900 VAR at 0.025 s and then it becomes a near zero value at 0.1 s.

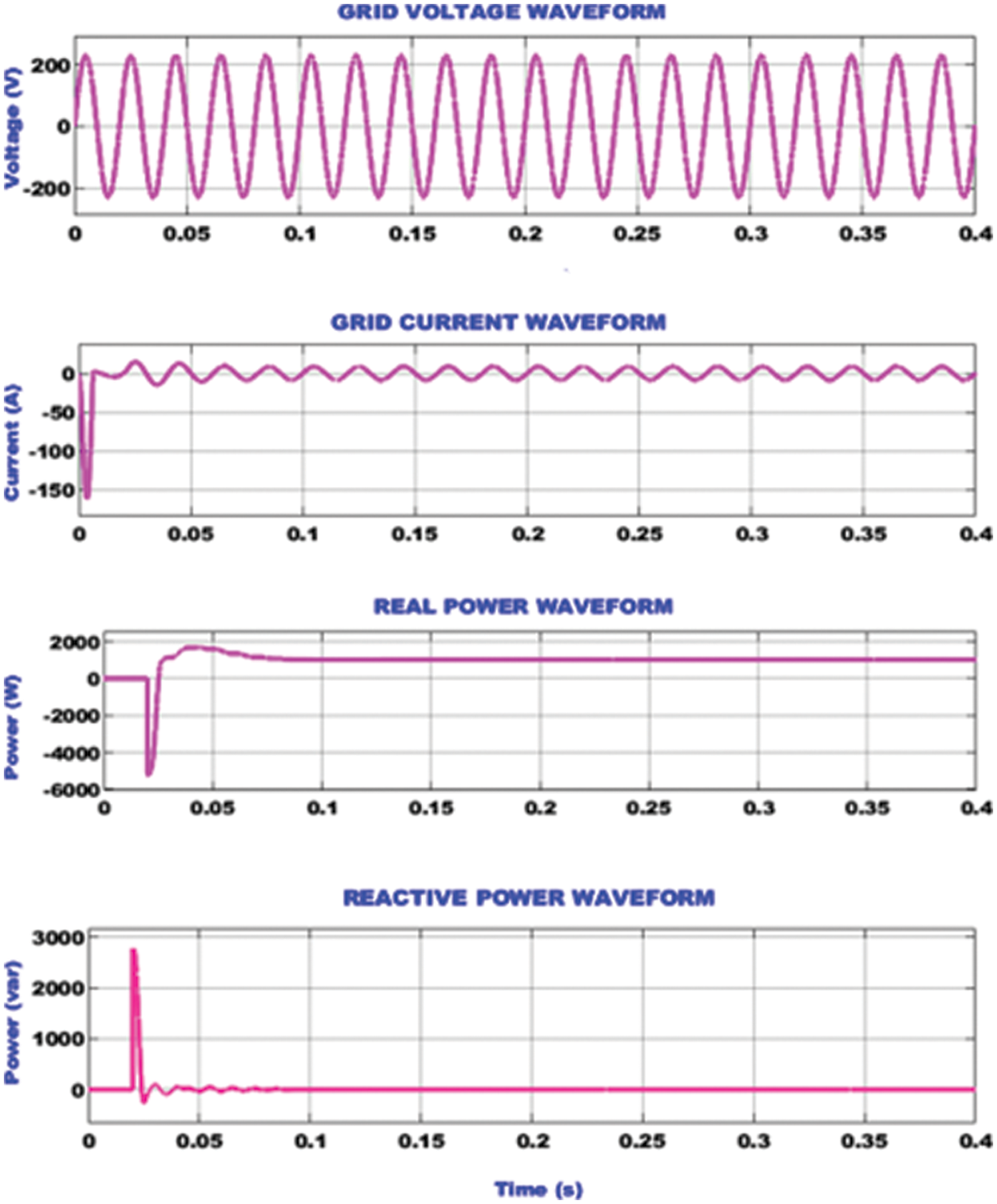
Figure 9: Grid side waveforms representing the voltage, current, real power and reactive power

The waveforms representing the current, back emf, speed and torque of the BLDC motor are depicted in Fig. 10. The above waveforms are used to analyse the operation of BLDC motor under variable speed conditions. The speed of the motor is initially around 1500 rpm till 0.35 s and then it is increased to 2000 rpm at 0.36 s. The impact of the speed variation is seen in the current, back emf and torque waveforms of the motor. At 0.36 s, the motor current raises from 5 to 15 A and then recovers to provide a steady output of 5 A again. Similarly, the motor torque also experiences an abrupt increase at 0.36 s from 2 to 11 Nm and again recovers quickly to 2 Nm. The back emf of the motor increases with the increase in speed at 0.36 s from 60 to 80 V.

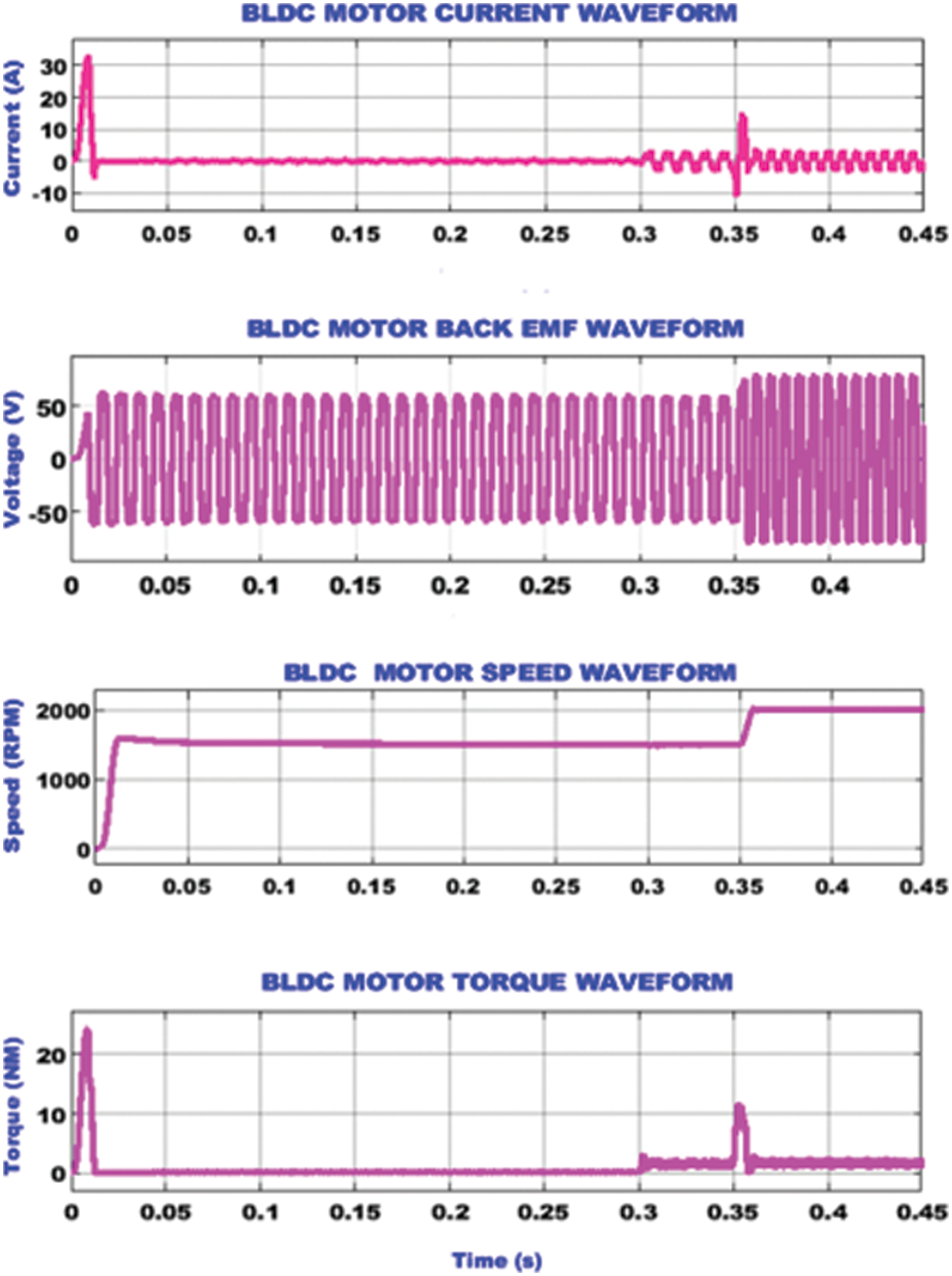
Figure 10: BLDC motor waveforms under variable speed

The BLDC motor parameter waveforms under constant speed condition is seen in Fig. 11. The speed of the BLDC motor is not varied and maintained to be constant at a speed of 1500 rpm from 0.02 s. The BLDC motor current, which is zero in the beginning gets raised to a magnitude of 5 A from 0.3 s. Since the motor is running with a constant speed, the back emf is also maintained at a constant value of 60 V. Similar to the motor current, the torque also becomes 2 Nm from 0.3 s.

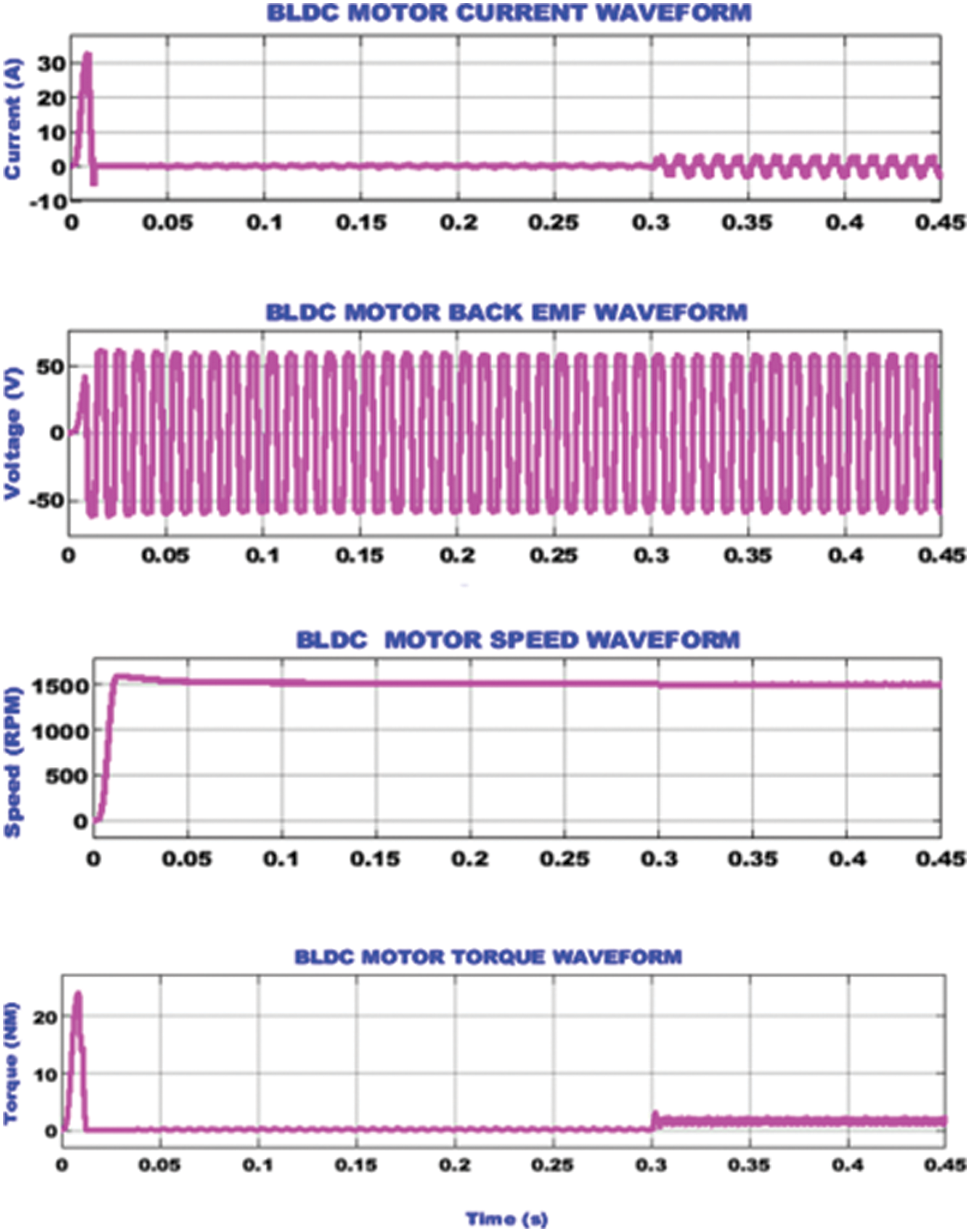
Figure 11: BLDC motor waveforms under constant speed

4.1 Hardware Analysis

The hardware analysis of the proposed grid tied solar EV charging system developed with the assistance of TZSBLC is implemented with the assistance of FPGA Spartan 6 E controller and the obtained outcomes are analyzed in detail subsequently. The hardware prototype is clearly portrayed in Fig. 12 in an optimal manner.

Figure 12: Hardware prototype

The hardware results representing the voltage and current output derived from the PV is given in Fig. 13. The PV output gets improved with the raise of temperature. The output current derived from the PV remains stable with slight fluctuations.

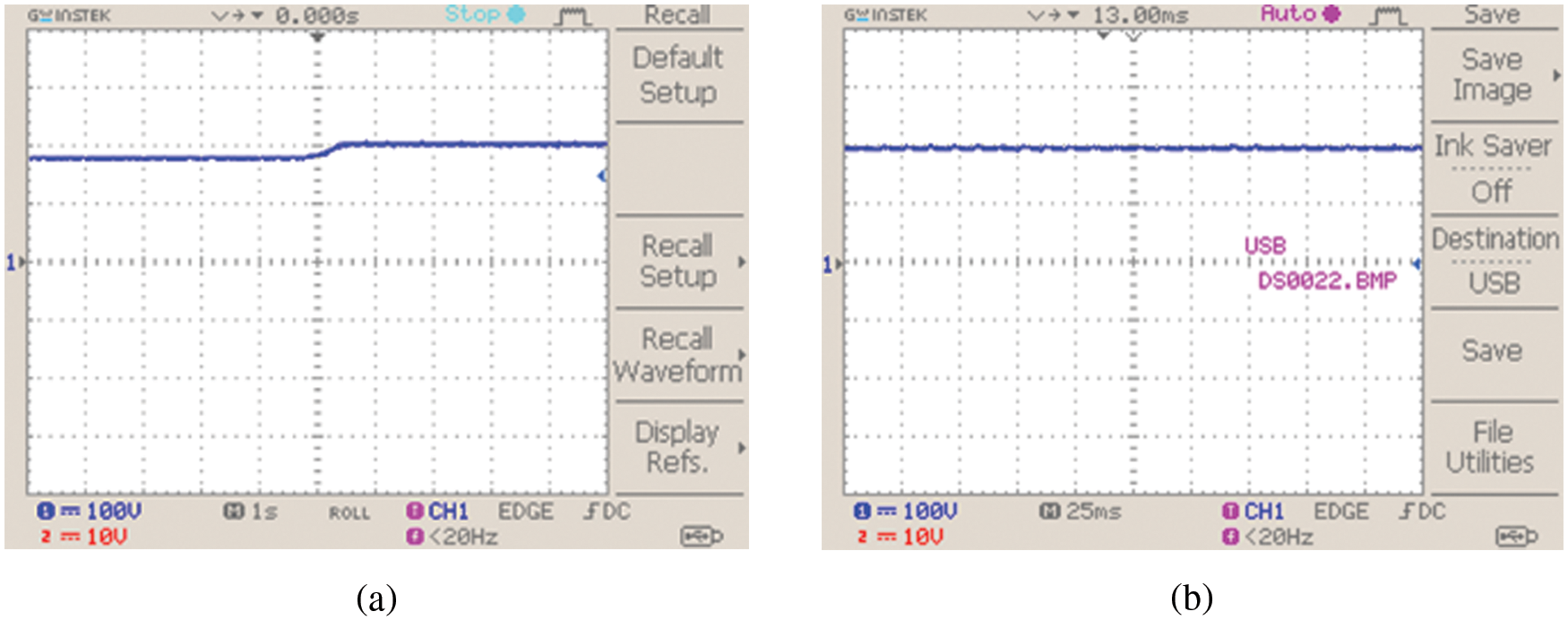
Figure 13: PV system (a) voltage and (b) current waveforms

The waveforms representing the output voltage of the TZSBLC with optimization and without optimization is given in Fig. 14. Without the aid of optimization, the converter output is affected by peak overshoot conditions as indicated from the figure but the problem of peak overshoot condition is eliminated and a stable output of 330 V is obtained with the aid of suitable optimization technique.

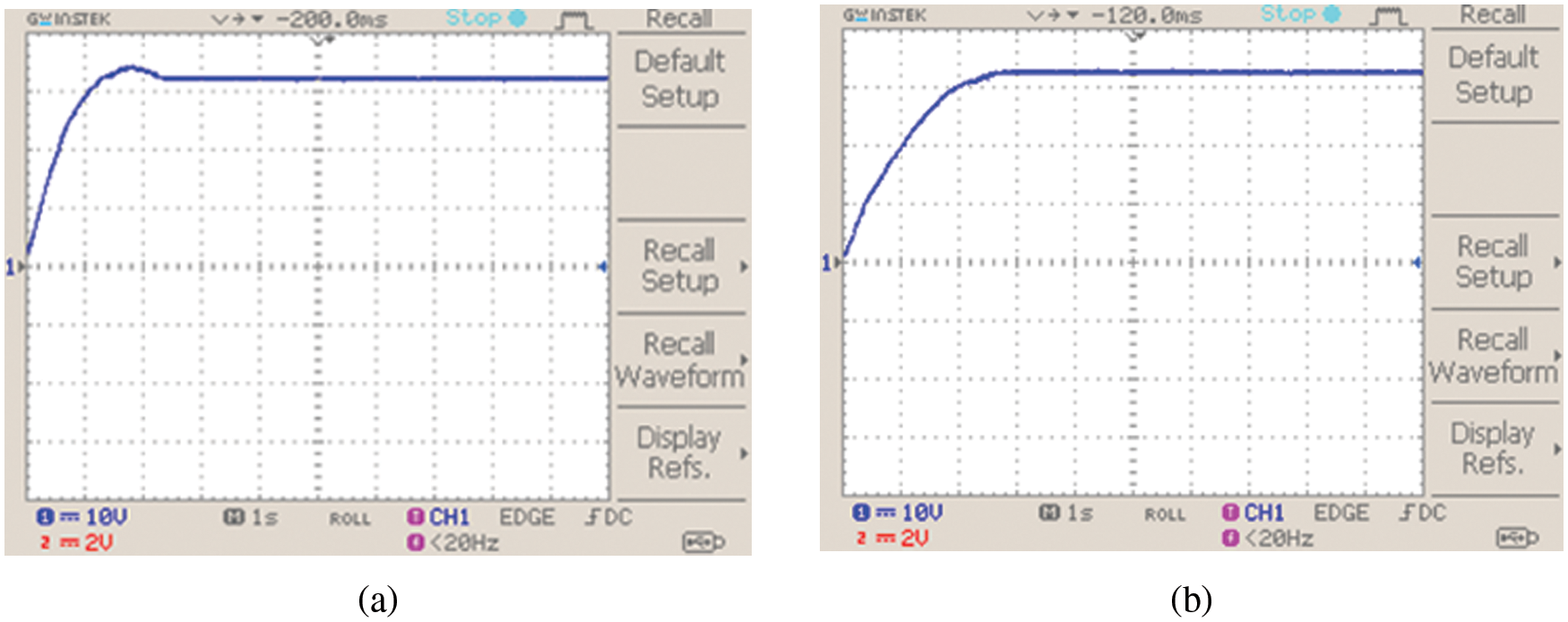
Figure 14: TZSBLC output voltage (a) without optimization and (b) with optimization

The BLDC motor’s reference speed is set to 1500 rpm. After the application of the proposed hybrid optimized controller, the speed remains stable and it is effectively regulated as illustrated in Fig. 15b. The reference and actual speeds are respectively highlighted in blue and red colours. The Fig. 15a represents the BLDC motor’s speed response characteristics without the application of optimization controller.

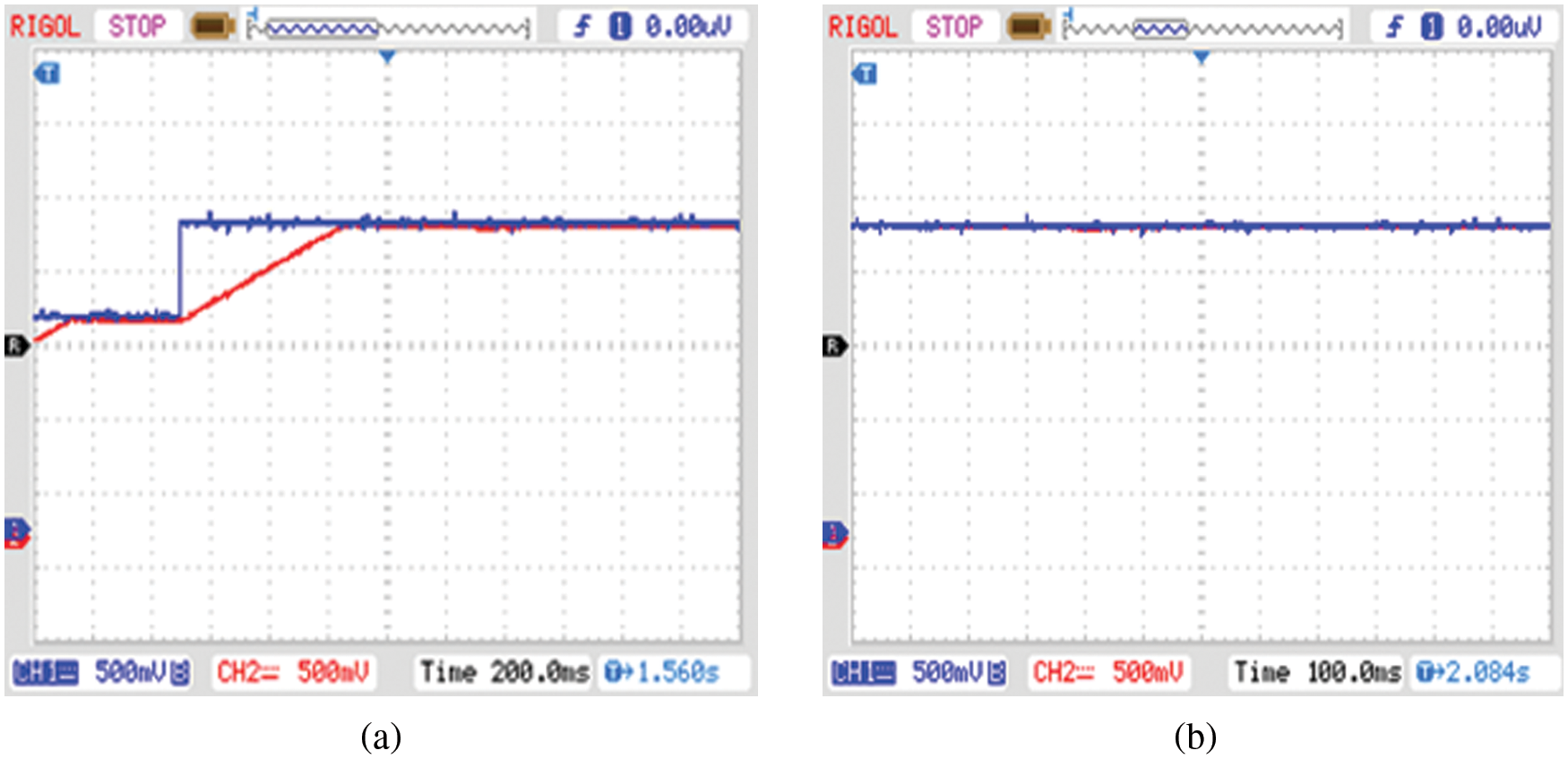
Figure 15: Speed waveform (at 1500 rpm) (a) without optimization controller and (b) with optimization controller

The BLDC motor’s speed and torque are effectively regulated and maintained stable without peak over shoot issues by using the proposed closed loop speed control technique as specified in the Fig. 16.

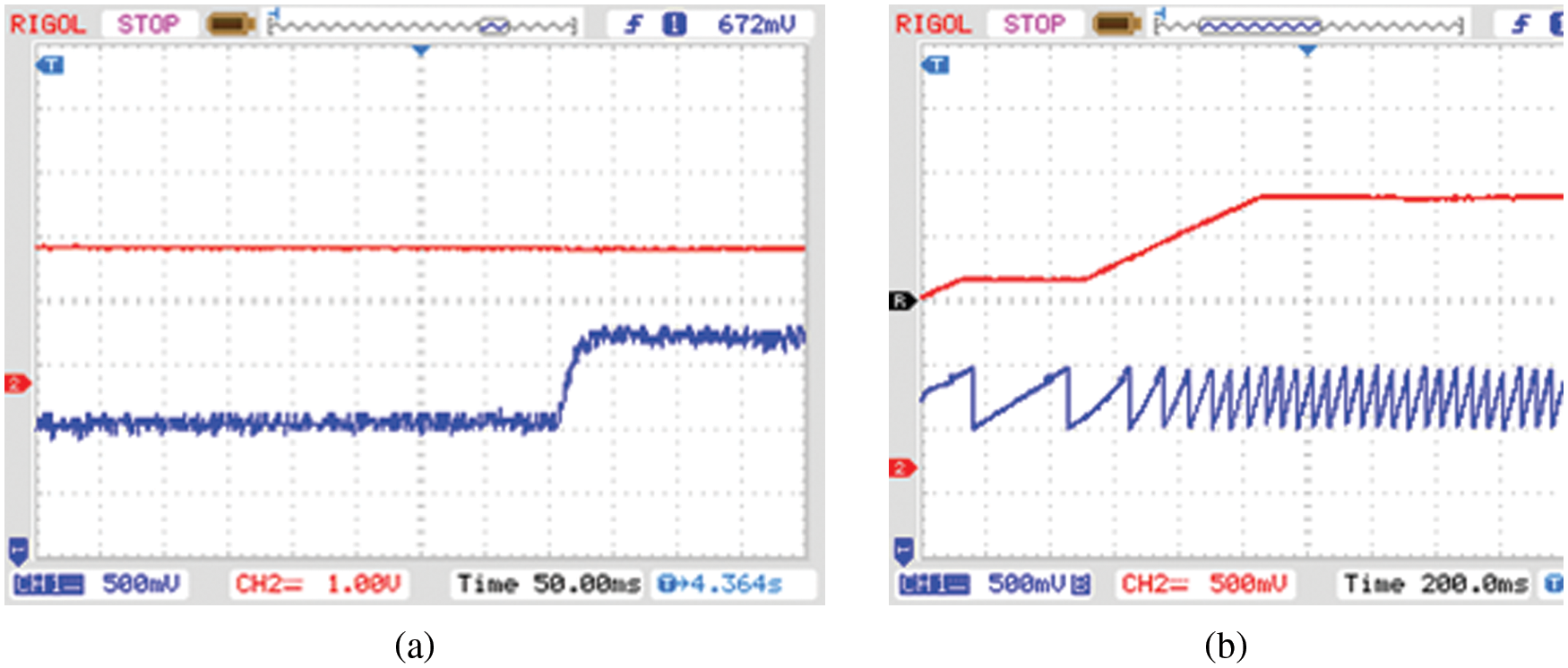
Figure 16: (a) Speed and (b) torque waveform

By using the PI controller, effective grid voltage synchronization is achieved so that a constant 230 V AC supply is fed to the grid from the inverter as represented in Fig. 17.

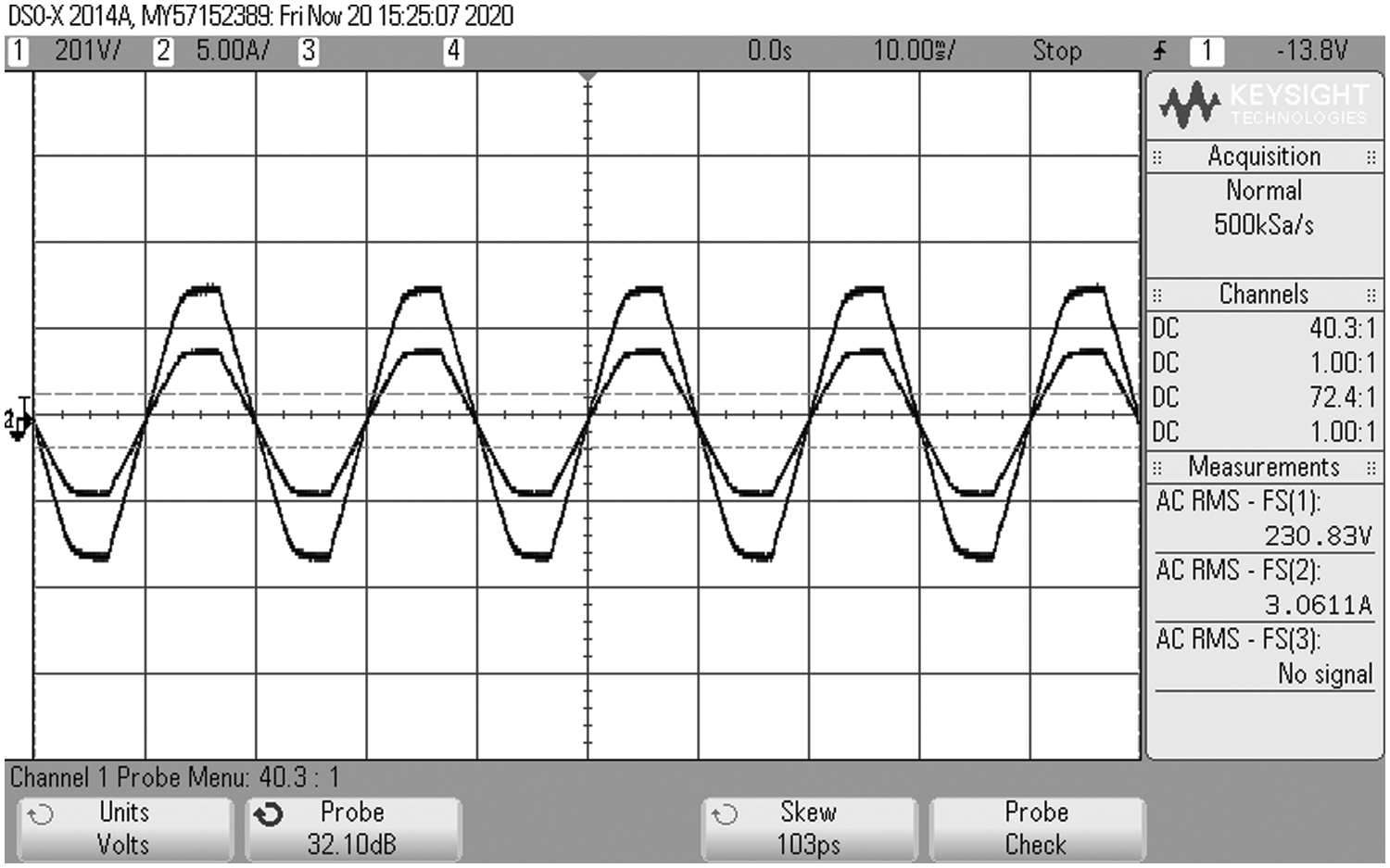
Figure 17: Grid voltage and current waveforms

The proposed trans Z-Source based Luo converter voltage gain is compared with other existing converetes such as Boost, Cuk, SEPIC and Luo as represented in Fig. 18a, which illustrates that the proposed converter owns optimum voltage gain than the other converters as it delivers high gain ratio of 1:16 . Hence, it is proved that the trans Z-Source based Luo converter is evidently capable enough in enhancing the input voltage in a wider range.

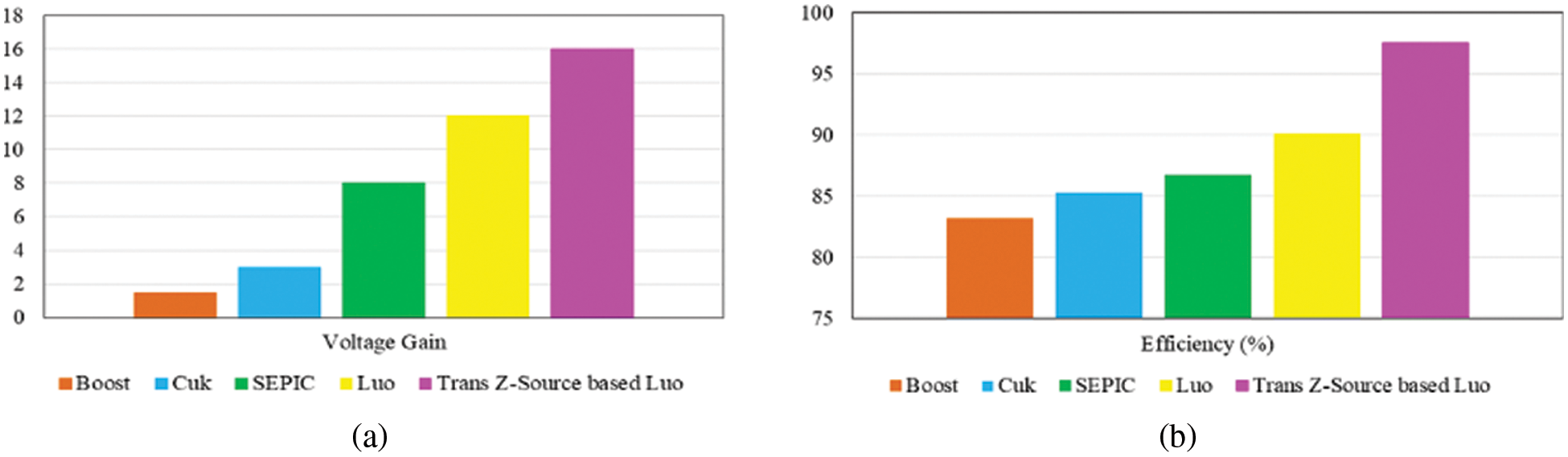
Figure 18: Comparative analysis of (a) voltage gain (b) efficiency

The efficiency is the significant parameter in analysing the performance of the converter and so the efficiency of the Trans Z-Source based Luo converter is analogised with other conventional converters that are specified in the aforementioned section. As represented in Fig. 18b, the outcome of this comparative analysis validates that the introduced converter provides maximum efficiency of 97.6% that is extremely optimal than the other converters that already exist.

The introduced controller takes less settling time of 0.05s , which is extremely lesser than the other existing controllers and this settling time comparison is remarkably highlighted through the graphical illustration in Fig. 19a for maximizing the clarity of obtained outcomes.

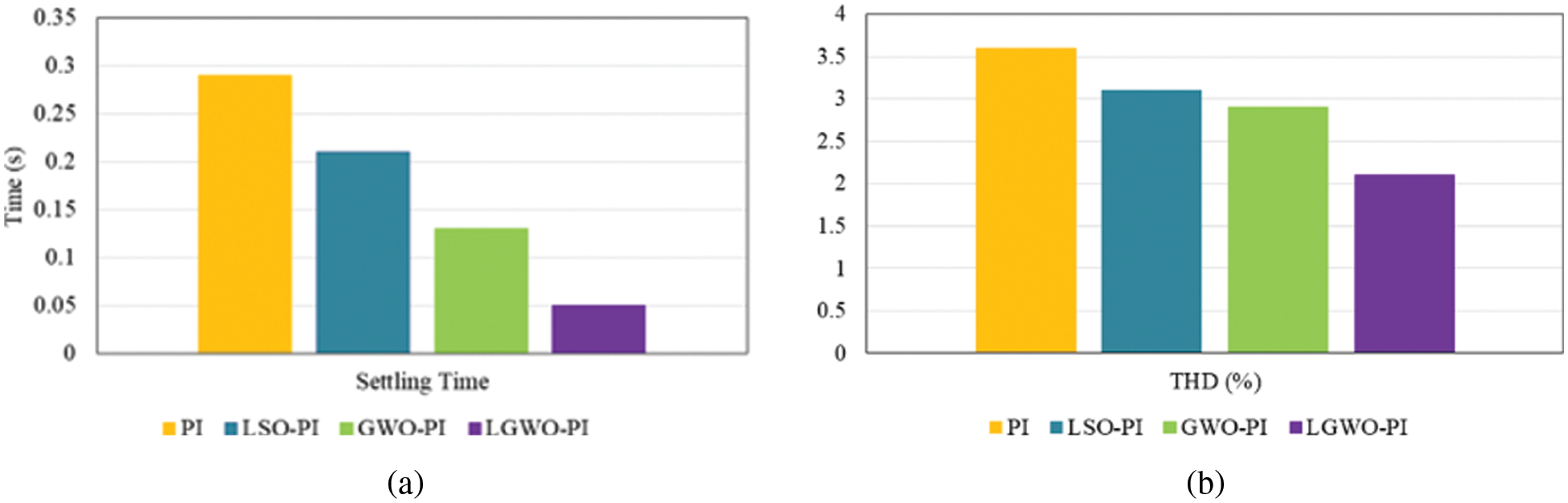
Figure 19: Comparison of (a) settling time (b) THD

The attained THD using the introduced LGWO-PI controller is analogized with other controllers like PI, LSO-PI and GWO-PI controllers as highlighted through the graphical representation in Fig. 19b. It validates that the proposed controller involves in minimizing the harmonic distortions in a wider range as it attain less THD of 2.1%, which is comparatively lower than the other controllers.

5  Conclusion

A novel robust hybrid LGWO-PI controller is designed with the objective of bringing significant enhancement to the operation of PV system, which is the major source of power supply in the proposed EV charging station. The development of an optimal control methodology for grid tied solar EV charging station aims towards boosting the adoption of EVs in addition to minimizing the over dependency on grid. The control approach proposed in this work for stabilizing and improving the output from the PV system includes a high gain TZSBLC and hybrid LGWO-PI controller. The selected BLDC motor drive for EVs offers excellent speed regulation, high efficiency in addition to less maintenance requirement. The reliability of the charging station is ensured with the inclusion of 1φ grid that guarantees uninterrupted power supply. The significance of the designed control methodology for strengthening the working of the charging station is analysed on the basis of experimental validation and MATLAB simulation. The novel hybrid LGWO-PI controller exhibits exceptional performance in enhancing the working of the TZSBLC, since the converter operates with an impressive efficiency of 97.6%.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Zahedmanesh, K. M. Muttaqi and D. Sutanto, “A cooperative energy management in a virtual energy hub of an electric transportation system powered by PV generation and energy storage,” IEEE Transactions on Transportation Electrification, vol. 7, no. 3, pp. 1123–1133, 2021. [Google Scholar]

 2.  A. Mohammad, R. Zamora and T. T. Lie, “Transactive energy management of PV-based EV integrated parking lots,” IEEE Systems Journal, vol. 15, no. 4, pp. 5674–5682, 2021. [Google Scholar]

 3.  A. Verma and B. Singh, “Multimode operation of solar PV array, grid, battery and diesel generator set based EV charging station,” IEEE Transactions on Industry Applications, vol. 56, no. 5, pp. 5330–5339, 2020. [Google Scholar]

 4.  Q. Chen, F. Wang, B. M. Hodge, J. Zhang, Z. Li et al., “Dynamic price vector formation model-based automatic demand response strategy for PV-assisted EV charging stations,” IEEE Transactions on Smart Grid, vol. 8, no. 6, pp. 2903–2915, 2017. [Google Scholar]

 5.  J. Liu, J. Wu, J. Qiu and J. Zeng, “Switched Z-source/quasi-Z-source DC-DC converters with reduced passive components for photovoltaic systems,” IEEE Access, vol. 7, pp. 40893–40903, 2019. [Google Scholar]

 6.  K. Kumar, N. Ramesh Babu and K. R. Prabhu, “Design and analysis of RBFN-based single MPPT controller for hybrid solar and wind energy system,” IEEE Access, vol. 5, pp. 15308–15317, 2017. [Google Scholar]

 7.  N. Rana and S. Banerjee, “Development of an improved input-parallel output-series buck-boost converter and its closed-loop control,” IEEE Transactions on Industrial Electronics, vol. 67, no. 8, pp. 6428–6438, 2020. [Google Scholar]

 8.  J. C. D. S. de Morais, J. L. D. S. de Morais and R. Gules, “Photovoltaic AC module based on a cuk converter with a switched-inductor structure,” IEEE Transactions on Industrial Electronics, vol. 66, no. 5, pp. 3881–3890, 2019. [Google Scholar]

 9.  K. S. Tey, S. Mekhilef, M. Seyedmahmoudian, B. Horan, A. T. Oo et al., “Improved differential evolution-based MPPT algorithm using SEPIC for PV systems under partial shading conditions and load variation,” IEEE Transactions on Industrial Informatics, vol. 14, no. 10, pp. 4322–4333, 2018. [Google Scholar]

10. R. Kumar and B. Singh, “BLDC Motor-driven solar PV array-fed water pumping system employing zeta converter,” IEEE Transactions on Industry Applications, vol. 52, no. 3, pp. 2315–2322, 2016. [Google Scholar]

11. M. Forouzesh, Y. Shen, K. Yari, Y. P. Siwakoti and F. Blaabjerg, “High-efficiency high step-up DC–DC converter with dual coupled inductors for grid-connected photovoltaic systems,” IEEE Transactions on Power Electronics, vol. 33, no. 7, pp. 5967–5982, 2018. [Google Scholar]

12. M. Das, M. Pal and V. Agarwal, “Novel high gain, high efficiency DC–DC converter suitable for solar PV module integration with three-phase grid tied inverters,” IEEE Journal of Photovoltaics, vol. 9, no. 2, pp. 528–537, 2019. [Google Scholar]

13. K. Nathan, S. Ghosh, Y. Siwakoti and T. Long, “A new DC–DC converter for photovoltaic systems: Coupled-inductors combined CUK-SEPIC converter,” IEEE Transactions on Energy Conversion, vol. 34, no. 1, pp. 191–201, 2019. [Google Scholar]

14. B. Singh and R. Kushwaha, “Power factor preregulation in interleaved luo converter-fed electric vehicle battery charger,” IEEE Transactions on Industry Applications, vol. 57, no. 3, pp. 2870–2882, 2021. [Google Scholar]

15. S. N. Singh, “Selection of non–isolated DC-DC converters for solar photovoltaic system,” Renewable and Sustainable Energy Reviews, vol. 76, pp. 1230–1247, 2017. [Google Scholar]

16. M. Mohammadi, J. S. Moghani and J. Milimonfared, “A novel dual switching frequency modulation for Z-source and quasi-Z-source inverters,” IEEE Transactions on Industrial Electronics, vol. 65, no. 6, pp. 5167–5176, 2018. [Google Scholar]

17. X. Ding, Y. Liu, D. Zhao and W. Wu, “Generalized cockcroft-walton multiplier voltage Z-source inverters,” IEEE Transactions on Power Electronics, vol. 35, no. 7, pp. 7175–7190, 2020. [Google Scholar]

18. T. Sreekanth, N. Lakshminarasamma and M. K. Mishra, “A Single-stage grid-connected high gain buck–boost inverter with maximum power point tracking,” IEEE Transactions on Energy Conversion, vol. 32, no. 1, pp. 330–339, 2017. [Google Scholar]

19. M. S. Ali, L. Wang, H. Alquhayz, O. U. Rehman and G. Chen, “Performance improvement of three-phase boost power factor correction rectifier through combined parameters optimization of proportional-integral and repetitive controller,” IEEE Access, vol. 9, pp. 58893–58909, 2021. [Google Scholar]

20. F. A. Alturki, H. O. Omotoso, A. A. Al-Shamma’a, H. M. H. Farh and K. Alsharabi, “Novel manta rays foraging optimization algorithm based optimal control for grid-connected PV energy system,” IEEE Access, vol. 8, pp. 187276–187290, 2020. [Google Scholar]

21. K. Y. Ahmed, N. Z. Bin Yahaya, V. S. Asirvadam, N. Saad, R. Kannan et al., “Development of power electronic distribution transformer based on adaptive PI controller,” IEEE Access, vol. 6, pp. 44970–44980, 2018. [Google Scholar]

22. M. H. Qais, H. M. Hasanien and S. Alghuwainem, “A grey wolf optimizer for optimum parameters of multiple PI controllers of a grid-connected PMSG driven by variable speed wind turbine,” IEEE Access, vol. 6, pp. 44120–44128, 2018. [Google Scholar]

23. M. I. Mosaad, H. S. M. Ramadan, M. Aljohani, M. F. El-Naggar and S. S. M. Ghoneim, “Near-optimal PI controllers of STATCOM for efficient hybrid renewable power system,” IEEE Access, vol. 9, pp. 34119–34130, 2021. [Google Scholar]

24. A. Ahmad, S. A. R. Kashif, A. Nasir, A. Rasool, S. Liaquat et al., “Controller parameters optimization for multi-terminal DC power system using ant colony optimization,” IEEE Access, vol. 9, pp. 59910–59919, 2021. [Google Scholar]

25. A. M. Hussien, R. A. Turky, A. Alkuhayli, H. M. Hasanien, M. Tostado-Véliz et al., “Coot bird algorithms–based tuning PI controller for optimal microgrid autonomous operation,” IEEE Access, vol. 10, pp. 6442–6458, 2022. [Google Scholar]

26. Y. Sun, S. Li, B. Lin, X. Fu, M. Ramezani et al., “Artificial neural network for control and grid integration of residential solar photovoltaic systems,” IEEE Transactions on Sustainable Energy, vol. 8, no. 4, pp. 1484–1495, 2017. [Google Scholar]

27. C. Zheng, T. Dragičević, Z. Zhang, J. Rodriguez and F. Blaabjerg, “Model predictive control of LC–filtered voltage source inverters with optimal switching sequence,” IEEE Transactions on Power Electronics, vol. 36, no. 3, pp. 3422–3436, 2021. [Google Scholar]