Selective Mapping Scheme for Universal Filtered Multicarrier

1  Introduction

A wide range of applications, such as the 4G to 5G evolution, Internet of Things (IoT) [1–3], will address future wireless systems. In order to efficiently handle these and other applications that demand features such as flexible resource allocation and low latency. Various alterations to the physical layer are required to meet these needs [4]. As a result of OFDM’s sensitivity to frequency and time offsets, high PAPR, and use of the cyclic prefix (CP), numerous possible waveforms for 5G wireless networks have been projected. GFDM, filter-bank multicarrier (FBMC), and UFMC waveforms reduce OOB emissions, making them more spectrally efficient [5] Filtering in the UFMC system minimises OOB emission and, as a result, ICI between various PRBs for each sub-band and physical resource block (PRB). CoMP (uplink coordinated multipoint) scenarios have also been realised with UFMC. Reference [6] When it comes to frequency division multiplexing (FBMC), [7] the UFMC approach can be seen as an in-between method between OFDM and the more robust FBMC. Reference [8] Power amplifier amplification efficiency is measured by the PAPR. Reference [9] High PAPR is a typical concern in multicarrier systems because nonlinear high power amplifiers distort the signal [10]. As a multicarrier system, UFMC is constrained by its high PAPR. Most of the PAPR works focuses on reducing PAPR in OFDM schemes, while only a few publications focus on UFMC and FBMC as 5G schemes. According to [11], the authors apply a tone reservation (TR) strategy in the FBMC system; [12,13] presented partial transmit sequence (PTS) and SLM in the UFMC and OFDM schemes correspondingly.

When used in conjunction with OFDM, SLM is a well-known PAPR reduction method [14]. SLM has been described in a variety of forms [15] SLM transmits the signal with the lowest PAPR between several signals that represent the same data. Non-coherent UFMC can also be treated with SLM. In this paper, we discuss how to improve SLM in the UFMC in order to reduce PAPR. It is possible to reduce PAPR by a much greater margin with the optimised version than with the regular SLM. The following are the bulk of our contributions:

1.    To reduce PAPR in UFMC, we suggest an OSLM (optimal SLM). Replacement of the constant for active sub-carrier in UFMC with complex number of ej represents the idea. Phase factor must be carefully selected in order to reduce the PAPR of the subsequent time series, and this is accomplished by solving a non-linear optimization problem.

2.    Another special situation of the suggested OSLM, in which equals zero, is also examined. Linear Integer Programming is used to approximate the optimization problem in this scenario. Estimated and original solutions are compared. Additionally, we devised a low-complexity iterative method for the suggested problem.

3.    In conclusion, we demonstrate that the suggested PAPR reduced UFMC has the same maximum likelihood (ML) detector as the standard UFMC. As a result, there is no loss in BER performance between the suggested approaches and the original non-coherent OFDM-IM.

2  UFMC System Ideal

It is a multicarrier technology that exchanges high data rates into parallel low data rates. Gray-coded 16-QAM N symbols, designated as S, are separated into M subbands to represent the data bits b. As a final step, the frequency-domain symbols Si are transformed into a time-domain signal s i by the use of an N-point IFFT (inverse fast Fourier transform). A length L is applied to each sub-band, and these time-domain signals are combined to give the output signal x of length N + L − 1 as depicted in Fig. 1. It is possible to express the transmitted signal in terms of

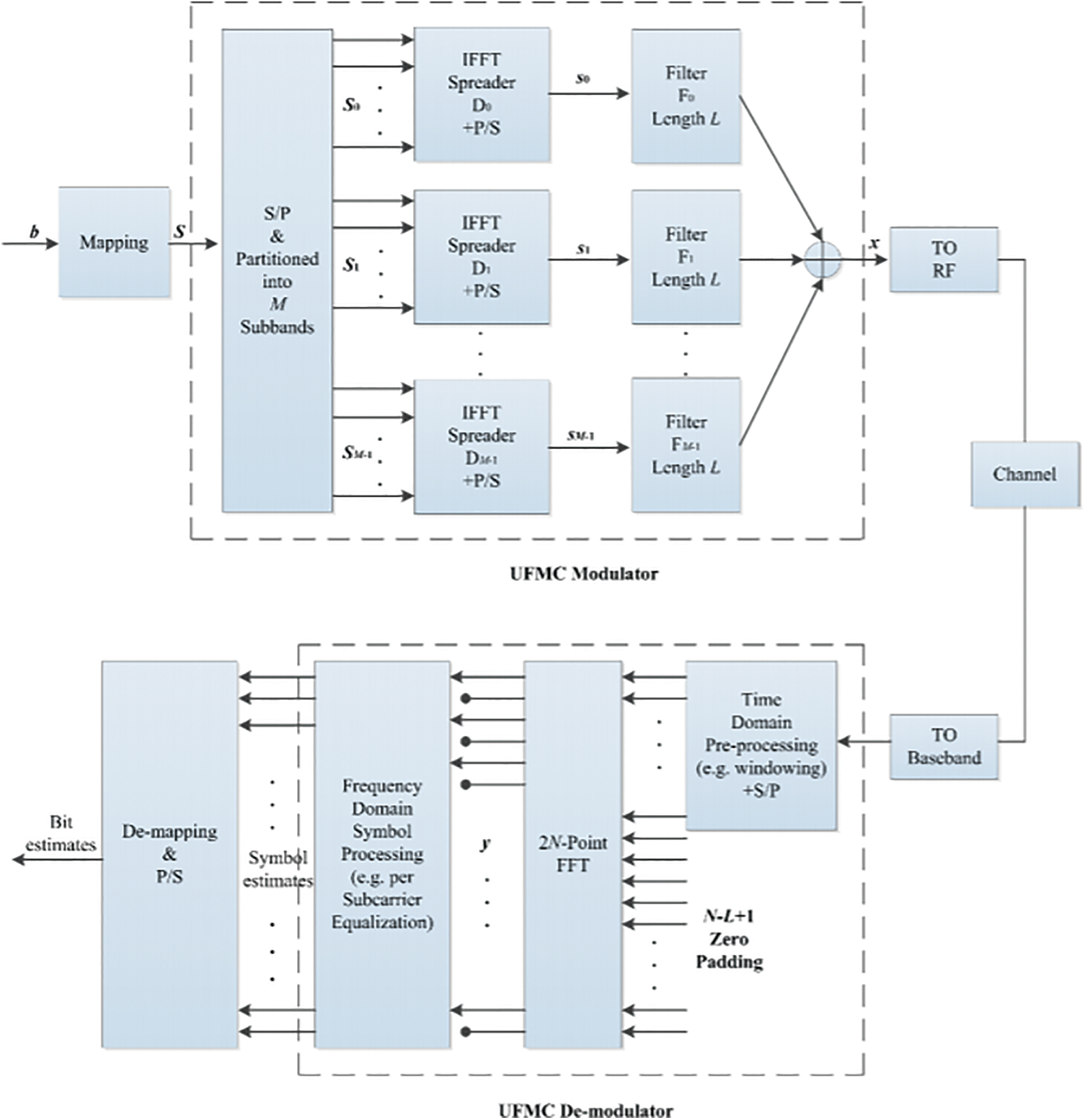
Figure 1: Block diagram of UFMC [4]

x(l)=∑i=0M−1⁡si(l)∗fi(l),l=0,1,….,N+L−2. (1)

where si(l)=1N∑k=0N−1⁡si(k)ej2πklN,l=0,1,….,N−1 signifies the N-point inverse Fourier transform on the ith sub-band, and ∗ signifies the linear convolution process.

Matrix conversion can also be used to describe the transmitted signal x as

x=∑i=0M−1⁡FiDiSi,X∈C(N+L−1)∗1 (2)

where Si is represent as the symbol vector transmitting on the ith sub-band and i(i=0,2,…,M−1) signifies the index of sub-band. Fi∈C(N+L−1)∗N is a Toeplitz matrix of the ith sub-band filter, where the coefficient of each sub-band filters are chosen to be normalized such that ∑l=0L−1⁡|fi(l)|2=1Di∈CN×Ni is the IFFT matrix, include the IFFT columns in reference to the exact sub-band location within the overall frequency range.

Let’s pretend that the frequencies are perfectly synchronised at this point. An N − L + 1 padding is used to zero pad the received signal before employing a 2-point FFT to turn the received sequence into the signal y (earlier channel equalisation) which may be signified as a vector.

y=DHH∑i=0M−1⁡FiDiSi+DHw, (3)

where {.}H as Hermitian operation. H∈C(N+L−1)∗(N+L+1) is the correspondent channel convolution matrix of h(t) . w=[w(0),w(1),…,w(N+L−2)]T is the AWGN vector at the receiver.

3  Proposed System Model

SLM-UFMC model incorporating PAPR difficult and projected efficient SLM-UFMC scheme are discussed in this part.

3.1 SLM-UFMC System Model

Fig. 2 depicts the block diagram for a UFMC transmitter based on an SLM. An S signal is multiplied by several U phase sequences Pku.Sku=S⊙Pku before the UFMC modulator, where the contestant with the lowest PAPR is broadcast. This is accomplished using a phase rotation vector of length N before the UFMC modulator. As a result, the transmitted signal is thus described.

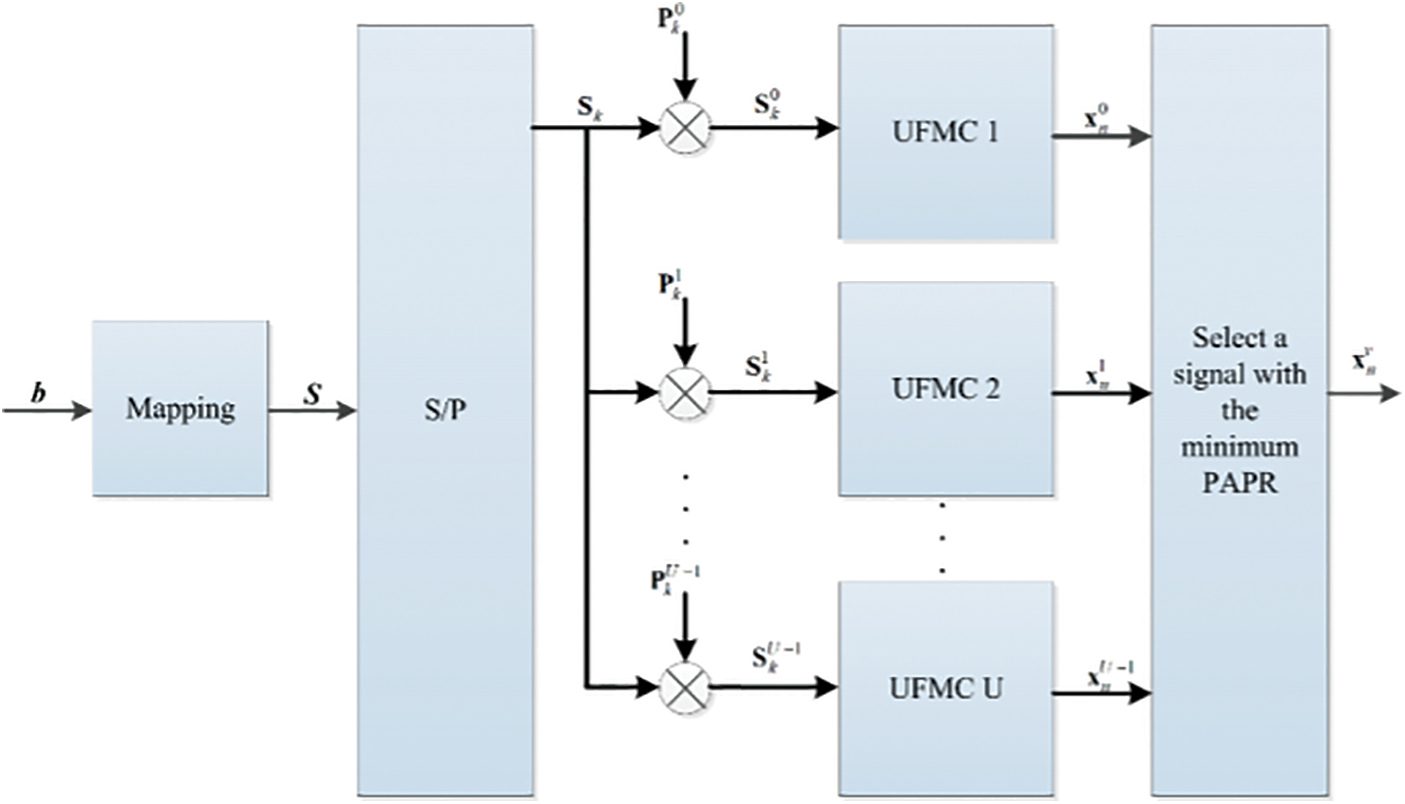
Figure 2: Block diagram of SLM-UFMC transmitter

xnv=∑i=0M−1⁡FiDiSiv=[x0v,x1v,…,xN+L−2v] (4)

where, V signifies the signal with the lowest PAPR from the set U, Pku and the best phase arrangement from the set Pku given by

Pku=[P0u,P1u,…,PN+L−2u]0≤u≤U−1. (5)

where Pku=ej∅ku and ∅ku is a range of 0 to 2π. Random discrete value.

The transmitted signal xnv PAPR in (4), can be stated as

PAPR=10log10PpeakPaverage=10log100≤n≤N+L−2max[|xnv|2]E[|xnv|2] (6)

where E[.] designates the predictable value operation, Ppeak is the maximum rapid power and Paverage is the average power of xnv .

3.2 Crow Search Algorithm

Crows (corvids) are regarded as the most intellectual birds in the animal kingdom. They have the greatest brain-to-body ratio of any mammal On the basis of a human brain-to-body ratio, they have a smaller brain than us. Many examples of crows’ ingenuity can be found. In mirror tests, they have shown that they are aware of their own bodies and have the ability to make tools Unlike humans, crows are able to recognise each other’s faces and warn each other when an unpleasant one is near. As a result, they are able to use tools, communicate in sophisticated ways, and remember where their food is hidden for months at a time. Fig. 2 shows the CSA pseudocode. This section outlines the step-by-step process for implementing CSA.

Step 1:Set up the problem and its modifying variables

The optimization problem, as well as the various choice variables and constraints, are all well stated. When the CSA parameters (flock size ( xnv )), extremesum of iterations (iter max), flight length ( fl ) and awareness probability (AP) are taken into consideration, the results are compared.

Step 2:The location and memory of crows must be established.

As the xnv members of the flock, the crows are placed in a random location in the d-dimensional search space. There are d possible solutions to the problem, and each crow represents one of them.

Crows=[X11X21…Xd1X12X22⋯Xd2⋮X1N⋮X2N⋮⋮⋯XdN] (7)

Each crow’s memory is set up in the beginning. Because the crows have no previous experience, it is presumed that they have hidden their food in the same places they did at the beginning of the

game.Memory=[m11m21…md1m12m22⋯md2⋮m1N⋮m2N⋮⋮⋯mdN] (8)

Step 3:Appraise fitness function

By putting the values of the choice variables into the objective function, we can calculate the quality of each crow’s position.

Step 4:Makenovel position

Suppose that crow I is looking to create a new role. In order to reach its goal, this crow picks a random crow from the flock and follows it to find the concealed food (mj). Eq. determines the new location of crow i. (2). All the crows are subjected to this procedure.

xi,iter+1={xi,iter+ri×fli,iter×(mj,iter−xi,iter)rj≥APj,iterarandompositionotherwise (9)

where APj,iter is the awareness probability of crow and rj is signified as a random sumamong and .

Step 5:New posts should be evaluated for their viability

Each crow’s new position is tested for its viability. If a crow’s new location is possible, the crow updates its position. Instead of moving to its new location, the crow remains at its current location.

Step 6:Perform an assessment of the new jobs’ fitness levels

Each crow’s new position is assigned a fitness function value.

Step 7:Update your memory

The crows’ memories are updated as follows:

mi,iter+1={xi,iter+1f(xi,iter+1)isbetterthatf(mi,iter)mi,itero.w (10)

where f(.) denotes the objective function value.

If the novel position of a crow has a better fitness function value than the one it has learned, the crow refreshes its memory by using the new location.

Step 8:Verify the criteria for dismissal.

Once itermax is achieved, the steps 4–7 are repeated. The optimal memory location in terms of the objective function value is presented as the solution to the optimization issue when the termination requirement is met. As a last step, the optimised value is evaluated as a signal with an optimal phase.

4  Results and Discussion

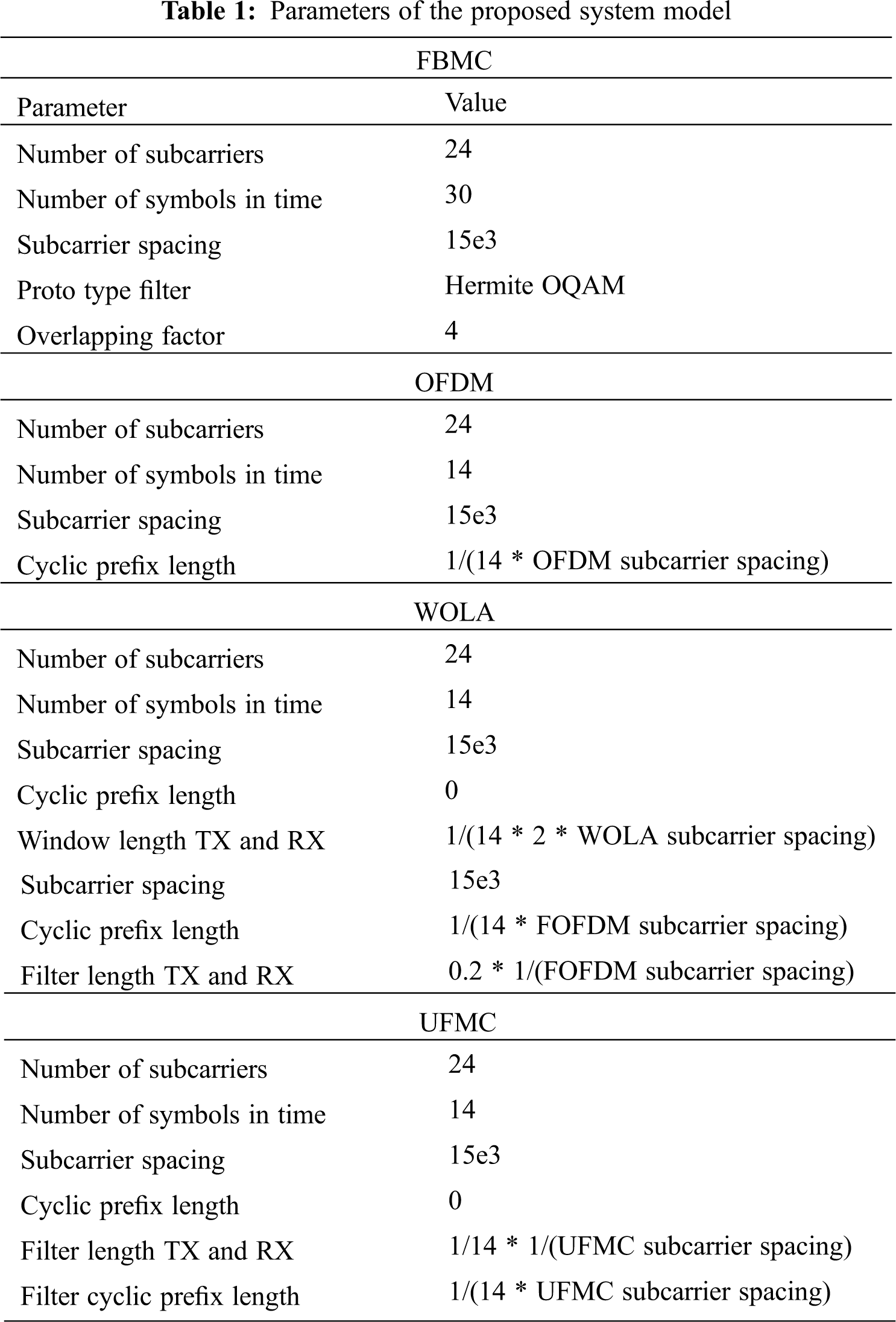
Assuming an AWGN channel, random data bits with QAM and 64 QAM modulation techniques are utilised to appraise and compare the proposed hybrid system performance. Initially, to ensure the proposed UFMC technique BER performance, UFMC is compared with conventional OFDM, FBMC, WOLA and FOFDM systems. To ensure the proposed UFMC system Pre-allocate Transmit Power and Pre-allocate Power Spectral Density are measure and plotted. The performance of the Optimized SLM UFMC technique, simulation results of PAPR and BER plots are presented. All the system evaluations are made with the Number of Monte Carlo repetitions over which we take the average is 1000. Simulation SNR in dB is [−5:2.5:30] SNR for OFDM in dB . The averages transmit power of all methods is the same! However, the SNR might be different due to filtering (in FOFDM and UFMC) or because a different bandwidth is used (different subcarrier spacing or different number of subcarriers). All the evaluations are made with fast fading channel. The parameters setting of the conventional and proposed system is summarized in Tab. 1.

4.1 UFMC Compared with Conventional Methods

System evaluation and comparison are done in this section, with the suggested model being compared to original SLM UFMC systems. The CCDF, which is distinct as the probability of PAPR exceeding a specific threshold PAPR0, is used to quantify PAPR reduction capacity. According to [14], the CCDF is defined. CCDF[PAPR(xn)]=prob(PAPR(xn)>PAPR0) (Figs. 3–7).

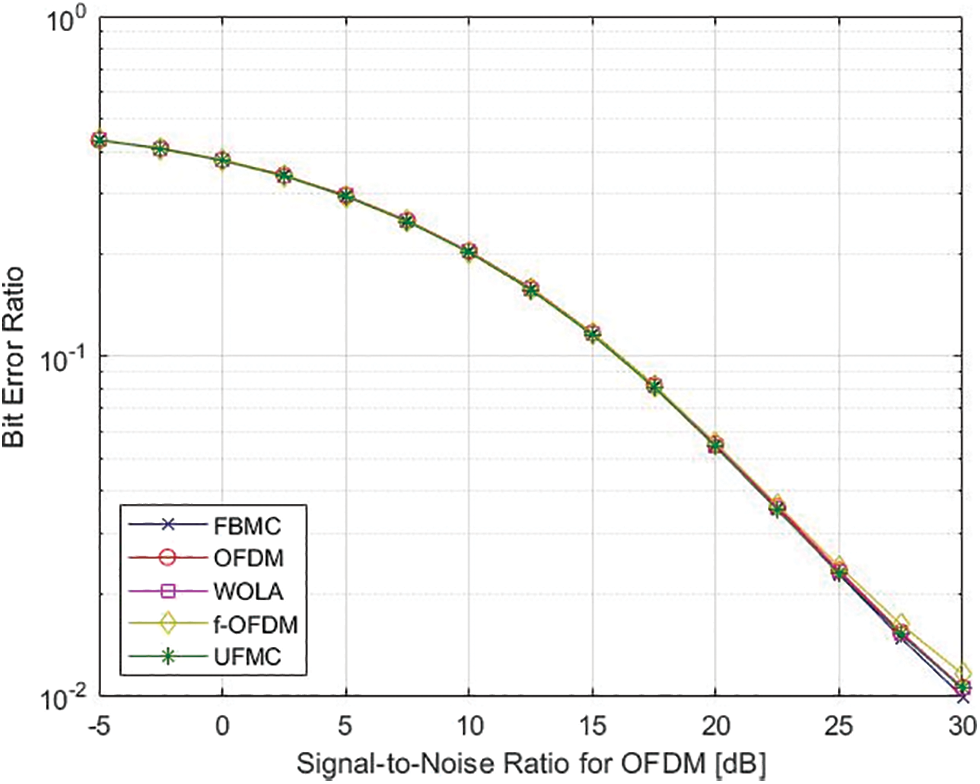
Figure 3: UFMC compared with conventional

Figure 4: Pre-allocate allocation power

Figure 5: Power spectral density

Figure 6: Performance

Figure 7: Bit error

5  Conclusion

In order to reduce PAPR, an effective UFMC SLM optimization technique is presented in this study. An SLM-UFMC system with PAPR reduction capabilities that outperforms any other system has been demonstrated by simulations. In order to reduce PAPR and BER, we devised an optimization problem. The suggested CSA with SLM-UFCM scheme reduces PAPR significantly compared to other schemes, according to simulation findings. Heuristic schemes have also been found to have a lower PAPR than previous SLMs and are beneficial for real-time implementations, as has been demonstrated. While this system’s principal advantage comes from using the side information index to de-randomize the data it receives, it is not without its drawbacks.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Gupta and R. K. Jha, “A survey of 5G network: Architecture and emerging technologies,” IEEE Access, vol. 3, pp. 1206–1232, 2015. [Google Scholar]

 2.  M. Agiwal, A. Roy and N. Saxena, “Next generation 5G wireless networks: A comprehensive survey,” IEEE Communications Surveys and Tutorials, vol. 18, no. 3, pp. 1617–1655, 2016. [Google Scholar]

 3.  Y. Liu, X. Chen, Z. Zhong, B. Ai, D. Miao et al., “Waveform design for 5G networks: Analysis and comparison,” IEEE Access, vol. 5, pp. 19282–19292, 2017. [Google Scholar]

 4.  J. Wen, J. Hua, W. Lu, Y. Zhang and D. Wang, “Design of waveform shaping filter in the UFMC system,” IEEE Access, vol. 6, pp. 32300–32309, 2018. [Google Scholar]

 5.  S. Han, Y. Sung and Y. H. Lee, “Filter design for generalized frequency-division multiplexing,” IEEE Transactions on Signal Processing, vol. 65, no. 7, pp. 1644–1659, 2016. [Google Scholar]

 6.  M. A. AboulDahab, M. M. Fouad and R. A. Roshdy, “A proposed preamble based channel estimation method for FBMC in 5G wireless channels,” in Proc. 35th National Radio Science Conf. (NRSC), Cairo, Egypt, pp. 140–148, 2018. [Google Scholar]

 7.  R. T. Kobayashi and T. Abrao, “FBMC prototype filter design via convex optimization,” IEEE Transactions on Vehicular Technology, vol. 68, pp. 1, 2018. [Google Scholar]

 8.  M. Wu, J. Dang, Z. Zhang and L. Wu, “An advanced receiver for universal filtered multicarrier,” IEEE Transactions on Vehicular Technology, vol. 67, no. 8, pp. 7779–7783, 2018. [Google Scholar]

 9.  V. Vakilian, T. Wild, F. Schaich, S. T. Brink and J. Frigon, “Universal-filtered multi-carrier technique for wireless systems beyond LTE,” in Proc. IEEE Globecom Workshops (Gc Wkshps), Abu Dhabi, United Arab Emirates, pp. 223–228, 2013. [Google Scholar]

10. W. Rong, J. Cai and X. Yu, “Low-complexity PTS PAPR reduction scheme for UFMC systems,” Cluster Computing, vol. 20, no. 4, pp. 3427–3440, 2017. [Google Scholar]

11. M. Laabidi, R. Zayani, D. Roviras and R. Bouallegue, “Papr reduction in FBMC/OQAM systems using active constellation extension and tone reservation approaches,” in Proc. IEEE Symp. on Computers and Communication (ISCC), Athens, Greece, pp. 657–662, 2015. [Google Scholar]

12. L. Dan, Q. Ma, F. Li and Y. Xiao, “Performance of subcarrier-index-modulation OFDM with partial transmit sequences for PAPR reduction,” in Proc. IEEE 87th Vehicular Technology Conf. (VTC Spring), Porto, Portugal, pp. 1–5, 2018. [Google Scholar]

13. L. Rujiprechanon, P. Boonsrimuang, S. Sanpan and P. Boonsrimuang, “Proposal of sub-optimum algorithm for trellis-based SLM reducing PAPR of FBMC-OQAM signals,” in Proc. Int. Workshop on Advanced Image Technology (IWAIT), Chiang Mai, Hong Kong, pp. 1–4, 2018. [Google Scholar]

14. X. R. Zhang, J. Zhou, W. Sun and S. K. Jha, “A lightweight CNN based on transfer learning for COVID-19 diagnosis,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1123–1137, 2022. [Google Scholar]

15. M. Wang, Z. Zhou and C. Ding, “Blockchain-based decentralized reputation management system for internet of everything in 6G-enabled cybertwin architecture,” Journal of New Media, vol. 3, no. 4, pp. 137–150, 2021. [Google Scholar]