Numerical Analysis for the Effect of Irresponsible Immigrants on HIV/AIDS Dynamics

1  Introduction

Acquired Immunodeficiency Syndrome (AIDS) is caused by the Human Immunodeficiency Virus (HIV). HIV/AIDS is the most destructive disease faced by humanity. There are serious consequences for the community, economy, and public health. People infected with Human Immunodeficiency Virus (HIV) may harbor the virus for many years without clinical signs of disease. Eventually, it destroys the body’s immune system, increases the risk of certain diseases, damages body organs such as the brain, kidneys, and heart, and results in death. Human Immunodeficiency Virus (HIV) deteriorates the blood deformation of some commonly used immune systems, which protect the body from disease. HIV/AIDS currently kills approximately 2 million people worldwide each year. Sexual relations with an infected person and exchanging infected blood normally cause Human Immunodeficiency Virus (HIV) transmission. The infected mother also transfers Human Immunodeficiency Virus (HIV) to her newborn. People with Acquired Immunodeficiency Syndrome (AIDS) are susceptible to many disease infections that do not normally cause disease in healthy people [1]. Mathematical and Numerical models have demonstrated importance in figuring out the dynamics of Human Immunodeficiency Virus (HIV) disease. These models have been widely used in HIV/AIDS epidemiological research to improve our understanding of the major factors contributing to a disease epidemic. Many researchers have worked intensively on various aspects of this dangerous disease. Busenberg et al. presented a simple model for the transmission of HIV/AIDS in India, and he concluded that the main reason for the spread of HIV/AIDS in the community was the sexual interaction between a core group of prostitutes and young unmarried men [2]. Coutsoudis et al. discussed the effects of free formula milk on infants of Human Immunodeficiency Virus (HIV) infected women [3]. Although it eliminates Human Immunodeficiency Virus (HIV) transmission but carries a risk of increased mortality, breastfeeding has several benefits but carries a risk of Human Immunodeficiency Virus (HIV) transmission. Ogundele et al. studied the mother-to-child transmission (MTCT) of HIV through breastfeeding [4]. Dunn et al. developed a Human Immunodeficiency Virus (HIV) transmission [5]. Newell studied the Human Immunodeficiency Virus (HIV) and concluded that its transmission can occurs before, during, or after birth [6]. An important impact on dangerous sexual behavior is the lack of awareness about HIV/AIDS. Zaleta studied heterosexual disease transmission and proposed a model for a heterosexually transmitted disease [7]. Greenhalgh et al. examined the effects of condom use on the sexual transmission of Human Immunodeficiency Virus (HIV) and Acquired Immunodeficiency Syndrome (AIDS) in a homogeneous male homosexual population [8]. Mukandavire et al. studied a model for heterosexual transmission of HIV/AIDS in a community and formulated a model [9]. The model divided the population into a gendered structure of males and females. The threshold and equilibria of the model were determined, and the stability was examined. The model has been expanded to focus on the impact of condom use as a unique strategic approach to HIV prevention without treatment. Male condom use was initially modeled, and the model was later expanded to include male and female condom use. Basic reproduction numbers were calculated for these models, and the models were analyzed numerically. Din et al. presented a modified model of Human Immunodeficiency Virus (HIV) CD4+T-cells [10]. Abueldahab et al. studied an epidemic model to observe the spread of Human Immunodeficiency Virus (HIV) in Khartoum [11]. Sanusi et al. developed a epidemic model to study and predict the spread of HIV/AIDS [12]. Shaikh et al. proposed the model of the dynamics of HIV/AIDS transmission in the existence of a conscious community using a fractional differential operator [13]. The conditions of existence and uniqueness of the model were obtained. The conditions necessary for disease control were examined to determine unconscious infectious agents’ role in spreading HIV/AIDS. Mickens introduced the concept of Nonstandard finite difference (NSFD) theory [14]. The theory has been widely used to solve mathematical models. Patidar studied developments and applications of Non-standard finite difference (NSFD) methods [15]. Jodar et al. developed two finite difference schemes based on the Nonstandard finite difference (NSFD) theory for an influenza mathematical model [16]. Raza et al. examined a stochastic model of HIV/AIDS based on Nonstandard finite difference (NSFD) theory in a bisexual population considering counseling and antiretroviral therapy. They concluded that the stochastic model of the HIV/AIDS epidemic is relatively more pragmatic than the deterministic model of HIV/AIDS. HIV/AIDS epidemic [17]. The Nonstandard finite difference (NSFD) stochastic scheme retained all the important properties of the disease dynamical model. Jawaz et al. studied a delay epidemic model with diffusion and developed Nonstandard finite difference (NSFD) based scheme to study HIV/AIDS, a delayed reaction-diffusion epidemic model [18]. Iqbal et al. studied a fractional-order HIV/AIDS transmission based on Nonstandard finite difference (NSFD) theory [19]. Ahmed et al. introduced a new Human Immunodeficiency Virus (HIV) CD4+T cells reaction-diffusion model [20]. Arifeen et al. studied the numerical techniques for the higher-order boundary value problems [21]. Shah et al. studied the fractional dynamics of HIV with source term for the supply of new CD4+ T-Cells depending on the viral load via Caputo Fabrizio derivative [22,23]. The well-known methods and infectious diseases models are studied in [24–35]. The rest of the paper is designed: An HIV/AIDS model is considered in Section 2. The existence analysis of the model is also studied in this section. Section 3 is devoted to numerical modeling. Sections 4 and 5 contain the simulation results and conclusions, respectively.

2  HIV/AIDS Model

In this work, we consider the HIV/AIDS model presented by [36] for the existence of a solution and reliable numerical study.

dSdt=Qo−C(β1I1+β2I2)SN−μS (1)

dI1dt=C(β1I1+β2I2)NS−γI1−(θ+δ+μ)I1 (2)

dI2dt=θI1−(δ+μ)I2 (3)

dAdt=δ(I1+I2)−(α+μ)A (4)

With initial conditions S(0)=S0≥0 , I1(0)=I10≥0,I2(0)=I20≥0 , A(0)=A0≥0 , β1>β2 .

The system (1)–(4) is developed assuming that HIV may be transferred in the population through sexual interaction and through infected blood or needle. Also, it is considered that the rate of irresponsible infective infecting people with the disease is higher than that of responsible infective. In the system (1)–(4), N represents the total size of the population, S is the variable that denotes the susceptible individuals, I1 represents the individuals who are irresponsible and infective, I2 is the infective people who are responsible, A is the size of the full-blown Acquired Immunodeficiency Syndrome (AIDS) populace, c represents the infective individuals who have sexual partners, β1 demonstrates the rate of contact of irresponsible infective, β2 is the rate of contact rate responsible infective, μ is the parameter which represents the natural rate of death. θ is the rate of conversion of irresponsible infective to responsible infective, δ represents the rate of the conversion rate of infective to full-blown Acquired Immunodeficiency Syndrome (AIDS), α is the Acquired Immunodeficiency Syndrome (AIDS)-induced rat of mortality, Qo represents the recruitment rate of susceptible into the population, γ is the recruitment rate of infective immigrants? Note that S=S(t) , I1=I1(t) , I2=I2(t) , A=A(t) , where t represents the time and N=S+I1+I2+A. Since N=S+I1+I2+A the system (1)–(3) can be modified as,

dNdt=Q0−μN−αA+γI1 (5)

dI1dt=C(β1I1+β2I2)(N−I1−I2−A)N−γI1−(θ+δ+μ)I1 (6)

dI2dt=θI1−(δ+μ)I2 (7)

dAdt=δ(I1+I2)−(α−μ)A (8)

and non-negative initial conditions are given as, N(0)=N0,I1(0)=I10,I2(0)=I20,A(0)=A0,β1>β2 .

2.1 Existence of the Solution

The model modified into total population N by the system (5)–(8) can be inverted in the form of Volterra integral equations,

N(t)=N0+∫0tF1(I2,N,A,I1)(s)ds (9)

I1(t)=I10+∫0tF2(N,I1,I2,A)(s)ds (10)

I2(t)=I20+∫0tF3(N,I1,I2,A)(s)ds (11)

N(t)=N0+∫0tF4(N,I1,I2,A)(s)ds (12)

For the sake of simplicity, the above system can be re-written as

xi(t)=x0i+∫0tFi(x1,x2,x3,x4)(s)ds,i=1,2,3,4. (13)

where x1=N(t) , x2=I1(t) , x3=I2(t) and x4=A(t) .

The classical solution of the deterministic model (5)–(8) together with the initial conditions x0i demands the solutions xi=1,2,3,4 , be continuously differentiable in the time domain. We supposed that the solution vector (x1(t),x2(t),x3(t),x4(t))∈C[0,ρ] . If each xi,i=1,2,3,4 is continuously differentiable, then the right-hand side Fi turns out to be continuous. Further, we assume that the RHS Fi satisfies the Lipschitz conditions,

‖Fi(x1i)−Fi(x2i)‖≤Li(r)‖x1i−x2i‖,i=1,2,3,4 (14)

The goal of the current section is to show the unique existence of the solution by the well-known Banach fixed theorem stated as.

Theorem (Contraction Mapping Principle)1. Let B be a closed-convex-bounded subset of a Banach space C and f be a continuous mapping B into itself. Further, if f has a contraction, then f has one and only one fixed point in B . To ensure the unique existence and corresponding explicit estimates for the system (9)–(12), we re-write the integral Eq. (13) in the operator notation

Xi=x0i+∫0tF(x1,x2,x3,x4)(s)ds, (15)

and we choose the space of continuous functions C0[0,ρ] as the target Banach space, equipped with the supremum norm ‖▀‖=max[0,ρ]|▀| . Further, we consider the closed convex and bounded subset B of the Banach space C0[0,ρ] defined by

Br(Θ)={xi,xi∈C0[0,ρ],‖xi‖≤r}. (16)

The application of the contraction mapping principle seeks the following two conditions,

•    Xi:Br(Θ)→Br(Θ) ,

•    Xi is the contraction

for the operators (15). We see the two conditions in the next two subsections.

2.2 Self-Mapping

In this subsection, we show the explicit estimates for Xi:Br(Θ)→Br(Θ) , i.e.,

Xi=x0i+∫0tFi(x1,x2,x3,x4)(s)ds .

⇒‖Xi‖≤|x0i|+∫0t‖Fi‖ds≤Ci+Ki(r)ρ≤r ,

ρ≤1Ki(r)[r−Ci] (17)

Here, x0i≥0,|x0i|=x0i=XCi,i=1,2,3,4 and ‖Fi‖≤Ki(r) . For positive length of continuity the following conditions is necessary,

r−Ci>0,orr>Ci, (18)

The sufficiently small initial conditions can be considered. For arbitrary initial needs, one may choose a larger ball radius. Still, the permissible restriction on the radius can be obtained after the second condition on the contractility of the operator.

Remark 1. The existence of the Schauder fixed point theorem can be guaranteed with the same conditions (17) and (18) with another state of relative compactness using the concepts of equicontinuity and the subsequent Arzela-Ascoli-Theorem.

2.3 Continuity

For the contraction condition, we consider the following two elements from Eq. (15),

X1i=x01i+∫0tFi(x1i,.,.)(s)ds (19)

X2i=x02i+∫0tFi(x2i,.,.)(s)ds (20)

From (19) and (20)

‖X1i−X2i‖=‖∫0t[Fi(x1i,.,.,.)−Fi(x2i,.,.,.)](s)ds‖ ≤∫0t‖Fi(x1i,.,.,.)−Fi(x2i,.,.,.)‖≤Li(r).ρ.‖x1i−x2i‖,i=1,2,3,4 .

The Lipschitz constants Li in this case will be estimated in the ball (16) using the radius of the ball. For contraction Li(r)ρ<1

⇒ρ<1Li(r). (21)

Condition (21) provides the second restriction on the choice of the length of the interval of continuity together with inequality (17). If both conditions are full-filled, then the following result has been established.

Theorem 2. Let the state functions xi,i=1,2,3,4 being the solutions of initial value problem (5)–(8) are Lipschitz continuous. The underlying problem possesses a unique solution vector (N,I1,I2,A) provided the conditions (17) and (21) are satisfied.

2.4 Analysis of Two Conditions of Contraction Mapping Principle

To understand the optimal behavior of the solution vector (N,I1,I2,A) , we again consider the inequalities (17) and (21)

ρ≤1Ki(r)[r−Ci] , ρ<1Li(r)

Let us have a comparison of the two functions appearing on the RHS of the above inequalities

1Ki(r)[r−Ci]=1Li(r)

The functions have a specific intersection point r∗ . This particular point r∗ is optimal radius, and using this exceptional value of the radius, we can use the following inequality for the unique solution and its length of continuity, i.e., ρ<1K(r∗)[r∗−Ci]=1Li(r∗).

The above important consideration leads to the important result of an optimal solution.

Theorem 3. Suppose the RHS of (5)–(8) are Lipschitz continuous (14), then the unique solution is continuous in the interval [0,1Ki(r∗)(r∗−Ci)] , where r∗ is the solution of the equation

1Ki(r)[r−Ci]=1Li(r).

2.5 Equilibrium Analysis

This section is dedicated to discussing the steady states of the system (5)–(8) and their stability analysis. For the steady states put dSdt=dI1dt=dI2dt=dAdt=0 . This implies that

Qo−C(β1I1+β2I2)SN−μS=0 , C(β1I1+β2I2)NS−γI1−(θ+δ+μ)I1=0 , θI1−(δ+μ)I2=0 , δ(I1+I2)−(α+μ)A=0 .

For the disease-free steady states, there are no infective and full-blown Acquired Immunodeficiency Syndrome (AIDS) patients. Hence I1=0,I2=0,A=0 and N=Qoμ , the DFE is (Eo,I1,I2,A)=(Qoμ,0,0,0) . The Jacobian matrix corresponding to Eo is given by

J=[−μγ0β1c−(θ+δ+μ−γ)0−αcβ200θ0δ−(δ+μ)0δ−(α+μ)]

=[β1c−(θ+δ+μ−γ)cβ2θ−(δ+μ)]

From this, we obtain the reproduction number Ro=θcβ2+(δ+μ)(γ+cβ1)(δ+μ)(θ+δ+μ) .

The disease persists at the endemic equilibrium state, and E*= gives the equilibrium point (N∗,I1∗,I2∗,A∗) . Where N∗=c[β1(δ+μ)+β2θ](θ+δ+μ)(α+δ+μ)(δ+μ)(δ+μ)

I1∗=Qo(δ+μ)(δ+μ)ξcμ[β1(δ+μ)+β2θ](θ+δ+μ)(α+δ+μ)+αδ(θ+δ+μ)ξ−(δ+μ)(δ+μ)ξγ

I2∗=θ(δ+μ)I1∗,A∗=δ(δ+μ+θ)(α+μ)(δ+μ)I1∗

We note here that E∗ is positive only when ξ>0 or Ro>1

Ro=θcβ2+(δ+μ)(γ+cβ1)(δ+μ)(θ+δ+μ).

3  Numerical Modeling

3.1 Forward Euler’s Scheme

The Euler method for the studied model can be obtained as follows

Nn+1=Nn+h[Qo−μNn−αAn+γI1n] (22)

I1n+1=I1n+h[C(β1I1n+β2I2n)(Nn−I2n−An)Nn−C(β1I1n+β2I2n)NnI1n+γI1n−(θ+δ+μ)I1n] (23)

I2n+1=I2n+h[θI1n−(δ+μ)I2n] (24)

An+1=An+h[δ(I1n+I2n)−(α−μ)An] (25)

3.2 Fourth Order Runge-Kutta Method

In this section, we make RK- 4 scheme for the studied model. Considering the system of Eqs. (5)–(8), we have,

Step-1

l1=Nn+h[Qo−μNn−αAn+γI1n]

m1=I1n+h[C(β1I1n+β2I2n)(Nn−I2n−An)Nn−C(β1I1n+β2I2n)NnI1n+γI1n−(θ+δ+μ)I1n]

n1=I2n+h[θI1n−(δ+μ)I2n]

Step-1I

l2=(Nn+l12)+h[Qo−μ(Nn+l12)−α(An+p12)+γ(I2n+n12)]

m2=(I1n+m12)+h[C(β1(I1n+m12)+β2(I2n+n12))((Nn+l12)−(I2n+n12)−(An+p12))(Nn+l12)−C(β1(I1n+m12)+β2(I2n+n12))(Nn+l12)(I1n+m12)+γ(I1n+m12)−(θ+δ+μ)(I1n+m12)]

n2=(I2n+n12)+h[θ(I1n+m12)−(δ+μ)(I2n+n12)]

p2=(An+p12)+h[δ((I1n+m12)+(I1n+n12))−(α−μ)(An+p12)]

Step-1II

l3=(Nn+l22)+h[Qo−μ(Nn+l22)−α(An+p22)+γ(I2n+n22)]

m3=(I1n+m22)+h[C(β1(I1n+m22)+β2(I2n+n22))((Nn+l22)−(I2n+n22)−(An+p22))(Nn+l22)−C(β1(I1n+m22)+β2(I2n+n22))(Nn+l22)(I1n+m22)+γ(I1n+m22)−(θ+δ+μ)(I1n+m22)]

n3=(I2n+n22)+h[θ(I1n+m22)−(δ+μ)(I2n+n22)]

p3=(An+p22)+h[δ((I1n+m22)+(I1n+n22))−(α−μ)(An+p22)]

Step-1V

l4=(Nn+l2)+h[Qo−μ(Nn+l2)−α(An+p2)+γ(I2n+n2)]

m4=(I1n+m3)+h[C(β1(I1n+m3)+β2(I2n+n3))((Nn+l3)−(I2n+n3)−(An+p3))(Nn+l3)−C(β1(I1n+m3)+β2(I2n+n3))(Nn+l3)(I1n+m3)+γ(I1n+m3)−(θ+δ+μ)(I1n+m3)]

n4=(I2n+n3)+h[θ(I1n+m3)−(δ+μ)(I2n+n3)]

p4=(An+p3)+h[δ((I1n+m3)+(I1n+n3))−(α−μ)(An+p3)]

Final Step

Nn+1=Nn+16[l1+2l2+2l3+l4]I1n+1=I1n+16[m1+2m2+2m3+m4]I2n+1=I2n+16[n1+2n2+2n3+n4]An+1=An+16[p1+2p2+2p+p4]} (26)

3.3 Non-Standard Finite Difference Scheme

Non-Standard finite-difference (NSFD) scheme for the studied model can be constructed as

N=Q0μ,I1=0,I2=0,A=0

Use Eq. (1)

dNdt=Qo−μNn+1−αAn+γI1n

Nn+1−Nnh=Qo−μNn+1−αAn+γI1n

Nn+1−Nn=hQo−μhNn+1−αhAn+γhI1n

(1+μh)Nn+1=Nn+hQo−αhAn+γhI1n

Nn+1=Nn+hQo−αhAn+γhI1n(1+μh) (27)

Similarly, we obtain

I1n+1=I1nNn+hC(β1I1n+β2I2n)(Nn−I2n−An)+γhNnI1nNn+hC(β1I1n+β2I2n)+Nnh(θ+δ+μ) (28)

I2n+1=I2n+hθI1n1+h(δ+μ) (29)

An+1=An+hδ(I1n+I2n)1+h(α+μ) (30)

3.4 Stability of the NSFD Scheme

Jacobian matrix for the system (26)–(29) is given by

J=[1(1+μh)γh(1+μh)01+hcβ1+γh1+h(θ+δ+μ)0−αh(1+μh)hcβ11+h(θ+δ+μ)00hθ1+h(δ+μ)0hδ1+h(α+μ)11+h(δ+μ)0hδ1+h(α+μ)11+h(α+μ)]

J=(11+μh)(11+h(α+μ))[1+hcβ1+γh1+h(θ+δ+μ)hcβ11+h(θ+δ+μ)hθ1+h(δ+μ)11+h(δ+μ)]

Clearly two Eigen value i.e., λ1=11+μh<1 and λ2=11+h(α+μ)<1 . The remaining two Eigen values are given by the matrix

=[1+hcβ1+γh1+h(θ+δ+μ)hcβ11+h(θ+δ+μ)hθ1+h(δ+μ)11+h(δ+μ)]

Since finding the Eigenvalue of the above matrix is quite tricky, the spectral radius (most considerable Eigen value) was calculated using MATLAB, which is depicted in Fig. 1. The most significant Eigen value is less than 1, which shows that the system (26)–(29) is stable.

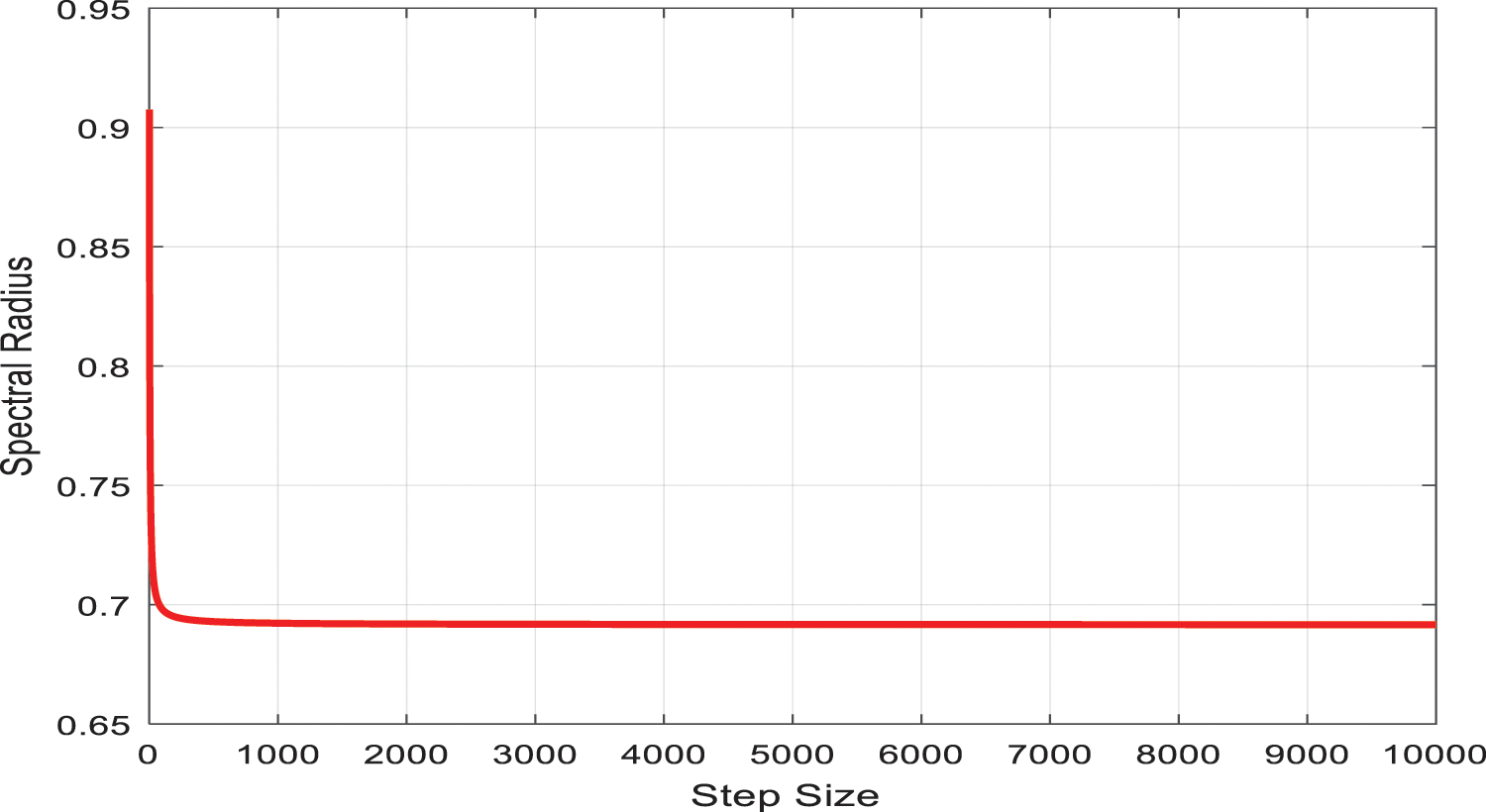
Figure 1: The spectral radius of the largest Eigenvalue

4  Numerical Simulation

In this portion, we discuss our findings. The following are values of the parameters used in our model. N(0) = 1, S(0) = 0.65, I1 (0) = 0.20, I2 (0) = 0.10, a(0) = 0.05, c = 10, β2 = 0.015, β1 = 0.08, μ = 0.02, θ = 0.955, δ = 0.25, α = 0.5, Qo = 0.40.

In Figs. 2a–2d and 3a–3d, all compartments of the proposed model by using the proposed numerical scheme with the time step size h=10 at disease-free equilibrium (DFE) and endemic equilibrium (EE) points respectively have shown.

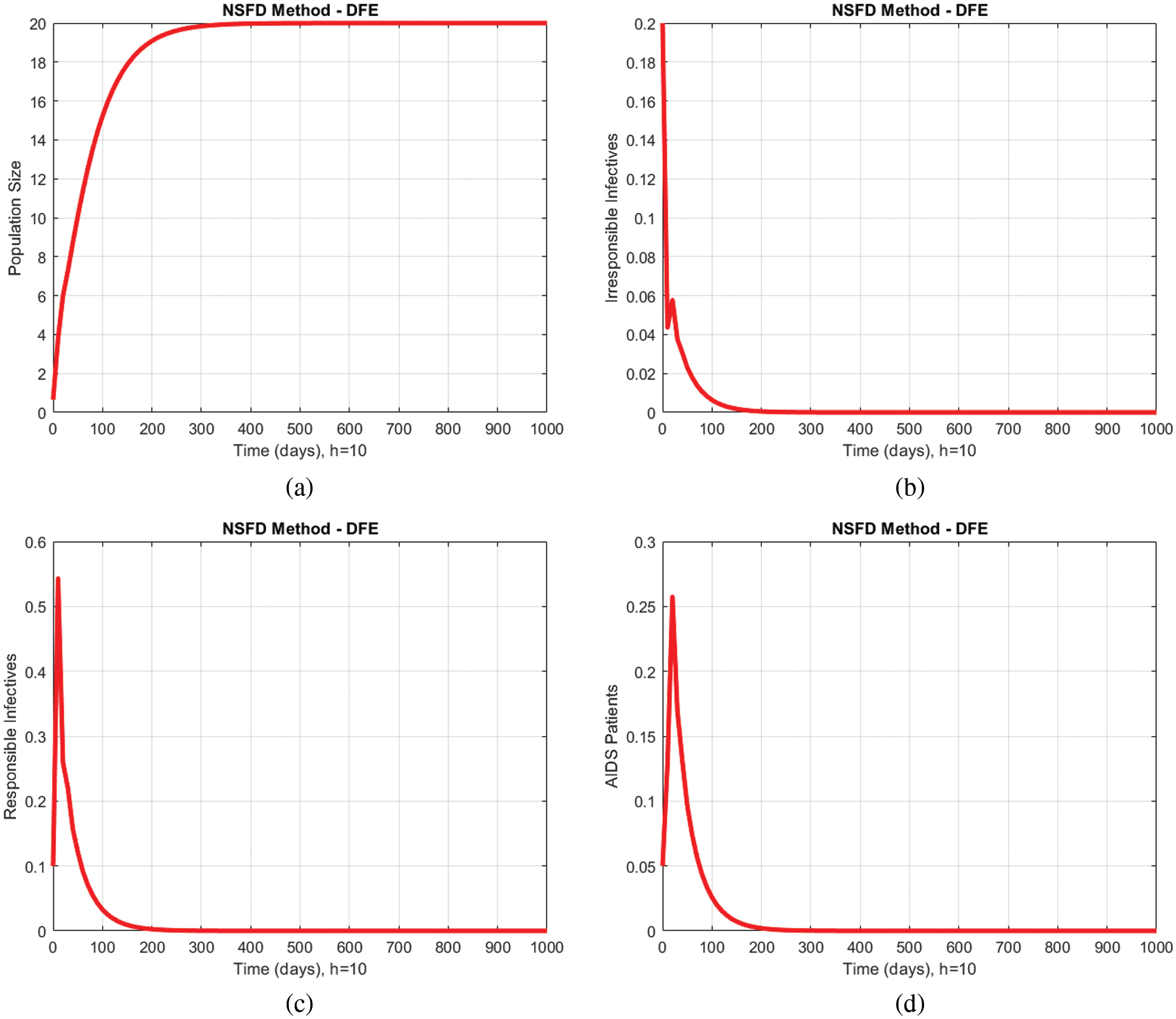
Figure 2: Numerical solutions of all compartments of the proposed model by using the proposed numerical scheme with time step size h=10 at disease-free equilibrium (DFE) point

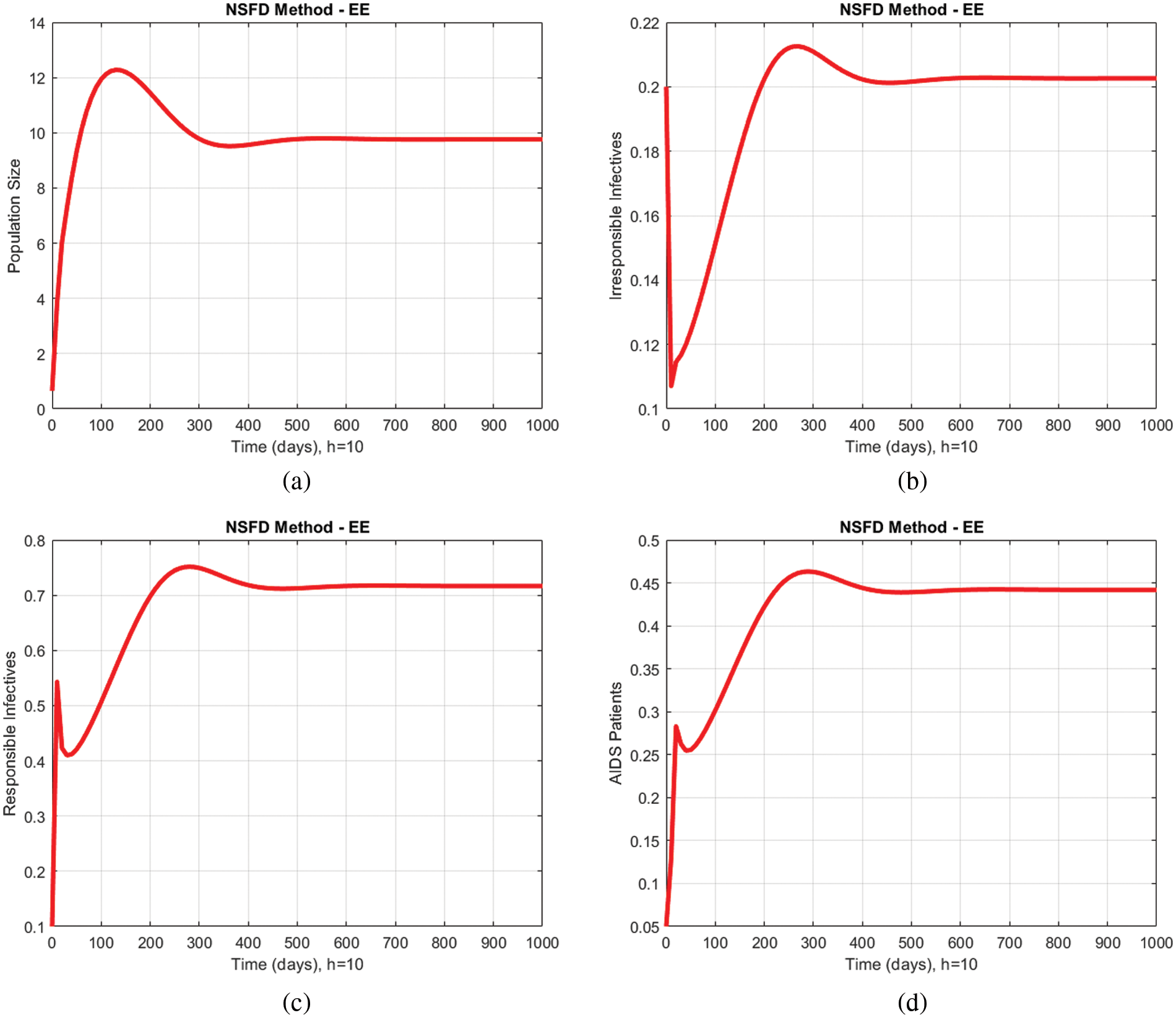
Figure 3: Numerical solutions of all compartments of the proposed model by using the proposed numerical scheme with time step size h=10 at endemic equilibrium (EE) point

4.1 Comparison of NSFD with Euler Method

Figs. 4a–4d shows a graphical comparison of the proposed method with the Euler technique describing the compartment of immunodeficiency patients for different values of h at the disease-free equilibrium (DFE) point. The Euler method produces a negative value at a minimal value of h and then at a considerable discount. These graphs do not make sense as negative values of the immunodeficiency patients cannot be possible. From this, it can be concluded that the Euler method is unreliable in reflecting the actual behavior of the disease dynamics of the model. On the other hand, the proposed method reflects positivity at the same values of h, which shows that the proposed method is a reliable tool for showing the model’s behavior.

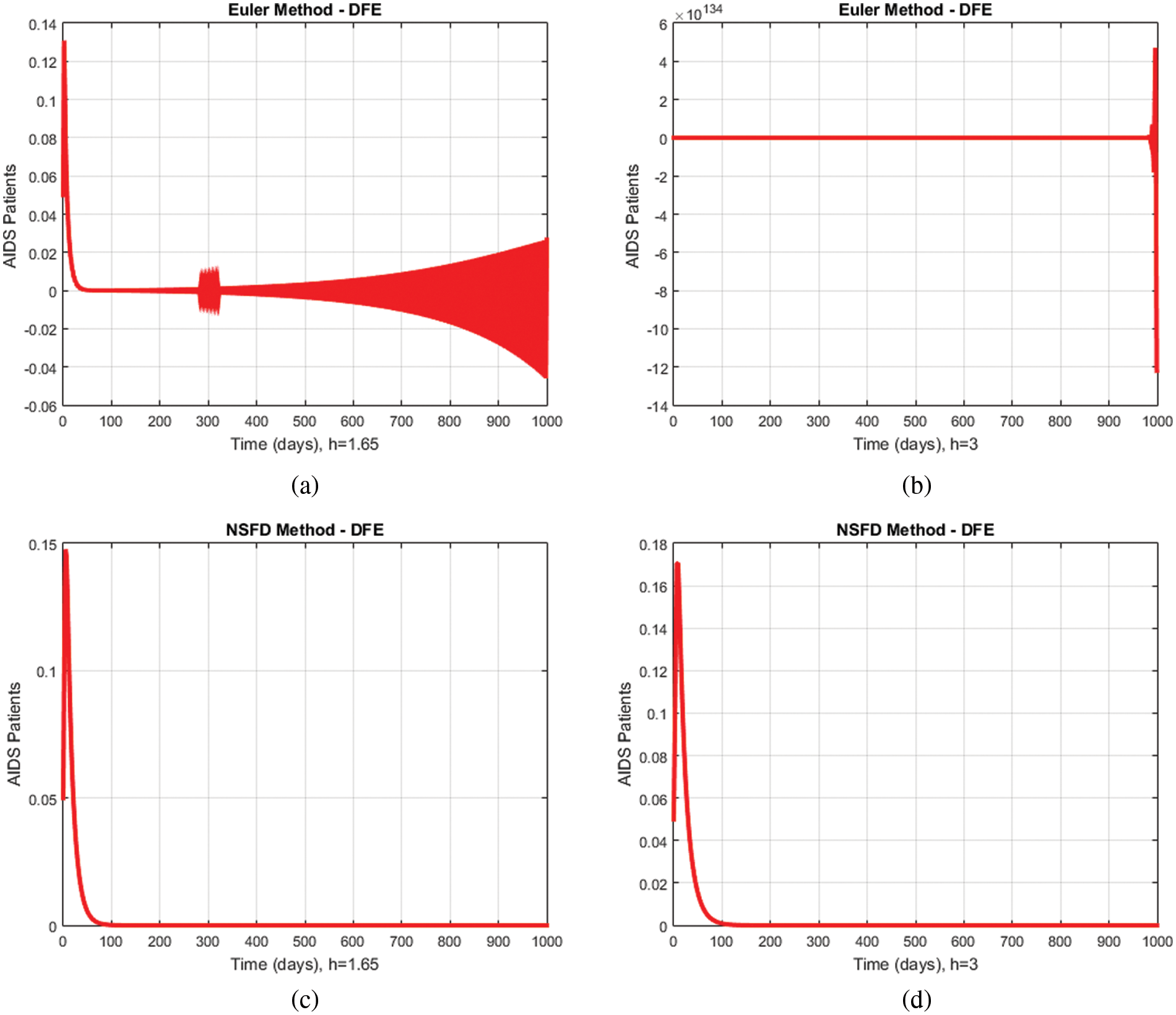
Figure 4: Comparison graphs of the proposed method with the Euler model technique for different values of h at the disease-free equilibrium (DFE) point

Fig. 5 presents another comparison between the proposed method and the Euler technique showing the portion of immunodeficiency patients for different values of h at the endemic equilibrium (EE) point. In Figs. 5a–5d, the Euler method initially shows positivity and converges to the actual equilibrium point at a step size h=2.65 . When the step size is increased to 4, the Euler diverges. The proposed method remains convergent to the essential equilibrium points for both values of h , which shows that the latter is superior in dealing with disease dynamical systems.

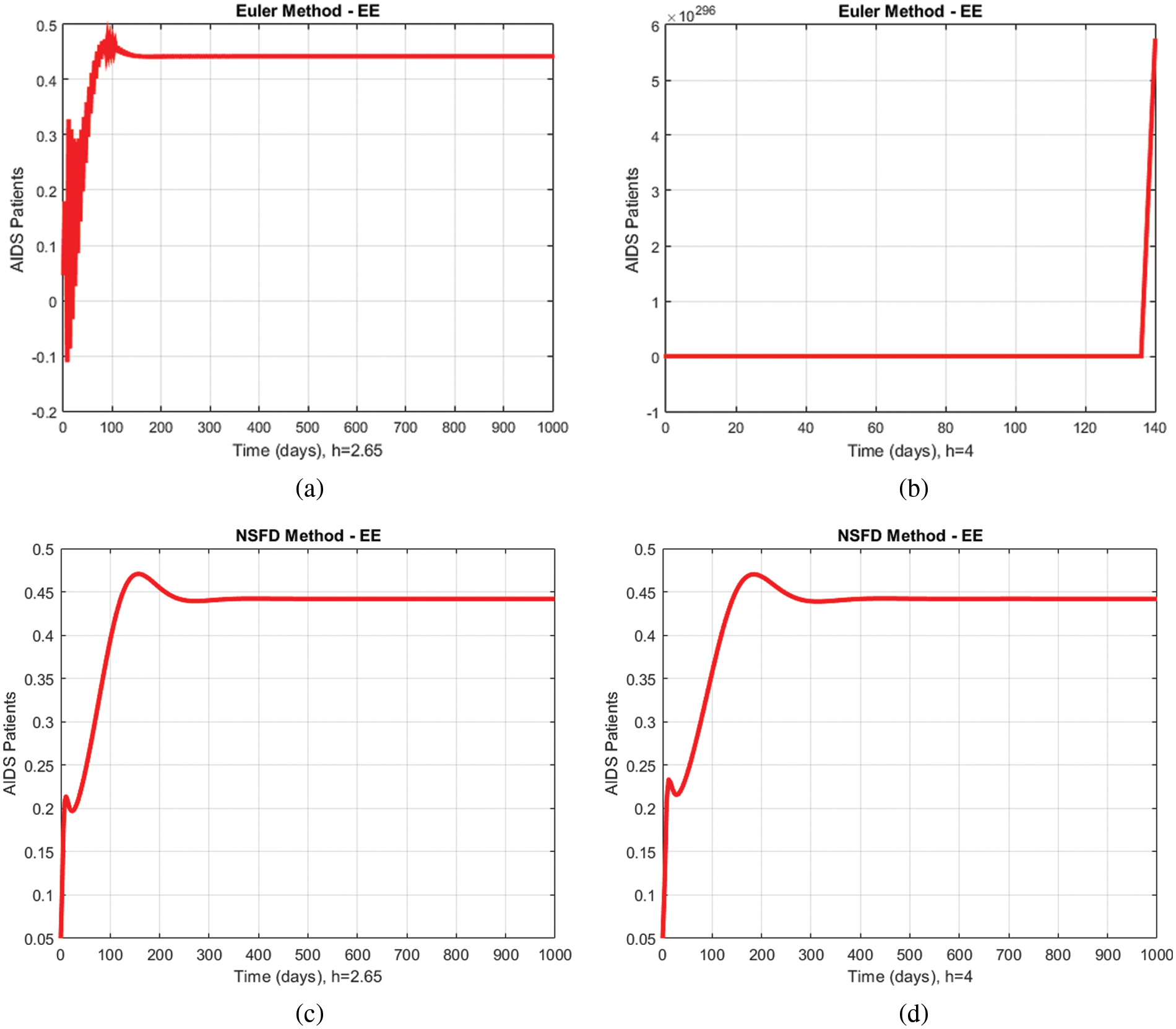
Figure 5: Comparison graphs of the proposed method with the Euler technique of immunodeficiency patients for different values of h at endemic equilibrium (EE) point

4.2 Comparison of NSFD with Runge Kutta Method

A comparison of the proposed method and the Runge Kutta technique describing the proportions of immunodeficiency for different values of h at the disease-free equilibrium (DFE) point is presented in Fig. 6. The Runge Kutta method initially remains positive at h=2.296 , but later starts producing negative values. At h=4 , the Runge Kutta remains stable at the start but diverges at the end. On the other hand, the convergence of the proposed method remains the same, and even the increase in the step size does not affect it.

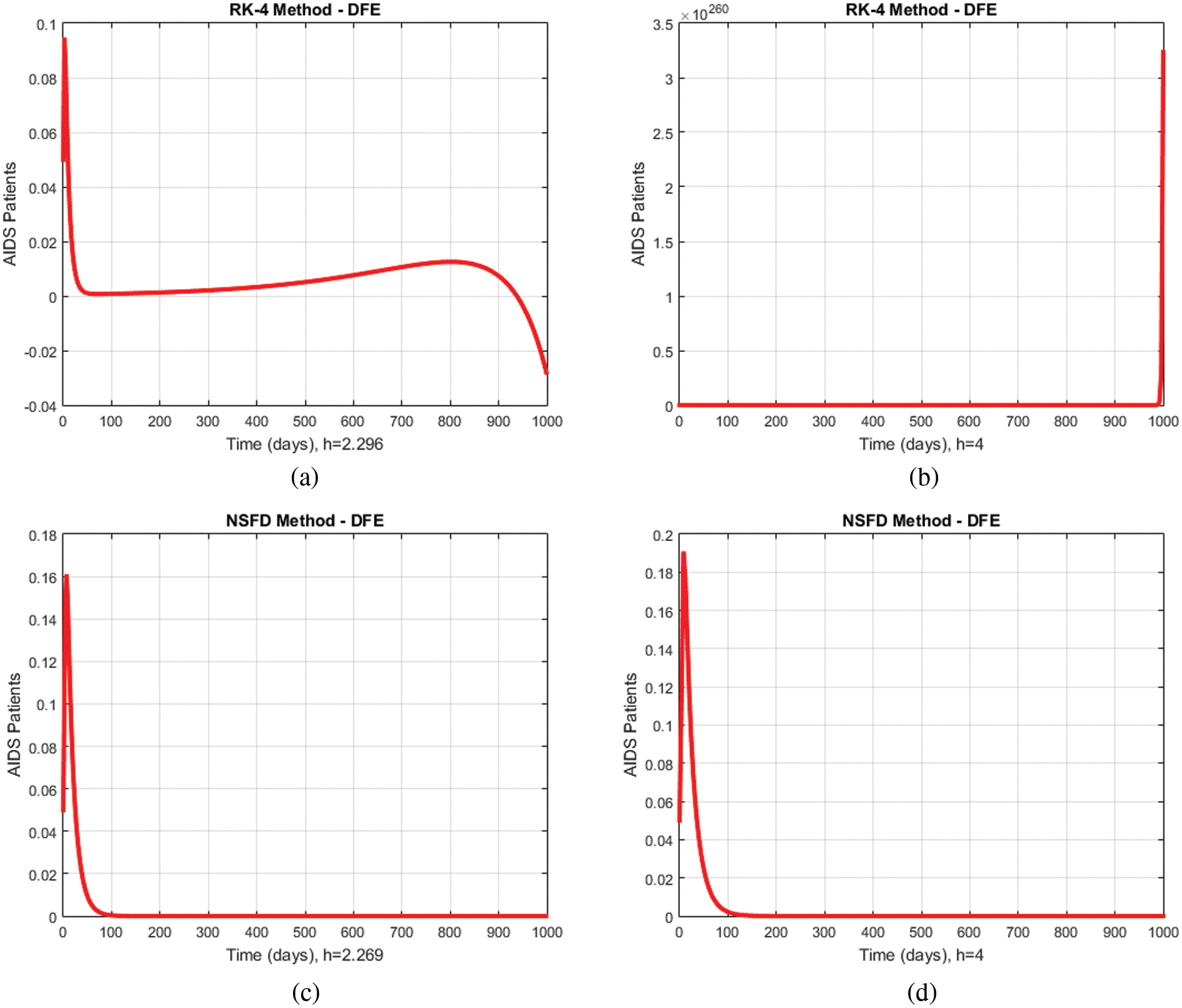
Figure 6: Comparison graphs of the proposed method with Runge Kutta technique of immunodeficiency patients for different values of h at disease-free equilibrium (DFE) point

In Figs. 7a–7d, a comparison of the proposed method and the Runge Kutta technique describing the compartment of the immunodeficiency patients for different values of h at the endemic equilibrium (EE) point is shown. The Runge Kutta method remains convergent but produces some oscillations at h=3.9 . An increase in the value of the step size results in a divergence of the technique. Again, the proposed method gives convergent solutions at all values of step sizes.

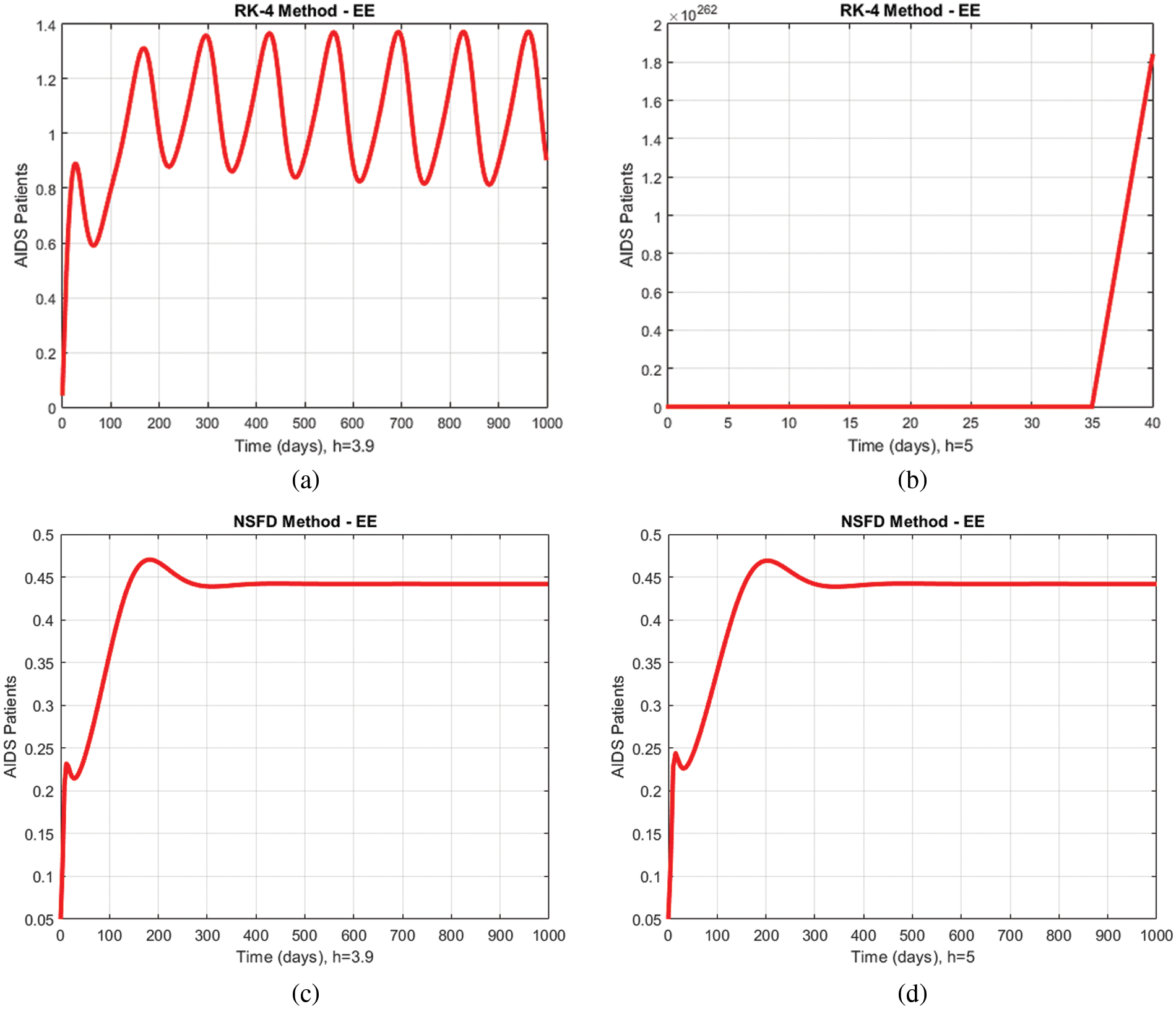
Figure 7: Comparison graphs of the proposed method with Runge Kutta technique of immunodeficiency patients for different values of h at endemic equilibrium (EE) point

5  Conclusion

The effect of irresponsible immigrants on human immunodeficiency has been studied in this article. The existence of the solutions incorporating the contraction mapping principle and self-mapping is discussed. Euler, Runge Kutta, and Non-standard Finite Difference (NSFD) methods are formulated to solve the studied model. Numerical experiments are performed at disease-free equilibrium (DFE), and endemic equilibrium (EE) points at different time-step sizes. The obtained results are analyzed and compared. We concluded that the Euler and Runge Kutta methods fail to converge at large time step sizes, while the proposed method gives results that combine to actual steady states for any time step size. Moreover, the Non-standard Finite Difference (NSFD) method is bounded, dynamically consistent, and preserves the positivity of the solution, which are essential requirements when modeling a prevalent disease.

Acknowledgement: Thanks to our families and colleagues who supported us morally.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

 1.  J. Chin and S. K. Lwanga, “Estimation and projection of adult aids cases: A simple epidemiological model,” Bulletin of the World Health Organization, vol. 69, no. 4, pp. 399–406, 1991. [Google Scholar]

 2.  S. Busenberg, K. Cooke and H. Y. Heng, “A model for HIV in Asia,” Mathematical Biosciences, vol. 128, no. 1, pp. 185–201, 1995. [Google Scholar]

 3.  A. Coutsoudis, A. E. Goga, N. Rollins and H. M. Coovadia, “Free formula milk for infants of HIV infected women: Blessing or curse,” Health Policy and Planning, vol. 17, no. 2, pp. 154–160, 2002. [Google Scholar]

 4.  M. O. Ogundele and J. B. S. Coulter, “HIV transmission through breastfeeding: Problems and prevention,” Annals of Tropical Pediatrics, vol. 23, no. 2, pp. 91–106, 2003. [Google Scholar]

 5.  D. T. Dunn, B. H. Tess, L. C. Rodrigues and A. E. Ades, “Mother-to-child transmission of HIV: Implication of variation in maternal infectivity,” AIDS, vol. 12, no. 16, pp. 162211–162216, 1998. [Google Scholar]

 6.  M. L. Newell, “Mechanism and timing of mother-to-child transmission of HIV-1,” AIDS, vol. 12, no. 8, pp. 832–837, 1998. [Google Scholar]

 7.  C. M. K. Zaleta, “Structured models for heterosexual disease transmission,” Mathematical Biosciences, vol. 160, no. 1, pp. 83–108, 1999. [Google Scholar]

 8.  D. Greenhalgh, M. Doyle and F. Lewis, “A mathematical treatment of aids and condom use,” Mathematical Medicine and Biology: A Journal of the IMA, vol. 18, no. 3, pp. 225–262, 2001. [Google Scholar]

 9.  Z. Mukandavire and W. Garira, “Sex-structured HIV/AIDS model to analyse the effects of condom use with application to Zimbabwe,” Journal of Mathematical Biology, vol. 54, no. 5, pp. 669–699, 2007. [Google Scholar]

10. S. T. M. Din, A. Nazir, B. Almohsin, N. Ahmed, U. Khan et al., “On mathematical model of HIV CD4+ T-cells,” Alexandria Engineering Journal, vol. 60, no. 1, pp. 995–1000, 2021. [Google Scholar]

11. S. M. Abueldahab and F. K. Mutombo, “SIR model and HIV/AIDS in khartoum,” Open Access Library Journal, vol. 8, no. 4, pp. 01–10, 2021. [Google Scholar]

12. W. Sanusi, S. Annas, M. I. Pratama and M. Rifandi, “Analysis and simulation of SIPA model for HIV-AIDS transmission,” Journal of Physics: Conference Series, vol. 21, no. 1, pp. 01–09, 2021. [Google Scholar]

13. A. Shaikh, K. S. Nisar, V. Jadhav, S. K. Elagan and M. Zakarya, “Dynamical behaviour of HIV/AIDS model using fractional derivative with Mittag-Leffler kernel,” Alexandria Engineering Journal, vol. 61, no. 4, pp. 2601–2610, 2022. [Google Scholar]

14. R. E. Mickens, “A fundamental principle for constructing nonstandard finite difference schemes for differential equations,” Journal of Difference Equations and Applications, vol. 11, no. 2, pp. 645–653, 2005. [Google Scholar]

15. K. C. Patidar, “Nonstandard finite difference methods: Recent trends and further developments,” Journal of Difference Equations and Applications, vol. 22, no. 6, pp. 817–849, 2016. [Google Scholar]

16. L. Jodar, R. J. Villanueva, A. J. Arenas and G. C. Gonzalez, “Nonstandard numerical methods for a mathematical model for influenza disease,” Mathematics and Computers in Simulation, vol. 79, no. 3, pp. 622–633, 2008. [Google Scholar]

17. A. Raza, M. Rafiq, D. Baleanu, M. S. Arif, M. Naveed et al., “Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population,” IET Systems Biology, vol. 13, no. 6, pp. 305–315, 2019. [Google Scholar]

18. M. Jawaz, N. Ahmed, D. Baleanu, M. Rafiq and M. A. Rehman, “Positivity preserving technique for the solution of HIV/AIDS reaction-diffusion model with time delay,” Frontiers in Physics, vol. 7, no. 1, pp. 1–10, 2020. [Google Scholar]

19. Z. Iqbal, N. Ahmed, D. Baleanu, W. Adel, M. Rafiq et al., “Positivity and boundedness preserving numerical algorithm for the solution of fractional nonlinear epidemic model of HIV/AIDS transmission,” Chaos Solitons & Fractals, vol. 134, no. 1, pp. 1–19, 2020. [Google Scholar]

20. N. Ahmed, M. Rafiq, W. Adel, H. Rezazadeh, I. Khan et al., “Structure preserving numerical analysis of HIV and CD4+ T-cells reaction-diffusion model in two space dimensions,” Chaos Solitons & Fractals, vol. 139, no. 1, pp. 1–18, 2020. [Google Scholar]

21. S. U. Arifeen, S. Haq, A. Ghafoor, A. Ullah, P. Kumam et al., “Numerical solutions of higher-order boundary value problems via wavelet approach,” Advances in Difference Equations, vol. 347, no. 1, pp. 1–19, 2021. [Google Scholar]

22. Z. Shah, R. Jan, P. Kumam, W. Deebani and M. Shutaywi, “Fractional dynamics of HIV with source term for the supply of new CD4+ T-cells depending on the viral load via Caputo Fabrizio derivative,” Molecules, vol. 26, no. 6, pp. 1806–1820, 2021. [Google Scholar]

23. T. Q. Tang, Z. Shah, R. Jan, W. Deebani and M. Shutaywi, “A robust study to conceptualize the interactions of CD4+ T-cells and human immunodeficiency virus via fractional-calculus,” Physica Scripta, vol. 96, no. 12, pp. 1–20, 2021. [Google Scholar]

24. A. Raza, A. Ahmadian, M. Rafiq, S. Salashour, M. Naveed et al., “Modeling the effect of delay strategy on transmission dynamics of HIV/AIDS disease,” Advances in Difference Equations, vol. 663, no. 1, pp. 1–19, 2020. [Google Scholar]

25. A. Raza, A. Ahmadian, M. Rafiq, S. Salahshour and I. R. Laganà, “An analysis of a nonlinear susceptible-exposed-infected-quarantine-recovered pandemic model of a novel coronavirus with delay effect,” Results in Physics, vol. 21, no. 1, pp. 1–7, 2021. [Google Scholar]

26. A. Raza, M. S. Arif, M. Rafiq, M. Bibi, M. Naveed et al., “Numerical treatment for stochastic computer virus model,” Computer Modeling in Engineering and Sciences, vol. 120, no. 2, pp. 445–465, 2019. [Google Scholar]

27. M. S. Arif, A. Raza, K. Abodayeh, M. Rafiq and A. Nazeer, “A numerical efficient technique for the solution of susceptible infected recovered epidemic model,” Computer Modeling in Engineering and Sciences, vol. 124, no. 2, pp. 477–491, 2020. [Google Scholar]

28. W. Shatanawi, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Essential features preserving dynamics of stochastic dengue model,” Computer Modeling in Engineering and Sciences, vol. 126, no. 1, pp. 201–215, 2021. [Google Scholar]

29. M. A. Noor, A. Raza, M. S. Arif, M. Rafiq, K. S. Nisar et al., “Non-standard computational analysis of the stochastic COVID-19 pandemic model: An application of computational biology,” Alexandria Engineering Journal, vol. 61, no. 1, pp. 619–630, 2021. [Google Scholar]

30. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Numerical analysis of stochastic vector-borne plant disease model,” Computers, Materials and Continua, vol. 63, no. 1, pp. 65–83, 2020. [Google Scholar]

31. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Stochastic numerical analysis for impact of heavy alcohol consumption on transmission dynamics of gonorrhoea epidemic,” Computers, Materials and Continua, vol. 62, no. 3, pp. 1125–1142, 2020. [Google Scholar]

32. A. Raza, J. Awrejcewicz, M. Rafiq, N. Ahmed, M. S. Ahsan et al., “Dynamical analysis and design of computational methods for nonlinear stochastic leprosy epidemic model,” Alexandria Engineering Journal, vol. 61, no. 10, pp. 8097–8111, 2022. [Google Scholar]

33. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Stochastic analysis of nonlinear cancer disease model through virotherapy and computational methods,” Mathematics, vol. 10, no. 3, pp. 1–18, 2022. [Google Scholar]

34. A. Raza, M. Rafiq, J. Awrejcewicz, N. Ahmed and M. Mohsin, “Dynamical analysis of coronavirus disease with crowding effect, and vaccination: A study of third strain,” Nonlinear Dynamics, vol. 107, no. 4, pp. 3963–3982, 2022. [Google Scholar]

35. A. Raza, J. Awrejcewicz, M. Rafiq and M. Mohsin, “Breakdown of a nonlinear stochastic Nipah virus epidemic model through efficient numerical methods,” Entropy, vol. 23, no. 12, pp. 1–20, 2021. [Google Scholar]

36. M. I. Daabo and B. Seidu, “Modelling the effect of irresponsible infective immigrants on the transmission dynamics of HIV/AIDS,” Advances in Applied Mathematical Biosciences, vol. 3, no. 1, pp. 31–40, 2012. [Google Scholar]