An Energy-Efficient Multi-swarm Optimization in Wireless Sensor Networks

1  Introduction

WSNs are made up of several sensor nodes that collect information from the execution surroundings and communicate it to the gateways via energy-efficient connectivity for more observation or analysis. In the domain of the Internet of Things, WSNs have a broad collection of applications, including home automation, management, and manufacturing inspections. Among the most important quality factors for WSNs is target covering, which represents the wireless sensor nodes’ network coverage capacities, which has a direct impact on data gathering. The system was considered deceased when the actual sensing range of WSNs falls beneath threshold exposure [1]. The energy-efficient system consumes less energy while transforming data.

A WSN technology is capable of completing unachievable tasks on and near the ground surface. Importantly, wireless networks change the world into a compact community in the business world as a result of the great achievement of WSN technologies and information communications systems [2]. Oceanographic, environmental control, farming, and engineering are among the fields where WSN has reached a new level. Massive numbers of smart, cost-effective rechargeable battery sensor nodes are created in ad-hoc wireless personal area networks (WPAN). It consists of a Central Processing Unit (CPU), a radio module, and a power source coupled to it [3].

Energy is the biggest issue when more sensor devices are demanded from the user. This motivates our research to choose energy-efficient communication in WSN. The lifespan of the networks is extended by observing areas that are separated into clusters. Every cluster has a large number of sensor nodes. Only one sensor serves as cluster head (CH), with the others serving as cluster members. The data is gathered from individual sensors in the given area. During the CH selection process in each area, the nodes with the highest power residues relative to those other nodes are selected as CH [4].

Numerous studies have been conducted on transmitting data strategies that used optimize WSN power usage and information reduction technologies used to decrease data transmission energy [5,6]. Data aggregation, on the other hand, is a broad topic with numerous issues that need to be investigated. As a result, the primary emphasis is routing protocol optimization, which will be covered in-depth in this section. To finish the observation of the target region, the data collected from the node is sent to the base station (BS) [7]. The energy consumption for such transferring of information of the same length increases as the transmission length grows, particularly in the case when the base station is located distant from the data gathering system. As a result of limited bandwidth, the intensive transmission job may degrade the consumer perceptions of the sink nodes and induce queue latencies [8].

Each sensor node in the EH (Energy Harvesting)-WSNs has the potential to gather energy from ambient, including breeze, sunlight, and thermal power, and store it in its own battery charger [9]. Whenever the total energy harvested is greater than or equal to the amount of energy consumed, continuous coverage can be achieved for the whole-energy monitoring of WSNs [10]. As a result, the Mobile Location Centre of WNSs is determined not simply by EH effectiveness other than by power usage [11]. Because the WSN node may send information during the energy-harvesting stage, the energy-efficient procedure for the EH networks should be rewritten to contract with changeable facts routes and broken nodes [12].

In [13], the routing protocol is designed using a Particle Swarm Optimization (PSO) technique to minimize intra-cluster distances and so achieve an energy-efficient routing mechanism. To optimize the clustering approach utilizing the heuristic algorithm, [14] proposes a fuzzy-enhanced blossom breeding based on an algorithm, threshold-sensitive, energy-efficient grouping procedure. The cluster head nodes are determined by taking into account all of the sensor characteristics, namely residual energy, node centralization, and ranges to BS. In [15] optimizes the previous stable election protocol (SEP) to ensure a balanced energy allocation among cluster head nodes and node density.

The main contribution of the proposed technique is given below:

•   An adaptive hierarchical clustering-based routing helps in the transmission of data in the cluster and reduces energy consumption.

•   It efficiently chooses the Cluster Head (CHs) selection.

•   The Genetic algorithm helps to minimize the cost optimization problems.

•   The Multi swarm optimization optimizes the routing process and efficiently improves the network’s lifetime.

The rest of our research article is written as follows: Section 2 discusses the related work on various Wireless Sensor Network and Routing methods. Section 3 shows the algorithm process and general working methodology of the proposed work. Section 4 evaluates the implementation and results of the proposed method. Section 5 concludes the work and discusses the result evaluation.

2  Related Work

Whenever there is an inconsistency in the communications network’s transfer of information, an energy hole is generated, causing the SNs to die prematurely, reducing the lifespan of the network [16,17]. The author in [18,19], who offered a strategy wherein the transmitted signal was changed dependent on the distances between CHs and their users, fixed this problem. The implementation of a firefly optimization technique also increased the network’s longevity. This method was applied against conventional methods in a variety of scenarios. According to the findings of their research, this algorithm produced better outcomes in terms of network life. The author, on the other hand, makes no mention of the SNs’ total power maximization while preserving the optimal CH range.

Researchers [20] proposed the PSO-UFC (PSO-based Unequal and Fault-Tolerant Clustering technique). The current Energy-Balanced Unequal Clustering (EBUC) method’s imbalanced grouping and fault-tolerant difficulties were solved in the method suggested for long-term network effectiveness. A shortage of imbalance in the clustering method was used to equalize intra- and inter-cluster energy use amongst Master CHs to remedy an unbalance in a clustering algorithm MCs). Moreover, in the PSO-UFC protocol, the internet connection was restored by selecting an extra CH termed Surrogate CH in the event of an impulse MCH failure.

The author [21] projected an improved Cuckoo Search (CS), based on power balancing node clustering protocol due to a new optimization problem using the uniform dispersion of CHs. The author proposed an upgraded Harmony Search (HS) routing protocol to transmit packets of data among CHs and the sink in another paper. The efficiency of the provided combined clustering and routing system was assessed using energy cost, the amount of alive and dying nodes, and network longevity. In comparison to existing protocols, the novel Cuckoo-Harmony Search-based combined route and grouping method revealed more results. When constructing state-of-the-art meta-heuristic algorithms with merged routing and clustering, the researcher disregards incorporating the lifespan and end-to-end delay elements. Tab. 1 shows the traditional routing protocols that were used.

3  Proposed Methodology

In the proposed method, multi-Swarm optimization with Genetic Algorithms and Adaptive hierarchical clustering-based routing is used for optimal CHs selection and data transmission. Fig. 1 shows the architecture of the suggested method. It consists of a system model, energy model, and fitness function.

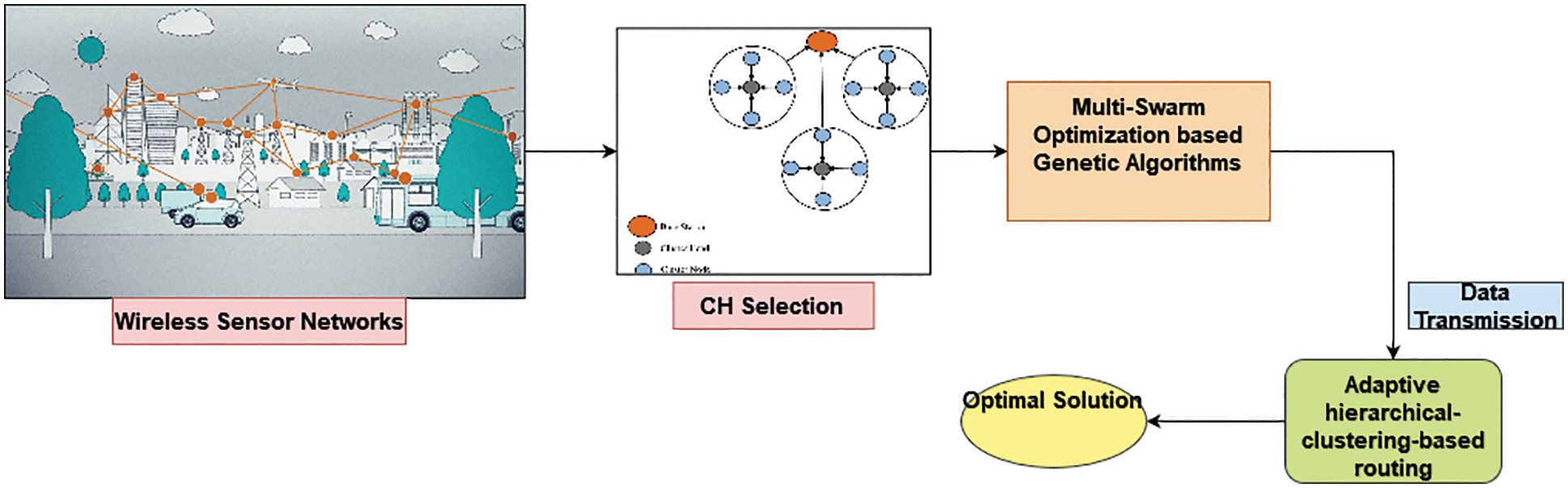
Figure 1: Architecture of the proposed method

3.1 System Model

The system model in this study effort comprises a base station (BS) and sensors (N) that maintains a homogenous distribution due to the random placement throughout the transmission range. As a result, the networks are populated with a huge amount of devices that are distributed throughout the service area for the improvement of network access. The network’s subcategories and secret aspects are covered. The network, that comprises the BS and sensor nodes, is perfectly stable. At the start, every node has the same amount of energy. The BS would have no energy constraints and has very high computing energy [25–43].

The main cluster head (PCH) and secondary cluster head (SCH) are selected on a regular basis based on the communication range and localization. The nodes optimize the energy based on the data transmission. The sleeping and waking node idea is implemented in the network to reduce energy usage. Each cluster members are multi-weighted, allowing for changing remaining energy to be maintained. The BS and PCH are located inside the network’s communication range, and the nodes get the capability to broadcast their address information to their neighbor nodes. In fact, one-hop transmission has a significant impact on energy. As a result, p-jump is a preferred idea. In this study, multi-weight clustering would be described, which employs resource scheduling in groups to minimize energy consumption and improve WSN energy efficiency.

3.2 Energy Model

In this model, there are two types of power loss were used. One is free space power loss (fd2) and the next one is multipath fading power loss (fd4), and the communication system is chosen based on the data transmission between both the origin and the sinks. If the range is much fewer than the threshold value (fdth), the free space modeling is used as a channel model; otherwise, the multi-path fading design is used as channel estimation. The following is a mathematical expression of the data’s energy use depending on the distance factor:

ENtx(l,fd)={l∗ENene+l∗ENtm∗fd2,iffd≤fdthl∗ENene+l∗ENam∗fd4,iffd>fdth (1)

Here, ENene is denoted as the entire amount of energy dissipapre-bit bit, ENtm, ENam is a network’s transmitter and amplifier.

fdth=ENtmENam (2)

The sink’s energy utilization is expressed as

ENrx(l)=l∗ENene (3)

3.3 Fitness Function

In sort to extend the life span of WSN networks, several clustering approaches are used to solve this problem. By providing the most effective solution for selecting the best cluster-head (CHs). All of these strategies rely on the fitness function. The fitness function determines the structure’s relative value. A greater appropriateness score indicates a more effective design. The fitness function in our research takes into account power consumption as well as the distances between the cluster members and the BS, as well as the range among member nodes and the cluster members. Our method’s fitness function multi-pathn FI is given by

FI=∑i⁡(ωi∗fi)∀fi∈{E,D} (4)

Assigns weights to the basic fitness parameters at random (wi). The weights for each variable are w1 and w2. The amount of energy used to pass on all of the gathered data to the BS is provided by: Those weight values are modified according to the design requirements.

EN=∑i=1o⁡EN(i,ch)+∑i=1p⁡(m∗Rx)+∑i=1p⁡EN(i,bs) (5)

The entire distance range is expressed as:

Dis=∑i=1o⁡Dis(i,ch)+∑i=1p⁡Dis(i,bs) (6)

Here o and p represents cluster members and Dis(i, ch) denotes detachment ranges from the node to CH.

3.4 Multi Swarm Optimization

The multi-PSO swarm is discussed in this paper that does not generalize instantaneously because the swarms do not communicate. If the time is appropriate to acquire other swarm, there may be communication; nevertheless, one swarm diminishes as a result of a variety of data exchange topologies. Therefore, two multi-swarm approaches are proposed. A multi-population form of CPSO is Multi-Charged Particle Swarm Optimization (CPSO). In place of standard atom targets, Multi-Quantum Swarm Optimization (MQSO) uses quantum swarm relying on quantum.

In CPSO, a certain number of particles receive a charge that repels other charged particles. Particles which have been assigned a value, while neutral particles are those that have not been given a charge. Particle speeds are updated using a standard updating formula with an additional option dependent on their closeness towards other particles.

ve→i(t+1)=wve→i(t)+co1r→1(t)(pbest→−x→i(t))+co2r→2(t)(gbest→−x→i(t)) (7)

Here ve→i is represented as a particles speed of i, x→i is the particles point.

The following is the CPSO velocity updating formula:

ve→i(t+1)=wve→i(t)+co1r→1(t)(pbest→−x→i(t))+co2r→2(t)(gbest→−x→i(t))+∑∀j≠i⁡aij (8)

The angular velocity of particles i and j is provided.

aij={CQiCQj||x→i−x→j||(x→i−x→j)ifpcore<||x→i−x→j||≤p0otherwise (9)

Here CQi denotes the charges of element i and p and pcore determine the radius of impact of the acceleration term.

The MQSQ method is used to calculate multi-modal dynamic issues. For explore multiple promising peaks in parallel, a swarm is partitioned into sub swarms. In concluding the searching in the local optimum, diversity is raised but probability is diminished. Furthermore, such swarms consist of two sorts of particles: i) PSO particles that pursue the normal PSO method but aim to obtain a greater location; (ii) quantum particles which orbit it around sub swarm attractor in a radius rcloud to maintain variety in addition to the proposed method. The issue of diversity defeat is addressed by quantum particles. The location of quantum element is designed using the Eq. (10):

p→i∈BAn(γcloud) (10)

3.4.1 Genetic Algorithm

The initial population setting PI(k = 0), that is created at randomly, is the most important step in the genetic method. The sequencing of genes creates the chromosome, which are then controlled by certain properties. Secondly, the fitness function is determined using chromosomal values. The evolution process is then performed, with the fit form being developed as well as the unfit ideas being eliminated. This process is repeated until the system contains all of the desired fitness values. Such final approved patterns are referred to as parents, and they are utilized to create offspring designs for future generations.

Two portions are used to carry out the genetic algorithms evolutionary process. Mutation and crossovers are the terms used to describe them. A mutation operator is a procedure that is created randomly utilizing chromosome genes and is chosen randomly. The likelihood of mutation in our study is pim(k) = 0.03. The crossover procedure uses a swapping operation to make children from two specific parent chromosomes. We utilize a single point crossover with pic(k) = 0.6 as the threshold.

3.4.2 Adaptive Hierarchical-Clustering Based Routing

The hierarchical clustering (HC) method is a rapid clustering technique that may autonomously achieve agglomerative clustering based on node placement. Humans are not required to designate the cluster leader or the number of clusters during the clustering stage. The agglomerative HC method is used to minimize the data communication approach within every cluster, and it achieves an acceptable clustering after placement of the WSN nodes. As a result, during the evaluation phase of WSNs, signal is obtained from nodes and integrated into data packages by CHs. CHs are responsible for sending these data correspondence to the base station, indicating that the CHs consume additional power than other nodes in the network. The clustering technique can be used to optimize data transport while also guaranteeing excellent energy consumption.

Assuming that R nodes were ideally positioned in the placement area, and also that the node positions are stable and determined ahead of time. These R nodes will be considered the starting clusters, as per the concept of the aggregate hierarchical clustering algorithm:

CLi={Xi},i∈R (11)

Here CLi denotes the ith cluster that has been created. For every clustering iteration, the maximum Euclidean distance among any two clusters will be computed and used as the clustering price.

The two components with the nearest proximity would then merge to form a original cluster till the requisite amount of clusters was reached or the provided the required was met.

Dis(CLR+a,CLR+b)=Dis(Xi,Xk) (12)

The cluster labels are represented by R + a and R + b. The longest range among deployed sensor nodes Dismax is chosen and modified as the clustering discontinuation criterion TH in this paper.

TH=σDismax

=σmax{(Xi−Xj)2+(Yi−Yj)2},i,j∈R,i≠j (13)

Here Xi = (Xi, Yi), Xj = (Xj, Yj) signifies the ith and jth node positions, and denotes the practical component, that is calculated as the proportion of distances among nodes inside the confident range.

The maximum range and reliable information range among the deployed sensor nodes that can ensure a variance among clusters and limit the variance within the established cluster, work together to determine clustering ending. As a result, combining the assurance range with the node topology could result in additional sensible node clustering.

The energy usage of every cluster might rise as the threshold distance increases in order to transport a particular amount of information to the base station. Therefore, the amount of clusters would drop as a result, reducing the data package’s transfer size. When it comes to increasing energy efficiency, optimizing the threshold range could be beneficial. As a result, by optimizing the node topology, the suggested environment-adaptive hierarchical clustering might boost the MLC of WSNs.

4  Result Analysis

The suggested MSO-GAHC technique is examined in this part by evaluating its effectiveness to that of GA, MWCSGA, MSO-TS and MSO-GAHC based clustering. The analytical tests are run on a Dell OptiplexTM 3020 PC including an Intel Core i7–4770 3.4 GHz processor, 8 MB caches, integrated Intel graphics, 16 GB RAM, 1 TB HDD, and Windows 10 operating system. As the simulated environment, Matlab R2019a is utilized. Tab. 2 lists the network parameters that were utilized.

Tests with 200 to 1500 nodes and 0 to 500 rounds are undertaken. The amount of clusters generated, the average end-to-end delay in secs, the overall packet loss rates, the lifespan computations, and theaverage energy released in joules are all factors to consider. In Fig. 2 shows that the energy consumption used for each round. The proposed method MSO-GAHC achieves better energy usage compared with other algorithms. It takes less energy for each round.

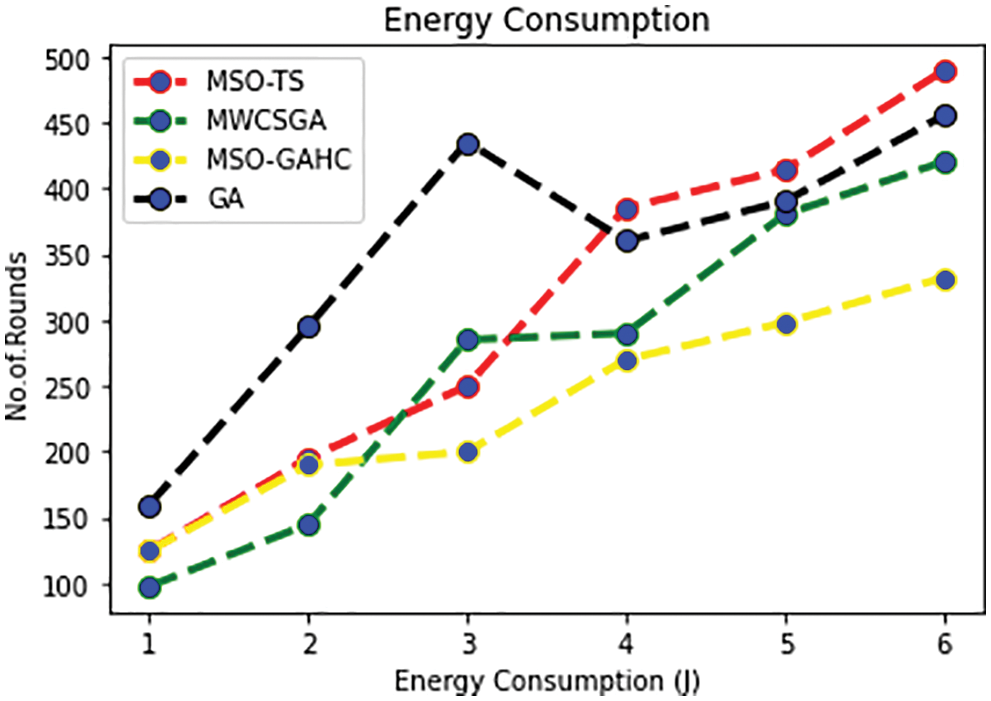
Figure 2: Energy consumption

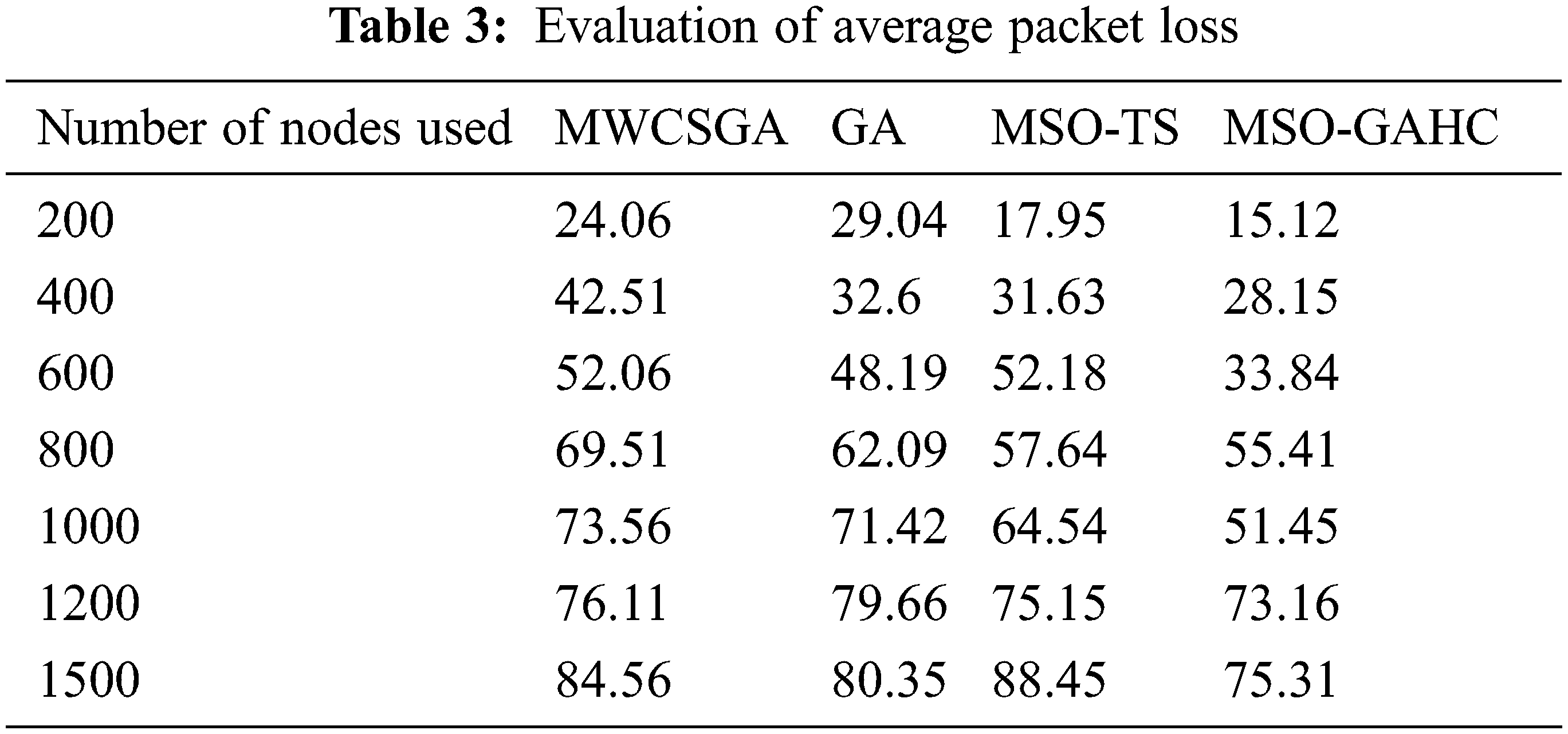
In Fig. 3 the average packet loss rate is evaluated. The proposed method achieves better performance compared with other algorithms. It achieves lower average packet loss rate. In Tab. 3 the evaluations are shown.

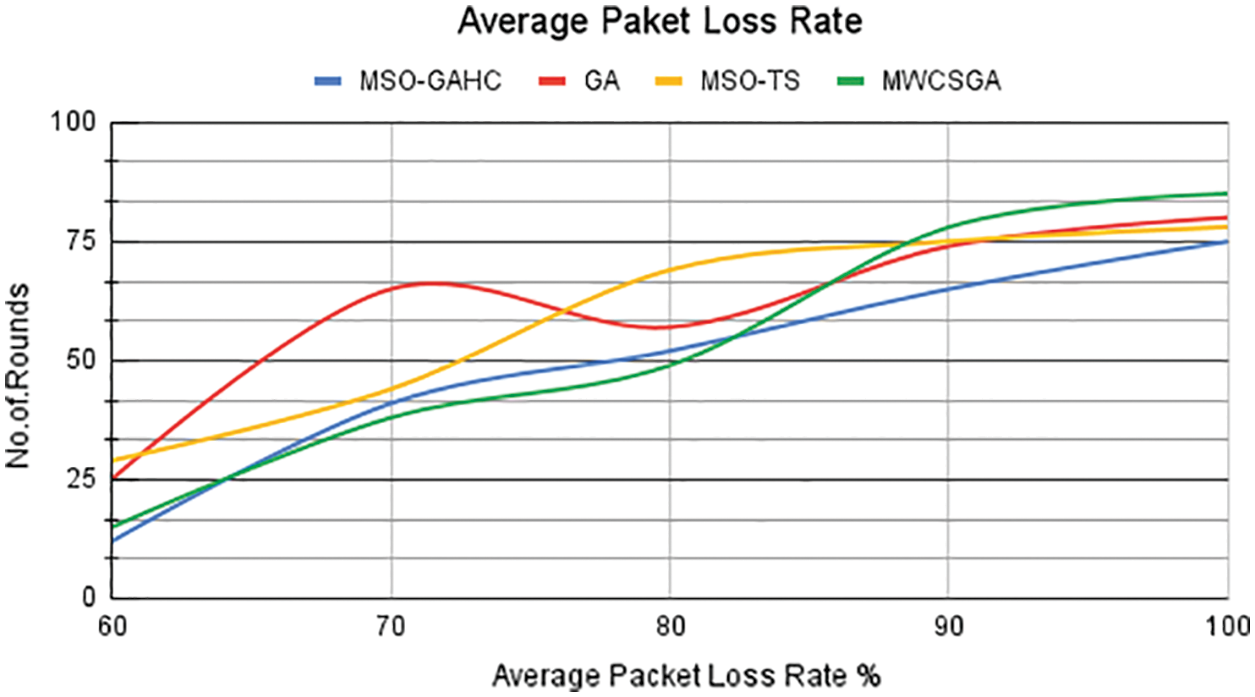
Figure 3: Average packet loss rate

In Fig. 4 shows that the proposed method achieves lower end-to-end delay. Comparing with other algorithms such as GA, MWCSGA and MSO-TS the proposed method MSO-GAHC outperforms better.

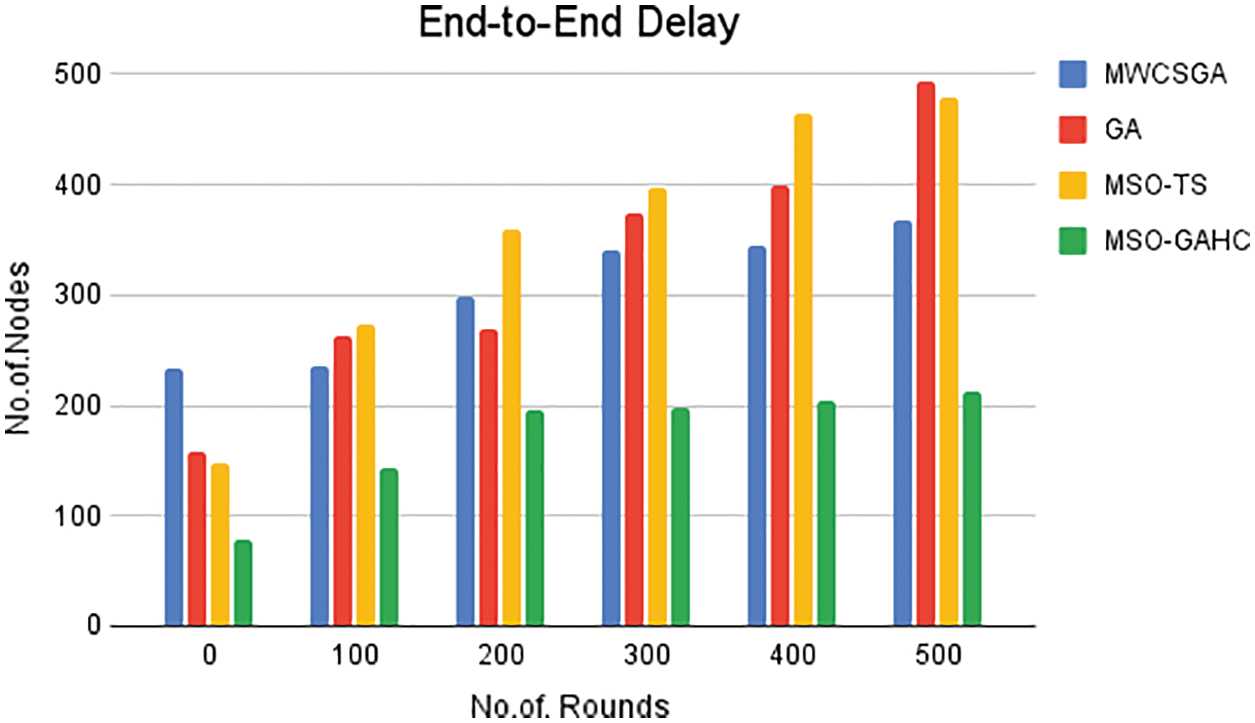
Figure 4: End-to-End delay

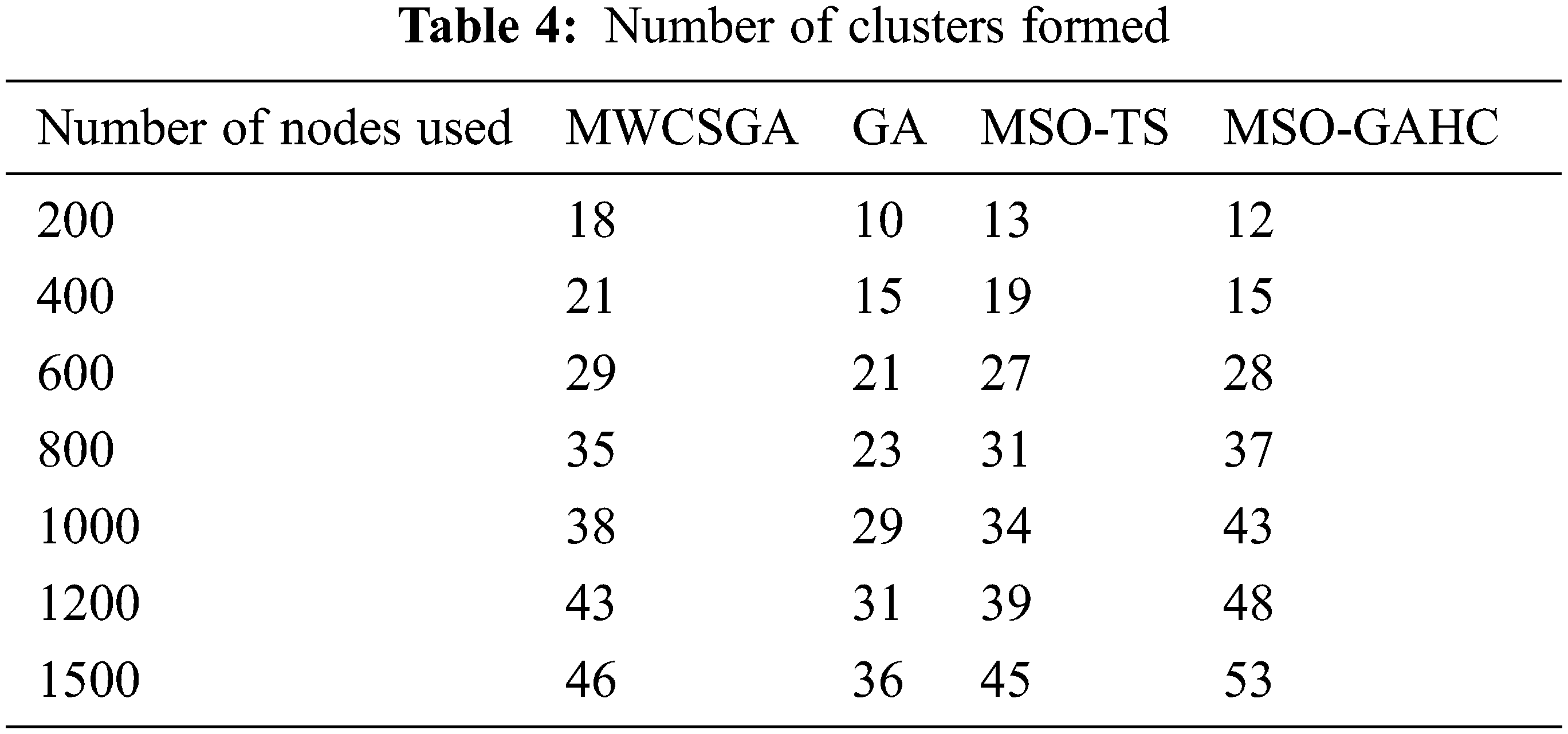
In Fig. 5 shows that the amount of clusters formed. The proposed method MSO-GAHC has higher amount of clusters formed during every round. Comparing with other algorithms it forms a clusters 50%, 30%, 12%. In Tab. 4 depicts the amount of clusters formed.

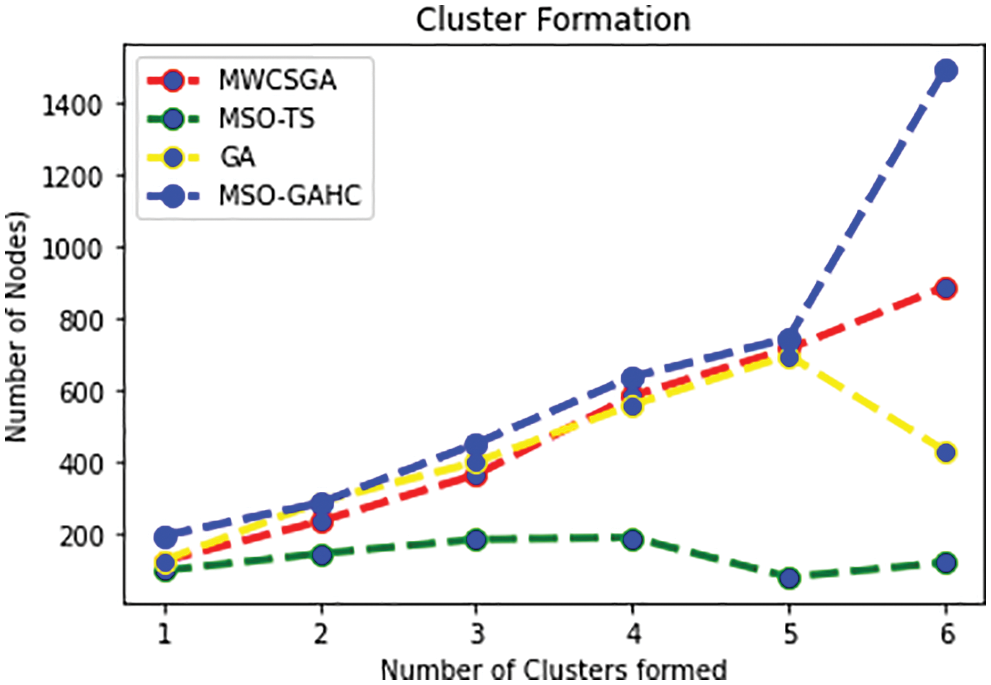
Figure 5: Cluster formation

The highest packets processed during a given period of time are described as network throughput. The throughput evaluation of the nodes is compared in Fig. 6 for several algorithms such as GA, MWCSGA, MSO-TS and MSO-GAHC. The simulations test is carried out with 1500 nodes in this environment. The proposed method achieves highest throughput compared with other algorithms.

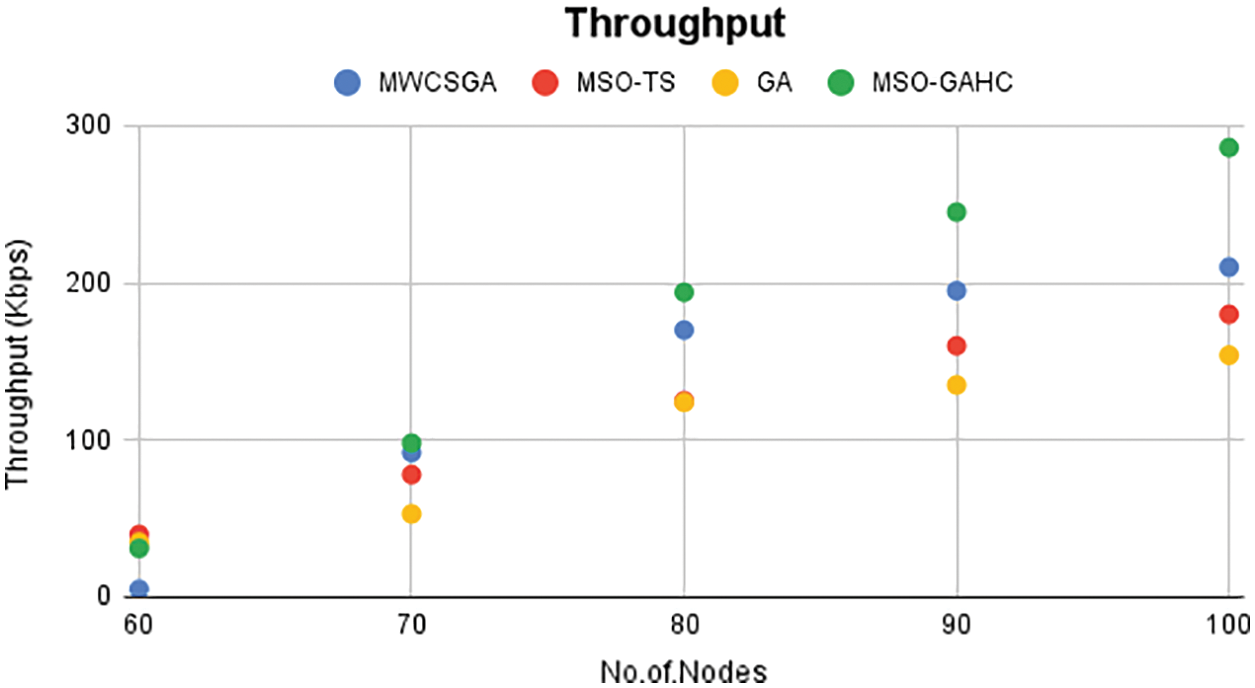
Figure 6: Throughput

5  Conclusion

A most essential criterion for operating WSNs successfully and reliably is energy conservation, and energy consumption is given a lot of weight in major technical issues and resource management. The most important objective of this study is to use a hybrid heuristic algorithm to develop WSN CH selection. As a result, an algorithm which is based on multi-Swarm optimization based on Genetic Algorithm and Adaptive Hierarchical clustering (MSO-GAHC) based routing protocol is used. The suggested method is developed for optimizing the WSN and CH selection routing. The solution provided is both energy efficient and networks responsive. The presented technique selects effective 53 CHs in reaction to the networks. The nodes could perform environment-adaptive clustering based on their ranges from one another that can decrease data transmission energy consumption and improve the network’s architectural connectivity. The suggested approach optimizes routing and extends the network’s lifetime by selecting effective CHs. The experimental outcome shows that the proposed technique increases the cluster formation; throughput also decreases the average packet loss rate, standard end-to-end delay. The suggested method achieves minimum energy consumption for every round compared with GA, MWCSGA and MSO-TS.

Acknowledgement: The authors express their gratitude to Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R323), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest regarding the publication of the paper.

References

 1.  S. Suganthi, N. Umapathi, M. Mahdal and M. Ramachandran, “Multi swarm optimization based clustering with tabu search in wireless sensor network,” Sensors, vol. 22, no. 5, pp. 1736, 2022. [Google Scholar]

 2.  B. Han, F. Ran, J. Li, L. Yan, H. Shen et al., “A novel adaptive cluster based routing protocol for energy-harvesting wireless sensor networks,” Sensors, vol. 22, no. 4, pp. 1–20, 2022. [Google Scholar]

 3.  N. Ajmi, A. Helali, P. Lorenz and R. Mghaieth, “MWCSGA—Multi weight chicken swarm based genetic algorithm for energy efficient clustered wireless sensor network,” Sensors, vol. 21, no. 3, pp. 791, 2021. [Google Scholar]

 4.  S. Kaur and R. Mahajan, “Hybrid meta-heuristic optimization based energy efficient protocol for wireless sensor networks,” Egyptian Informatics Journal, vol. 19, no. 3, pp. 145–150, 2018. [Google Scholar]

 5.  S. Loganathan and J. Arumugam, “Energy efficient clustering algorithm based on particle swarm optimization technique for wireless sensor networks,” Wireless Personal Communications, vol. 119, no. 1, pp. 815–843, 2021. [Google Scholar]

 6.  Z. Wan, S. Liu, W. Ni and Z. Xu, “An energy-efficient multi-level adaptive clustering routing algorithm for underwater wireless sensor networks,” Cluster Computing, vol. 22, no. 6, pp. 14651–14660, 2021. [Google Scholar]

 7.  X. Fu, Y. Yang and O. Postolache, “Vulnerability of clustering wireless sensor networks against cascading failures,” IEEE Systems Journal, vol. 13, no. 2, pp. 1431–1442, 2018. [Google Scholar]

 8.  D. W. Sambo, B. O. Yenke, A. Forster and P. Dayang, “Optimized clustering algorithms for large wireless sensor networks: A review,” Sensors, vol. 19, no. 2, pp. 322–345, 2019. [Google Scholar]

 9.  M. Sajwan, D. Gosain and A. K. Sharma, “CAMP: Cluster aided multi-path routing protocol for wireless sensor networks,” Wireless Networks, vol. 25, no. 5, pp. 2603–2620, 2019. [Google Scholar]

10. B. Shah, A. Abbas, G. Ali, F. Iqbal, A. M. Khattak et al., “Guaranteed lifetime protocol for IoT based wireless sensor networks with multiple constraints,” Ad Hoc Networks, vol. 104, no. 3, pp. 102158, 2020. [Google Scholar]

11. L. Wenxing, W. Muqing and W. Yuewei, “Design of multi energy space based energy-efficient algorithm in novel software-defined wireless sensor networks,” International Journal of Distributed Sensor Networks, vol. 13, no. 7, pp. 1–15, 2017. [Google Scholar]

12. N. Mittal, U. Singh, R. Salgotra and M. Bansal, “An energy efficient stable clustering approach using fuzzy-enhanced flower pollination algorithm for WSNs,” Neural Computing and Applications, vol. 32, no. 11, pp. 7399–7419, 2020. [Google Scholar]

13. T. Behera, M. S. Kumar, S. U. Chandra, S. Mohammad and H. Amir, “I-SEP: An improved routing protocol for heterogeneous WSN for IoT-based environmental monitoring,” IEEE Internet of Things Journal, vol. 7, no. 1, pp. 710–717, 2019. [Google Scholar]

14. N. Khademi and S. Sharifian, “A hierarchical routing protocol for EH-WSNs,” Wireless Networks, vol. 26, no. 6, pp. 4303–4317, 2020. [Google Scholar]

15. U. N. Nisha and A. M. Basha, “Triangular fuzzy-based spectral clustering for energy-efficient routing in wireless sensor network,” The Journal of Supercomputing, vol. 76, no. 6, pp. 4302–4327, 2020. [Google Scholar]

16. R. Thiagarajan, “Energy consumption and network connectivity based on novel-LEACH-POS protocol networks,” Computer Communications, vol. 149, no. 3, pp. 90–98, 2020. [Google Scholar]

17. Y. Xu, O. Ding, R. Qu and K. Li, “Hybrid multi-objective evolutionary algorithms based on decomposition for wireless sensor network coverage optimization,” Applied Soft Computing, vol. 68, no. 5, pp. 268–282, 2018. [Google Scholar]

18. T. Kaur and D. Kumar, “Particle swarm optimization-based unequal and fault tolerant clustering protocol for wireless sensor networks,” IEEE Sensors Journal, vol. 18, no. 11, pp. 4614–4622, 2018. [Google Scholar]

19. V. Varsha, J. Singh and M. Bala, “Tabu search based energy efficient clustering protocol for wireless sensor networks,” Global Journal of Computers & Technology, vol. 5, no. 2, pp. 302–309, 2017. [Google Scholar]

20. G. P. Gupta, “Improved cuckoo search-based clustering protocol for wireless sensor networks,” Procedia Computer Science, vol. 125, no. 10, pp. 234–240, 2018. [Google Scholar]

21. G. P. Gupta and S. Jha, “Integrated clustering and routing protocol for wireless sensor networks using cuckoo and harmony search based metaheuristic techniques,” Engineering Applications of Artificial Intelligence, vol. 68, no. 12, pp. 101–109, 2018. [Google Scholar]

22. G. Shanthi and M. Sundarambal, “FSO–PSO based multihop clustering in WSN for efficient medical building management system,” Cluster Computing, vol. 22, no. 5, pp. 12157–12168, 2019. [Google Scholar]

23. L. Nagarajan and S. Thangavelu, “Hybrid grey wolf sunflower optimisation algorithm for energy-efficient cluster head selection in wireless sensor networks for lifetime enhancement,” IET Communications, vol. 15, no. 3, pp. 384–396, 2021. [Google Scholar]

24. M. Abouhawwash and K. Deb, “Karush-kuhn-tucker proximity measure for multi-objective optimization based on numerical gradients,” in Proc. 2016 on Genetic and Evolutionary Computation Conf. Companion, ACM, Denver Colorado USA, pp. 525–532, 2016. [Google Scholar]

25. A. H. El-Bassiouny, M. Abouhawwash and H. S. Shahen, “New generalized extreme value distribution and its bivariate extension,” International Journal of Computer Applications, vol. 173, no. 3, pp. 1–10, 2017. [Google Scholar]

26. A. H. El-Bassiouny, M. Abouhawwash and H. S. Shahen, “Inverted exponentiated gamma and its bivariate extension,” International Journal of Computer Application, vol. 3, no. 8, pp. 13–39, 2018. [Google Scholar]

27. A. H. El-Bassiouny, H. S. Shahen and M. Abouhawwash, “A new bivariate modified weibull distribution and its extended distribution,” Journal of Statistics Applications & Probability, vol. 7, no. 2, pp. 217–231, 2018. [Google Scholar]

28. M. Abouhawwash and M. A. Jameel, “KKT proximity measure versus augmented achievement scalarization function,” International Journal of Computer Applications, vol. 182, no. 24, pp. 1–7, 2018. [Google Scholar]

29. H. S. Shahen, A. H. El-Bassiouny and M. Abouhawwash, “Bivariate exponentiated modified weibull distribution,” Journal of Statistics Applications & Probability, vol. 8, no. 1, pp. 27–39, 2019. [Google Scholar]

30. M. Abouhawwash and M. A. Jameel, “Evolutionary multi-objective optimization using benson’s karush-kuhn-tucker proximity measure,” in Int. Conf. on Evolutionary Multi-Criterion Optimization, East Lansing, Michigan, USA, Springer, pp. 27–38, 2019. [Google Scholar]

31. M. Abouhawwash, M. A. Jameel and K. Deb, “A smooth proximity measure for optimality in multi-objective optimization using benson’s method,” Computers \& Operations Research, vol. 117, no. 2, pp. 104900, 2020. [Google Scholar]

32. M. Abouhawwash, K. Deb and A. Alessio, “Exploration of multi-objective optimization with genetic algorithms for PET image reconstruction,” Journal of Nuclear Medicine, vol. 61, no. 1, pp. 572–572, 2020. [Google Scholar]

33. M. Abdel-Basset, R. Mohamed, M. Elhoseny, M. Abouhawwash, Y. Nam et al., “Efficient MCDM model for evaluating the performance of commercial banks: A case study,” Computers, Materials & Continua, vol. 67, no. 3, pp. 2729–2746, 2021. [Google Scholar]

34. B. Gomathi, S. Balaji, V. K. Kumar, M. Abouhawwash, S. Aljahdali et al., “Multi-objective optimization of energy aware virtual machine placement in cloud data center,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1771–1785, 2022. [Google Scholar]

35. M. Kumar, K. Venkatachalam, M. Masud and M. Abouhawwash, “Novel dynamic scaling algorithm for energy efficient cloud computing, ” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1547–1559, 2022. [Google Scholar]

36. R. S. Ram, K. Venkatachalam, M. Masud and M. Abouhawwash, “Air pollution prediction using dual graph convolution LSTM technique,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1639–1652, 2022. [Google Scholar]

37. A. J. Basha, N. Rajkumar, M. A. AlZain, M. Masud and M. Abouhawwash, “Fog-based self-sovereign identity with RSA in securing IoMT data,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1693–1706, 2022. [Google Scholar]

38. G. Ravikumar, K. Venkatachalam, M. A. AlZain, M. Masud and M. Abouhawwash, “Neural cryptography with fog computing network for health monitoring using IoMT,” Computer Systems Science and Engineering, vol. 44, no. 1, pp. 945–959, 2023. [Google Scholar]

39. R. Rajdevi, K. Venkatachalam, M. Masud, M. A. AlZain and M. Abouhawwash, “Proof of activity protocol for IoMT data security,” Computer Systems Science and Engineering, vol. 44, no. 1, pp. 339–350, 2023. [Google Scholar]

40. G. Ravikumar, K. Venkatachalam, M. Masud and M. Abouhawwash, “Cost efficient scheduling using smart contract cognizant ethereum for IoMT,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 865–877, 2022. [Google Scholar]

41. N. Mittal, H. Singh, V. Mittal, S. Mahajan, A. K. Pandit et al., “Optimization of cognitive radio system using self-learning salp swarm algorithm,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3821–3835, 2022. [Google Scholar]

42. K. S. Bhuvaneshwari, J. Uma, K. Venkatachalam, M. Masud, M. Abouhawwash et al., “Gaussian support vector machine algorithm based air pollution prediction,” Computers, Materials & Continua, vol. 71, no. 1, pp. 683–695, 2022. [Google Scholar]

43. A. Garg, A. Parashar, D. Barman, S. Jain, D. Singhal et al., “Autism spectrum disorder prediction by an explainable deep learning approach,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1459–1471, 2022. [Google Scholar]