A Joint Optimization Algorithm for Renewable Energy System

1  Introduction

In recent years, with the increasing scarcity of coal resources and the rising demand for environmental protection, research on renewable energy power generation has been deepened, and large-scale new energy power generation has played an increasingly important role in the energy market [1–5]. However, due to the randomness, volatility, uncertainty and other objective problems of distributed energy resources (DER) [6–11], the structure, form and operation control methods of traditional power systems need to be changed accordingly, including power plants, power grids and users in the power system. The entire power system within the system needs to adapt to it [12–15].

In this context, the concept of virtual power plant (VPP) emerged. Without changing the distributed energy resources, through certain control and communication strategies, a large number of distributed power sources, energy storage, loads, etc., are assembled to participate in the electricity market [16–19]. Dispatching operation solves the problem of lack of effective coordination and control between independent distributed energy generation [20–22], and provides new ideas for power market operation.

At present, domestic and foreign literatures have reported on the role of VPP in new energy power consumption. Reference [23] proposes a method to control a virtual power plant containing wind turbines and cogeneration units to achieve the goal of smoothing wind power fluctuations and reducing power generation costs. In view of the difficulty of grid-connected scheduling of large-scale wind farms, the authors in [24] proposed a virtual power plant concept that equivalently aggregates wind turbines in a certain area with conventional water, thermal power units and energy storage equipment, and realizes the power grid power for the unit equipment in the area. Reference [25] discussed the problems and possible solutions of access to clean energy such as wind power in view of existing power environment, but did not give specific solutions and analysis. Reference [26] proposed a day-ahead clearing model for the power pool market considering wind power, drawing on the idea of “ex-post electricity price”, and generating a multi-scenario model based on the results of probabilistic wind power forecasting, taking into account the economy and safety of system operation. Reference [27] established a multi-party electricity price linkage game model including traditional power generators, wind power suppliers, power suppliers, energy storage service providers and users based on multi-agent technology. Reference [28] proposed a multi-agent two-layer optimization model including supply side and demand side. The bidding game behaviors of market members such as wind power companies, electric vehicle aggregators, and retailers providing demand response are analyzed. Based on multi-scenario stochastic programming, reference [29] established a single-period day-ahead market clearing model considering network constraints including wind power. Aiming at the randomness of wind power output, the day-ahead energy and reserve market were jointly optimized, but the production of thermal power units was not considered. Reference [30] proposed a hybrid bidding mode and clearing algorithm in the power market, using segmented bidding for basic loads, clearing them according to the queuing method, and using time-sharing bidding for fluctuating loads, providing a brand-new idea for market bidding.

On this basis, this paper is based on the bidding mechanism in the electricity market, under the framework of VPP, taking VPP revenue maximization as the objective function, coordinating the output of wind power, photovoltaic and other new energy sources, and establishing a mixed integer linear model in conjunction with electric vehicles, so as to conduct the VPP optimal design of joint scheduling, and the effectiveness of the bidding strategy is verified by a simulation example.

2  The Complementary Strategy of Wind-Solar Load-Storage

2.1 VPP Bidding Mechanism

The essence of VPP is to centrally control and dispatch equipment such as new energy power stations and energy storage in different regions and at multiple levels, and complete market operations [31]. In the operation of the power grid, the dispatch center does not directly control these generator sets or energy storage equipment, but participates in the operation and dispatch of the power grid as a whole by controlling the VPP [32]. Therefore, like conventional power plants, VPPs can also participate in power market transactions and system adjustments.

Because domestic use of new energy is currently restricted, this article treats VPP as the receiver of the electricity market price, assuming that changes in output and strategic optimization have no effect on the market price. It is also assumed that VPP bidding in the day-ahead energy market occurs hourly, and that the power generating output and electricity per unit time are set to be the same in value, with the unit being MW. When the output deviation of the new energy source causes an output penalty, VPP employs wind power generation and solar power production as new energy power grid connections.

VPP purchases electric energy from the energy market during the load trough period to arrange electric vehicle charging, and during the load peak period, the electric vehicle battery provides backup for new energy and, at the same time, acts as a controllable power source by controlling the deviation between the actual charge and discharge power, and the preferred operating point (POP) provides tuning services to the system. On the one hand, electric vehicles participate in the operation of virtual power plants as an energy storage part and as a load part on the other hand.

2.2 New Energy Participation in the Market

When new energy participates in the day-ahead energy market submits the day-ahead bidding output for each time period t of the next day to the Independent System Operation Organization (ISO), and accepts the ISO dispatched power generation after winning the bid. The VPP bidding revenue Rn in time T can be expressed as:

Rn=∑t=1T⁡λe,tPn,b,tΔt (1)

In the formula, Pn,b,t are the bidding output of new energy units; λe,t is the price of the energy market in the day before; Δt is the length of the unit period.

The spares provided by electric vehicles for VPP new energy bidding output through charging and discharging are Pev,c,t and Pev,dc,t . Assuming that the actual output of new energy is greater than, and less than the output of the bidding, the deviations are Ppc,h,t and Ppc,1,t , respectively. The corresponding penalty coefficients are γpc,h, h and γpc,1, respectively, then the new energy output deviation caused by the economic penalty Cpc is as follows:

Cpc=∑t=1T⁡λe,t(γpc,hPpc,h,tuh,t+γpc,1Ppc,1,tu1,t) (2)

Ppc,h,t=Pn,r,t+Pev,dc,t−Pev,c,t−Pn,b,t (3)

Ppc,1,t=Pn,b,t+Pev,c,t−Pev,dc,t−Pn,r,t (4)

In the formula: Pn,r,t is the actual output of the new energy unit; uh,t , u1,t are 0–1 variables, uh,t is 1 when Ppc,h,t>0 and u1,t is 1 when Ppc,1,t>0 . γpc,h and γpc,1 are all greater than 0.

2.3 Electric Vehicle Participation in the Market

When the electric vehicles in the VPP participate in the regulation market bidding, they can simultaneously provide up-reserve, down-reserve and rotating reserve services.

The VPP’s revenue from managing EVs is divided into revenue from discharging the grid when idle, and electricity bills charged to owners for charging EVs. The gross revenue can be expressed as:

RBEV=∑t∈T⁡(λt,uPBEV,dc,u,t+λt,dPBEV,dc,d,t+λt,rPBEV,dc,r,t)+λc∑t∈T⁡PBEV,dri,tΔt (5)

where PBEV,dc,u,t , PBEV, PBEV,dc,d,t , PBEV,dc,r,t are the up-regulated, down-regulated, and spinning reserve power provided by the electric vehicle to the grid in period t, respectively. PBEV,dri,t is the charging power of the electric vehicle in period t;λt,u,λt,d and λt,r are the capacity prices for adjusting the market’s upward adjustment, downward adjustment, and spinning reserve, respectively. λc is the unit electricity price charged by VPP to car owners, and VPP provides electric vehicle users with preferential electricity prices to attract them to participate in the adjustment.

The number of electric cars that can be dispatched in a given period of time, as well as the continuous connection time between electric vehicles and virtual power plants, are both unpredictable in the process of managing electric vehicles using VPP. In this research, the number of electric cars participating in dispatching is considered to be big enough, ignoring the appropriate adjustment coefficient and treating all electric vehicles as comparable to one electric vehicle [33]. Similarly, it is believed that the wind turbines bidding in the VPP on the power market have adequate photovoltaic panels and the same type. One wind turbine and one solar array are the same.

This paper assumes that VPP purchases electricity from the bilateral contract market and real-time energy market to charge electric vehicles in order to reduce the cost of electricity purchase [34]. Then, the electricity purchase cost of electric vehicle is shown in Eq. (6) as follows:

Cev,pur=λs,tQc+∑t=1T⁡λpur,tE(Pev,c,t)Δt (6)

In the formula: λs,t is the electricity purchase price of the virtual power plant from the bilateral contract market; λpur,t is the electricity purchase price in the real-time energy market; E(Pev,c,t) is the expected value of the actual charging power of the electric vehicle; Qc represents the electricity purchased from the contract market by the virtual power plant to charge electric vehicles

Qc=∑t=1T⁡Pev,dc,t (7)

The cost of the virtual power plant is mainly composed of two parts: the power purchase cost Cev,pur and the electric vehicle battery loss cost Cev,dc . The loss cost of electric vehicle battery discharge is

Cev,dc=∑t=1T⁡cdisE(Pev,dc,t)udc,tΔtηdc (8)

In the formula: E(Pev,dc,t) is the expectation of the actual discharge power of the electric vehicle value; ηdc is the battery discharge efficiency; cdis is a constant, which is the cost of discharge loss per unit of electricity, and the unit is USD/(MW⋅h).

3  Wind-Solar Load-Storage Complementary Optimization Model

3.1 Objective Function

Under the VPP environment, the optimal decision-making objective of the joint operation of wind turbines, photovoltaics and electric vehicles is to maximize the total profit of the consortium.

maxR=Rn+RBEV−Cpc−Cev,pur−Cev,dc (9)

In the formula: R is the final total revenue of the virtual power plant; Rn is the income obtained by virtual power plants participating in market bidding.

3.2 Constraints

(1)   The output of fans and photovoltaics is about:

uh,t+u1,t=1 (10)

Pn,min,t≤Pn,r,t≤Pn,max,t (11)

Eq. (10) is the deviation constraint between the actual output and bidding output of new energy units in the same period t, and Eq. (11) is the approximate upper and lower limit of the output of new energy units in each period.

(2)   The output of electric vehicles is about:

udc,t+uc,t=1 (12)

St+1=St−E(PEV,dc,t)/ηdc−E(PEV,dc,t)ηc (13)

St,min≤St≤St,max (14)

S1=S24 (15)

PBEV,dc,d,t+PPOP,t+Pev,dri+Pev,c,t−Pev,dc,t≤Pev,max (16)

PPOP,t+Pev,c,t−PBEV,dc,u,t−PBEV,dc,r,t−Pev,dc,t≥−Pev,max (17)

PBEV,dc,d,t,Pev,dri,t,Pev,c,t,Pev,dc,t≥0 (18)

The electric vehicle battery charge and discharge constraints are shown in Eqs. (12–17). We can see that Eq. (12) is the charge-discharge state constraint. In Eq. (13), St is the state of charge (SOC) value of the electric vehicle battery in the period t, and the SOC value of the battery at each moment is determined by the previous period. Considering that the electric vehicle has factors such as driving demand and battery loss, the battery cannot be fully charged and discharged, so the SOC is constrained in Eq. (14), where St,min and St,max are the minimum and maximum values of St , respectively. In Eq. (15), the daily initial charge state of the battery is the same as that at the end of the previous day. In addition, it is also necessary to consider the battery discharge constraints of electric vehicles, see Eqs. (16)–(17), where Pev,max is the maximum charge and discharge power constraint. In Eq. (18), the value of the model decision variable is limited to be non-negative.

4  Solution

The analysis in Section 3 indicates that the optimal decision-making model for the combined operation of wind-solar-load-storage in the virtual power plant environment is a multi-period, large-scale mixed integer linear programming model (MILP). In this paper, based on the General Algebraic Modeling System (GAMS) optimization platform, the CPLEX commercial optimization software is called to carry out the optimization solution [35]. Among them, for the linear programming problem, CPLEX uses the simplex method to solve it, as shown in Fig. 1.

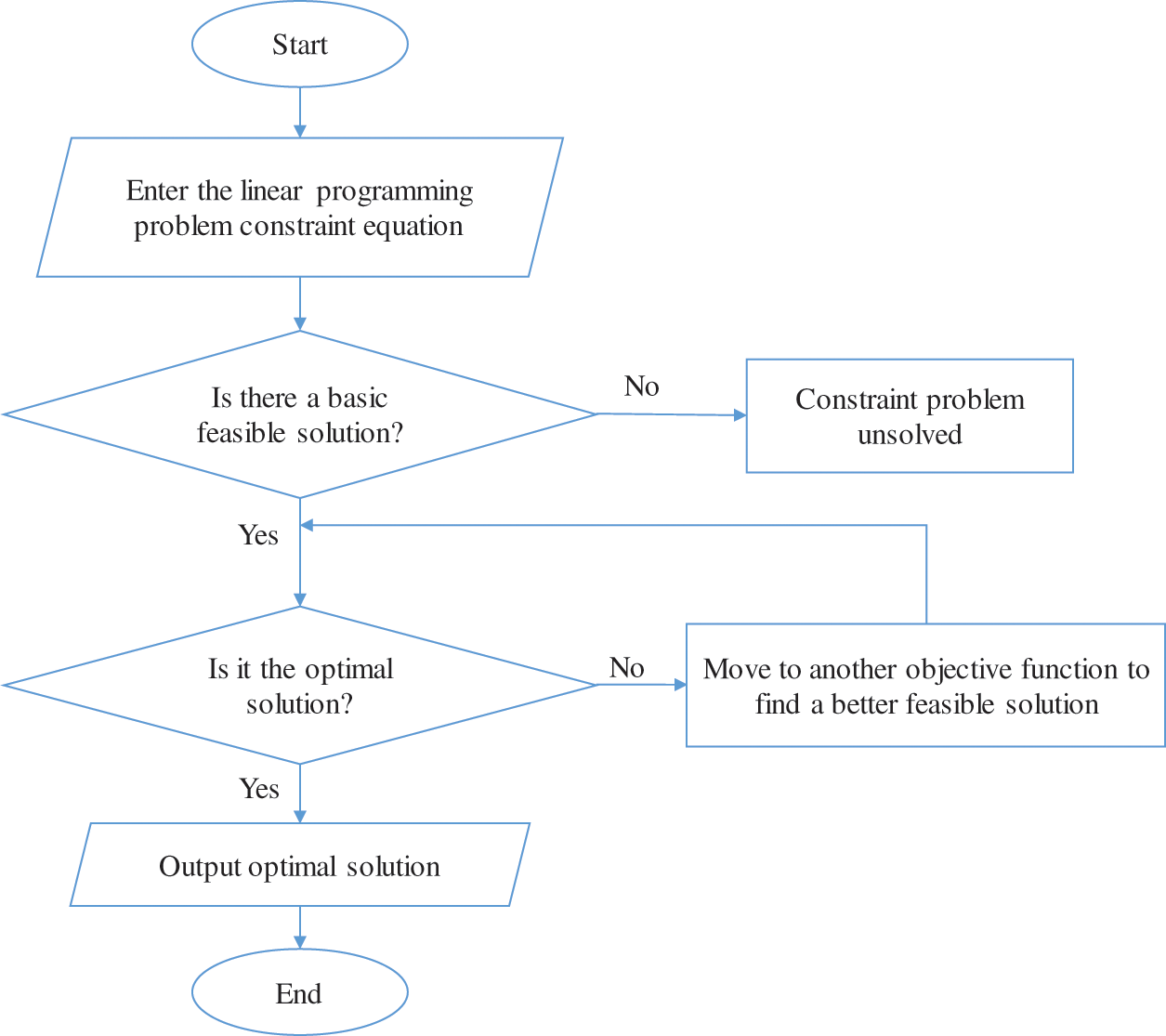
Figure 1: Proposed algorithm flowchart

5  Case Analysis

In order to verify the usability of the model, this study gives a numerical example of a virtual power plant deploying wind turbines, photovoltaics, and electric cars to participate in energy market operations. Taking into account the market impact of uncertainty in new energy power production output, the calculation example eventually achieves the advantages of virtual power plants in numerous sets of scenarios and performs appropriate analysis.

5.1 Basic Data

For the output of wind turbines and photovoltaic units, it is considered that the new energy in the virtual power plant has an output range and that the output swings between the higher and lower output limits during 24 h. The specific data are shown in Fig. 2.

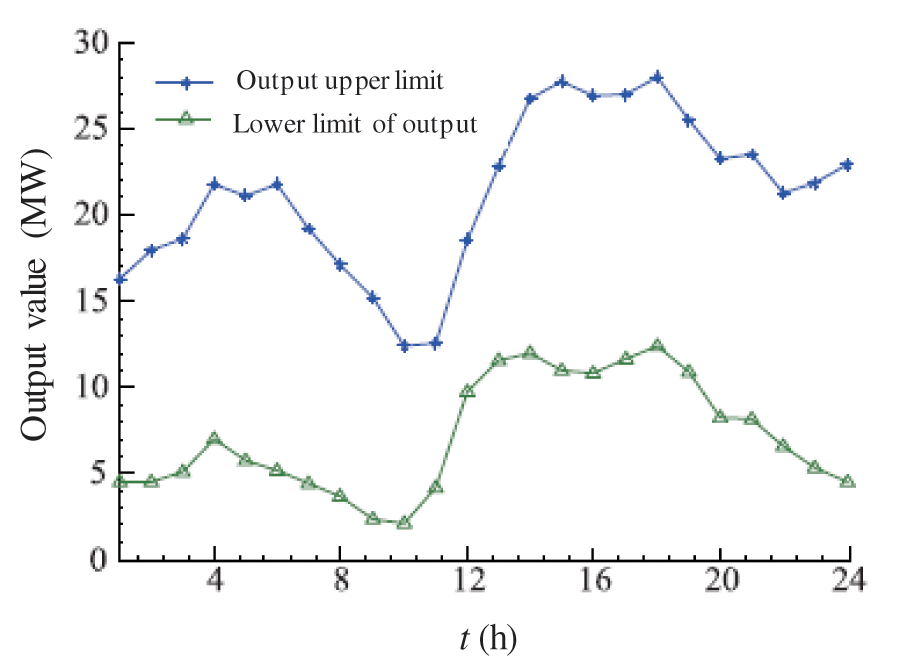
Figure 2: Illustration of energy output with time

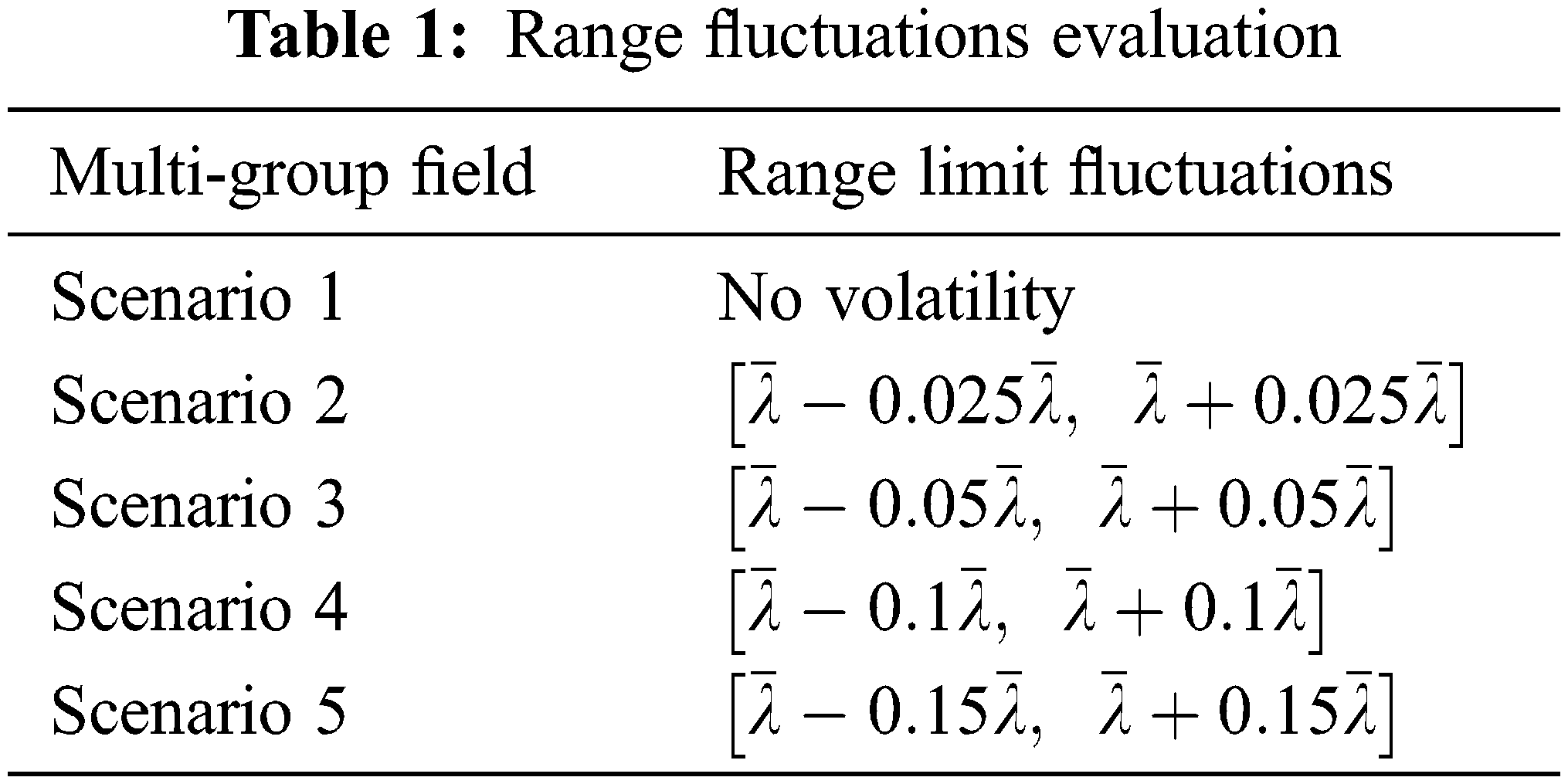
Because new energy output is unknown, it is difficult to anticipate its maximum and lowest output in the day-ahead market. Therefore, the upper and lower limits of new energy output are set as fluctuation ranges [λ¯−λ^,λ¯+λ^] , where λ^ is volatility.

For the volatility, a total of five groups of scenarios are simulated, and the volatility values in the five groups of scenarios are 0%, 2.5%, 5%, 10%, and 15%, respectively, as shown in Table 1.

It is assumed that the expected output value of the joint bidding of new energy units of the virtual power plant in the next 24 h is shown in Fig. 3.

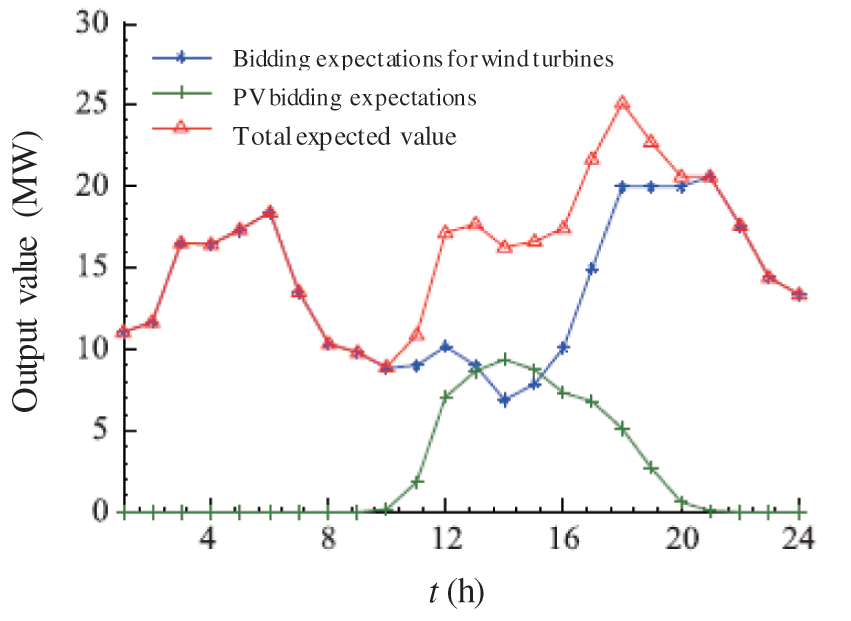
Figure 3: Comparison of the output of the PV and wind power

Given that electric cars engage in regulation market bidding while also providing up, down, and rotating reserve services, the energy price of reserve capacity in the regulation market is depicted in Fig. 4.

Figure 4: Comparison of the price capacity reservation

Assume that the purchase cost of unit battery capacity in the virtual power plant is 400 USD/(kW⋅h). The battery’s maximum charging and discharging power is 3 kW. The battery’s average charge and discharge efficiency are both 0.95. The cost of charging an electric car is 0.14 USD/(kWh). The cost of transmission and distribution is 0.07 USD/(kWh). The energy price on the generating side of the virtual power plant obtained via bilateral contracts is 0.06 US dollars/(kWh), and the contracted electricity is anticipated to be 288 MWh during the optimization period (24 h). Set t to 1, indicating that there are 24 time periods every day. When the actual output of the new energy unit is greater than or less than the bidding value, the penalty coefficients are 0.95 and 1.05, respectively.

5.2 Solving Data

According to the assumption, the virtual power plant compensates for the difference between the actual value of the new energy output and the bidding value by dispatching electric vehicle charging and discharging, avoiding the corresponding default penalty, and finally increasing the virtual power plant’s total revenue in the electricity market environment. The optimization outcomes of the virtual power plant’s ultimate income under five sets of scenarios may be achieved by solving the calculation example, as illustrated in Fig. 5. The actual output of the virtual power plant in the electricity market under the five scenarios is shown in Fig. 6.

Figure 5: Revenue evaluation under various fluctuation scenarios

Figure 6: Actual output comparison under various fluctuation scenarios

It can be seen from Figs. 5∼6 that when the expected value of VPP bidding is the same, with the increase of the fluctuation degree of the new energy output in the five groups of scenarios, the total income brought by the VPP stroke-light-load-storage complex gradually increases. Finally, the optimization results, the actual output of new energy is gradually decreased. According to the comparison of the five groups of scenarios, and analyze the reasons for this situation, we can draw the following conclusions:

1)   As the output fluctuation range of the new energy group increases, the risk of the VPP bidding result violating the bidding also increases, the scheduling role played by the VPP increases accordingly, and the income also increases.

2)   By deploying electric cars, VPP regulates the fluctuation of new energy output, and the backup output given by electric vehicles to stabilize the output fluctuation of new energy units grows as the fluctuation increases.

3)   The VPP dispatches electric cars to offer backup for new energy units while also participating in market bidding regulation and providing backup energy storage for the system to get advantages.

6  Conclusion

In this study, exploratory research on the collaborative engagement of new energy units and electric cars in bidding in the electricity market under the VPP environment is presented. This paper mainly builds a wind-light-load-storage collaborative bidding optimization model, and combines relevant examples to conduct a multi-scenario model.

The calculation example results show that by constructing an optimization model and studying the operation strategy of wind-sun-load-storage joint optimization, the profitability of VPP can be effectively improved, the volatility of new energy’s own output can be stabilized to a certain extent, and the market competitiveness can be improved. Finally, it is expected that the work done in this paper can provide useful reference for new energy consumption and VPP development to a certain extent.

Acknowledgement: The authors would like to express their appreciation to Agencia Nacional de Investigación y Desarrollo (ANID) for the support received through the project Fondecyt regular 1200055.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. Bashir, M. H. Alsharif, I. Khan, M. A. Albreem, A. Sali et al., “MIMO-Terahertz in 6G nano-communications: Channel modeling and analysis,” Computers, Materials & Continua, vol. 66, no. 1, pp. 263–274, 2020. [Google Scholar]

 2.  F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communications under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 19, no. 1, pp. 1–9, 2019. [Google Scholar]

 3.  Q. Alsafasfeh, O. A. Saraereh, A. Ali, L. A. Tarawneh, I. Khan et al., “Efficient power control framework for small-cell heterogeneous networks,” Sensors, vol. 20, no. 5, pp. 1–14, 2020. [Google Scholar]

 4.  K. M. Awan, M. Nadeem, A. S. Sadiq, A. Alghushami, I. Khan et al., “Smart handoff technique for internet of vehicles communication using dynamic edge-backup node,” Electronics, vol. 9, no. 3, pp. 1–17, 2020. [Google Scholar]

 5.  W. Shahjehan, S. Bashir, S. L. Mohammed, A. B. Fakhri, A. A. Isaiah et al., “Efficient modulation scheme for intermediate relay-aided IoT networks,” Applied Sciences, vol. 10, no. 6, pp. 1–12, 2020. [Google Scholar]

 6.  B. M. Lee, M. Patil, P. Hunt and I. Khan, “An easy network onboarding scheme for internet of things network,” IEEE Access, vol. 7, pp. 8763–8772, 2018. [Google Scholar]

 7.  O. A. Saraereh, A. Alsaraira, I. Khan and B. J. Choi, “A hybrid energy harvesting design for on-body internet-of-things (IoT) networks,” Sensors, vol. 20, no. 2, pp. 1–14, 2020. [Google Scholar]

 8.  T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–15, 2019. [Google Scholar]

 9.  M. Waqas, Y. Niu, Y. Li, M. Ahmed, D. Jin et al., “A comprehensive survey on mobility-aware D2D communications: Principles, practice and challenges,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 1863–1886, 2020. [Google Scholar]

10. M. Ahmed, Y. Li, M. Waqas, M. Sheraz, D. Jin et al., “A survey on socially aware device-to-device communications,” IEEE Communications Surveys & Tutorials, vol. 20, no. 3, pp. 2169–2197, 2018. [Google Scholar]

11. F. S. Shaikh and R. Wismuller, “Routing in multi-hop cellular device-to-device (D2D) networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 22, no. 3, pp. 2622–2657, 2018. [Google Scholar]

12. M. Haus, M. Waqas, A. Y. Ding, Y. Li, S. Tarkoma et al., “Security and privacy in device-to-device (D2D) communication: A review,” IEEE Communications Surveys & Tutorials, vol. 19, no. 2, pp. 1054–1079, 2017. [Google Scholar]

13. O. Hayat, R. Ngah, S. Z. M. Hashim, M. H. Dahri, R. F. Malik et al., “Device discovery in D2D communication: A survey,” IEEE Access, vol. 7, pp. 131114–131134, 2019. [Google Scholar]

14. N. Voropai, “Electric power system transformations: A review of main prospects and challenges,” Energies Journal, vol. 13, no. 21, pp. 1–28, 2020. [Google Scholar]

15. A. C. Brent, “Renewable energy for sustainable development,” Sustainability Journal, vol. 13, no. 12, pp. 1–23, 2021. [Google Scholar]

16. R. Butt, S. Kazmi, M. Alghassab, Z. Khan, A. Altamimi et al., “Techno-economic and environment impact analysis of large-scale wind farms integration in weak transmission grid from mid-career repowering perspective,” Sustainability Journal, vol. 14, no. 5, pp. 1–17, 2022. [Google Scholar]

17. E. Borghini, C. Giannetti, J. Flynn and G. Todeschini, “Data-driven energy storage scheduling to minimize peak demand on distribution systems with PV generation,” Energies Journal, vol. 14, no. 12, pp. 1–17, 2021. [Google Scholar]

18. L. Li, Y. Fan, X. Su and G. Qiu, “Probabilistic load flow calculation of power system integrated with wind farm based on kriging model,” Energy Engineering, vol. 118, no. 3, pp. 565–580, 2021. [Google Scholar]

19. Y. Wang, X. Shen and Z. Dai, “A probabilistic power flow calculation method considering the uncertainty of the static frequency characteristic,” Global Energy Interconnection, vol. 2, no. 1, pp. 45–53, 2019. [Google Scholar]

20. H. Rouzbahani, H. Karimpour and L. Lei, “A review on virtual power plant for energy management,” Sustainable Energy Technologies and Assessments, vol. 47, no. 3, pp. 1031–1045, 2021. [Google Scholar]

21. B. Goia, T. Cioara and I. Anghel, “Virtual power plant optimization in smart grids: A narrative review,” Future Internet Journal, vol. 14, no. 5, pp. 1–25, 2022. [Google Scholar]

22. P. Pal, A. K. Parvathy, K. Devabalaji, S. Antony, S. Ocheme et al., “IoT-Based real time energy management of virtual power plant using PLC for transactive energy framework,” IEEE Access, vol. 9, pp. 97643–97660, 2021. [Google Scholar]

23. M. Rashid, F. Granelli, M. Hossain, M. Alam, F. Ismail et al., “Development of cluster-based energy management scheme for residential usages in the smart grid community,” Electronics, vol. 9, no. 9, pp. 1–16, 2020. [Google Scholar]

24. P. Pal, P. Krishnamoorthy, D. Rukmani, S. Antony, S. Ocehem et al., “Optimal dispatch strategy of virtual power plant for day-ahead market framework,” Applied Sciences, vol. 11, no. 9, pp. 1–18, 2021. [Google Scholar]

25. N. Holjevac, T. Baskarad, J. Dakovic, M. Krpan, M. Zidar et al., “Challenges of high renewable energy sources integration in power systems–the case of Croatia,” Energies Journal, vol. 14, no. 4, pp. 1–23, 2021. [Google Scholar]

26. A. Heydari, G. Memarzadeh, D. Garcia, F. Keynia and L. Santoli, “Interval prediction algorithm and optimal scenario making model for wind power producers bidding strategy,” Optimization and Engineering, vol. 22, no. 5, pp. 1807–1829, 2021. [Google Scholar]

27. J. Lee, M. Kim and H. Kim, “A Multi-agent based optimization model for microgrid operation with hybrid method using game theory strategy,” Energies Journal, vol. 14, no. 3, pp. 1–17, 2021. [Google Scholar]

28. J. Zhang, Y. Zheng, M. Yao, H. Wang and Z. Hu, “An agent-based two-stage trading model for direct electricity procurement of large consumers,” Sustainability Journal, vol. 11, no. 18, pp. 1–19, 2019. [Google Scholar]

29. J. Roungkvist, P. Enevoldsen and G. Xydis, “High-resolution electricity spot price forecast for the danish power market,” Sustainability Journal, vol. 12, no. 10, pp. 1–18, 2020. [Google Scholar]

30. S. Singh, M. Fozdar, H. Malik, M. Moreno and F. Marquez, “Influence of wind power on modeling of bidding strategy in a promising power market with a modified gravitational search algorithm,” Applied Sciences, vol. 11, no. 10, pp. 1–19, 2021. [Google Scholar]

31. R. Subramanya, M. Ojanpera, S. Sierla, T. Holtta and J. Valtakari, “A virtual power plant solution for aggregating photovoltaic systems and other distributed energy resources for northern european primary frequency reserves,” Energies Journal, vol. 14, no. 5, pp. 1–14, 2021. [Google Scholar]

32. W. Tayari, S. Elghali, E. Forushani and M. Benbouzid, “Virtual power plants optimization issue: A comprehensive review on methods, solutions, and prospects,” Energies Journal, vol. 15, no. 10, pp. 1–24, 2022. [Google Scholar]

33. N. Li, X. Wang, Z. Zhu and Y. Wang, “The reliability evaluation research of distribution system considering demand response,” Energy Reports, vol. 6, no. 2, pp. 153–158, 2020. [Google Scholar]

34. X. Liu, “Research on bidding strategy of virtual power plant considering carbon-electricity integrated market mechanism,” International Journal of Electrical Power & Energy Systems, vol. 137, no. 2, pp. 1759–1778, 2022. [Google Scholar]

35. O. D. Montoya, J. Fuentes, F. Moya, J. Barrios and H. Chamorro, “Reduction of annual operational costs in power systems through the optimal siting and sizing of STATCOMs,” Applied Sciences, vol. 11, no. 10, pp. 1–14, 2021. [Google Scholar]