Outsourced Privacy-Preserving kNN Classifier Model Based on Multi-Key Homomorphic Encryption

1  Introduction

With its development, outsourced classification services [1–3] have been used in medical diagnosis, image retrieval, anomaly detection and Internet of Things [4]. K-Nearest Neighbor (kNN) is a common technique used to solve classification problems in machine learning [5,6]. Outsourced kNN classification services are more and more widely used in practical applications [7]. For example, many medical technology companies have models trained on medical records datasets that can be deployed in the cloud to provide intelligent medical diagnosis services to patients. Models trained by many fintech companies can be deployed in the cloud to provide customers with credit risk forecasting services. However, privacy concerns restrict the development of outsourced classification services [8]. For example, in the training phase, the training data may be stolen by the adversary, resulting in the leakage of user sensitive information (medical data, home address). In the classification phase, the adversary may access the target model through inference attacks to obtain model information. It will seriously damage the property rights of the model owners and cause significant economic losses to the model owners by obtaining the entire model by a reverse attack method [9]. It hinders the wider application of outsourced classification services to a certain extent, so it is very important to ensure data and model privacy [10].

In response to the above problems, many scholars usually use homomorphic encryption to construct a client-server two-party model [11], in which the server has a kNN classifier, and the client inputs encrypted features to start the evaluation. Classification over encrypted data is more challenging than traditional machine learning model classification, and there are still two problems:

(1)   First, once the classifier is handed over to the cloud server, it will damage the copyright of the user’s classifier models, and a three-party model needs to be used for processing. Tai et al. [12] proposed a privacy-preserving two-party classifier evaluation protocol, which significantly improves efficiency. Lu et al. [13] proposed a new scheme to realize secure outsourced storage and kNN query in the cloud, protect the privacy of data owners and query users from the cloud, and data owners do not need to query online. However, the above schemes are stored in the server, and the adversary attacks the server and steals the models.

(2)   Second, the data sources in the existing scheme use the same public key to encrypt data, and the security assumption is based on the fact that the server cannot collude with any model owner. Once they collude, the cloud server can decrypt and obtain models. Recently, Mandal et al. [14] proposed a scheme to support a large number of users to jointly learn a shared machine learning model, where coordinated by a centralized server from multiple devices. They designed two privacy-preserving protocols for training linear and logistic regression models based on an additive homomorphic encryption scheme. However, each user has the same public key and private key, as long as A obtains the encrypted data of B, it can decrypt and learn the data of B.

Based on the above research, we further propose an outsourced privacy-preserving kNN classifier model based on multi-key homomorphic encryption (kNNCM-MKHE) for prediction. Outsourced to third-party evaluators, models are not leaked to unauthorized entities. In this paper, we focus on the scenario where predictive models from multiple owners are sent to the evaluator for collaborative evaluation. Due to the diversity of data, collaborative machine learning has become popular to improve accuracy. In medical diagnosis, many hospitals and medical laboratories collaborate to provide a better diagnosis. Compared with other methods, our proposed method can support the joint evaluation of multi-party models, use different keys, and prevent parties from collusion. The privacy of multi-party models and data is protected. We highlight contributions below:

•   First, we proposed an outsourced privacy-preserving kNN tripartite model, which allows multiple model owners to outsource kNN classification services to an untrusted party. Each model owner encrypts their models so that none of them can get access to the classifiers, while the evaluator remains unaware of the model or user query data. It protects data and model confidentiality.

•   Secondly, we designed a secure computing protocol based on multi-key homomorphic encryption, which supports the computation of encrypted data with different public keys and provides security proofs. The calculation processes of kNN are analyzed, and the basic operations are extracted. Since the public and private keys of each model owner are different, even if any model owner colludes with the evaluator, no information will be disclosed to the evaluator. At the same time, collusion between model owners is prevented.

2  Related Work

In order to take advantage of the computing power provided by the cloud, more and more models are outsourced computing on the cloud, for example, Support Vector Machine (SVM) [15], neural network [16,17], and deep learning [18–20]. Wang et al. [21] proposed a decision tree query scheme over encrypted data and designed corresponding security protocols, including secure binary decomposition and secure minimum protocol, which solved the complex problem of multi-party framework construction and improved computing efficiency. It protected the privacy of training data, user queries, and query results. Yu et al. [22] proposed an efficient blockchain-based distributed network Iterative Dichotomiser 3 (ID3) decision tree classification framework for expanding the amount of training data, it can make more training data sharing without sacrificing data privacy. Existing privacy-preserving medical pre-diagnosis schemes are all experimented on single-label datasets, while. Dan et al. [23] proposed a scheme that will consider multi-label instances. Boldyreva et al. [24] designed an outsourced security approximate kNN model, which can perform secure approximate kNN search and updates. Meanwhile, they designed a generic construction based on locality-sensitive hashing, symmetric encryption, and an oblivious map. Liang et al. [25] used multiple keywords and an improved k-nearest neighbor technology to improve search accuracy. Compared to [25], our protocol supports multiple model owners to upload their models and prevents collusion between models. Liu et al. [26] implemented a secure kNN classification scheme in cloud servers for Cyberspace (CKKSKNNC) based on the CKKS homomorphic encryption and supports batch calculation. Compared to our protocol, it supports floating-point numbers computing. However, the protocol we designed to allow multiple model owners to jointly evaluate the results.

Since the cloud server is run by a third party, users cannot fully trust it. Therefore, how to perform privacy-preserving machine learning on cloud data from different data providers becomes a challenge. Li et al. [27] proposed a new scheme to secure datasets from different providers and cloud datasets. To protect the privacy requirements of different providers, their datasets are encrypted using different public keys of a double decryption algorithm (DD-PKE). Jiang et al. [28] and Zou et al. [29] proposed a secure privacy protection outsourcing scheme under multi-key in cloud computing, which combines the double decryption mechanism with the Multi-key HE scheme to solve the privacy protection collaborative deep learning encryption with different public keys. A secure neural network in federated learning is proposed, allowing different clients to encrypt their local models with different keys, relying on two non-colluding cloud servers. The client uploads the encrypted local model to the first cloud server, and the second server can decrypt it by a trapdoor. The experimental results show that the accuracy is high, but the efficiency is not high. [29] implements the k-means clustering scheme. However, the cost of computation and communication is high.

There have also been recent efforts in secure machine learning under two-server [30]/three-server [31,32], /four-server [33] models, where three/four servers must participate in online interactions. Two and more cloud service providers need to come to an agreement and collaborate on the service. Reaching the agreement among more cloud service providers is expected to be a bit more complicated.

3  Preliminary

Multi-key HE supports extensions of Somewhat Homomorphic Encryption (SWHE) to compute encrypted data under different keys. The existing Multi-key HE scheme with extended ciphertexts is a multi-key variant of the BGV scheme. Multi-key BGV scheme (MKBGV) [34] compares with the traditional single-key homomorphic encryption, it is more suitable for computing multi-user data in a cloud environment.

Definition 1 (Multi-key homomorphic encryption). Multi-key homomorphic encryption is defined as follows:

Setup ( 1κ ,  1K, 1L ): Given the security parameters κ , the number of keys K , maximum circuit depth L, return a public parameter pp;

Gen(pp) : Given the public parameter pp, generate key pair ( pkmi, skmi ) and ( pkc, skc ), where i=1, …, K . They also generate the evaluation helper,

Enc(pk, μ) : Given the public parameter pp , public key, and the plaintext μ , then output ciphertext c=(c0, c1) ;

Ext(pk¯, c) : Extend c to c¯ under concatenated key pk¯={pkc, pkm} , and output two sub-vectors c¯=(cc, cm) , where is in the form c¯={(cc,0, cc,1)|(cm,0, cm,1)} ;

Dec(sk¯, c¯) : Decrypt an extended c¯=(cc, cm) under the concatenated secret key sk¯={skc, skm} . Each model owner computes ρmi=cm,0smi+temi , then compute cm,1−∑i=1ncm,0smi .

4  System and Adversary Model

4.1 System Model

Our system architecture is illustrated in Fig. 1. There are three entities: User ( U ), Model Owners ( MOsi ), and Evaluator ( E ).

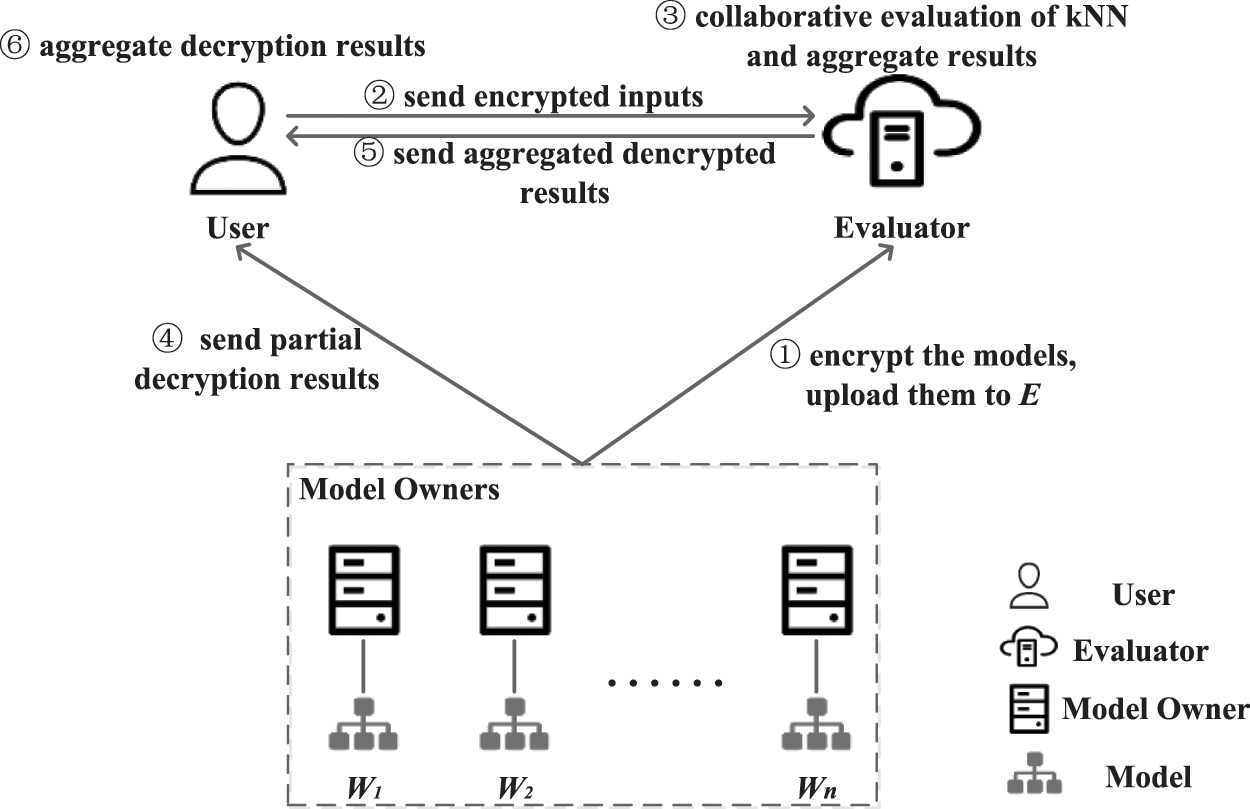
Figure 1: The system architecture

Each model owner MOsi (e.g., hospital) has a kNN model wi (the classifier’s core), which can be used to evaluate the data (health condition of patients). They upload encrypted models to the evaluator (e.g., cloud server) for collaborative evaluation of kNN. The collections of kNN contributed by all MOsi , which is evaluated in the E. Each kNN model wi produces one result, and E produces an encrypted aggregate classification result. The user (e.g., patient) sends encrypted inputs xi (e.g., weight, height, blood pressure, medical history and other private information) to the evaluator, and the evaluator returns an encrypted classification result to the patient. The patient obtains the final classification result through decryption. Each entity is described as follows.

(1)   Model Owners ( MOsi ): Each model owner has a classification model W. MOsi encrypt models and upload them to E. MOsi can perform classification work using W. The confidentiality of W is protected by homomorphic encryption. Finally, each model owner will participate in the partial decryption.

(2)   User ( U ): The U has query data x=(x1, …, xd) and desires to predict the class to which x belongs. U sends an encrypted input to the E for computations to obtain the C(W, x) without revealing any information to other entities.

(3)   Evaluator ( E ): After receiving an encrypted query data under the key of the U, the E will perform secure counting protocols to obliviously aggregate each unique class label. The evaluator then sends the class labels with their associated counts to the U.

4.2 Adversary Model

Consistent with previous existing works on privacy-preserving machine learning, all participants are assumed to be semi-honest, which means that each participant performs the computing task honestly with protocols, but is curious about original data and tries to extract private data from intermediate results generated in the process of computing execution. We follow prior works under semi-honest. In our system, it is considered that evaluator and model owners might be corrupted by such an adversary.

For the evaluator entity, we consider that the user’s input data and the model owner’s model should not be known to the evaluator, because the user input data contains private information and the model is private property. Both are encrypted and uploaded to the evaluator. The evaluator cannot decrypt it alone. Even if the evaluator is attacked, it is safe.

For the model owners’ entity, the trained model W is the knowledge of the model owners. It is encrypted and outsourced to E to provide classification service for legally authenticated U. It is valuable and private; the privacy of models requires that neither the E, an external eavesdropper should not derive any useful information about the plaintext of model W. Even if the model owner is attacked or colluded with other model owners, models will not be leaked due to the different keys.

5  Our Proposed Design

5.1 Overview

There are three phases of interactions between different parties, as shown in Fig. 2. In the first phase, each model owner MOsi encrypts the model W. Upload the encrypted models to the evaluator. The user sends an encrypted input to the evaluator. In the second phase, the evaluator evaluates each model with model owners. Once it is done, each model outputs a class label. The evaluator will perform a secure computing protocol to aggregate the number of each class label. Then, it sends the class labels with their associated counts to the user. In the final phase, each model owner sends a decryption component to the user, then, the evaluator aggregates decryption results, finally, the user uses the secret key and decryption component to decrypt it.

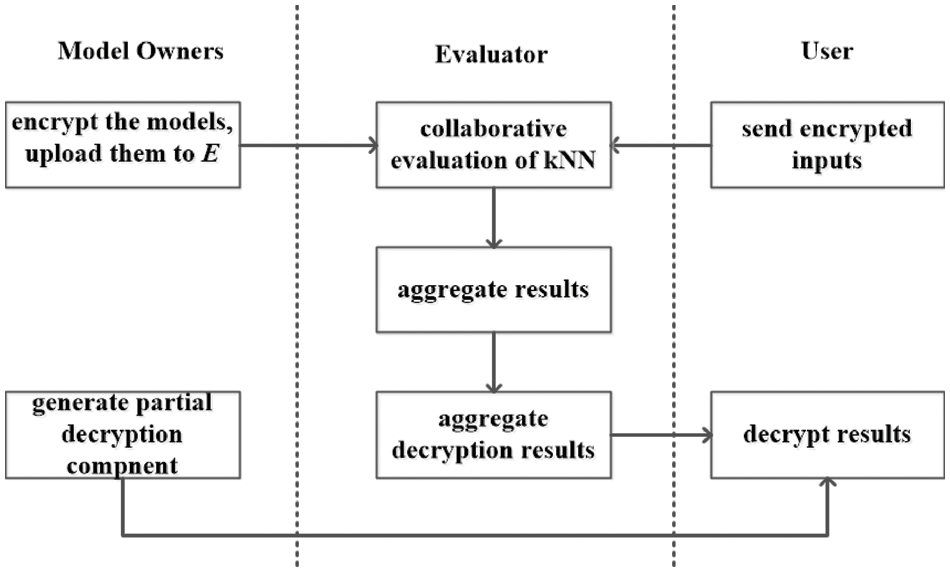
Figure 2: The system architecture

5.2 Symbol Description

There are two encryption schemes used in this scheme: AES and SWHE. In order to facilitate the description of the subsequent communication protocol and the ciphertext classification process, a description of the relevant symbols is given, as shown in Table 1.

5.3 Communication Protocol

The communication protocols of kNNCM-MKHE include comparison protocol, dot product protocol, and minimum protocol. The comparison protocol is used to compare two ciphertext data; the dot product protocol is used to realize the euclidean distance calculation of two encrypted vectors; the minimum protocol is used to realize the conversion from multiple encryption schemes. The following is a detailed introduction to three communication protocols.

5.3.1 Comparison Protocol

It is assumed that there are two parties in the MUX protocol, which is mainly used to implement if-else expressions over ciphertext. The U inputs encrypted data and E inputs private key for decryption. The MUX expressions are shown in Protocol 1.

The Comparison protocol is built on the MUX protocol. The protocol is jointly participated by U and E. The input of MOsi is two binary data encrypted by the bit and the input of E is the private key for decryption. Comparison protocol is to first compare bit-by-bit except for the highest bit, and the comparison results are obtained via the formula res=an⋅(bn+1)+(an+bn+1)⋅c . If res=1 , then a<b ; if res=0 , then a≥b . MUX protocol is called during protocol execution. Protocol 2 is shown as followed.

5.3.2 Dot Product Protocol

The dot product protocol calculates two SWHE encrypted ciphertext vectors, and returns an encrypted result, which represents the square of the euclidean distance between the encrypted data to be tested and each encrypted training data.

In the dot product protocol, the input of E is the test data [[xi]] and the training data [[yi]] . SWHE cannot perform root arithmetic, so the protocol uses sum of squares instead of root arithmetic calculation. The dot product protocol is euclidean distance calculation.

Protocol 3 is a description of the dot product protocol.

5.3.3 Minimum Protocol

The minimum protocol is to compare m encrypted ciphertext data and obtain the subscript of the minimum value. The core idea is to first compare the values, assign the smaller value to the one with the smaller subscript, then, assign 0 to the larger subscript, and record the original smaller subscript. And then continue to compare the new array until the number of arrays is 1, which is the minimum value.

In the minimum value, the input data is an array storing the encrypted euclidean distance, and the input data of E is the corresponding private key used for decryption. [[dmin]] represents the minimum encryption value, and [[dflag]] represents the comparison result of the two encrypted data.

5.4 Classification Process

The classification process is divided into three phases between different parties. In the first phase, each model owner MOsi and user U generate respective keys. In the second phase, E and U performs the kNN classification based on the above secure protocols to obtain an encrypted result. In the final phase, jointly decrypt, and U gets the decryption result. The specific process is described as follows.

5.4.1 Build Multiple Keys

Each model owner generates an AES key kmi , the SWHE key pkmi , which is used to encrypt the models before sending them to the E. Then, generate an evaluation helper element KeyGen(pp)→((pkmi, skmi), ekmi′) and a joint key pkm=∑i=1npkmi and evaluation helper element ekm′=∑i=1nekmi′ .

The user independently generates an AES key and a SWHE key pair (pkc, skc) and ekc′ , which is used later to generate the evaluation key ekc .

Model owner and user encrypt their AES key using the SWHE key to get [kmi]m, [kc]c . Then, they send them to the evaluator.

5.4.2 Classification Process

In the classification process, U is the requester of the classification service and has the data x to be classified, which is classified by the evaluator; E is the responder of the classification service, responsible for providing the classification service. MOsi has uploaded the encrypted model before the classification process.

This section uses the above protocol to construct the classification process. First, convert the type of data from floating-point numbers to integers and encrypt it. Secondly, calculate the euclidean distance through Protocol 3, and then obtain the minimum value in the distance array through protocol 4, the idea is to compare the values in the array to get the smaller of the two values, and assign the larger value to 0. The small squares form a new array, and then continue to compare the new array until the number of arrays is 1, and the value is the minimum value. Loop k times to obtain k nearest neighbors samples, and finally use the method introduced in Protocol 6 to count the number of categories to obtain the classification result. Among them, each protocol is regarded as a module, and the modules are connected through the modular sequence combination to construct the kNNCM-MKHE classifier, so that the user can only know the final classification result, but not the distance between the test sample and the training sample; make the evaluation was unable to obtain the user’s input x.

Protocol 5 is a description of the kNNCM-MKHE classification process.

The collaborative evaluation process of kNNCM-MKHE is as follows:

Step 1: Each MOsi sends models to the E, then MOsi and U send [kmi]m, [kc]c to the E to start evaluation;

Step 2: U input the data to be classified x, and convert each data x into bit-wise representation (xl−1, xl−2, .., x0) . U encrypts each bit using AES key to get ⟨xl−1⟩, ⟨xl−2⟩, .., ⟨x0⟩ . And send ⟨xl−1⟩, ⟨xl−2⟩, .., ⟨x0⟩ to E;

Step 3: Upon receiving ⟨xl−1⟩, ⟨xl−2⟩, .., ⟨x0⟩ , E extends ciphertexts [x]=AESdec(⟨x⟩, [km]) . Then, extend each of [[x]]=Ext(pk¯, [x]) using the extended SWHE key pk¯ ;

Step 4: U and each model in the E call Protocol 3 to calculate the euclidean distance until all data is traversed. U obtains the encrypted result and saves it in the array d;

Step 5: Each model the E calls Protocol 4 to obtain a minimum value in the array d, saves its corresponding category to the array lab, resets the minimum value to the maximum value, and calls protocol cyclically until k nearest neighbors are obtained. Finally, U obtains the categories of k nearest neighbor, and the results are stored in the array lab .

Step 6: U performs category statistics, counts the number of each category in the array lab , and the category in a model with the most occurrences ci′ . Then, aggregate the ci′ in each model to get the final collaborative evaluation result ci .

In the classification process, the U finally obtains an array of k-nearest neighbor data categories, which represents the number of neighbors, ck representing the categories. Count the number of occurrences of each category in the array lab, the most occurrences are the category to which the data to be classified belongs. Protocol 6 category statistic is a specific description of the function.

5.4.3 Decryption the Result

After classification, the results are extended ciphertexts using pk¯ . Each result is c¯={(cc,0, cc,1)|(cm,0, cm,1)} . The user can decrypt (cc,0, cc,1) and model owners decrypt (cm,0, cm,1) . Evaluator sends cm,0 to each model owner. Then, each model owner constructs ρmi=cm,0smi+temi and returns it to the evaluator. Finally, the evaluator aggregates the result ρ=∑i=1nρi=cm,0sm+tekm and sends it to the user. The user decrypts the result using ρ and skc . Fig. 3 illustrates the decryption process.

Figure 3: Some functions of x

6  Security Analysis

The encryption scheme used by our proposed system is secure against semi-honest adversaries. The evaluator converts AES ciphertext to the SWHE ciphertext under the secret key pkc and the model owner joint key pkm . MKHE provides semantic security unless all keys are compromised by the adversary.

For all model owners, the model is their private property and cannot be known by other parties. The model is encrypted before being sent to the evaluator, so the model is secure for the evaluator and the user. The model owner does not participate in the subsequent classification process, so user query data and classification results are also secure for the model owner.

The user’s view consists of feature vector x and class labels, which have been ciphertext computed on the evaluator. The feature vector x is encrypted by the user, only the user has the decrypted private key, and no other party except the user can decrypt it. The obtained class labels need to be decrypted jointly by the evaluator and the user, which protects the security of the class labels.

In the classification process, first, the square of the euclidean distance between the test and training data is calculated by the dot product protocol. It is secure under the semi-honest model. The evaluator only sends encrypted ciphertext data to the user, and does not receive any input from the user, which ensures the security of being classified. Finally, call the random permutation function to replace the subscript of the array d, and then call the minimum value protocol to obtain the value. Since each minimum value protocol uses the random permutation function to replace the index of the array, the evaluator cannot know the real value. The user cannot only obtain the minimum value of the refreshed ciphertext, and cannot obtain the size relationship of the data to be compared, which ensures that the size relationship of the array elements will not be leaked to the user.

To sum up, the constructed kNNCM-MKHE is secure under the semi-honest model.

7  Evaluation

Our scheme is implemented in C++ on Ubuntu18.04.2 64-bit version, Intel(R) Core(TM) i7-9700M CPU (3.00 GHz) 32 GB RAM. We constructed the kNNCM-MKHE based on the multi-key BGV scheme [34] using NTL and GMP. We evaluate the performance of the Heart Disease (HD), Breast Cancer (BC), and Credit Approval (CA) datasets [35], which is consisting of 70% training examples and 30% testing examples. The key length in the encryption scheme is 1024 bits, and the security parameters are λ=100 .

First, the comparison protocol is evaluated from four aspects: user, evaluator running time, exchange data volume, and exchange times for the encrypted data of two-bit lengths. The experimental results are shown in Table 2. The running time is related to the comparison bit length. The longer the bit length, the longer the user and evaluator running time, and the greater the amount of data exchanged.

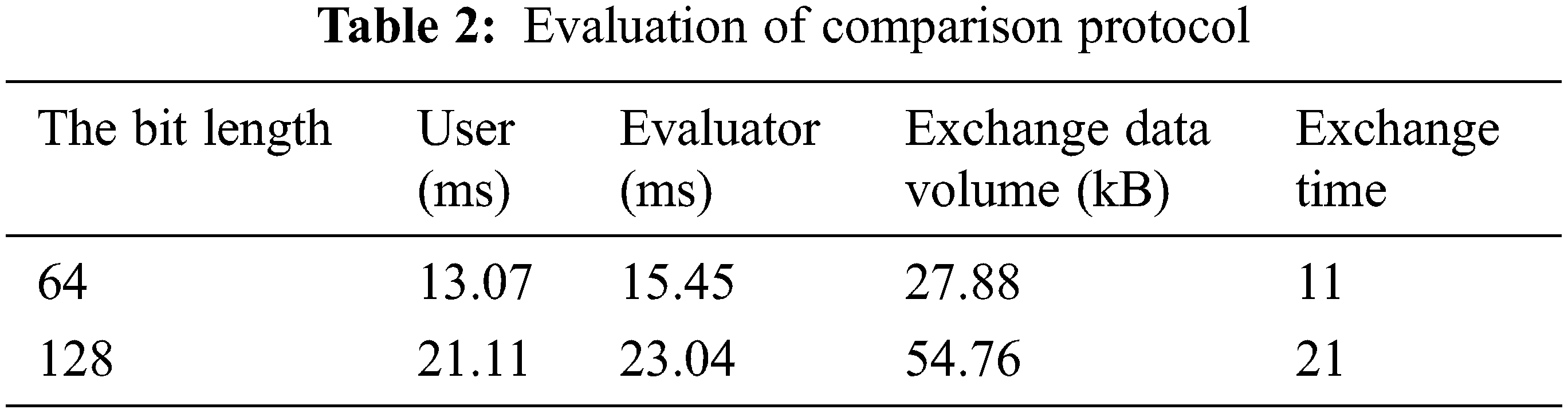
This experiment evaluates the calculation and comparison time of the user and the evaluator, the total amount of exchanged data and the number of exchanges. The specific experimental results are shown in Table 3.

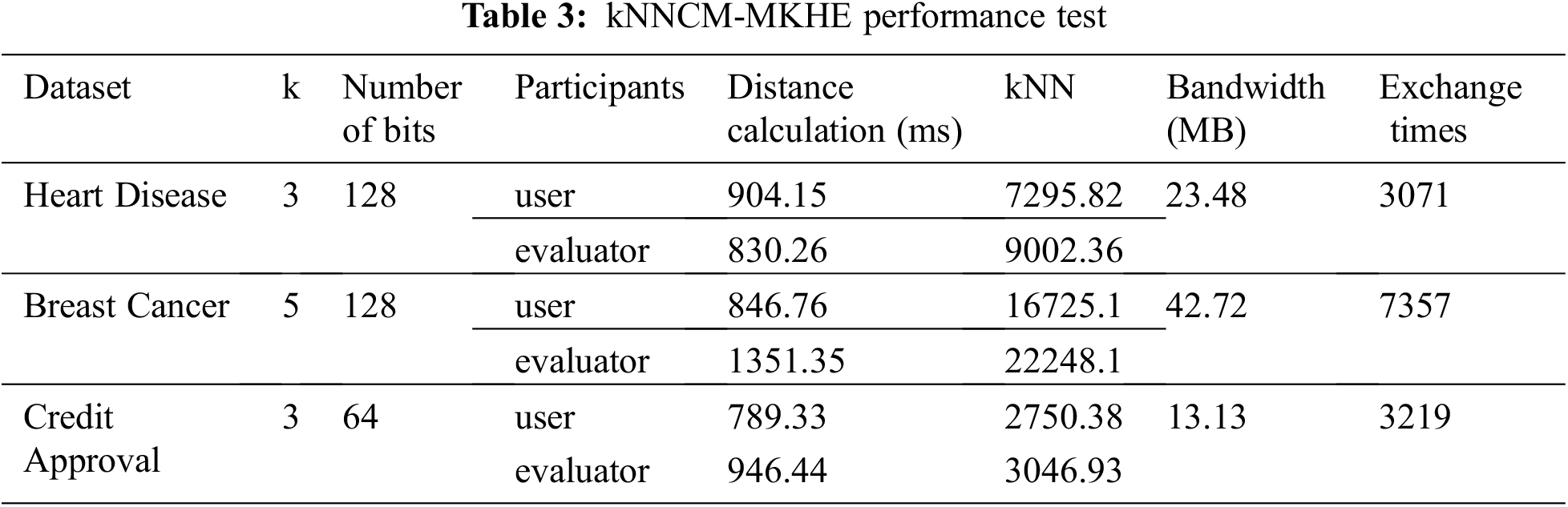
To validate the performance of kNNCM-MKHE, experiments on the running time of kNNCM-MKHE when the number of model owners varies, as shown in Fig. 4.

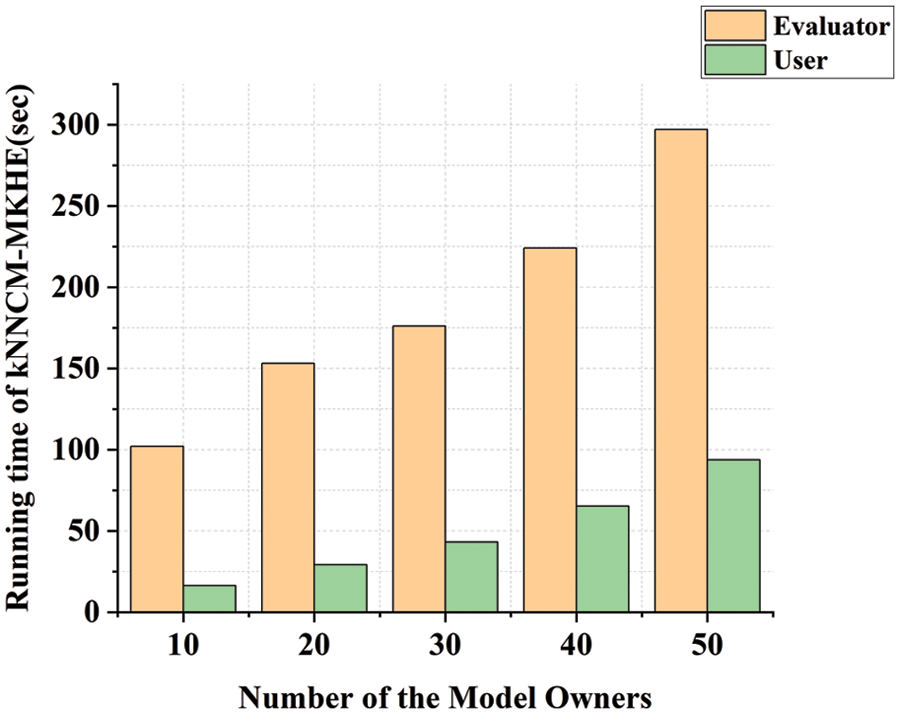
Figure 4: The running time of kNNCM-MKHE (ms)

In the kNNCM-MKHE process, the evaluator and user are mainly involved, and it can be seen that the evaluator bears most of the computational overhead. At the same time, as the number of model owners increases, so does the running time of the evaluator and user.

Table 4 shows the comparison of evaluation time and accuracy under kNN plaintext and kNNCM-MKHE when n changes, n represents the total number of data.

It can be seen from Table 4, evaluation over encrypted data is much slower compared to unencrypted data. Because computations on encrypted data are much more complex than plaintext computations. As the number of datasets increases, so does the evaluation time and accuracy rate, which proves that the proposed model is effective.

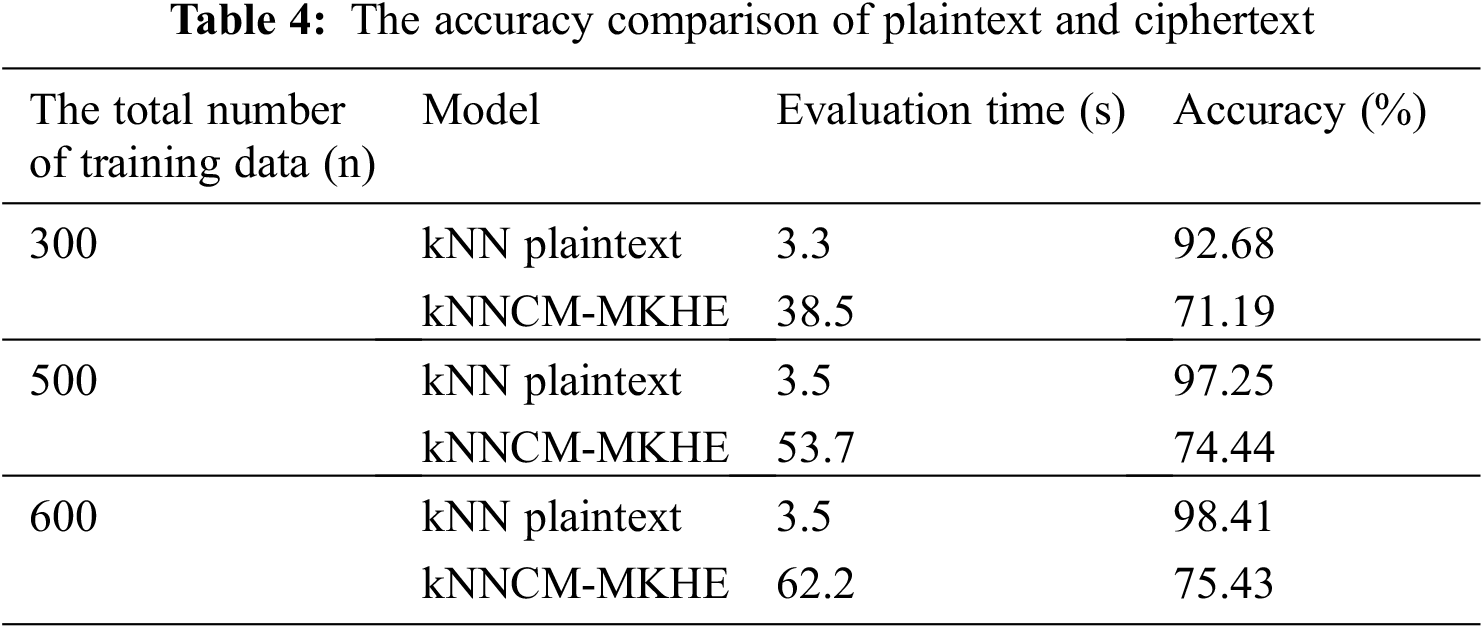
Fig. 5 shows the average running time of each stage on the three datasets of kNNCM-MKHE, including mode, euclidean distance, decrypt encrypted data and kNN neighbor.

Figure 5: The average running time of stage for kNNCM-MKHE three datasets (ms)

As can be seen from Fig. 5, the longest time consuming stage is finding k-nearest neighbor samples, and for Heart Disease and Credit Screening data, the k value is the same as the number of training samples, and the bits compared are 128 and 64, respectively. The time to find k nearest neighbors is almost half of Heart Disease. It can be seen that the number of bits is positively correlated with the samples of k nearest neighbors.

8  Conclusion

In this paper, we proposed a kNNCM-MKHE scheme that allows model owners to provide their encrypted models to outsource kNN classifier service, so that none of them can get access to other’s classifiers. Compared with previous works, our system protects data and models confidentiality. More importantly, we designed a secure computing protocol based on MKBGV to support the computation over encrypted data with different public keys and provided security proofs. Experiments have proved that collaborative evaluation of multiple model owners is feasible.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant No. 61872069, in part by the Fundamental Research Funds for the Central Universities under Grant N2017012.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Asma, P. Z. Hu, W. Harry and H. W. Sherman, “Blindfolded evaluation of random forests with multi-key homomorphic encryption,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 4, pp. 1821–1835, 2021. [Google Scholar]

2. J. Tang, Z. Xia, L. Wang, C. Yuan and X. Zhao, “Oppr: An outsourcing privacy-preserving jpeg image retrieval scheme with local histograms in cloud environment,” Journal on Big Data, vol. 3, no. 1, pp. 21–33, 2021. [Google Scholar]

3. T. Li, Z. Huang, P. Li, Z. Liu and C. Jia, “Outsourced privacy-preserving classification service over encrypted data,” Journal of Network & Computer Applications, vol. 106, no. 15, pp. 100–110, 2018. [Google Scholar]

4. C. C. Luo, Z. Y. Tan, G. Y. Min, J. G. Wei, W. Shi et al., “A novel web attack detection system for internet of things via ensemble classification,” IEEE Transactions on Industrial Informatics, vol. 17, no. 8, pp. 5810–5818, 2021. [Google Scholar]

5. B. Xie, T. Xiang and X. F. Liao, “Access-oblivious and privacy-preserving k nearest neighbors classification in dual clouds,” Computer Communications, vol. 187, pp. 12–23, 2022. [Google Scholar]

6. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]

7. Q. Liu, Z. Yang, X. Liu and S. Mbonihankuye, “Analysis of the efficiency-energy with regression and classification in household using k-nn,” Journal of New Media, vol. 1, no. 2, pp. 101–113, 2019. [Google Scholar]

8. Z. Xia, L. Jiang, X. Ma, W. Yang, P. Ji et al., “A privacy-preserving outsourcing scheme for image local binary pattern in secure industrial internet of thing,” IEEE Transactions on Industrial Informatics, vol. 16, no. 1, pp. 629–638, 2019. [Google Scholar]

9. X. Ma, F. Zhang, X. Chen and J. Shen, “Privacy preserving multi-party computation delegation for deep learning in cloud computing,” Information Sciences, vol. 459, pp. 103–116, 2018. [Google Scholar]

10. J. So, B. Guler and A. S. Stimehr, “CodedPrivateML: A fast and privacy-preserving framework for distributed machine learning,” IEEE Journal on Selected Areas in Information Theory, vol. 2, no. 1, pp. 441–451, 2021. [Google Scholar]

11. M. DeCock, R. Dowsley, C. Horst, R. Katti, A. Nascimento et al., “Efficient and private scoring of decision trees, support vector machines and logistic regression models based on pre-computation,” IEEE Transactions on Dependable & Secure Computing, vol. 16, no. 2, pp. 217–230, 2018. [Google Scholar]

12. R. K. H. Tai, J. P. K. Ma, Y. Zhao and S. S. M. Chow, “Privacy-preserving decision trees evaluation via linear functions,” Springer, vol. 10493, pp. 494–512, 2017. [Google Scholar]

13. Z. Lu, Y. Zhu and A. Castiglione, “Efficient k-nn query over encrypted data in cloud with limited key-disclosure and offline data owner,” Computers & Security, vol. 69, pp. 84–96, 2016. [Google Scholar]

14. K. Mandal and G. Gong, “PrivFL: Practical privacy-preserving federated regressions on high-dimensional data over mobile networks,” in Proc. SIGSAC, Los Angeles, CA, USA, pp. 57–68, 2019. [Google Scholar]

15. X. Liu, R. Deng, K. K. R. Choo and Y. Yang, “Privacy-preserving outsourced support vector machine design for secure drug discovery,” IEEE Transactions on Cloud Computing, vol. 8, no. 2, pp. 610–622, 2018. [Google Scholar]

16. A. Nitin, S. S. Ali, J. K. Matt and G. Adrià, “QUOTIENT: Two-party secure neural network training,” in Proc. SIGSAC, Los Angeles, CA, USA, pp. 1231–1247, 2019. [Google Scholar]

17. R. Xu, J. Joshi and C. Li, “Nn-emd: Efficiently training neural networks using encrypted multi-sourced datasets,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 4, pp. 2807–2820, 2021. [Google Scholar]

18. Y. Feng, X. Yang, W. Fang, S. T. Xia and J. Shao, “An accuracy-lossless perturbation method for defending privacy attacks in federated learning,” in Proc. WWW’22, New York, NY, US, pp. 732–742, 2022. [Google Scholar]

19. R. Xu, J. Joshi and C. Li, “Cryptonn: Training neural networks over encrypted data,” in Proc. ICDCS, Dallas, Texas, USA, pp. 1–14, 2019. [Google Scholar]

20. S. Cai, D. Han, X. Yin, D. Li and C. Chang, “A hybrid parallel deep learning model for efficient intrusion detection based on metric learning,” Connection Science, vol. 34, pp. 551–577, 2022. [Google Scholar]

21. C. Wang, A. Wang, J. Xu, Q. Wang and F. Zhou, “Outsourced privacy-preserving decision tree classification service over encrypted data,” Journal of Information Security and Applications, vol. 53, pp. 273–286, 2020. [Google Scholar]

22. J. Yu, Z. Qiao, W. Tang, D. Wang and X. Cao, “Blockchain-based decision tree classification in distributed networks,” Intelligent Automation and Soft Computing, vol. 29, no. 3, pp. 713–728, 2021. [Google Scholar]

23. Z. Dan, Z. Hui, L. Xi, L. Hui, W. Feng et al., “CREDO: Efficient and privacy-preserving multi-level medical pre-diagnosis based on ML-kNN–ScienceDirect,” Information Sciences, vol. 514, pp. 244–262, 2020. [Google Scholar]

24. A. Boldyreva and T. Tang, “Privacy-preserving approximatek-nearest-neighbors search that hides access, query and volume patterns,” Proceedings on Privacy Enhancing Technologies, vol. 4, pp. 549–574, 2021. [Google Scholar]

25. Y. R. Liang, Y. P. Li, Q. Cao and F. Ren, “Vpams: Verifiable and practical attribute-based multi-keyword search over encrypted cloud data,” Journal of Systems Architecture, vol. 108, pp. 324–341, 2020. [Google Scholar]

26. J. Liu, C. Wang, Z. Tu, X. A. Wang and Z. Li, “Secure knn classification scheme based on homomorphic encryption for cyberspace,” Security and Communication Networks, vol. 5, pp. 1–12, 2021. [Google Scholar]

27. P. Li, T. Li, H. Ye, J. Li, X. Chen et al., “Privacy-preserving machine learning with multiple data providers,” Future Generation Computer Systems, vol. 87, pp. 341–350, 2019. [Google Scholar]

28. Z. L. Jiang, H. Guo, Y. Pan, Y. Liu and J. Zhang, “Secure neural network in federated learning with model aggregation under multiple keys,” in Proc. CSCC, Washington, DC, USA, pp. 47–52, 2021. [Google Scholar]

29. Y. Zou, Z. Zhao, S. Shi, L. Wang and B. Wang, “Highly secure privacy-preserving outsourced k-means clustering under multiple keys in cloud computing,” Security and Communication Networks, vol. 2020, pp. 1–11, 2020. [Google Scholar]

30. Y. Zheng, H. Duan, C. Wang, R. Wang and S. Nepal, “Securely and efficiently outsourcing decision tree inference,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 3, pp. 1841–1855, 2020. [Google Scholar]

31. P. Mohassel and P. Rindal, “ABY3: A mixed protocol framework for machine learning,” in Proc. SIGSAC, Los Angeles, CA, USA, pp. 35–52, 2018. [Google Scholar]

32. S. Wagh, D. Gupta and N. Chandran, “Securenn: 3-party secure computation for neural network training,” Privacy Enhancing Technologies, vol. 3, pp. 26–49, 2019. [Google Scholar]

33. R. Rachuri and A. Suresh, “Trident: Efficient 4pc framework for privacy-preserving machine learning,” in Proc. NDSS, San Diego, California, pp. 1–26, 2021. [Google Scholar]

34. C. Long, Z. Zhang and X. Wang, “Batched multi-hop multi-key FHE from ring-LWE with compact ciphertext extension,” Theory of Cryptography Conference, vol. 10678, pp. 1–31, 2017. [Google Scholar]

35. D. Dua and C. Graff, “UCI Machine Learning Repository,” Irvine, CA: School of Information and Computer Sciences, 2017. [Online]. Available: http://archive.ics.uci.edu/ml [Google Scholar]