Genetic Algorithm Combined with the K-Means Algorithm: A Hybrid Technique for Unsupervised Feature Selection

1  Introduction

Feature selection aims to identify the minimum size subset of features that is necessary and sufficient to stay close to the original class distribution. Irrelevant or redundant features whose presence does not improve the proximity to the original class distribution can be dropped [1]. Consequently, learning with the subset of selected features will be easier, less expensive, and more effective in terms of accuracy and computational time [2,3].

Most of the feature selection techniques are dedicated to supervised learning. Unsupervised feature selection is known to be a more difficult problem due to the unavailability of class labels that could facilitate efficient exploration of the search space of the problem. Few studies have tackled this problem. The literature offers four types of machine learning approaches to deal with the feature selection: namely wrapper, filter, embedded, and hybrid [4]. Wrapper approaches [5–7] proceed by implicitly enumerating subsets of features and assessing their learning contributions according to a specific clustering algorithm, which is run for every candidate subset of features. Wrapper approaches are time-consuming because they generally must explore all possible feature subsets. In addition, wrapper effectiveness is restricted to the specific learning algorithm used to assess the subset of features. On the other hand, filter approaches [8–13] filter the features based on their intrinsic properties. Embedded method is a built-in feature selection mechanism that incorporates feature selection into the learning process and uses its properties to guide feature evaluation [4]. In hybrid methods, they try to combine the advantages of other methods [4,14].

The mathematical formulation of the unsupervised feature selection problem leads to a hard combinatorial optimization problem (see Section 4). Even when the number k of features to select is a priori known, the state space of the potential solutions is huge; it is of order Ckn  that is the number of ways to choose k features among n. For that reason, rather than solving the optimization problem in an exact manner, many metaheuristics and evolutionary algorithms have been proposed to deal with this problem [15–20]. Unsupervised Feature Selection problem (UFS) can be considered as an optimization problem, where the objective function is to select the smallest subset of features that minimizes the redundancy and maximizes the relevance toward the goal. UFS is a hard optimization problem; the size of the search space is O (2n) where n is the number of features. Exact optimization methods must explore the whole search space to determine the optimal solution. However, these types of methods are time-consuming due to the huge size space of the problem, especially when the number of features is relatively large. Metaheuristics constitute a more adequate and suitable alternative to solve such hard optimization problems as only some promising regions of the search space are explored to determine a near-optimal solution. On the one hand, metaheuristics can exploit all the different types of concepts of similarity and feature variance developed in the context of filter approaches, and on the other hand they can overcome the drawbacks of wrapper approaches by intelligently exploring the huge search space of exponential size in a reasonable time to find a near-optimal solution of the problem. The main difficulty lies in the designing of a significant objective function of the UFS optimization problem enabling us to guide the search toward potential solutions. These types of methods combine and take advantage of metaheuristic techniques developed in artificial intelligence and existing statistical concepts designed for unsupervised feature selection that we are seeking to design in this paper.

Genetic Algorithm (GA) is a powerful population-based search metaheuristic that has demonstrated its effectiveness and superiority in solving the famous hard combinatorial optimization problems the Quadratic Assignment Problem (QAP) [21,22], the Traveling Salesman Problem (TSP) [23,24], and the DNA Fragment Assembly Problem [25]. On the other hand, few GAs have been developed for the UFS problem and even those developed are very basic, in the sense that they used classical and generic known GA operators of the literature. For these reasons, we consider it worth investigating properly and adequately designed genetic algorithms in the context of unsupervised feature selection.

In this paper, we propose a hybrid technique, called GAk-MEANS, which combines the genetic algorithm approach with the classical k-Means algorithm. In order to efficiently explore the huge search space of the UFS problem and to guide the search to the potential solutions, we modeled the UFS as a multi-criteria optimization problem. For this purpose, we designed a new fitness function based on the k-Means algorithm. Our fitness function stands out from the others existing fitness functions in the literature because it is properly designed with respect to the characteristics of the optimization problem modeling UFS itself, rather than adapting existing fitness functions of the literature. The main contributions of this research are as follows:

•   We proposed a hybrid technique for unsupervised feature selection called GAk-MEANS, which combines the genetic algorithm (GA) approach with the classical k-Means algorithm to find a low-dimensional subset of features. The proposed technique is experimentally evaluated using a set of datasets that vary in dimensionality.

•   The initial population plays a major role in the effectiveness of any genetic algorithm performance. Thus, we investigated how to generate an initial population to enhance the performance of genetic algorithms that solve the UFS problem. In this paper, we carefully generate a set of initial individuals to improve the search and converge quickly to a satisfactory near-optimal solution.

•   Designing an efficient fitness function for a genetic algorithm is a substantial and challenging task. In the proposed algorithm, a new fitness function relying on the k-RMeans algorithm is designed to assess the quality of a subset of features, and specially to direct the exploration of the search space of the problem toward potential (near-optimal) solutions.

•   We designed a new smart crossover operator to ensure the exchange of the best-selected feature subsets to create a better subset of features.

•   We designed a new suitable mutation operator based on the feature similarity measure to diversify the search and maintain the fitter individual.

Our approach, GAk-MEANS, can be categorized as a hybrid filter-wrapper approach as it assesses a subset of features based on their similarities independently from any learning algorithm (as in the filter approach). However, it stands out from the traditional filter approaches by allowing the consideration and the assessment of several candidate solutions instead of only the first one selected based on the similarity coefficients (as in the wrapper approach).

The designed hybrid technique is implemented and tested using five different datasets. The performances of GAk-MEANS have been compared with the results of other genetic algorithms, namely the genetic algorithm using the Sammon Error Function, and the genetic algorithm using the Sum of Squared Error Function. Moreover, the performance of GAk-MEANS is compared against the state-of-the-art statistical approaches for unsupervised feature selection techniques.

Experimental results show that GAk-MEANS consistently selects the subsets of features that result in better classification accuracy compared to others.

2  Background Information

2.1 Relevant and Irrelevant Features Definitions

Real-world data suffers from the existence of many irrelevant, redundant, and noisy features. Removing these features by feature selection reduces the computational cost in terms of both time and space [14]. Removing irrelevant features before learning is beneficial. Some relevant features could be redundant. For instance, when one feature strongly correlates with some other feature. In this case, one of these features could be removed, hence improving the learning process.

2.2 Similarity Measure between Two Features

The similarity measure is a way of measuring how data samples are related or close to each other. Data samples are related if their corresponding features are related. Without loss of generality, we can assume that all features are vector samples from real numbers. Some of the most popular similarity measures are described below:

Euclidean distance is the basis of many measures of similarity and dissimilarity [26]. The Euclidean distance between features X and Y is the square root of the sum of squared differences between corresponding elements of the two features, as shown in Eq. (1) [26].

dEuclidean(X,Y)=∑in(xi−yi)2(1)

Euclidean distance is only appropriate for data measured on the same scale. The correlation coefficient is (inversely) related to the Euclidean distance between standardized versions of the data.

Another commonly used distance measure is the Manhattan distance. The Manhattan distance between features X and Y is the sum of the absolute differences between the corresponding elements of the two features, see Eq. (2) [26].

dManhattan(X,Y)=∑1n|xi−yi|(2)

The following is a definition of the correlation between the vectors X and Y [27]:

r(X,Y)=1n∑imxiyi−μXμYσXσY(3)

where μX and μY are the means of X and Y respectively, and σX and σY are the standard deviations of X and Y. The numerator of the equation is called the covariance of X and Y and is the difference between the mean of the product of X and Y subtracted from the product of the means.

In this paper, the designed fitness function is based on the k-RMeans algorithm, where the k-RMeans algorithm is a relaxed version of k-Means that can rely on any feature similarity measure.

2.3 Genetic Algorithm

Genetic algorithm (GA) is a well-known population-based metaheuristic algorithm that is inspired by the biological evolution processes [28,29]. The fundamental components of GA are chromosome representation, fitness function, and biological-inspired operators which are selection, mutation, and crossover. The fitness function evaluates the closeness of the solution to the optimal solution of a specific problem, which means it decides how suitable a solution is. In the genetic algorithm, the creation of the fitness function is a very important step [30]. Genetic algorithms begin by generating an initial population of candidate solutions. The natural selection procedure begins with the selection of the fittest individuals (solutions) from a population by employing a fitness function to obtain a better population. The generation of the new solutions occurs by using crossover and mutation operations [31].

3  Related Work

3.1 Machine-Learning Techniques for Unsupervised Feature Selection

In this section, some of the state-of-the-art unsupervised feature selection methods [14] based on mathematical/statistical modeling are presented. Different feature selection algorithms exploit various types of criteria to define the relevance of features. Current UFS are classified into Similarity-Based methods, Sparse-Learning-Based methods, and other recent methods. The state-of-the-artwork for Similarity-Based methods and Sparse-Learning-Based methods are described in this section.

Similarity-Based methods assess feature importance by their ability to preserve data similarity. These include Laplacian Score [32], and SPEC [33]. The Laplacian Score (LS) method assumes that the local structure of the data space defines the underlying classes/clusters. To model the local geometric structure, LS constructs a nearest neighbor graph where two data points are probably in the same class/cluster, if they are close to each other. LS computes for each feature its Laplacian Score to find the top features that respect this graph structure. Since Laplacian Score evaluates each feature individually, the task of selecting the k features can be solved by picking the most k relevant features. Obviously, LS is unable to discover redundant features.

SPEC realizes that both supervised and unsupervised feature selection methods select the features that separate the data points into subsets according to their similarity, in most cases. It proposes that, analyzing the spectrum of the graph induced by the data points pairwise similarity is a generic framework in both settings. SPEC shows that many algorithms, including Laplacian Score, are just special cases of the proposed generic framework.

Sparse-learning-based methods select the features by removing the least useful ones. They use a spare regularizer to weigh the importance of a feature and force the coefficient of the non-useful features to be very small or exactly zero, and hence, to be removed. Examples of sparse-learning-based methods are Multi Cluster Feature Selection (MCFS) [34], and Nonnegative Discriminative Feature Selection (NDFS) [35].

In the experimental evaluation section, we compared the performance and results obtained by the proposed method GAk-MEANS with the results of these statistical methods.

There are some recent works that proposed unsupervised feature selection algorithms. For example, Miao et al. [36] proposed a new UFS approach, called Regularized Local Linear Embedding (GLLE), which aims at preserving the local invariance of feature subspace by integrating local linear embedding (LLE) and manifold regularization constrained in feature subspace into a unified framework. Moreover, they proposed an iterative optimization algorithm to solve the resulting model. Nie et al. [37] proposed a new feature selection approach, called unsupervised feature selection with RSOGFS, to solve the original ℓ 2, 0-norm constrained problem rather than tackling its relaxed or approximate problem. Instead of selecting a good individual one at a time, RSOGFS selects a good feature subset. Miao et al. [38] proposed a new regularized self-representation unsupervised feature selection method, which employs ℓ 2, 1–2 as sparse regularization to perform feature selection. Also, an iterative CCCP algorithm to the resulting non-convex problem with proven global convergence is provided. Several experiments using real-world datasets show that the proposed method performs better than several state-of-the-art methods.

Some methods for solving the unsupervised feature selection problem include a metaheuristic artificial intelligent (AI) strategy, and a machine learning (ML) strategy such the methods mentioned above. Metaheuristics in artificial intelligent are intelligent techniques intended to explore the search space of the UFS optimization problem to find a near-optimal solution in a reasonable time as only some promising regions of the search space are explored to determine a near-optimal solution. For this purpose, some metaheuristics have been designed to deal with the UFS optimization problem, which will be discussed in the following sections.

3.2 Metaheuristics Techniques for Solving UFS

Metaheuristics are a type of generic algorithm that can be used to solve a wide range of optimization problems. Recently, few metaheuristics have been designed to deal with the UFS optimization problem. For example, evolutionary approaches as the binary bat algorithm [16] and genetic algorithm approaches are used to solve UFS problem [17–20]. Furthermore, ant colony optimization [15] has recently been used to solve UFS problem. In this section, some metaheuristics algorithms for solving UFS problem are presented.

Ant colony optimization (ACO) is one of the most well-known swarm-based algorithms. Dadaneh et al. [15] designed an unsupervised probabilistic ACO-based method for feature selection (UPFS). In each step of the ACO algorithm, to select the next potential feature, they calculate the amount of redundancy between the current feature and all those which have been selected thus far. In addition, they utilize a matrix to hold ant related pheromone which shows the rate of the copresence of every pair of features in solutions, then the features are ranked based on a probability function extracted from the matrix. In general, there are some limitations and drawbacks of ant colony algorithm [39]. As a result of numerous parameters that are involved in ACO, incorrect selection of starting value can lead to a local optimum. In addition, individual ants will move randomly when the problem size is too large, causing the entire algorithm to take longer to run, reducing the efficiency of finding the best solution. The pheromone-related parameters that were chosen in the formula are mostly based on experience. Thus, when selecting the pheromone parameters without experience and theoretical arguments, then the obtained results could be greatly scattered because of the inefficiency and poor convergence of the algorithm.

Ramasamy et al. [16] proposed a wrapper-based unsupervised feature selection method with the modified binary bat approach that applies k-Means clustering algorithm. They used a fitness function which is evaluated based on the cluster quality measured using Sum of Squared Error. Binary bat algorithm has some weaknesses that may negatively affect its performance [40]. One of the important factors through which the efficacy of most swarm intelligence algorithms is determined its ability to produce a mutation. Besides, the diversity of the population achieves the continued ability to develop in the algorithm, but bat algorithm lacks these features and thus cannot jump out from the local optima area, where the diversity decreases whenever the problem dimensions increase [41]. Another determinant is that in the standard bat algorithm, the movement to a new location (a new solution) is not performed unless it is better than the current global solution, and this leads to limiting the movement of the search agents [42].

There are few numbers of metaheuristics algorithms that have been proposed to deal with the UFS optimization problem. Metaheuristic algorithms including the genetic algorithm have proven their efficiency in solving optimization problems, through a balance between exploration and random search [40]. In the next section, we present a number of recent works to solve UFS problem by using genetic algorithms.

3.3 Genetic Algorithms for Solving UFS

To the best of our knowledge, there are many unsupervised feature selection methods reported in the literature, but few of them discuss unsupervised feature selection using genetic algorithms.

Shamsinejadbabki et al. [17] introduced an approach to unsupervised feature selection for text clustering based on genetic algorithm that evaluates groups of terms by utilizing a new Term Variance measuring technique. They used a genetic-based algorithm to find the most valuable groups of terms (vector feature) depending on the new measure. The proposed method’s main limitation, according to the author, is that it is time-consuming in which finding the best-fitting groups of words with a GA is a process that takes a long time.

Abualigah et al. [18] proposed a new method called Feature Selection technique using GA Algorithm for the Text Clustering (FSGATC), which is a genetic algorithm used to solve the unsupervised feature selection problem. This method is used to create a new subset of informative features to obtain more accurate clusters. They used mean absolute difference (MAD) as a fitness function in GA for feature selection technique using the weight scheme called (term frequency-inverse document frequency) for each position, which is a statistical measure that evaluates how relevant a word is to a document in a collection of documents. MAD is a measure used in FS domain to assign a relevance score for features by calculating the difference of the mean value, then computing the difference between the mean and median of xij, where xij is the value of the feature j in document i. The optimal solution is the one with the highest fitness value.

Agrawal et al. [19] proposed an approach for unsupervised feature selection using genetic algorithm. They incorporated the genetic feature selection method and greedy feature selection algorithm as discussed by Farahat et al. [43], which selects one feature at each iteration such that the reconstruction error for the novel set of features is in the least amount. The implementation of the greedy feature selection algorithm is to compute the reconstruction error for every candidate feature, and then select the feature with the minimum error. The proposed greedy feature selection by Ahmed K. Farahat, as noted by the author, is less effective for very big data instances, which is one of the method’s disadvantages. In addition, there is insufficient information regarding the implementation of the genetic algorithm operations and their parameters.

Saxena et al. [20] proposed a new method for unsupervised feature selection where a genetic algorithm has been utilized to select a subset of features by taking Sammon error as the fitness function, where Sammon error is related to Sammon mapping that belongs to the multidimensional scaling algorithms family for mapping a high-dimensional space to a lower-dimensional space. Sammon error is a function to evaluate how good a given projection is in preserving the original structure, by assessing the difference in the distance between each pair of points in the higher and the lower dimensionality space, which can be used as a measure of quality of the selected feature. A lower value of the Sammon error denotes a higher topology preservation and a better set of selected features.

As mentioned in the introduction, GA algorithms proved their effectiveness and superiority to solve the well-known combinatorial hard optimization problem such as the Traveling Salesman Problem (TS) and the Quadratic Assignment Problem (QAP). On the other hand, to the best of our knowledge, a few numbers of UFS approaches in the literature are utilizing genetic algorithms and are still inadequate and unsatisfactory which also creates a motivation to research in this field. Furthermore, most genetic algorithms for solving UFS problems rely on the basic classical operators and generic fitness functions which do not consider the structural aspect and characteristics of the UFS optimization problem. Thus, there is a need for designing a more appropriate genetic algorithm for UFS by developing more adequate fitness function and biological-inspired operators. The modeling of the unsupervised feature selection as an optimization problem enables us to design a new proper fitness function to the UFS problem that naturally guides the search towards feasible and potential region of solutions. Our fitness function is distinct from other fitness functions of the literature because it is properly designed with respect to the characteristics of the UFS problem, rather adapting existing fitness functions of the literature. Similarly, this modelling allowed us to introduce proper smart crossover and mutation operators to explore the huge search space of the UFS problem rather adapting existing classical known operators as the famous one-point crossover. At the end, these new different algorithmic contributions to UFS deserve to be investigated in order to know their impacts on several UFS datasets of the literature.

4  UFS as a Multi-Criteria Optimization Problem

We model the unsupervised feature selection as a Multi-Criteria Optimization problem. More formally, given a similarity measure between the features of data samples, and let C1, …, Ck be a set of k clusters where each cluster is a grouping of similar features according to the similarity measure. Let Pij be the similarity measure of the two features i and j (i  <  j). The best subset of features should fulfill the following three objective functions (given in points 1, 2, 3) subject to the two constraints (given in point 4):

The huge search space of the optimization problem will be explored using the designed hybrid technique detailed in the following section. The three objective functions are handled explicitly via the fitness function, the crossover and mutation operators designed for this purpose.

5  The Hybrid Technique GAk-MEANS

In this section, we describe the designed GA concepts for the UFS problem. We start by encoding a possible solution of UFS, then we introduce the simple variant of the k-Means algorithm which will be used in defining the fitness function of an individual and generating the initial population of the hybrid technique GAk-MEANS. We describe how to calculate an individual’s fitness function value, and the newly designed crossover and mutation operators for UFS. Some definitions are introduced below to illustrate the proposed algorithm of the hybrid technique.

•   Definition 1. (Nearest features vs. farthest features): A feature j in a cluster C is the nearest (resp. farthest) feature to some feature i in C, according to a given similarity measure, if j is the most (resp. least) similar feature to i. That is for i, j∈C, maxj Pij (resp. minj Pij).

•   Definition 2. The eccentricity of a feature i into a cluster C is the similarity value with the farthest feature to i in C.

•   Definition 3. The center of a cluster C is the feature in C with minimum eccentricity.

Fig. 1 gives an overview of the different steps for the hybrid technique GAk-MEANS. Next, each step will be explained in detail.

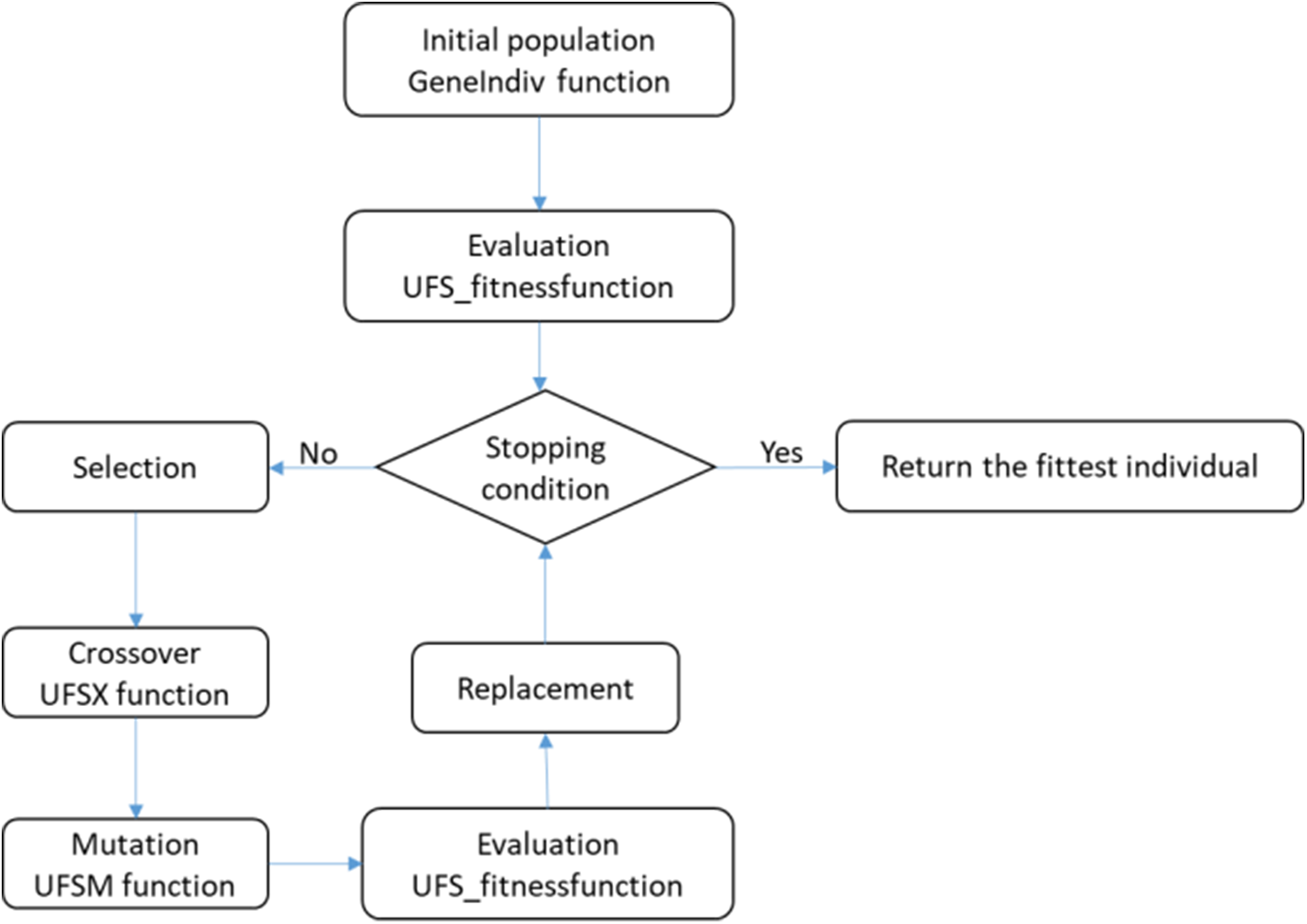
Figure 1: GAk-MEANS flowchart

5.1 Encoding of Individuals

An individual I is a set of integer numbers where each number represents a feature, and the cardinality of a set I indicates the number of features in the individual I.

5.2 Initial Population

The first step in any GA algorithm is to create the first generation of the population. The population is a set of individuals; each individual consists of a subset of k features (LB <= k <= UB). Basically, the genetic algorithms generate the initial population randomly.

In this paper, we carefully improve a set of initial individuals in order to improve the search and to converge quickly to a satisfied near-optimal solution. Table 1 shows the procedure of GeneIndiv (I, k) relying on k-RMeans algorithm to improve a given individual of size k from the initial population. The value of k is randomly selected in the interval [LB, UB] for each generated individual.

5.3 k-RMeans Algorithm

Given a subset of k features, k-RMeans aims to partition the features of F into k clusters where intra-clusters similarity is maximized. k-RMeans is a Relaxed variant of k-Means algorithm that is simply one iteration of k-Means. Let I be a subset of k features of F, we create for each feature I a cluster. k-RMeans assigns every feature i of F not in I to the cluster whose the center feature is the nearest feature to i. k-RMeans relies on the concept of eccentricity to compute the center of a cluster as seen in Table 2.

k-RMeans algorithm can use any feature similarity measure (feature correlation: Person, Euclidian distance, symmetric uncertainty, etc.).

5.4 Fitness Function

The fitness function assesses the quality of an individual, a subset of k features (k <= n) where n set of all features. For UFS, we defined a new fitness function relying on the k-RMeans algorithm. The fitness value of an individual is the ratio of intra-cluster similarities to inter-cluster similarities. More formally, the fitness function of an individual I is computed as follows:

Fitness (I)=∑k∑i∈Ck,j=center of Ck Pij ∑ icenterofCi,i<jjcenterofCjPij(4)

This fitness function is defined from the objective functions 2 and 3 of the optimization problem described in Section 4. A good individual is one who has a higher fitness function value. In our experiments, we used Euclidean distance to infer the similarity. Thus, the lower fitness function, the better the individual.

5.5 Selection

The roulette wheel selection is used at this step to select the potentially useful solutions for recombination based on the fitness values of the individuals.

5.6 The Crossover Operator UFSX

The crossover operator explores the search space of the UFS solution by building a new offspring from two individual parents. UFSX is a new smart crossover operator that we designed to generate a new offspring by getting closer to the optimal solution. Let’s I1 and I2 be two individuals. UFSX crossover builds a new offspring in O (k1 k2) as shown in Table 3.

The new crossover UFSX creates offspring with a smaller number of features and selects features from the candidate set that are less similar. Thus, UFSX creates offspring that are closer to the optimal solution.

5.7 The Mutation Operator UFSM

The mutation operator aims to diversify the search in order to explore different promising regions of the search space of the problem. We designed a new mutation operator UFSM that involves exchanging a randomly selected feature i of the individual I with the less similar feature in F-I. The time complexity of UFSM operator is O (k n) where n is the number of features in the original set F, and k is the number of features included in the mutant individual, as shown in Table 4.

5.8 Replacement and Stopping Condition

The final step is to replace the old population with the new population based on the selection strategy. GAk-MEANS algorithm terminates at the end to announce the best solution in hand when the predetermined number of generations is reached.

6  Evaluation Framework

We implemented GAk-MEANS algorithm for UFS problem using Spyder (Python 3.8) software. Next, we explain the used datasets, the experiments settings, and the performance measures.

6.1 Datasets

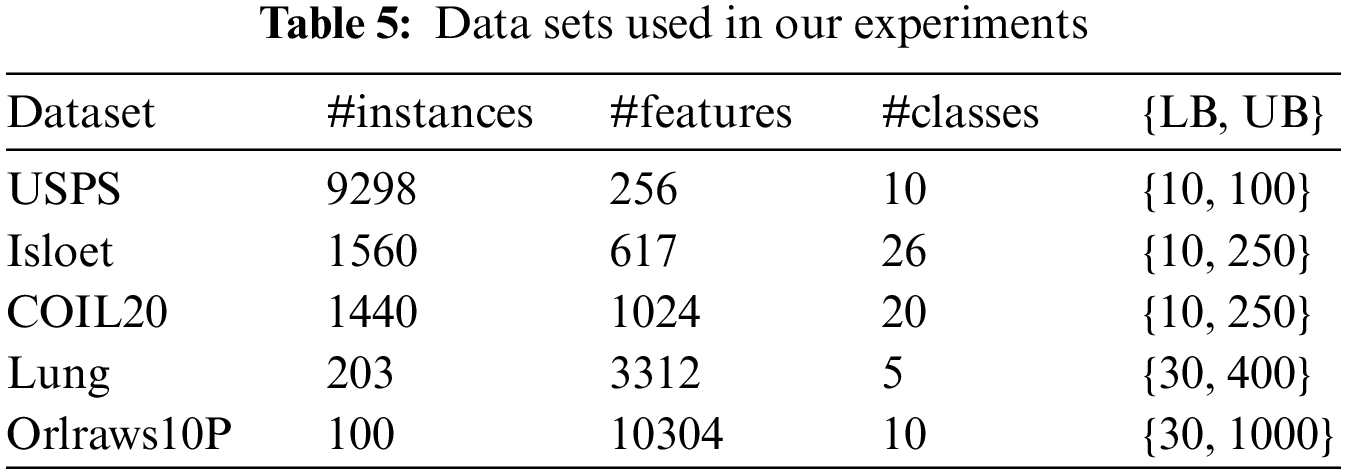
Experiments have been conducted on 5 datasets of various types. The datasets are hand-written image dataset USPS [44], face image datasets COIL20 [45], spoken letter recognition dataset Isolet [46], biological dataset Lung [47], and face image dataset Orlraws10P [48]. Datasets description is summarized in Table 5, which shows a considerable diversity in the number of instances, features, and classes. LB refers to the lower bound of k, and UB refers to the upper bound of k. The search for an optimal value of k is handled implicitly during the exploration of the search space of the UFS problem. The value of k is changed gradually, and for each value make a run of GAk-MEANS. The best solution according to the classification accuracy with the small value of k is returned.

6.2 GA Parameters Settings

There are some user-specified parameters that have been learnt from our comprehensive experiments by changing the experimental parameters and carrying out multiple runs of the algorithm with different parameters’ values including the population size, probability of crossover operation, probability of mutation operation, and number of iterations. Population size is the number of individuals in a population. The probability of crossover operation referred to the probability of crossover to occur in each iteration. For each individual, a randomly generated floating-point value is compared to the crossover probability, and if it is less than the probability, crossover is performed; otherwise, the offspring are identical to the parents. The probability of mutation operation is the probability of mutation occurrence for the individual. For each individual, a randomly generated floating-point value is compared to the mutation probability, and if it is less than the probability, mutation is performed. The number of iterations, also called number of generations, refers to the number of cycles before the termination. Table 6 shows these parameters.

6.3 Performance Measure

Results are evaluated in terms of the number of selected features, accuracy, and time. Classification accuracy is measured as the percentage of the samples that were correctly classified. The accuracy of each method was measured by using naïve Bayes classifier with 10-cross-validation. To evaluate the goodness of the final set of features, the accuracy of the original data with full set of features was compared with the accuracy of the data containing only selected features.

7  Results and Discussion

This section presents the results of the experiments on GAk-MEANS and analyses its performance in terms of classification accuracy, run time, and the number of selected features. In addition, the performance of GAk-MEANS has been compared with the results of other genetic algorithms. Furthermore, the performance of GAk-MEANS is compared with the state-of-the-art unsupervised feature selection techniques.

7.1 Evaluating the Performance of GAk-MEANS

The performance of GAk-MEANS is shown in Table 7. Results were averaged over 10 independent runs. F and Fs refer to the total number of original features and selected features, respectively. ACC refers to the classification accuracy and STDDEV(ACC) refers to the Standard Deviation of accuracy.

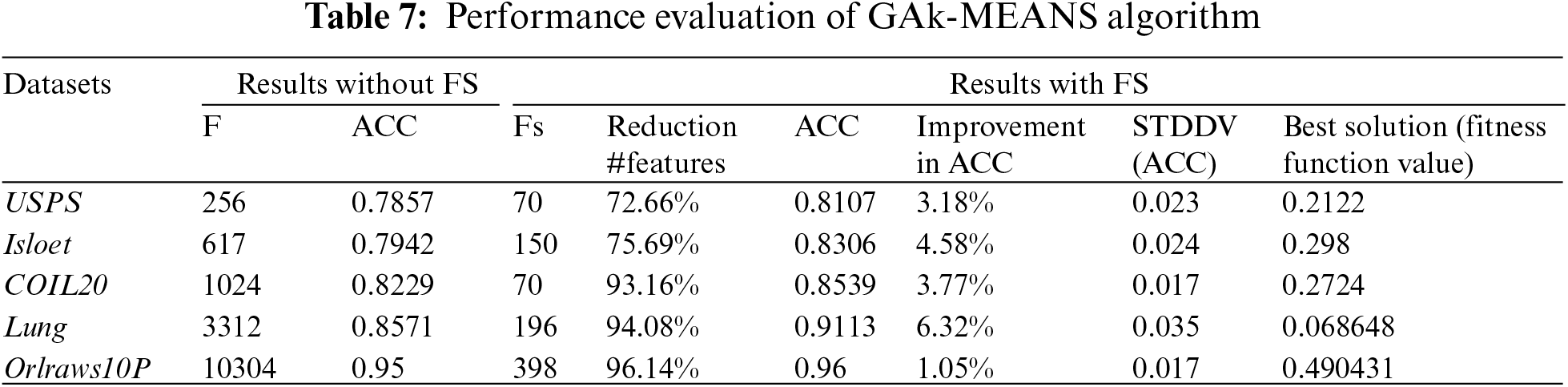
Fig. 2 shows the values of the accuracy in the y-axis and the number of selected features in the x-axis for each dataset. We observed that accuracy increases with a reduction in the number of features.

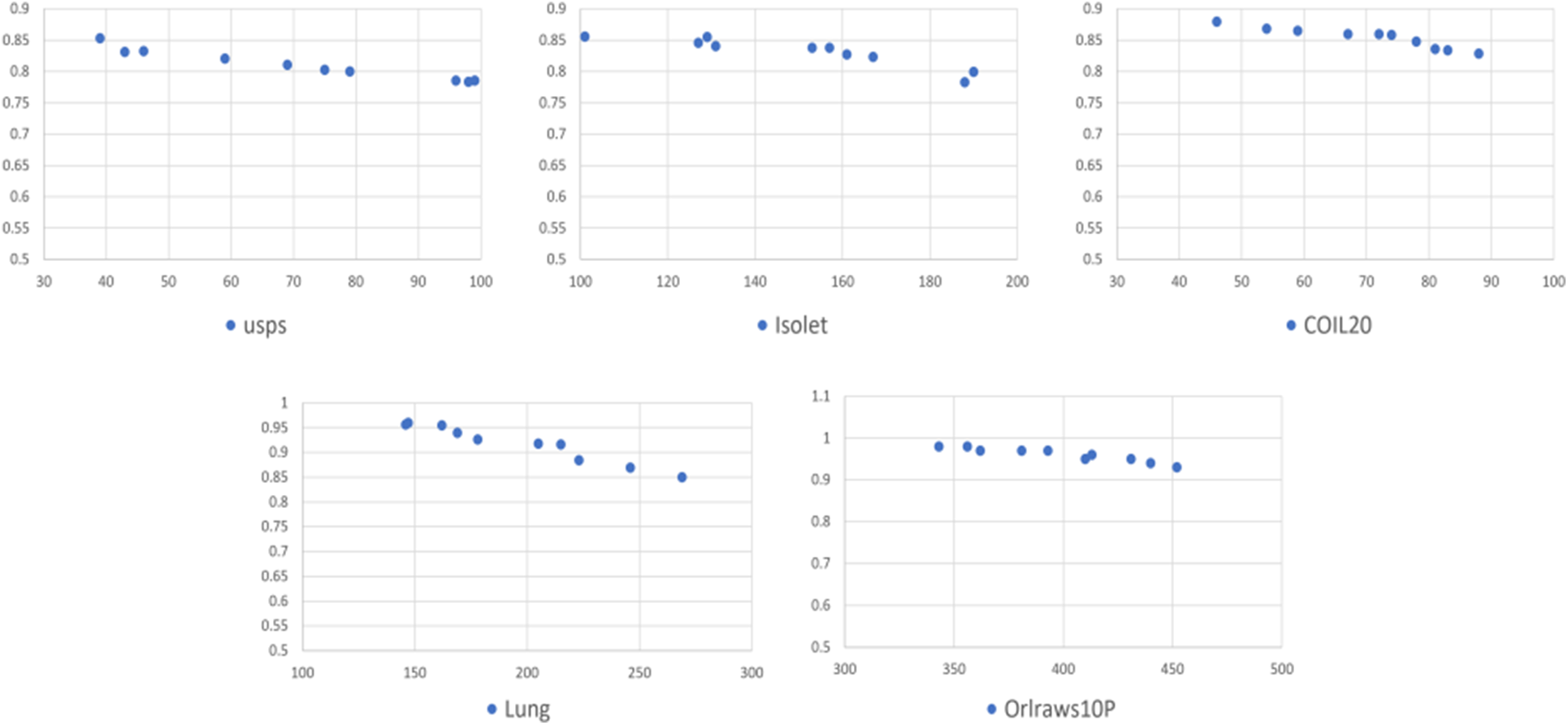
Figure 2: The accuracy and the number of selected features for each dataset

Based on the results, we observed that GAk-MEANS has the ability to select a small number of features. After applying GAk-MEANS algorithm on the given datasets and the dimension size had become smaller, we found that, the selected subset of features by our proposed method had a higher classification accuracy than all features’ accuracy. The positive effect of a small number of features is clearly visible if we look at the results of the accuracy as shown in Table 7. In particular, GAk-MEANS is able to significantly reduce the size of the features by 86.35% on average (72%–96%, 14%), which leads to an increase of the accuracy by 3.78% on average (1.05%–6.32%) compared to using all features.

7.2 Comparisons of GAk-MEANS and Other Genetic Algorithms

Table 8 compares GAk-MEANS performance to other genetic algorithms. In particular, GAk-MEANS are compared with the genetic algorithm using Sammon Error Function (GA-SEF) [20], and the genetic algorithm using Sum of Squared Error Function (GA-SSEF) [16]. Table 8 shows the result on different datasets.

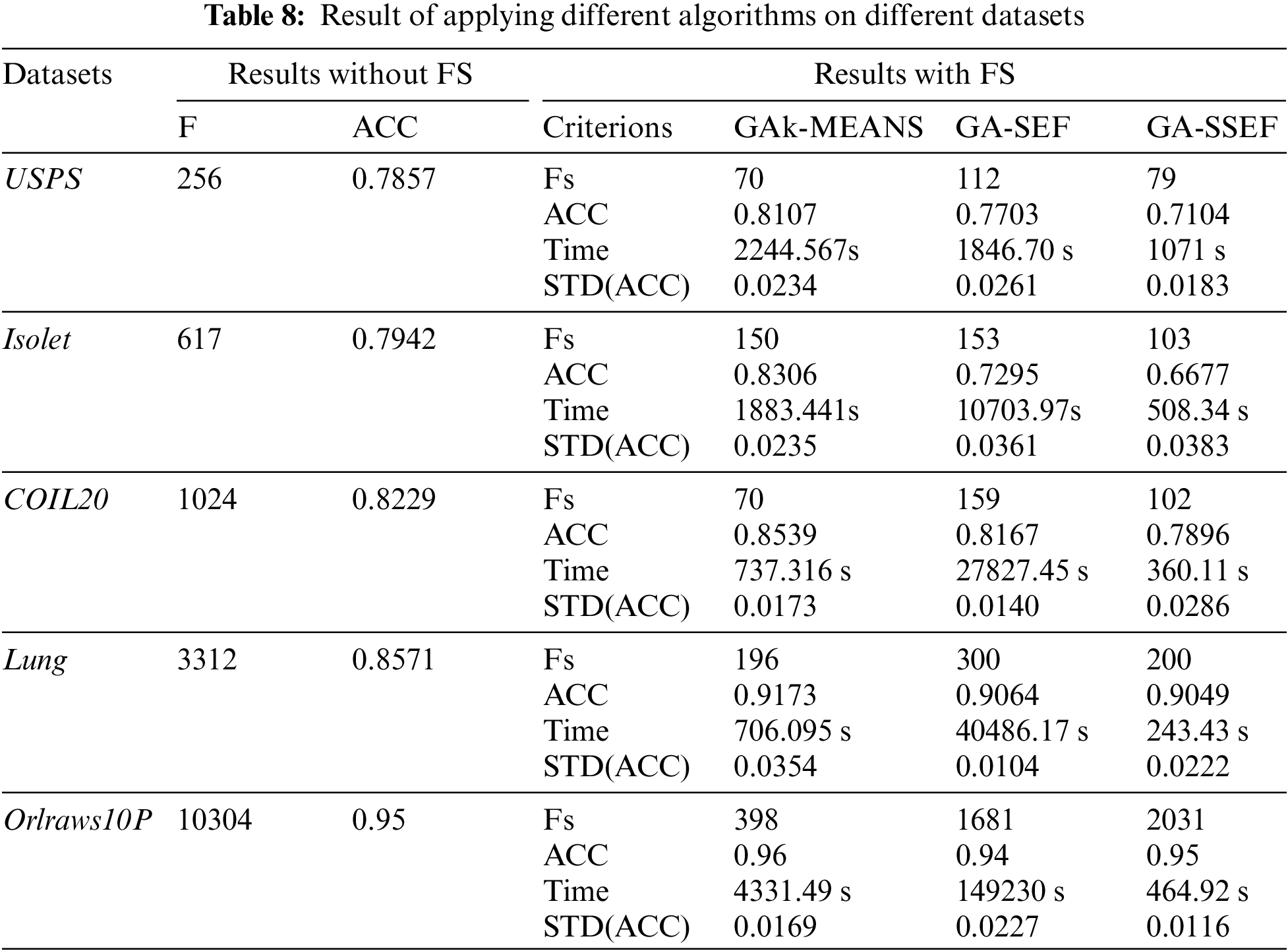
Table 9 shows the percentage of the improvement in GAk-MEANS compared to other algorithms in terms of reducing the number of features, improving the accuracy, and reducing the time.

When comparing with the genetic algorithm using the Sammon Error Function, GAk-MEANS on average is able to reduce the size of the features by 41.29% and improve the accuracy by 5.37% with reduced time by 70.71%. When comparing with the genetic algorithm using the Sum of Squared Error Function, GAk-MEANS on average is able to reduce the size of the subset of selected features by 15.91% and improve the accuracy by 9.81% with an increase in time by 3 factors. Based on the result, we observed that our proposed algorithm consumes less time than the Sammon Error function, but more time than the Sum of Squared Error Function. According to the results of applying these different algorithms, we found that the proposed algorithm overcomes the comparative methods by selecting a small number of features that provide superior classification accuracy in a reasonable period of time.

The proposed GAk-MEANS gave better performance based on the classification accuracy and time overall datasets. Our algorithm achieves a higher level of dimensionality reduction by selecting a smaller number of features than other methods. The superior performance of GAk-MEANS could be attributed to several factors. A new fitness function is designed to guide the search toward the promising regions involving relevant solutions. Furthermore, a new smart crossover and mutation operators are used instead of classical operators to increase the diversity of the population with greater fitness and provide a mechanism for escaping from a local optimum. Unlike other genetic algorithms, which randomly generate the initial population, in GAk-MEANS algorithm we developed a procedure to carefully generate the initial individuals; each individual regroups in a cluster a subset of similar features intended to improve the search and to converge quickly to a satisfied near-optimal solution.

7.3 Comparisons of GAk-MEANS and Machine-Learning Techniques

In this section, we conducted experiments to compare the performance of GAk-MEANS and the state-of-the-art ML based unsupervised feature selection methods. Four ML methods are compared with the proposed algorithm; similarity-based methods: Laplacian Score (LS) and SPEC, sparse learning-based methods: MCFS, and NDFS. We specified the number of selected features to be uniform in all methods for each dataset, according to the obtained number of selected features from GAk-MEANS in Section 6. Table 10 shows the result of applying these different methods on different datasets in terms of the accuracy and time consuming.

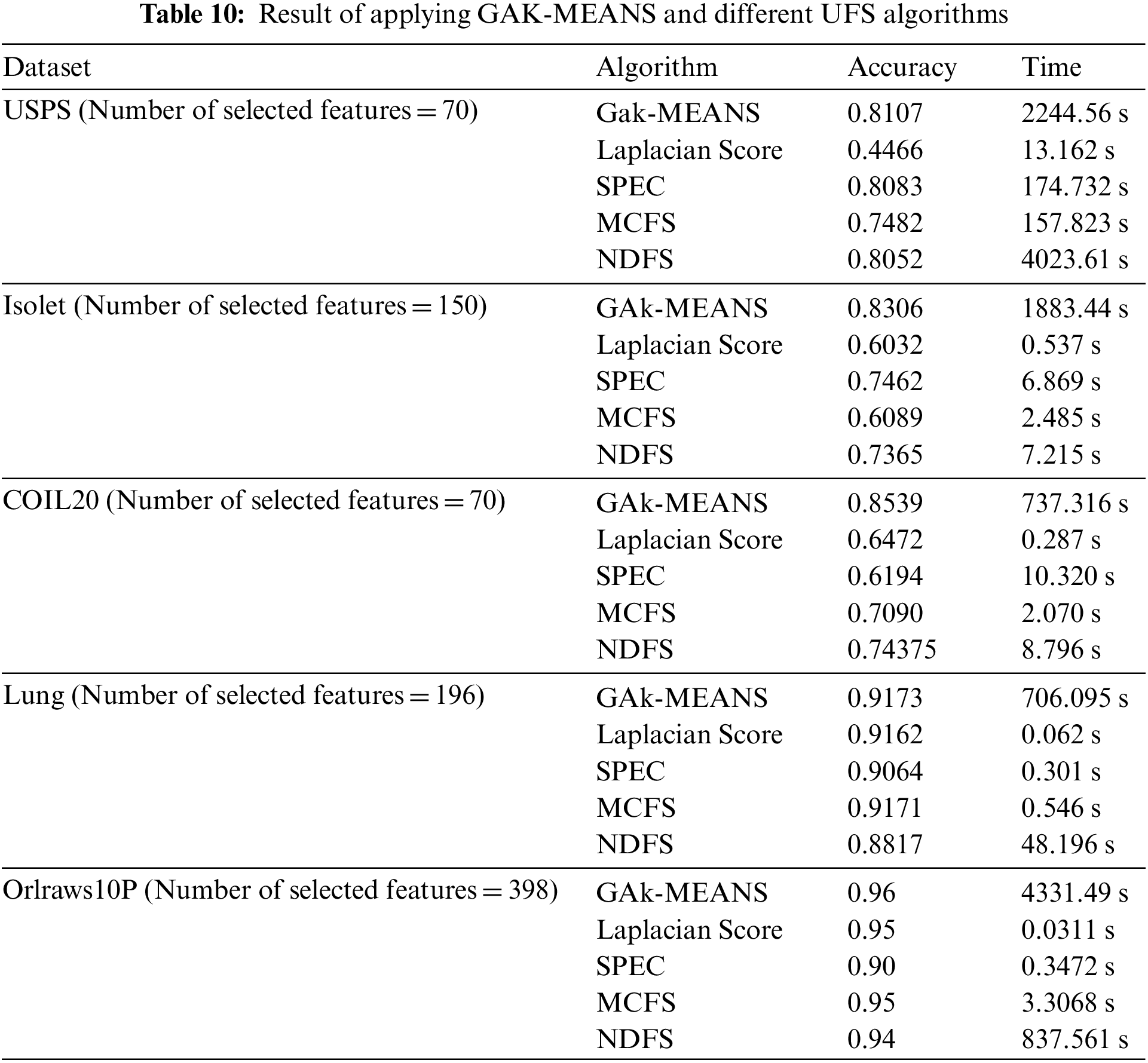
Based on Table 10 we observed that, in the case of USPS dataset, GAk-MEANS outperformed ML methods where the rate of improvement is 15.47%. According to the time metric, NDFS consumes more time than all methods. Regarding the Isolet dataset, GAk-MEANS outperformed ML methods where the improvement rate is 23.29%. In the case of COIL20 dataset, GAk-MEANS outperformed ML methods where the rate of improvement is 25.60%. Regarding the Lung dataset, GAk-MEANS outperformed ML method where the rate of improvement is 1.32%. In the case of Orlraws10P dataset, GAk-MEANS outperformed ML methods where the rate of improvement is 2.67%. Based on the result, we make the following observations: GAk-MEANS outperforms the Laplacian Score, SPEC, MCFS, and NDFS for all datasets in terms of accuracy. On the other hand, GAk-MEANS consumes more time than other methods, except in the case of USPS where NDFS method consumes more time than other approaches.

Based on the results, we found that GAk-MEANS can increase the accuracy by 13.67% on average with 88.76% average increase in time. We observed that, for Lung and Orlraws10P datasets, since the number of features is challenging and greater than the number of samples, the performance of GAk-MEANS is better than other algorithms, but the improvement rate is small. On the other hand, for USPS, Isolet, and COIL20 where the number of features is less than in Lung and Orlraws10P, and less than the number of samples, GAk-MEANS performs better than other algorithms.

8  Conclusion

In this paper, a new genetic algorithm combined with the k-Means algorithm for unsupervised feature selection is proposed to find a low-dimension subset of features. The proposed method is evaluated by using a set of datasets varying in dimensionality. The experiments demonstrate the effectiveness of the proposed method where the number of features is reduced, and the classification accuracy is better than using all features. It also overcomes the other comparative methods by obtaining better classification accuracy with a small number of selected features based on five common datasets. GAk-MEANS can significantly reduce the size of the subset of selected features by 86.35% on average, which leads to an increase of the accuracy by 3.78% on average compared to using all features. When comparing with the genetic algorithm using the Sammon Error Function, GAk-MEANS on average can reduce the size of the subset of selected features by 41.29% and improve the accuracy by 5.37% with reduced time by 70.71%. When comparing with the genetic algorithm using the Sum of Squared Error Function, GAk-MEANS on average can reduce the size of the subset of selected features by 15.91% and improve the accuracy by 9.81% with an increase in time by 3 factors. When compared with the machine-learning based methods, we observed that GAk-MEANS is able to increase the accuracy by 13.67% on average with 88.76% average increase in time. Finally, according to this study, we can conclude that carefully designed genetic algorithms can lead to competitive techniques for solving the UFS problem.

Acknowledgement: The authors extend their appreciation to the Deanship of Scientific Research at Imam Mohammad bin Saud Islamic University for funding and supporting this work through Graduate Students Research Support Program.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. H. Cho, S. H. Moon and Y. H. Kim, “Genetic feature selection applied to kospi and cryptocurrency price prediction,” Mathematics, vol. 9, no. 20, pp. 2574, 2021. [Google Scholar]

2. J. Lee, H. Jang, S. Ha and Y. Yoon, “Android malware detection using machine learning with feature selection based on the genetic algorithm,” Mathematics, vol. 9, no. 21, pp. 2813, 2021. [Google Scholar]

3. F. Nie, Z. Wang, L. Tian, R. Wang and X. Li, “Subspace sparse discriminative feature selection,” IEEE Transactions on Cybernetics, vol. 52, no. 6, pp. 4221–4233, 2022. [Google Scholar] [PubMed]

4. J. C. Ang, A. Mirzal, H. Haron and H. N. Hamed, “Supervised, unsupervised, and semi-supervised feature selection: A review on gene selection,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 13, no. 5, pp. 971–989, 2016. [Google Scholar] [PubMed]

5. F. Beiranvand, V. Mehrdad and M. B. Dowlatshahi, “Unsupervised feature selection for image classification: A bipartite matching-based principal component analysis approach,” Knowledge-Based Systems, vol. 250, pp. 109085, 2022. [Google Scholar]

6. A. Got, A. Moussaoui and D. Zouache, “Hybrid filter-wrapper feature selection using whale optimization algorithm: A multi-objective approach,” Expert Systems with Applications, vol. 183, pp. 115312, 2021. [Google Scholar]

7. A. Kaur, K. Guleria and N. Kumar Trivedi, “Feature selection in machine learning: Methods and comparison,” in Int. Conf. on Advance Computing and Innovative Technologies in Engineering (ICACITE), Greater Noida, India, 2021. [Google Scholar]

8. X. Zhu, Y. Wang, Y. Li, Y. Tan, G. Wang et al., “A new unsupervised feature selection algorithm using similarity-based feature clustering,” Computational Intelligence, vol. 35, no. 1, pp. 2–22, 2018. [Google Scholar]

9. X. F. Song, Y. Zhang, D. W. Gong and X. Z. Gao, “A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data,” IEEE Transactions on Cybernetics, vol. 52, no. 9, pp. 9573–9586, 2022. [Google Scholar] [PubMed]

10. A. M. Usman, U. K. Yusof and M. Sabudin, “Filter-based feature selection using information theory and binary cuckoo optimization algorithm,” Journal of Information Technology Management, vol. 14, pp. 324–338, 2022. [Google Scholar]

11. F. Song, Z. Guo and D. Mei, “Feature selection using principal component analysis,” in 2010 Int. Conf. on System Science, Engineering Design and Manufacturing Informatization, Yichang, China, 2010. [Google Scholar]

12. S. Solorio-Fernández, J. A. Carrasco-Ochoa and J. F. Martínez-Trinidad, “A review of unsupervised feature selection methods,” Artificial Intelligence Review, vol. 53, no. 2, pp. 907–948, 2019. [Google Scholar]

13. J. Park, M. W. Park, D. W. Kim and J. Lee, “Multi-population genetic algorithm for multilabel feature selection based on label complementary communication,” Entropy, vol. 22, no. 8, pp. 876, 2020. [Google Scholar] [PubMed]

14. J. Li, K. Cheng, S. Wang, F. Morstatter, R. P. Trevino et al., “Feature selection: A data perspective,” ACM Computing Surveys, vol. 50, no. 6, pp. 1–45, 2017. [Google Scholar]

15. B. Z. Dadaneh, H. Y. Markid and A. Zakerolhosseini, “Unsupervised probabilistic feature selection using ant colony optimization,” Expert Systems with Applications, vol. 53, pp. 27–42, 2016. [Google Scholar]

16. R. Ramasamy and S. Rani, “Modified binary bat algorithm for feature selection in unsupervised learning,” International Arab Journal of Information Technology, vol. 15, no. 6, pp. 1060–1067, 2018. [Google Scholar]

17. P. Shamsinejadbabki and M. Saraee, “A new unsupervised feature selection method for text clustering based on genetic algorithms,” Journal of Intelligent Information Systems, vol. 38, no. 3, pp. 669–684, 2011. [Google Scholar]

18. L. M. Abualigah, A. T. Khader and M. A. Al-Betar, “Unsupervised feature selection technique based on genetic algorithm for improving the text clustering,” in 2016 7th Int. Conf. on Computer Science and Information Technology (CSIT), Amman, Jordan, 2016. [Google Scholar]

19. N. Agrawal and S. Gonnade, “An approach for unsupervised feature selection using genetic algorithm,” International Journal of Engineering Sciences and Research Technology, vol. 6, no. 1, pp. 1790–1794, 2017. [Google Scholar]

20. A. Saxena, N. R. Pal and M. Vora, “Evolutionary methods for unsupervised feature selection using Sammon’s stress function,” Fuzzy Information and Engineering, vol. 2, no. 3, pp. 229–247, 2010. [Google Scholar]

21. Z. H. Ahmed, “A hybrid algorithm combining lexisearch and genetic algorithms for the quadratic assignment problem,” Cogent Engineering, vol. 5, no. 1, pp. 1423743, 2018. [Google Scholar]

22. F. Niebles, I. Escobar, L. Agudelo and G. Jimenez, “A comparative analysis of genetic algorithms and QAP formulation for facility layout problem: An application in a real context,” in Advances in Swarm Intelligence 7th Int. Conf., vol. 624, pp. 59–75, 2016. [Google Scholar]

23. A. Hussain, Y. S. Muhammad, M. Nauman, I. Hussain, A. Mohamad et al., “Genetic algorithm for traveling salesman problem with modified cycle crossover operator,” Computational Intelligence and Neuroscience, vol. 2017, pp. 1–7, 2017. [Google Scholar]

24. R. Liu and Y. Wang, “Research on TSP solution based on genetic algorithm,” in 2019 IEEE/ACIS 18th Int. Conf. on Computer and Information Science (ICIS), Beijing, China, 2019. [Google Scholar]

25. H. Bennaceur, M. Almutairy and N. Alqhtani, “An investigative study of genetic algorithms to solve the DNA assembly optimization problem,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 10, pp. 139–150, 2020. [Google Scholar]

26. S. S. Patel, N. Kumar, J. Aswathy, S. K. Vaddadi, S. A. Akbar et al., “K-means algorithm: An unsupervised clustering approach using various similarity/dissimilarity measures,” in Intelligent Sustainable Systems, Singapore, pp. 805–813, 2022. [Google Scholar]

27. G. Puccetti, “Measuring linear correlation between random vectors,” Information Sciences, vol. 607, pp. 1328–1347, 2022. [Google Scholar]

28. S. Katoch, S. S. Chauhan and V. Kumar, “A review on genetic algorithm: Past, present, and future,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 8091–8126, 2021. [Google Scholar] [PubMed]

29. K. Wu, J. Liu, M. Li, J. Liu and Y. Wang, “Multi-mode active suspension control based on a genetic k-means clustering linear quadratic algorithm,” Applied Sciences, vol. 11, no. 21, pp. 10493, 2021. [Google Scholar]

30. H. Kour, P. Sharma and P. Abrol, “Analysis of fitness function in genetic algorithms,” International Journal of Scientific and Technical Advancements, vol. 1, no. 3, pp. 87–89, 2015. [Google Scholar]

31. A. Lambora, K. Gupta and K. Chopra, “Genetic algorithm—A literature review,” in 2019 Int. Conf. on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, 2019. [Google Scholar]

32. X. He, D. Cai and P. Niyogi, “Laplacian score for feature selection,” in NIPS’05: Proc. of the 18th Int. Conf. on Neural Information Processing Systems, Vancouver, pp. 507–514, 2005. [Google Scholar]

33. Z. Zhao and H. Liu, “Spectral feature selection for supervised and unsupervised learning,” in Proc. of the 24th Int. Conf. on Machine Learning, Corvalis, 2007. [Google Scholar]

34. D. Cai, C. Zhang and X. He, “Unsupervised feature selection for multi-cluster data,” in Proc. of the 16th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, Washington DC, USA, 2010. [Google Scholar]

35. Z. Li, Y. Yang, J. Liu, X. Zhou and H. Lu, “Unsupervised feature selection using nonnegative spectral analysis,” in Proc. of the AAAI Conf. on Artificial Intelligence, Toronto,Ontario, Canada, vol. 26, no. 1, pp. 1026–1032, 2021. [Google Scholar]

36. J. Miao, T. Yang, L. Sun, X. Fei, L. Niu et al., “Graph regularized locally linear embedding for unsupervised feature selection,” Pattern Recognition, vol. 122, pp. 108299, 2022. [Google Scholar]

37. F. Nie, D. Xia, T. Lai, W. Rong and L. Xuelong, “Unsupervised feature selection with constrained ℓ₂,o-norm and optimized graph,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, no. 4, pp. 1702–1713, 2022. [Google Scholar] [PubMed]

38. J. Miao, Y. Ping, Z. Chen, X. -B. Jin, P. Li et al., “Unsupervised feature selection by non-convex regularized self-representation,” Expert System Application, vol. 173, pp. 114643, 2021. [Google Scholar]

39. G. Wang, “A comparative study of cuckoo algorithm and ant colony algorithm in optimal path problems,” MATEC Web of Conf., Shanghai, vol. 232, pp. 03003, 2018. [Google Scholar]

40. S. U. Umar and T. A. Rashid, “Critical analysis: Bat algorithm-based investigation and application on several domains,” World Journal of Engineering, vol. 18, no. 4, pp. 606–620, 2021. [Google Scholar]

41. L. Jun, L. Liheng and W. Xianyi, “A double-subpopulation variant of the bat algorithm,” Applied Mathematics and Computation, vol. 263, pp. 361–377, 2015. [Google Scholar]

42. E. A. Hassan, A. I. Hafez, A. E. Hassanien and A. A. Fahmy, “A discrete bat algorithm for the community de-tection problem,” in Int. Conf. on Hybrid Artificial Intelligence Systems, Cham, Springer, pp. 188–199, 2015. [Google Scholar]

43. A. K. Farahat, A. Ghodsi and M. S. Kamel, “An efficient greedy method for unsupervised feature selection,” in 2011 IEEE 11th Int. Conf. on Data Mining, Vancouver, BC, Canada, pp. 161–170, 2011. [Google Scholar]

44. J. Hull, “A database for handwritten text recognition research,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 16, no. 5, pp. 550–554, 1994. [Google Scholar]

45. S. A. Nene, S. K. Nayar and H. Murase, Columbia Object Image Library (COIL-20), 1996. [Online]. Available: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=31fda8bf27aa5a18d55ef36631264322cc5b45fe [Google Scholar]

46. D. Dua and C. Graff, UCI Machine Learning Repository. Irvine, CA: University of California, School of Information and Computer Science, 2019. [Google Scholar]

47. D. Nardone, “Biological datasets for SMBA,” 2019. [Online]. Available: https://zenodo.org/record/2709491 [Google Scholar]

48. D. Cai, X. He, J. Han and H. -J. Zhang, “Orthogonal laplacianfaces for face recognition,” IEEE Transactions on Image Processing, vol. 15, no. 11, pp. 3608–3614, 2006. [Google Scholar] [PubMed]