Enhancing Classification Algorithm Recommendation in Automated Machine Learning: A Meta-Learning Approach Using Multivariate Sparse Group Lasso

1  Introduction

The increasing implementation of machine learning (ML) in diverse fields has greatly transformed data-driven decision-making. However, the growing number of available algorithms makes selecting the most suitable one for a particular task challenging. This challenge, known as the Algorithm Selection Problem (ASP), is becoming more complex and computationally demanding [1]. Conventional approaches, which rely on comprehensive trial-and-error techniques are not only time-consuming and resource-intensive but also require a high level of expertise, specifically when dealing with large datasets and multiple algorithms [2].

In response to these challenges, Automated Machine Learning (AutoML) is a rapidly expanding field within machine learning that attempts to overcome these challenges and automates the entire process of applying machine learning to real world problems [3]. AutoML systems are designed to recommend not just the most suitable machine learning algorithms but also optimal hyperparameters and preprocessing methods for a specific dataset. By intelligently narrowing down the search space and offering customized recommendations, AutoML greatly decreases the manual effort and expertise needed, hence enhancing the accessibility of advanced machine learning techniques for both novice and experienced practitioners.

Recently, meta-learning has been receiving huge attention as one of the most promising ways to advance algorithm selection within the AutoML pipeline [4]. Generally described as learning to learn [5,6], meta-learning learns from past experiences derived from a wide range of machine learning tasks to recommend the most appropriate algorithm or set of algorithms to use on a given task. For algorithm recommendation systems, meta-learning is the process of building a knowledge base by systematically analyzing a wide variety of datasets, their descriptive meta-features, and the performance of different algorithms on the datasets. The acquired knowledge is then used to train a meta-model that learns the complex associations between meta-features and algorithm performance. To recommend an appropriate algorithm for a particular dataset, the first step is to extract and analyze its meta-features. Based on this extracted information, a trained meta-model can then predict which algorithms are likely to perform best on the given dataset. In essence, meta-learning operates as an “algorithm selection expert,” providing tailored recommendations by analyzing the data. This approach streamlines the machine learning process by helping users identify the most suitable algorithms without requiring extensive trial and error or specialized domain knowledge [7,8].

Meta-learning has demonstrated its effectiveness in recommending algorithms across a variety of fields. In time series forecasting, for instance, it assists in identifying the most appropriate algorithms for accurate predictions [9]. Similarly, in clustering tasks, meta-learning aids in selecting methods that best suit specific datasets [10]. In the domain of classification, notably the most studied domain in meta-learning for algorithm recommendation, has seen numerous studies demonstrating its success for example in these studies [11–14]. Furthermore, meta-learning has also been vital in identifying optimal pre-processing techniques, improving the overall performance of machine learning workflows [15–18]. Additionally, it has significantly contributed to automating hyper-parameter tuning, allowing for the selection of optimal configurations that enhance algorithm performance [5,19,20].

Although considerable advances have been made in the area of AutoML for algorithm recommendation, especially in classification, many current methods often overlook the group structures that exist within meta-features. These meta-features are typically organized based on their origins or the relationships they represent [1]. In the literature, meta-features are grouped according to their relationships with various dataset attributes, such as statistical properties, information-theoretic characteristics, or model-based attributes. However, current methods frequently treat these meta-features in isolation [21]. This neglect of group structures introduces challenges, most notably high dimensionality. When meta-features from the same group are treated independently, it complicates the feature space and leads to redundancy, thereby increasing computational costs and reducing the efficiency of feature selection. The overlap of information within these groups can degrade the performance of meta-models by incorporating an excess of irrelevant or redundant features.

In addition to high dimensionality, sparsity within meta-feature spaces adds another layer of complexity. Meta-features are often sparse, with only a few features or groups proving truly informative [3]. This aspect of sparsity is currently not yet properly exploited. Current methods do not handle both intra-group and inter-group sparsity. Ignoring this dual-level sparsity may lead to risks of overfitting models by selecting too many features or underfitting, where the most relevant groups are not being captured. Furthermore, the failure to address sparsity across groups diminishes the interpretability and effectiveness of algorithm recommendations. It becomes difficult to identify which specific groups of meta-features are most influential, obscuring the decision-making process of the model and making it challenging to determine which meta-features contribute most to predictive performance.

To overcome these limitations, this paper proposes a novel approach to algorithm recommendation within the context of meta-learning by framing it as a multivariate sparse group lasso regression task (Meta-MSGL). This approach directly addresses the challenges of managing high-dimensional, sparse, and structured meta-feature spaces, improving both the efficiency of feature selection and the accuracy of algorithm recommendations. The key contributions of this paper are as follows:

1.    Multivariate Sparse Group Lasso (MSGL) for Meta-Learning: We propose the Meta-MSGL framework, which extends traditional Lasso and Group Lasso methods by introducing multivariate sparse group regularization. This allows the model to handle both individual and group-level sparsity, which is particularly important for addressing high-dimensional meta-features and mitigating multicollinearity, a challenge not fully addressed in previous algorithm recommendation methods.

2.    Effective Meta-Feature Selection: Unlike prior works that either treat meta-features independently or lack structured regularization, our method simultaneously considers meta-feature groups, leading to improved accuracy in classifier selection by reducing redundancy and selecting only the most relevant groups of meta-features.

3.    Robust Performance Across Diverse Datasets: Through extensive empirical evaluation on 145 datasets, we demonstrate that Meta-MSGL outperforms established baseline methods across key metrics, including average classification accuracy (ACA), average recommendations accuracy (ARA), and normalized discounted cumulative gain (NDCG). The structured feature selection and regularization lead to more reliable algorithm recommendations, particularly in high-dimensional spaces.

The remainder of this paper is organized as follows: Section 2 provides an overview of existing meta-learning methods for algorithm recommendation. In Section 3, we provide details of the proposed meta-learning framework. Section 4 outlines our experimental design and results. Finally, in Section 5, we conclude the paper.

2  Background and Related Works

In AutoML, various methodologies regarding meta-learning for algorithm recommendation have been explored. This section reviews main approaches, including multi-label methods, instance-based methods, and regression-based methods.

2.1 Multi-Label Methods

Wang et al. [22] introduces a multilabel learning-based approach for recommending classification algorithms, treating the task as a multilabel problem. Meta-data is generated by evaluating 13 classification algorithms across 84 UCI datasets, with five groups of meta-features characterizing the datasets. A multiple comparison procedure, specifically the Friedman test followed by Holm’s procedure, is used to label algorithms (meta-labels) for each dataset. The recommendation model is then constructed using the multilabel k-nearest neighbors (ML-kNN) algorithm [23], with k set to 1%, 5%, 10%, and 10% of the training dataset size to determine the best configuration. For a new dataset, extracted meta-features are input into the trained ML-kNN model, which predicts suitable algorithms by identifying the k-nearest neighbors and aggregating their labels. While the method exhibited enhanced accuracy in recommendations compared to single-label approaches, it has several limitations. These include the requirement to train the meta-learner on each group of meta-features separately, as well as the increased computational complexity associated with the meta-labeling process.

Zhu et al. [11] proposed the EML (Ensemble of ML-KNN) method for classification algorithm recommendation, addressing key limitations in existing methods that often rely on single learners or simple combinations of meta-features. The EML method is structured as a two-layer learning framework where the first layer (Tier-1) constructs 31 different meta-datasets by combining five types of meta-features, each used to train an ML-KNN model. The outputs from these models serve as features for the second layer (Tier-2), where binary classifiers are trained using AdaBoost with C4.5 as the base classifier. This ensemble approach improves recommendation accuracy by leveraging the diversity and accuracy of multiple ML-KNN models. Empirical validation on 183 datasets using 20 classification algorithms demonstrated that EML outperforms existing methods (ML-KNN, random walk with restart (RWR), and OBOE (Collaborative Filtering for AutoML Model Selection) across several metrics, including Hamming Loss, F-measure, Accuracy, and Hit Ratio.

Zhu et al. [24] propose a classification algorithm recommendation method based on link prediction within a heterogeneous network called the Data and Algorithm Relationship (DAR) Network, utilizing 131 datasets, five groups of meta-features, and 21 classification algorithms. The method involves three steps: meta-data collection, DAR network construction, and algorithm recommendation via link prediction. The DAR Network consists of two node types (datasets and algorithms) and two edge types (dataset-algorithm and dataset-dataset). Dataset nodes are connected to their k-nearest neighbors (with k=5) based on Euclidean distance, forming dataset-dataset edges, while dataset-algorithm edges connect datasets to suitable algorithms identified through statistical tests. Link prediction techniques (Katz, Local Random Walk, and Superposed Random Walk) estimate the likelihood of links between new datasets and algorithms, recommending the most suitable classifiers, and improving recommendation accuracy.

Yang et al. [25] developed OBOE, a collaborative filtering method for time-constrained model selection and hyperparameter tuning. OBOE constructs a low-rank approximation of an error matrix, predicting model performance based on latent meta-features inferred from cross-validated errors. This method offers quick, accurate recommendations under time constraints, but its effectiveness may be limited if the error matrix does not exhibit low-rank properties.

Although the multi-label approaches have shown success, they have several limitations such as training meta-models separately on each group of meta-features, which restricts the full utilization of feature diversity. Moreover, depending on statistical tests such as the Friedman test for meta-label estimation may fail to consider potentially significant algorithms, therefore restricting the recommendations. The method that takes into account all meta-features at the same time could improve the accuracy and adaptability of meta-models and provide more extensive recommendations for algorithms and comprehensive algorithm suggestions.

2.2 Instance-Based Methods

Instance-based approaches utilize the notion of similarity, through the analysis of dataset meta-features, to suggest appropriate algorithms. These methods are adaptable and scalable, as demonstrated by the European METAL project, which led to the development of the Data Mining Advisor (DMA). DMA uses the K-Nearest Neighbors (KNN) algorithm as a meta-learner, extracting meta-knowledge from 67 datasets and 10 algorithms. It recommends algorithms by identifying the K most similar datasets in the meta-knowledge database and aggregating performance data from these datasets. A key advantage of this approach is its ability to manage small training sets and incorporate new meta-examples without retraining the meta-model, making it effective in expanding meta-knowledge bases [26].

Wang et al. [2] proposed a clustering-based approach where datasets are grouped based on feature vectors using the EM algorithm. This method evaluates the performance of 17 classification algorithms on 84 UCI datasets, grouping similar datasets in the meta-knowledge database via clustering. To recommend an algorithm for a new dataset, the system identifies the closest cluster and suggests algorithms that perform well in that cluster. However, the complexity of feature extraction, clustering, and the reliance on training data quality poses challenges, especially when new datasets or algorithms are introduced.

Although instance-based methods offer advantages, they encounter challenges. Determining the optimal value for the parameter k is sometimes challenging, as it directly influences recommendation accuracy and computational efficiency. Moreover, these methods might exhibit limitations in terms of scalability when dealing with large meta-knowledge bases and high-dimensional meta-features. To address these difficulties, several authors, such as Lee et al. [27] and Wang et al. [2], have investigated the incorporation of unsupervised learning approaches with instance-based methods. Their objective is to enhance the adaptability and generalizability of these methods.

2.3 Regression-Based Methods

In the context of meta-learning for algorithm recommendation, regression methods have been found beneficial in modeling the association between meta-features and algorithm performance. Such models are very flexible, handle continuous target variables well, and suit a wide variety of algorithm recommendation tasks, making them very popular for performance prediction and algorithm selection. For instance, using ridge regression, Leyva et al. [28] found it is possible to predict classifier performance more accurately than with simpler models. In another work, Garcia et al. [29] conducted work involving random forest regression, which shows how flexible different regression methods are in this context.

Reif et al. [30] conducted a comprehensive assessment of the predictive capability of regression models among five separate groups of meta-features: simple, statistical, information-theoretic, model-based, and landmarking. This evaluation was conducted utilizing data from 54 UCI datasets. The work integrated an automated feature selection technique that improved the regression models, thereby increasing prediction accuracy and decreasing computational expenses.

Lai et al. [31] introduced a scalable digital twin framework that utilizes an adaptive ensemble surrogate model to predict performance across varying conditions. While their method focuses on real-time system optimization, our approach specifically targets algorithm recommendation in AutoML pipelines, leveraging multivariate sparse group Lasso to handle high-dimensional meta-features.

Furthermore, Bensusan et al. [32] examined linear regression models to determine the association between meta-features and the performance of algorithms. Although simple regression methods offered meaningful insights, their research emphasized the need to develop more advanced models to tackle non-linear connections. The primary advantage of regression-based methods in the field of AutoML is to offer readily available and easily understandable performance estimates. In addition to providing dependable predictions across diverse datasets, they also aid in the identification of the most influential meta-features, therefore contributing to the development of more precise and efficient models and facilitating informed decision-making in algorithm selection.

AutoML systems, such as Auto-sklearn [33] and A Tree-based Pipeline Optimization Tool for Automating Machine Learning (TPOT) [34], have introduced more advanced techniques for model selection and hyperparameter optimization. These frameworks automate the machine learning pipeline by integrating diverse classifiers and search strategies to identify optimal configurations for different tasks. However, these systems primarily focus on general model selection and hyperparameter tuning and do not specifically target the problem of meta-feature selection in the context of algorithm recommendation. In contrast, our approach, Meta-MSGL, leverages multivariate sparse group Lasso to handle high-dimensional meta-features while addressing the challenges of multicollinearity and redundant meta-features, leading to more precise algorithm recommendations.

3  Methodological Framework (Meta-MSGL): Multivariate Sparse Grouped Lasso Regression

In this study, we propose a novel framework for classification algorithm recommendation, leveraging the Multivariate Sparse Group Lasso (MSGL) regression. This approach is designed to handle the high dimensionality and multicollinearity that often arise in meta-feature-based algorithm recommendations. Our key contribution lies in modeling both intra-group and inter-group sparsity within meta-features, allowing for more efficient and accurate classification algorithm recommendations across diverse datasets. Unlike existing methods that treat meta-features independently or fail to fully exploit group structures, MSGL enables the simultaneous selection of relevant features both within and across predefined meta-feature groups. By imposing structured sparsity, our method improves performance and computational efficiency.

To solve this challenging optimization problem, we employ the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) with adaptive restart, which efficiently handles the non-smooth regularization terms involved in MSGL. This innovation ensures that the model is not only accurate but also interpretable, as it allows us to identify the most critical meta-features for algorithm recommendation.

In this section, we describe the methodology used in this study. We first introduce the necessary notations and present the basic formal definition of algorithm selection. We then frame this problem as a multi-objective, multivariate sparse group lasso regression task and explain our approach to solving it. To present our approach, we first define the following notations:

•   D={D1,D2,…,DN} represents a set of N classification problems;

•   A={A1,A2,…,Ak} represents a set of k potential candidate classification algorithms;

•   F:D↦Rm is a function that extracts m features from each classification problem Di∈D, known as meta-features, which are represented in the space Rm;

•   X={X1,X2,…,XN}⊆Rm corresponds to the meta-features of the N classification problems in D, as extracted by the function F. For each i where 1≤i≤N, Xi represents the meta-features of problem Di, specifically Xi=F(Di);

•   Y={Y1,Y2,…,YN} represents the meta-labels for the N classification problems in D. Here, Yi denotes the performance scores of the candidate algorithms in A for dataset Di.

Given these notations, and following the framework proposed by Smith [35], the algorithm recommendation process can be formally defined as follows:

1.    Construct a mapping function ϕ:X↦Y that models the intricate associations between the meta-features X of classification tasks and the corresponding performance scores Y of the candidate algorithms.

2.    For a new dataset dnew, apply the function ϕ(F(dnew)) to recommend the algorithms most likely to achieve optimal performance on the given task.

In the field of algorithm selection through meta-learning, the construction of the mapping function is a process that seeks to align the inherent biases and capabilities of candidate algorithms with the meta-features characterizing classification tasks. Each algorithm operates under specific data assumptions, such as linearity, smoothness, or feature independence, influencing its performance across diverse scenarios. As elaborated in Section 2, various methodologies have been employed to construct such a mapping function, each leveraging distinct underlying assumptions and computational paradigms, including instance-based approaches, multi-label learning techniques, and ranking-based approaches. In this paper, we formulate the meta-learning task of classifier recommendation as an optimization problem, specifically a multi-objective multivariate sparse group lasso regression task.

3.1 MSGL Optimization Problem: A Detailed Derivation

To establish a formal definition of our problem, we introduce two fundamental matrices that represent the data utilized for our meta-learning process: the Meta-Feature matrix (X) and the Meta-Label matrix (Y). The meta-feature Matrix, denoted by X∈Rn×p, stores the meta-features of datasets. Each row xi of X represents a single dataset, and each column corresponds to a specific meta-feature. Mathematically, this can be expressed as:

X=[x11x12⋯x1px21x22⋯x2p⋮⋮⋱⋮xn1xn2⋯xnp](1)

Here n is the number of datasets, p is the number of meta-features, and xij represents the value of the j-th meta-feature for the i-th dataset.

The Meta-Label matrix, denoted by Y∈Rn×q, contains the performance scores of the candidate algorithms on the datasets. Each row yi corresponds to a dataset at the meta-level, and each column represents a specific candidate algorithm. Mathematically, this can be expressed as:

Y=[y11y12⋯y1qy21y22⋯y2q⋮⋮⋱⋮yn1yn2⋯ynq](2)

Here q is the number of algorithms, and yij represents the performance (classification accuracy) of the j-th algorithm on the i-th dataset.

For the accurate construction of the mapping function ϕ:X↦Y, the central task involves learning a coefficient matrix B∈Rp×q. Each element bjk of this matrix quantifies the association between the j-th meta-feature and the performance of the k-th algorithm. If bjk is positive and large, it indicates that the meta-feature strongly and positively influences the algorithm’s performance. Conversely, a negative bjk suggests a negative influence. A value close to zero implies that the meta-feature has little or no impact on the algorithm’s performance. By learning the values in B, we create a model that can predict the performance matrix Y given the meta-feature matrix X. The foundation of our approach lies in the standard linear regression model, where we aim to predict a response variable (algorithm performance) based on a set of predictor variables (meta-features). In matrix form, this model is expressed as:

Y=XB+E(3)

where Y is the meta-label matrix (actual performance), X is the meta-feature matrix, B is the coefficient matrix we want to learn, and E is the error matrix, representing the difference between the actual and predicted performance. To find the optimal coefficient matrix B, we minimize the sum of squared errors, known as the ordinary least squares (OLS) objective:

LOLS(B)=12n‖Y−XB‖F2(4)

While OLS regression is a powerful tool, it can lead to overfitting when the number of features is large relative to the number of observations. To overcome this issue, we introduce regularization techniques. In particular, we employ the Lasso (Least Absolute Shrinkage and Selection Operator) regularization, which adds an L1 penalty on the coefficients:

LLasso(B)=LOLS(B)+λ1∑j=1p‖Bj⋅‖2(5)

where λ1 is a hyperparameter that controls the strength of the regularization. The L1 penalty encourages sparsity by driving some coefficients to exactly zero, effectively performing feature selection.

In many real-world scenarios, features naturally exhibit inherent grouping structures. This is especially relevant in our meta-learning problem, where meta-features are categorized into eight predefined groups based on established literature, which have been consistently validated across various studies [19]. Conventional Lasso regularization does not explicitly consider this group structure, which can lead to sub-optimal feature selection [36]. To address this, we introduce the group Lasso regularization, which adds L2 penalty on groups of coefficients. This approach leverages domain-specific groupings to enforce sparsity at both the individual feature and group levels.

LGroupLasso(B)=LLasso(B)+λ2∑g∈𝒢‖Bg‖F(6)

where λ2 is a hyperparameter controlling the strength of the group-level regularization, 𝒢 is a set of groups of meta-features, and Bg is the submatrix of B containing the coefficients for the meta-features in group g. This penalty encourages sparsity at the group level, meaning that either all features within a group are selected or the entire group is discarded.

By integrating the OLS loss with both Lasso and group Lasso regularization, we formulate our final optimization problem, thus defining the grouped multivariate sparse Lasso:

minBLGroupLasso(B)=minB{12n‖Y−XB‖F2+λ1∑j=1p‖Bj⋅‖2+λ2∑g∈𝒢‖Bg‖F}(7)

The above general optimization problem we aim to solve is derived from the principles of penalized regression, specifically the multivariate sparse grouped Lasso [37].

The first term in the equation, 12n‖Y−XB‖F2, quantifies the difference between the actual performance matrix Y and the predicted performance matrix XB. This is measured using the Frobenius norm which is defined as the square root of the sum of the squares of all elements in a matrix.

‖Y−XB‖F2=∑i=1n∑k=1q(yik−∑j=1pxijbjk)2(8)

Each term in the summation quantifies the squared difference between the observed performance of the k-th algorithm on the i-th dataset yik and its predicted performance based on the meta-features and coefficients ∑jxijbjk. Minimizing this term encourages the model to learn coefficients that result in precise predictions of algorithm performance across the datasets.

The second term, λ1∑j=1p‖Bj⋅‖2, promotes sparsity at the individual feature level. The ℓ2 norm (‖⋅‖2) of each row Bj⋅ (representing the coefficients for a single meta-feature across all algorithms) is calculated as follows:

‖Bj⋅‖2=∑k=1qbjk2(9)

This factor quantifies the extent of coefficients associated with a particular meta-feature. Incorporating this term into the objective function, weighted by λ1, encourages the model to assign zero or near-zero coefficients to irrelevant or redundant meta-features, thereby effectively implementing feature selection and prioritizing the most impactful meta-features for predicting algorithm performance.

The third term, λ2∑g∈𝒢‖Bg‖F, promotes structured group-level sparsity, a critical component of our feature selection strategy. Meta-features naturally cluster into distinct groups 𝒢, where features within each group collectively contribute to modeling the mapping function ϕ:X↦Y. By penalizing the Frobenius norm of the submatrix Bg corresponding to each group, our method induces sparsity across entire groups. This approach effectively reduces the coefficients of less relevant groups to zero, improving recommendation accuracy and reducing the computational cost of meta-feature extraction.

The balance between prediction accuracy and model complexity is determined by the hyper-parameters λ1 and λ2. These parameters are optimized through cross-validation, a systematic procedure that evaluates the model’s performance across various data subsets, ensuring an optimal trade-off between model complexity and accuracy. To further ensure the robustness of our model and mitigate overfitting, we employed nested cross-validation throughout the training process. Nested cross-validation is a more stringent validation method compared to traditional k-fold cross-validation, as it optimizes hyperparameters in an inner loop while evaluating model performance in an outer loop. This approach ensures that the model’s hyperparameters do not overfit to any particular training set, and it provides a more reliable estimate of the model’s ability to generalize to unseen data. Moreover, the regularization inherent in the multivariate sparse group Lasso model plays a critical role in controlling overfitting. The inclusion of both ℓ1 (Lasso) and ℓ2 (group Lasso) penalties reduces the risk of overfitting by driving irrelevant or redundant meta-features and meta-feature groups to zero, thus maintaining model simplicity while preserving predictive accuracy.

The overall loss function, combining both the data-fitting term and regularization terms, plays a key role in controlling model complexity and ensuring the selection of relevant meta-features. By minimizing the squared error between the predicted and actual performance values, the model achieves high predictive accuracy. Simultaneously, the L1 and group regularization terms work together to prevent overfitting by enforcing sparsity, both at the feature and group levels. This structured approach to regularization helps the model generalize well to unseen datasets by selecting only the most important meta-features.

By minimizing the combined objective function, the resulting coefficient matrix B not only predicts algorithm performance with high accuracy but also enhances the ranking and recommendation process. Our approach identifies key meta-features at both individual and group levels, leading to a model that is both precise and computationally efficient. The integration of Lasso regularization controls sparsity, utilizing the relationships between meta-features to enhance recommendation accuracy and minimize redundancy.

3.2 Fast Iterative Shrinkage-Thresholding Algorithm for MSGL (FISTA)

The multivariate sparse group Lasso regression problem we have formulated is the main component of our meta-learning framework. However, appropriately solving this problem requires an adequate optimization approach due to its inherent complexity, which involves both individual and group-level sparsity. To manage this complexity, it is important to employ an algorithm capable of efficiently handling the smooth and non-differentiable components of the objective function. In this part, we present the mathematical formulation of the Fast Iterative Shrinkage-Thresholding Algorithm (FISTA) with adaptive restart. We follow the approach proposed by Beck et al. [38] and enhanced by the adaptive restart scheme of Donoghue et al. [39]. This optimization algorithm is particularly well-suited to solving our MSGL problem because it ensures accurate minimization of the objective function while maintaining both predictive accuracy and computational efficiency. We here provide a step-by-step derivation of the algorithm and show how it addresses our specific optimization problem.

FISTA is designed to minimize composite objective functions of the form f(B)=g(B)+h(B), where g(B) is a smooth and differentiable function, while h(B) is convex but non-differentiable. The algorithm works by iteratively updating the coefficient matrix B through two main steps. First, it uses the gradient of the smooth function g(B) to guide the update. Then it applies a proximal operator to handle the non-smooth function h(B). This approach makes FISTA particularly effective for solving our optimization problem where both smooth and non-smooth components are involved. In our case, in our formulated optimization problem in Eq. (7), the smooth component g(B) represents the prediction error and is defined as:

g(B)=12n‖Y−XB‖F2

This term represents the squared Frobenius norm of the residuals, where Y denotes the meta-labels, X the design matrix of meta-features, and B the coefficient matrix. Minimizing g(B) ensures accurate modeling of the mapping function ϕ. The non differentiable component h(B) is expressed as:

h(B)=λ1∑j=1p‖Bj⋅‖2+λ2∑g∈𝒢‖Bg‖F(10)

This term incorporates the Lasso and group Lasso regularizations, promoting sparsity in individual meta-features and groups of meta-features. By minimizing h(B), we achieve a more interpretable model by selecting the most relevant meta-features.

The gradient of g(B), which guides the direction of optimization, is given by:

∇g(B)=1nXT(XB−Y)(11)

The gradient indicates the direction in which g(B) gets the greatest increase. Throughout each iteration of FISTA, the gradient plays an important role in guiding the update of B, gradually bringing it closer to the optimal solution. The update involves a shrinkage-thresholding step that enforces the sparsity constraints determined by h(B). The proximal operator for the non-differentiable part h(B) is defined as:

proxηh(U)=arg⁡minB{12‖B−U‖F2+ηh(B)}(12)

The above operator works well in addressing the non-smooth component of our objective function through the implementation of a proximal gradient step. It ensures that the updated solution maintains the sparsity properties induced by the regularization terms. In our case, h(B) includes both ℓ2 and Frobenius norms. Here is the proximal operator for this combined norm:

proxη(λ1‖⋅‖2+λ2‖⋅‖F)(U)={‖U‖F−η(λ1+λ2)‖U‖FU,if ‖U‖F>η(λ1+λ2)0,otherwise(13)

To improve the performance of FISTA, we have implemented an adaptive restart strategy based on the recommendation made by Donoghue et al. [39]. This technique can automatically restart the algorithm when the objective function shows a specific non-monotonic behavior. This facilitates faster convergence by ensuring that the iterations do not become stuck.

The FISTA algorithm starts by initializing the coefficient matrix B(0) and the auxiliary variable Z(0) as zero matrices. Additionally, the momentum parameter t0 is set to 1. This sets the starting point for the iterative optimization process.

During each iteration k, the algorithm proceeds by first computing the gradient of the smooth part of the objective function, given by ∇g(Z(k))=1nXT(XZ(k)−Y), and updating the coefficients using B(k)=proxηh(Z(k)−η∇g(Z(k))). Here, the proximal operator is applied to enforce sparsity according to the grouped multivariate sparse Lasso regularization. Following this, the momentum parameter tk+1 is updated according to the formula tk+1=1+1+4tk22, which accelerates convergence by incorporating information from previous iterations. The auxiliary variable is then updated using Z(k+1)=B(k)+(tk−1tk+1)(B(k)−B(k−1)), which combines current and previous estimates to further speed up convergence.

To avoid potential stalling, the algorithm includes an adaptive restart mechanism. If the condition ⟨B(k)−B(k−1),Z(k)−B(k)⟩>0 is met, indicating that the momentum is not aiding convergence, the momentum term is reset to tk=1. This periodic resetting ensures that the optimization process remains efficient by mitigating the negative effects of potential stalling phases. A common convergence criterion is to check if the relative change in the objective function value falls below a predefined tolerance. The algorithm stops iterating when:

|f(B(k+1))−f(B(k))||f(B(k))|<tol(14)

In summary, the combination of FISTA with adaptive restart offers an efficient solution to our MSGL optimization problem. By effectively minimizing the composite objective function, this approach balances the trade-offs between prediction accuracy, sparsity, and computational efficiency, resulting in a robust and interpretable model (Algorithm 1).

3.3 Meta-Learning Via MSGL

Within this subsection, we show how Meta-MSGL is used for the recommending classifiers. To illustrate, we consider q candidate algorithms within the algorithm search space 𝒜, defined as 𝒜={a1,a2,…,aq}, and n datasets, denoted as 𝒟1,𝒟2,…,𝒟n. For each dataset, the classification performance of these algorithms is evaluated using balanced classification accuracy, and the results are compiled into the Meta-Label Matrix Y. The performance matrix Y is constructed as Y=[y1,y2,…,yn]∈Rn×q, where each row vector yi=[yi1,yi2,…,yiq]⊤ represents the performance of the q algorithms on dataset 𝒟i. The performance matrix Y is obtained through tenfold cross-validation, using stratified dataset splitting to address class imbalance typically found in real-world datasets. Alongside, for each dataset, a set of meta-features is computed to characterize its properties, compiled into the Meta-Feature Matrix X. This matrix is defined as X=[x1,x2,…,xn]⊤∈Rn×p, where each row vector xi=[xi1,xi2,…,xip] represents the values of p meta-features for dataset 𝒟i.

The training of the GMSL model begins with the initialization of the matrix B to zero, and the setting of hyperparameters λ1 and λ2. The optimization is performed using FISTA with adaptive restart, iteratively updating B by considering the gradient of the smooth part and applying the proximal operator to manage the non-smooth part. As the iterations proceed, the Lasso and group Lasso penalties progressively drive certain coefficients in B towards zero. Upon completion of the optimization, we obtain the coefficient matrix B=[B(1),B(2),…,B(p)], which includes zero columns as anticipated.

The vector v∈Rr′, where r′<p, contains the indices of the non-zero columns of B, which are used to identify the chosen meta-features. The association between the chosen meta-features and the performance of candidate algorithms over the n datasets is shown below:

Y=B[:,v]X[v,:](15)

Here X[:,v] and B[v,:] denote the submatrices formed by selecting the columns of X and the corresponding rows of B indexed by v. This meta-feature selection offers multiple benefits: it decreases the total number of predictors thereby lowering the model complexity, it improves accuracy by eliminating irrelevant or redundant meta-features and it enhances efficiency in the algorithm recommendation phase by requiring only the chosen meta-features to be extracted for a dataset.

3.4 Algorithm Recommendation Using Meta-MSGL

For a new dataset Dnew, the performance of each candidate algorithm Ai from the available pool of algorithms A is estimated using the trained GMSL (Grouped Multivariate Sparse Lasso) model. The process is as follows:

1.    Meta-feature Extraction: Extract relevant meta-features of Dnew, represented as xv=Fv(Dnew), here xv∈Rr′ and Fv refers to the extraction of meta-features specifically indexed by v, which have been selected during the meta-model training phase.

2.    Performance Estimation: Using the selected meta-features, the trained meta-model estimates the performance of each algorithm:

yDnew=B[:,v]xv(16)

where yDnew∈Rq and (yDnew)j, j=1,2,…,q, represents the predicted performance of the j-th algorithm in the search space A.

The algorithm(s) predicted to achieve the best performance on Dnew are then recommended based on these predictions. To facilitate selection, the predicted performance values yDnew=[y1,y2,…,ym]⊤ are ranked in descending order:

[yi1,yi2,…,yim],whereyi1≥yi2≥⋯≥yim(17)

This ranking serves as an elementary step to prioritize algorithms. The configuration with the highest predicted value is recommended for Dnew, while the ranking helps in understanding the relative performance of the other algorithms.

3.5 Metafeature Extraction and Selection

Our methodology employs an extensive set of meta-features across eight categories: General, Statistical, Landmarking, Information Theory, Clustering, Model-Based, Itemset, and Complexity. Unlike prior studies with limited meta-features, our approach effectively handles the high dimensionality and multicollinearity inherent in these diverse groups. Due to space limitations, we cannot provide detailed descriptions, mathematical formulations, and extensive discussions of the eight meta-feature groups here. For a comprehensive overview of these meta-features, including their formulations and detailed descriptions, we refer readers to [40,41].

Inconsistencies in extraction techniques can affect reproducibility across studies [42]. To address this, we utilize the standardized reproducible meta-feature extraction (MFE) framework [43] available in R and Python, specifically using the Python package pymfe for meta-feature extraction. Post-extraction, we apply preprocessing steps: (1) normalize measures to [0,1] using min-max scaling; (2) remove constant or missing-value-dominant measures; and (3) eliminate duplicate measures, retaining only one instance.

We have shown the multicollinearity by calculating correlation matrices and eigenvalues from meta-features extracted from 145 UCI datasets in Fig. 1. Some eigenvalues nearing zero indicate high correlation, potentially degrading linear regression model performance if not addressed. The Meta-MSGL method facilitates the selection of the most informative meta-features, mitigating multicollinearity and reducing redundancy. By managing a broad range of meta-features, our methodology significantly enhances the accuracy and reliability of classification algorithm selection in AutoML systems.

Figure 1: Multicollinearity is present between the different groups (eight) of meta-features. The near-zero eigenvalues indicate that some meta-feature variables are strongly correlated with each other

4  Experimental Evaluation

In this section, we conduct an empirical investigation to evaluate the effectiveness of our proposed approach. We begin by detailing the experimental setup which includes the datasets, classification algorithms, and evaluation metrics used. We then present the results, highlight key findings, and compare the performance of our approach with four existing benchmark methods.

4.1 Datasets and Candidate Algorithms

This study utilizes 145 classification datasets sourced from OpenML [44], with 105 datasets allocated for training and validation, and 40 datasets randomly selected as the test set. The datasets were split such that 80% of the datasets were used for model training and cross-validation, while 20% were reserved for independent testing. The training set was further divided into training and validation subsets using 10-fold cross-validation to tune the hyperparameters λ1 and λ2. The test set was used only for final evaluation after all model parameters were tuned. This setup ensures that the model’s performance is evaluated on unseen data, providing a robust assessment of its generalizability. The dataset details are provided in the supplementary materials.

To ensure a thorough evaluation, we included 17 classification algorithms in our meta-learning setup. These algorithms are widely used in previous studies on classifier selection. The algorithms include probabilistic learners such as Bayesian Network (weka.classifiers.bayes.BayesNet) and Naive Bayes (weka.classifiers.bayes.NaiveBayes), tree-based learners like C4.5 (weka.classifiers.trees.J48), Random Tree (weka.classifiers.trees.RandomTree), and Random Forest (weka.classifiers.trees.RandomForest), rule-based learners including Ripper (weka.classifiers.rules.JRip) and PART (weka.classifiers.rules.PART), an instance-based learner, K-Nearest Neighbors (weka.classifiers.lazy.KStar), and a Support Vector Machine, SMO (weka.classifiers.functions.SMO). We also included several ensemble methods, such as AdaBoostM1 combined with Naive Bayes, KStar, PART, and J48, as well as Bagging combined with Naive Bayes, KStar, PART, and J48. This diverse selection of algorithms enables a thorough assessment of different classification methods, ensuring the collection of high-quality meta-data essential for adequate training the meta-learner.

We used WEKA version 3.8.2 [45], a Java-based open-source data mining software, to implement these candidate classifiers at the meta-level. We followed the default settings provided by WEKA for each classifier. This included using a polynomial kernel for the Support Vector Machine and a linear search for the K-Nearest Neighbors algorithm, aligning with configurations used in previous studies.

4.2 Evaluation Against Benchmark Approaches

To assess the effectiveness of our proposed method, we compared it with four established baseline methods, each representing a different approach to recommending classification algorithms:

1.    Wang et al. (2014) - Meta-MLkNN: This method uses multilabel learning, treating the task of recommending classification algorithms as a multilabel problem, implemented through the ML-kNN algorithm [22].

2.    Zhu et al. (2018) - Meta-DAR: This method uses link prediction within a heterogeneous network called the Data and Algorithm Relationship (DAR) Network to recommend classifiers [24].

3.    Zhu et al. (2021) - Meta-EML: An ensemble approach that uses ML-KNN as the base learner to recommend classification algorithms based on meta-features [11].

4.    Giraud-Carrier et al. (2005) - Meta-DMA: An instance-based method developed under the European METAL project, using KNN to recommend algorithms [46].

Each of the above baseline method is described in detail in the Section 2. These baseline methods were chosen because they are well-known in the literature, allowing for a thorough comparison with our proposed method.

4.3 Performance Evaluation Metrics

Our study evaluates the effectiveness of each method using three widely recognized metrics: classification accuracy rate (CA), recommendation accuracy rate (RA), and normalized discounted cumulative gain (NDCG). These metrics are commonly used in meta-learning (MtL) research for algorithm recommender systems, as demonstrated in studies such as [42,47]. Each of these metrics provides insight into the effectiveness of the different meta-learning frameworks for algorithm recommendation. Below, we define each of these metrics:

1.    Classification Accuracy Rate (CA): CA is frequently employed to assess the efficacy of a recommended classification algorithm 𝒜 on a given problem 𝒟. To address the issue of class imbalance commonly encountered in classification tasks, we consider the balanced CA [47].

The average cumulative accuracy (ACA) across N datasets is defined as:

ACA=1N∑i=1NCA𝒜𝒟i×100%,(18)

The notation CA𝒜𝒟i represents the performance of the recommended algorithm 𝒜 on the problem 𝒟i. The range of both CA and ACA is the interval [0,1], and greater values of both CA and ACA are favored, suggesting that the recommended methods are more appropriate for the dataset.

2.    Recommendation Accuracy (RA): While Classification Accuracy (CA) is a key metric for algorithm selection, it may not always differentiate well between multiple algorithms that achieve similar CA values on a given problem. To address this limitation, Recommendation Accuracy (RA) evaluates how close a recommended algorithm is to the optimal solution. Let CA𝒜,b𝒟i and CA𝒜,w𝒟i represent the best and worst CA values, respectively, among candidate algorithms for problem 𝒟i. The RA for algorithm 𝒜 on 𝒟i is then defined as:

RA𝒜𝒟i=CA𝒜𝒟i−CA𝒜,w𝒟iCA𝒜,b𝒟i−CA𝒜,w𝒟i,(19)

This formula normalizes the CA of a given algorithm within the range of possible CA values for that problem. RA values range from 0 to 1, with higher RA indicating that the recommended algorithm is closer to the optimal one. To evaluate performance across multiple problems, the Average Recommendation Accuracy (ARA) is calculated over N problems as:

ARA=1N∑i=1NRA𝒜𝒟i×100%,(20)

Similar to RA, ARA values range from 0 to 1, with higher values indicating that the recommended algorithms are consistently closer to the optimal solutions across the entire problem set.

3.    Normalized Discounted Cumulative Gain (NDCG)

The Normalized Discounted Cumulative Gain (NDCG) is a metric used to assess the quality of ranked lists, particularly in recommender systems, by evaluating how closely the predicted rankings of items align with their ideal rankings based on true relevance. For a given dataset (query) 𝒟i, the NDCG at a specific rank position p (where 0<p≤m) is defined as NDCG𝒟ip=DCG𝒟ip/IDCG𝒟ip. The Discounted Cumulative Gain (DCG) at position p is calculated as DCG𝒟ip=∑j=1p2π[(x𝒟ipred)j]−1log2⁡(j+1), where x𝒟ipred denotes the vector of predicted performance scores. The Ideal DCG (IDCG), computed similarly, arranges items in the optimal order based on their true scores, given by IDCG𝒟ip=∑j=1p2π[(x𝒟i)j]−1log2⁡(j+1). Here, π[(⋅)j] indicates the rank of the jth entry in the respective vector. The overall NDCG across N datasets is calculated as:

NDCG@p=1N∑i=1NNDCG𝒟ip.(21)

Again, NDCG@p values lie within the range (0,1], with larger values indicating better ranking performance. The results presented in the current paper are calculated on setting the value of p=3.

4.4 Results and Discussion

Our experimental analysis comprises two distinct phases. In the first phase, we conduct an in-depth examination of the Meta-MSGL model, focusing on three key questions. (1) Which meta-features are essential for constructing the Meta-MSGL model? (2) Can meta-features selection help mitigate multicollinearity in the Meta-MSGL model? (3) How does meta-feature selection influence the recommendation performance of Meta-MSGL? In the second phase, we directly compare the performance of Meta-MSGL against four baseline meta-learning methods. This comprehensive two-phase approach allows us to thoroughly evaluate the strengths and weaknesses of Meta-MSGL, specifically within the context of meta-learning for classification algorithm recommendation.

4.4.1 Evaluating the Effectiveness of Metafeature Selection in Meta-MSGL

A comprehensive grid search was conducted to determine the optimal settings and assess the impact of various meta-features on the meta-model. It involved extensive experimentation with different parameter combinations. Here, we present the results of varying the regularization parameter λ1 ( 0.0, 0.3, 0.6, 0.9, 1.2, and 1.5) while maintaining a constant value of λ2 at 0.1 and 0.4. During the training of our Meta-GMSR model, the maximum number of iterations was set to 5000.

Fig. 2 illustrates these results, showing the ratio of retained measures to the total number of measures for each λ value. The feature selection process using the Group Lasso model reveals how variations in λ1 and λ2 impact the retention of critical meta-features across different groups. For λ2=0.1, the model initially selects all 105 meta-features when no regularization is applied (λ1=0.0). As λ1 increases, the number of selected features decreases significantly. At λ1=0.3, 45 features are retained, with model-based and complexity features showing the highest retention rates (52.94% and 68.18%, respectively), while statistical and structural features are more selectively retained (14.29% and 16.67%, respectively). The number of selected features decreases to 28 and 21 respectively as regularization strength increases (λ1 = 0.6 and λ1 = 0.9). Notably information-theoretic and simple features demonstrate significant retention, particularly under moderate regularization. At λ1 = 0.3 their retention rates are 25% and 47.06%, respectively.

Figure 2: The influence of λ on metafeature selection. The count of chosen meta-features is shown in parentheses on the horizontal axis. A ratio of zero signifies the meta feature’s removal from the model

A similar pattern is observed for λ2=0.4, with greater reductions in the number of selected features as λ1 increases. At the start, all 105 features are selected at λ1=0.0. At λ1=0.3, the model retains only 29 features, with a significant emphasis on simplicity (35.29%) and complexity (50%), as well as moderate retention of model-based features (23.53%). As λ1 increases, the same pattern continues, resulting in the model retaining only 10 features at λ1=1.5.

Across both λ2 settings, complexity features consistently demonstrate high retention rates. Other groups such as model-based, simple, and information-theoretic features also play important roles, particularly with moderate regularization. This diverse selection of features highlights the significance of these feature groups in enhancing the overall performance of the meta-model. Overall, the combination of these different feature groups contributes to a more robust and comprehensive meta-learning framework that can adapt to a wide range of tasks. The reduction in statistical and structural features under stronger regularization indicates that these groups may have higher redundancy or contribute less to the model’s performance.

In summary, retaining complexity-based, model-based, simple, and information-theoretic features is crucial for preserving the model’s predictive performance across varying levels of regularization. Each of these meta-feature groups plays a key role in improving the model’s decision-making process. For example, complexity and model-based features provide essential insights into the structure and behavior of datasets, while information-theoretic features capture relationships between variables that enhance algorithm selection. The reduced significance of statistical and structural features suggests that they contribute less to the meta-learning task, often introducing redundancy. This highlights the value of incorporating diverse, relevant meta-feature groups to optimize meta-learning models and improve both accuracy and interpretability.

4.4.2 Analysis of Eigenvalues to Assess Multicollinearity Reduction

Here we evaluate the effectiveness of the Meta-MSGL model in reducing multicollinearity by analyzing the smallest eigenvalues of the correlation matrix for selected meta-features. The results for both λ2 values (0.1 and 0.4) across varying levels of λ1 are shown in Fig. 3. Due to space limitations, we only display six of the smallest eigenvalues. The results indicate that when λ equals 0, the variables are highly correlated with many eigenvalues approaching zero. As λ increases this problem diminishes leading to a smaller proportion of selected measures. This outcome demonstrates that the Meta-MSGL model effectively eliminates redundant and correlated measures, thereby improving overall model performance. The consistent trends observed for both λ values in Fig. 3 further highlight the stability of the Meta-MSGL model. Additionally, when comparing Fig. 3 with Fig. 1, it is clear that the combined meta-features show stronger correlations than individual meta-features. This is evident from the greater number of eigenvalues near zero. This observation implies that similar measures are present across different meta-features and that the feature selection process effectively removes these redundancies.

Figure 3: Smallest six eigenvalues of the meta feature correlation matrix for the various λ values. Near-zero eigenvalues indicate high multicollinearity within the meta features

4.4.3 Impact of Meta-features Selection on Meta-MSGL Performance

Here, we illustrate how meta-feature selection impacts the performance of Meta-MSGL. The ACA, ARA, and hit rate (HR) results are presented in Fig. 4. The impact of feature selection on the Meta-MSGL performance is evident. When all meta-features are used with λ2=0.01, the model demonstrates how feature selection affects the outcomes. Specifically, with λ1=1.5, the model attains an ACA of 74.8%, an ARA of 78.5%, and an NDCG of 84.5%, illustrating the performance metrics for this feature selection level. At λ1=0.3, the model achieves stronger performance, with an ACA of 76.11%, an ARA of 84.5%, and an HR of 86.83%. When λ2=0.04, the model demonstrates a slight improvement over its performance at λ2=0.01. Notably, at λ1=1.5, the model records an ACA of 75.1%, an ARA of 77.0%, and an HR of 84.5%. The best results, however, are seen at λ1=0.3, where the ACA rises to 77.18%, the ARA reaches 86.07%, and the HR peaks at 88.83%. These outcomes suggest that increasing λ2 enhances the model’s overall performance.

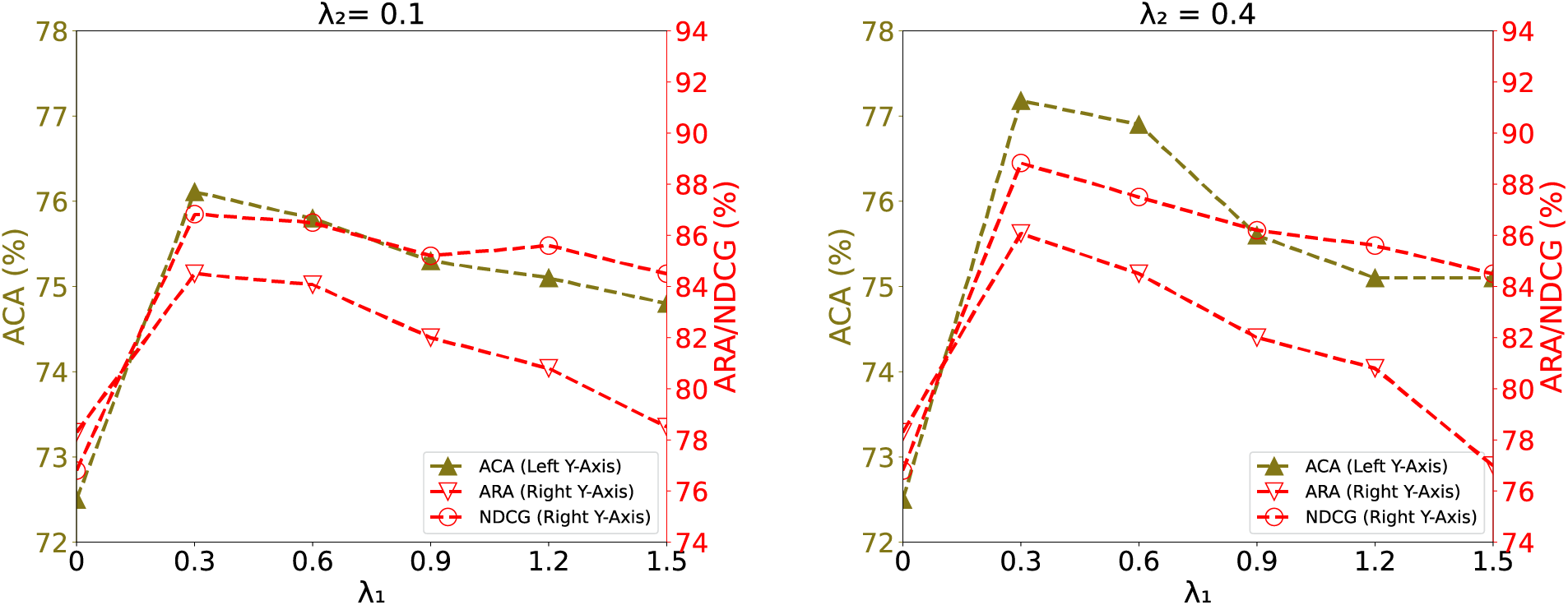
Figure 4: Analyzing SGLasso recommendations: how varying sparsity affects accuracy

The optimal performance is observed at λ2=0.04 and λ1=0.3, where the model achieves its highest values: 77.18% (ACA), 86.07% (ARA), and 88.83% (NDCG). However, the performance of Meta-MSGL is sensitive to parameter choices, as demonstrated through a grid search over various λ1 and λ2 values. Lower values of λ1 result in the inclusion of more meta-features, potentially introducing noise, while higher values reduce the number of selected meta-features, risking underfitting. Similarly, higher values of λ2 progressively eliminate entire groups of meta-features, impacting overall performance. Our analysis suggests that λ1 values between 0.3 and 0.6, and λ2 values between 0.01 and 0.04 provide robust performance, ensuring that the model generalizes well across datasets without being overly sensitive to parameter variations. This sensitivity analysis highlights the importance of balancing sparsity with feature selection to maximize the model’s effectiveness.

4.5 Comparisons With MtL Baselines

In this section, we compare the performance of Meta-MSGL with several baseline meta-learning methods, namely Meta-EML, Meta-MLkNN, Meta-DAR, and Meta-DMA, using three key metrics: ACA, ARA, and NDCG. The results, summarized in Table 1, are averaged across all testing datasets.

The performance of Meta-MSGL is consistently high on the three metrics. The achieved ACA is 77.18% ARA is 86.07% and the average normalized discounted cumulative gain is 88.83%. The results indicate that Meta-MSGL is able to reliably produce recommendations and sustain good classification performance across the datasets. The high NDCG score further confirms its efficiency in prioritizing algorithms based on predictive performance on datasets. Meta-EML performs comparably to Meta-MSGL particularly in the ARA and NDCG metrics achieving scores of 83.52% and 84.75%, respectively. Although it falls slightly short of the performance of Meta-MSGL the minor difference indicates that Meta-EML is still effective in most scenarios on ARA and NDCG metrics. In contrast, the performance of Meta-MLkNN is significantly lower compared to Meta-MSGL and Meta-EML. It achieved an ACA of 72.25% ARA of 79.53% and NDCG of 80.15%. This suggests that Meta-MLkNN recommendations are less reliable on many datasets.

Meta-DAR and Meta-DMA show consistently lower performance compared to the other methods with ACA scores of 66.48% and 64.88%, respectively. Their ARA and NDCG scores are also significantly lower. Meta-DAR achieves 72.58% and 74.90%, while Meta-DMA scores 70.02% and 69.87%. These results highlight limitations in their ability to handle diverse datasets effectively. Its lower NDCG scores on NDCG@3 indicate that Meta-DAR and Meta-DMA have a limitation in not only providing adequate recommendations for the best predictive algorithm in each testing data set but also in the top three recommended algorithms.

4.5.1 Classification Accuracy (CA)

To further illustrate the performance differences across each testing problem, we present scatter plots in Figs. 5–7. In these plots, the datasets are ordered in ascending order according to the performance of Meta-MSGL. In terms of the CA metric on each testing dataset, Meta-MSGL performed better compared to the baseline methods on most of the datasets. It should be noted that algorithm recommended by Meta-MSGL achieves accuracy levels higher than 90% on 9 datasets and retains high accuracy on 22 datasets when a more moderate accuracy level of 80% is taken into account. The results indicate that Meta-MSGL is not only able to recommend algorithms that attain performance comparable to the best available candidate for a specific dataset but also consistently achieves high classification accuracy.

Figure 5: Comparison of CA performance across individual testing datasets among Meta-MSGL, Meta-EML, Meta-MLkNN, Meta-DAR, and Meta-DMA

Figure 6: Comparison of RA performance across individual testing datasets among Meta-MSGL, Meta-EML, Meta-MLkNN, Meta-DAR, and Meta-DMA

Figure 7: Comparison of NDGC performance across individual testing datasets among Meta-MSGL, Meta-EML, Meta-MLkNN, Meta-DAR, and Meta-DMA

Meta-EML and Meta-MLkNN also acheived reliable performance by reaching over 90% accuracy on 6 and 5 datasets, respectively. However they display greater variability than Meta-MSGL particularly in datasets like column3C and thoracic-surgery where their performance is less stable. When the accuracy threshold is reduced to 80% Meta-EML remains competitive by achieving this level on 18 datasets, while Meta-MLkNN achieves it on 14 datasets. This indicates that although both Meta-EML and Meta-MLkNN are effective, their sensitivity to certain dataset characteristics may affect their overall reliability in consistently maintaining high accuracy across diverse datasets.

In contrast, Meta-DAR and Meta-DMA show poor performance by reaching the 90% accuracy threshold in only one dataset each and even not achieving 80% in most cases. Their lower classification accuracy values highlight significant limitations in adapting to diverse datasets. As a result, these methods may recommend algorithms that are not well-suited to the task, which leads to poorer classification accuracy across a broader range of datasets.

4.5.2 Recommendation Accuracy (RA)

Fig. 6 presents scatter plot to show the variations in performance among the meta-learning methods on the RA metric for each testing problem. As can be observed Meta-MSGL performs better than the baseline methods on the majority of the datasets. It achieves above 90% recommendation accuracy in 17 datasets and exceeds 80% on 31 datasets, which indicates its advantage over the baselines. In comparison, Meta-EML exhibits competitive performance closely following Meta-MSGL achieving 90% RA on 15 datasets and exceeding 80% on 29 datasets. Although slightly less effective than Meta-MSGL Meta-EML remains a strong contender showcasing its ability to recommend algorithms with high accuracy in a substantial number of cases. This indicates that Meta-EML’s meta-learning approach while effective does not match the precision of Meta-MSGL in all scenarios. Although Meta-EML performance is not as high as Meta-MSGL, it still demonstrates its capability to accurately recommend algorithms on most of the datasets.

Meta-MLkNN shows a noticeable drop in performance reaching the 90% accuracy threshold in only 9 datasets and exceeding 80% in 21 datasets. This suggests that Meta-MLkNN is less effective in consistently identifying and recommending algorithms. In addition, Meta-DAR and Meta-DMA showed considerably lower performance. Meta-DAR achieved 90% accuracy on only 5 datasets and Meta-DMA on 3. When considering the 80% accuracy threshold, Meta-DAR and Meta-DMA reached it in only 10 and 11 datasets respectively. The overall evaluation indicates that while Meta-MSGL and Meta-EML consistently recommend algorithms effectively for most datasets, Meta-MLkNN, Meta-DAR, and Meta-DMA show notable inconsistency and decreased efficacy.

4.5.3 Normalized Discounted Cumulative Gain (NDCG)

The Normalized Discounted Cumulative Gain (NDCG@3) metric assesses the ranking quality of the recommendations, highlighting the importance of correctly ordering the top 3 relevant algorithms according to their performance. Meta-MSGL consistently demonstrates superior ranking capabilities, maintaining high NDCG scores on most datasets. As can be noted from Fig. 7, Meta-MSGL consistently demonstrated superior ranking capabilities with high NDCG scores across diverse datasets, exceeding 90% in 19 datasets. This indicates the Meta-MSGL accurately identifies and ranks top-performing algorithms, ensuring recommendations are both reliable and informative.

Meta-EML and Meta-MLkNN also achieve considerably high NDCG scores, but not as high as Meta-MSGL. Meta-EML exceeds 90% in 10 datasets, while Meta-MLkNN achieves this in 4. These methods perform generally well on NDCG metric implying that, while they may not always provide the highest-ranked algorithm, their rankings are generally close to optimal. However, their performance variability indicates that they do not consistently match Meta-MSGL performance on this metric. In contrast, Meta-DAR and Meta-DMA exhibit significantly lower NDCG scores, failing to reach the 90% threshold in any dataset. Their weaker performance in ranking algorithms effectively reflects their limitations in utilizing the available meta-features.

Overall, the results on NDCG metric show that Meta-MSGL is the most effective method for ensuring that recommended algorithms are both accurate and correctly prioritized. Meta-EML and Meta-MLkNN offer reasonably good rankings but are less reliable, whereas Meta-DAR and Meta-DMA performanc is much lower.

While Meta-MSGL demonstrates superior performance across a wide range of datasets, certain datasets present unique challenges that affect its recommendation accuracy. Specifically, datasets with high dimensionality, class imbalance, or substantial noise can introduce variability in the performance of the model. For instance, datasets such as ‘thoracic-surgery’ and ‘column3C’ exhibit variability in classification accuracy due to significant noise and imbalance between classes, which complicates the recommendation process. Meta-MSGL’s ability to mitigate these challenges is attributed to its multivariate sparse group Lasso framework, which effectively reduces the impact of irrelevant meta-features. However, in cases where the meta-features are highly correlated or exhibit high variance, the method’s ability to discern subtle differences in algorithm performance may be affected. Future work could explore more refined noise-handling techniques or alternative meta-feature extraction methods to further enhance the model’s robustness to such dataset-specific characteristics.

4.5.4 Statistical Validation of Meta-MSGL Performance

To evaluate the statistical significance of the performance differences between Meta-MSGL and the baseline methods, we conducted Wilcoxon signed-rank tests at a significance level of 0.05. The results, presented in Table 2 provide insight into whether the observed performance advantages of Meta-MSGL are statistically significant. The null hypothesis in each case affirms that Meta-MSGL performs either worse or equally compared to the other baseline methods (Meta-EML, Meta-MLkNN, Meta-DAR, and Meta-DMA) across the three key metrics: CA, RA and NDCG.

The test reveal that Meta-MSGL significantly outperforms the baseline methods on the three evaluation metrics. Meta-MSGL shows a consistent and statistically significant advantage, secifically when compared to Meta-MLkNN, Meta-DAR, and Meta-DMA, with p-values of 0.0 across all metrics. When compared to Meta-EML, Meta-MSGL also demonstrates significant improvements, especially in RA and NDCG, though the competition is closer, as reflected in the slightly higher p-values. These results confirm that Meta-MSGL superior performance is not only practical but also statistically significant, making it the most reliable choice for algorithm selection and ranking tasks.

While the proposed Meta-MSGL model demonstrates strong performance in classification algorithm recommendation, it is not without limitations. First, the model’s performance is sensitive to the choice of regularization parameters λ1 and λ2, which require careful tuning to achieve optimal results. Second, the computational complexity of the MSGL approach can increase with the size of the meta-feature groups and the number of candidate algorithms, leading to potentially higher training times for larger datasets.

5  Conclusion

In this paper, we have introduced a novel framework to address critical challenges in automated machine learning (AutoML), specifically focusing on the classification algorithm recommendation problem within the context of meta-learning. By leveraging multivariate sparse group lasso, our approach effectively manages the high-dimensional, sparse, and structured nature of meta-feature spaces. This dual-level sparsity, enforced both within and across groups, enhances the accuracy of feature selection and algorithm recommendations. This results in more precise and effective algorithm recommendations, addressing the limitations of existing methods that treat meta-features in isolation and fail to account for the interrelatedness of these features.

The empirical validation of our approach on a diverse set of benchmark datasets has demonstrated its superior performance compared to state-of-the-art meta-learning methods. However, our model does present some limitations, particularly regarding its sensitivity to the regularization parameters λ1 and λ2, which require careful tuning to achieve optimal results. Additionally, the computational cost of training the model can be higher for larger datasets due to the complexity of handling multiple groups of meta-features. Another limitation is the need for retraining when new datasets or meta-features are introduced, which could affect the model’s scalability in continuously evolving environments.

Future work can address these limitations by integrating our framework with adaptive meta-learning techniques, such as dynamic hyperparameter tuning and incremental learning for continuous adaptation to new data. Further, expanding the considered meta-features and datasets, as well as enhancing the method’s scalability and efficiency, will open new opportunities for improving the performance and applicability of the framework across various domains.

Acknowledgment: The authors would like to thank Universiti Tunku Abdul Rahman, Kampar, Malaysia, and the School of Software, Dalian University of Technology, Dalian, China for supporting this study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contributions to the paper as follows: Irfan Khan conceived and conducted the study, designed the experiments, and prepared the draft manuscript. Xianchao Zhang provided supervision and guidance throughout the research. Ramesh Kumar Ayyasamy offered technical assistance and support during the study. Saadat M. Alhashmi and Azizur Rahim contributed by reviewing the manuscript and providing critical feedback. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data supporting the findings of this study are provided within the paper. For any additional information or further inquiries, the authors may be contacted.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

References

1. Deng L, Xiao M. A new automatic hyperparameter recommendation approach under low-rank tensor completion e framework. IEEE Transact Pattern Anal Mach Intell. 2023;45(4):4038–50. doi:10.1109/TPAMI.2022.3195658. [Google Scholar] [PubMed] [CrossRef]

2. Wang G, Song Q, Zhu X. An improved data characterization method and its application in classification algorithm recommendation. Appl Intell. 2015;43:892–912. doi:10.1007/s10489-015-0689-3. [Google Scholar] [CrossRef]

3. Khan I, Zhang X, Ayyasamy RK, Ali R. AutoFe-Sel: a meta-learning based methodology for recommending feature subset selection algorithms. KSII Trans Internet Inf Syst. 2023 Jul;17(7):1773–93. doi:10.3837/tiis.2023.07.002. [Google Scholar] [CrossRef]

4. Carneiro D, Guimar M, Carvalho M, Novais P. Using meta-learning to predict performance metrics in machine learning problems. Expert Syst. 2023;40(1):e12900. doi:10.1111/exsy.12900. [Google Scholar] [CrossRef]

5. Marinho TL, Carvalho D, Pimentel BA. Optimization on selecting XGBoost hyperparameters using meta-learning. Expert Syst. 2024 Apr;41(9):e13611. doi:10.1111/exsy.13611. [Google Scholar] [CrossRef]

6. Jiang K, Cao B, Fan J. A robust framework for multimodal sentiment analysis with noisy labels generated from distributed data annotation. Comput Mod Eng Sci. 2024;139(3):1–10. doi:10.32604/cmes.2023.046348. [Google Scholar] [CrossRef]

7. Xu C, Zhu Y, Zhu P, Cui L. Meta-learning-based sample discrimination framework for improving dynamic selection of classifiers under label noise. Knowl Based Sys. 2024;295:111811. doi:10.1016/j.knosys.2024.111811. [Google Scholar] [CrossRef]

8. Khan I, Zhang X, Kumar R, Alhashmi SM, Ali R. MtL-NFW: a meta-learning framework for automated noise filter selection and hyperparameter optimization in auto-ML. Research Square. 2024 Jul. doi:10.21203/rs.3.rs-4638344/v1. [Google Scholar] [CrossRef]

9. Abanda A, Mori U, Lozano JA. Time series classifier recommendation by a meta-learning approach. Pattern Recognit. 2022;128(1):108671. doi:10.1016/j.patcog.2022.108671. [Google Scholar] [CrossRef]

10. Pimentel BA, de Carvalho ACPLF. A new data characterization for selecting clustering algorithms using meta-learning. Informat Sci. 2019;477:203–19. doi:10.1016/j.ins.2018.10.043. [Google Scholar] [CrossRef]

11. Zhu X, Ying C, Wang J, Li J, Lai X, Wang G. Ensemble of ML-KNN for classification algorithm recommendation. Knowl Based Syst. 2021;221(1):106933. doi:10.1016/j.knosys.2021.106933. [Google Scholar] [CrossRef]

12. Pio PB, Rivolli A, Carvalho ACPLFD, Garcia LPF. A review on preprocessing algorithm selection with meta-learning. Knowl Inf Syst. 2023;66(1):1–28. doi:10.1007/s10115-023-01970-y. [Google Scholar] [CrossRef]

13. Shao X, Wang H, Zhu X, Xiong F, Mu T, Zhang Y. EFFECT: explainable framework for meta-learning in automatic classification algorithm selection. Informat Sci. 2023;622(92):211–34. doi:10.1016/j.ins.2022.11.144. [Google Scholar] [CrossRef]

14. Garouani M, Ahmad A, Bouneffa M, Hamlich M. Autoencoder “kNN meta” model based data character-ization approach for an automated selection of AI algorithms. J Big Data. 2023;10(1):1–18. doi:10.1186/s40537-023-00687-7. [Google Scholar] [CrossRef]

15. Garcia LPF, de Carvalho ACPLF, Lorena AC. Noise detection in the meta-learning level. Neurocomputing. 2016;176:14–25. doi:10.1016/j.neucom.2014.12.100. [Google Scholar] [CrossRef]

16. Tornede A, Gehring L, Tornede T, Wever M, Hüllermeier E. Algorithm selection on a meta level. USA: Springer; 2023. doi:10.1007/s10994-022-06161-4 [Google Scholar] [CrossRef]

17. Oreski D, Oreski S, Klicek B. Effects of dataset characteristics on the performance of feature selection techniques. Appl Soft Comput. 2017;52:109–19. doi:10.1016/j.asoc.2016.12.023. [Google Scholar] [CrossRef]

18. Corrales DC, Ledezma A, Corrales JC. A case-based reasoning system for recommendation of data cleaning algorithms in classification and regression tasks. Appl Soft Comput. 2020;90(4):106180. doi:10.1016/j.asoc.2020.106180. [Google Scholar] [CrossRef]

19. Deng L, Chen WS, Xiao M. Metafeature selection via multivariate sparse-group lasso learning for automatic hyperparameter configuration recommendation. IEEE Trans Neural Netw Learn Syst. 2024;35(9):12540–52. doi:10.1109/TNNLS.2023.3263506. [Google Scholar] [PubMed] [CrossRef]

20. Mantovani RG, Rossi ALD, Alcobaça E, Vanschoren J, de Carvalho ACPLF. A meta-learning recommender system for hyperparameter tuning: predicting when tuning improves SVM classifiers. Informat Sci. 2019;501(13):193–221. doi:10.1016/j.ins.2019.06.005. [Google Scholar] [CrossRef]

21. Horváth T, Mantovani RG, de Carvalho ACPLF. Hyper-parameter initialization of classification algorithms using dynamic time warping: a perspective on PCA meta-features. Appl Soft Comput. 2023;134(2):109969. doi:10.1016/j.asoc.2022.109969. [Google Scholar] [CrossRef]

22. Wang G, Song Q, Zhang X, Zhang K. A generic multilabel learning-based classification algorithm recommendation method. ACM Transact Knowl Disc Data. 2014;9:1–30. doi:10.1145/262947. [Google Scholar] [CrossRef]

23. Zhang ML, Zhou ZH. ML-KNN: a lazy learning approach to multi-label learning. Pattern Recognit. 2007;40(7):2038–48. doi:10.1016/j.patcog.2006.12.019. [Google Scholar] [CrossRef]

24. Zhu X, Yang X, Ying C, Wang G. A new classification algorithm recommendation method based on link prediction. Knowl-Based Syst. 2018;159:171–85. doi:10.1016/j.knosys.2018.07.015. [Google Scholar] [CrossRef]

25. Yang C, Akimoto Y, Kim DW, Udell M. OBOE: collaborative filtering for AutoML model selection. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining. 2019; Anchorage AK, USA. p. 1173–83. [Google Scholar]

26. Sousa AFM, Prudêncio RBC, Ludermir TB, Soares C. Active learning and data manipulation techniques for generating training examples in meta-learning. Neurocomputing. 2016;194:45–55. doi:10.1016/j.neucom.2016.02.007. [Google Scholar] [CrossRef]

27. Lee JW, Giraud-Carrier C. Automatic selection of classification learning algorithms for data mining practitioners. Intell Data Anal. 2013;17:665–78. doi:10.3233/IDA-130599. [Google Scholar] [CrossRef]

28. Leyva E, Caises Y, González A, Pérez R. On the use of meta-learning for instance selection: an architecture and an experimental study. Informat Sci. 2014;266:16–30. doi:10.1016/j.ins.2014.01.007. [Google Scholar] [CrossRef]

29. Garcia LPF, Lorena AC, Matwin S, Carvalho AD. Ensembles of label noise filters: a ranking approach. Data Min Knowl Disc. 2016;30(5):1192–216. doi:10.1007/s10618-016-0475-9. [Google Scholar] [CrossRef]

30. Reif M, Shafait F, Goldstein M, Breuel T, Dengel A. Automatic classifier selection for non-experts. Pattern Anal Appl. 2014;17(1):83–96. doi:10.1007/s10044-012-0280-z. [Google Scholar] [CrossRef]

31. Lai X, He X, Pang Y, Zhang F, Zhou D, Sun W, et al. A scalable digital twin framework based on a novel adaptive ensemble surrogate model. J Mech Des. 2022 Nov;145(2):021701. doi:10.1115/1.4056077. [Google Scholar] [CrossRef]

32. Bensusan H, Kalousis A. Estimating the predictive accuracy of a classifier. In: De Raedt L, Flach P, editors. Machine learning: ECML 2001. Berlin, Heidelberg: Springer; 2007. vol. 2167, p. 25–36. doi:10.1007/3-540-44795-4_3. [Google Scholar] [CrossRef]

33. Feurer M, Klein A, Eggensperger K, Springenberg JT, Blum M, Hutter F. Efficient and robust automated machine learning. Adv Neural Inf Process Syst. 2015;2015:2962–70. [Google Scholar]

34. Olson RS, Moore JH. TPOT: a tree-based pipeline optimization tool for automating machine learning. In: International Conference on Machine Learning. New York, NY, USA; 2016. p. 66–74. [Google Scholar]

35. Smith-Miles KA. Cross-disciplinary perspectives on meta-learning for algorithm selection. ACM Comput Surv. 2008;41:1–25. doi:10.1145/1456650.14566. [Google Scholar] [CrossRef]

36. Tugnait JK. Sparse-group lasso for graph learning from multi-attribute data. IEEE Transact Signal Process. 2021;69:1771–86. doi:10.1109/TSP.2021.3057699. [Google Scholar] [CrossRef]

37. Li Y, Nan B, Zhu J. Multivariate sparse group lasso for the multivariate multiple linear regression with an arbitrary group structure. Biometrics. 2015;71(2):354–63. doi:10.1111/biom.12292. [Google Scholar] [PubMed] [CrossRef]

38. Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm. Soci Indust Appl Math J Imag Sci. 2009;2(1):183–202. doi:10.1137/080716542. [Google Scholar] [CrossRef]

39. O’Donoghue B, Candès E. Adaptive restart for accelerated gradient schemes. Foundat Computat Mathem. 2015;15(3):715–32. doi:10.1007/s10208-013-9150-3. [Google Scholar] [CrossRef]

40. Smith MR, Martinez T, Giraud-Carrier C. An instance level analysis of data complexity. Mach Learn. 2014;95(2):225–56. doi:10.1007/s10994-013-5422-z. [Google Scholar] [CrossRef]

41. Rivolli A, Garcia LPF, Soares C, Vanschoren J, Carvalho ACPLFD. Meta-features for meta-learning. Knowl-Based Syst. 2022;240(2):101–8. doi:10.1016/j.knosys.2021.108101. [Google Scholar] [CrossRef]

42. Khan I, Zhang X, Rehman M, Ali R. A literature survey and empirical study of meta-learning for classifier selection. IEEE Access. 2020;8:10262–81. doi:10.1109/ACCESS.2020.2964726. [Google Scholar] [CrossRef]

43. Alcobaça E, Siqueira F, Rivolli A, Garcia LPF, Oliva JT, de Carvalho ACPLF. MFE: towards reproducible meta-feature extraction. J Mach Learn Res. 2020;21(111):1–5. [Google Scholar]

44. Rijn JNV, Bischl B, Torgo L, Gao B, Umaashankar V, Fischer S, et al. OpenML: a collaborative science platform. In: Joint European Conference on Machine Learning and Knowledge Discovery in Databases. 2013; Prague, Czech Republic. p. 645–9. [Google Scholar]

45. Kotthoff L, Leyton-brown K. Auto-WEKA 2.0: automatic model selection and hyperparameter optimization in WEKA. J Mach Learn Res. 2017;18:1–5. [Google Scholar]

46. Giraud-Carrier C. The data mining advisor: meta-learning at the service of practitioners. In: Fourth International Conference on Machine Learning and Applications (ICMLA'05). 2005; Los Angeles, CA, USA. p. 113–9. [Google Scholar]

47. Deng L, Xiao MQ. Latent feature learning via autoencoder training for automatic classification configuration recommendation. Knowl Based Syst. 2023;261(3):110218. doi:10.1016/j.knosys.2022.110218. [Google Scholar] [CrossRef]