Execution of Bioconvective Radiative Dissipative Non-Newtonian Magnetohydrodynamic Flow Comprising Stratification with BVP4C Approach Configured with Vertical Plane

1  Introduction

A nanofluid changes the heat transfer mechanism in coolants. Moreover, the coolant has a greater thermal conductivity. Due to its increasing need in many industrial processes, heat transfer has recently been a focus of major study. An important aspect of nanoparticle research is improving thermal conductivity. Nanofluids exhibit excellent potential for achieving increased thermal conductivity in many applications. A term used to describe these fluids is nanofluids [1]. Nanofluids consist of a uniform combination of nanoparticles with a base fluid. When compared to base fluids, nanofluids exhibit superior thermophysical properties, including viscosity, diffusivity, conductivity, and heat transfer quantities [2]. Magnetized ferrofluids consist of a base fluid suspended in a colloidal dispersion of nanoscale ferromagnetic particles. It has several uses and was made artificially [3–5]. Heat treatment furnaces, lasers, avionics, nuclear power plants, cooling agents, fiber optics, robotics, speakers, filters, refrigeration, drawing plastic, computer peripherals, and semiconductor and crystal processing are just a few of the many applications for ferrofluids. Ghadikolaei et al. [6] use numerical analysis to delve into the topic of nano C2H6O2-CNTs flow between revolving channels. Hamid et al. [7] used numerical analysis to investigate the behavior of nanofluid thermal transfer using several models of nanoparticles. Magnetized radiative Williamson nanofluids with heat sink were the subject of research by Hamid et al. [8].

An electromagnetic wave is distributed through a medium as radiation. An example of thermal radiation therapy is when doctors transmit heat below the skin friction into muscles and tissues to treat a pathological condition. Nuclear power stations, turbines, and many propulsion mechanisms for satellites, airplanes, and planetary vehicles are just a few examples of the various solar and power technology processes that rely on heat transmission, which is affected by thermal radiation. The majority of the radiation emitted by Earth’s objects falls into the ultraviolet region of the electromagnetic spectrum. That’s why radiation analysis plays such a pivotal role in revealing the conversation systems’ thermal properties. The effects of radiation on nano liquid via permeable entrenched cone were investigated by Chamkha et al. [9]. Over a flexible rotating disk, Ijaz et al. [10] investigated the activation energy behavior of nano Sisko liquid with radiation. The impact of Rosseland’s nonlinear/linear radiation on natural laminar steady convection over an isothermal plate was studied by Pantokratoras [11]. Stratification and activation energy were taken into account by Ijaz et al. [12] for Maxwell nanofluid convective flow. Using radiative flux in Rosseland’s estimate for radiation, Mushtaq et al. [13] examine the steady and 3D boundary flow, across a stretched sheet. The activation energy for Casson radiative flow using the Cattaneo model was numerically simulated via Ijaz et al. [14]. Microorganisms that swim oxytactically or chemotactically were explored by Childress et al. [15].

Industrial operations with significant flow rates regularly exhibit stratified flows. An example of stratified flow regime is used by pipelines that transport gas-condensate. By mixing liquids with varying density and temperatures, or by fluctuating concentration, fluid stratification occurs naturally. In this case, the variations in mass and energy transmission are stratified twice. One example of stratification is the removal of heat from bodies of water such as lakes, rivers, and oceans. A power-law liquid in a porous media was studied by Cheng [16] for its fluctuations in temperature and concentration stratification. They demonstrated that increasing the thermal stratification parameter reduces the rate of change in energy transfer. Local skin friction is reduced when the stratification parameter is increased, according to Hossain et al. [17], who investigated the issue of spontaneous convective flow in a vertical cone with a thermal stratification parameter. Fluid stratification’s effects in various contexts were investigated by Daniel et al. [18] and Ibrahim et al. [19].

There has been an increase in interest in non-Newtonian fluid flow due to its increased industrial and technological benefits in recent years. Viscoelastic fluids are non-Newtonian fluids with both elastic and viscous properties. The rate of strain at a specified point is non-linear when it comes to such fluids. An Oldroyd-B fluid is a special non-Newtonian fluid whose transport behavior cannot be appropriately described by a simple shear flow’s typical relation between shear stress and shear rate. This has led to many constitutive equations for these fluids being proposed. Oldroyd’s name is associated with the Oldroyd-B fluid, an expansion of Maxwell fluid, providing a satisfactory explanation for retardation and relaxation times behavior [20]. Siddiqui et al. [21] examined Oldroyd-B liquid flow amongst parallel plates, which is one of the research projects on Oldroyd-B fluids. In their subsequent investigation on Oldroyd-B fluid’s time-dependent flow, Jamil et al. [22] used the Hankel transform to solve the model equation. Brownian motion impact on Oldroyd-B transient fluid across an overextended surface was considered by Awad et al. [23]. Mixing chemicals with radiation and an Oldroyd-B, Irfan et al. [24] investigated the flow across a stretched cylinder surface. Over a spinning disk, Abbas et al. [25] studied a thin film response of an Oldroyd-B liquid with homogeneous/heterogeneous. The incompressible Oldroyd-B liquid model’s global regularity was the subject of Ye’s [26] research.

Brownian motion and thermophoresis effect are significant because they can affect the behavior and movement of particles in multiple systems. Brownian motion describes the random movement of nanoparticles in a fluid caused by their collisions with one another. Thermophoresis is a temperature gradient that causes nanoparticles to diffuse. It is essential to understand these effects in fields such as biotechnology, environmental science, and materials science to design and optimize processes. Using analytical methods, Pasha et al. [27] investigated the effect of Brownian motion, thermophoresis, and magnetic factors between two plates; they found that the fluid’s thermal panels had grown in size due to an increase in thermophoretic and Brownian motion. When discussing fluid flow on a surface, both of these concepts have substantial effects on heat transmission. As a result of its effects on mixing and the fluid’s effective thermal conductance, Brownian motion improves heat transmission. This effect makes cooling or heating the sheet more effective by increasing convective heat transfer close to the surface. On the other hand, thermophoresis may either improve or impede heat transmission, depending on the properties of the particles and the circumstances of the flow. Particles may collect close to the surface of the sheet as a result of thermophoresis, forming a layer of thermal resistance that prevents heat from transferring. Alternatively, thermophoresis may improve heat transmission in some situations by removing particles from the surface, which lowers thermal resistance and increases convective heat transfer. Researchers Thirupathi et al. [28] observed that the thermal and concentration distributions have grown with an increase in the thermal Biot number in their study of three-dimensional gyrating nanofluid flow over an extended sheet with influences of heat sink/source. There has been an increase in thermal distribution with the development in volume fractions, according to Sheri et al. [29], who studied the effects of mass and thermal transportation on convective nanofluid flow.

To improve the mixing of nanoparticles and fluids, movable microorganisms are used, since they are responsible for the biological transmission process. During metabolic energy consumption, an organism’s motility refers to its capacity to move self-propelled. Magneto slip nano flow comprehending motile microbes onto a vertical platform was conveyed by Khan et al. [30]. Researchers Kuznetsov [31] solved the bio convection problem with nanoliquid and motile microorganisms analytically by using the Galeriken and a linear instability approach. Using gyrotactic microbes as a model, Elbashbeshy et al. [32] investigated the incompressible nano-liquid flow over a porous elongating surface. The results showed that when the porosity of the material was decreased, the dragging force at the surface was also decreased. Researchers Thumma et al. [33] looked at how heat dissipation affected the stationary point flow of 3-dimensional multi-holomorphic fluid on a sinusoidal cylinder with a circular shape. When investigating the heating mechanism of Carbon nanotubes with slip effects, Raza et al. [34] found that the thermal profiles of single-wall carbon nanotubes have grown over time. In their study, Souayeh et al. [35] examined the behavior of gyrotactic microorganisms in an incompressible tri-hybrid nanofluid flow over a stretched surface. Radiation factor and Brownian motion improved the microbiological profile, according to their results. Utilizing influences of varied thermal conductance, Haq et al. [36] investigated the Darcy-Forchheimer flow of Williamson bio-convective nanofluid. Using magneto hydro dynamics and the behavior of motile microorganisms, Makkar et al. [37] examined bio-convective fluid flow on an expanding surface. Based on the results, the author concluded that a high-volume chemical reaction resulted in a decrease in fluid concentration. By simulating the reviewed Fick’s and Fourier’s laws on a cylinder with chemical reactivity, microorganisms, and dual diffusive effects computationally, Haq et al. [38] found that concentration and thermal distributions decrease as mass and relaxation times increase. The effects of activation energy and microorganisms on optimizing entropy for bio-convective and chemically reactive nanofluid flows were investigated by Hussain et al. [39]. The magnetized bio-convective nanofluid flow on a gyratory disk with the activation energy as an effect was mathematically and theoretically investigated by Haq et al. [40]. The numerical analysis of the bio-convective nanofluid flow on a stretched cylinder by Saleem et al. [41] revealed an increase in heat distribution with an increase in the Eckert number. Dinarvand et al. [42] studied an application of a mass-based hybrid nanofluid model. The nanofluid flow with physical properties can be found in [43]. The hybrid nanofluid flow of blood with homogeneous and heterogeneous reactions and the optimization of heat transfer nanofluid blood flow have been discussed in [44,45]. A numerical scheme for a time-dependent electroviscous and hybrid nanofluid has been presented in [46].

Currently, a vertically stretched sheet with nonlinear radiation has not been investigated for mixed convection MHD flow over a bioconvection flow. Accordingly, an objective and novelty of the present study is to address and perform thermal radiation impact towards heat transfer phenomena along with Oldroyd-B nanofluid and triple stratified medium in the energy equation of physical flow system. A gap in the research was filled by this study. The purpose of this study is therefore to cover this topic. The relevant Partial Differential Equations are transformed into nonlinear differential equations because of their similar flow characteristics. Runge-Kutta fourth-fifth is used to obtain a numerical solution for the proposed system. To evaluate the flow and heat transfer rate characteristics, the flow-controlling parameters at the center of this study are represented graphically and tabularly. To determine the accuracy of the proposed method, we compared the results of this study to those reported in previous studies. The quality of an agreement is noticeable. This work pertains to bioinspired nanofluid-enhanced fuel cells and nanomaterial manufacturing processes.

In this study, the following main research questions are addressed:

1.    What is the impact of thermal radiation parameters on temperature behavior?

2.    What effect does Lewis number have on concentration pattern?

3.    In what ways does bioconvection Lewis number affect motile density?

2  Mathematical Formulation

Flow of Oldroyd-B viscoelastic nanofluid is presented, which results from a non-isothermal vertical surface containing microorganisms and floating nanoparticles. Fig. 1 shows the process of flow.

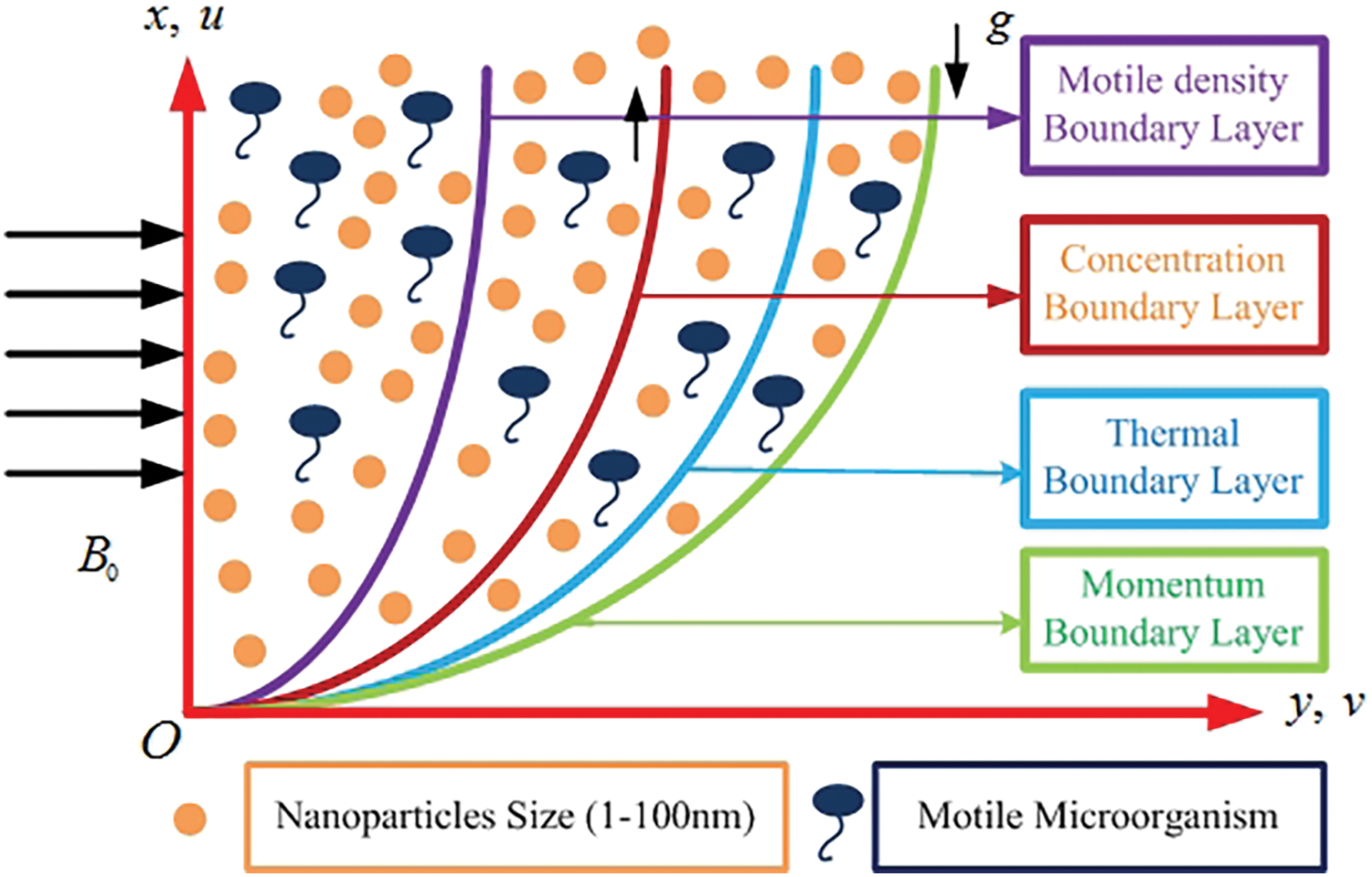
Figure 1: Physical flow process

•   The x^1 and y^1 are the coordinates that expand towards the surface and normal to that.

•   The uw=ax^1, increasing the sheet towards vertical direction, where a>0,stretching speed.

•   Radiation and dissipation are assumed.

•   Induced magnetic field is neglected.

•   Wall temperature Tw is varied towards x^1-direction.

•   Assuming Ohm’s law applies, the flow occurs.

•   The magnetic field is kept constant.

•   The surface of a non-isothermal vertical chamber contains floating nanoparticles and microbes that travel through gyro-tactic motion is assumed.

•   Governing equations under the above norms are [47]:

∂u^1∂x^1+∂v^1∂y^1=0,(1)

u^1∂u^1∂x^1+v^1∂u^1∂y^1=υρf∂2u^1∂y^21−A1(u^21∂2u^1∂x^21+v^21∂2u^1∂y^21+2u^1v^1∂2u^1∂x^1∂y^1)−σρfB02u^1−σρfB02A1υρf∂u^1∂y^1+υA2(u^1∂3u^1∂x^1∂y^12+v^1∂3u^1∂y^31−∂u^1∂x^1∂2u^1∂y^21+∂u^1∂y^1∂2u^1∂x^1∂y^1)+1ρf(1−C^∞)ρfgβ(T^−T^∞)−(ρp−ρf)g(C^−C^∞)−(n^−n^∞)gγ(ρm−ρf),(2)

u^1∂T^∂x^1+v^1∂T^∂y^1=αf∂2T^∂y^21+τ[DB∂C^∂y^1∂T^∂y^1+DTT∞(∂T^∂y^1)2]−1(ρc)f∂qr∂y^1+μf(ρc)f(∂u^1∂y^1)2(3)

u^1∂C^∂x^1+v^1∂C^∂y^1−DB∂2C^∂y^21=DTT∞∂2T^∂y^21,(4)

u^1∂n^∂x^1+v^1∂n^∂y^1−Dm∂2n^∂y^21=−bWc(C^w−C^0)[∂∂y^1(n^∂C^∂y^1)].(5)

The boundary conditions are [42]:

u^1=u^w=ax^1,v^1=0,T^=T^w=T^0+b1x^1,C^=C^w=C^0+d1x^1,n^=n^w=n^0+e1x^1,as y^1=0,(6)

u^1→0,∂u^1∂y^1→0,T^=T^∞=T^0+b2x^1,C^=C^∞=C^0+d2x^1,n^=n^∞=n^0+e2x^1,as y^1→∞.(7)

Stratification refers to the process of forming separate layers with different densities. In thermal and mass stratification, differences in concentration and temperature are prevented from exchanging or mixing liquids with different densities to develop the activities of living organisms. Heat transfer from thermal sources, such as condensers of power plants, can be done in many ways, including dissipating heat into the atmosphere through oceans, lakes, and rivers, storing thermal energy, for instance with solar ponds, and transferring heat from thermal sources, such as lakes and seas.

Radiative warmth flux is:

qr=−4σ∗3k∗∂T^4∂y^1=−16σ∗3k∗T^3∂T^∂y^1,(8)

Therefore, Eq. (3) becomes

u^1∂T^∂x^1+v^1∂T^∂y^1=∂∂y^1[(αf+16σ∗T^33(ρc)fk∗)∂T^∂y^1]+τ[DB∂C^∂y^1∂T^∂y^1+DTT∞(∂T^∂y^1)2]+μf(ρc)f(∂u^1∂y^1)2(9)

Considered non-dimensions are:

η=y^1(aυ)1/2,Ψ=(aυ)1/2x^1f(η),u^1=∂Ψ∂y^1,v^1=−∂Ψ∂x^1,u^1=uwf′(η),v^1=−(aυ)1/2f(η),θ(η)=T^−T^∞T^w−T^0,θw=T^wT^∞,T^=T^∞(1+(θw−1)θ),ϕ(η)=C^−C^∞C^w−C^0,Γ(η)=n^−n^∞n^w−n^0.

α1=A1aandβ1=A2a,M=(σB02aρf)1/2,λ=βγ(1−C^∞)(T^w−T^0)auw,Nr=(ρp−ρf)(C^w−C^0)βρf(T^w−T^0),Pr=υcpk,Nt=τDT(T^w−T^0)υT^0,Nb=τDB(C^w−C^0)υ,Ec=uw2cp(T^w−T^0),Le=αfDB,Lb=υDmand Pe=bWcDm,Ω=n^∞n^w−n^0,S1=b2b1,S2=d2d1 and S3=e2e1;Rd=16σ∗T∞33kk∗.(10)

An obtained ordinary differential equation:

f1′′′+(1+Mα1)f1f1′′−f1′2+α1(2f1f1′f1′′−f12f1′′′)+β1(f1′′2−f1f1iv)−Mf1′+λ(θ−Nrϕ−RbΓ)=0,(11)

1Pr[{1+Rd(1+(θw−1)θ)3}θ′]′+f1θ′−f1′θ−S1f1′+Nbθ′ϕ′+Ntθ′2+Ecf1′′2=0,(12)

ϕ′′−PrLef1ϕ′−PrLef1′ϕ−PrLeS2f1′+NtNbθ′′=0,(13)

Γ′′+Lb(f1Γ′−f1′Γ)−LbS3f1′−Pe[ϕ′′(Γ+Ω)+ϕ′Γ′]=0.(14)

Related BCs are:

f1(0)=0,f1′(0)=1,θ(0)=1−S1,ϕ(0)=1−S2,Γ(0)=1−S3,f1′(0)=0=f1′′(0),θ(∞)=ϕ(∞)=0=Γ(∞).(15)

The Nux, Shx, Nnx are:

Nux=x^1qwk(T^w−T^0),Shx=x^1qmDB(C^w−C^0),Nnx=x^1qnDn(n^w−n^0),qw=[−k∂T^∂y^1+qr]y^1=0,qm=[−DB∂C^∂y^1]y^1=0,qn=[−Dn∂n^∂y^1]y^1=0.(16)

Nur=NuxRe−0.5=−(1+Rdθw3)θ′(0),Shr=ShxRe−0.5=−ϕ′(0),Xnr=NnxRe−0.5=−Γ′(0).(17)

where Re=uwx^1υ.

3  Method of Solution

One of the main advantages of bvp4c is it adapts to stiff problems and complex boundary conditions to provide reliable solutions. An error tolerance of this method 10−3 ≤ η ≤ 10−8.

The bvp4c is used here to solve (11)–(14) with (14).

Reduced 1st order differential equation system is:

y1′=y2,y2′=y3,y3′=y4,y4′=1β1y1[y4+(1+Mα1)y1y3−y22+α1(2y1y2y3−y12y4)+β1y32−My2+λ(y5−Nry7−Rby9)],y5′=y6,y6′=−11+Rd(1+(θw−1)y5)3[Pr(y1y6−y2y5−Sy2+Nby8y6+Nty62+Ecy32)+3Rdy62(1+(θw−1)y5)2(θw−1)],y7′=y8,y8′=PrLe(y2y7+y1y8+S2y2)−NtNby6′,y9′=y10,y10′=Lb(y2y9−y1y10+S3y2)+Pe[y8′(y9+Ω)+y10y8],(18)

where y1=f1,y2=f1′,y3=f1′′,y4=f1′′′,y5=θ,y6=θ′,y7=ϕ,y8=ϕ′,y9=Γ,y10=Γ′.

Following is an equivalent boundary condition:

y1=0,y2=1,y5−1+S1=0,y7−1+S2=0,y9−1+S3=0,At η=0,(19)

y2→0,y3→0,y5→0,y7→0,y9→0,as η→∞.(20)

Convergence Concerns: Convergence can be challenging for bvp4c, especially for problem types that are highly nonlinear or complex. Convergence of the solver depends on a good initial guess for the solution. Generating Mesh: bvp4c automatically adapts the mesh, but it may not generate a sufficiently detailed mesh when problems exist with sharp gradients or complex behaviors. Enormous Systems: Large systems of ODEs can be computationally expensive and memory-constrained with bvp4c.

4  Validation of Results

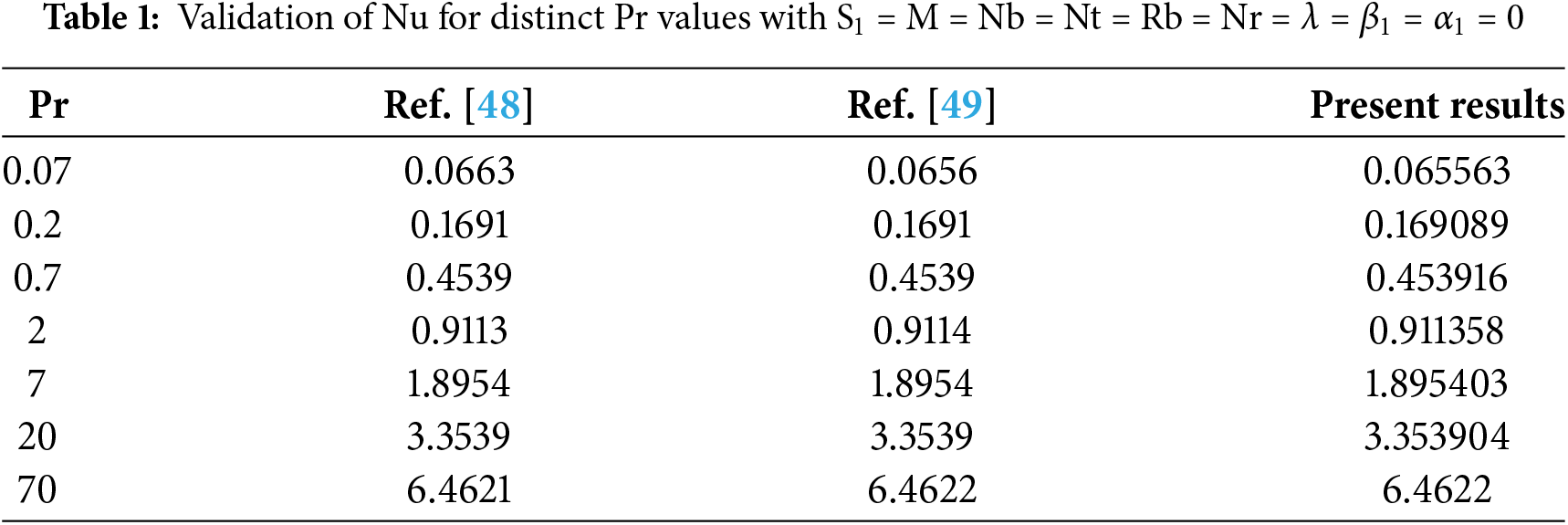
As part of the approval process for the proposed method and results, Table 1 shows a comparison of the study results with previous outcomes in [48,49] for approval purposes. Exam results demonstrate a profound understanding of this study. Validation of Nu for distinct Pr values with S1 = M = Nb = Nt = Rb = Nr = λ = β1 = α1 = 0. There is decent agreement between the results.

Future Scope: In the future, the model can be modified as follows:

1.    While the present problem focuses on two-dimensional flows, it may be extended to three-dimensional flows as well.

2.    Second-order slip is a noteworthy advancement over conventional first- or no-order slip.

3.    This model will produce entropy at a calculated rate.

4.    Models such as this could have applications in biomedical engineering and biotechnology.

5  Results and Discussion

Oldroyd-B nanofluid flow over a stretchy sheet with swimming microbes is analyzed with graphs in this work. As a consequence, the flow-controlling parameters are used to analyze velocity profiles, motile densities, nanoparticle concentrations, and temperature profiles. The impact of thermophoresis and Brownian motion on magnetohydrodynamic nanofluids in bioconvection boundary layer flows has been illuminated by the present investigation. The calculations might have implications for biofuel cell materials production and other applications (Khan et al. [50], Eswaramoorthi et al. [51], Bhatti et al. [52]). Through graphs, we have examined the effects of different parameters on the solution of the problem to understand its physics. The impact of the Deborah number or material parameter (α1) on f1′ distribution is seen in Fig. 2. Because of the viscoelastic properties of the fluid, the relaxation time, which is related to the parameter (α1), indicates a decrease in velocity. Rheologists often use Deborah’s number (De) to describe the fluidity of materials under various flow conditions. Physically, as the elasticity and viscosity effects are in inverse proportion, increasing viscosity decreases fluid velocity. A plot of the material parameter (β1) is shown in Fig. 3. As the material parameter (β1) increases, the fluid velocity strengthens. Physically, β1 includes retardation time, which increases the velocity of fluid particles. A dimensionless velocity can be affected by a magnetic parameter (M) in Fig. 4. A significant decrease in the velocity of the flow occurs throughout the fluid domain as the magnetic parameter is strengthened. An electrically conducting fluid is subjected to the Lorentz force when a magnetic field is applied to it. Therefore, the fluid’s velocity decreases. A dimensionless velocity can be affected by a buoyancy ratio parameter (Rb) as seen in Fig. 5. A higher buoyancy ratio leads to a reduction in velocity and the momentum barrier layer becomes thinner. In light of the dynamic viscosity correlation, and also in light of the governing equations, it decreases in velocity. Deborah number/material parameter (α1) influences the temperature profile, as seen in Fig. 6. When Deborah’s number is greater, boundary layer thickness can be effective. Fig. 7 is drawn to illustrate the impacts on temperature in more detail. Material parameter (β1) comprises retardation time, which decreases temperature, and this tendency is physically significant for that reason. The effect of the mixed convection parameter on the momentum field and the other field is seen in Fig. 8. The same value causes a little drop in the thermal field, as seen in Fig. 8. From a physical standpoint, forced convection loses ground to natural convection as the mixed convection parameter increases. Fig. 9 shows how the dimensionless temperature is affected by the Brownian motion parameter. Fig. 9 confirms that when Nb rises, θ(η) also increases. Physically, raising the nanofluid temperature causes an upsurge in thermal energy, which increases the number of collisions between nanofluid particles. Fig. 10 shows that the dimensionless temperature increases when Nt, the thermophoresis parameter, is increased. Physically, a very fast flow away from the stretched sheet is created by thermophoretic force, which is itself caused by a temperature differential. This moves the fluid away from the surface that is being stretched and makes it more heated. Changing the thermal radiation parameter (Rd) on the flow temperature influences is shown in Fig. 11. As the thermal radiation parameter rises, the flow temperature grows. Physically, Thermo-radiation improves heat transmission, since thermal layer thickness grows concerning the radiation intensity and growth in Rd improves the temperature distribution. The working fluid’s temperature and thermal layer thickness are both increased when the thermal radiation parameter’s value increases. Fig. 12 also shows that a larger thermal stratification parameter (S1) results in a thicker thermal boundary layer. The temperature of the fluid dropped because, as S1 rises, physically, the temperature differential between the distant and heated surfaces drops. Lewis number effect on dimensionless concentration is seen in Fig. 13. An obvious effect of increasing Le values is a sharp drop in the nanoparticle volume fraction. Physically, a dimensionless Lewis number is the heat diffusivity divided by the mass diffusivity. Fig. 14 shows Nb influence on the concentration of nanoparticles in the boundary layer region. The figure clearly demonstrates that when the parameter and Solutal boundary layer thickness increase, the Brownian motion decreases, and the concentration changes become minor. Physically, when the Brownian motion parameter increases, the nanoparticles’ concentration drops because their random motion is accelerated. The thermophoresis parameter (Nt) effect on the concentration profile is seen in Fig. 15. As shown in Fig. 15, the concentration profile in the flow domain grows exponentially with increasing values of the thermophoresis parameter. A higher thermophoresis produces a thicker concentration boundary layer, while a higher mass transfer rate results in a thicker mass boundary layer. Accordingly, the resistance to mass diffusion increases with an increase in the thermophoresis parameter. Fig. 16 confirms the enhancement of the concentration profile by mass stratification (S2). While increasing the mass stratification (S2), a decrease in the volume fraction between the reference nanoparticles and the surface concentration is noticed. Consequently, there is a lower concentration dispersion. Fig. 17 displays the variations in motile microbe profiles vs. different values of the Lewis bioconvection number. While the bioconvection Lewis number reduces microorganism profiles. For larger levels of Lb, the microbial diffusivity drops, leading to a lower motile density. Fig. 18 shows the impact on the motile density of the variation in the constant concentration Ω of microorganisms. It was also noted that the density profile decreased as Ω increased. Figuratively, Fig. 19 confirms Peclet number Pe impact on the two-dimensionally mobile bacteria. There will be a significant reduction in microbial density as the concentration of Pe rises. By establishing this connection, heat transfer can occur through conduction as well as convection. Greater Peclet numbers indicate that convection dominates conduction for heat transfer. Fig. 20 shows how the cell motility stratification parameter S3 affects the cell motility density in nanofluids. The results demonstrated that the boundary layer thickness values of motile microorganisms decreased as the S3 value increased. The relationship between the heat transfer rate and Eckert number is seen in Fig. 21. The rate of heat transmission decreases, and Eckert’s number rises. The thermal layer is therefore thinner as a result. As the thermophoresis parameter values increase, Fig. 22 displays the characteristics of the mass transfer rate. The Sherwood number is shown to have grown. As the values of Lb increase, Fig. 23 reveals the characteristics of the motile organism’s rate of density. The density rate of motile organisms decreases as Lb grows.

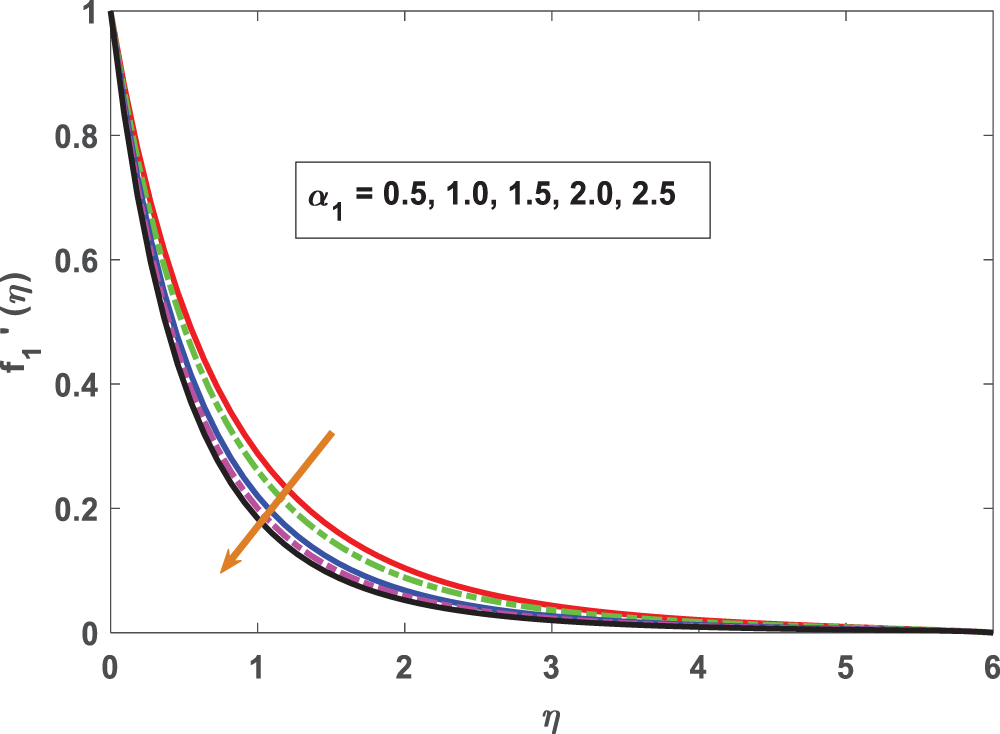
Figure 2: Profiling of velocity under Deborah number (α1)

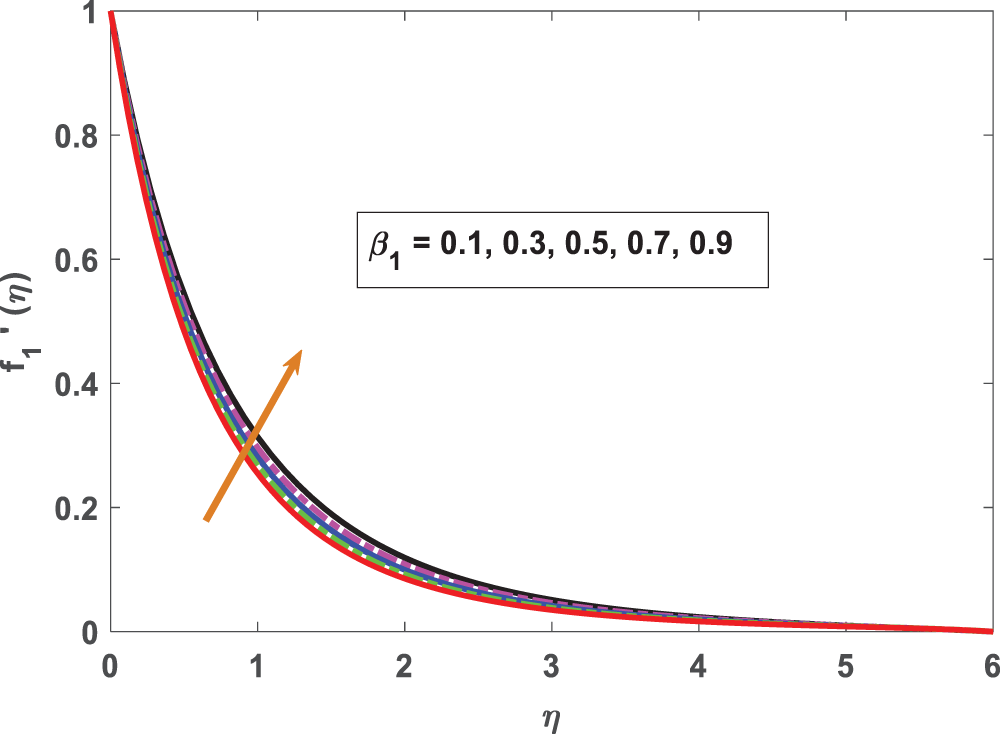
Figure 3: Profiling of velocity under material parameter (β1)

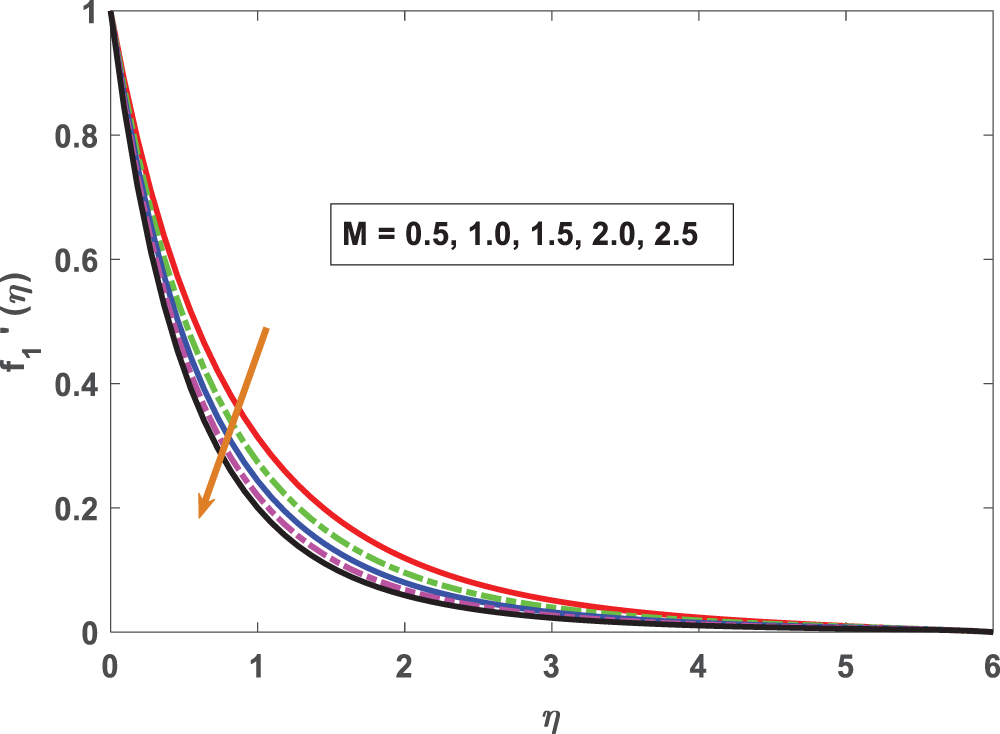
Figure 4: Profiling of velocity under magnetic parameter (M)

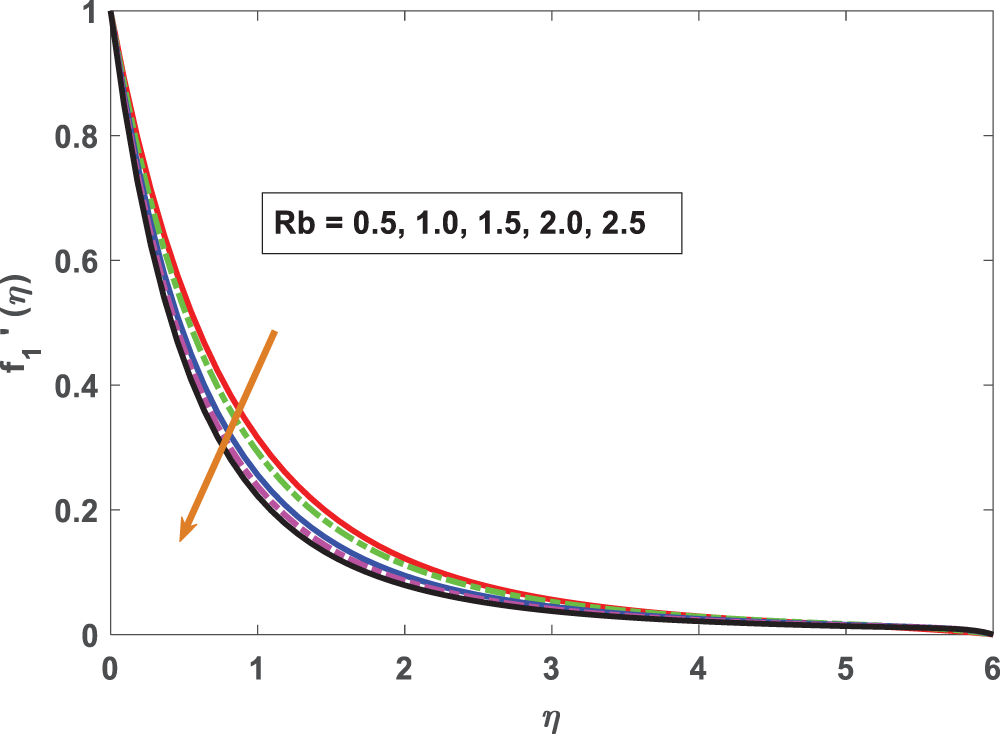
Figure 5: Profiling of velocity under buoyancy ratio parameter (Rb)

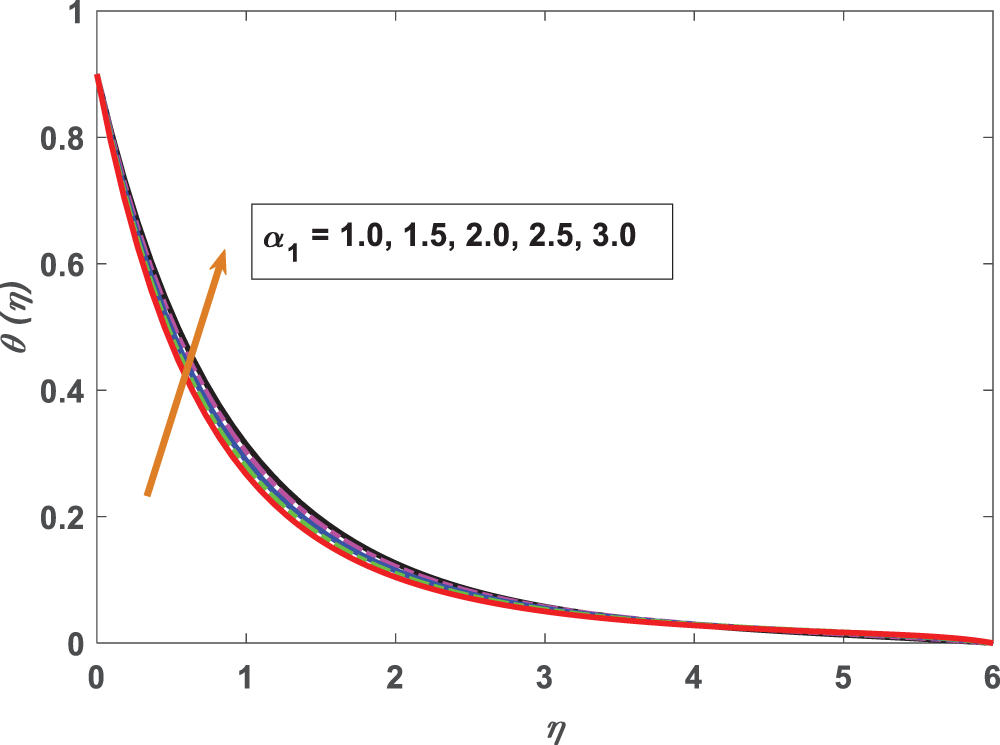
Figure 6: Profiling of temperature under Deborah number (α1)

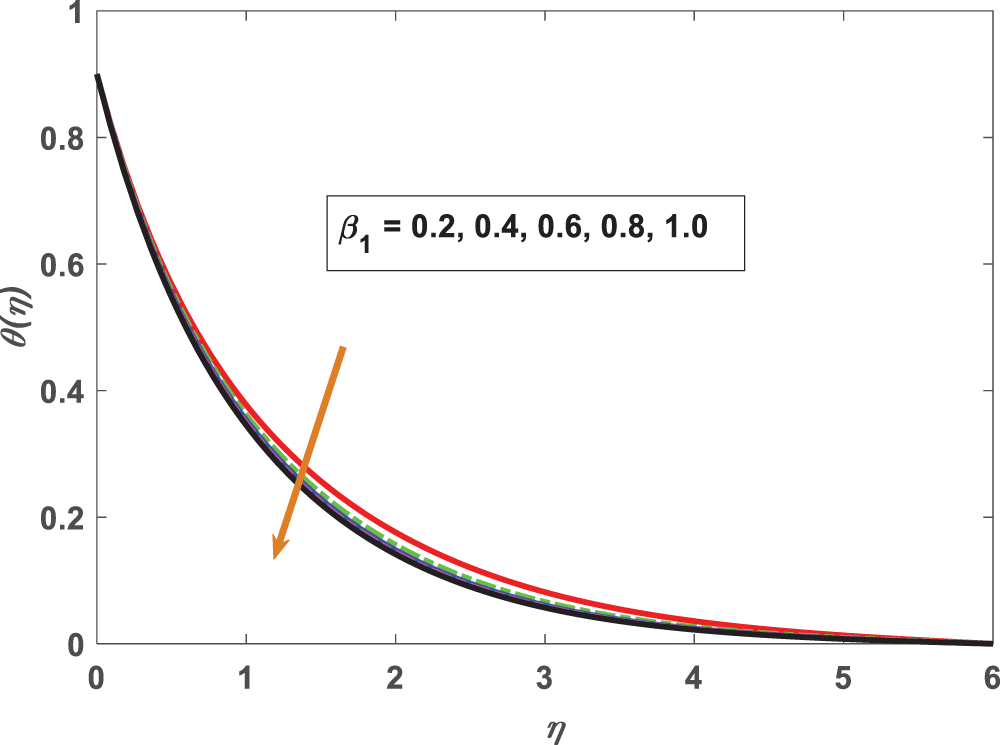
Figure 7: Profiling of temperature under material parameter (β1)

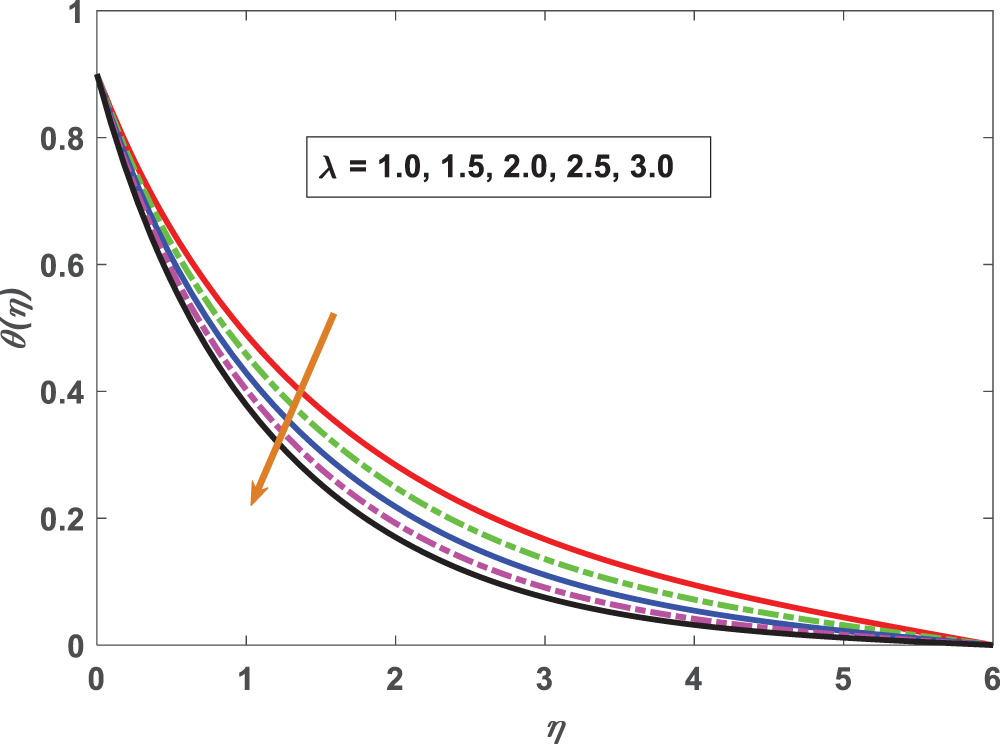
Figure 8: Profiling of temperature under mixed convection parameter (λ)

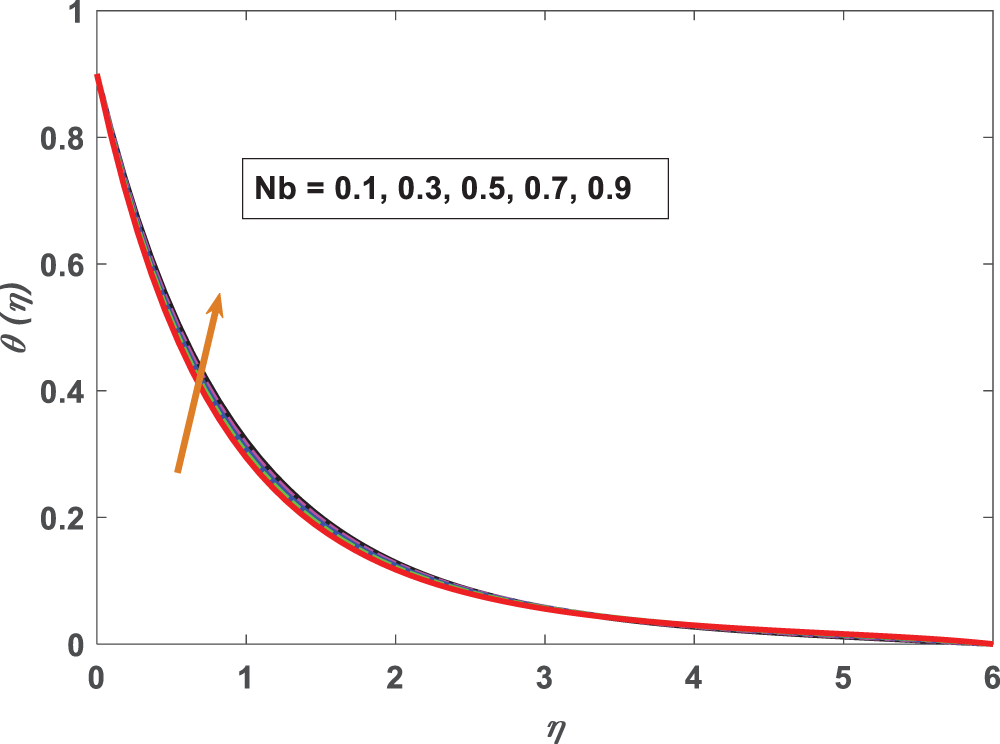
Figure 9: Profiling of temperature under Brownian motion parameter (Nb)

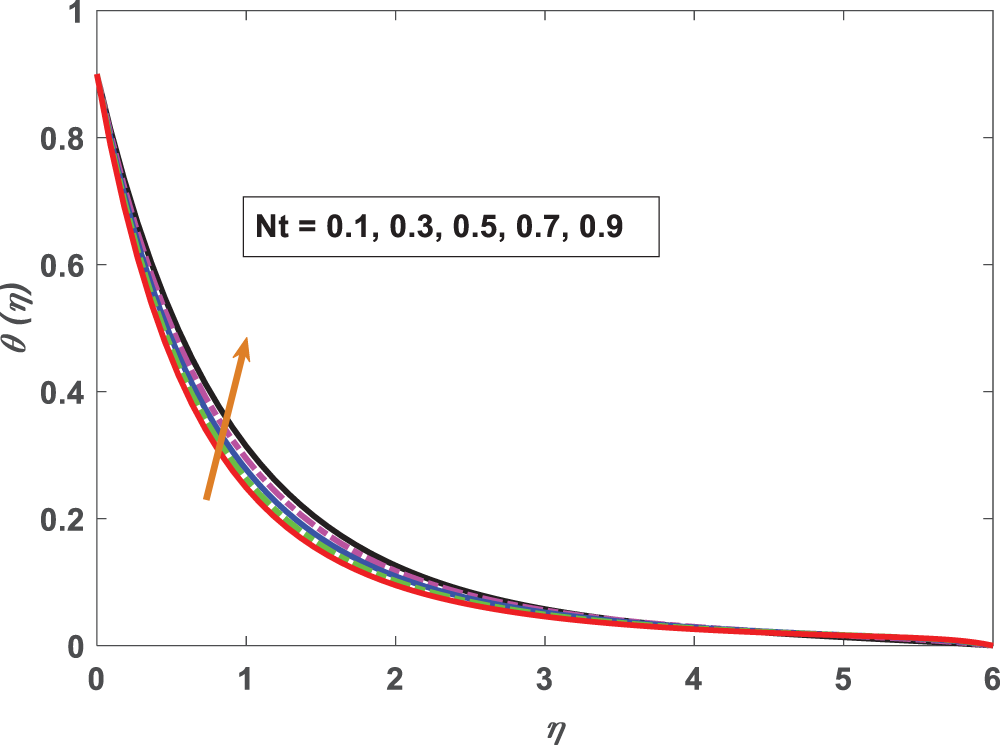
Figure 10: Profiling of temperature under Thermophoresis parameter (Nt)

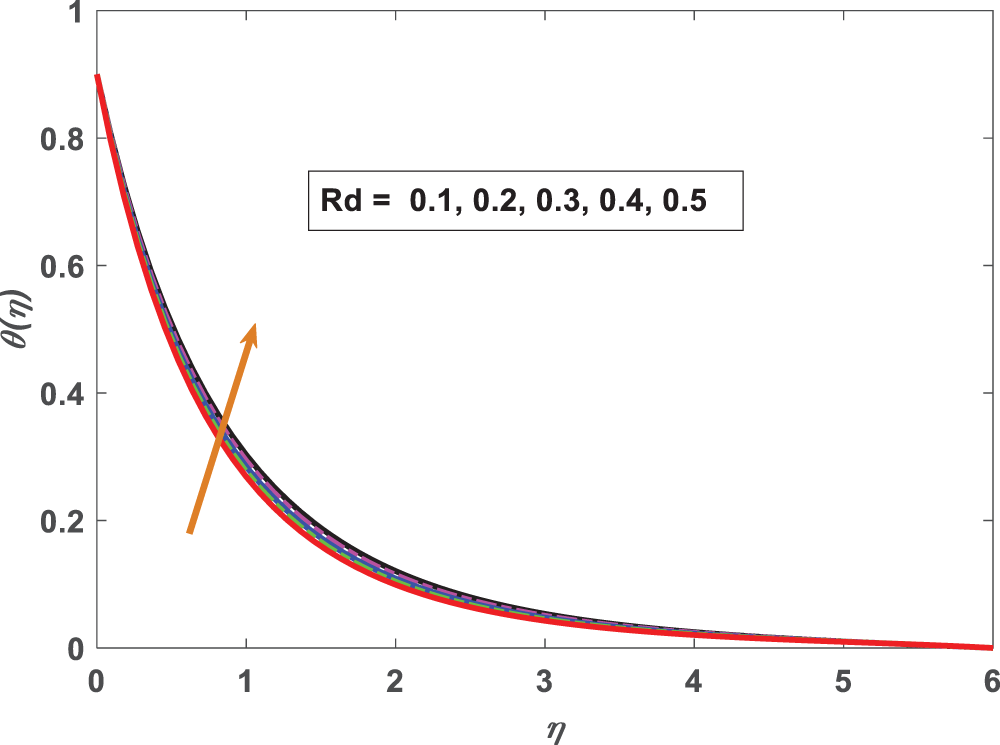
Figure 11: Profiling of temperature under radiation parameter (Rd)

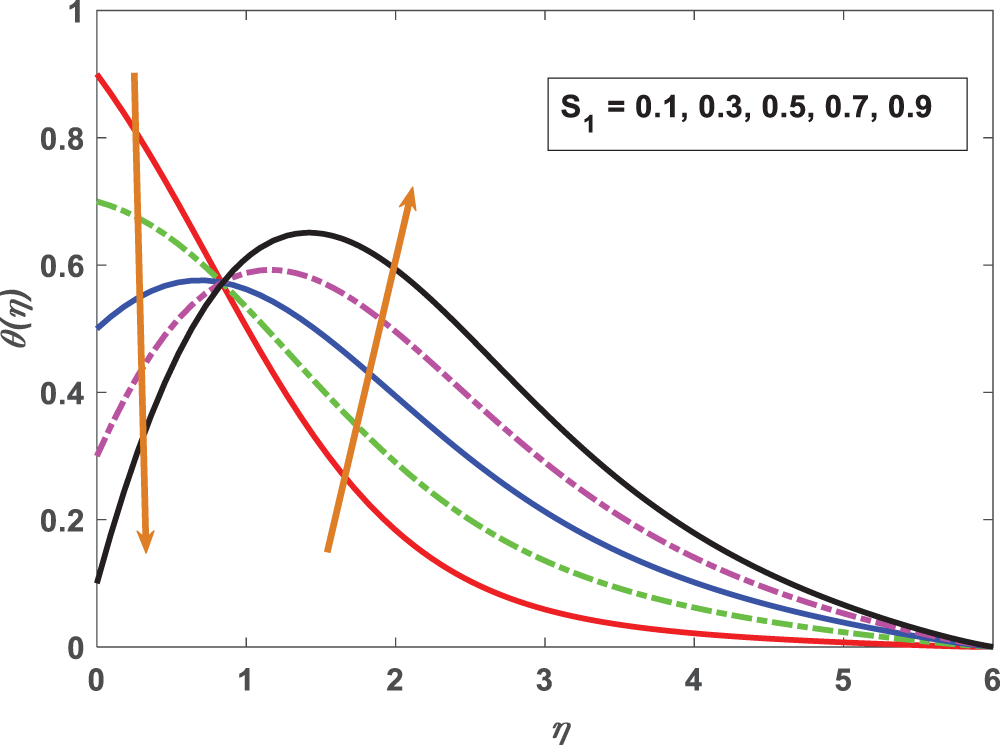
Figure 12: Profiling of temperature under thermal stratification parameter (S1)

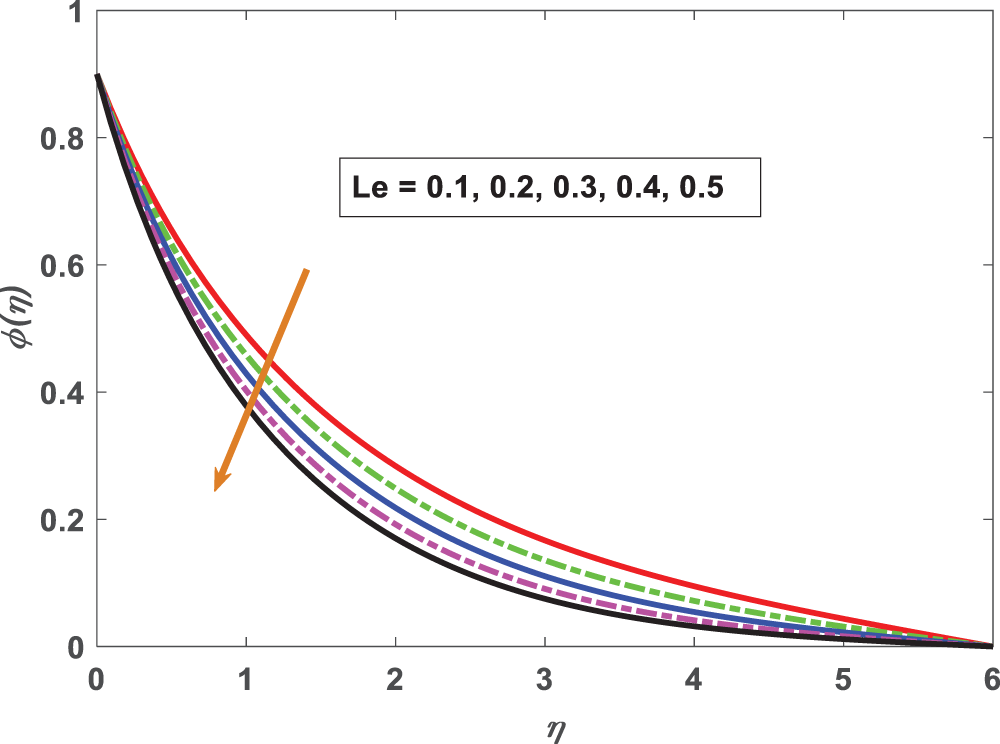
Figure 13: Profiling of concentration under Lewis parameter (Le)

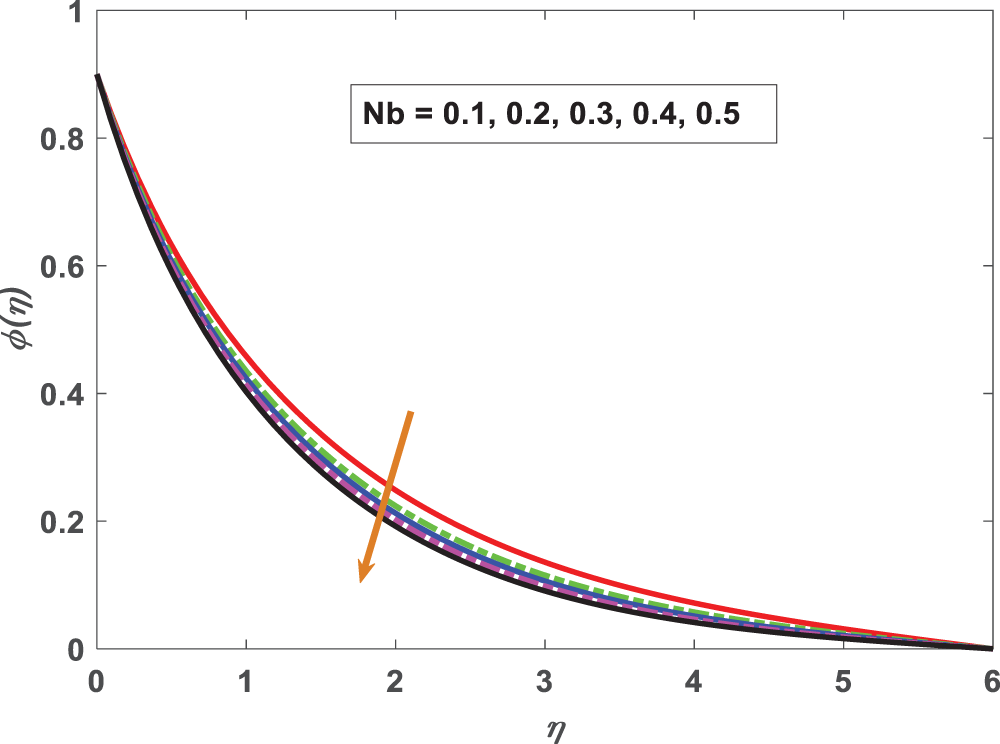
Figure 14: Profiling of concentration under Brownian motion parameter (Nb)

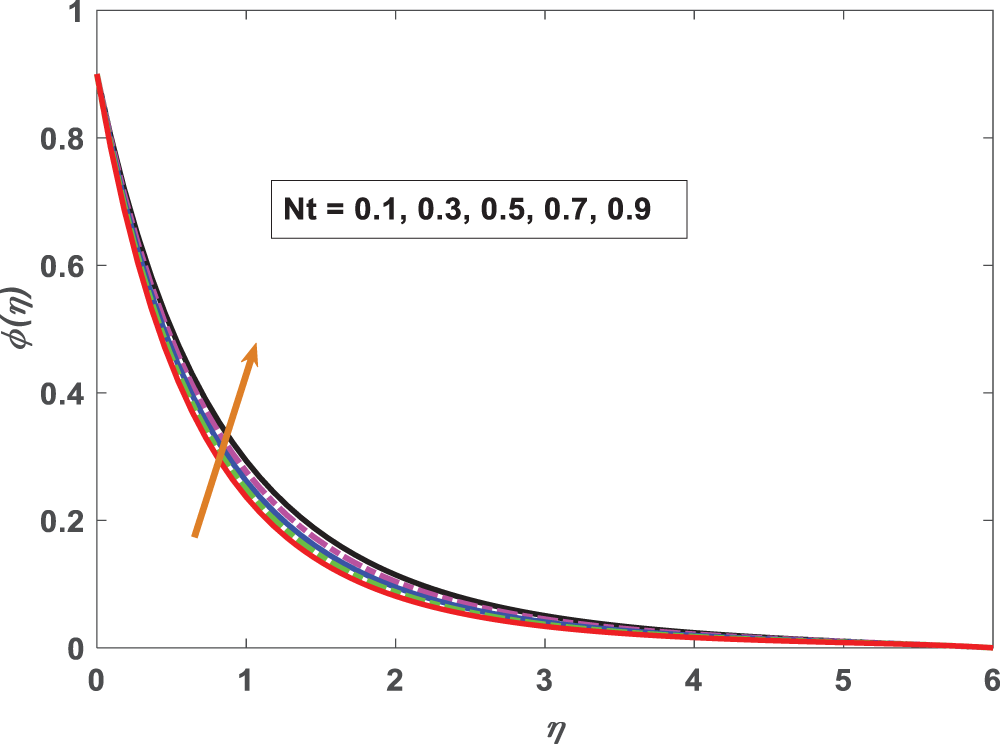
Figure 15: Profiling of concentration under Thermophoresis parameter (Nt)

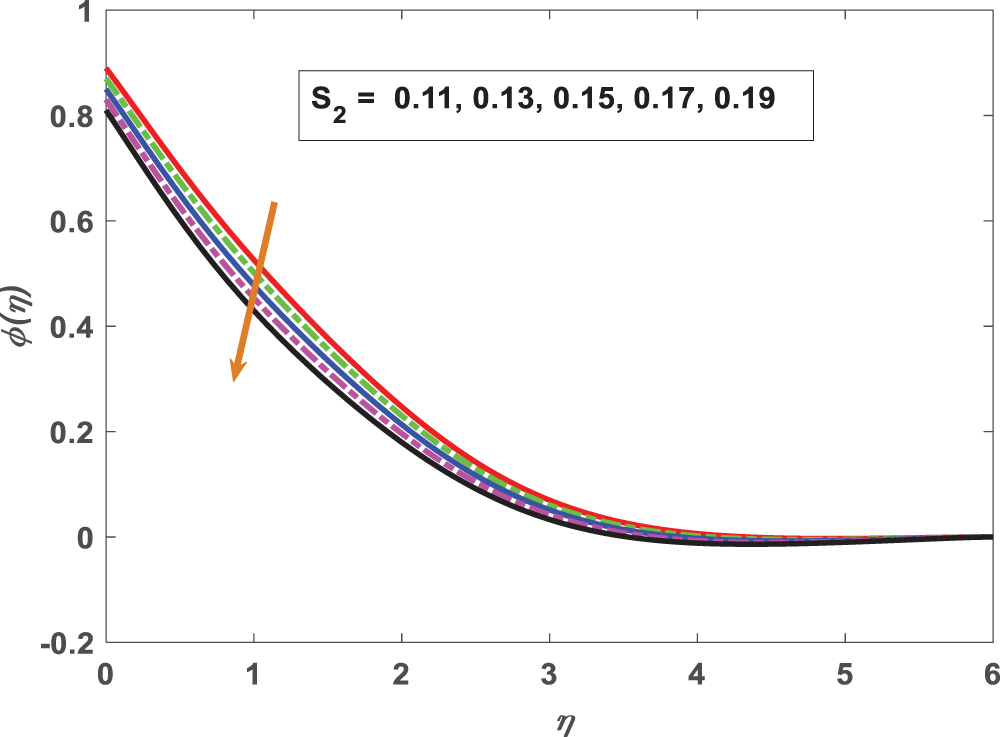
Figure 16: Profiling of concentration under mass stratification parameter (S2)

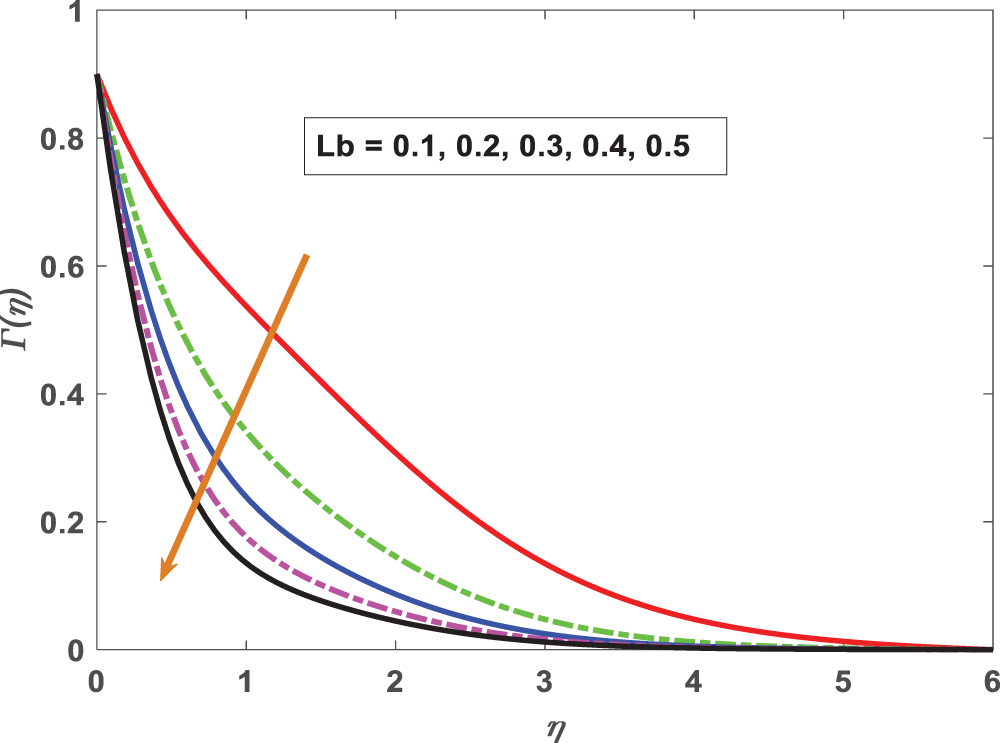
Figure 17: Profiling of motile density under bio-convective Lewis number (Lb)

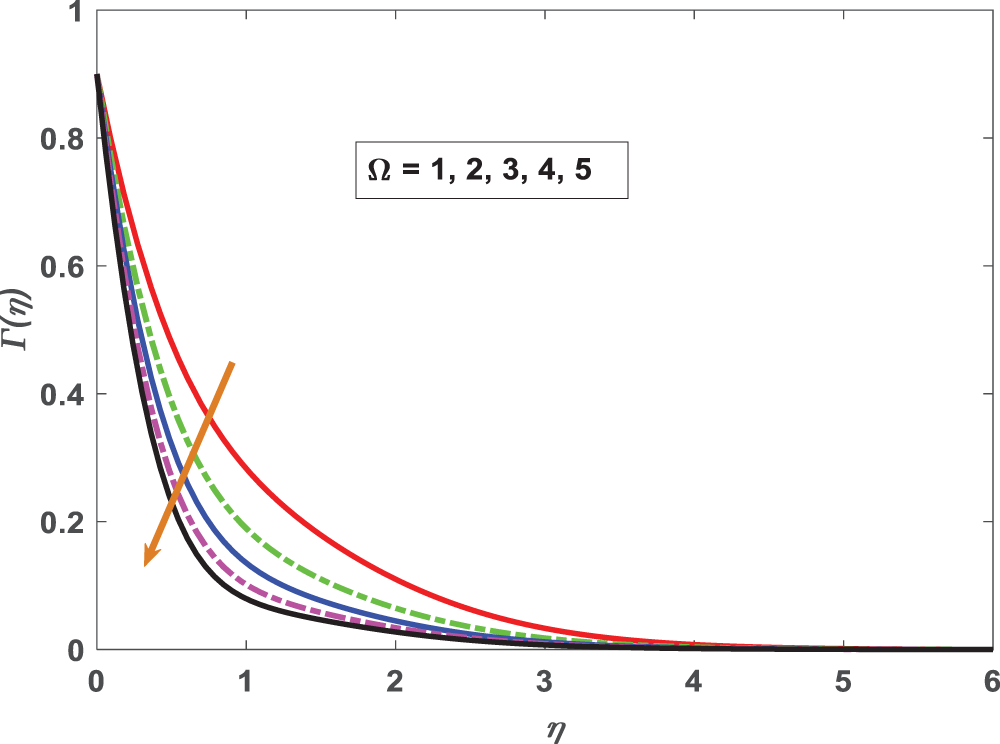
Figure 18: Profiling of motile density under Microorganisms concentration difference parameter (Ω)

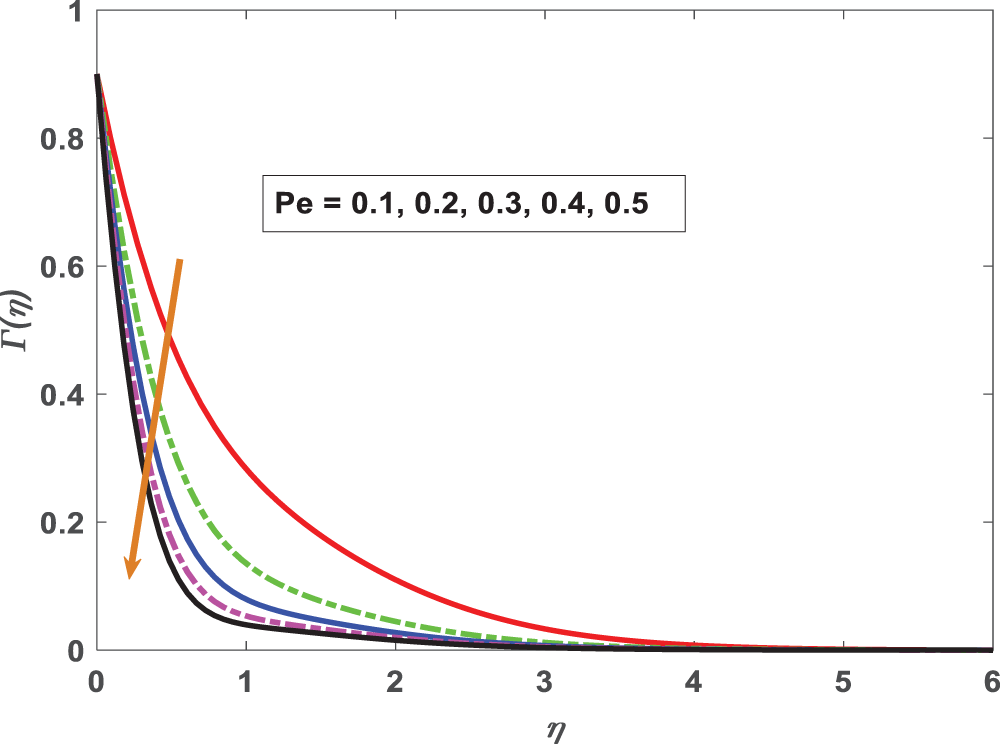
Figure 19: Profiling of motile density under Peclet number (Pe)

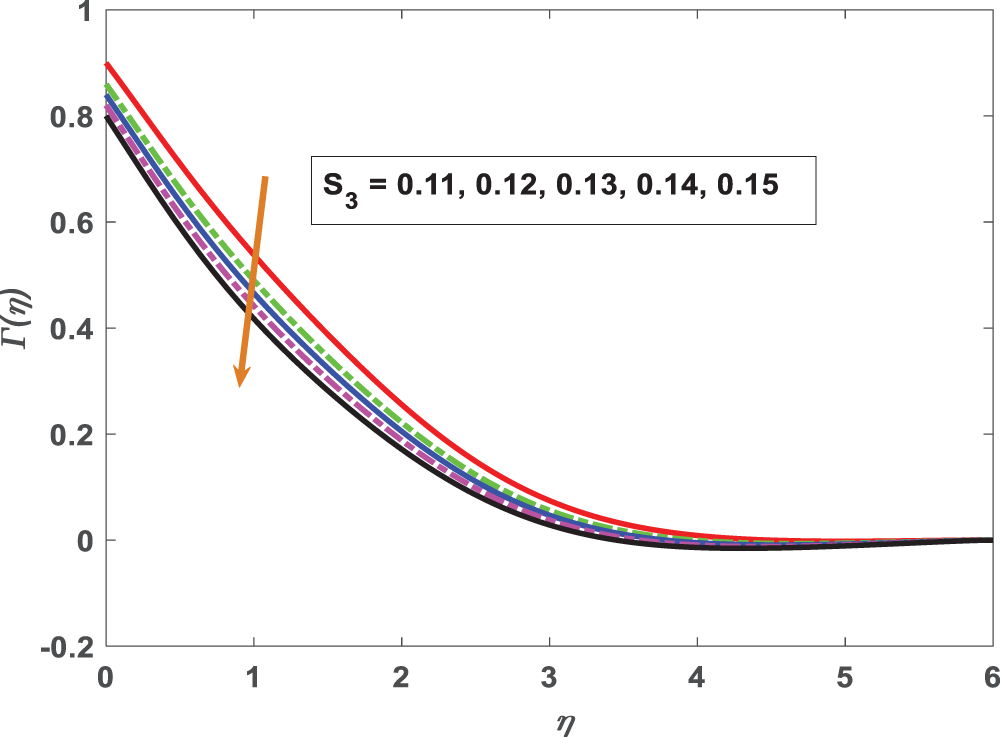
Figure 20: Profiling of motile density under Motile density stratification parameter (S3)

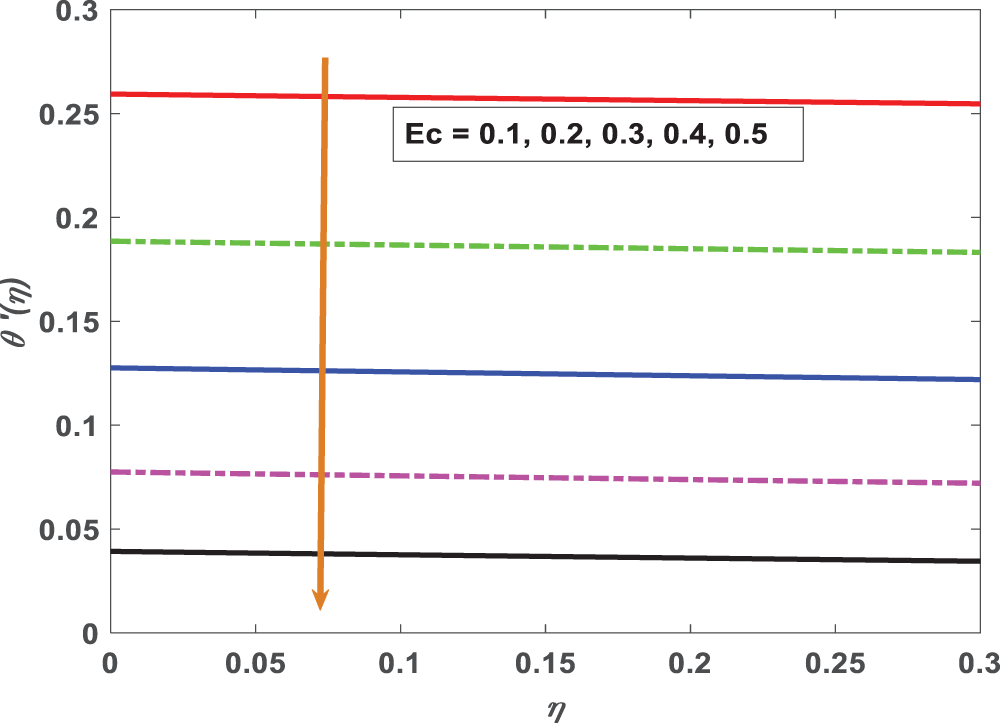
Figure 21: Nusselt number variations under Eckert number

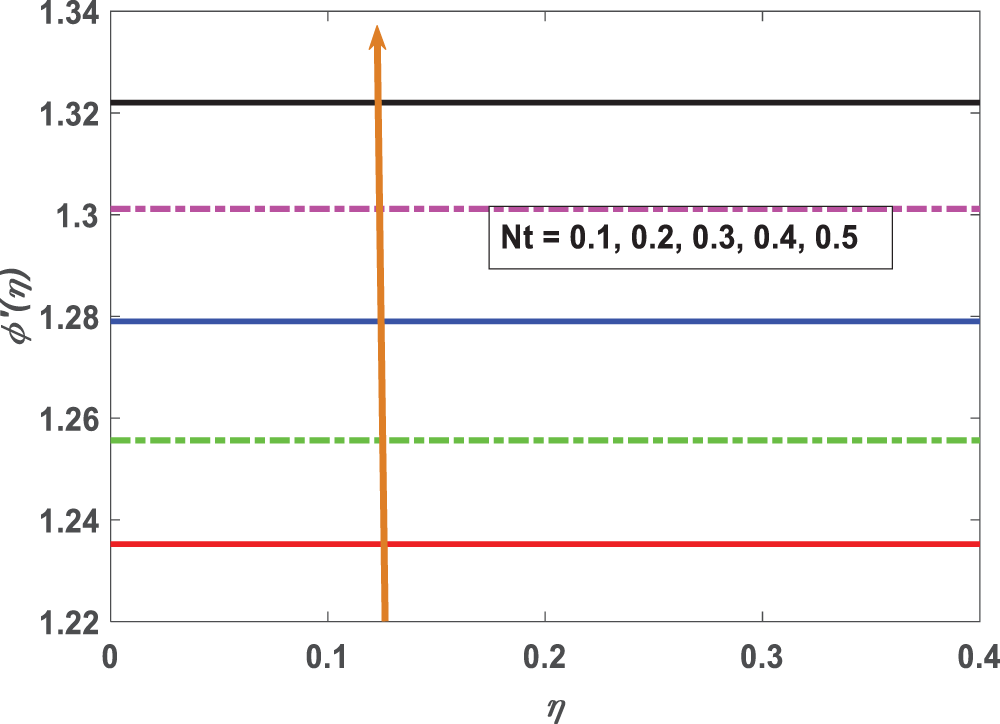
Figure 22: Sherwood number variations against Thermophoresis parameter

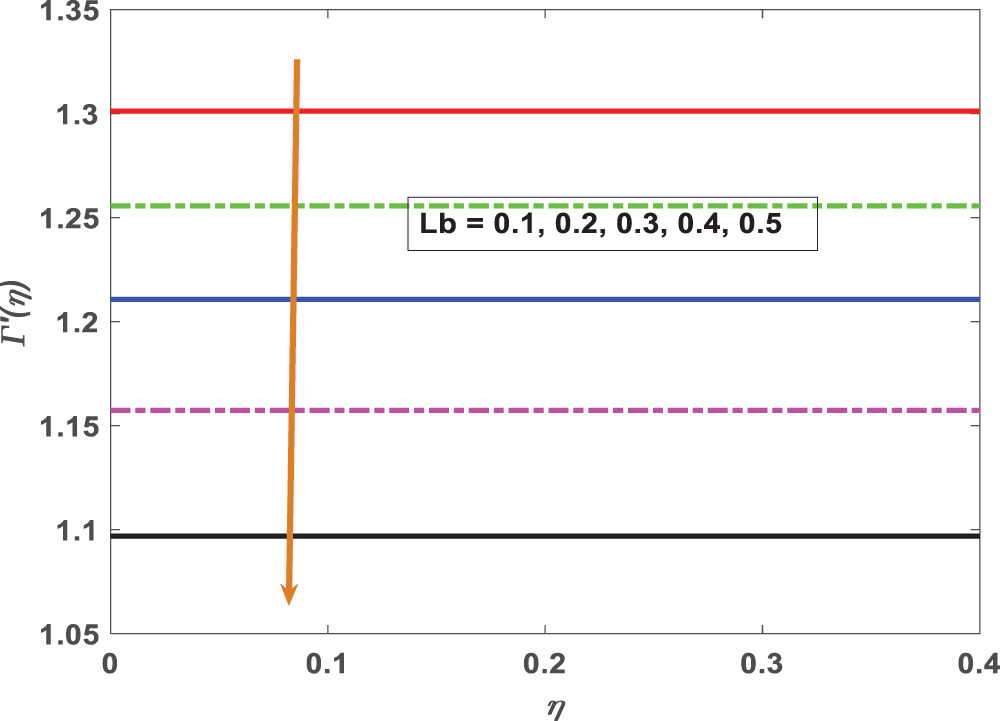
Figure 23: Motile density variations against Lewis number (Lb)

6  Conclusions and Limitations

The impact of thermal radiation and two-phase nanofluid on magnetohydrodynamic bioconvection boundary layer flows has been illuminated by the present investigation. The calculations might have implications for biofuel cell materials production.

•   Strengthening Deborah’s number slows down the fluid velocity.

•   Reinforcing material parameters, the fluid velocity strengthens.

•   A significant decrease in the velocity of the flow occurs throughout the fluid domain as the magnetic parameter is strengthened, subjected to the Lorentz force.

•   A higher buoyancy ratio leads to a reduction in velocity and the momentum barrier layer becomes thinner.

•   When Deborah’s number is greater, boundary layer thickness can be effective.

•   Material parameter comprises retardation time, which decreases fluid temperature.

•   The thermal field is lowered with mixed convection parameters.

•   Dimensionless temperature is affected by the Brownian motion parameter.

•   Raising the nanofluid temperature causes an upsurge in thermal energy, which increases the number of collisions between nanofluid particles.

•   Fluid temperature increases when Nt the thermophoresis parameter is increased.

•   As the thermal radiation parameter rises, the flow temperature grows.

•   Increasing Lewis number values is a sharp drop in the nanoparticle volume fraction. Bioconvection Lewis number reduces microorganism profiles.

•   A significant reduction in microbial density as the concentration of Peclet number rises.

Convergence region fluid flow has certain limitations:

1.    Measures of physical limits that are appropriate.

2.    Each parameter value was selected based on the applied correlations.

3.    If we ignore the thermal radiation effect −1(ρc)f∂qr∂y^1 from Eq. (3), the rest of the results are splendid agreement, is noticed.

4.    To ensure that the problem is accurate and reliable, validation is necessary.

5.    Research has been limited to settings where turbulence is severe since it hasn’t been made to account for turbulent flow during high Reynolds number settings.

6.    Accordingly, the validity of the scheme depends on specific examples, making it necessary to expand it to cover more complex fluid scenarios and behaviors.

Acknowledgement: The authors want to extend heartfelt thanks to the reviewers for their careful, unbiased and constructive suggestions, which led to this revised manuscript.

Funding Statement: U. F. -G. was supported by the Mobility Lab Foundation, a governmental organization of the Provincial Council of Araba, and the local council of Vitoria-Gasteiz. S. Noeiaghdam was supported by the Henan Academy of Sciences ( Project No. 241819246).

Author Contributions: Gurram Dharmaiah: Writing—review & editing, Writing—original draft, Validation, Software, Methodology. Jupudi Lakshmi Rama Prasad: Writing—review & editing, Validation, Methodology, Formal analysis. Chegu Ramprasad: Writing—review & editing, Validation, Software, Methodology, Formal analysis. Unai Fernandez-Gamiz: Writing—review & editing, Validation, Software, Methodology, Formal analysis. Samad Noeiaghdam: Writing—review & editing, Validation, Methodology, Formal analysis. Saeed Dinarvand: Supervision and Conceptualization. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Ethics Approval: Not applicable.

Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.

Nomenclature

References

1. Nkurikiyimfura I, Wang Y, Pan Z. Heat transfer enhancement by magnetic nanofluids: a review. Ren Sub Energy Rev. 2013;21:548–61. doi:10.1016/j.rser.2012.12.039. [Google Scholar] [CrossRef]

2. Vadasz JJ, Govender S, Peter V. Heat transfer enhancement in nano-fluids suspensions: possible mechanisms and explanations. Int J Heat Mass Transf. 2005;48(13):2673–83. doi:10.1016/j.ijheatmasstransfer.2005.01.023. [Google Scholar] [CrossRef]

3. Frey NA, Peng S, Cheng K, Sun S. Magnetic nanoparticles: synthesis, functionalization, and applications in bioimaging and magnetic energy storage. Chem Soc Rev. 2009;9(38):2532–42. doi:10.1039/B815548H. [Google Scholar] [PubMed] [CrossRef]

4. Colombo M, Carregal-Romero S, Casula MF, Gutiérrez L, Morales MP, Böhm IB, et al. Biological applications of magnetic nanoparticles. Chem Soc Rev. 2012;11(41):4306–34. doi:10.1039/C2CS15337H. [Google Scholar] [PubMed] [CrossRef]

5. Singamaneni S, Bliznyuk VN, Binek C, Tsymbal EY. Magnetic nanoparticles: recent advances in synthesis, self-assembly and applications. J Mater Chem. 2011;42(21):16819–45. doi:10.1039/C1JM11845E. [Google Scholar] [CrossRef]

6. Ghadikolaei SS, Hosseinzadeh K, Hatami M, Ganji DD, Armin M. Investigation for squeezing flow of ethylene glycol (C2H6O2) carbon nanotubes (CNTs) in rotating stretching channel with nonlinear thermal radiation. J Mol Liq. 2018;263:10–21. doi:10.1016/j.molliq.2018.04.141. [Google Scholar] [CrossRef]

7. Hamid M, Usman M, Khan ZH, Haq RU, Wang W. Numerical study of unsteady MHD flow of Williamson nanofluid in a permeable channel with heat source/sink and thermal radiation. Eur Phys J Plus. 2018;133(12):1–12. doi:10.1140/epjp/i2018-12322-5. [Google Scholar] [CrossRef]

8. Hamid M, Zubair T, Usman M, Khan ZH, Wang W. Natural convection effects on heat and mass transfer of slip flow of time-dependent Prandtl fluid. J Comput Des Eng. 2019;6(4):584–92. doi:10.1016/j.jcde.2019.03.004. [Google Scholar] [CrossRef]

9. Chamkha AJ, Abbasbandy S, Rashad AM, Vajravelu K. Radiation effects on mixed convection about a cone embedded in a porous medium filled with a nanofluid. Meccanica. 2012;48(2):275–85. doi:10.1007/s11012-012-9599-1. [Google Scholar] [CrossRef]

10. Ijaz M, Ayub M, Khan H. Entropy generation and activation energy mechanism in nonlinear radiative flow of Sisko nanofluid: rotating disk. Heliyon. 2019;5:e01863. doi:10.1016/j.heliyon.2019.e01863. [Google Scholar] [PubMed] [CrossRef]

11. Pantokratoras A. Natural convection along a vertical isothermal plate with linear and nonlinear Rosseland thermal radiation. Int J Therm Sci. 2014;84:151–7. doi:10.1016/j.ijthermalsci.2014.05.015. [Google Scholar] [CrossRef]

12. Ijaz M, Ayub M. Nonlinear convective stratified flow of Maxwell nanofluid with activation energy. Heliyon. 2019;5(1):e01121. doi:10.1016/j.heliyon.2019.e01121. [Google Scholar] [PubMed] [CrossRef]

13. Mushtaq A, Mustafa M, Hayat T, Alsaedi A. On the numerical solution of the nonlinear radiation heat transfer problem in a three-dimensional flow. Z Naturforsch. 2014;69:705–13. doi:10.5560/zna.2014-0059. [Google Scholar] [CrossRef]

14. Ijaz M, Ayub M, Zubair M, Malik MY. Numerical simulation of Joule heating and Arrhenius activation energy for nonlinear radiative flow of Casson nanofluid with Cattaneo-Christov heat flux model. Phys Scr. 2019;95(2):025401. doi:10.1088/1402-4896/ab41ac. [Google Scholar] [CrossRef]

15. Childress S, Levandowsky M, Spiegel EA. Pattern formation in a suspension of swimming microorganisms equations and stability theory. J Fluid Mech. 1975;69(3):591–613. doi:10.1017/S0022112075001577. [Google Scholar] [CrossRef]

16. Cheng CY. Combined heat and mass transfer in natural convection flow from a vertical wavy surface in a power-law fluid saturated porous medium with thermal and mass stratification. Int Commun Heat Mass Trans. 2009;36(4):351–6. doi:10.1016/j.icheatmasstransfer.2009.01.003. [Google Scholar] [CrossRef]

17. Hossain MA, Paul SC, Mandal AC. Natural convection flow along a vertical circular cone with uniform surface temperature and surface heat flux in a thermally stratified medium. Int J Numer Methods Heat Fluid Flow. 2002;12(3):290–305. doi:10.1108/09615530210422965. [Google Scholar] [CrossRef]

18. Daniel YS, Aziz ZA, Ismail Z, Salah F. Double stratification effects on unsteady electrical MHD mixed convection flow of nanofluid with viscous dissipation and Joule heating. J Appl Res Tech. 2017;15(5):464–76. doi:10.1016/j.jart.2017.05.007. [Google Scholar] [CrossRef]

19. Ibrahim W, Makinde OD. The effect of double stratification on boundary-layer flow and heat transfer of nanofluid over a vertical plate. Comput Fluids. 2013;86:433–41. doi:10.1016/j.compfluid.2013.07.029. [Google Scholar] [CrossRef]

20. Oldroyd JG. On the formulation of rheological equations of state. Proc Royal Soc Lond Ser A Math Phys Sci. 1950;200(1063):523–41. doi:10.1098/rspa.1950.0035. [Google Scholar] [CrossRef]

21. Siddiqui AM, Haroon T, Zahid M, Shahzad A. Effect of slip condition on unsteady flows of an Oldroyd-B fluid between parallel plates. World App Sci J. 2011;13(11):2282–7. [Google Scholar]

22. Jamil M, Fetecau C, Imran M. Unsteady helical flows of Oldroyd-B fluids. Comm Nonlinear Sci Num Sim. 2011;16(3):1378–86. doi:10.1016/j.cnsns.2010.07.004. [Google Scholar] [CrossRef]

23. Awad FG, Ahamed SMS, Sibanda P, Khumalo M, Dao M. The effect of thermophoresis on unsteady Oldroyd-B nanofluid flow over stretching surface. PLoS One. 2015;10(8):e0135914. doi:10.1371/journal.pone.0135914. [Google Scholar] [PubMed] [CrossRef]

24. Irfan M, Khan M, Gulzar MM, Khan WA. Chemically reactive and nonlinear radiative heat flux in mixed convection flow of Oldroyd-B nanofluid. Appl Nanosci. 2020;10(8):3133–41. doi:10.1007/s13204-019-01052-y. [Google Scholar] [CrossRef]

25. Abbas SZ, Khan WA, Waqas M, Irfan M, Asghar Z. Exploring the features for flow of Oldroyd-B liquid film subjected to rotating disk with homogeneous/heterogeneous processes. Comp Met Prog Biomed. 2020;189:105323. doi:10.1016/j.cmpb.2020.105323. [Google Scholar] [PubMed] [CrossRef]

26. Ye Z. Global regularity of the high-dimensional Oldroyd-B model in the corotational case. J Math Anal App. 2020;486(2):123867. doi:10.1016/j.jmaa.2020.123867. [Google Scholar] [CrossRef]

27. Pasha P, Nabi H, Peiravi MM, Pourfallah M, Domiri Ganji D. The application of analytical methods in the investigation effects of Magnetic parameter and Brownian motion on the fluid flow between two equal plates. Int J Eng. 2021;34:2341–50. doi:10.5829/ije.2021.34.10a.15. [Google Scholar] [CrossRef]

28. Thirupathi T, Mishra SR, Abbas MA, Bhatti MM, Abdelsalam SI. Three-dimensional nanofluid stirring with non-uniform heat source/sink through an elongated sheet. App Math Comp. 2022;421:126927. doi:10.1016/j.amc.2022.126927. [Google Scholar] [CrossRef]

29. Sheri SR, Thumma T. Heat and mass transfer effects on natural convection flow in the presence of volume fraction for copper-water nanofluid. J Nanofluids. 2016;5:220–30. doi:10.1166/jon.2016.1214. [Google Scholar] [CrossRef]

30. Khan WA, Makinde OD, Khan ZH. MHD boundary layer flow of a nanofluid containing gyrotactic microorganisms past a vertical plate with Navier slip. Int J Heat Mass Transf. 2014;74:285–91. doi:10.1016/j.ijheatmasstransfer.2014.03.026. [Google Scholar] [CrossRef]

31. Kuznetsov AV. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic microorganisms. Int Commun Heat Mass Transf. 2010;37(10):1421–5. doi:10.1016/j.icheatmasstransfer.2010.08.015. [Google Scholar] [CrossRef]

32. Elbashbeshy EMA, Asker HG. Fluid flow over a vertical stretching surface within a porous medium filled by a nanofluid containing gyrotactic microorganisms. Eur Phys J Plus. 2022;137:541. doi:10.1140/epjp/s13360-022-02682-y. [Google Scholar] [CrossRef]

33. Thumma T, Mishra SR, Swain K, Ijaz Khan M, Khan NM. Effect of dissipation energy on magnetohydrodynamic 3D stagnation point flow of micropolar nanofluid past a sinusoidal circular cylinder. Waves Random Complex Media. 2022;16:1–26. doi:10.1080/17455030.2022.2102271. [Google Scholar] [CrossRef]

34. Raza A, Thumma T, Khan SU, Boujelbene M, Boudjemline A, Chaudhry IA, et al. Thermal mechanism of carbon nanotubes with Newtonian heating and slip effects: a Prabhakar fractional model. J Ind Chem Soci. 2022;99(10):100731. doi:10.1016/j.jics.2022.100731. [Google Scholar] [CrossRef]

35. Souayeh B, Ramesh K. Numerical scrutinization of ternary nanofluid flow over an exponentially stretching sheet with gyrotactic microorganisms. Mathematics. 2023;11(4):981. doi:10.3390/math11040981. [Google Scholar] [CrossRef]

36. Haq F, Saleem M, El-Zahar ER, Gouadria S, Khan MI. Darcy-Forchheimer flow of magnetized bioconvective Williamson nanofluid with variable thermal conductivity. J Magn. 2021;26(4):378–88. doi:10.4283/JMAG.2021.26.4.378. [Google Scholar] [CrossRef]

37. Makkar V, Poply V, Sharma N. Three-dimensional magnetohydrodynamic nonNewtonian bioconvective nanofluid flow influenced by gyrotactic microorganisms over stretching sheet. Heat Transf. 2023;52:548–62. doi:10.1002/htj.22706. [Google Scholar] [CrossRef]

38. Haq F, Rahman MU, Khan MI, Sayfutdinovna Abdullaeva B, Tamam N. Computational analysis of revised Fourier and Fick’s law to investigate features of chemically reactive flow of nanofluid with microorganisms and activation energy. Int J Model Simul. 2024:1–13. doi:10.1080/02286203.2023.2301212. [Google Scholar] [CrossRef]

39. Hussain S, Haq F, Ghazwani HA, Saleem M, Hussain A. Entropy optimization in bio-convective chemically reactive flow of micropolar nanomaterial with activation energy and gyrotactic microorganisms. Case Stud Therm Eng. 2024;55:104131. doi:10.1016/j.csite.2024.104131. [Google Scholar] [CrossRef]

40. Haq F, Rahman MU, Khan MI, Abdullaeva BS, Altuijri R. Mathematical modeling and theoretical analysis of bioconvective magnetized Sutterby nanofluid flow over rotating disk with activation energy. Bionanoscience. 2023;13:1849–62. doi:10.1007/s12668-023-01166-2. [Google Scholar] [CrossRef]

41. Saleem M, Haq F, Ullah A, Ur Rahman M, Bafakeeh OT. Numerical investigation of irreversibility in bioconvective flow of Sisko nanofluid with Arrhenius energy. J Comput Biophys Chem. 2023;22:295–308. doi:10.1142/S2737416523400057. [Google Scholar] [CrossRef]

42. Dinarvand S, Behrouz M, Ahmadi S, Ghasemi P, Noeiaghdam S, Fernandez-Gamiz U. Mixed convection of thermomicropolar AgNPs-GrNPs nanofluid: an application of mass-based hybrid nanofluid model. Case Stud Therm Eng. 2023;49:103224. doi:10.1016/j.csite.2023.103224. [Google Scholar] [CrossRef]

43. Saeed A, Shah RA, Khan MS, Gamiz UF, Fwaz MZB, Noeiaghdam S, et al. Theoretical analysis of unsteady squeezing nanofluid flow with physical properties. Math Biosci Eng. 2022;19(10):10176–91. doi:10.3934/mbe.2022477. [Google Scholar] [PubMed] [CrossRef]

44. Sharma BK, Sharma P, Mishra NK, Noeiaghdam S, Fernandez-Gamiz U. Bayesian regularization networks for micropolar ternary hybrid nanofluid flow of blood with homogeneous and heterogeneous reactions: entropy generation optimization. Alex Eng J. 2023;77:127–48. doi:10.1016/j.aej.2023.06.080. [Google Scholar] [CrossRef]

45. Sharma M, Sharma BK, Khanduri U, Mishra NK, Noeiaghdam S, Fernandez-Gamiz U. Optimization of heat transfer nanofluid blood flow through a stenosed artery in the presence of Hall effect and hematocrit dependent viscosity. Case Studies Therm Eng. 2023;47:103075. doi:10.1016/j.csite.2023.103075. [Google Scholar] [CrossRef]

46. Khan MS, Mei S, Shabnam, Fernandez-Gamiz U, Noeiaghdam S, Khan A. Numerical simulation of a time-dependent electroviscous and hybrid nanofluid with darcy-forchheimer effect between squeezing plates. Nanomater. 2022;12:876. doi:10.3390/nano12050876. [Google Scholar] [PubMed] [CrossRef]

47. Elanchezhian E, Nirmalkumar R, Balamurugan M, Mohana K, Prabu KM, Viloria A. Heat and mass transmission of an Oldroyd-B nanofluid flow through a stratified medium with swimming of motile gyrotactic microorganisms and nanoparticles. J Therm Anal Calorim. 2020;141:2613–23. doi:10.1007/s10973-020-09847-w. [Google Scholar] [CrossRef]

48. Khan WA, Pop I. Boundary-layer flow of a nanofluid past a stretching sheet. Int J Heat Mass Transf. 2010;53:2477–83. doi:10.1016/j.ijheatmasstransfer.2010.01.032. [Google Scholar] [CrossRef]

49. Makinde OD, Aziz A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int J Therm Sci. 2011;50:1326–32. doi:10.1016/j.ijthermalsci.2011.02.019. [Google Scholar] [CrossRef]

50. Khan MI, Zeeshan A, Ellahi R, Bhatti MM. Advanced computational framework to analyze the stability of non-newtonian fluid flow through a wedge with non-linear thermal radiation and chemical reactions. Mathematics. 2024;12:1420. doi:10.3390/math12101420. [Google Scholar] [CrossRef]

51. Eswaramoorthi S, Divya S, Thamaraikannan N, Roopadevi B, Loganathan K. Passive control of bio-convective flow on Eyring-Powell nanofluid over a slippery surface with activation energy and magnetic impact. Part Diff Equa Appl Mathe. 2024;11:100884. doi:10.1016/j.padiff.2024.100884. [Google Scholar] [CrossRef]

52. Bhatti MM, Abbas MA, Muhammad S. Optimizing fluid flow efficiency: third-grade hybrid nanofluid flow with electro-magneto-hydrodynamics in confined vertical spaces. In: Nanofluids. Elsevier; 2024. p. 243–75. doi:10.1016/B978-0-443-13625-2.00012-7. [Google Scholar] [CrossRef]