Hybrid Deep Learning Enabled Load Prediction for Energy Storage Systems

1  Introduction

With an increased number of industries and rapid development of population, electricity grids become a complex process for managing the electricity demand for industrial and household purposes [1]. The increasing demand for electricity at certain times results in number of challenges such as failure of transformers, short circuits. To resolve this problem of communication of electrical energy through conventional grids, it is essential to forecast the consumption pattern of the customer to efficiently transport the electricity [2]. A smart grid (SG) could reasonably forecast the electricity demand and thus transfer the electrical energy based on the forecasted demands [3]. A SG through its smart prediction and sensing could resolve various problems of the conventional grids namely reduction of power usage, demand forecasting, reduce the risk of short circuits thus saving the loss of properties and lives [4]. SG has different stakeholders and it is linked to many other smart regions like smart buildings, smart vehicles, smart cities, smart power plants, and so on. In smart grid environments, there are several possibilities to save the energy cost of smart homes that are advanced from traditional homes by adapting three mechanisms, that is home automation, internal networks, and intelligent controls [5]. For instance, dynamic electricity prices are employed for reducing energy costs. It is significant to effectively handle the energy storage system (ESS). The ESS provides added value to enhance supply reliability and power quality [6]. With this regard, we consider need to forecast the ESS charge and energy consumption. Fig. 1 illustrates the process of ESS.

Figure 1: Energy storage systems

Despite the urgency and importance of making a transition from renewable energy (RE) to the smart grids, still it remains a challenge for developing an efficient and effective short-term load prediction because of this uncertainty, complexity, and variability of the RE resource [7]. Still, thorough information mining and data cleaning are inadequate for present prediction model in modelling future short-term load as noise could be hard to remove. Furthermore, uncertainty still exists and could not be explained well in machine learning (ML)-based prediction method, particularly for determining and parameter fine-tuning [8].

In addition to prediction precision, the robustness is often neglected in present research. The expansion of novel methods and advanced technologies with artificial intelligence to manage problems in the smart grid is indispensable. Especially, energy storage systems, distributed generation resources, and advanced control/operation are tackled in the SG. Generally, emerging an efficient and effective short-term load prediction method using higher accuracy and strength becomes a topmost priority for urban sustainability growth [9]. Artificial Intelligence (AI) is effectively employed for solving several industrial issues like neural networks (NN), fuzzy logic control, evolutionary computation, hybrid intelligent system, and so on. In recent times, deep learning (DL) network has gained considerable interest since they are capable of managing nonlinear problem [10].

This study develops an improved whale optimization with deep learning enabled load prediction (IWO-DLELP) scheme for ESS in smart grid platforms. The proposed IWO-DLELP model initially undergoes pre-processing in two stages namely min-max normalization and feature selection. Next, partition clustering approach is applied for the decomposition of data into distinct clusters with respect to distance and objective functions. In addition, IWO with bidirectional gated recurrent unit (BiGRU) model is employed to the prediction of load and the hyperparameters are tuned by the use of IWO algorithm. The simulation analysis of the IWO-DLELP model is performed and the outcomes are investigated under several aspects.

2  Related Works

Hong et al. [11] projected the short-term residential load forecasting (LF) structure that creates utilize of Spatio-temporal correlation present from appliance load data with DL. Several time series were conducted from the structure for describing consumed power performances and its internal Spatio-temporal connection. And this approach dependent upon deep neural network (DNN) and iterative ResBlock was presented for learning the correlation amongst distinct consumed power actions to short-term load forecasting (STLF). In [12], a DL approach was established for forecasting the current load accurately. The researchers presented a method that is dependent upon selective, extracting, and classifier of historic information. Grey Correlation based random forest (RF) and Mutual Information (MI) was carried out for feature selection (FS) and kernel principal component analysis (KPCA) was utilized to feature extracted and improved convolution neural network (CNN) was utilized to classifier.

Usman et al. [13] presented a DL based algorithm to forecast price and demand on big data utilizing deeper long short term memory (LSTM). Because of adaptive and automated feature learning of DNN, process of big data has simpler with LSTM as related to completely data driven techniques. The presented method was estimated utilizing a famous real electricity market information. In [14], a Bayesian DL was utilized for resolving this difficult problem. Especially, a novel multitasks probabilistic load forecasting (PLF) structure dependent upon Bayesian DL was presented for quantifying the shared uncertainty across various customer groups but accounting for its variances. Moreover, a clustering based pooling approach was planned for increasing the data diversity and volume of the structure.

In [15], a fast and accurate STLF technique was presented. The abstractive feature in the historical information was removed utilizing modified mutual information (MMI) approach. The factored conditional RBM (FCRBM) was allowed using learned for predicting the electrical load. At last, the presented genetic wind driven optimization (GWDO) technique was utilized for optimizing the efficiency. Syed et al. [16] presented a new hybrid clustering based DL technique to STLF at the distributing transformer level with improved scalability. It examines the gain from trained timeand the efficiency with respect to accuracy if clustering based DL modeling was utilized to STLF. A k-Medoid based technique was utilized to cluster but the predict methods were created for various clusters of load profiles. In [17], STLF and mid-term LF (MTLF) are presented utilizing smart-metered data developed in real-life distributing grid with distinct typical and ML approaches. Data pre-processed was complete for transforming the raw data into suitable format by extracting the outliers existing from the data sets. The effective meteorological variable attained with correlation analysis together with past loaded was utilized for training the LF method.

3  The Proposed Model

In this study, a new IWO-DLELP algoithm has been presented to effectually forecast the electric load in SG environment for designing proficient ESS. The proposed IWO-DLELP model encompasses pre-processing, partition clustering, BiGRU based prediction, and IWO based hyper parameter tuning. For optimal tuning of the hyperparameters involved in the BiGRU, the IWO algorithm is utilized and it results in enhanced predictive performance. Fig. 2 depicts the working process of IWO-DLELP technique.

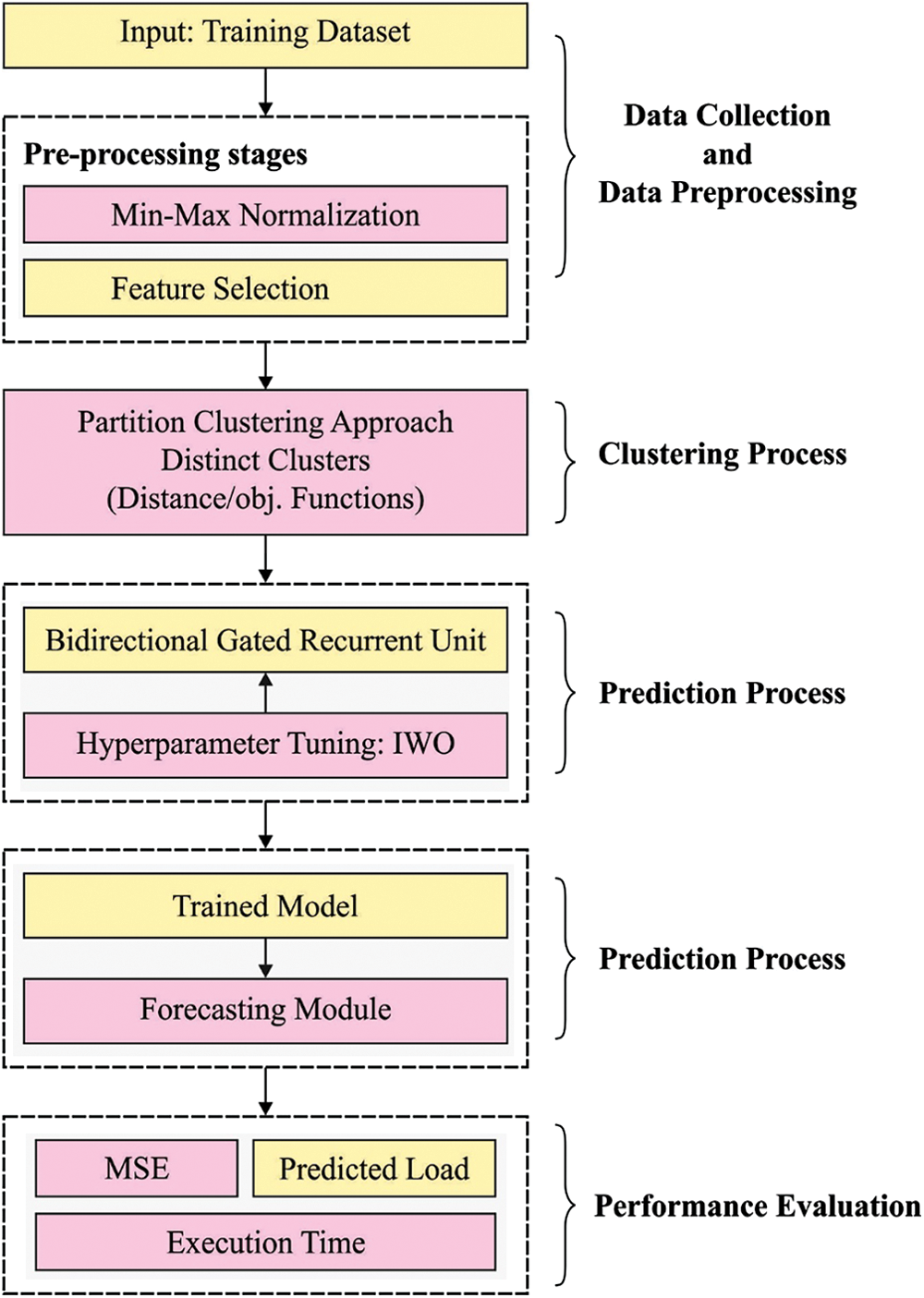
Figure 2: Overall process of IWO-DLELP technique

3.1 Data Pre-processing

Initially, the input dataset is pre-processed in two stages such as min-max normalization and feature selection. For incorporating the non-distorting scaler, mini-max normalization scale is utilized as defined in Eq. (1):

am′=c+(am−min(a))(q−p)(max(a)−min(a))(1)

where am′ and am indicates new and actual attribute values, min(a) represents least value, and [p, q] is the scaling range. In order to elect optimal features, feature importance score gets determined by the use of permutation feature importance approaches. In addition, a top-down search enabled model named Sequential Backward Search (SBS) approach is applied for addressing the multi-collinearity among distinct features in contrast to individual feature technique [18].

3.2 Partition Clustering

At this stage, the decomposition of input data into different set of clusters was carried out using the partition clustering approach [18].

Partitional clustering methodology attempts to decompose the data (Rodriguez et al., 2019) according to an objective and distance function and it is utilized for measuring the quality of cluster attained whereas, distance function is utilized for identifying the similarity amongst data objects. An arithmetical explanation of the search problem is assumed that D characterizes the whole dataset, n denotes the data object number, and d indicates the feature number, that is, D ={x1, x2, . . . , xn}. Partitional clustering model tries to detect the optimal set of centers C=C1, C2, …, CK that partition the data set D into K disjoint cluster.

F=1n∑i=1n min d(Cj,xi)(2)

Whereas Cj indicates class j and d(C, x) corresponding to the squared Euclidean distance among the point xi and the center of class Cj. SI method uses the objective function (2) to estimate the quality of solution.

3.3 BiGRU Based Load Prediction Model

The clustered data are processed by the BiGRU model to estimate the electricity load in the SG environment. The central component of gated recurrent neural network (GRNN) is the gated recurrent unit (GRU) that is a different from existing popular long- and short-term memory networks [19]. The iteration equation is as follows:

{ztσ(ωzSt+λzht−1+bz)rtσ(ωrSt+λrht−1+br)h~t tanh(ωhSt+rt⊗(λhht−1)+bh),ht(l−zt)⊗ht−1+zt⊗h~t(3)

where ⊗ refers to the cross product function. Reset threshold rt and upgrade threshold zt control the data upgrade of all the hidden states. ω∗ and λ∗ signifies the co-efficient matrices. b∗ implies the bias vector that is exploited for adaptably selecting and removing historical data which generates the existing semantics. BiGRU was utilized for extracting the condataual semantic data feature of data. The way one GRU has positive order way of the input order, and the other is reverse order way of the input order. If the feature extracting was executed on the input order, the GRUs from the 2 ways could not share the state. The state alteration rules of GRU follow the transition occurrence amongst the comparable states. But, at the similar moments, the output results of GRUs from the 2 ways were spliced as resultant of total BiGRU layer. This not only assumes the above semantic data, along with assumes the subsequent semantic data as follows:

ei=χaT tanh (ωahi+b),(4)

where hi refers to the hidden state outcome ωa signifies the arbitrary initialized weight matrix, χa stands for the arbitrary initialized vector, and b represents the offset vector. Afterward, compute the weighted score θ as follows:

θ=exp (ei)∑k=1L exp (eik).(5)

Based on Eq. (6), the resultant vector ci weight by dynamic adaptive weighted as:

ci=∑j=1Lθ⋅hj.(6)

It is obvious that the attention model relates the target matrix with weighted matrix from the NN with a perception functions. Afterward, utilize the softmax function for regularizing it for obtaining the probability distribution.

3.4 IWO Based Hyperparameter Tuning

For ideal tuning of the hyper parameter involved in the BiGRU model, the IWO algorithm is utilized [20]. It employs two methods for exploration: the initial diversification technique chooses an arbitrary whale x→rand(t) from the present swarm to be the prey as follows:

a=2−t(2/Maxiteration);A=2ar−a;C=2r(7)

D→=|C⋅X→rand(t)−X→(t)|(8)

X→(t+1)=X→rand(t)−A⋅D→(9)

Whereas r denotes an arbitrary value, r indicates the present iteration amount, Max Iteration signifies the maximal amount of iterations, a denotes a variable that has a reducing value; || signifies the component-wise absolute value, D→ shows the distance among present swarm member X→(t) and the arbitrary whale x→rand(t),C indicates a controlling coefficient, and (⋅) shows an component-wise multiplication:

D→=|C⋅X∗⟶(t)−X→(t)|(10)

X→(t+1)=X∗⟶(t)−A⋅D→(11)

Whereas x∗⟶(t) indicates the optimum solution at iteration r and the parameter C,A are provided. WOA selects among the two divergence methodologies according to the accurate value of A variable. For the intensification stage, WOA considering the optimal solution X∗⟶(t) to be the prey and designs a spiral formula among the present whale x→(t):

D→=|X∗⟶(t)−X→(t)|(12)

X→(t+1)=D→⋅ebl⋅ cos (2πl)+X∗⟶(t)(13)

Whereas t denotes number of iterations, D→ indicates the distance among present swarm member and the optimal solution, b denotes a constant and l denotes an arbitrary value in the within [−1, 1]. WOA selects among the exploration and exploitation stages arbitrarily based on the value of p variable that has a value in the range.

x¯(t+1)={X∗⟶(t)−A⋅D→if p<0.5D→⋅ebl⋅cos⁡(2πl)+X∗⟶(t)if p≥0.5(14)

where p denotes an arbitrary value. Alternating the two stages ensures the balance among diversification and intensification methods, applying all the 50% of the time. Generally, the operation and structure of WOA are simpler that facilitate its improvement.

To optimize the efficiency of the conventional algorithm, the IWO approach is derived by the use of levy flight (LF) concept. LF was firstly established by the French mathematician in 1937 named Paul Levy [21].

Levy(β) ∼u=t−1−β, 0<β≤2(15)

β indicates Levy index for altering the stability. The Levy arbitrary amount is evaluated by:

Levy(β)∼φ×μ|v|1/β(16)

In which μ & v indicates regular distribution, Γ shows standard Gamma function, β=1.5, & φ as follows:

φ=[Γ(1+β)×sin⁡(π×β2)Γ((1+β2)×β×2β−12) ]1β.(17)

For gaining a tradeoff amongst the exploitation and exploration capacities of metaheuristic model, LF approach is employed to upgrade searching agent position as follows:

Xilevy=Xi+r⊕levy(β)(18)

In which Xilevy indicates position of i th searching agent Xi after that upgrading and r indicate arbitrary vector in zero and one ⊕ designates dot product. The IWO algorithm computes an objective function with the minimization of mean square error (MSE), as defined in Eq. (19):

MSE=∑Ni|yi−y^i|2N(19)

where y states the number of rounds, yi indicates the experimental value, and y^i symbolizes forecasted values, correspondingly.

4  Experimental Validation

The experimental analysis of the IWO-DLELP method is performed using the historical hourly load dataset of 3 USA power grids, collected from openly accessible PJM electricity market. The three power grids are formula electric (FE) grid, Dayton grid, and East Kentucky Power Cooperative (EKPC) grid. The proposed is simulated using Python tool.

Table 1 and Fig. 3 showcases the predictive outcomes of the IWO-DLELP model with existing models such as mutual information-based artificial neural network (MI-ANN), bi-level, ANN-based accurate and fast converging (AFC-ANN), and factored conditional restricted Boltzmann machine (FCRBM) under distinct hours on FE grid [22]. The experiment value indicates that the IWO-DLELP model has accomplished effectual results with the least difference among the actual and predicted values. For instance, on hour 1 with actual load of 671.8923 kW, the IWO-DLELP technique has obtained predicted value of 670.3248 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have attained predicted values of 670.0814, 684.6426, 646.4398, and 652.2836 kW respectively. Besides, on hour 10 with actual load of 717.9577 kW, the IWO-DLELP technique has reached predicted value of 714.9781 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have attained predicted values of 714.5973, 705.7591, 698.4807, and 720.5594 kW respectively.

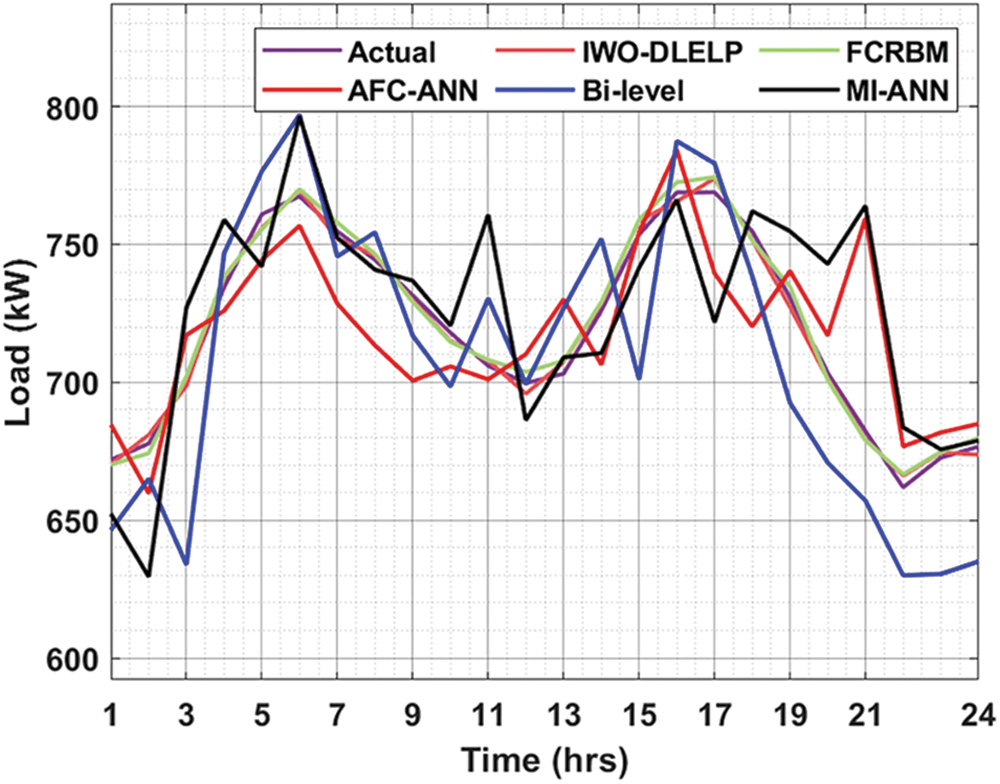
Figure 3: Actual and predicted values of IWO-DLELP model on FE grid

Table 2 and Fig. 4 demonstrates the overall predictive results of the IWO-DLELP model with recent techniques under diverse hours on Dayton grid. The results reported that the IWO-DLELP model has attained proficient results with the minimal variation amongst the actual and predicted values. For instance, on hour 1 with actual load of 175.3224 kW, the IWO-DLELP technique has gained predicted value of 172.5558 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have achieved values of 178.5829, 168.5829, 171.5829, and 169.8923 kW respectively. In addition, on hour 10 with actual load of 215.6234 kW, the IWO-DLELP technique has attained predicted value of 714.9781 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have provided predicted values of 215.9234, 217.4214, 216.4214, and 222.9577 kW respectively.

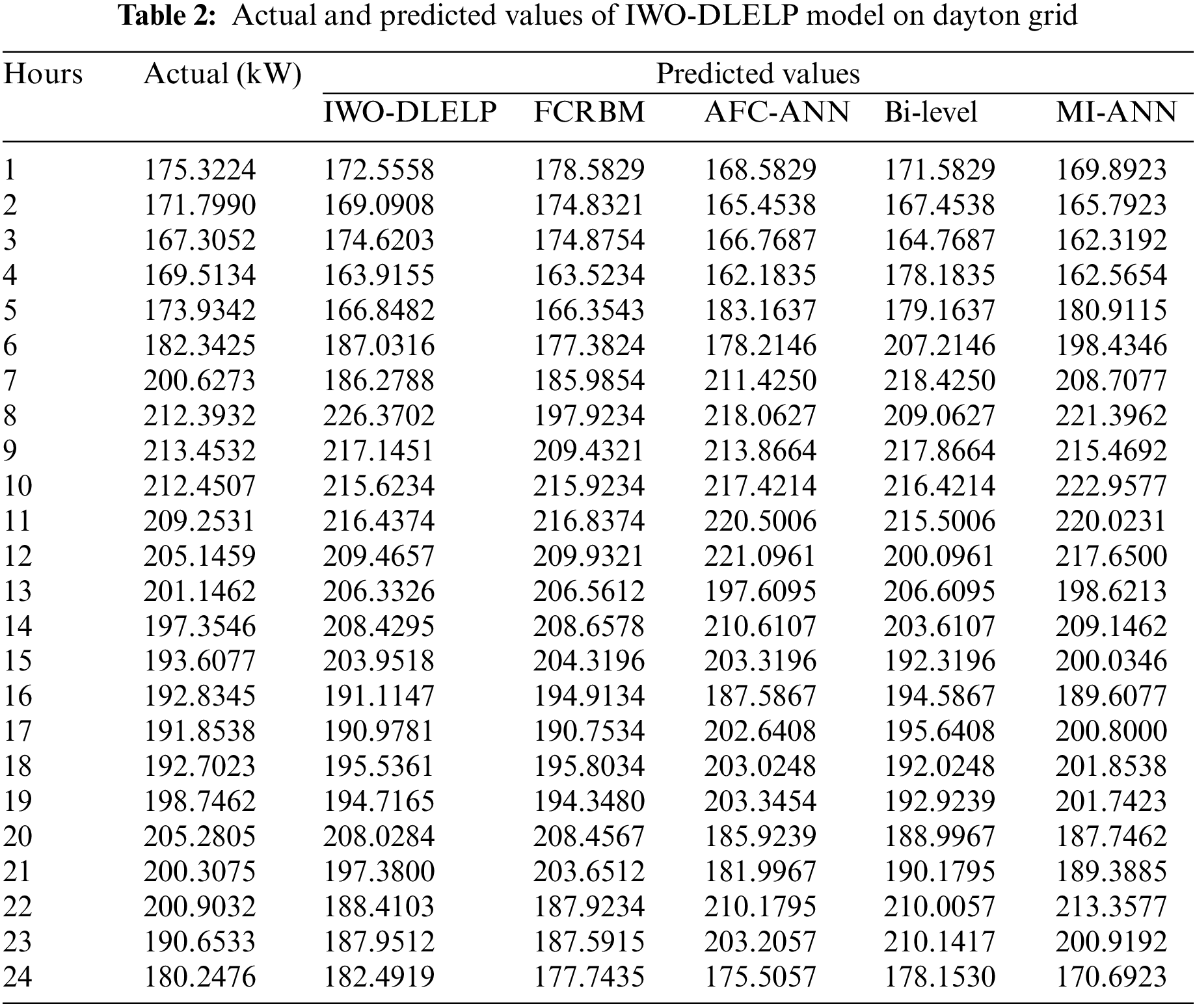
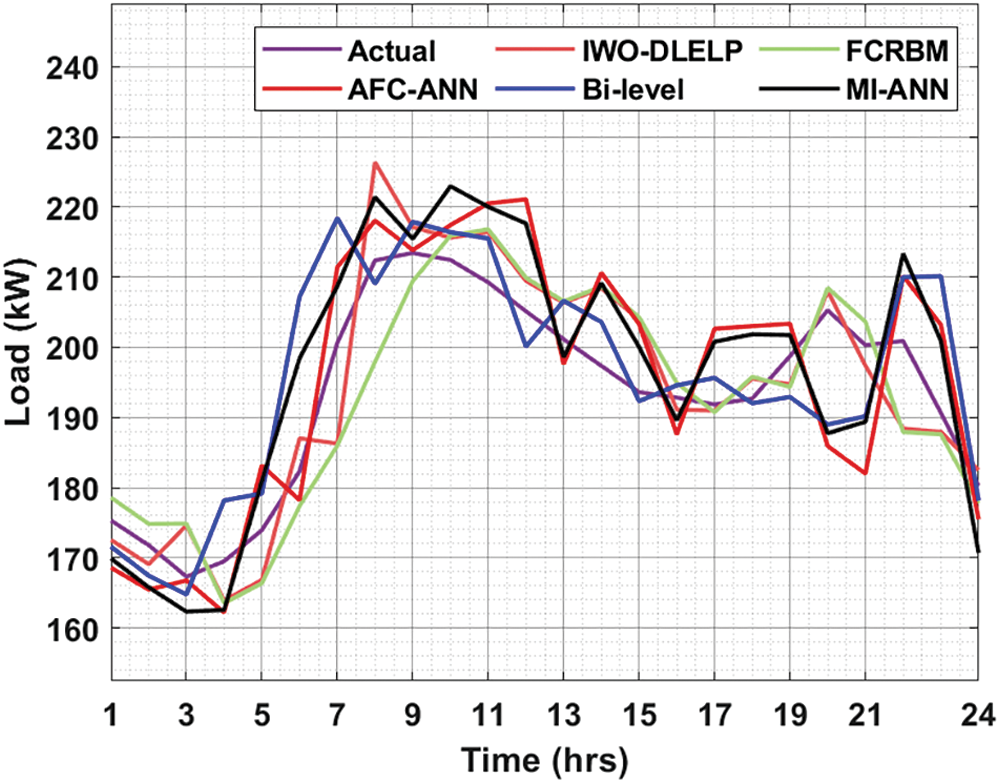
Figure 4: Actual and predicted values of IWO-DLELP model on dayton grid

Table 3 and Fig. 5 highlights the comprehensive prediction outcomes of the IWO-DLELP model with recent techniques under distinct hours on EKPC grid. The table values indicated that the IWO-DLELP model has reached proficient outcomes over the other methods with the minimal variation between the original and predicted values. For instance, on hour 1 with actual load of 132.8923 kW, the IWO-DLELP technique has gained predicted value of 134.9866 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have depicted predicted values of 136.5019, 138.9234, 138.9234, and 139.8923 kW respectively. Meanwhile, on hour 10 with actual load of 150.4692 kW, the IWO-DLELP technique has exhibited predicted value of 151.6949 kW whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN models have demonstrated predicted values of 148.8664, 150.4214, 153.1423, and 150.4000 kW respectively.

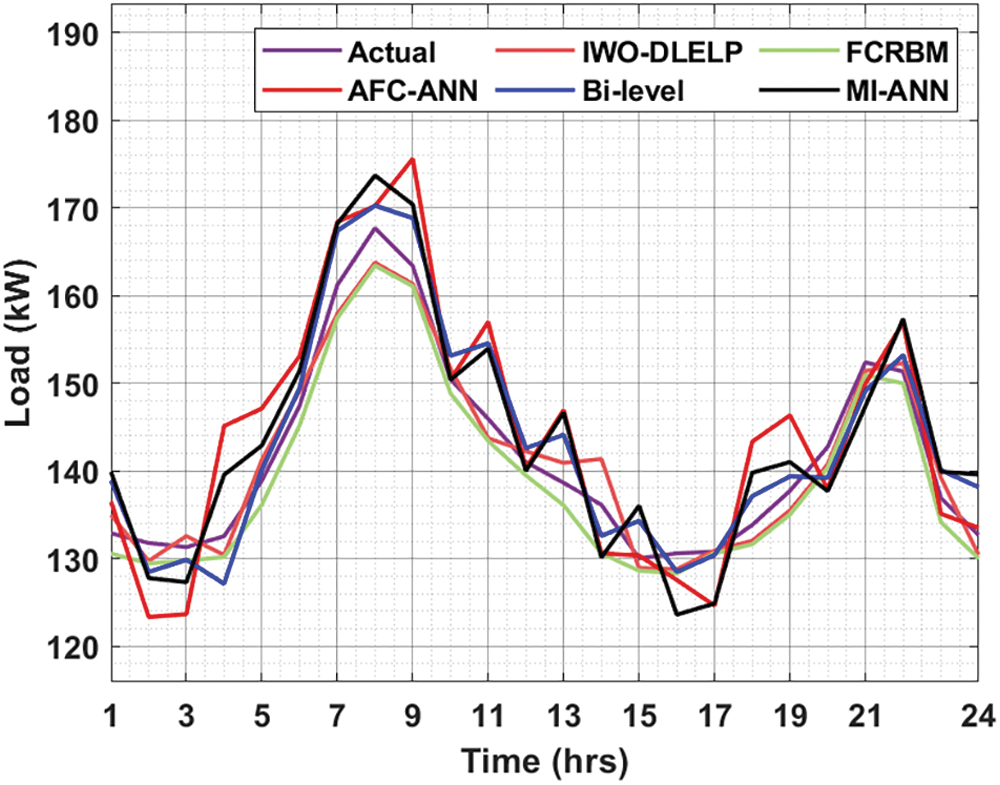
Figure 5: Actual and predicted values of IWO-DLELP model on EKPC grid

A comparative MSE inspection of the IWO-DLELP with recent methods is made under distinct hours in Fig. 6 on FE grid. The results indicated that the IWO-DLELP model has accomplished proficient results with the minimal MSE values under several hours. For instance, with 1 h, the IWO-DLELP model has obtained lower MSE of 1.5675 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have attained higher MSE of 1.8109, 12.7503, 25.4525, and 19.6087 respectively. At the same time, with 15 h, the IWO-DLELP model has obtained lesser MSE of 5.0218 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have attained higher MSE of 5.3567, 0.7382, 52.5910, and 12.1071 correspondingly. Along with that, within 24 h, the IWO-DLELP approach has reached lower MSE of 2.9242 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN algorithms have attained higher MSE of 3.1591, 8.2589, 41.6143, and 2.2147 correspondingly.

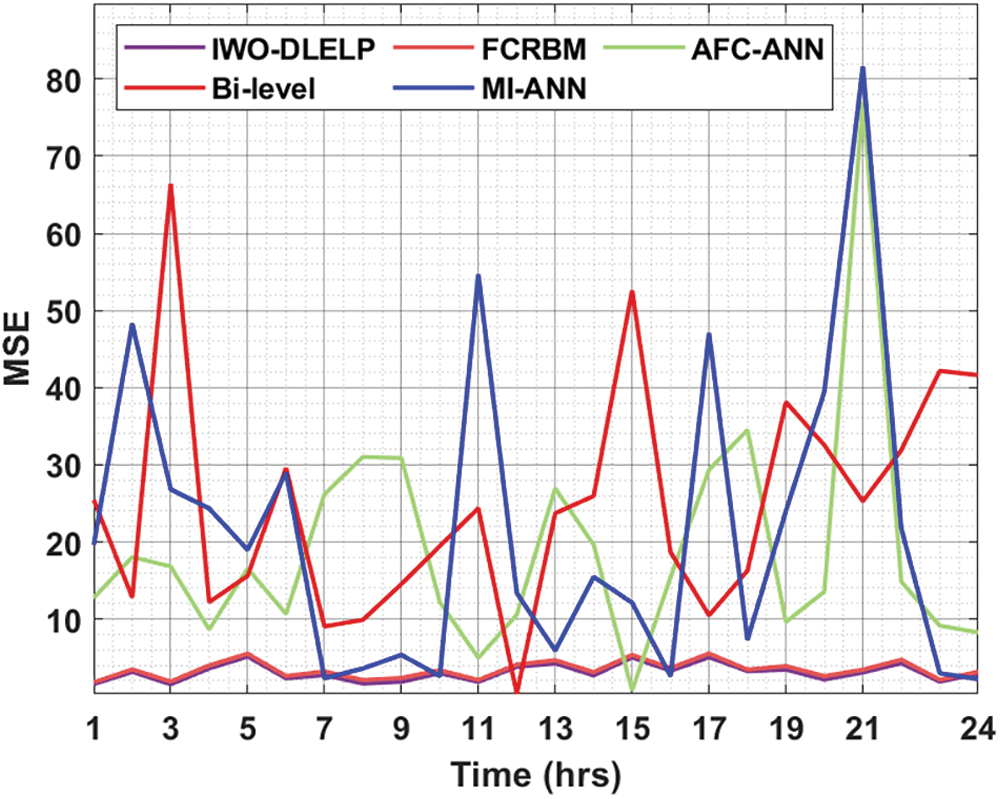
Figure 6: MSE analysis of IWO-DLELP technique under FE grid dataset

A brief MSE inspection of the IWO-DLELP with recent methods is made under distinct hours in Fig. 7 on Dayton grid. The outcomes exposed that the IWO-DLELP model has accomplished proficient results with the lesser MSE values under different hours. For instance, with 1 h, the IWO-DLELP algorithm has reached lower MSE of 2.7666 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have attained higher MSE of 3.2605, 6.7395, 3.7395, and 5.4301 correspondingly. Followed by, with 15 h, the IWO-DLELP model has obtained lesser MSE of 10.3441 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have attained higher MSE of 10.7119, 9.7119, 1.2881, and 6.4269 correspondingly. Next, within 24 h, the IWO-DLELP technique has obtained reduced MSE of 2.2443 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN methods have attained higher MSE of 2.5041, 4.7419, 2.0946, and 9.5553 respectively.

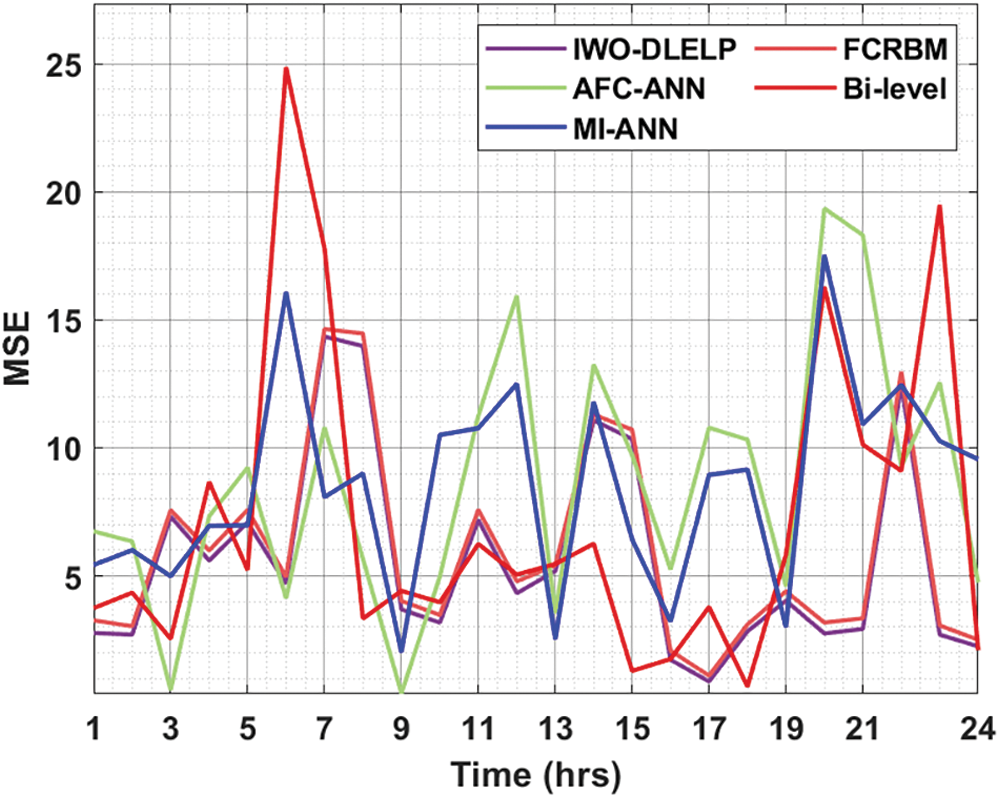
Figure 7: MSE analysis of IWO-DLELP technique under Dayton grid dataset

A detailed MSE inspection of the IWO-DLELP with recent methods is made under distinct hours in Fig. 8 on EKPC dataset. The results indicated that the IWO-DLELP model has accomplished proficient results with the minimal MSE values in several hours. For instance, with 1 h, the IWO-DLELP approach has obtained lower MSE of 2.0943 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have reached higher MSE of 2.3094, 3.6096, 6.0311, and 7.0000 correspondingly. Simultaneously, with 15 h, the IWO-DLELP model has obtained lower MSE of 1.0995 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN techniques have attained maximum MSE of 1.4239, 0.3256, 4.2760, and 6.0000 respectively. Lastly, within 24 h, the IWO-DLELP methodology has obtained decreased MSE of 2.2625 whereas the FCRBM, AFC-ANN, Bi-level, and MI-ANN approaches have attained maximum MSE of 2.6866, 0.8308, 5.4607, and 6.9130 correspondingly. After examining the results and discussion, it is ensured that the IWO-DLELP model has accomplished superior results over the other methods.

Figure 8: MSE analysis of IWO-DLELP technique under EKPC dataset

5  Conclusion

In this study, a new IWO-DLELP technique has been presented to effectually forecast the electric load in SG environment for designing proficient ESS. The proposed IWO-DLELP model encompasses pre-processing, partition clustering, BiGRU based prediction, and IWO based hyperparameter tuning. The simulation analysis of the IWO-DLELP model is performed and the results are inspected under several aspects. The comparison study reported the enhanced outcomes of the IWO-DLELP model over the recent methods interms of distinct evaluation measures. Therefore, the IWO-DLELP technique can be utilized for the promising load prediction performance in the SG environment. In future, metaheuristics based feature selection models can be derived to enhance the predictive performance.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Liu, Z. Xiao, R. Zhu, J. Wang, L. Liu et al., “Edge sensing data-imaging conversion scheme of load forecasting in smart grid,” Sustainable Cities and Society, vol. 62, pp. 102363, 2020. [Google Scholar]

2. S. Kaneriya, S. Tanwar, A. Nayyar, J. P. Verma, S. Tyagi et al., “Data consumption-aware load forecasting scheme for smart grid systems,” in 2018 IEEE Globecom Workshops (GC Wkshps), Abu Dhabi, United Arab Emirates, pp. 1–6, 2018. [Google Scholar]

3. T. Ahmad and H. Chen, “Potential of three variant machine-learning models for forecasting district level medium-term and long-term energy demand in smart grid environment,” Energy, vol. 160, pp. 1008–1020, 2018. [Google Scholar]

4. I. K. Nti, M. Teimeh, O. N. Boateng and A. F. Adekoya, “Electricity load forecasting: A systematic review,” Journal of Electrical Systems and Information Technology, vol. 7, no. 1, pp. 13, 2020. [Google Scholar]

5. L. Zhang, J. Wen, Y. Li, J. Chen, Y. Ye et al., “A review of machine learning in building load prediction,” Applied Energy, vol. 285, pp. 116452, 2021. [Google Scholar]

6. T. Ahmad, H. Zhang and B. Yan, “A review on renewable energy and electricity requirement forecasting models for smart grid and buildings,” Sustainable Cities and Society, vol. 55, pp. 102052, 2020. [Google Scholar]

7. T. O. Ajewole, W. A. Salami, A. O. Adeniran and M. O. Omoigui, “Reliability analysis of the pre-privatization Nigerian electric power distribution systems,” Environmental Quality Management, vol. 28, no. 2, pp. 97–103, 2018. [Google Scholar]

8. M. Xia, H. Shao, X. Ma and C. W. de Silva, “A stacked gru-rnn-based approach for predicting renewable energy and electricity load for smart grid operation,” IEEE Transactions on Industrial Informatics, vol. 17, no. 10, pp. 7050–7059, 2021. [Google Scholar]

9. A. Li, F. Xiao, C. Zhang and C. Fan, “Attention-based interpretable neural network for building cooling load prediction,” Applied Energy, vol. 299, pp. 117238, 2021. [Google Scholar]

10. S. D. Khan, L. Alarabi, and S. Basalamah, “Toward smart lockdown: A novel approach for COVID-19 hotspots prediction using a deep hybrid neural network,” Computers, vol. 9, no. 4, pp. 99, 2020. [Google Scholar]

11. Y. Hong, Y. Zhou, Q. Li, W. Xu and X. Zheng, “A deep learning method for short-term residential load forecasting in smart grid,” IEEE Access, vol. 8, pp. 55785–55797, 2020. [Google Scholar]

12. K. Thiyagarajan and R. S. Kumar, “Real time energy management and load forecasting in smart grid using compactrio,” Procedia Computer Science, vol. 85, pp. 656–661, 2016. [Google Scholar]

13. M. Usman, Z. A. Khan, I. U. Khan, S. Javaid and N. Javaid, “Data analytics for short term price and load forecasting in smart grids using enhanced recurrent neural network,” in 2019 Sixth HCT Information Technology Trends (ITT), Ras Al Khaimah, United Arab Emirates, pp. 84–88, 2019. [Google Scholar]

14. Y. Yang, W. Li, T. A. Gulliver and S. Li, “Bayesian deep learning-based probabilistic load forecasting in smart grids,” IEEE Transactions on Industrial Informatics, vol. 16, no. 7, pp. 4703–4713, 2020. [Google Scholar]

15. L. Barolli, F. K. Hussain and M. Ikeda, “Complex, intelligent, and software intensive systems,” in Proc. of the 13th Int. Conf. on Complex, Intelligent, and Software Intensive Systems (CISIS-2019), Advances in Intelligent Systems and Computing, vol. 611, Sydney, Australia, Cham: Springer, 2020. [Google Scholar]

16. D. Syed, H. A. Rub, A. Ghrayeb, S. S. Refaat, M. Houchati et al., “Deep learning-based short-term load forecasting approach in smart grid with clustering and consumption pattern recognition,” IEEE Access, vol. 9, pp. 54992–55008, 2021. [Google Scholar]

17. S. Rai and M. De, “Analysis of classical and machine learning based short-term and mid-term load forecasting for smart grid,” International Journal of Sustainable Energy, vol. 40, no. 9, pp. 821–839, 2021. [Google Scholar]

18. M. Pellegrini, “Short-term load demand forecasting in smart grids using support vector regression,” in 2015 IEEE 1st Int. Forum on Research and Technologies for Society and Industry Leveraging a Better Tomorrow (RTSI), Torino, Italy, pp. 264–268, 2015. [Google Scholar]

19. L. M. Nkomo and B. K. Daniel, “Sentiment analysis of student engagement with lecture recording,” Tech Trends, vol. 65, no. 2, pp. 213–224, 2021. [Google Scholar] [PubMed]

20. K. K. A. Ghany, A. M. AbdelAziz, T. H. A. Soliman and A. A. E. -M. Sewisy, “A hybrid modifiedstep whale optimization algorithm with tabu search for data clustering,” Journal of King Saud University—Computer and Information Sciences, vol. 34, no. 3, pp. 832–839, 2022. [Google Scholar]

21. G. Iacca, V. C. D. S. Junior and V. V. D. Melo, “An improved jaya optimization algorithm with lévy flight,” Expert Systems with Applications, vol. 165, pp. 113902, 2021. [Google Scholar]

22. G. Hafeez, K. S. Alimgeer and I. Khan, “Electric load forecasting based on deep learning and optimized by heuristic algorithm in smart grid,” Applied Energy, vol. 269, pp. 114915, 2020. [Google Scholar]