A Novel S-Box Generation Methodology Based on the Optimized GAN Model

1  Introduction

S-box is the core nonlinear component of a block cipher, and its cryptographic properties usually determine the security strength of a block cipher. The main indicators used to measure the cryptographic properties of an S-box include nonlinearity, differential uniformity, algebraic degree, strict avalanche criterion, and transparency order, etc. Methods to generate an S-box with good cryptographic properties can be random generation, cryptographic structure construction, and mathematical function generation, etc. Since the search space of an S-box can be large and different indicators can perform differently, traditional construction methods cannot generate S-boxes that perform well under all indicators at the same time. Therefore, how to efficiently generate S-boxes with excellent cryptographic properties appears to be the key task in the design of block ciphers.

In the design of S-boxes, intelligent search algorithms, such as heuristic algorithms, machine learning algorithms, and deep learning algorithms, can efficiently search the optimal solution in a large space and improve the efficiency of global optimization. During the past decade, some classic intelligent search algorithms such as hill climbing [1], genetic algorithm [2,3], neural network [4,5], cellular automata [6], chaotic maps [7,8] were used to generate S-boxes with excellent cryptographic properties.

Currently, the main works are still about how to generate 4/8 bit S-boxes with intelligent search algorithms, and existing works show that the generated 4-bit S-boxes have excellent cryptographic properties due to the smaller searching space [9]. However, most 8-bit S-boxes generated by the above methods may have relatively weak cryptographic properties under certain indicators, since it is usually difficult to search S-boxes that maintain good cryptographic properties under different indicators in a huge searching space. Deep learning has the advantages of strong learning ability, wide coverage, and good adaptability. So, deep learning can greatly improve our ability to solve complex problems, and it has been widely used in image recognition, natural language processing, autonomous driving, recommendation system, and so on. In light of this, deep learning may provide a new way to design S-boxes that maintain good cryptographic properties under different indicators.

This paper focuses on the design of cryptographic S-boxes based on deep learning, the main contribution is as follows.

(1) This paper studies the generation method of 8-bit S-boxes based on the GAN model. Specially, the sample dataset is constructed based on the S-box of AES with affine equivalence. Then, three models are respectively built and cross-trained to generate 8-bit S-boxes based on three extended frameworks of GAN, i.e., DCGAN, WGAN, and WGAN-GP.

(2) The optimized model WGP-IM based on the WGAN-GP model is proposed, the main idea is to construct loss function constraints for WGAN-GP to select S-boxes with excellent cryptographic properties. In WGP-IM, the loss functions of the generator are constrained by designing loss functions, including bijection loss, differential uniformity loss, and nonlinearity loss. The WGP-IM model is then cross-trained to generate 8-bit S-boxes with excellent cryptographic properties.

(3) In order to evaluate the efficiency of the proposed method, we test the cryptographic properties of the S-boxes generated with the enhanced WGP-IM model. The test results show that the enhanced WGP-IM model can generate S-boxes with excellent properties, including a reduced differential uniformity of 8, and the nonlinearity up to 104, and so on. Compared with existing S-box generation methods, the proposed method can efficiently generate S-boxes with excellent cryptographic properties, and it only takes a few seconds to generate an 8-bit S-box after the model has been trained. Besides, the method is simpler and has good generality to generate S-boxes.

The rest of this paper is organized as follows: Section 2 introduces related works. Preliminaries on generative adversarial networks and affine equivalence are described in Section 3. Based on the sample dataset constructed by affine equivalence, DCGAN, WGAN, and WGAN-GP models can be used for training and generating 8-bit S-boxes, which is shown in Section 4. In order to optimize cryptographic properties of the generated 8-bit S-boxes, an optimized model WGP-IM is proposed to generate S-boxes, which is shown in Section 5. The cryptographic properties of the generated S-boxes and existing S-boxes are evaluated and compared in Section 6. Finally, Section 7 summarizes the paper.

2  Related Works

Intelligent search algorithms have the merit of automatic search, which can reduce the search space of optimal solution and improve the efficiency of global search by setting up reasonable constraints. In order to improve the efficiency to generate S-boxes and optimize cryptographic properties of the generated S-boxes, many intelligent search algorithms were proposed.

In 2007, Yin et al. used genetic algorithm and heuristic mutation strategy to generate S-boxes [2]. In 2017, multi-objective genetic algorithm was used to generate S-boxes [3]. In 2020, in order to further enhance the nonlinearity of the generated S-boxes, Wang et al. [10] regarded the Boolean function as the chromosome of the S-box and proposed a novel genetic algorithm to construct a bijective S-box with high nonlinearity.

Besides, neural networks have been used in the generation of S-boxes. In 2010, neural network was proposed to generate S-boxes [4]. In 2015, Zhang et al. presented a new scheme to generate S-boxes based on neural network [5]. In 2020, in order to resist side channel attacks, Aljuffri et al. [11] trained the neural network model S-NET, and used its output results to replace S-boxes to break the linear relationship between the hypothetical leakage and the real leakage of a cryptographic chip, the results applied to AES proved that it could resist common side channel cryptanalyses.

Notice that, cellular automata are also commonly used to generate S-boxes. In 2018, Ghoshal et al. proposed an optimal 4-bit S-box generation method with cellular automata rules, and they showed that the hardware implementation cost of the method can be low [6]. Based on the work of Ghoshal et al. [6], Zhang et al. [12] proposed an S-box generation method based on Cellular automata (CA) rules, and they generated 4-bit S-boxes with better cryptographic properties than existing ones. In 2020, Huang et al. [13] proposed the neural network implementation method of CA-based S-box, and a weight threshold search algorithm which can efficiently implement the neural network structure of CA-based S-boxes was proposed.

Chaotic maps are a type of mathematical function that exhibit complex, non-linear behavior, it has advantages in randomness, and it has been used to generate S-boxes earlier. In 2017, Çavuşoğlu et al. [7] proposed a new approach for designing strong S-box generation algorithms based on chaotic scaled Zhongtang system, which utilized a new random number generator with complex and interesting dynamic features. In 2022, Manzoor et al. [8] proposed a dynamic and key-dependent substitution box using an innovative chaotic map and permutation process, which was compared with other S-boxes based on chaotic maps and demonstrated its suitability for cryptographic applications.

Recently, more construction methods have been proposed. In 2019, Zahid et al. [14] proposed using cubic polynomial mapping to construct a strong S-box. In the same year, cryptographic S-boxes were also constructed using cubic fractional transformation (CFT) [15]. In 2020, Zahid et al. proposed a new S-box based on modular approach [16]. In 2021, Alhadawi et al. [17] proposed an 8-bit S-box generation method based on the Cuckoo Search (CS) algorithm and the discrete space chaotic mapping, which has good randomness and a small number of adjustable parameters. In order to further optimize the nonlinearity and the differential uniformity of S-boxes, Long et al. [18] proposed a new S-box generation method based on the discrete chaotic mapping and the improved Artificial Bee Colony algorithm (ABC). Besides, various design methods for S-boxes have been proposed. Specifically, Rashidi [19] proposed a method to generate an S-box based on inversion and affine transformation, which exhibited better hardware implementation compared to the AES S-box with similar cryptographic properties. In 2023, in order to achieve a lower area and higher security for the inversion of the S-box in [19] over a finite field, Rashidi rewrote the original equation of inversion to optimize the S-box [20]. And Rashidi [21] also constructed two 8-bit S-boxes with lower hardware resources and lower critical path delay (CPD).

Furthermore, the emergence of side-channel attacks (SCA), post-quantum cryptography (PQC), and lightweight cryptography (LWC), have prompted the design of cryptographically strong S-boxes to meet specific needs. In detail, different styles of SCA can exploit the unintended physical leakage to extract sensitive information from cryptographic devices [22–25]. PQC can solve the hard mathematical problems in classical cryptography in a much shorter time than current computing power [26–29]. LWC refers to the field of cryptography that focuses on developing efficient and secure cryptographic algorithms suitable for resource-constrained devices [30,31]. The generation of cryptographically strong S-boxes that meets the above specific needs becomes a new design concern for the generation of S-boxes.

3  Preliminaries

3.1 Generative Adversarial Networks

GAN is an unsupervised deep learning model proposed by Ian Goodfellow et al. based on the zero-sum game idea in game theory [32]. GAN usually includes two parts, i.e., generator G and discriminator D. The generator tries to learn the sample distribution in the real dataset, and extracts the feature distribution from the real data samples. Moreover, the generator generates fake samples, and then it feeds the generated samples to the discriminator. The discriminator is essentially a binary classifier, which judges whether the input sample is the real data or the generated data, and optimizes the parameters of the generator. Through cross-training, the generator generates a generated data that approximates the real data, and the discriminator discriminates the authenticity of the sample. The GAN structure is shown in Fig. 1.

Figure 1: Generative adversarial network architecture

Formally, the objective function of GAN is given as follows:

minGmaxDV(D,G)=minGmaxDEx∼Pdata(x)[log⁡D(x)]+Ez∼Pg(z)[log⁡(1−D(G(z)))](1)

where Pg(z) is the distribution of the noise z, x is the real data, Pdata(x) is the distribution of the real data and G(z) is the output of a generator. Generator G receives the random noise z, and Xfake is the generated data G(z), which is mapped from known priors Pg(z). The discriminator D receives both the generated data Xfake and the real data Xreal, and then it judges whether the data comes from the generator or the dataset according to the probability D(x) of the real data distribution Pdata(x).

During the model training process, the generator and the discriminator are cross-trained. After certain rounds of training, the generator G can reach the optimal generation ability, and the discriminator D can also reach the optimal discriminant ability. In this case, Pdata(x) and Pg(z) gradually converge to reach the Nash equilibrium and the discriminator prediction approaches to 0.5. Then, the generated data and the real data can be indistinguishable.

Based on the cross-training style, GAN can obtain excellent results with back propagation. However, there are some issues exist in GAN. For instance, the training is unstable, the gradient is easy to disappear and it is unsuitable to process discrete data. In order to solve these problems, GAN has been extended to form some new architecture in recent years, e.g., DCGAN [33], WGAN [34], WGAN-GP [35], CycleGAN [36], and StyleGAN [37] were proposed consecutively.

3.2 Affine Equivalence

Note that the model training of GAN needs a large number of data samples to learn and extract the feature distribution of the real data. According to the feature distribution, the generator can output the generated data to approximate the real data. It is easier to output results with excellent properties if samples have excellent properties, since the excellent properties can be learned and used by the model. Therefore, the AES S-box is selected as the data sample. The algebraic degree of the AES S-box is 7, its differential uniformity is 4, its nonlinearity is 112, and its transparency order is 7.86 [38].

In order to construct a large number of S-box sample datasets for training, an 8-bit S-box dataset is constructed based on the selected S-boxes with the affine equivalence technique. The definition of affine equivalence is given as follows:

Definition 1 [39]. Two n-bit S-boxes S2 and S1 are affine equivalence if there exit two invertible n × n matrices A, B ∈ (n, F2) and constants a,b∈F2n such that:

S2(x)=B⋅(S1(A⋅x⊕a))⊕b(2)

If S1 and S2 are affine equivalent, the differential uniformity and nonlinearity of the S-box remain unchanged under the affine transformation, which inherits the excellent cryptographic properties of the original S-box.

Based on the affine equivalence property, a large number of 8-bit S-boxes can be constructed to form a sample dataset. Then, data preprocessing is performed on the sample dataset. Note that in the preprocessing phase, each sample is converted into a matrix of 2Dim/2 × 2Dim/2, where Dim is the size of the S-box. In this case, the preprocessed sample dataset will be used as the real input data for GAN model training.

4  Generate S-Box Based on the Extended Architecture of GAN

This section describes how to train model and generate 8-bit S-boxes by based on three extended architecture of GAN, i.e., DCGAN, WGAN, and WGAN-GP, respectively.

4.1 Generate S-Box Based on DCGAN

With the increase of the number of neural network layers, the computing speed of the model will be significantly decreased. DCGAN will remove the fully connected layer, and it only uses the convolutional layer to decrease the calculation burden so that the model is more stable. In order to avoid influencing the convergence speed, the random input of the generator is directly connected with the feature input of the convolutional layer. Similarly, the output layer of the discriminator is connected with the output feature of the convolutional layer.

The DCGAN model can learn the hidden information in the S-box sample dataset by means of the powerful feature extraction ability of Convolutional Neural Networks (CNN). Combined with the excellent generation ability of GAN to do cross-training, S-Boxes with excellent cryptographic properties may be generated.

The transposed convolution layer of the generator includes 4 layers, and the neurons of each layer are respectively set to 64, 32, 16 and 1. The generator inputs the random noise z, which is extended to 2n bits through the transposed convolution layer and converted into a matrix. Moreover, the output of the generator can be denoted as Xfake = G(z). In order to improve the fitting ability of the model, DCGAN uses nonlinear activation function LeakyReLU in the training process. LeakyReLU has the ReLU function, and it will result in a small slope for negative value inputs. Thus, it overcomes the problem that the ReLU function does not learn and cannot back propagate after entering the negative region. Besides, it avoids sparse gradients during training, and reduces the probability of gradient disappearing in the process of training. Therefore, it is more suitable for CNN training. The expression of the LeakyReLU function is given as follows:

LeakyReLU(x)={x,ifx≥0xa,ifx<0, a∈(1,+∞)(3)

where x is the output of the upper layer and a is a fixed slope.

In the last layer of the transposed convolution, Tanh function is used as the activation function. Tanh function not only has the merits of Sigmoid function, but also limits the output range to [−1, 1]. The formula of Tanh function is given as follows:

Tanh(x)=ex−e−xex+e−x(4)

where x is the output of the upper layer.

The convolutional layer of the discriminator also includes 4 layers. The neurons in each layer are respectively set to 16, 32, 64, and 128, the convolution kernel is 5 × 5, and the stride is 2. The convolution operation preserves the information of the spatial structure to extract local features. The discriminator receives the real data Xreal and the generated data Xfake. The first three layers and the last layer of the convolutional layer use LeakyReLU and Tanh as activation functions respectively. Moreover, the discriminator outputs the true and false probability distribution of the generated data and the real data, and judges whether the input data is a real sample or a generated sample. Softmax function is used in the final classification. The expression of the Softmax function is given as follows:

Softmax(x)=eVx∑j=1neVj(5)

where V is the array needs to be classified, Vx is the x-th element in V, and n is the length of the array V.

Ahead of cross-training, the number of rounds Epoch and the values of different parameters should be set. Cross-training is also referred to as adversarial training, which includes two stages, i.e., the generation stage and the discrimination stage. In the first stage, the generator G is fixed and the discriminator D is trained. In the second stage, the trained discriminator D is fixed and the generator G is trained.

In the cross-training process, back-propagation needs to be performed according to the output of the discriminator to optimize the generator and the discriminator. Back-propagation is a gradient descent process, and its goal is to minimize the difference between the output and the real data, i.e., to minimize the loss function. Cross entropy is set to be the loss function, which describes the difference between two probability distributions. The expression of cross-entropy is given as follows:

Hy′(y)=∑i=0K−1y′ilog⁡(yi)(6)

where y is the real probability distribution, y′ is the predicted probability distribution, and K is the number of samples.

In the discriminant stage, according to the maximum maxV(D, G) of the difference between Pdata(x) and Pg(z), the discriminator distinguishes the generated data and the real data, and then updates the parameters of the discriminator according to the discriminant result.

In the generation stage, according to the difference between Pdata(x) and Pg(z), maxV(D, G) should be minimized so that the difference between two distributions is the smallest, which can be denoted as minmaxV(D, G). Moreover, the generator fits the probability distribution Pg(z) of the randomly generated noise z to the real distribution Pdata(x) as much as possible with the activation function, and maps the random noise z to the generated data G(z), and after that updates the parameters of the generator.

The training would be ended when Pdata(x) = Pg(x), i.e., Pdata(x)Pdata(x)+Pg(x) tends to 0.5. In this case, an S-box is generated.

4.2 Generate S-Box Based on WGAN

Due to the difference of the data in nature, the overlap between the real data distribution Pdata and the generated data distribution Pg is negligible. However, Jensen-Shannon (JS) in GAN is not suitable to measure the distance between data without overlap, which induces the result that it is difficult to converge for the discriminator in the process of training and good results cannot be obtained.

Different from DCGAN, WGAN mainly improves GAN from the view of the loss function, which uses the wasserstein distance to measure the difference of distributions between the real data and the generated data. In addition to computing the difference between two different data distributions without overlapping, the wasserstein distance also provides a continuous and effective gradient for the generator. The WGAN [34] value function is given as follows:

minGmaxD∈LV(D,G)=minGmaxD∈L{Ex∼Pdata(x)[D(x)]−Ez∼Pg(z)[D(G(z))]}(7)

where L is the set of K-Lipschitz functions, which requires that the function gradient value is not larger than a finite constant K. The limitation of the L set makes the gradient of the discriminator D smooth enough so that it will not become infinite or infinitesimal. Without the limitation of the L set, the discriminator will be difficult to converge in the training process. Eq. (7) shows that under the condition that the discriminator D satisfies the L set, if x is a sample of Pdata, the output of the discriminator D should be as large as possible, while if it is a sample of Pg, the output of the discriminator D should be as small as possible.

Both the process of model training and generating S-box with the WGAN model can be similar to those with the DCGAN model, and the WGAN model also includes two stages, i.e., the generator stage and the discriminator stage.

The generator contains 1 fully connected layer and 2 2D convolutional layers. The generator first receives input random noise z of dimension 256 × 1, and converts it into a feature map whose size is 4 × 4 with 512 channels after going through a fully connected layer. Then, it goes through 2 2D convolutional layers, the convolution kernel is 5 × 5, the stride is 1, the padding is 0 and the number of channels can be 256 and 1. Before entering into the convolutional layer, bilinear interpolation is used for upsampling to double the size of the feature map. Except to the last 2D convolutional layer, the other two layers need to be normalized with the Batch Normalization function and activated by the LeakyReLU function. Finally, the generator model is instantiated to convert the input random noise z into a vector of dimension (16, 16, 1).

The discriminator contains 3 2D convolutional layers, 1 flatten layer and 1 fully connected layer. The 3 2d convolution layers are followed by the flatten layer and the full connection layer. The convolution kernel of the 2D convolution layer is 5 × 5, the stride is 1, the padding is 0, and the channel number can be 128, 256 and 512 respectively. The activation function of the 2D convolutional layers is LeakyReLU, and the last two convolutional layers need to be normalized by the Batch Normalization function before activation. In this case, the discriminator model is instantiated to convert the input vector of dimension (16, 16, 1) into a binary classification output (true or false).

4.3 Generate S-Box Based on WGAN-GP

Actually, WGAN limits the parameters of the discriminator in order to ensure that the network can meet the Lipschitz limit, which causes the gradient value of the function lies in intervals of two extreme values after the discriminator is updated. This induces the result that most of the weights will fall on two extreme values after the WGAN model cutting the weights to a certain range, therefore the fitting effect of the deep neural network can be not that well.

WGAN-GP is an improved version of WGAN, with major improvement to the Lipschitz constraints. In order to solve the problem of WGAN gradient explosion and find a suitable way to meet the Lipschitz constraint, the gradient penalty is used in WGAN-GP to meet the Lipschitz constraint and improve the stability of model training. The optimized objective function of WGAN-GP [35] is as follows:

minGmaxDV(D,G)=minGmaxD{Ex∼Pdata(x)[D(x)]−Ez∼Pg(z)[D(G(z))]−λEy∼Ppenalty[(||∇yD(y)||2−1)2]}(8)

where, y~Ppenalty indicates sampling from the real data distribution Pdata and the generated data distribution Pg, rather than the whole network. Compared with (7), (8) replaces the Lipschitz restriction of the discriminator with gradient penalty. Lipschitz restriction is used to limit the gradient of the discriminator so that it will not exceed K, while the gradient penalty is used to set an additional loss term to relate the gradient with K.

The process of model training and generating S-box with the WGAN-GP model is similar to that with the DCGAN model.

In the WGAN-GP model, the generator consists of 1 fully connected layer and 3 2D convolutional layers. The generator receives input the random noise z of dimension 256 × 1, which is converted into a feature map of size 4 × 4 with 1024 channels after going through a fully connected layer. Subsequently, the feature map goes through 3 2D convolution layers with the convolution kernel of 5 × 5, the stride is 1, the padding is 0, and the number of channels can be 512, 256, and 1, respectively. The bilinear interpolation method is used for upsampling before entering the convolutional layer to double the size of the feature map. Except for the last 2D convolutional layer, the other three layers need to be normalized with the Batch Normalization function and activated with the LeakyReLU function. Finally, the generator model is instantiated to convert the input random noise z into a vector of dimension (16, 16, 1).

The discriminator contains 3 2D convolutional layers, 1 data flatten layer and 1 fully connected layer. The convolution kernels of the 2D convolutional layers are all 5 × 5, the stride is 1, the padding is 0, and the number of channels can be 128, 256 and 512, respectively. Different from WGAN, the 2D convolution layer of the WGAN-GP model discriminator directly uses the LeakyReLU activation function, and it does not need to use Batch Normalization for normalization, otherwise it will introduce the interdependence of different samples in the same batch, which causes the result that the discriminator cannot impose gradient penalty on each data independently. Finally, the discriminator model is instantiated to convert the input vector of dimension (16, 16, 1) into a binary classification output (true or false).

5  Generate S-Box with the WGP-IM Model

The S-box generation results of the WGAN-GP model show that the optimal differential uniformity of the generated 8-bit S-box is 12, and the optimal nonlinearity is 94. In light of this, the S-box generation results of the WGAN-GP model can be worse than the S-box generation results of the DCGAN model and the WGAN model. The reason may be that the WGAN-GP model imposes a gradient penalty on each data independently, while it does not constrain the cryptographic properties of the S-box in the gradient penalty. Therefore, the model cannot extract the properties related to the S-box in the sample dataset, and the generated S-boxes have worse cryptographic properties.

In order to obtain 8-bit S-boxes with excellent cryptographic properties, an improved model WGP-IM based on the WGAN-GP model is proposed. In order to extract the properties related to S-boxes in the process of model training, some loss functions including bijection loss Lb, differential uniformity loss LDU and nonlinearity loss LNF are added.

The loss function of the adversarial loss Ladv in the original WGAN-GP is as follows:

Ladv=−Ez∼Pg(z)[D(G(z))](9)

where z∼Pg(z) is the distribution of the noise z served as the input of the generator, and G(z) represents the output of the generator.

First the generated S-boxes need to satisfy the bijection property, which will be judged by the deduplication number of elements in the truth table of the generated S-box, and the loss function of the bijective loss Lb is given as follows:

Lb=Ez∼Pg(z)[‖fb(fS(G(z)))−N‖2](10)

where N is the size of the truth table of the S-box in the input sample set, fS is the function of converting the input data to an S-box, fb is the deduplication number of elements in the truth table of the input S-box and ‖⋅‖ is the F norm.

In order to reduce the differential uniformity of the S-box generated by the generator, a differential uniformity loss LDU is established. It judges the similarity between the generated data and the real data in the feature space by comparing the differential uniformity between the generated S-boxes and the real S-boxes. The loss function of the differential uniformity loss LDU is given as follows:

LDU=Ez∼Pg(z),x∼Pdata(x)[‖DU(fS(G(z)))−DU(fS(x))‖2](11)

where x∼Pdata(x) is the distribution of the real data, DU is the differential uniformity function of an S-box, and fS is the function that converts the input data to an S-box.

Similar to the differential uniformity loss function, the loss function of the nonlinearity loss LNF is given as follows:

LNF=Ez∼Pg(z),x∼Pdata(x)[‖NF(fS(G(z)))−NF(fS(x))‖2](12)

where NF is the nonlinearity function of S-box.

In order to balance the influence of the above loss functions, the weighted calculation method is used to establish an objective loss function LG for the generator, and the method is as follows:

LG=λ1Ladv+λ2Lb+λ3LDU+λ4LNF(13)

where λ1, λ2, λ3 and λ4 are loss coefficients of different loss functions that satisfy λ1+λ2+λ3+λ4=1.

The loss function LD of the discriminator network of the WGP-IM model uses the loss function of WGAN-GP [35] as follows:

LD=Ex∼Pdata(x)[D(x)]−Ez∼Pg(z)[D(G(z))]−λEy∼Ppenalty[(||∇yD(y)||2−1)2](14)

Similarly, based on the generated S-box sample set, the WGP-IM model is built, and the loss function of the generator in the original WGAN-GP network is replaced with the objective loss function LG, which can help the generator to learn the hidden properties in the S-box sample set and generate 8-bit S-boxes with excellent cryptographic properties after the model reaches Nash equilibrium.

6  Experiments and Analysis

The generative adversarial network extension models DCGAN, WGAN, WGAN-GP, and an improved WGP-IM model are implemented with Python to generate 8-bit S-boxes. Both Intel Xeon CPU E7-4850 CPU and NVIDA Quadro M6000 GPU are used as the computation unit, the operate system is Windows Server 2012 R2 Standard operating system, and application software includes TensorFlow-gpu 2.50 deep learning platform, Python 3.8.0 and CUDA 9.0/CuDNN v7.0.5.

The model training for DCGAN, WGAN, WGAN-GP, and WGP-IM can be automatically performed by using different optimizers and setting different parameters. The optimizers used by these models are Adam, RMSProp, Adam and Adam, the learning rate can be set to 0.0002, 0.0008, 0.0001 and 0.0002 respectively, the number of batches is set to 128, and the number of training rounds is set to 5000. The λ of the discriminator network in WGAN-GP and WGP-IM can be empirically set to 10 [35].

6.1 Influence of Loss Coefficients in WGP-IM Model on Cryptographic Properties

The training results of the WGP-IM model are influenced by loss coefficients. In order to analyze the influence of loss coefficients on cryptographic properties of S-boxes, different combinations of loss coefficients are set, which can be seen from Table 1, and the WGP-IM model is trained based on different combinations of loss coefficients. The differential uniformity and the nonlinearity of S-boxes generated with the WGP-IM model based on different combinations of loss coefficients can be seen from Figs. 2 and 3.

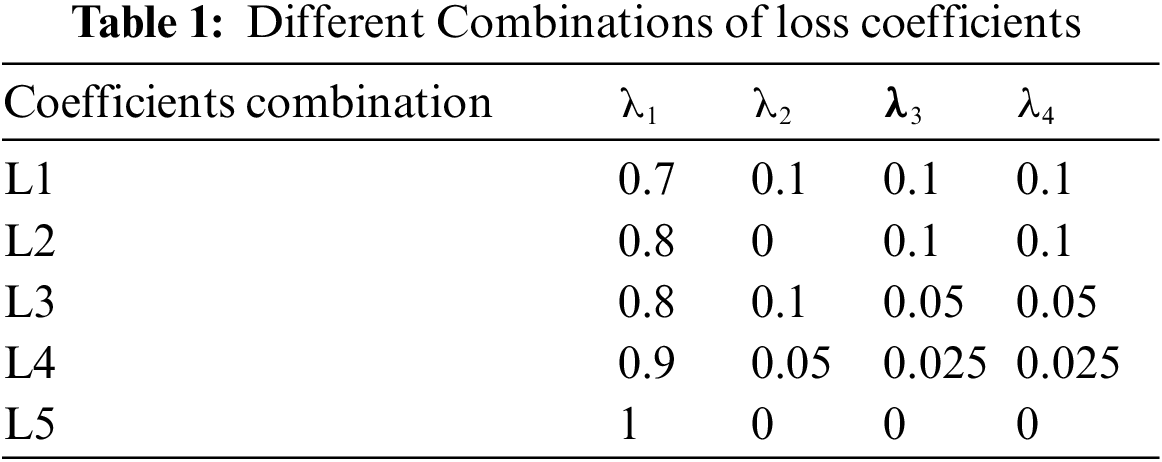
Figure 2: Differential uniformity of S-boxes in different cases

Figure 3: Nonlinearity of S-boxes in different cases

Fig. 2 shows that the differential uniformity of the generated S-boxes are reduced with the number of training rounds. Therefore, the WGP-IM models can better learn the feature of the sample data and the differential uniformity of the generated S-boxes can be better by increasing the number of training rounds. Moreover, the WGP-IM model generates S-boxes with the worst differential uniformity based on the coefficient combination L1, which indicates that if the adversarial loss coefficient is too small, the additional loss will induce the model to generate an inferior result. The differential uniformity of the S-boxes generated with the WGP-IM models based on the coefficient combinations L3 and L4 can be better than that of the S-boxes generated with the WGP-IM model based on the coefficient combination L5 without additional loss. In fact, the differential uniformity of the generated S-Boxes with the WGP-IM model based on the coefficient combination L3 can be the best among five cases, which indicates that the model with reasonable loss functions and loss coefficients can generate S-Boxes with good differential uniformity. Similarly, Fig. 3 shows that the nonlinearity of the S-Boxes generated with the WGP-IM model based on the coefficient combination L3 can be the best among five cases.

The above experimental results illustrate that the adversarial loss can influence the training stability and the convergence speed of the model. In this case, by constructing suitable loss functions and setting reasonable loss coefficients according to the training target, one can maintain a good training stability and convergence speed of the model, which can make the model better learn the features of the added loss function and therefore optimize the output data of the corresponding features. According to the above experimental results, in the subsequent experiments, the loss coefficients λ1, λ2, λ3 and λ4 of the generator in WGP-IM model can be set to 0.8, 0.1, 0.05 and 0.05, respectively.

6.2 Cryptographic Properties Evaluation of S-Boxes Generated with Different Models

In the first place, the S-box dataset is created by using affine equivalence. Then, DCGAN, WGAN, WGAN-GP, and WGP-IM are respectively built and cross-trained, which takes approximately three days to complete the cross-training phase. After the model training phase is finished, an 8-bit S-box can be generated in a few seconds. In order to evaluate the cryptographic properties of the generated S-boxes, many indicators including Bijection, strict avalanche criterion (SAC), algebraic degree (degF), differential uniformity (δF), differential approximation probability (DAP), nonlinearity (NF), linear approximation probability (LAP), transparency order (TO) [38], and boomerang uniformity (βF) [40] are implemented using Python programming language. And the evaluated results for the generated S-boxes according to the above implemented indicators can be shown in Table 2.

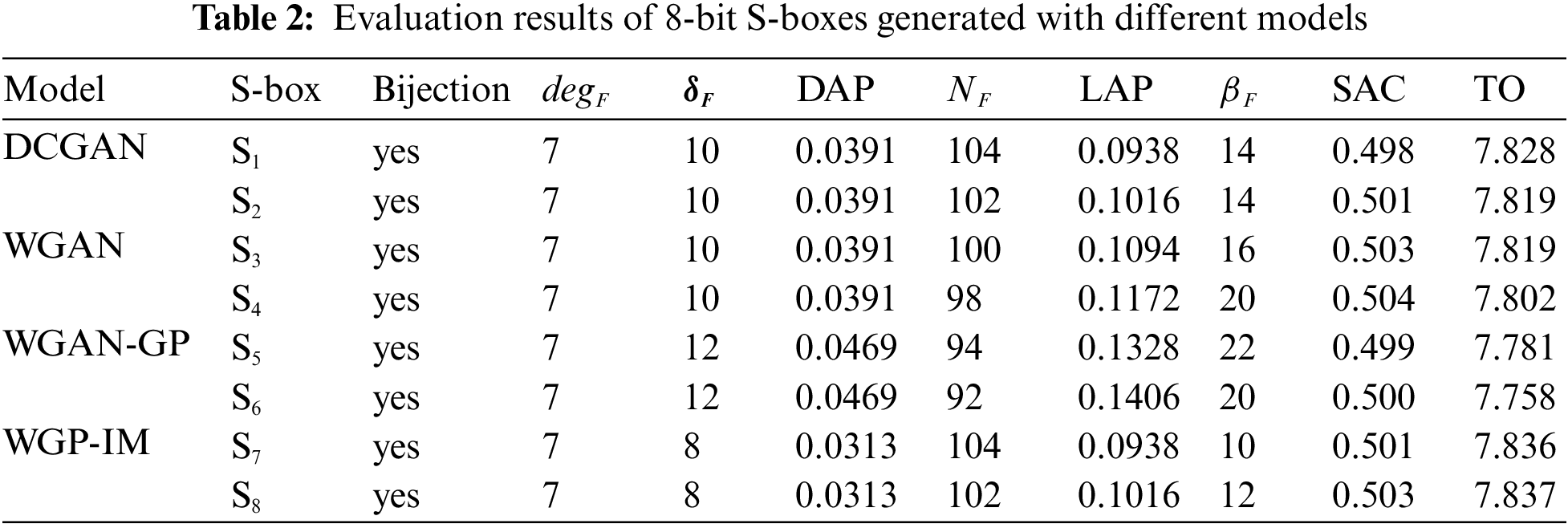
Firstly, we can see from Table 2 that the S-boxes generated by different models satisfy the bijectivity criterion. Secondly, Table 2 shows that as a measure of the ability of the S-box to resist algebraic attacks, the algebraic degree of all S-boxes is 7, this is the optimal value for 8-bit S-boxes.

Differential uniformity is a measure to evaluate the resistance of an S-box to differential cryptanalysis, and the smaller its value, the stronger the resistance of an S-box to differential cryptanalysis. In Table 2, the S-boxes generated by the WGP-IM model have the optimal differential uniformity, which is a significant improvement. Additionally, similar to differential uniformity, DAP also is a measure to evaluate the resistance of an S-box to differential cryptanalysis by describing the probability of output differences given input differences during a differential attack. The Table 2 reveals that the S-boxes generated by the WGP-IM model are the best, with an optimal DAP of 0.0313.

Nonlinearity is a measure used to evaluate the resistance of an S-box to linear analysis, and the larger its value, the stronger the resistance of an S-box to d linear analysis. The optimal nonlinearity of the generated S-boxes can reach 104, which are generated by DCGAN and WGP-IM models. Similarly, LAP describes the probability of a linear approximation, and the smaller its value, the stronger the resistance to linear analysis. The results in Table 2 show that the S-boxes generated by the WGP-IM and DCGAN model have the best results.

According to the method proposed in [40], we calculate the boomerang uniformity of the generated S-boxes, and the result in Table 2 shows that the boomerang uniformity of the S-boxes generated by the WGP-IM model can be the best, which is 10. The SAC is an indicator that can be used to evaluate the influence of the input bit on the output bit of an S-box. If the probability that the output bit variates with the input bit is 0.5, the S-box satisfies SAC. Based on this, the average SAC of each S-box is evaluated, and it can be seen from Table 2 that the SAC of all S-boxes can be close to 0.5, which indicates that the S-boxes generated by different models can have good SAC performance.

TO can be used to evaluate the resistance of the generated S-boxes to differential power analysis (DPA) attacks, the smaller the TO of an S-box, the stronger its ability to resist DPA attacks. According to the definition of TO and Nonlinearity, we know that both indexes are related to the Walsh spectrum. When the value of the Walsh spectrum of an S-box is larger, the TO of the S-box is smaller, and the NF of the S-box is smaller. According to the method proposed in [38], the TO value of the generated S-boxes are calculated, and the results in Table 2 show that the S-box generated by the WGAN-GP model has the smallest TO, which is 7.758.

Overall, Table 2 shows that the S-boxes generated by the improved WGP-IM model have excellent cryptographic properties because lost function constrains are added.

6.3 Comparison of the Cryptographic Properties of Different S-boxes Generated with Different Algorithms

The performance of the above four generated S-Boxes S1, S3, S5, and S7 together with those of existing S-Boxes under different indicators are evaluated, and the evaluation results can be shown in Table 3.

Table 3 shows that most S-boxes can achieve the optimal algebraic degree. Among them, the AES S-box has the optimal differential uniformity, DAP, boomerang uniformity, nonlinearity, and LAP, but its transparency order is the worst. Meanwhile, Inversion1 and Inversion2 have almost the same cryptographic properties as AES because they are generated by inversion and affine transformation based on AES S-boxes, furthermore, their hardware implementation area is smaller than that of AES S-boxes. Of course, the characteristics of S-boxes are similar to the AES S-boxes.

The S-boxes of Iceberg, Clefia, Zorro, Fox, and Fast are generally not good. For the S-boxes generated with intelligent algorithms, the S-box generated with the artificial bee colony (ABC) algorithm can be better than the S-boxes generated by the Genetic algorithm, the Cuckoo algorithm, Iceberg, Clefia, Zorro, Fox, Fast, DCGAN, WGAN, and WGAN-GP. The properties of the S-boxes generated by WGP-IM are approximate to the S-boxes generated by ABC.

In terms of resistance to DPA, compared the S-boxes generated by ABC, Genetic, AES, Inversion1, Inversion2, the S-box generated by the WGP-IM model can also perform well according to its TO value. Of course, the S-box generated by Fast has the smallest TO value. Nevertheless, because the differential uniformity of all S-boxes in Table 3 can be not 256, the S-boxes may be unable to resist Differential Fault Analysis (DFA). If it is necessary for the generated S-boxes to resist DFA, it is necessary to construct a non-zero linear structure for the generated S-boxes.

Compared with existing S-box generation methods, the method based on the WGP-IM model can efficiently generate lots of S-boxes with excellent properties, and it only takes a few seconds to generate an 8-bit S-box after the model is trained. Besides, the method is simpler and has good generality for generating different n-bit S-boxes.

7  Conclusions and Future Works

In this paper, based on the optimized GAN model, an efficient S-Box generation method is proposed. The S-box of AES is used as a sample to construct a data set based on affine equivalence. Moreover, three models based on DCGAN, WGAN, and WGAN-GP are built and cross-training is performed to generate 8-bit S-boxes. Finally, an optimized WGP-IM model based on WGAN-GP is proposed to optimize the cryptographic properties of the generated S-boxes with additional loss functions constraint. The experimental results show that the optimized model can generate S-boxes with better cryptographic properties, and it can generate S-boxes more efficiently than many existing methods. As a new S-box generation method, it can improve the efficiency to generate S-boxes.

In future works, we will apply the loss function constraints to other deep learning models or heuristic algorithms to explore the construction of S-boxes with better cryptographic properties. In addition, we will also consider incorporating more cryptographic indicators into loss function constraints, such as transparency order, etc., and evaluate the cryptographic properties of the generated S-boxes by weighing these constraints.

Acknowledgement: Previous S-boxes generation methods and GAN model are the basis of our research. We are thankful to all the researchers that led us to develop a new method to generate S-boxes.

Funding Statement: This work is supported in part by the National Natural Science Foundation of China (62062026, 62272451), the Innovation Research Team Project of Guangxi in China (2019GXNSFGA245004), the Key Research and Development Program of Guangxi in China (2022AB05044), and the Scientific Research Project of Young Innovative Talents of Guangxi (guike AD20238082).

Author Contributions: Study method and design: RunLian Zhang, Rui Shu; model implementation: Rui Shu; draft manuscript preparation: RunLian Zhang, Rui Shu; analysis and interpretation of results: Rui Shu, XiaoNian Wu; manuscript revise: YongZhuang Wei, HaiLong Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No new dataset was generated or analyzed during this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Millan, A. Clark and E. Dawson, “Boolean function design using hill climbing methods,” Information Security and Privacy, vol. 1587, no. 1, pp. 1–11, 1999. [Google Scholar]

2. X. Ying and J. Yang, “Construction of S-boxes based on genetic algorithm,” Application Research of Computers, vol. 3, pp. 91–93, 2007. [Google Scholar]

3. T. Kapuściński, R. K. Nowicki and C. Napoli, “Comparison of effectiveness of multi-objective genetic algorithms in optimization of invertible S-boxes,” in Artificial Intelligence and Soft Computing, Zakopane, Poland, pp. 466–476, 2017. [Google Scholar]

4. M. N. A. Noughabi and B. Sadeghiyan, “Design of S-boxes based on neural networks,” in 2010 Int. Conf. on Electronics and Information Engineering, Kyoto, Japan, pp. 172–178, 2010. [Google Scholar]

5. X. Zhang, F. Chen, B. Chen and Z. Cao, “A new scheme for implementing S-box based on neural network,” in 2015 Int. Conf. on Computational Science and Computational Intelligence (CSCI), Las Vegas, NV, USA, pp. 571–576, 2015. [Google Scholar]

6. A. Ghoshal, R. Sadhukhan, S. Patranabis, N. Datta, S. Picek et al., “Lightweight and side-channel secure 4 × 4 S-boxes from cellular automata rules,” IACR Transactions on Symmetric Cryptology, vol. 2018, no. 3, pp. 311–334, 2018. [Google Scholar]

7. Ü. Çavuşoğlu, A. Zengin, I. Pehlivan and S. Kaçar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled Zhongtang system,” Nonlinear Dynamics, vol. 87, pp. 1081–1094, 2017. [Google Scholar]

8. A. Manzoor, A. H. Zahid and M. T. Hassan, “A new dynamic substitution box for data security using an innovative chaotic map,” IEEE Access, vol. 10, pp. 74164–74174, 2022. [Google Scholar]

9. W. Zhang, Z. Bao, V. Rijmen and M. Liu, “A new classification of 4-bit optimal S-boxes and its application to PRESENT, RECTANGLE and SPONGENT,” in Int. Workshop on Fast Software Encryption 2015, Istanbul, Turkey, pp. 494–515, 2015. [Google Scholar]

10. Y. Wang, Z. Zhang, L. Y. Zhang, J. Feng, J. Gao et al., “A genetic algorithm for constructing bijective substitution boxes with high nonlinearity,” Information Sciences, vol. 523, pp. 152–166, 2020. [Google Scholar]

11. A. Aljuffri, P. Venkatachalam, C. Reinbrecht, S. Hamdioui and M. Taouil, “S-NET: A confusion based countermeasure against power attacks for SBOX,” in Int. Conf. on Embedded Computer Systems, Samos, Greece, pp. 295–307, 2020. [Google Scholar]

12. R. Zhang, Y. Sun, Y. Wei and Y. Li, “A new automatic search method for cryptographic S-box,” Journal of Computer Research and Development, vol. 57, no. 7, pp. 1415–1423, 2020. [Google Scholar]

13. J. Huang and J. Guan, “Research on properties and neural networks implementation of cellular automata based S-boxes,” Acta Electronica Sinica, vol. 48, no. 12, pp. 2462–2468, 2020. [Google Scholar]

14. A. H. Zahid and M. J. Arshad, “An innovative design of substitution-boxes using cubic polynomial mapping,” Symmetry, vol. 11, pp. 437–447, 2019. [Google Scholar]

15. A. H. Zahid, M. J. Arshad and M. Ahmad, “A novel construction of efficient substitution-boxes using cubic fractional transformation,” Entropy, vol. 21, pp. 245–258, 2019. [Google Scholar] [PubMed]

16. A. H. Zahid, E. A. Solami and M. Ahmad, “A novel modular approach based substitution-box design for image encryption,” IEEE Access, vol. 8, pp. 150326–150340, 2020. [Google Scholar]

17. H. S. Alhadawi, M. A. Majid, D. Lambi and M. Ahmad, “A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 7333–7350, 2021. [Google Scholar]

18. M. Long and L. Wang, “S-box design based on discrete chaotic map and improved artificial bee colony algorithm,” IEEE Access, vol. 9, pp. 86144–86154, 2021. [Google Scholar]

19. B. Rashidi, “Compact and efficient structure of 8-bit S-box for lightweight cryptography,” Integration, the VLSI Journal, vol. 76, pp. 172–182, 2021. [Google Scholar]

20. B. Rashidi, “Lightweight 8-bit S-box and combined S-box/S-box−1 for cryptographic applications,” International Journal of Circuit Theory and Applications, vol. 49, pp. 2348–2362, 2023. [Google Scholar]

21. B. Rashidi, “Lightweight cryptographic S-boxes based on efficient hardware structures for block ciphers,” The ISC International Journal of Information Security, vol. 15, pp. 137–151, 2023. [Google Scholar]

22. M. M. Kermani and A. R. Masoleh, “A high-performance fault diagnosis approach for the AES subbytes utilizing mixed bases,” in 2011 Workshop on Fault Diagnosis and Tolerance in Cryptography, Nara, Japan, pp. 80–87, 2011. [Google Scholar]

23. M. Mozaffari-Kermani and A. Reyhani-Masoleh, “Fault detection structures of the S-boxes and the inverse S-boxes for the advanced encryption standard,” Journal of Electronic Testing, vol. 25, pp. 225–245, 2009. [Google Scholar]

24. A. Aghaie, M. M. Kermani and R. Azarderakhsh, “Fault diagnosis schemes for secure lightweight cryptographic block cipher RECTANGLE benchmarked on FPGA,” in 2016 IEEE Int. Conf. on Electronics, Circuits and Systems (ICECS), Monte Carlo, Monaco, pp. 768–771, 2016. [Google Scholar]

25. M. M. Kermani and R. Azarderakhsh, “Reliable architecture-oblivious error detection schemes for secure cryptographic GCM structures,” IEEE Transactions on Reliability, vol. 68, no. 4, pp. 1347–1355, 2019. [Google Scholar]

26. M. M. Kermani and R. Azarderakhsh, “Reliable hash trees for post-quantum stateless cryptographic hash-based signatures,” in 2015 IEEE Int. Symp. on Defect and Fault Tolerance in VLSI and Nanotechnology Systems (DFTS), Amherst, MA, USA, pp. 103–108, 2015. [Google Scholar]

27. A. Jalali, R. Azarderakhsh, M. M. Kermani and D. Jao, “Supersingular isogeny diffie-hellman key exchange on 64-bit ARM,” IEEE Transactions on Dependable and Secure Computing, vol. 16, no. 5, pp. 902–912, 2019. [Google Scholar]

28. M. Anastasova, R. Azarderakhsh and M. M. Kermani, “Fast strategies for the implementation of SIKE round 3 on ARM Cortex-M4,” IEEE Transactions on Circuits and Systems I: Regular Papers, vol. 68, no. 10, pp. 4129–4141, 2021. [Google Scholar]

29. A. Jalali, R. Azarderakhsh, M. M. Kermani and D. Jao, “Towards optimized and constant-time CSIDH on embedded devices,” in Constructive Side-Channel Analysis and Secure Design, Darmstadt, Germany, pp. 215–231, 2019. [Google Scholar]

30. A. C. Canto, M. M. Kermani and R. Azarderakhsh, “Reliable CRC-based error detection constructions for finite field multipliers with applications in cryptography,” IEEE Transactions on Very Large Scale Integration (VLSI) Systems, vol. 29, no. 1, pp. 232–236, 2021. [Google Scholar]

31. S. B. Sarmadi, M. M. Kermani, R. Azarderakhsh and C. Y. Lee, “Dual-basis superserial multipliers for secure applications and lightweight cryptographic architectures,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 61, no. 2, pp. 125–129, 2014. [Google Scholar]

32. I. J. Goodfellow, J. P. Abadie, M. Mirza, B. Xu, D. W. Farley et al., “Generaive adversarial networks,” ArXiv Preprint ArXiv:1406.2661, 2014. [Google Scholar]

33. A. Radford, L. Metz and S. Chintala, “Unsupervised representation learning with deep convolutional generative adversarial networks,” ArXiv Preprint ArXiv:1511.06434, 2015. [Google Scholar]

34. M. Arjovsky, S. Chintala and L. Bottou, “Wasserstein generative adversarial networks,” in Int. Conf. on Machine Learning, Sydney, Australia, pp. 214–223, 2017. [Google Scholar]

35. I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin and A. Courville, “Improved training of wasserstein GANs,” in Int. Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 5769–5799, 2017. [Google Scholar]

36. J. -Y. Zhu, T. Park, P. Isola and A. A. Efros, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in 2017 IEEE Int. Conf. on Computer Vision (ICCV), Venice, Italy, pp. 2242–2251, 2017. [Google Scholar]

37. T. Karras, S. Laine and T. Aila, “A style-based generator architecture for generative adversarial networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 12, pp. 4217–4228, 2021. [Google Scholar] [PubMed]

38. E. Prouff, “DPA attacks and S-boxes,” in Int. Workshop on Fast Software Encryption, Paris, France, pp. 424–441, 2005. [Google Scholar]

39. G. Leander and A. Poschmann, “On the classification of 4 bit S-boxes,” in Int. Workshop on the Arithmetic of Finite Fields, Madrid, Spain, pp. 156–176, 2007. [Google Scholar]

40. C. Cid, T. Huang, T. Peyrin, Y. Sasaki and L. Song, “Boomerang connectivity table: A new cryptanalysis tool,” in Advances in Cryptology—EUROCRYPT 2018, Tel Aviv, Israel, pp. 683–718, 2018. [Google Scholar]

41. J. Daemen and V. Rijmen, “The advanced encryption standard process,” in The Design of Rijndael, 2nd ed., Berlin, Heidelberg, GER: Springer, pp. 1–8, 2020. [Google Scholar]

42. F. X. Standaert, G. Piret, G. Rouvroy, J. J. Quisquater and J. D. Legat, “ICEBERG: An involutional cipher efficient for block encryption in reconfigurable hardware,” in Int. Workshop on Fast Software Encryption, Delhi, India, pp. 279–298, 2004. [Google Scholar]

43. T. Shirai, K. Shibutani, T. Akishita, S. Moriai and T. Iwata, “The 128-bit blockcipher CLEFIA,” in Int. Workshop on Fast Software Encryption, Luxembourg, Luxembourg, pp. 181–195, 2007. [Google Scholar]

44. B. Gérard, V. Grosso, M. Naya-Plasencia and F. X. Standaert, “Block ciphers that are easier to mask: How far can we go?,” in Cryptographic Hardware and Embedded Systems—CHES 2013, Santa Barbara, CA, USA, pp. 383–399, 2013. [Google Scholar]

45. P. Junod and S. Vaudenay, “FOX: A new family of block ciphers,” in Int. Workshop on Selected Areas in Cryptography, Waterloo, Canada, pp. 114–129, 2004. [Google Scholar]