MOALG: A Metaheuristic Hybrid of Multi-Objective Ant Lion Optimizer and Genetic Algorithm for Solving Design Problems

1  Introduction

In recent years, to solve difficult problems, computers have recently gained a lot of popularity across a variety of industries. The use of computers to solve issues and develop systems is the focus of the field of computer-aided design. In the prior, direct human engagement was needed for solving complex problems. More time and resources were also needed. Similarly, there has been a significant advancement in the field of optimization.

Gaining the most from the other options is what is meant by optimization. Based on the number of objectives taken, optimization problems are mainly classified as Single objective optimization problems (SOOPs) and Multi-objective optimization problems (MOOPs). SOOPs are the problems having one objective and MOOPs have more than one objective. In SOOPs, a single solution, however for MOOPs a set of trade-off solutions called Pareto-optimal solutions is obtained. Edgeworth and Pareto developed the optimality notion for MOOPs in their books in 1881 and 1906, respectively [1,2]. Finding solutions to problems with many objectives is the major goal of this effort, which is MOO. The key problem in MOO is dealing with many objectives, which are generally in conflict with one another. Traditional optimization approaches are based on gradient-based calculation. So, to solve real-world complex problems it becomes difficult [3]. To overcome this problem metaheuristic techniques came into existence and are problem-independent and capable of finding near-optimal solutions [4]. In those stochastic optimization techniques, they begin the optimization procedure by improving a group of randomly selected solutions to a given problem over a predetermined number of steps. Metaheuristic algorithms are categorized based on the natural phenomenon they mimic such as evolutionary algorithms, and swarm intelligence-based algorithms. The fundamental idea behind the application of evolutionary algorithms is survival of the fittest means weak must phased out. The most prominent are Genetic Algorithm (GA) [5], Differential Evolution (DE) [6], and Non-dominated Sorting Genetic Algorithm (NSGA) [7]. Swarm intelligence-based algorithms draw inspiration from the social behavior seen across living organisms. Some of the algorithms can be seen as Grey Wolf Optimizer (GWO) [8], Particle Swarm Optimization (PSO) [9], Artificial Hummingbird Algorithm (AHA) [10], Artificial Bee Colony (ABC) [11], Ant Colony Optimization (ACO) [12], Cuckoo Search (CS) Algorithm [13], ALO [14], Monarch Butterfly Optimization (MBO) [15], Firefly Algorithm (FA) [16]. Some other algorithms are the Moth Search Algorithm (MSA) [17], Thermal Exchange Optimization (TEO) [18], Gravitational Search Algorithm (GSA) [19], and Binary Waterwheel Plant Optimization Algorithm [20]. To address the shortcomings of individual algorithms and enhance their effectiveness, hybrid algorithms are gaining more prominence these days. Some of these algorithms incorporate different areas such as structural optimization [21], combinatorial optimization [22], and energy and renewable energy [23].

The two key components of Metaheuristic algorithms are exploration and exploitation. The perfect balance between them is the performance assessment of any algorithm in solving given MOOPs. Exploration refers to the search for the unexplored area and exploitation refers to the search for the immediate area to deliver an accurate search and convergence.

No Free Lunch theorem (NFL) for optimization encourages experts to develop the algorithms and enhance the ones that are already in use [24]. It asserts that no algorithm is superior to another for all OPs. In response to this, numerous novel algorithms and hybrid ones have been evolved to address challenging OPs of the real world.

This paper proposes the hybrid of MOALO and GA for solving MOOPs. As best, this is the first comprehensive hybrid between MOALO and GA employed to solve MOOPs and design problems. According to the NFL, one single algorithm cannot have the expertise to solve all the existing problems. Real-world problems are more complex nowadays and also have many objectives to satisfy, so to solve those problems more and more algorithms are needed. For handling challenging real-world situations, metaheuristic and hybrid metaheuristic algorithms are preferable. Inspired by this, two metaheuristics have been chosen MOALO and GA, this hybrid will try to overcome the limitation of MOALO of efficiency and accuracy and GA’s computational effort to converge.

This work’s primary contributions can be specified as follows:

•   A hybridization strategy that combines MOALO and GA has been put forward as a means of tackling MOOPs and mitigating the limitations of each method.

•   Next, the use of performance metrics like generational distance (GD), inverted generational distance (IGD), spacing, spread, and hypervolume (HV) has been statistically implemented to test the overall performance in comparison to other existing algorithms.

•   Hybrid has been subjected to testing on constrained, unconstrained benchmark problems and design problems.

The remaining portion of the paper is presented as Section 2 covers the literature. MOALO, GA, and the proposed hybrid MOALG are included in Sections 3 and 4. Section 5 concludes the evaluation metrics involved. Section 6 and Section 7 display the outcomes of the MOALG algorithm. Section 8 solves the engineering design problems and discussion of the outcomes. Section 9 serves as the concluding section, providing a comprehensive summary of the work and exploring potential future research areas.

2  Related Work

2.1 The Beginnings of Multi-Objective Optimization

A general MOOP [25]:

Minimize:fz(o), z=1,2,…Z(1)

Subject to:

hm(o)≥0,m = 1, 2, …D

kn(o)=0, n = 1, 2, …J

Lbk≤uk≤Ubk, k = 1, 2, …v

where Z-Number of objectives, D-Inequality constraints, kn-n-th equality constraints, hm-m-th inequality, J-Equality constraints, V-Number of variables and [Lbk, Ubk]-k-th variable boundaries.

2.2 Existing Metaheuristic Multi-Objective Optimization Algorithms

Different algorithms have been employed to resolve MOOPs including the Multi-objective Bat algorithm [26], the MO version of the bat algorithm that is inspired by bat echolocation. MO Bee Algorithm [27] is inspired by honeybees well-known for their efficient foraging behavior, in which they explore their surroundings in search of the best resources to exploit. Inspired by forensic investigation techniques another well-known algorithm is MO Forensic-based Investigation Algorithm (MOFBI) [28]. Mrijalili’s and other’s hard work gave us an algorithm that follows the hunting behavior of grey wolves (MOGWO) [29]. MOPSO, MO version of PSO [30]. Some of the recently proposed algorithms (see Table 1) are the MOCryStAl [31], MOMVO [32], and MO Thermal Exchange Optimization (MOTEO) algorithm [33].

3  Background of MOALO and GA

3.1 Multi-Objective Ant Lion Algorithm (MOALO)

Seyedali Mirjalili established the ant lion algorithm in 2015. The ALO algorithm is inspired by antlion and ant interaction in the trap. To resolve MOOPs, MOALO [43] is an enhanced version of ALO. Similar to ALO, they have antlions and ants as population.

The fundamental ALO processes to modify ants and antlions position and finally calculate the global optimum for a specific problem of optimization are:

1. Ants are the prime agents of search in ALO. So, in the initialization process, random values are assigned for the ants set.

2. At each iteration each ant’s fitness value is measured by the use of an objective function.

3. It is assumed that antlions are at one place and ants move randomly around antlions and over the search space.

4. Antlion populations are never determined. In the first iteration, antlions are expected to be where the ants are, but as the ants improve, they move to new positions in successive iterations.

5. Each ant is assigned an antlion and the position gets updated as the ant becomes fitter.

6. The best antlion obtained is defined as elite and affects the ant’s movement.

7. By the successive iterations, any antlion that outperforms the elite will get replaced by the elite.

8. The steps numbered 2 and 7 are executed iteratively multiple times until a certain condition is met, which serves as the termination criterion for the algorithm.

9. For the global optimum value the elite antlion’s position and fitness value are considered.

The changes made to MOALO set it apart from ALO since they used archives to store Pareto optimum solutions. To solve this issue of identifying Pareto optimal solutions with large diversity, “leader selection and archive maintenance” have been used. Concerning assessing the distribution of solutions within the archive, the niching technique was utilized. A further modification was the use of the roulette wheel selection and elitism, which was employed in selecting a non-dominated solution.

3.2 Genetic Algorithm

Genetic algorithm (GA) was first discovered by Holland and extensions by Goldberg in the 1960s influenced by Darwin’s evolutionary theory [5]. Firstly, a random set of solutions is generated which are expressed as chromosomes defined as population. After that fitness function of each chromosome is calculated. Solutions that are best in terms of fitness function are selected to generate the next population and undergo “crossover and mutation”. This procedure is executed till the defined condition is satisfied.

Basic operators involved in GA for finding the optimal solutions are defined as:

1. Selection: For the next generation to benefit from good individuals, the selection operator must make sure that they do so. So, the best solution should move to the reproduction process for the next generation, and the bad solution left behind. Selection operators are designated as Tournament Selection, Random Selection, Rank-Based Selection, Elitist Selection, Roulette wheel selection, and Boltzmann Selection.

2. Crossover: Two or more parents’ genetic material are combined to form one or more new individuals. Single-point, Uniform, Two-point, and Arithmetical crossover are the defined operators.

3. Mutation: In GA, maintaining genetic diversity is crucial for the success of the process of optimization. To preserve genetic diversity, one common strategy is to alter “one or more gene values” of the population to create a new individual. This alteration can be done in various ways, such as by randomly selecting a gene value or by using a mutation operator to change the gene value based on a specific probability distribution. The mutation is normally applied at low probability. Lip bit, Non-uniform, Uniform, and Gaussian are mutation operators defined.

4  Hybrid Multi-Objective Ant Lion Optimizer Algorithm with Genetic Algorithm (MOALG)

MOALG is developed in this paper which is a hybridised algorithm. The population of ants and antlions is generated randomly in the proposed hybrid like ALO [14]. Following the identification of each ant and antlion’s fitness value, random walks in the search space’s boundaries and the area of antlions are conducted like MOALO [43]. In MOALG, after the first iteration archive is updated by utilizing the operator’s selection, crossover, and mutation to improve the solutions. After that the solutions again go through the ranking process and the archive is updated. Then, antlion selection, elitism, random walk of ants, and other steps of MOALO are completed.

4.1 Steps of Proposed MOALG

This section involves the steps utilized in the proposed hybrid MOALG. The following steps are:

1. Initialization

The population of ant and antlion is generated by

x=rand(Ub−Lb)+Lb(2)

2. Random walks

The ant’s random walk (RW) is entitled as:

X(t)=[0,cumsum(2r(t1),…,cumsum(2r(tp)−1)](3)

where iteration is illustrated by t as RW steps

The stochastic function is illustrated as r(t)

r(t) is 1 if rand>0.5, otherwise 0, if not. “rand” is used to generate a random number spread uniformly over the range [0,1]. Since Eq. (2) should not be the only equation for position updating of ants and every search space should have a boundary. So RW should be normalized:

Xit=(Xit−ai)×(dit−cit)(bi−ai)+cit(4)

where at the iteration,dit,cit is the maximum and minimum of RW, of ith variable, respectively.

3. Trapping, building trap by antlion

By modifying the RW of ants around antlions, ALO facilitates the entrapment of ants in antlion pits. The equation proposed for this is as follows:

cit=Antlionjt−ct(5)

dit=Antlionjt−dt(6)

Antlionjt demonstrates as the selected antlion’s position jth antlion. To imitate this, ALO employs a Roulette wheel operator. More ants are drawn to the fitter antlions due to the roulette wheel.

4. Sliding ants towards antlion

To simulate the movement of ants towards antlions in a simulation using random walks, it is often necessary to decrease the boundaries of the random walks adaptively. This adaptive adjustment of the boundaries is done to simulate the ants sliding over to the antlion.

ct=ctI(7)

dt=dtI(8)

where

I=1+10wtT(9)

I is a ratio. t, T are the current and maximum number of iterations, respectively.

The parameter “w” in the Eq. (9) for “I” enables precise adjustment of the exploitation accuracy level as shown in Table 2.

5. Catching prey and re-building the pit

The next step is to update the position after catching the ants. The equation below is expressed in this context:

Antlionjt=Antit if f(Antit)>f(Antlionjt)(10)

where t is determined by the current iteration and ith and jth are ant and selected antlion’s position, respectively.

6. Elitism

The final phase is elitism, where the antlion having the fittest value is saved during optimization at each iteration. The following process is shown:

Antit=(RAt+REt)2(11)

RAt and REt-RW around the antlion selected by “roulette wheel” and elite, respectively.

7. Use of leader selection

The solutions with the fewer neighboring solutions are chosen for the antlions.

Pi=cNi(12)

8. Archive maintenance

The solution with the densely packed neighboring is discarded when the archive is full to free up space for new solutions.

Pi=Nic(13)

where c > 1 and is a constant. At ith solution, Ni is a variety of neighboring solutions.

After finding the fitness of each ant and elite. In MOALG, the Archive has been updated by applying the ranking process. From the archive, two solutions are selected as parent 1 and parent 2 by the roulette wheel selection. The new generation (offspring) is generated by applying a one-point crossover operator with a certain probability Pc as 0.9 [44].

After that, elements of the new offspring mutate at a certain probability Pm as 0.01. The ranking process is again applied in the archive which is followed by the selection of the elite. After that, all the steps are followed same as of MOALO.

A random walk around antlion includes steps Eqs. (3) and (4) and which includes antlion’s pits entrapment Eqs. (5) and (6). After that, the building trap and ants falling towards the antlion include Eqs. (7) and (8). The last step includes a random walk around the antlion and elite in which the position of the ant is updated including Eq. (11). For storing the non-dominated solutions, an archiving approach has been employed and for finding the high diversity among the Pareto optimal solutions niching have been employed. This antlion is composed of individuals from the least populated neighboring and the solutions with the densely packed neighboring are discarded when the archive is full to free up space for new solutions Eqs. (12) and (13). The computational complexity is entitled O(mn2), where m and n are some objectives and individuals, respectively. The Pseudocode of MOALG is presented in Algorithm 1 and the flowchart is shown in Fig. 1.

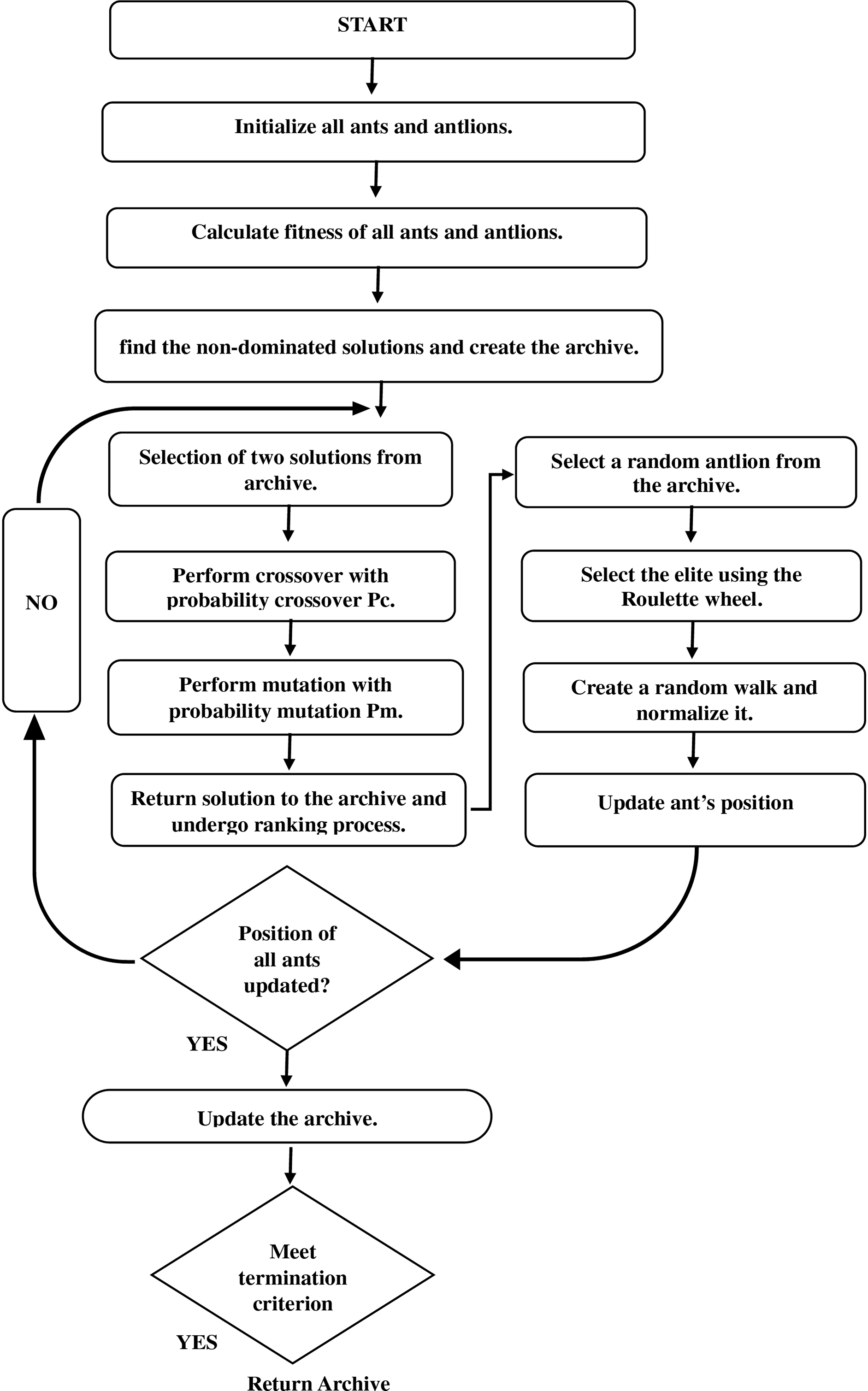
Figure 1: Flowchart of MOALG

5  Evaluation Method

In this section, the MOALG algorithm’s efficiency for test problem having many objectives, and unconstrained and constrained problem have been assessed. These problems are employed to test the MOO handling of non-convex and non-linear situations. The algorithm was programmed in MATLAB 2021. To complete the work at that point, the computer’s following features are employed: 8 GB of RAM of Intel Core i9 with CPU (1.19 GHz).

5.1 Performance-Based Metrics for Multiple-Objective

When analyzing the Pareto-optimal solutions those retrieved by the MOO techniques are frequently evaluated using the following criteria [45]:

1. Uniformity: The Pf has an evenly distributed range of good solutions.

2. Convergence: The solutions that come closest to the Pf are the best.

3. Coverage: The exact solution should cover the Pf as much as possible.

5.1.1 GD

Veldhuizen (1998) addressed the GD [46] to evaluate the distance between the obtained and true Pf.

GD=∑p=1mdim(14)

di=((∑i=1n(PfI,po−PfI,pt)2)12)

where m,n are the number of Pareto-optimal solution and objective functions, respectively. PfI,po and PfI,pt indicate pth obtained Pareto front (OPF) and the nearest point on true Pareto front (TPF) for the i-th objective. An algorithm with more effective convergence and coverage has a lower GD value.

5.1.2 IGD

It is common practice to compare meta-heuristics using IGD [47], which evaluates distance calculations from each reference point.

IGD=∑i=1ndi2m(15)

5.1.3 Spacing (S)

Spacing [48,49] is entitled as

S=1m−1∑p=2m(Dp−D¯)2(16)

where in the OPF, Dp represents the absolute difference between two consecutive solutions and is defined as

Dp=|∑in|Pfi,p−1o−Pfi,pt|

D¯ is an average of calculated Dp values. Here, for the OPF small value of S indicates uniform spacing. A smaller spacing value corresponds to an improved uniform distribution of solutions.

5.1.4 Spread (Δ)

Deb in 2002 [50] addressed this indicator and used it to determine how extensively the generated non-dominated solutions have been spread out. It is defined in mathematical form as

Δ=∑j=1ndj+∑p=2m|dp−d¯|∑j=1ndj+(m−1)d¯(17)

where dj-Euclidean distance between TPF and OPF. dp-Euclidean distance between two consecutive Pf and d¯-an average of calculated dp.

A smaller value of spread denotes a more diverse and even distribution of the non-dominated solutions.

5.1.5 HV

Brest in 2006 [51] addressed this indicator and used it to quantify the solution spreading in the objective space by measuring the volume occupied by them.

HV=⋃i=1Kvi(18)

K-non-dominated set of solutions and vi-hypercube.

For, each xi belongs to K, using a reference point W and for vi at diagonal corners place the solution xi. So, vi union is used to calculate HV. An algorithm having a large value of HV is considered to be better.

5.2 Experimental Setup

The results of MOALO, MSSA, MOPSO, MOMVO, and MOCryStAl have been compared to MOALG. The Pareto optimal curve of MOALO and MOALG is shown in Fig. 2. The initial parameter for each algorithm is displayed in Table 3. A maximum of 1000 iterations and 100 search agents and an archive size of 100 and 30 independent runs were allotted for each experiment.

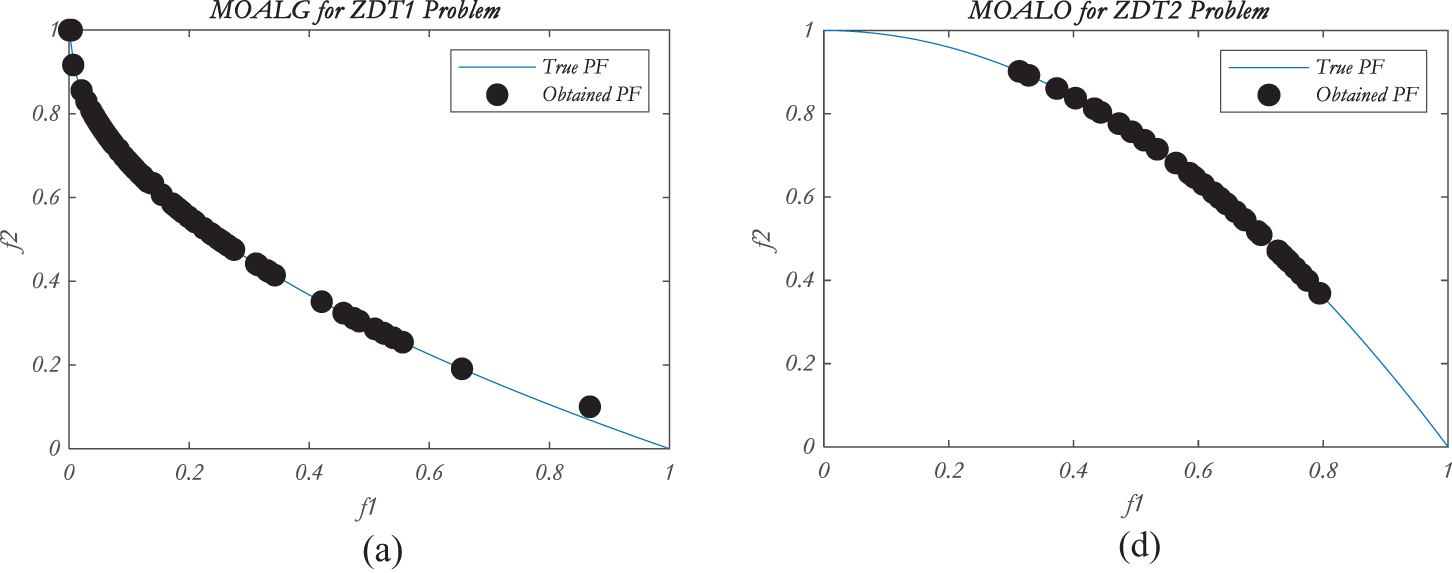
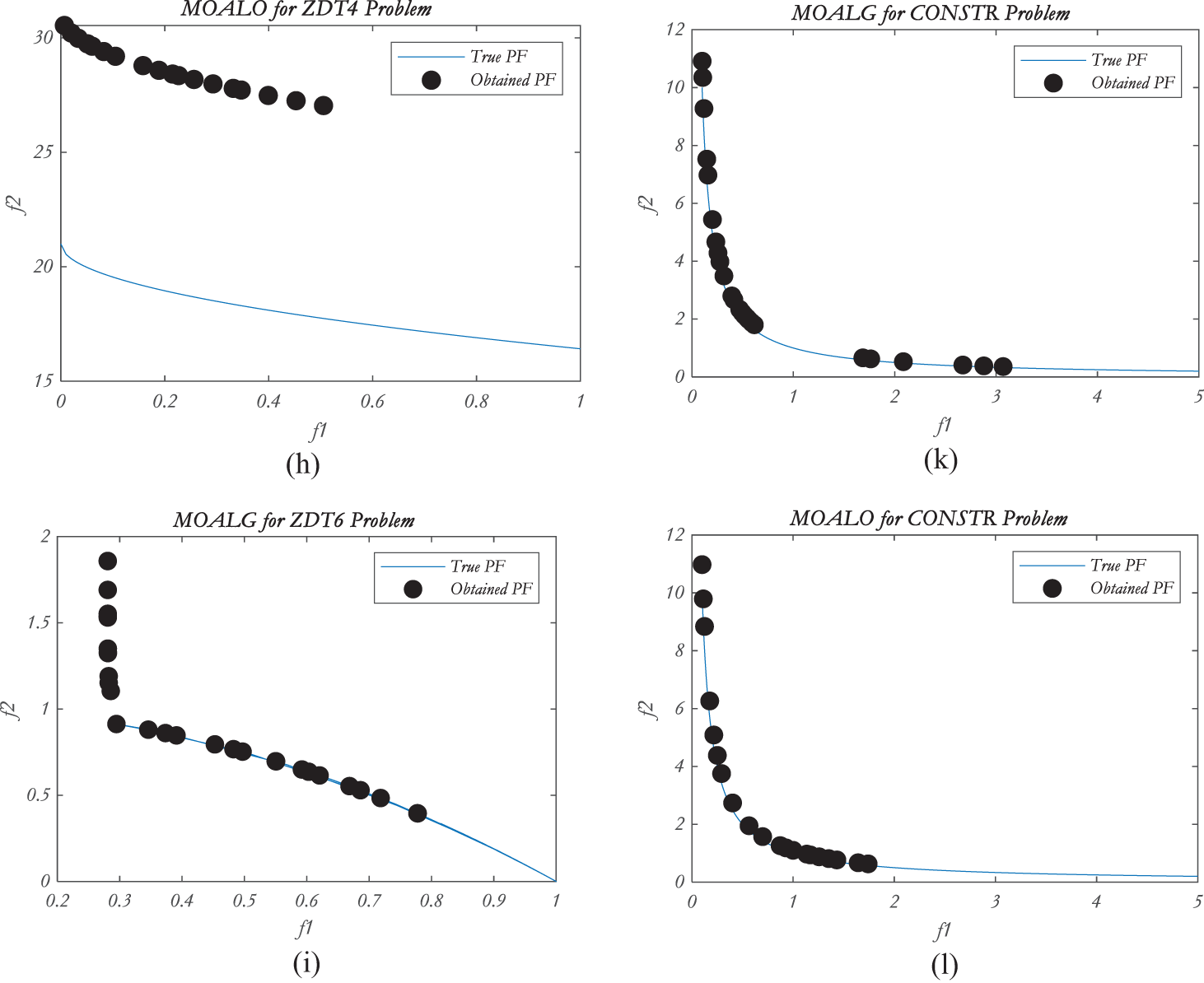
Figure 2: Pareto optimal front for the ZDT problems and CONSTR

6  Results

This section examines the performance of existing algorithms on various benchmark functions constrained and unconstrained problems for performance metrics such as spread, spacing, HV, GD, and IGD. MOALG outperforms various algorithms in GD and IGD results. Spread, spacing, and HV results indicate convergence and diversity, MOALG surpasses the MOALO algorithm on various benchmark functions.

Tables 4 and 5 display the outcomes of GD and IGD performance metrics, demonstrating superior convergence. In Table 4, for the unconstrained problem ZDT1, ZDT4, ZDT6 [52] and for the constrained CONSTR [53] problem, MOALG outperforms other existing algorithms. In Table 5, for the unconstrained problems, ZDT3, ZDT4, and ZDT6 the proposed hybrid MOALG gives competitive results. As well as for the constrained problem CONSTR it proves to be the best in terms of mean which shows MOALG has better convergence property.

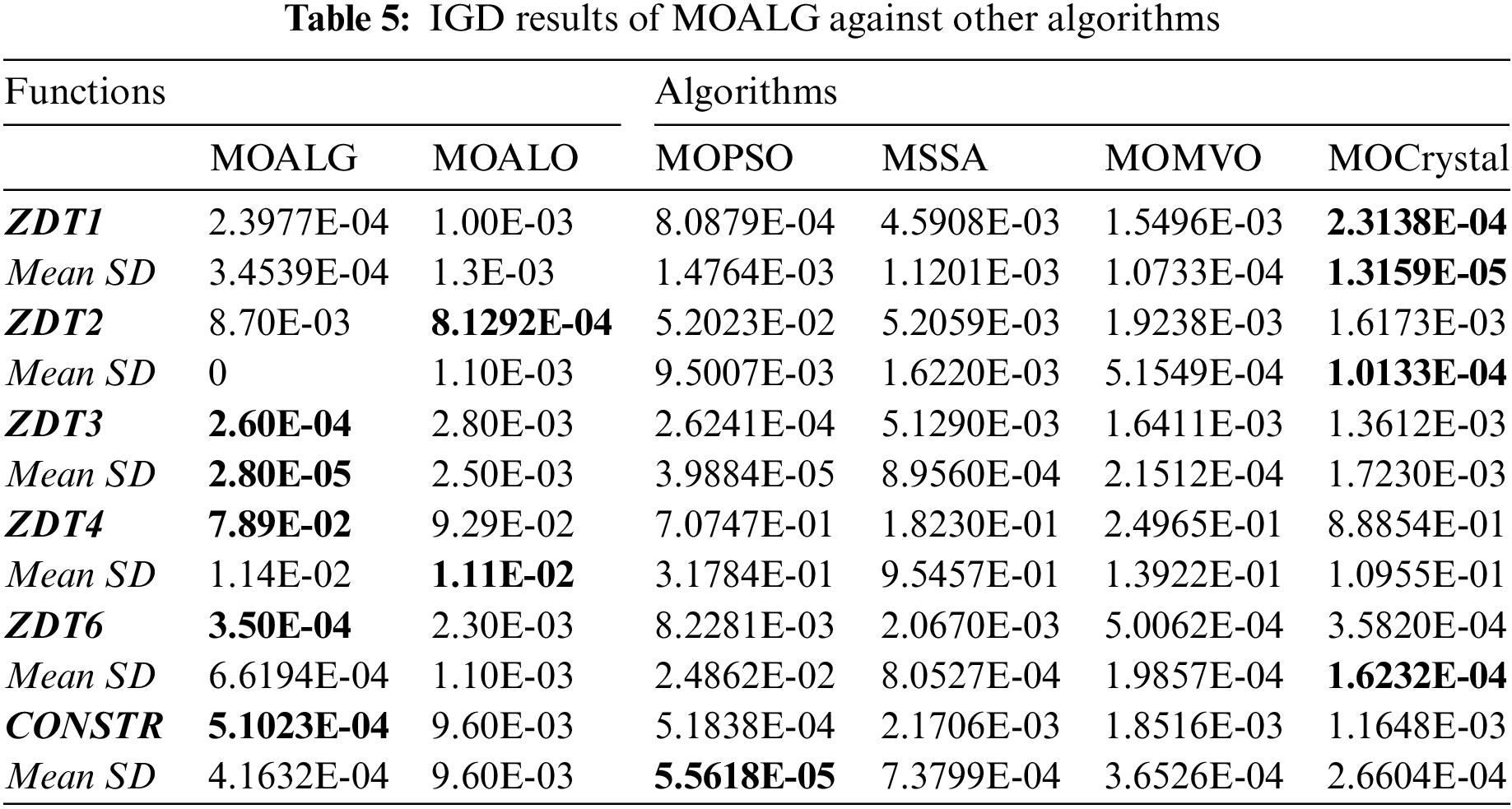
In Table 6, the results of the spread indicator in terms of mean have been displayed. So, due to the diversity of non-dominated solutions and better distribution MOALG outperforms MOALO for all constrained and unconstrained problems. Table 7 shows spacing which means better uniform distribution of solutions, MOALO has better results in all problems except ZDT3.

Table 8 shows the results of hypervolume, which means that if any algorithm has a higher HV value that means better convergence and diversity simultaneously. MOALG obtained a better HV score for four problems ZDT1, ZDT3, ZDT4, and CONSTR, and for the rest of the problems, MOALO proved to be better. Fig. 2 shows the visualization of the Obtained and True Pareto fronts. For the ZDT1 problem, MOALG has obtained the efficient Pareto front as compared to the MOALO concerning the convergence to the TPF and distributing the non-dominated solutions to the entire PF. For ZDT2, MOALG did not perform well and has a disconnected Obtained PF. The test problem, ZDT3, MOALG, and MOALO have competitive results, but if the results of HV are seen, it is obvious that for convergence and diversity together MOALG performs better than MOALO. Similarly, for ZDT4 both the algorithms are not performing well but MOALG has better results than MOALO for GD, Spread, and HV performance metrics. For the rest of the problem, ZDT6 the proposed algorithm solutions that are non-dominated are closer to True PF, and the same for CONSTR which is a constrained problem solutions are diverse on True PF and convergence can also be seen in the Fig. 2. As a result, it can be concluded that MOALG is capable of creating better solutions those are close to True PF and performs better than MOALO. The time taken by MOALG to complete 1000 iterations is 1 min 3 s whereas by MOALO is 33 s. Which is slightly more in MOALG. This can be ignored as the results of MOALG are better than MOALO.

7  Results Obtained for Engineering Design Problem

Two design problems have been solved. Four-bar truss design problem [54] is a structural optimization problem where objective functions are volume and displacement. The cross-sectional area relates to design variables. Welded beam [55] has objective functions fabrication cost and deflection of the beam which should be minimized.

7.1 Experimental Results

Tables 9 and 10 show that MOALG surpasses other algorithms in design problems. The findings of the four-bar truss design problem are provided in Table 9, and the results of the welded beam design problem are provided in Table 10. Fig. 3 gives the representation of True PF and Obtained PF. MOALG shows better performance and coverage in truss-bar problems. For welded beam problems, hybrid outperforms another algorithm for GD, IGD, Spread, and HV showing convergence and diversity together. The notations used for MOALG are represented in Table 11.

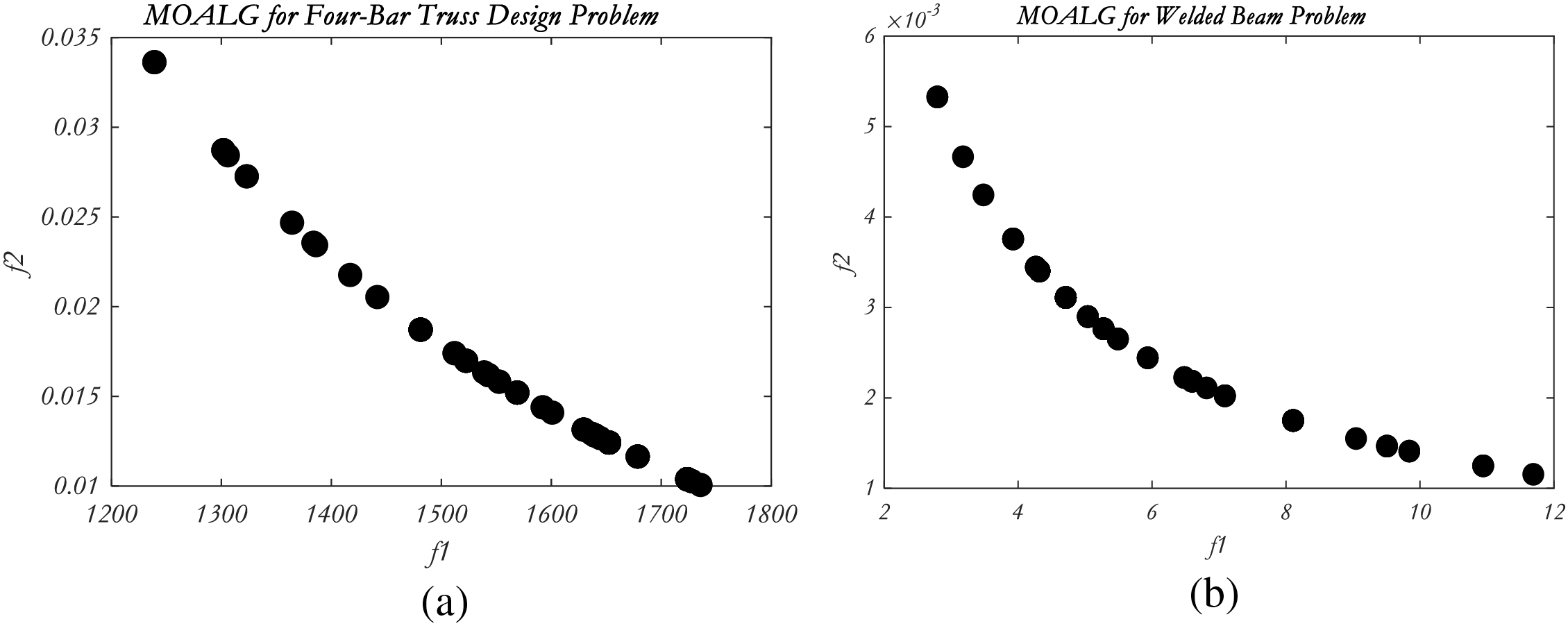
Figure 3: True PF and obtained PF for four-bar truss and welded beam design problem

8  Conclusion

This paper proposed a hybrid of MOALO and GA named MOALG. Selection mechanism and crossover, mutation operator have been used for bettering of non-dominated solutions in the archive. The primary objective behind the development of MOALG is to overcome the limitations of ALO of getting caught in a local optimum and more computational effort to converge GA. The algorithm tests various problems using performance metrics such as GD, IGD, Spread, Spacing, and HV. For the comparison, the other competitive algorithms were utilized as MOALO, MOPSO, MSSA, MOMVO, and MOCryStAl. MOALG has been observed to benefit from strong convergence and coverage. MOALG has performed better than MOALO which can be seen through the numerical and statistical results. It can be viewed that MOALG can also find the Pareto optimal front of any shape. Another conclusion is that as per the NFL theorem, MOALG can perform better for other problems as well.

For future work, MOALG can be tested for various engineering design problems and many other real-life problems of multi-objectives.

Acknowledgement: The authors wish to acknowledge the resources of Chandigarh University, Mohali, India, Soonchunhyang University, Korea, Michigan State University, USA, and Mansoura University, Egypt for carrying out the research work.

Funding Statement: This work was supported by the National Research Foundation of Korea (NRF) Grant funded by the Korea government (MSIT) (No. RS-2023-00218176), and the Soonchunhyang University Research Fund.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: R. Sharma, A. Pal, N. Mittal; data collection: S. Van, L. Kumar; analysis and interpretation of results: R. Sharma, Y. Nam; draft manuscript preparation: L. Kumar, R. Sharma, A. Pal, M. Abouhawwash. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is available from the authors upon reasonable request from the authors.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. G. D. Allen and F. Y. Edgeworth, “Mathematical psychics,” Econ. J., vol. 42, no. 166, pp. 307, 1932. [Google Scholar]

2. V. Pareto, Manual of Political Economy. Oxford, England: Oxford University Press, 1906. [Google Scholar]

3. S. Kumar, G. G. Tejani, and S. Mirjalili, “Modified symbiotic organisms search for structural optimization,” Eng. Comput., vol. 35, no. 4, pp. 1269–1296, 2019. doi: 10.1007/s00366-018-0662-y. [Google Scholar] [CrossRef]

4. S. M. Almufti, “Historical survey on metaheuristics algorithms,” Int. J. Sci. World, vol. 7, no. 1, pp. 1–12, 2019. [Google Scholar]

5. J. H. holland. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. London, England: MIT Press, 1992. [Google Scholar]

6. K. Storn and R. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” J. Global Optim., vol. 1, pp. 341–359, 1997. doi: 10.1023/A:1008202821328. [Google Scholar] [CrossRef]

7. N. Srinivas and K. Deb, “Muiltiobjective optimization using nondominated sorting in genetic algorithms,” Evol. Comput., vol. 2, no. 3, pp. 221–248, 1994. [Google Scholar]

8. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007. [Google Scholar] [CrossRef]

9. R. Eberhart and J. Kennedy, “New optimizer using particle swarm theory,” in Proc. Sixth Int. Symp. Micro Mach. Human Sci., Nagoya, Japan, 1995, pp. 39–43. [Google Scholar]

10. W. Zhao, L. Wang, and S. Mirjalili, “Artificial hummingbird algorithm: A new bio-inspired optimizer with its engineering applications,” Comput. Methods. Appl. Mech. Eng., vol. 388, pp. 114194, 2022. doi: 10.1016/j.cma.2021.114194. [Google Scholar] [CrossRef]

11. B. Akay and D. Karaboga, “Artificial bee colony algorithm for large-scale problems and engineering design optimization,” J. Intell. Manuf., vol. 23, no. 1, pp. 1001–1014, 2012. doi: 10.1007/s10845-010-0393-4. [Google Scholar] [CrossRef]

12. M. Dorigo and K. Socha, “Ant colony optimization,” in Handbook of Approximation Algorithms and Metaheuristics, Santa Barbara, USA: CRC Press, 2007, vol. 1, pp. 26-1–26-14. [Google Scholar]

13. X. S. Yang and S. Deb, “Engineering optimisation by cuckoo search,” Int. J. Math. Model. Numer. Optim., vol. 1, no. 4, pp. 330–343, 2010. doi: 10.1504/IJMMNO.2010.035430. [Google Scholar] [PubMed] [CrossRef]

14. S. Mirjalili. “The ant lion optimizer,” Adv. Eng. Softw., vol. 83, pp. 80–98, 2015. doi: 10.1016/j.advengsoft.2015.01.010. [Google Scholar] [CrossRef]

15. G. G. Wang, S. Deb, and Z. Cui, “Monarch butterfly optimization,” Neural. Comput. Appl., vol. 31, no. 7, pp. 1995–2014, 2019. [Google Scholar]

16. X. Yang, “Firefly algorithm, stochastic test functions and design optimisation,” Int. J. Bio-Inspired Computing, vol. 2, no. 2, pp. 78–84, 2010. [Google Scholar]

17. G. G. Wang. “Moth search algorithm: A bio-inspired metaheuristic algorithm for global optimization problems,” Memet. Comput., vol. 10, no. 2, pp. 151–164, 2018. doi: 10.1007/s12293-016-0212-3. [Google Scholar] [CrossRef]

18. A. Kaveh and A. Dadras, “A novel meta-heuristic optimization algorithm: Thermal exchange optimization,” Adv. Eng. Softw., vol. 110, pp. 69–84, 2017. doi: 10.1016/j.advengsoft.2017.03.014. [Google Scholar] [CrossRef]

19. E. Rashedi, H. Nezamabadi-pour, and S. Saryazdi, “GSA: A gravitational search algorithm,” Inf. Sci., vol. 179, no. 13, pp. 2232–2248, 2009. doi: 10.1016/j.ins.2009.03.004. [Google Scholar] [CrossRef]

20. A. A. L. I. Alhussan et al., “A binary waterwheel plant optimization algorithm for feature selection,” IEEE Access, vol. 11, pp. 94227–94251, 2023. [Google Scholar]

21. D. Golbaz, R. Asadi, E. Amini, H. Mehdipour, and M. Nasiri, “Layout and design optimization of ocean wave energy converters: A scoping review of state-of-the-art canonical, hybrid, cooperative, and combinatorial optimization methods,” Energy Rep., vol. 8, pp. 15446–15479, 2022. doi: 10.1016/j.egyr.2022.10.403. [Google Scholar] [CrossRef]

22. E. H. Houssein, M. A. Mahdy, M. J. Blondin, D. Shebl, and W. M. Mohamed, “Hybrid slime mould algorithm with adaptive guided differential evolution algorithm for combinatorial and global optimization problems,” Expert Syst. Appl., vol. 174, pp. 114689, 2021. doi: 10.1016/j.eswa.2021.114689. [Google Scholar] [CrossRef]

23. B. Alexander and M. Wagner, “Optimisation of large wave farms using a multi-strategy evolutionary framework,” in Proc. Genet. Evol. Comput., New York, USA, 2020, pp. 1150–1158. [Google Scholar]

24. D. Whitley and J. Rowe, “Focused no free lunch theorem,” in Proc. 10th Annual Conf. Genet. Evol. Comput., Atlanta, GA, USA, 2008, pp. 811–818. [Google Scholar]

25. P. Ngatchou, A. Zarei, and M. A. El-Sharkawi, “Pareto multi objective optimization,” in Proc. 13th Int. Conf. Intell. Syst. Appl. Power Syst., Arlington, VA, USA, 2005, pp. 84–91. [Google Scholar]

26. X. S. Yang. “Bat algorithm for multi-objective optimisation,” Int. J. Bio-Inspir. Com., vol. 3, no. 5, pp. 267–274, 2011. [Google Scholar]

27. R. Akbari, R. Hedayatzadeh, K. Ziarati, and B. Hassanizadeh, “A multi-objective artificial bee colony algorithm,” Swarm Evol. Comput., vol. 2, pp. 39–52, 2012. doi: 10.1016/j.swevo.2011.08.001. [Google Scholar] [CrossRef]

28. J. S. Chou and D. N. Truong, “Multiobjective forensic-based investigation algorithm for solving structural design problems,” Autom. Constr., vol. 134, pp. 104084, 2022. doi: 10.1016/j.autcon.2021.104084. [Google Scholar] [CrossRef]

29. S. Mirjalili, S. Saremi, S. M. Mirjalili, and L. D. S. Coelho, “Multi-objective grey wolf optimizer: A novel algorithm for multi-criterion optimization,” Expert Syst. Appl., vol. 47, pp. 106–119, 2016. doi: 10.1016/j.eswa.2015.10.039. [Google Scholar] [CrossRef]

30. C. A. Coello and M. S. Lechuga, “MOPSO: A proposal for multiple objective particle swarm optimization,” in Proc. Congress Evol. Comput., NW, Washington DC, USA, vol. 2, 2002, pp. 1051–1056. [Google Scholar]

31. N. Khodadadi, M. Azizi, S. Talatahari, and P. Sareh, “Multi-objective crystal structure algorithm (MOCryStAlIntroduction and performance evaluation,” IEEE Access, vol. 9, pp. 117795–117812, 2021. [Google Scholar]

32. S. Mirjalili, P. Jangir, S. Z. Mirjalili, S. Saremi, and I. N. Trivedi, “Optimization of problems with multiple objectives using the multi-verse optimization algorithm,” Knowl.-Based Syst., vol. 134, pp. 50–71, 2017. [Google Scholar]

33. S. Kumar, P. Jangir, G. G. Tejani, and M. Premkumar, “MOTEO: A novel physics-based multiobjective thermal exchange optimization algorithm to design truss structures,” Knowl.-Based Syst., vol. 242, pp. 108422, 2022. doi: 10.1016/j.knosys.2022.108422. [Google Scholar] [CrossRef]

34. A. Kaveh, T. Bakhshpoori, and E. Afshari, “An efficient hybrid particle swarm and swallow swarm optimization algorithm,” Eng. Comput., vol. 143, pp. 40–59, 2014. doi: 10.1016/j.compstruc.2014.07.012. [Google Scholar] [CrossRef]

35. J. Luo, Y. Qi, J. Xie, and X. Zhang, “A hybrid multi-objective PSO-EDA algorithm for reservoir flood control operation,” Appl. Soft Comput., vol. 34, pp. 526–538, 2015. doi: 10.1016/j.asoc.2015.05.036. [Google Scholar] [CrossRef]

36. C. Lu, L. Gao, X. Li, Q. Pan, and Q. Wang, “Energy-efficient permutation flow shop scheduling problem using a hybrid multi-objective backtracking search algorithm,” J. Clean. Prod., vol. 144, pp. 228–238, 2017. doi: 10.1016/j.jclepro.2017.01.011. [Google Scholar] [CrossRef]

37. I. Tariq et al., “MOGSABAT: A metaheuristic hybrid algorithm for solving multi-objective optimisation problems,” Neural. Comput. Appl., vol. 32, no. 8, pp. 3101–3115, 2020. [Google Scholar]

38. G. Dhiman, “MOSHEPO: A hybrid multi-objective approach to solve economic load dispatch and micro grid problems,” Appl. Intell., vol. 50, no. 1, pp. 119–137, 2020. [Google Scholar]

39. A. Mohammadzadeh, M. Masdari, F. S. Gharehchopogh, and A. Jafarian, “A hybrid multi-objective metaheuristic optimization algorithm for scientific workflow scheduling,” Clust. Comput., vol. 24, no. 2, pp. 1479–1503, 2021. doi: 10.1007/s10586-020-03205-z. [Google Scholar] [CrossRef]

40. M. A. Deif, A. A. A. Solyman, M. H. Alsharif, S. Jung, and E. Hwang, “A hybrid multi-objective optimizer-based SVM model for enhancing numerical weather prediction: A study for the seoul metropolitan area,” Sustain., vol. 14, no. 1, pp. 1–17, 2022. doi: 10.3390/su14010296. [Google Scholar] [CrossRef]

41. M. H. Marghny, E. A. Zanaty, W. H. Dukhan, and O. Reyad, “A hybrid multi-objective optimization algorithm for software requirement problem,” Alex. Eng. J., vol. 61, no. 9, pp. 6991–7005, 2022. doi: 10.1016/j.aej.2021.12.043. [Google Scholar] [CrossRef]

42. R. K. Avvari and V. D. M. Kumar, “A novel hybrid multi-objective evolutionary algorithm for optimal power flow in wind, PV, and PEV systems,” J. Oper. Autom. Power Eng., vol. 11, no. 2, pp. 130–143, 2023. [Google Scholar]

43. S. Mirjalili, P. Jangir, and S. Saremi, “Multi-objective ant lion optimizer: A multi-objective optimization algorithm for solving engineering problems,” Appl. Intell., vol. 46, no. 1, pp. 79–95, 2017. [Google Scholar]

44. A. Yaghoubzadeh-Bavandpour, O. Bozorg-Haddad, B. Zolghadr-Asli, and V. P. Singh, “Computational intelligence: An introduction,” Stud. Comp. Intell., vol. 1043, pp. 411–427, 2022. [Google Scholar]

45. J. S. Chou and D. N. Truong, “Multiobjective optimization inspired by behavior of jellyfish for solving structural design problems,” Chaos, Solit. Fractals, vol. 135, pp. 109738, 2020. doi: 10.1016/j.chaos.2020.109738. [Google Scholar] [CrossRef]

46. J. A. Nuh, T. W. Koh, S. Baharom, M. H. Osman, and S. N. Kew, “Performance evaluation metrics for multi-objective evolutionary algorithms in search-based software engineering: Systematic literature review,” Appl. Sci., vol. 11, no. 7, pp. 1–25, 2021. [Google Scholar]

47. N. Khodadadi, L. Abualigah, E. S. M. El-Kenawy, V. Snasel, and S. Mirjalili, “An archive-based multi-objective arithmetic optimization algorithm for solving industrial engineering problems,” IEEE Access, vol. 10, no. 1, pp. 106673–106698, 2022. doi: 10.1109/ACCESS.2022.3212081. [Google Scholar] [CrossRef]

48. A. J. Nebro, J. J. Durillo, and C. A. C. Coello, “Analysis of leader selection strategies in a multi-objective particle swarm optimizer,” in Proc. IEEE Congr. Evol. Comput., Cancun, Mexico, 2013, pp. 3153–3160. [Google Scholar]

49. J. D. Knowles and D. W. Corne, “Approximating the nondominated front using the pareto archived evolution strategy,” Evol. Comput., vol. 8, no. 2, pp. 149–172, 2000. [Google Scholar] [PubMed]

50. A. Zhou, Y. Jin, Q. Zhang, B. Sendhoff, and E. Tsang, “Combining model-based and genetics-based offspring generation for multi-objective optimization using a convergence criterion,” in Proc. IEEE Congr. Evol. Comput., Vancouver, BC, Canada, 2006, pp. 892–899. [Google Scholar]

51. J. Brest, S. Greiner, B. Bošković, M. Mernik, and V. Zumer, “Self-adapting control parameters in differential evolution: A comparative study on numerical benchmark problems,” IEEE Trans. Evolut. Comput., vol. 10, no. 6, pp. 646–657, 2006. [Google Scholar]

52. E. Zitzler, K. Deb, and L. Thiele, “Comparison of multiobjective evolutionary algorithms: Empirical results,” Evol. Comput., vol. 8, no. 2, pp. 173–195, 2000. doi: 10.1162/106365600568202. [Google Scholar] [PubMed] [CrossRef]

53. K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, “A fast and elitist multiobjective genetic algorithm: NSGA-II,” IEEE Trans. Evol. Comput., vol. 6, no. 2, pp. 182–197, 2002. doi: 10.1109/4235.996017. [Google Scholar] [CrossRef]

54. C. A. Coello and G. T. Pulido, “Multiobjective structural optimization using a microgenetic algorithm,” Struct. Multidiscipl. Optim., vol. 30, no. 5, pp. 388–403, 2005. doi: 10.1007/s00158-005-0527-z. [Google Scholar] [CrossRef]

55. T. Ray and K. M. Liew, “A swarm metaphor for multiobjective design optimization,” Eng. Optim., vol. 34, no. 2, pp. 141–153, 2002. [Google Scholar]

Appendix

Appendix A: Multi-Objective Unconstrained ZDT Test Problems

ZDT1:

f1=u1,f2=h(1−f1h) where h=1+9d−1∑i=2dui

0≤ui≤1,1≤i≤30

ZDT2:

f1=u1,f2=h(1−(f1h)2)where h=1+9d−1∑i=2dui

0≤ui≤1,1≤i≤30

ZDT3:

f1=u1,f2=h(1−f1h−f1hsin⁡(10πf1))where h=1+9d−1∑i=2dui

0≤ui≤1,1≤i≤30

ZDT4:

f1=u1,f2=h(1−f1h)where h=1+10(d−1)+∑i=2d(ui2−10cos⁡(4πui))

0≤u1≤1,1≤i≤10,−5≤ui≤5

ZDT6:

f1=1−exp⁡(−4u1)sin6⁡(6πu1),f2=h(1−(f1h)2)where h=1+9(∑i=2duid−1)0.25

0≤i≤10,0≤ui≤1

Appendix B: Multi-Objective Constrained Test Problems

CONSTR:

A convex Pareto-front is obtained here equation containing two constraints:

f1=x1,f2=1+x2x1 and g1=6−(x2+9x1)

0.1≤x1≤1,0≤x2≤5

Appendix C: Multi-Objective Engineering Design Problems

FOUR-BAR-TRUSS DESIGN PROBLEM:

This is a well-known field in structural optimization were f1 and f2 are volume and displacement.

Minimize:

f1=200×x1+sqrt(2×x2+sqrt(x3)+x4) and

f2=0.01×((2x1)+(2×sqrt(2)x2)−(2×sqrt(2)x3)+(2x1))

1≤x1≤3,1.4142≤x2≤3,1.4142≤x3≤3,1.4142≤x4≤3

WELDED BEAM DESIGN PROBLEM:

Minimize:f1=1.10471×x12 × x2+0.04811×x3×x4×(14+x2)

Minimize:f2=65856000/(30×106×x4×x33)

where g1(x)=τ−13600, g2(x)=σ−30000, g3(x)=x1−x4, g4(x)=6000−P

0.125≤x1≤5, 0.1≤x2≤10, 0.1≤x3≤10, 0.125≤x4≤5

Q=6000×(14+x22), D=sqrt×(x224+(x1+x3)2)4),

J=2×(x1×x2×sqrt(2)×(x2212+(x1+x3)24)), α=6000sqrt(2)×x1×x2, β=Q×DJ