Multivariate Broadcast Encryption with Group Key Algorithm for Secured IoT

1  Introduction

The Internet of Things (IoT) is ease technology in which devices are associated to the network and may communicate with one another over it. In a number of traditions, the Internet of Things (IoT) is infiltrating our life. Technology has become an indispensible aspect of our life, from smart watches to isolated security doors. Its influence upon our life would almost certainly continue to grow. Transmitting information to a collection of things attached via networks is a critical component of most IoT applications.

To put it another way, an IoT platform necessitates multi-hop communication delicate and fragile information that is vulnerable to data loss. Broadcast Encryption (BE) is a fast and strong cryptographic building block that allows a broadcaster to transmit encrypted information to a group of authorized strategy, providing a natural approach to IoT. BE enables broadcasters to effectively multiplex. It also assures the safety and privacy of the information of the consumers [1].

BE [2] was the first to demonstrate a cryptographic device. Reference [3,4] enables again for distribution of encrypted files over a broadcast station in such a way that only authorized customers can recover it. With considerable detail, given a subset S of the world, a transmitter can encrypt content to S using public keys, and the client could only recover encoded material if something corresponds to the set S with their secret keys. Additional quality which BE should get is collusion resistance, which means that even if all clients (not in S) conspire collectively, still would not be able to learn anything at all about the transmitted information (this is known as collusion resistant BE). The author [5] created a fully collusion-resistant BE with a small private key and decryption key. In addition, [6,7] developed the concept of identity-based BE (IB-B).

Authorization is the process of confirming an object’s identification, or in other terms, determining whether or not a person. It is critical to use an effective and trustworthy authentication method because it plays such an important role in establishing encrypted channel and secret transmitting data. When a system is heavily populated and large devices are linked to one another, identification has become a difficult task in terms of memory, electricity, communications, and computational resources. In line with the verification phase, the added security precaution of private key sharing amongst users on the network places an unacceptably high computation complexity on devices with limited, particularly when using common cryptographic techniques. Instead of one-to-one authentication, group authentication schemes (GASs) have been proposed as a method to lower the computational complexity of authenticated key negotiation procedures [8].

The cloud is a promising tool for service delivery to Iot systems. Fog and edge are cloud branches which work together and provide effective services [9]. The cloud offers resources with the help of techniques such as Virtual Functions (VFs) and Software Defined Networking (SDN). To implement transversal end-to-end information security, proposes SDN-centered group identity. The number of assaults against Iot systems has risen dramatically lately. Millions of Iot systems are being used as robots in Cyber attacks. One of approaches to avoid the acquisition of connected systems and limit threats is to establish network access. Because Iot systems have limited resources, applying complex encryption primitive people in real-time ABE is challenging. One technique to avoid illegal network access and ensure safe group-based interaction is to use group identity. There are three people in charge of the team.

The proposed Tree based algorithms and Group Key Establishment with Multivariate public key cryptosystem based on Broadcast Encryption provides front and back security. The research helps to identify the solutions for:

•   How the tree based algorithms provide security?

•   How the group keys are generated?

•   How the MPKC-BE reduces the cost of the system?

•   How GKE authenticate the group communications?

The major contribution of the proposed system is given below:

1.    The important protection characteristics that a grouping must obey are a forward secrecy, reverse secrecy, and collisions resistance.

2.    A creation of a group key doesn’t really necessitate possessing additional users’ shares for every participant in the organization. In those other terms, a member of a group can recover the shared secrets using public data supplied by the group admin. In this method, the security dangers associated with sharing member information between peer is fully eliminated, and communication costs among members are considerably reduced.

3.    The price of retrieving a key or authenticating a number of consumers is independent of the value of participants. Some group identification techniques based on iteration method, on either side, set up the team functional dependent on the amount of members.

4.    BE may be utilized as just a major structure element in IoT systems since it is an effective and accurate cryptographic key component which offers a logical answer by enabling a transmitter to transmit encrypted information to a set of systems.

The rest of our research article is written as follows: The Section 2 consists of brief study of existing Software Defined Network (SDN), Group Key Establishment (GKE) and Multivariate public key cryptosystem with Broadcast Encryption (BE). Section 3 describes the working principal of the proposed model. Section 4 evaluates the result and gives a comparison of different algorithms. Section 5 conclusion of the research work

2  Related Work

In paper [10] is a centralized message passing tree-based groups management solution that distributes key codes by encoding it in crypto items. These consumers are the massive tree leaf node. Each has such a private personal key, and thus a series of intermediary values that may be used to go into the root of the tree and retrieve the collective key. So communication cost of this tree-based key management is reduced to log (dn), wherein d is indeed the level of a key trees and n represents the number of individuals in the team. The one-way functional tree (OFT) method is a version of the method wherein the know about in order is produced by nodes itself in a bottom-up approach [11]. Every person has a private key, which has a one-way functionality that provides the blind key. These nodes with key cryptography key KEK are indeed a mixture of the blinding keys from of the sub tree.

In [12] proposes an OFT system based on a randomly generated encoder. With credentials produced to use a randomly generated encoder, the users are assigned from of the leaf node to all other nodes. Because the keys could be retrieved even when a nodes was taken, the system is much more secured than OFT. When comparing to the Logical key hierarchy (LKH) system, the price of rekeying is lower. In [13] proposes a compact authenticated key agreement strategy for IoT devices and user groups based on the structure. User groups join to devices group in order to collect information from subscribed gadgets. The combination of the item id as well as private keys is being used to restore the key even when a device connects. For prevent collusion efforts, the tree is updated whenever a member joins the grouping. This updates the devices IDs. In comparison to the typical LKH method, the suggested methodology is computationally inexpensive.

In [14] proposes high-intensity tree-based authenticated key agreement solution. The Diffie-Hellman analysis is used to identify an intermediary key that use the security support efficient and the adjoining paired node’s blinded secret. Even so, using the Diffie-Hellman technique in IoT resource-constrained devices is not viable. In [15] proposes two traffic one-way functional tree (OFT) architectures. The Random OFT method conducts a hashing on the old items just on route to the base of a joining node, and the existing values on the reverse side tree. Whenever a node connects, the method OFT uses digital node to calculate values.

This approach provides an improved collision-resistant OFT in terms of crash resistance and calculation time. As during join process, the computing burden on the membership devices still is greater than the previous OFT. In [16] uses a binary tree to implement a unique strategy. The approach has low memory requirements and reduces network cost by using one-way key generation for packet regular routines. Despite the fact that tree-based access control is fast, maintaining a binary tree adds significant overhead [17].

Its existence of systems with low power and computing capabilities necessitates the use of e protocol. In all other terms, given the ubiquitous use of these devices and their ability to communicate with one another without the limited funding, data protection and identification are most pressing concerns for energy various measures. Traditional approaches for authenticated key agreements that use a key exchange protocol [18–20] really aren’t appropriate again for architecture of the device system for various purposes: A need of significant processing burden even during administration of effective key methods is among the main factors, as is the overburdening of replying to every device queries independently.

They may divide security in two groups based on significant updates: State ful and Connectionless network security. Cryptographic keys of users could be changed after joining state ful security [21]. This secret is really only transferred once during the initial configuration of the stateless security [22–24]. The issue including which sort of BE is better for IoT network naturally arises. Given the tiny size of connected systems as well as the fact because not every IoT device is suitable for constant updates and maintenance, we chose stateless broadcasts encrypting as just a cryptography core component for use in IoT systems.

The process is based on MPKC that increases the reliability in the face of quantum-based assaults if the security problem is NP-hard. The suggested program’s execution simply necessitates limited fields multiplies and addition. Because our model is built on an blockchain security, it is generally quick and uses only low-cost computational resources, making it appropriate for application on low-cost devices [25,26], such as RFID technology and wireless chips.

3  Proposed Methodologies

A hybrid new important management method is developed to combine the Logical key hierarchy (LKH) and OFT schemes and Group Key Establishment with Multivariate public key cryptosystem based on Broadcast Encryption. A centralized trustworthy system, which is in charge of key distribution and upgrades, is used to maintain group keys. To provide longitudinal access controls, Software Defined Network (SDN) based security controllers are employed for group administration services. Cloud service providers provide a variety of security features. There are just a few software security answers available. The architecture of the proposed method is given in Fig. 1.

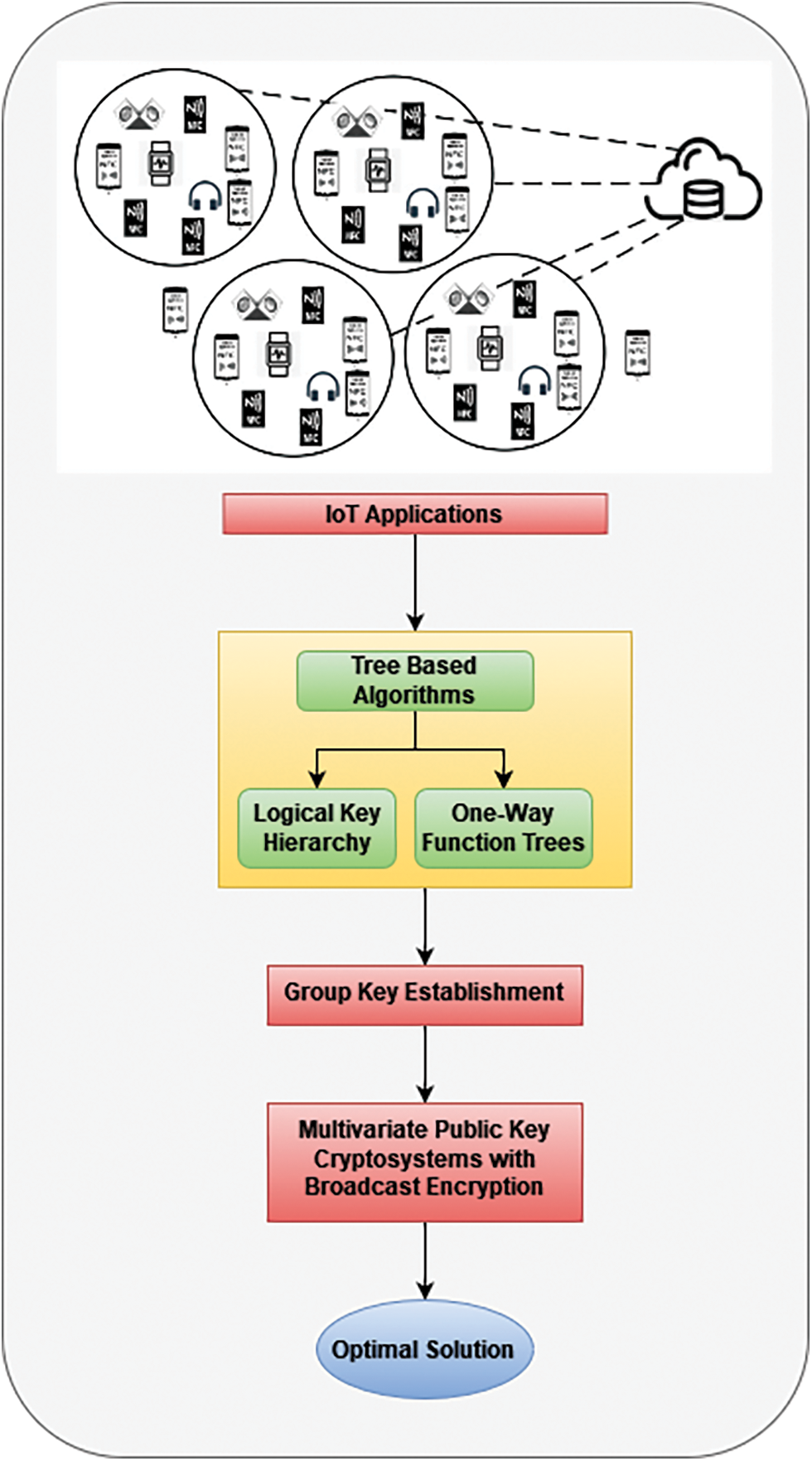
Figure 1: System architecture

3.1 Tree Based Algorithm

Each participant has their own secret key (SI) that they exchange with key management system. The leaf node is made up of people. A node secrets and a blinded node secret are associated with each node in the key tree. The nodes secrets is being used to transmit private keys, while the blindfolded network secrets is disseminated to neighboring nodes in order to create intermediary codes. A specific node secret SI is assigned to each user. The blinded node secret (Bli) of different nodes is a one-way function of node secret f(SI). The XOR of blinded node secret of left and right child nodes Blli XOR Blri is used to derive the IK node secret SIKi. IK node’s blinded node secret BlIKi is indeed the one-way functional of IK node’s secret f(Blli XOR Blri). Because it is not transmitted to the next sub trees, KEK nodes do not have a blinded node secret. The KEK is computed asf(BlIKlixorBlIKri).

User Join Procedure

Whenever an users join, as shown in Fig. 2. The entering users nodes 10 is offered a new network private S10, which is encrypted with own private key s10, and a blind nodes hidden Bl9 of cluster 9. A blind network secretBl10 of network 10 is sent to node 9. The intermediary key IK5 node secretSIK5 = Bl9 xorBl10 and blinded secretBlIK5 = f(Bl9 xorBl10) are calculated from both networks 9 and 10. IK6’s modified blinded nodes secrets are distributed to nodes 9 and 10. By conducting one-way operation just on current blinded node secrets of IK5, upgraded BlIK6 is created. The key encryption key (KEK) is calculated and the grouping key (GK) is obtained by vertices 9, 10, 11, 12.

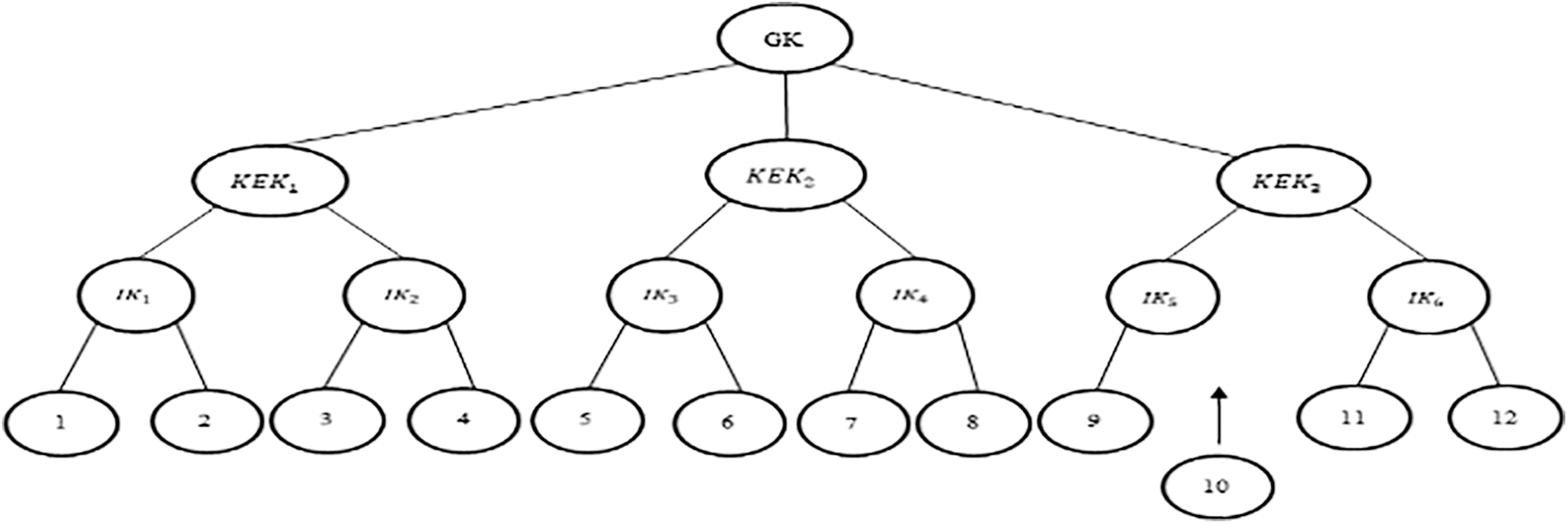
Figure 2: User 10 joins adjacent to leaf node 9 [1]

3.2 SDN Based Security Controller for Group Management

The trusted key management system (KMS) is used for group member managers and operational delivery in a centralized authenticated key agreement system. In [2], group management is handled by an SDN-based protection manager. For the presented design, an SDN-based Security Controller can also be used for combining the sensors and effective key distribution. SDN is a central management system enabling of software-based virtualization of communication networks. In systems like VANETS [11], SDN can be used for grouping and cluster head choice. SDN is utilized to organize devices in our company. To avoid sending unwanted messages, the network connection among non-group equipment can be turned off. As the components that make up a series or those that interact frequently can be grouped together.

The protection surveillance program, house entertainment area, light system management, water management system, temperature, and air-conditioning system, for example, are all included in a monitoring platform. A group of gadgets is accountable for video surveillance, and another group is charged for illumination regulation. It cans efficiently broadcast and multicast messages using a share similar key. This lowers statement cost while also reducing the propagation of assaults such as node replication assaults, which occur when a device in a smart home system is taken.

A common group key is used to communicate among the members in the grouping. A connection demand is issued to the risk administrator for inter-group interaction. The demand is passed to the user’s admin devices, which grants or denies requests after verifying the node as a valid group member. Whereas if application is granted, both devices will receive a session key for one-time interaction. Fig. 3. shows the SDN security controller.

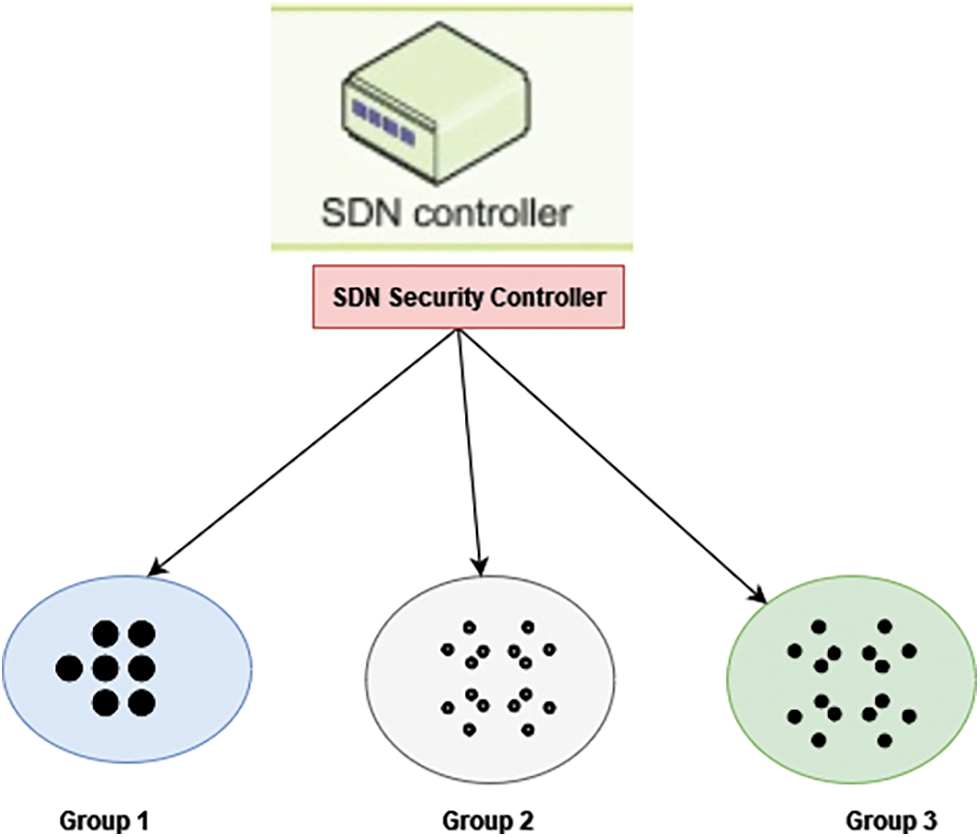
Figure 3: SDN security controller

3.3 Analysis of Security

     i)  Situation: The one-way functions must be powerful enough the result can only be computed if both input data were available.

    ii)  Theorem 2: Whenever a user joins the proposed scheme, the entering users do not have any unapproved already utilized secrets, ensuring backwards secrecy.

Proof: When users 10 join at time T1 as shown in Fig. 2, the user is given its very own node secretS10 and neighboring blinded node secret Bl9, which are used to construct the intermediate secret SIK5 and blind secretBlIK5. For compute a new KEK, the updated intermediate blinded node secretBlIK6 is given. As a result, the new users have no access to every already utilized key, providing reverse secrecy.

iii)   Forwarding Secrecy Theorem 1

If a users exits the proposed technique, the departing users does not have any unauthorized future keys, ensuring forward secrecy.

Users A knows the keys node 9 blindfolded node secretBl9 intermediary node secretSIK5, blinded indirect route secretBlIK5, blinded intermediate node secretBlIK6 and KEK when user 10 departs at time T2 . Because the network secrets of its adjacent node moves, all the keys accessible to users 10 changes as well, with the exception of the blinded access point secretBlIK6. Despite this, 10 are unable to create the KEK without having the modified blinded indirect route secretBlIK5. As a result, user A does not have any unauthorized future keys, guaranteeing forward secrecy.

Strike by collision

The one functional trees is collision resistant, as according Liu’s theorem, if and only if an arbitrary number of users U1, U2,…,Un cannot conspire to calculate some unknown node secret, such as the groups key [2].

The suggested technique is crash resistant, according to the third hypothesis.

Proof:

A collusion attack is only possible if a group of bad users work together to obtain any unauthorized node secret, allowing them to access the group’s keys for an unauthorized time frame T. The one and only key accessible to the departing users at time T1 is intermediary blinded node secretBlIK6, as according theorem 1. At time T2, the leaving user colludes with a joining user to obtain KEK. The new user does not have any already used unauthorized keys, as according theorem 2. As a result, the suggested technique is resistant to collisions.

3.4 Multivariate Encryption

There are three algorithms that make up a multivariate encryption system are:

•   (PuK,SeK) Gen(η): Gen produces the combination of public and private keys (p,{s, f, t}) given a security parameters.

•   CiText←Encrypt (M,PuK): Provided a word M FNQ, the en-cryptor calculates Y = Pu(M) ∈ FMQ and returns Y as a CiText encrypted message.

•   M←Decrypt (CiText,SeK): With a cipher-text CiText = Y FMQ, the de-cryptor performs α = s − 1(y), β = f − 1(β), and M = t − 1(β) iteratively to return the messages M.

3.5 Multivariate Identity-Based Broadcast Encryption (MulIB-BE)

It contains four algorithms:

     i)  Initial setup of MulIB-BE.,

    ii)  Key Extracted by MulIB-BE.,

   iii)  Encryption using MulIB-BE,

    iv)  Decryption using MulIB-BE.

Where Nu represents the number of users for whom the broadcaster intends to make the BE (u1,…, un). Let Id = (id1, id2,…, idn) represent the identification number for every member MulIB-BE is being used. The transmitter creates the masters public key MPK and the master private key MSK during installation. This broadcasters produces the private key for each user using the master secret key MSK and iNui = 1. With SAuth and a subset of u1,…, un authorized users, the broadcaster uses the MulIB-BE. Encrypt technique to generate its combination (hdr,Ke) by using masters public key MPK.

For retrieve a key from of the cipher-text, the user’s Ui with the identifier γi uses the method MulIB-BE. Decrypt. Let’s now go into the specifics of the suggested program’s architecture.

• (MSK,MPK) ←Initial setup of MulIB-BE (N,η) : A transmitter creates MPK = (P(d), iNi = 1) with shared secret key MSK = (S(d),F(d),T(d)) given N and the secure parameters. In this case, I FNq is such that Det (1,…,N) 6 = 0 and d is a N tuple (d1,…, dN) such that:

1. S(d)¯:Fqm→Fqm is the form of linear invertible chart

S(d)¯(Y1…Ym)=(S1(d¯)(Y1…Ym),…,Sm(d¯)(Y1…Ym)) (1)

Also with that

Si(d¯)(Y1…Ym)=∑⁡S(i,j)(d¯)(d1~,…,dN~)Yj+S(i,0)(d¯)((d1~,…dN~)) (2)

Therefore each quadratic polynomial in ∑⁡S(i,j)(d¯)(d1~,…,dN~) is d1~,…,dN~ .

2.    T(d~):Fqn→Fqn is the form of linear invertible chart

Ti(d¯)(Y1…Yn)=(Ti(d¯)(Y1…Yn),……,Ti(d¯)(Y1…Yn)) (3)

Also with that

Ti(d¯)(Y1…Yn)=∑⁡T(i,j)(d¯)(d1~,…,dN~)Yj+T(i,0)(d¯)((d1~,…,dN~) (4)

Therefore each quadratic polynomial in ∑⁡T(i,j)(d¯)(d1~,…,dN~) is d1~,…,dN~ .

3.    F(d)¯:Fqn→Fqm has m multivariate polynomials ( F1(d¯),…….,Fm(d¯) )

Fk(d¯)=∑i,j⁡αkijYiYj+∑i⁡bkiYi+ck (5)

Here αkij , bki , ck represents the quadratic equation of d1~,…,dN~ .

4.Pk(d¯)=∑i,j⁡αkijYiYj+∑i⁡bkiYi+ck (6)

3.6 Group Key Establishment

The key object in the strategy is an inner product space vs. The concept arose from the insight that a finite-dimensional subspace of a vector space v has had an endless number of foundation, however once a user has a base again for subspace, this has the same privileges as everyone else who does have a foundation for same subspace. This same secret information are constructed with the predetermined subspace and besides collective members, no one else can create this same group secret. The team members can generate the secured key and create a secure communications system once the first transmission of basis to members of the group is accomplished. Users can also communicate directly with the group leader and yet another friend in the community.

In certain numbers i, j, let Gsi signify a group and Usij denote a member of it. A group-manager, as defined by GMi, is a person who is in charge of a company. In comparison to the other members of the group, Gsi is thought to have even more computing capacity and energy resources. The group manager is intended to conduct the verification of a user in the group in general. It’s worth noting that the suggested technique also outlines how any member of the Gsi group can authenticate. A subset Wi of a preset global product or process that results E is used by all units in the system. For example, E may be all equations more than a finite set F, which would have been an indefinite dimensions unit vector.

The foundation For Wi, Bi = {Vi1,…,Vin} is chosen to become a secrets of a group leader GMi.

Wi=span(Bi)=span{Vi1,……,Vin} (7)

Because of the nature of sub-domain Wi, it is possible to choose an endless number of bases for it, and in certain cases, knowing every basis for Wi will suffice to reveal the secret key. On either side, the individual’s structure necessitates awareness of the chosen platform in order to reveal the group’s overall secrets. In those other terms, understanding Wi’s subspace enables somebody to learn about the group’s secret. As a result, the organization manager will keep Wi and the chosen base Bi under wraps. When dispersing personal secret, the group manager GrMi uses a bring new possibilities function fi(x). A polynomial of great degree d can be used as the chosen function fi(x). According to the information security within next section, the number d may be larger than the expected users in the group Gri. The essential data is held confidential by the group manager:

Bi,j={fi(xi,j)vi1,fi(xi,j)r2vi2,fi(xi,j)r3vi3,…,fi(xi,j)rnvin} (8)

here r2, r3,…, rn are integers randomly picked by GrMi, the unit person in charge.

If some individuals’ interests are acquired, the secrecy of group interaction in proposals is unlikely to be breached by an attacker. In those other phrases, because each individuals personal confidential communications is self sufficient of one another, if an adversary obtains all members’ private keys except one, the adversary cannot obtain any data about it member’s secret or construct the function from which the group manager generates the secrets of other users as long as the degree is bigger than the amount of end user undergoing verification.

3.7 Authentication of Users in the Group

This suggested program’s initial portion is in responsibility of group verification. Let Uij to be a user who will be authorized by GrMi, the group manager. A group manager chooses a vectors uin the universality E at randomly so that u ∉ Wi. u is published by the group manager. Uij, the user, calculates

ki=Projw,u (9)

A function fi belongs to the manager GM (x). Anyone, such as the group manager, has access to the user Uij’s publically available xij. The management next verifies to see if the formula below is correct.

Tvi1=fi(xij) (10)

T=fi(xij)vi1 (11)

In some circumstances, GM might have to complete validation for each of its users individually. If a non-member tries to penetrate the group in this situation, the administrator will quickly recognize them throughout the authentication phase. In reality, the procedure necessitates the knowledge of a point (x, f(x)) on the f(x) graph, as well as the subspace W and the basis already obtained via GM. Its way to spot someone attempting to mimic a member of the group protects the system from a DOS attack. A random vector is used in the initial step of the authentication process to generate a connection between two senders and receivers. Because the random vectors differ by activity, a repeat attack cannot be accommodated during the verification stage.

3.8 Group Secret is Established

The non-member may rejoin the group conversation because of the procedure of establishing shared secrets. In those other terms, group authentication is the goal of the key establishment process. As just a result, the one-by-one authentication mechanism can be avoided in favor of the group key creation step. The collective secrets can be discovered under the guidance of the group leader or any other trustworthy member of a group. The group manager GMi is in charge of establishing the group secret in the following sections. A management randomly chooses vector o∈E that has the value o∉E . The organization secrets s is retrieved after this vector, which has been publicly disclosed.

s=Projwio (12)

It’s worth noting because calculating s necessitates the use of any basis for the subspace Wi; in other words, the projections of v onto the Wi subspace is the same irrespective of a reason used for W.

3.9 Adding User to a Group by Member

Sometimes in cases, the group manager GrMi may be unavailable to handle adding new members to the Gi unit, or either Gi user may be given the ability to join users for the group. In such instances, a group member can join a non-member, signified by UF, to the group, and also that users can safely converse with the other members. Surprisingly, the group manager can quickly identify the person who joined UF to the group. UF or may not be granted all member of the group capabilities until it’s a members through the group manager GMi. Take the group member Uij, who possesses the given foundation set:

Bij={fi(xi,j)vi1,fi(xi,j)r2vi2,fi(xi,j)r3vi3,…,fi(xi,j)rnvin} (13)

By join users UF to the group conversation, the sponsor Uij does not need to know the function f(x). Notice that now the user UF may readily grab the group secret s using its basis, and the new user’s funding source can be identified by anybody using its public key or by the group leader using the function f using its private key (x).

4  Result Analysis

A Hybrid Tree-based algorithm compared with Group Key Establishment (GKE) and Multivariate public key cryptosystem with Broadcast Encryption improves the security, efficiency of the system and reduces the power consumption and minimizes the cost.

4.1 Power Consumption

The power consumption of group communication is improved in all of the algorithms because the wide variety of turns improved. The end result suggests the strength intake of the proposed T-GKE-MBE techniques is decrease than that of the diverse techniques. The proposed set of rules has decrease strength intake.

Fig. 4. shows that the power consumption of the proposed T-GKE-MBE method in blue color bar. The proposed consumes less power and saves energy by consuming less power than existing techniques.

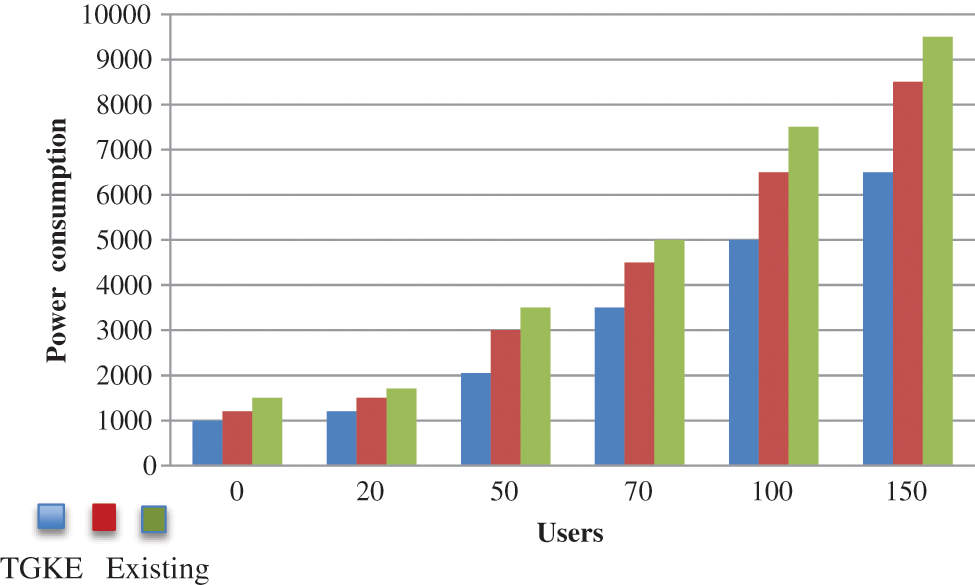
Figure 4: Power consumption

4.2 Accuracy

This is a metric which is used to predict the overall percentage of true positive and true negative elements throughout every component, and then it’s written like this:

A=Tp+TnTp+Tn+Fp+Fn (14)

Fig. 5 shows the accuracy of the proposed system. Thus the Proposed T-GKE-MBE achieves better results compared with Tree based and GKE method. The proposed method attains 7.96% of accuracy and the Tree based achieves 5.26%, the GKE 4.87% of accuracy.

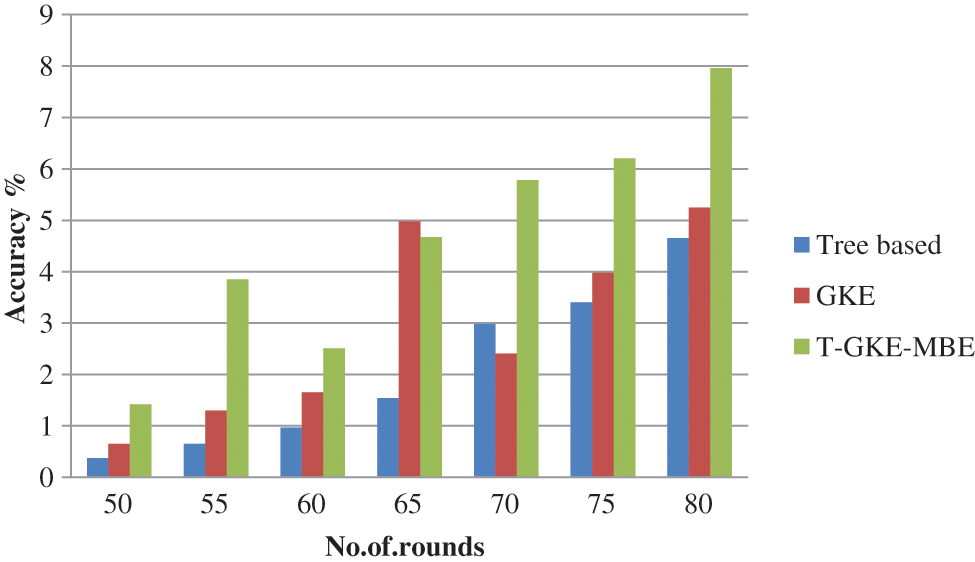
Figure 5: Accuracy

4.3 Execution Cost

Execution cost is based on the number of rounds and the number of seconds which take for completing the rounds. Initially, the data are given to the cloud server. It executes each task. In the proposed system it is minimized

Fig. 6. Shows the execution cost of the proposed system. Thus the Proposed T-GKE-MBE achieves better results compared with Tree based and GKE method. The proposed method attains 58.45 s of execution cost.

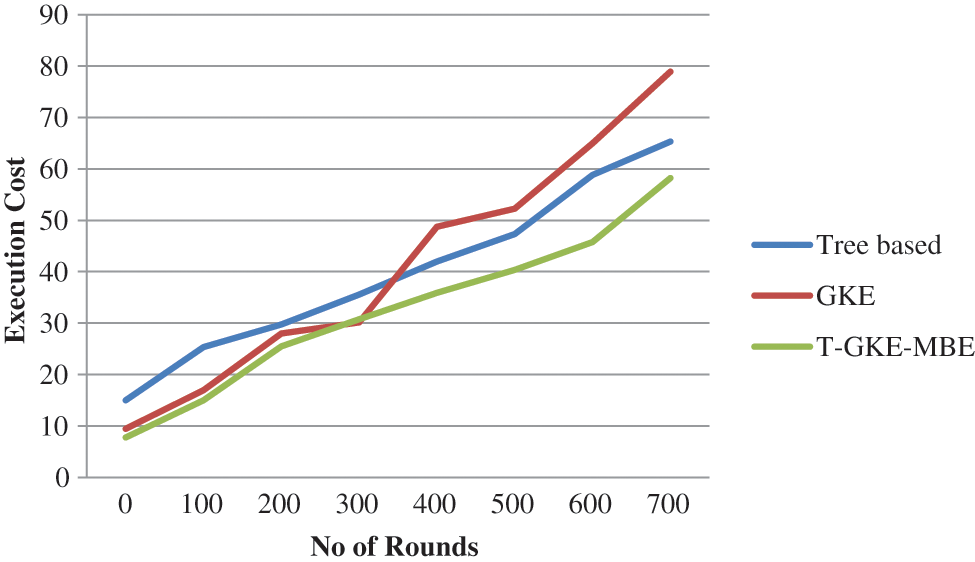
Figure 6: Execution cost

4.4 Execution Time

Execution time is evaluated by the no.of rounds and the no.of seconds which take for completing the rounds. Initially, the data are given to the cloud server. It executes each task.

Fig. 7. Shows the execution time of the proposed system. Compared with other algorithms the proposed method achieves better performance. The proposed takes less than 55 s than the other methods.

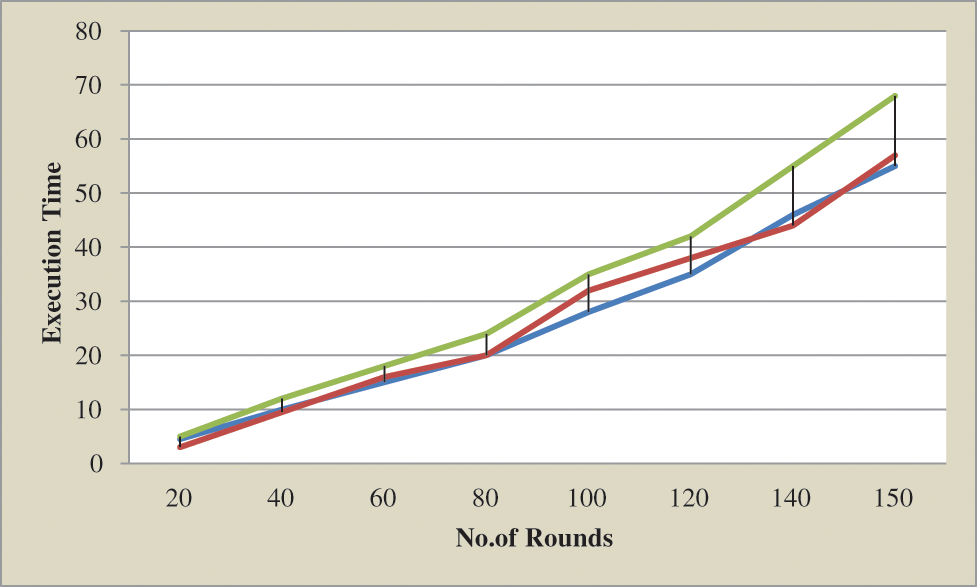
Figure 7: Execution time

5  Conclusion

Cloud data centers offer security as a service. With our study, we use SDN-based security controllers to deliver key exchange protocol as a service to secure inter-group and intra-group communications in Iot systems. LKH is a team communication technique that uses a tree-based key exchange protocol. In comparison to the LKH system, the OFT is a tree-based key management method with lower communication costs. The system employs a bottom-up strategy, with the ancestor keys being a consequence of the keys of the sibling node. However, the technique is vulnerable to a collision attack, which occurs when two or more users collide in order to generate unauthorized keys. Many collision-resistant OFT systems have been suggested, but they come at a higher cost. Our research presents a new tree-based group key management scheme that combines the LKH and OFT schemes. This method is well suited to Iot applications, which necessitate data transfer to a collection of devices that are connected via a connection in a secure and reliable manner. Using MulIB-BE as the cryptographic building block in the backend, we should be able to develop secure IoT systems in which a centralized device may broadcast data to linked devices while maintaining anonymity. Our approach is collision-resistant, according to security study. The proposed Hybrid Tree-based algorithm compared with Group Key Establishment (GKE) and Multivariate public key cryptosystem with Broadcast Encryption method improves the security, efficiency of the system and reduces the power consumption and minimizes the cost. In future blockchain based security algorithms can be suggested to improve the authentication of IoT.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Srivastava, S. K. Debnath, P. Stǎnicǎ and S. K. Pal, “A multivariate identity-based broadcast encryption with applications to the internet of things,” Advances in Mathematics of Communications, 2021. [Google Scholar]

 2.  A. Taurshia, G. J. W. Kathrine, S. David and S. S. Ilango, “A hybrid groupkey management service for static IoT applications,” Annals of the Romanian Society for Cell Biology, vol. 25, no. 4, pp. 4449–4455, 2021. [Google Scholar]

 3.  J. Shahid, R. Ahmad, A. K. Kiani, T. Ahmad, S. Saeed et al., “Data protection and privacy of the internet of healthcare things (IoHTs),” Applied Sciences, vol. 12, no. 4, pp. 1927, 2022. [Google Scholar]

 4.  A. Rawat, V. Daza and M. Signorini, “Offline scaling of IoT devices in IOTA blockchain,” Sensors, vol. 22, no. 4, pp. 1411, 2022. [Google Scholar]

 5.  S. S. Kareem, R. R. Mostafa, F. A. Hashim and H. M. El-Bakry, “An effective feature selection model using hybrid metaheuristic algorithms for IoT intrusion detection,” Sensors, vol. 22, no. 4, pp. 1396, 2022. [Google Scholar]

 6.  A. Carelli, A. Palmieri, A. Vilei, F. Castanier and A. Vesco, “Enabling secure data exchange through the IOTA tangle for IoT constrained devices,” Sensors, vol. 22, no. 4, pp. 1–17, 2022. [Google Scholar]

 7.  R. Sakai and J. Furukawa, “Identity based broadcast encryption,” IACR Cryptol. ePrint Arch, vol. 217, pp. 200–215, 2007. [Google Scholar]

 8.  L. Harn, “Group authentication,” IEEE Transactions on Computers, vol. 62, no. 9, pp. 1893–1898, 2012. [Google Scholar]

 9.  P. Hu, S. Dhelim, H. Ning and T. Qiu, “Survey on fog computing: Architecture, key technologies, applications and open issues,” Journal of Network and Computer Applications, vol. 98, pp. 27–42, 2017. [Google Scholar]

10. W. Shu, S. HashimotoHill, V. Woo, E. M. Eshleman, J. Whitt et al., “Microbiota-derived metabolite promotes HDAC3 activity in the gut,” Nature, vol. 586, no. 7827, pp. 108–112, 2020. [Google Scholar]

11. S. Rafaeli, L. Mathy and D. Hutchison, “An efficient one-way function tree implementation for group key,” Management, pp. 1–24, 2001. [Google Scholar]

12. Y. Ming, X. Yu and X. Shen, “Efficient anonymous certificate-based multi-message and multi-receiver signcryption scheme for healthcare internet of things,” IEEE Access, vol. 8, pp. 153561–153576, 2020. [Google Scholar]

13. Y. H. Kung and H. C. Hsiao, “GroupIt: Lightweight group key management for dynamic IoT environments,” IEEE Internet Things, vol. 5, pp. 5155–5165, 2018. [Google Scholar]

14. E. Festijo, Y. Jung and M. Peradilla, “Software-defined security controller-based group management and end-to-end security management,” Journal of Ambient Intelligence and Humanized Computing, vol. 10, no. 9, pp. 3365–3382, 2019. [Google Scholar]

15. Y. Sun, M. Chen, A. Bacchus and X. Lin, “Towards collusion-attack-resilient group key management using one-way function tree,” Computer Networks, vol. 104, pp. 16–26, 2016. [Google Scholar]

16. J. Pon Senni and A. V. Ram Prasad, “Efficient data sensing with group key management for intelligent automation system by one-way key derivation in wireless networks,” Journal of Ambient Intelligence Humanized Computer, vol. 12, no. 5, pp. 4655–4662, 2020. [Google Scholar]

17. M. Trnka, A. S. Abdelfattah, A. Shrestha, M. Coffey and T. Cerny, “Systematic review of authentication and authorization advancements for the internet of things,” Sensors, vol. 22, no. 4, pp. 1–11, 2022. [Google Scholar]

18. T. Vandervelden, R. De Smet, K. Steenhaut and A. Braeken. “Symmetric key based authentication among the nodes in a wireless sensor and actuator network,” Sensors, vol. 22, no. 4, pp. 1403, 2022. [Google Scholar]

19. D. Zoni, A. Galimberti and W. Fornaciari, “Efficient and scalable FPGA oriented design of QC-LDPC bit-flipping decoders for post-quantum cryptography,” IEEE Access, vol. 8, pp. 163419–163433, 2020. [Google Scholar]

20. F. Borges, P. R. Reis and D. Pereira, “A comparison of security and its performance for key agreements in post-quantum cryptography,” IEEE Access, vol. 8, pp. 142413–142422, 2020. [Google Scholar]

21. H. N. Almajed and A. S. Almogren, “SEEnc: A secure and efficient encoding scheme using elliptic curve cryptography,” IEEE Access, vol. 7, pp. 175865–175878, 2019. [Google Scholar]

22. M. T. Goodrich, J. Z. Sun and R. Tamassia, “Efficient tree-based revocation in groups of low-state devices,” Advances in Cryptology–CRYPTO, vol. 3152, pp. 511–527, 2004. [Google Scholar]

23. D. Halevy and A. Shamir, “The LSD broadcast encryption scheme, advances in cryptology,” CRYPTO, vol. 2442, pp. 47–60, 2002. [Google Scholar]

24. T. N. Tan and H. Lee, “High-secure fingerprint authentication system using ring-LWE cryptography,” IEEE Access, vol. 7, pp. 23379–23387, 2019. [Google Scholar]

25. A. Bogdanov, T. Eisenbarth, A. Rupp and C. Wolf, “Time-area optimized public-key engines: MQ-cryptosystems as replacement for elliptic curves?,” Cryptographic Hardware and Embedded Systems-CHES, vol. 5154, pp. 45–61, 2008. [Google Scholar]

26. B. Y. Yang, C. M. Cheng, B. R. Chen and J. M. Chen, “Implementing minimized multivariate PKC on low-resource embedded systems, security in pervasive computing,” Pervasice Computing, vol. 3934, pp. 73–88, 2006. [Google Scholar]