Training Neuro-Fuzzy by Using Meta-Heuristic Algorithms for MPPT

1  Introduction

Interest in MPPT techniques has been ongoing for many years, and numerous studies have been conducted on them. Studies on MPPT techniques aim to increase the efficiency of these algorithms, to reach the maximum power point rapidly, and to oscillating as little as possible around this point. It is seen in the literature that many traditional and artificial intelligence-based approaches are recommended for MPPT [1–3].

Mao et al. [4] compared traditional and intelligent MPPT control techniques. The popular MPPT techniques have been examined in terms of advantages and disadvantages. Within the scope of their study, it was emphasized that traditional MPPT techniques may be insufficient to reach the maximum power point. The MPPT techniques were here examined in three parts: traditional, intelligent and techniques under partial shading condition. These techniques were compared under the headings of complexity, tracking speed, cost, efficiency, accuracy and hardware implementation. Baba et al. [5] realized a review on the development and classification of MPPT techniques. They determined that the techniques assigned to reach the maximum power point differ in terms of their efficiency, performance, modernity, complexity and tracking speed. At the same time, traditional and advanced techniques were compared. It was stated that each technique has its own characteristics, limitations and applications. Motahhir et al. [6] investigated the maximum power point algorithms in PV energy systems and evaluated the most used MPPT algorithms in three groups. The first group is direct techniques such as hill climbing (HC), incremental conductance (INC) and perturb and observe (P&O). The second group is indirect such as namely fractional short-circuit current (FSCC), pilot cell and Fractional Open-Circuit Voltage (FOCV). The last group is including soft computing methods such as fuzzy logic control (FLC), Kalman filter, neural network, ABC algorithm, PSO etc. In addition, within the scope of their study, a comparative analysis of the above-mentioned algorithms for suitable and low-cost embedded system applications was realized. The gains obtained during the comparison were expressed under the sections such as real MPPT, steady-state oscillations, efficiency, tracking speed, analog/digital method, application complexity, sensor requirement, cost, reaching the globular MPP and using in commercial products.

Fuzzy, neural network, neuro-fuzzy and meta-heuristic optimization algorithms are among the artificial intelligence techniques used for MPPT. It is seen that neuro-fuzzy-based studies are particularly effective due to its strong structure. Rezvani et al. [7] presented an approach based on genetic algorithm (GA) and ANFIS to track PV power. ANFIS training was realized by utilizing GA. Hamouda et al. [8] developed a MPPT controller based on ANFIS and PSO to track the MPP belonging to PV generator. Andrew-Cotter et al. [9] used a ANFIS model for MPPT control of a three-phase grid-connected photovoltaic system. Parameters of membership functions of ANFIS were determined by using PSO. LSE was utilized to set the consequent parameters. The data set required for ANFIS training was obtained through P&O algorithm. It was reported that the proposed method is more effective than the conventional P&O based approach. Priyadarshi et al. [10] used a MPPT approach based on PSO and ANFIS to acquire rapid and maximal PV power with zero oscillation tracking. In a different study, Ndiaye et al. [11] utilized ANFIS and PSO for MPPT control. Padmanaban et al. [12] introduced a novel MPPT controller based on ANFIS and ABC algorithm. ABC algorithm determined parameters of membership functions. Priyadarshi et al. [13] proposed an approach based on ANFIS and FPA for MPPT for brushless dc motor-driven PV pumping systems. Basha et al. [14] studied on five MPPT techniques such as modified Variable Step Size-Radial Basis Functional Network (MVSS-RBFN), modified Hill-Climb with Fuzzy Logic Controller (MHC-FLC), ANFIS, P&O with PSO and adaptive CS. Pachaivannan et al. [15] proposed a MPPT technique by using crowded plant height optimization algorithm and ANFIS. Apart from these, there are also MPPT studies based on ANFIS [16,17].

In the light of the above information, it is seen that ANFIS is used extensively in MPPT studies. As is known, an effective training algorithm is utilized to get effective results with ANFIS. The number of algorithms trained in ANFIS for MPPT is limited. Within the scope of this study, ANFIS is trained using PSO, HS, BA, FPA, DE, ABC and CS for MPPT. There are three main innovations in this study. First, most of these algorithms are used for the first time in ANFIS training for MPPT. Second, for the first time, the ANFIS training performance of these algorithms has been evaluated in detail and the ANFIS training performances of seven heuristic algorithms are compared. Third, this study is important in terms of presenting the performance of different algorithms for MPPT. In general, PSO and GA are used more frequently in the literature. However, it is presented in the light of concrete information that there are algorithms that give better results than these.

2  Neuro-Fuzzy Model

Neuro-fuzzy models combine the advantages of neural networks and fuzzy logic. There are many neuro-fuzzy models proposed in the literature. ANFIS [18], proposed by Jang, is one of the most popular and successful neuro-fuzzy models. Therefore, ANFIS is used as the neuro-fuzzy model in this study. The related neuro-fuzzy model consists of two parts, antecedent and conclusion. These parts are connected to each other by IF-THEN rules. A neuro-fuzzy model consists of 5 layers as seen in Fig. 1. Descriptions of the layers are given below:

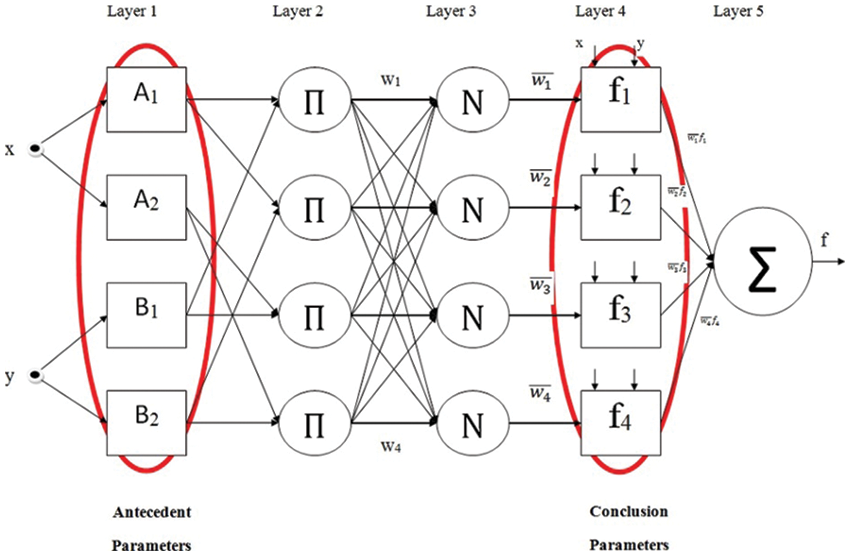
Figure 1: Display of parameters used in ANFIS training

Layer 1 is named as fuzzification layer. In this layer, fuzzy sets are obtained from input values by using membership functions (MFs). There are parameters that allow the shaping of the membership function. These parameters are called antecedent parameters. They are used in neuro-fuzzy training. Each membership function has a membership degree in the range [0, 1]. In the case of using the generalized bell function (Gbellmf), the membership degree is calculated using (1) and (2). μAi(x) denotes the obtained membership degree.

μAi(x)=gbellmf(x;a,b,c)=11+|x−ca|2b (1)

O11=μAi(x) (2)

Layer 2 is named as rule layer. Firing strengths are obtained for each rule by using the membership degrees obtained in Layer 1. wi  values are found by multiplying the membership values as (3):

O12=wi=μAi(x)∗μBi(y),i=1,2. (3)

Layer 3 is named as normalization layer. Normalized firing strengths are calculated for each rule by utilizing the firing strengths obtained in the previous layer. (4) is used for the relevant calculation.

O13=wi¯=wiw1+w2+w3+w4,i∈{1,2,3,4} (4)

Layer 4 is named as defuzzification layer. Weighted values of rules are calculated by using normalized firing strengths and a first order polynomial. { pi,qi,ri } parameters in the first order polynomial are called conclusion parameter. These parameters are other parameters used in neuro-fuzzy training.

O14=wi¯fi=wi¯(pix+qiy+ri) (5)

Layer 5 is named as the summation layer. The actual output of the model is found by summing the outputs obtained for each rule in Layer 4.

O15=∑i⁡wi¯fi=∑i⁡wifi∑i⁡wi (6)

It is aimed to adjust the antecedent and conclusion parameters in neuro-fuzzy training. As seen in Fig. 1, antecedent parameters belong to membership functions. Conclusion parameters are the coefficients of the first order polynomial in the defuzzification layer. An effective training algorithm is needed for an effective training process. In this study, neuro-fuzzy training is carried out using the meta-heuristic algorithms indicated in Fig. 2.

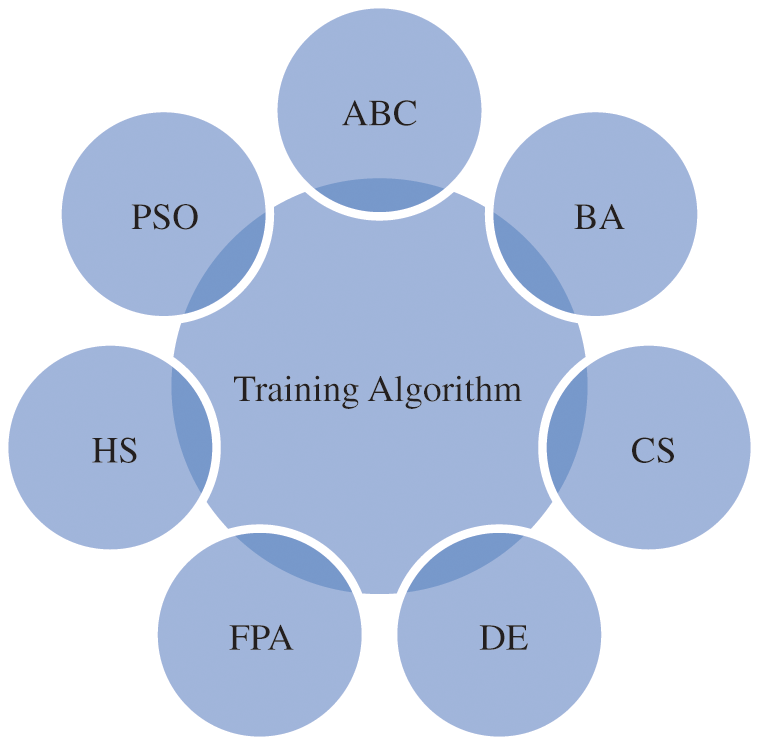
Figure 2: Metaheuristic algorithms used in neuro-fuzzy training

3  Maximum Power Point Tracking (MPPT)

MPPT techniques are most popular way to reach maximum power of alternative energy sources like solar, wind and fuel cell etc. MPPT techniques aim to get the maximum power from alternative energy sources at that moment. MPPT techniques can be created with many methods such as traditional methods, intelligent algorithms, and nature-inspired algorithms.

MPPT techniques are most commonly applied in energy sources that include wind turbines and solar panels. The characteristics of the energy produced by these sources depend on environmental conditions. Partial or total shade, dusting and variations due to panel temperature directly affect the output power of solar panels. The simplified electrical equivalent circuit of a PV cell is shown in Fig. 3. It is possible to calculate the output current and output voltage of a PV cell with the equations given below:

Ipv=Ipvcell−Id−Ip (7)

Vpv=Vd−Ipv∗Rs (8)

where; Ipvcell is PV cell current depending on temperature and solar radiation, Id is diode current, Ip is parallel resistor current, Vd is diode voltage drop, Ipv is PV cell output current and Rs is serial resistor.

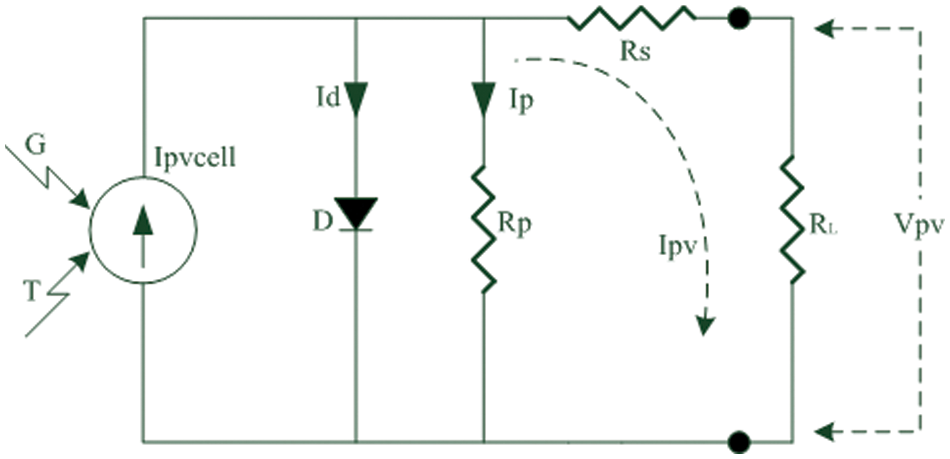
Figure 3: The simplified electrical equivalent circuit of a PV cell

4  Simulation Results

In this study, neuro-fuzzy training is performed by using PSO, HS, BA, ABC, FPA, DE and CS for MPPT. The data obtained from the solar simulator is used for MPPT. Solar array simulators are power electronics applications that behave as solar panels. There are a large number of commercial products that use a variety of strengths and techniques designed for this purpose. Solar array simulators can behave as solar panels in a single or array structure over the data they contain or that the user can enter from the outside. These data can be listed as solar radiation in (w/m2), ambient temperature in C0 and type/model of the panel. The solar panel data used in the study are produced by the solar array simulator. In this context, air temperature and solar radiation data pertaining to one day are entered into the solar array simulator. The input data is applied to the 250 W solar panel model of Kyocera Company. Namely, the inputs of the system consist of temperature and solar radiation. The output is the power value. The dataset consists of 509 samples. 408 of them are used in the training process. The other data is applied in the testing process. Due to the large values of the inputs and output, scaling is realized by using (9) in the range of [0, 1].

xn=(x−xmin)(xmax−xmin) (9)

The neuro-fuzzy model consisting of 2 inputs and 1 output given in Fig. 4 is used in this study. Temperature and solar radiation are inputs of the neuro-fuzzy model. The power is its output. The type and number of MFs affect the performance of the neuro fuzzy model. For this reason, different membership functions are utilized. Gbellmf, Trimf and Gaussmf are MFs used in applications. The analyzes are performed by using 2 and 3 MFs for each input. Gbellmf and Trimf are MFs with 3 parameters. Gaussmf has 2 parameters. These parameters determine the shape of the MFs. In addition, the number of MFs’ parameters directly affects the training and optimization process. When 2 Gbellmf or Trimf are used in the inputs, a total of 24 parameters are optimized. If 2 Gaussmf are used for each input, the total number of parameters is 20. If 3 Gbellmf or Trimf are utilized for each input, optimization of 45 parameters is required. In case of 3 Gaussmf, this number drops to 39.

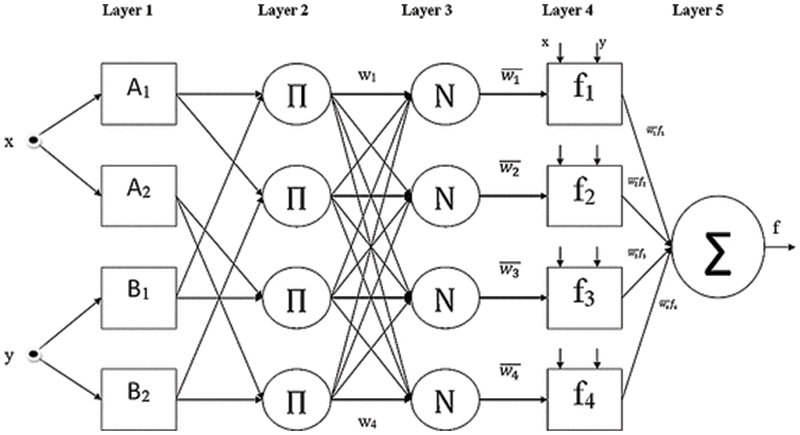
Figure 4: A neuro-fuzzy model with 2 inputs and 1 output

A block diagram of MPPT modeling based on neuro-fuzzy is given in Fig. 5. Here, temperature (t) and solar radiation (s) are given as inputs to the neuro-fuzzy model. The power value obtained using the neuro-fuzzy model is compared with the real power value. The error is calculated using the difference between each two outputs. The mean squarer error (MSE) is utilized as the error metric. Training of the neuro-fuzzy model continues until the stopping criterion is met. An error value or maximum number of generations can be used as the stopping criterion. It is expected that the error value decreases as the generations’ number increases. As seen in Fig. 5, neuro-fuzzy training is carried out using the existing samples.

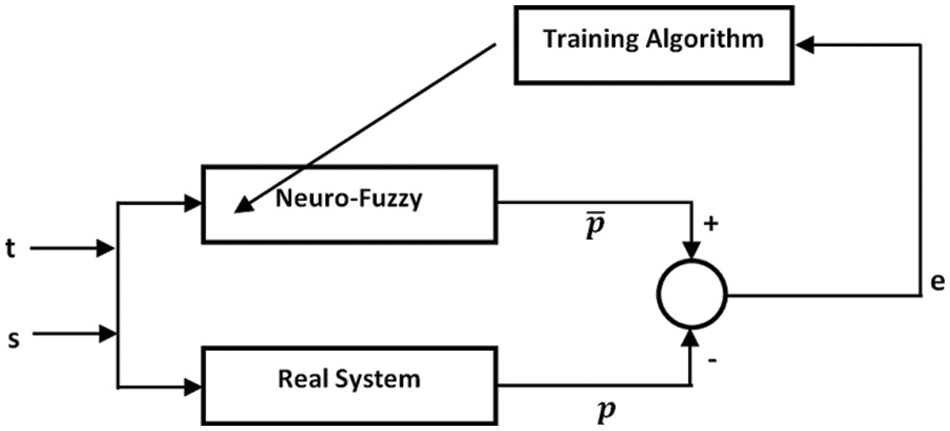
Figure 5: A block diagram of MPPT modeling

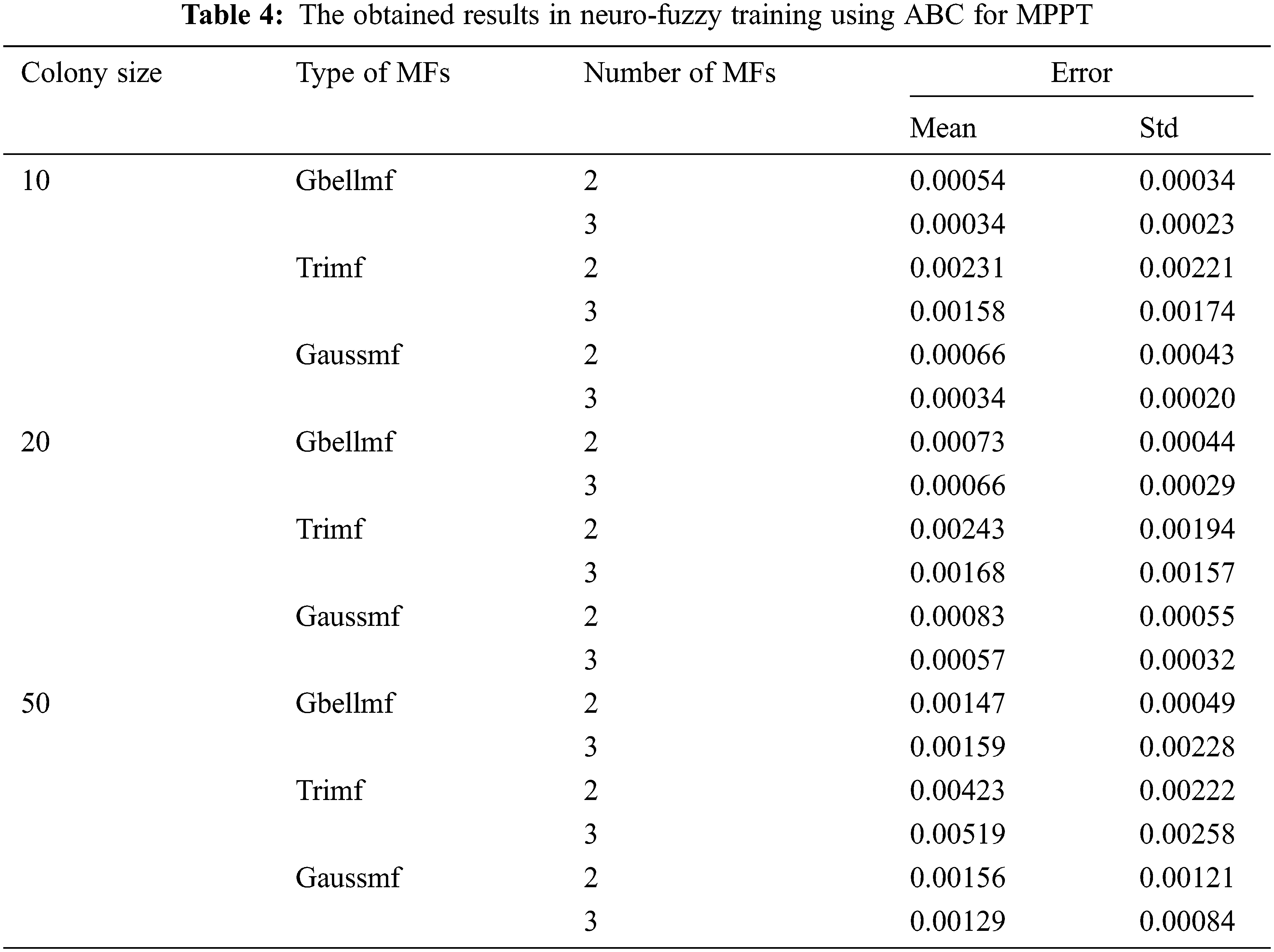
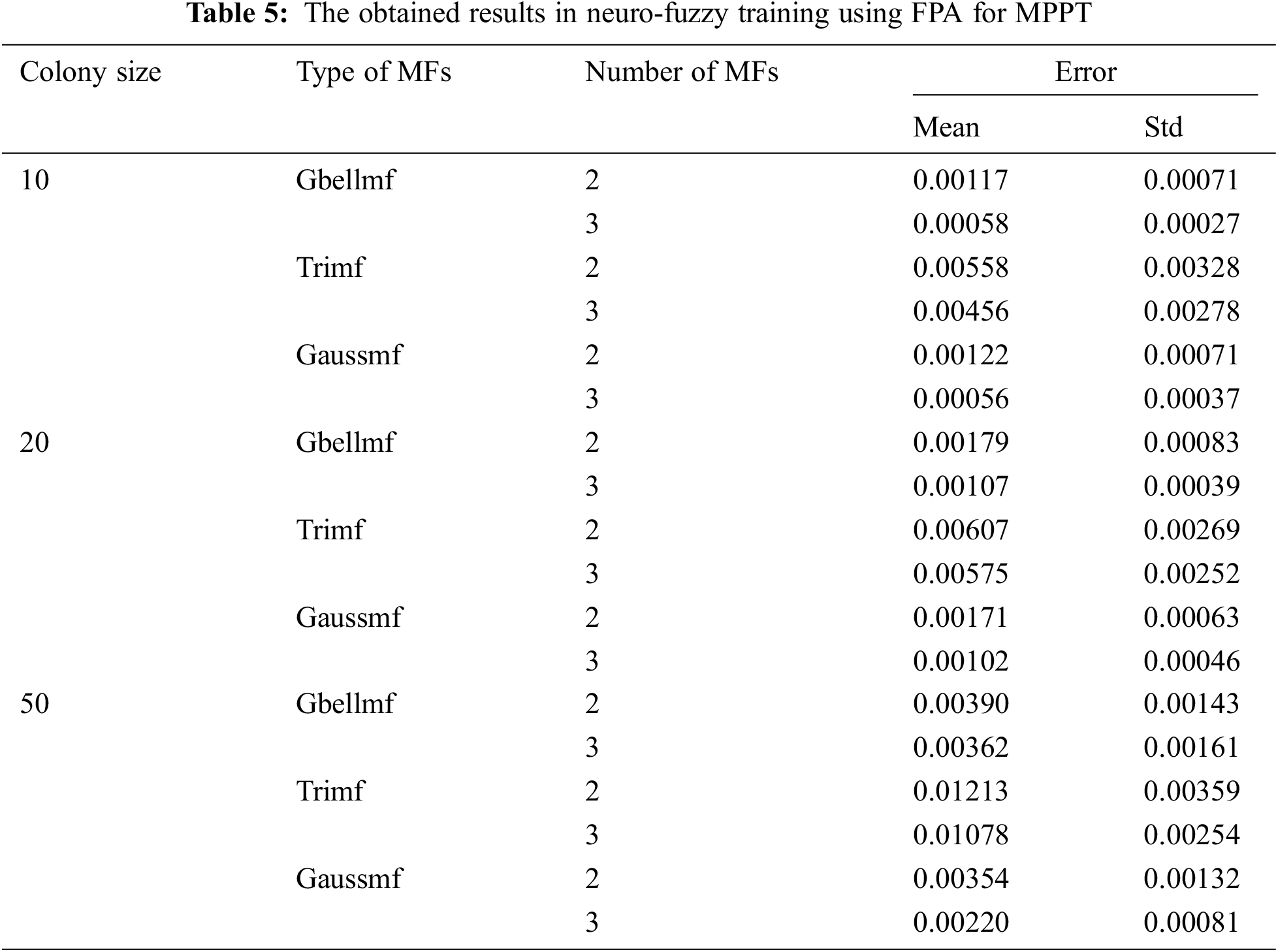
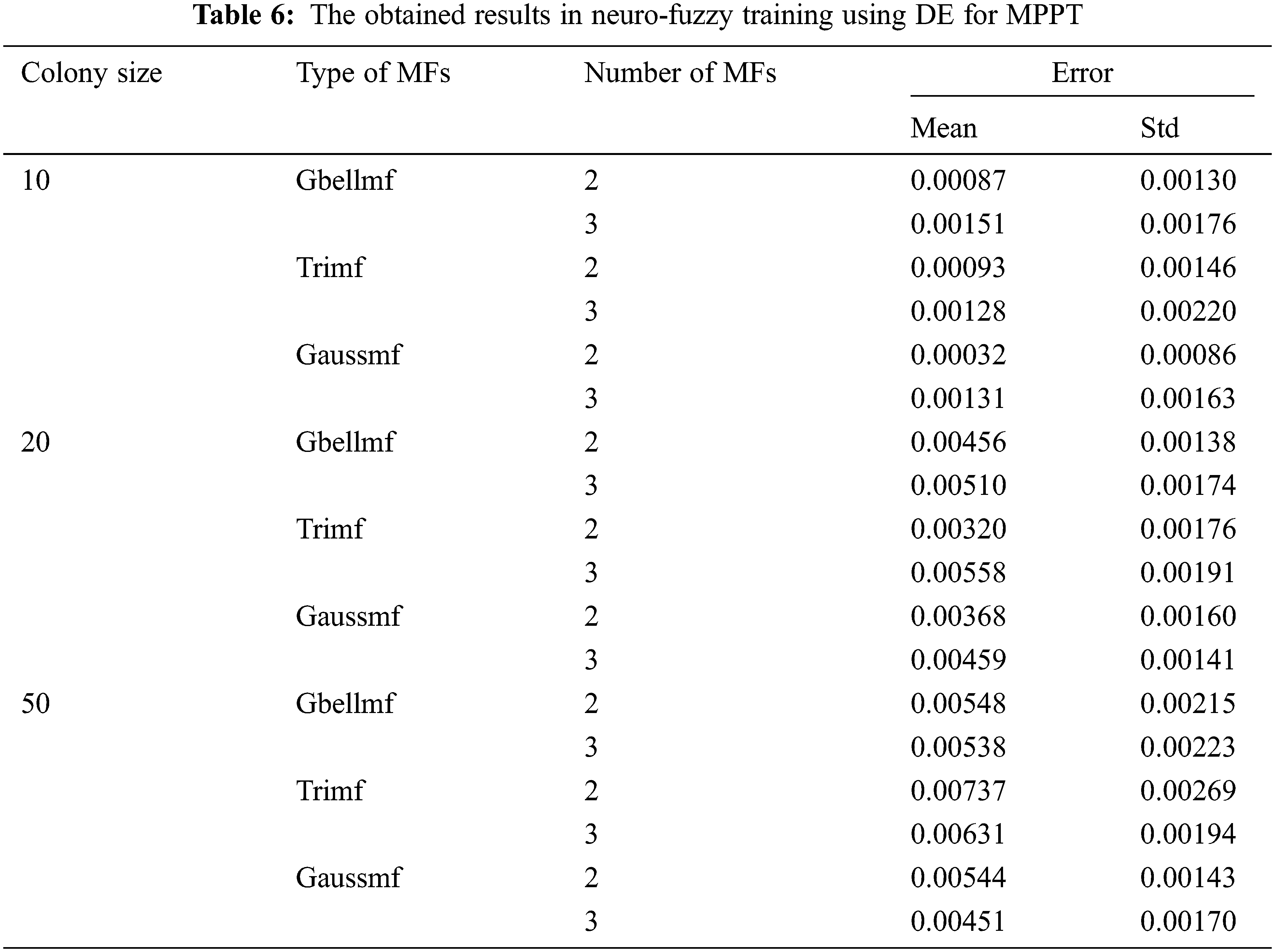
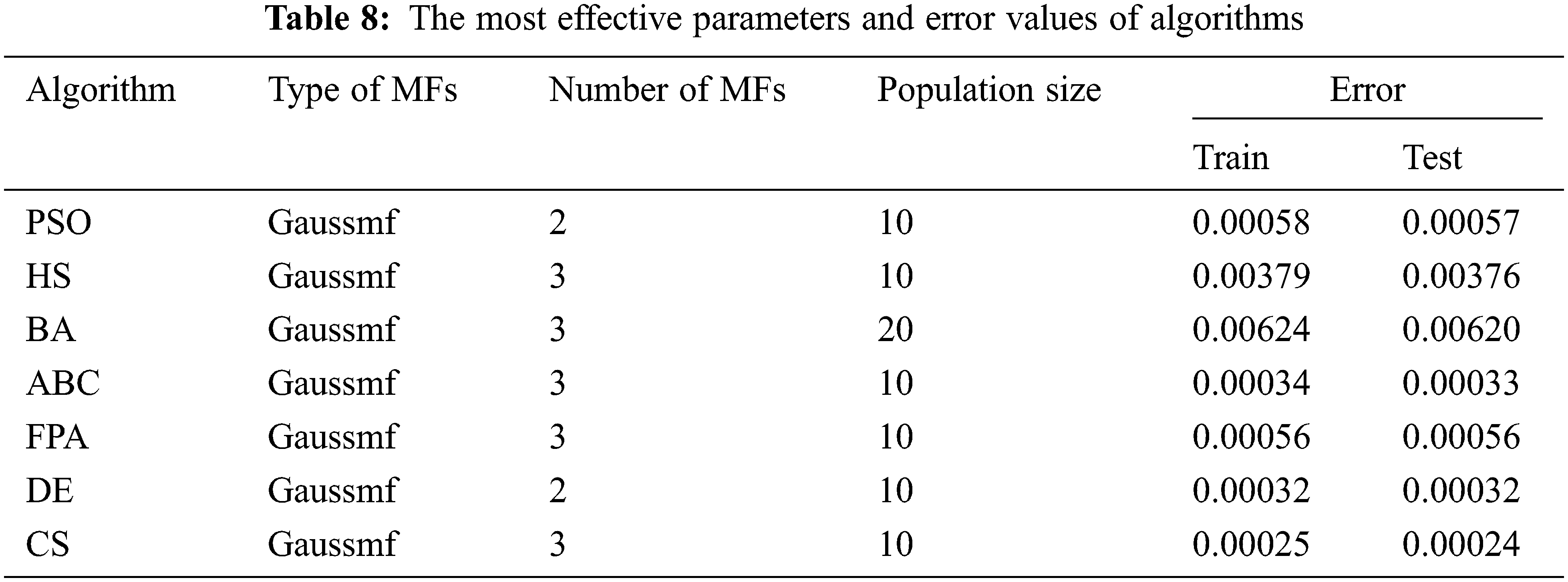
Neuro-fuzzy training is realized by using PSO, HS, BA, ABC, FPA, DE and CS, and the training results are presented in Tabs. 1–7. Colony size (n) is chosen as 10, 20 and 50 for each algorithm. The best results in PSO are obtained when n = 10. The increase in colony size negatively affects the performance. Gaussmf is more effective than other MFs. The best training error value is found as 0.00058 using 2 Gaussmf. The most ineffective MF is Trimf. As in PSO, the most effective results are obtained in HS when n = 10. Increasing the number of parameters generally increases the solution quality. The best training error value is achieved with 3 Gaussmf. In BA, colony size and type of MFs affect performance. The best training error value is obtained with 3 Gaussmf when n = 20. The increase in the number of population in ABC algorithm decreases the quality of the solution. The most effective solutions are obtained by utilizing 3 Gbellmf and 3 Gaussmf when n = 10. The effect of the colony size and membership functions on the solution in FPA is similar to ABC algorithm. The most effective solutions belong to 3 Gbellmf and 3 Gaussmf. The most effective results in DE are found as 0.00032 with 2 Gaussmf when n = 10. Increasing the number of parameters mostly improves the solution quality in CS. The most effective training error value is found as 0.00025 using 3 Gaussmf.

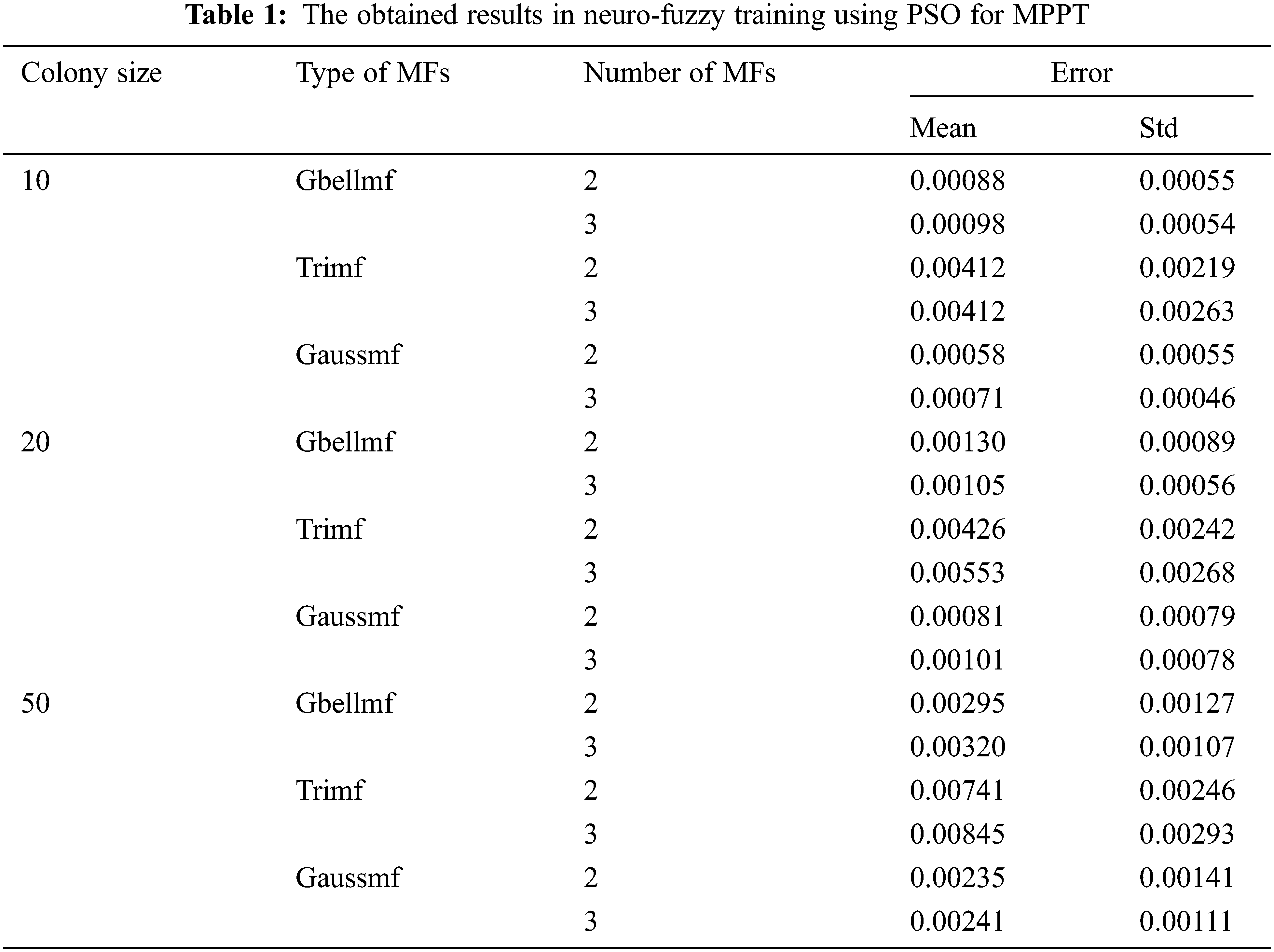
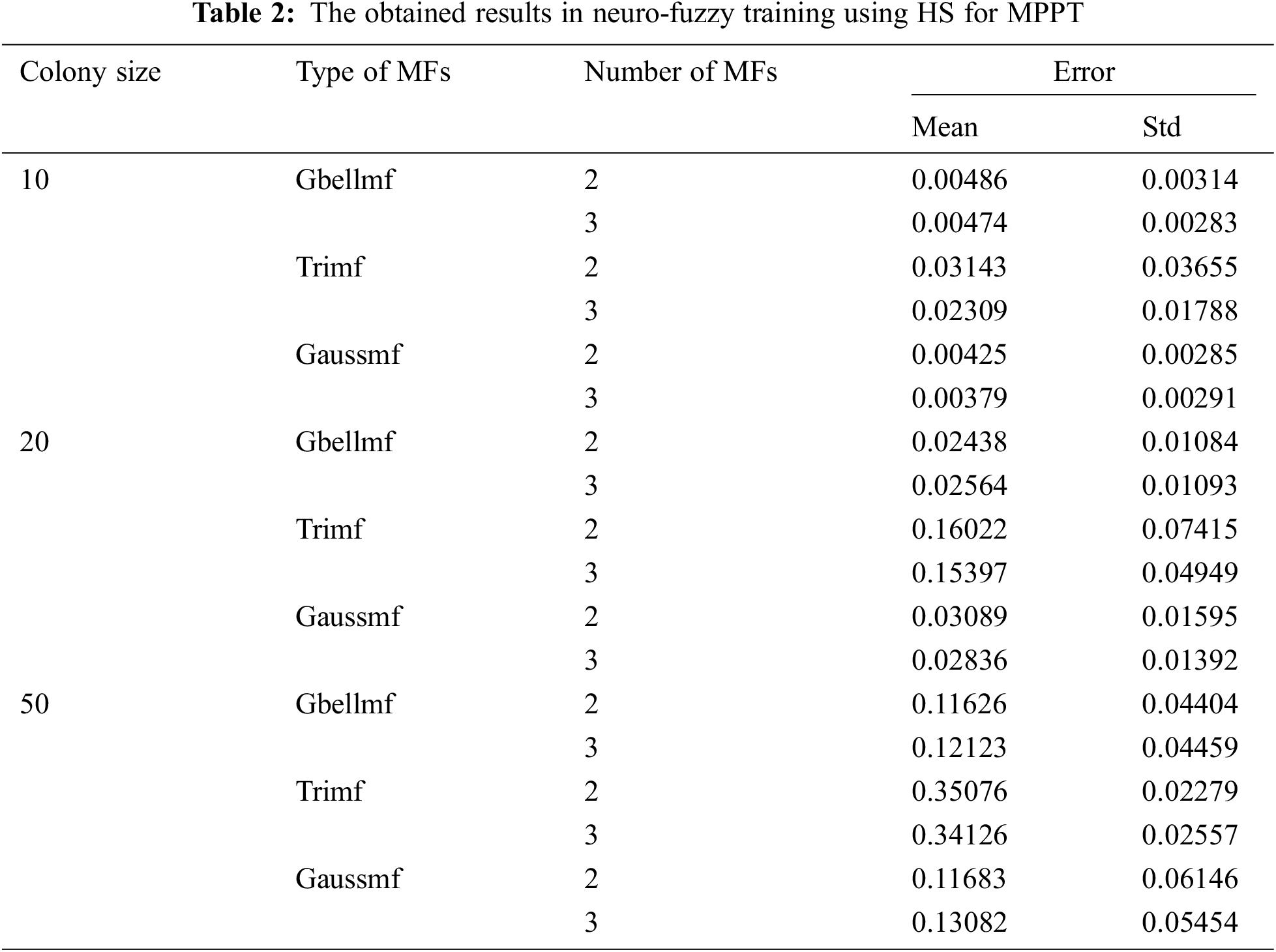
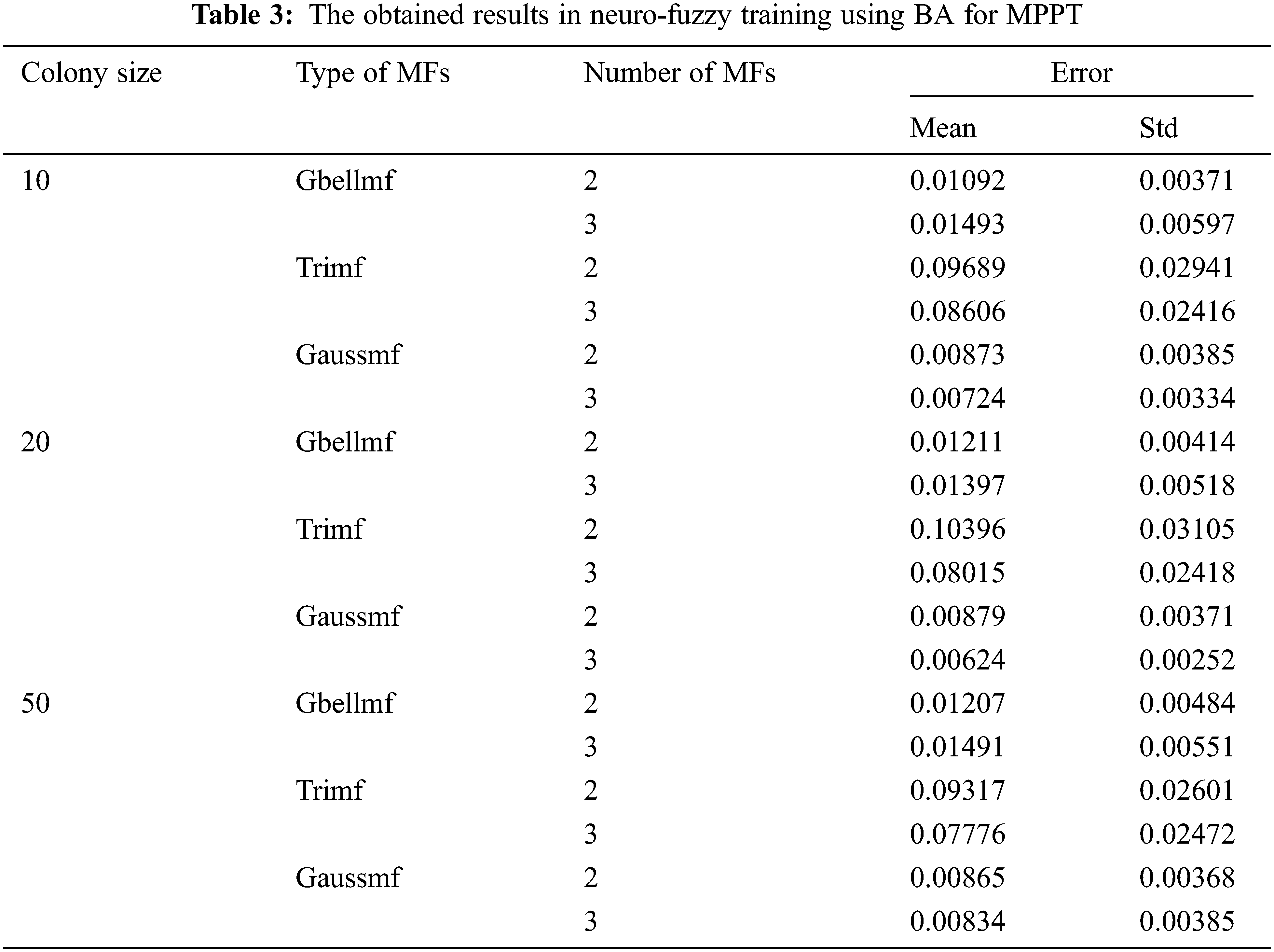
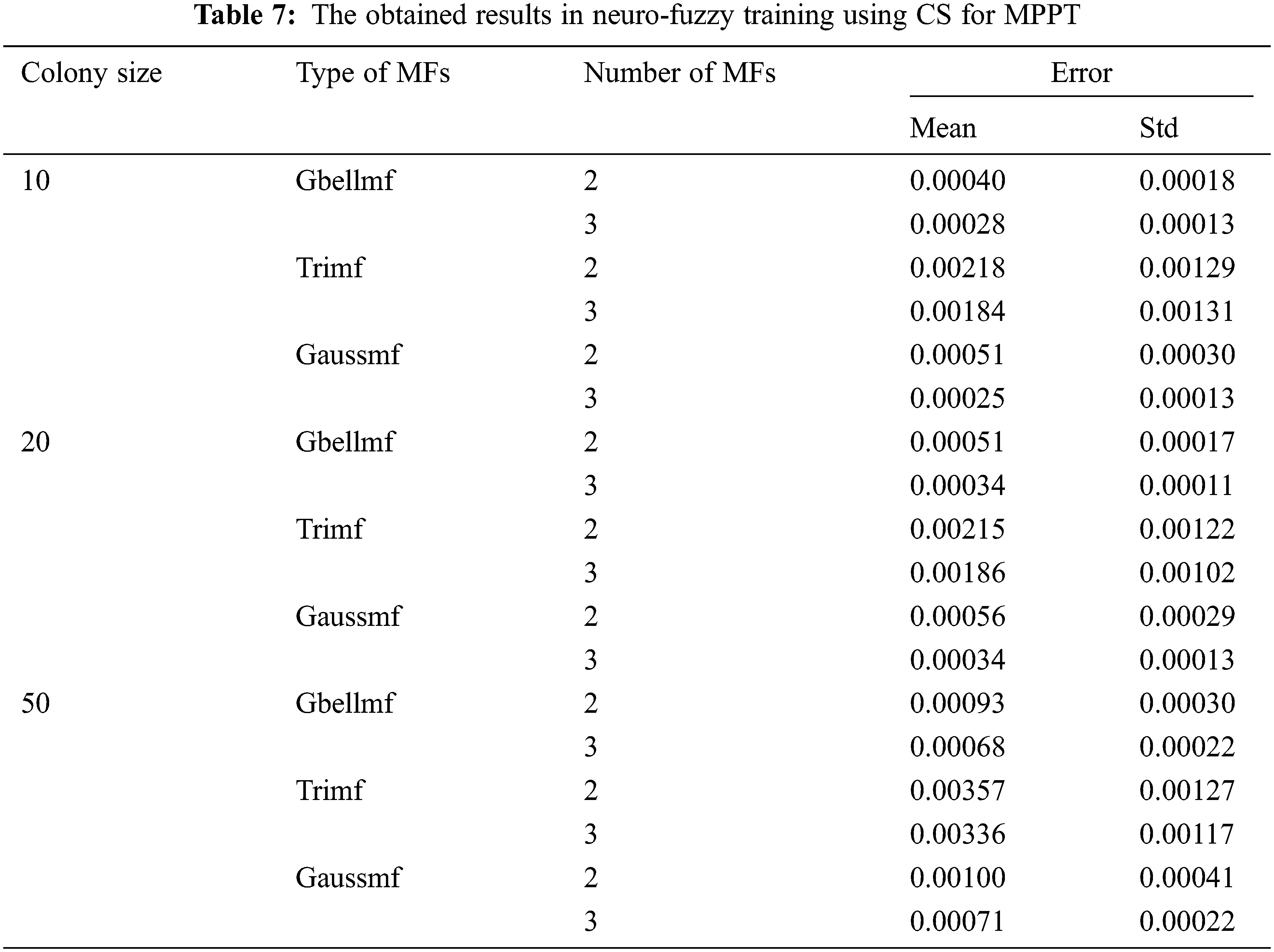
The effect of meta-heuristic algorithms on the results differs according to the MFs used. Tab. 8 presents the most effective results of meta-heuristic algorithms. The algorithms other than BA achieve the best results when n = 10. In BA, more effective results are found when n = 20. All algorithms are more efficient in Gaussmf. In PSO and DE, the best results are achieved by using 2 Gaussmf. For other algorithms, the best results belong to 3 Gaussmf. The worst results in all algorithms are obtained with Trimf. When all algorithms are evaluated together, the lowest training error value is found as 0.00025 with CS.

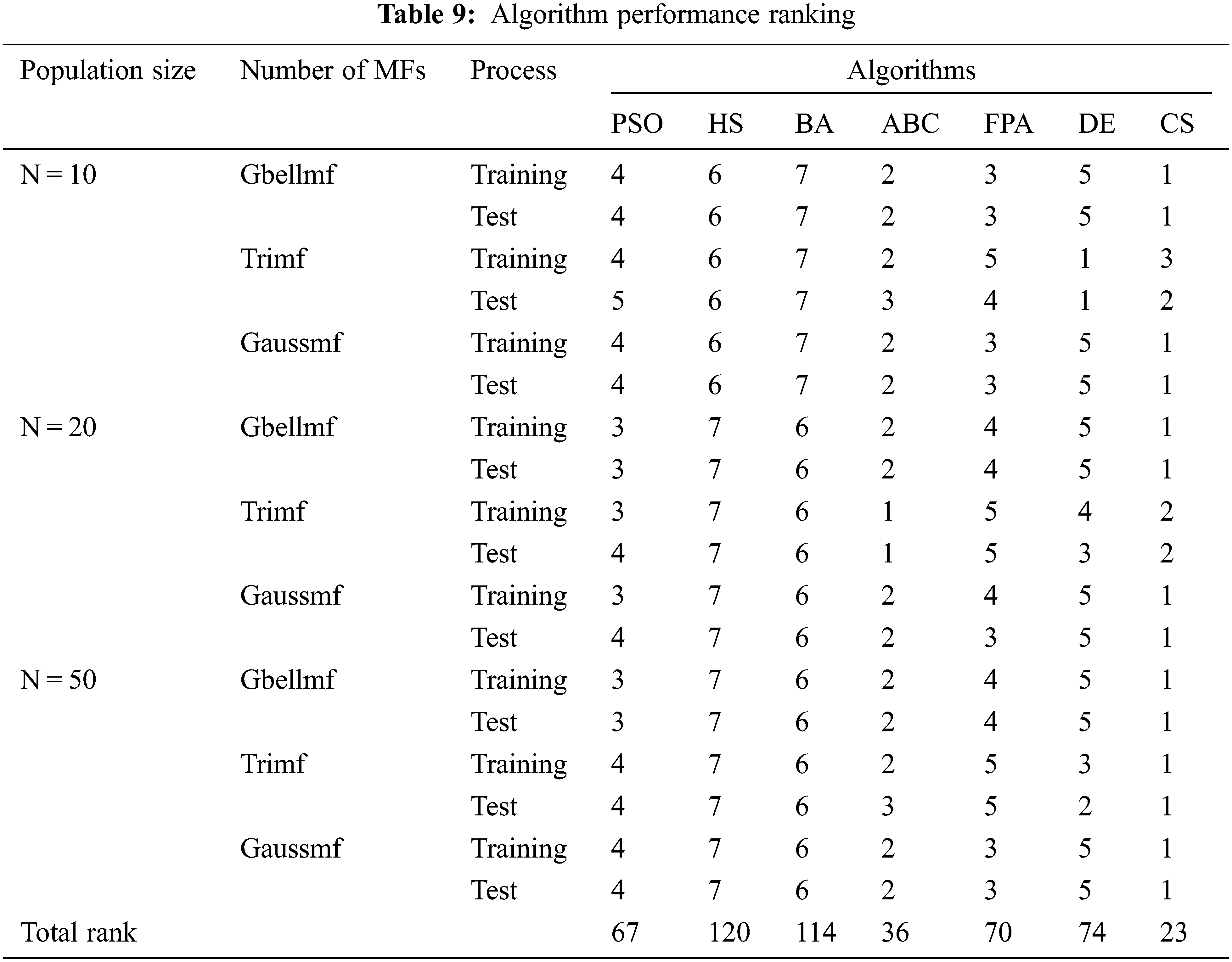
The success ranking of the algorithms varies according to colony size and the neuro-fuzzy structure chosen. Tab. 9 shows the success rankings of the algorithms. When n = 10 and n = 20, the best results other than Trimf are found with CS. In other words, CS is the first place in 14 out of 18 results. ABC algorithm is in first place for results obtained with Trimf when n = 20. When the all rankings in the 18 applications are taken into account, CS is in the 1st place with 23 points. ABC is second place with 36 points. PSO, FPA and DE have scores close to each other. The scores of PSO, FPA, and DE are 67, 70, and 74, respectively. It is seen that the worst results are obtained by using HS and BA. While BA is in the 5th place with 114 points, HS is in the last place with 120 points.

One of the important performance criteria of algorithms is convergence speeds. Convergence of related meta-heuristic algorithms on MPPT is compared in Fig. 6. This figure is created for n = 10 and the number of generations = 500. The convergence of CS is best in all generations. In the first 200 generations, the effective convergence after CS belongs to PSO. In the generations after 200, PSO loses its superiority and ABC is more effectively from it. After the 400th generation, the convergence speed of the PSO decreases and it falls behind FPA. In the first 300 iterations, BA is better than HS. But later, the development status of both algorithms has changed. It is seen that HS has better solution quality than BA. Fig. 7 compares the real output and the predicted output. It is seen that the real output and the predicted output generally overlap with each other, outside of BA. In other words, it is understood that the proposed approaches are effective in estimating the power values of the MPPT.

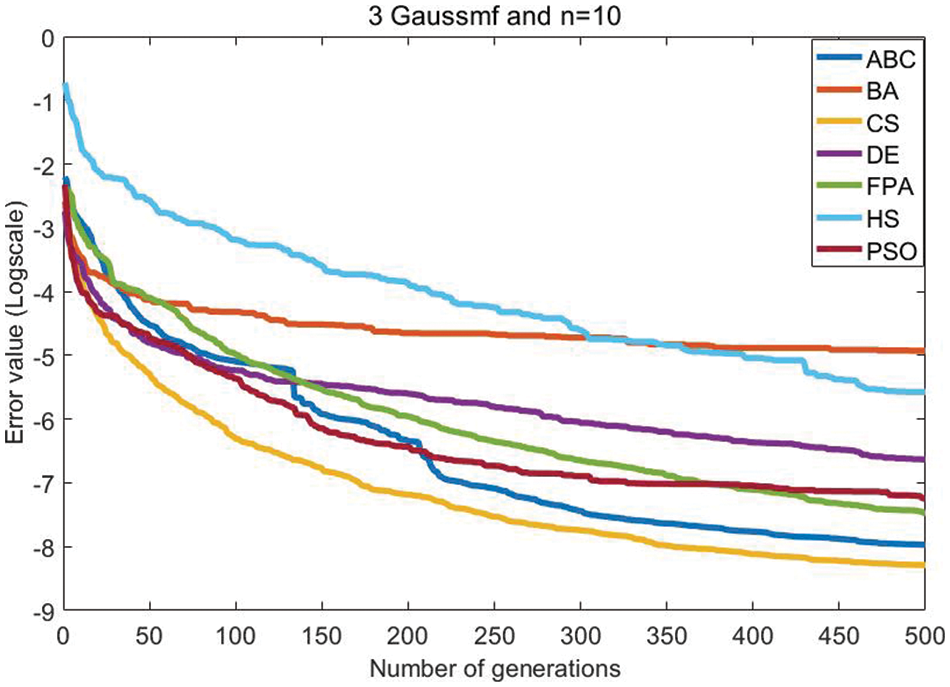
Figure 6: Comparing convergence of heuristic algorithms on MPPT

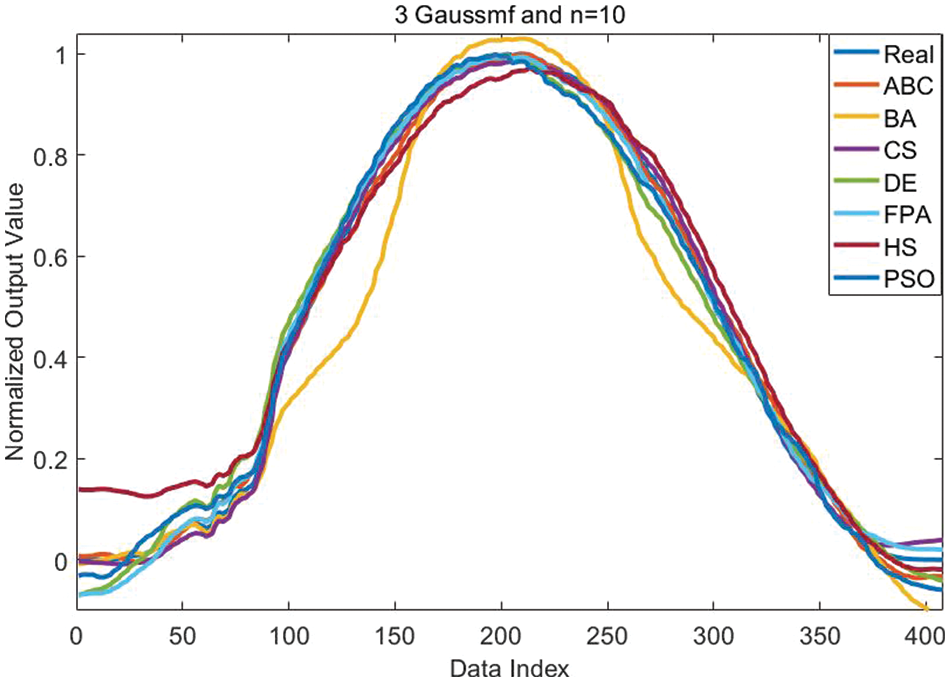
Figure 7: Comparison of real and predicted output

5  Discussion

In neuro-fuzzy training, the type of MFs, number of MFs, number of rules, colony size and number of generations directly affect performance. It is seen that different MFs are used in the literature. Within the scope of this study, the analyzes are carried out on three popular MFs such as Gbellmf, Trimf and Gaussmf. In MPPT, the effect of MFs is clearly observed. The best results are found by utilizing Gaussmf. The increase in the number of MFs directly affects the number of parameters to be used in training. At the same time, it also affects the solution quality. It can be positive in some cases and negative in other cases. In particular, the training algorithms are also a decisive factor. This is clearly observed in MPPT model based on the neuro-fuzzy.

The effect of training algorithms is very important in neuro-fuzzy training. Control parameters affect the performance of training algorithms. Colony size and number of maximum generations are common control parameters of algorithms. In neuro-fuzzy training for MPPT, increasing colony size negatively affects performance generally. The best results are generally obtained when the colony size is 10. Namely, increasing colony size often worsens solution quality. This situation can be analyzed on the CS and ABC algorithm, where the best results are obtained. When 2 Gbellmf, the obtained results for n = 10, 20 and 50 are 0.00040, 0.00051 and 0.00093 by using CS, respectively. When the ABC algorithm is evaluated, the errors obtained are 0.00054, 0.00073 and 0.00147, respectively. As can be seen, as the colony size increases, the quality of the solution deteriorates. A similar situation is mostly observed in other membership functions and meta-heuristic algorithms. Within the limitations of the study, it is seen that n = 10 is more effective for solving the related problem.

In addition to the solution quality, one of the important indicators in neuro-fuzzy training is the speed of convergence. Fast convergence enables to reach effective solutions in a short time. An algorithm can reach efficient solutions in high generations. If it cannot reach effective solutions in lower generations, it will have a disadvantage. It is important to achieve the best results in a short time in energy and electronics applications. Especially in the process of integrating artificial intelligence techniques such as neuro-fuzzy and artificial neural networks into embedded systems, this may affect the preferences. As with solution quality, convergence is affected by membership functions, colony size, and number of generations. The effect of convergence is discussed within the limitations of the study. Here, the convergence obtained with n = 10 and 3 Gaussmf is evaluated. Within this limitation, it was observed that the algorithms with the best convergence speed received CS and ABC.

As it is known, the training process takes place on known data. Predicted outputs are obtained as a result of the training process. As a result of an effective training process, it is expected that the error will be low. In other words, the real output used in the training process and the predicted output should be similar to each other. As the similarity increases, the acceptability of the training process will also increase. That’s why it’s important to compare real and predicted output. When the comparison chart is examined, the predicted output values in the first 100 and the last 50 data have moved away from the real output mostly. In other words, it shows that meta-heuristic algorithms have difficulty in predicting this data. In other data, the algorithms mostly achieved a good predictive output. It is seen that the predicted outputs obtained with CS and ABC exactly overlap with the real output. This means that the two algorithms produce acceptable results for MPPT estimation.

Temperature and solar radiation are given as an input to the neuro-fuzzy model in MPPT. As the output, power value is obtained. When the tables and figures are examined, it is seen that results very close to the real output value are obtained. This indicates that the relevant heuristic algorithms can be used for MPPT. It is true that CS and ABC algorithm will be more effective for precise calculations. However, it is possible to use other training algorithms within certain fault tolerance. The maximum number of generations can be increased to achieve better results. CS and ABC algorithm are recommended for studies requiring rapid results.

6  Conclusion

This study proposes a MPPT model based on neuro-fuzzy by using PSO, HS, BA, ABC, FPA, DE and CS. The proposed MPPT model takes as input values such as the temperature and solar radiation. It is obtained a power value as the output. For effective MPPT, neuro-fuzzy model is separately trained using related meta-heuristic algorithms. The effects of type of MF, number of MF, colony size and maximum number of generations on performance are investigated. All obtained results are compared with each other. It has been observed that CS and ABC algorithms are more effective than others in terms of both solution quality and convergence. For the proposed MPPT model, Gaussmf is generally more successful. More effective solutions are usually found when the colony size is 10. In particular, it is observed that the difference between the real output and the predicted output is low. This shows that the suggested approaches can be used in MPPT applications.

MPPT is one of the important topics studied in the literature. Variants of related algorithms can be developed to obtain more effective results on MPPT in future studies. It is possible to analyze the performance of different artificial intelligence techniques on MPPT. In addition, it seems from the results that the proposed method can be applied to different engineering problems other than MPPT.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. A. Qasim and V. I. Velkin, “Maximum power point tracking techniques for micro-grid hybrid wind and solar energy systems-A review,” International Journal on Energy Conversion, vol. 8, no. 6, pp. 223–234, 2020. [Google Scholar]

 2.  S. Lyden and M. Haque, “Maximum power point tracking techniques for photovoltaic systems: A comprehensive review and comparative analysis,” Renewable and Sustainable Energy Reviews, vol. 52, pp. 1504–1518, 2015. [Google Scholar]

 3.  M. Abo-Sennah, M. El-Dabah and A. E. -B. Mansour, “Maximum power point tracking techniques for photovoltaic systems: A comparative study,” International Journal of Electrical & Computer Engineering, vol. 11, no. 1, pp. 2088–8708, 2021. [Google Scholar]

 4.  M. Mao, L. Cui, Q. Zhang, K. Guo, L. Zhou et al., “Classification and summarization of solar photovoltaic MPPT techniques: A review based on traditional and intelligent control strategies,” Energy Reports, vol. 6, pp. 1312–1327, 2020. [Google Scholar]

 5.  A. O. Baba, G. Liu and X. Chen, “Classification and evaluation review of maximum power point tracking methods,” Sustainable Futures, vol. 2, pp. 100020, 2020. [Google Scholar]

 6.  S. Motahhir, A. El Hammoumi and A. El Ghzizal, “The most used MPPT algorithms: Review and the suitable low-cost embedded board for each algorithm,” Journal of Cleaner Production, vol. 246, pp. 118983, 2020. [Google Scholar]

 7.  A. Rezvani, M. Izadbakhsh, M. Gandomkar and S. Vafaei, “Implementing GA-ANFIS for maximum power point tracking in PV system,” Indian Journal of Science and Technology, vol. 8, no. 10, pp. 982, 2015. [Google Scholar]

 8.  N. Hamouda, B. Babes, S. Kahla, A. Boutaghane, A. Beddar et al., “ANFIS controller design using PSO algorithm for MPPT of solar PV system powered brushless DC motor based wire feeder unit,” in 2020 Int. Conf. on Electrical Engineering (ICEE), IEEE, Istanbul, Turkey, pp. 1–6, 2020. [Google Scholar]

 9.  J. Andrew-Cotter, M. N. Uddin and I. K. Amin, “Particle swarm optimization based adaptive neuro-fuzzy inference system for MPPT control of a three-phase grid-connected photovoltaic system,” in 2019 IEEE Int. Electric Machines & Drives Conf. (IEMDC), IEEE, San Diego, CA, USA, pp. 2089–2094, 2019. [Google Scholar]

10. N. Priyadarshi, S. Padmanaban, J. B. Holm-Nielsen, F. Blaabjerg and M. S. Bhaskar, “An experimental estimation of hybrid ANFIS–PSO-based MPPT for PV grid integration under fluctuating sun irradiance,” IEEE Systems Journal, vol. 14, no. 1, pp. 1218–1229, 2019. [Google Scholar]

11. A. Ndiaye and M. Faye, “Experimental validation of pso and neuro-fuzzy soft-computing methods for power optimization of PV installations,” in 2020 8th Int. Conf. on Smart Grid (icSmartGrid), IEEE, Paris, France, pp. 189–197, 2020. [Google Scholar]

12. S. Padmanaban, N. Priyadarshi, M. S. Bhaskar, J. B. Holm-Nielsen, V. K. Ramachandaramurthy et al., “A hybrid ANFIS-ABC based MPPT controller for PV system with anti-islanding grid protection: Experimental realization,” IEEE Access, vol. 7, pp. 103377–103389, 2019. [Google Scholar]

13. N. Priyadarshi, S. Padmanaban, L. Mihet-Popa, F. Blaabjerg and F. Azam, “Maximum power point tracking for brushless DC motor-driven photovoltaic pumping systems using a hybrid ANFIS-FLOWER pollination optimization algorithm,” Energies, vol. 11, no. 5, pp. 1067, 2018. [Google Scholar]

14. C. H. Basha and C. Rani, “Performance analysis of MPPT techniques for dynamic irradiation condition of solar PV,” International Journal of Fuzzy Systems, vol. 22, no. 8, pp. 2577–2598, 2020. [Google Scholar]

15. N. Pachaivannan, R. Subburam, M. Padmanaban and A. Subramanian, “Certain investigations of ANFIS assisted CPHO algorithm tuned MPPT controller for PV arrays under partial shading conditions,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 10, pp. 9923–9938, 2021. [Google Scholar]

16. S. Benhalima, A. Chandra and M. Rezkallah, “Real-time experimental implementation of an LMS-adaline-based ANFIS controller to drive PV interfacing power system,” IET Renewable Power Generation, vol. 13, no. 7, pp. 1142–1152, 2019. [Google Scholar]

17. D. Mlakić, L. Majdandžić and S. Nikolovski, “ANFIS used as a maximum power point tracking algorithm for a photovoltaic system,” International Journal of Electrical & Computer Engineering, vol. 8, no. 2, pp. 2088–8708, 2018. [Google Scholar]

18. J. -S. Jang, “ANFIS: Adaptive-network-based fuzzy inference system,” IEEE Transactions on Systems, Man, and Cybernetics, vol. 23, no. 3, pp. 665–685, 1993. [Google Scholar]