Cooperative NOMA Based on OAM Transmission for Beyond 5G Applications

1  Introduction

Currently, the wireless connection is the primary form of communication, meanwhile, the exponentially increasing demand makes it challenging to be fulfilled. For instance, one of 5G technologies the internet of things (IoT) requires enhanced mobile broadband (eMBB) which requires higher throughput than that available in 4G. Achieving sufficient throughput for 5G and beyond applications cannot be realized without upgrading the available network infrastructure [1].

Typically, a traditional wireless system is based on orthogonal transmission by ensuring an exclusive frequency band, time-slot, or code for each link between any transmitter and receiver, hence communications among different links do not interfere with each other. The spectral efficiency of this way is not sufficient for the new era of communications [2]. Resulting in the introduction of non-orthogonal multiple access (NOMA) for simultaneous use of the same resources by more than one user but with different levels of power. Particularly, NOMA assigns less power to users with better channel states, where these users decode their information by applying successive interference cancellation (SIC) [3]. Currently, NOMA is under consideration for 3GPP Release 16 standards of 5G systems [4].

Cooperative communication through adding relays exploits the broadcast nature of the wireless channel via providing an alternative link to avoid bad transmission [5–8]. After the successfulness of applying cooperative communication in 5G, employing relays in NOMA networks (this is known as cooperative NOMA networks) enhanced the network performance with higher diversity gain and higher throughput as well [9].

Combining different 5G techniques to overcome their shortcomings is popular in the current literature. As an example, authors in [10] utilized cooperative communication to overcome the millimeter-wave (mm-wave) enormous pathloss. In addition to mm-wave and NOMA, several advanced radio spectrum efficiency enhancement techniques are expected to play a role in the transition to 5G and beyond 5G technologies.

One of the promising techniques for improving spectrum efficiency is orbital angular momentum (OAM) orders which are possessed by electromagnetic waves. As shown in [11], an electromagnetic wave has a special form of radiation which is OAM. OAM beams are generated by a circular antenna array. The OAM mode is defined by its rotating phase front, so it is a phase-dependent phenomenon. This contrasts with the ordinary beams which have rotating electric field vectors.

OAM phase fronts have an azimuthal phase dependence of exp(jl∅) in their spatial phase distribution where l is an integer denotes the OAM order, and ∅ denotes the azimuthal angle in the cylindrical coordinates (r,∅,z) . The OAM beams have amplitude nulls at the centers of the beams. Furthermore, the size of the null region of the radio beams widens with the vertical distance to the transmitting array, this is known as beam divergence, due to the structure of the beam which has a conic shape [12]. Due to phase differences among OAM orders, the orthogonality among orders is preserved. The orthogonal OAM orders extremely increase the system throughput by transmitting over different orders of OAM without occupying an additional frequency spectrum [13].

The promising results of cooperative communication and OAM transmission inspired the authors in [14] to combine the two technologies. The results of [14] show that the cooperative OAM based solution is able to overcome the OAM beam divergence limitation, hence, higher throughput is realized.

Motivated by the success of cooperative NOMA with ordinary radiation and the superiority of OAM compared to ordinary radiation in raising system throughput, in addition to the encouraging results of [14], this paper proposes the combining of cooperative NOMA and OAM transmission. This can be accomplished by transmitting all users’ messages over the available OAM orders but each message has a different level of power. Similar to the case in ordinary NOMA, successive interference cancellation SIC helps each user decodes its own message. To the best of the authors’ knowledge, no previous studies have employed OAM transmission in the cooperative NOMA network. This employment shows several advantages to both OAM and the cooperative NOMA network.

The relay cooperation part of the proposed system mitigates the main shortcoming usually encountered in the implementation of OAM transmission which is the beam divergence. Rather than using extremely large receivers or raising the frequency to mitigate beam divergence, relay cooperation reduces the distance between the transmitter and the receiver. In addition, relays can help with avoiding deep fading situations.

On the other hand, the OAM transmission has orthogonal orders that can help cooperative NOMA to achieve higher throughput than what traditional cooperative NOMA can achieve. For the suitability of ordinary cooperative NOMA, the link connecting the relay to the weakest user (which has the worst channel conditions) should at least support ordinary orthogonal multiple access (OMA) transmission. Therefore, we suggest the replacement of ordinary transmission with OAM waves which makes these orthogonal links support a higher rate of data transmission. To summarize, this paper proposes a novel system that employs OAM transmission, which has the ability to increase the number of data streams, in cooperative NOMA networks to reach higher throughput levels that are suitable for 5G and beyond 5G applications.

The organization of this paper is as follows: Section 2 includes the system model for the proposed cooperative NOMA network that employs OAM transmission. Numerical simulation experiments of the proposed system in addition to comparison with other available systems are thoroughly discussed in Section 3. Finally, Section 4 concludes this paper.

2  System Model

2.1 Cooperative NOMA Network

The system model of the OAM-base cooperative NOMA network is shown in Fig. 1. There are a source node S, a half-duplex decode-and-forward (DF) relay node denoted as R, and two users U1 and U2. The system model can be extended to any number of users as in [15]. The channel coefficients for S to R, R to U1 and R to U2 links are denoted as hsr , hru1 and hru2 respectively. All channels are assumed to have flat Rayleigh fading coefficients that remain unchanged within the time-slot and change independently from one time-slot to another. Without losing of generality, we assume that the transmit powers at all transmit nodes are Pt and the noise variances at all receiving nodes are σ2 .

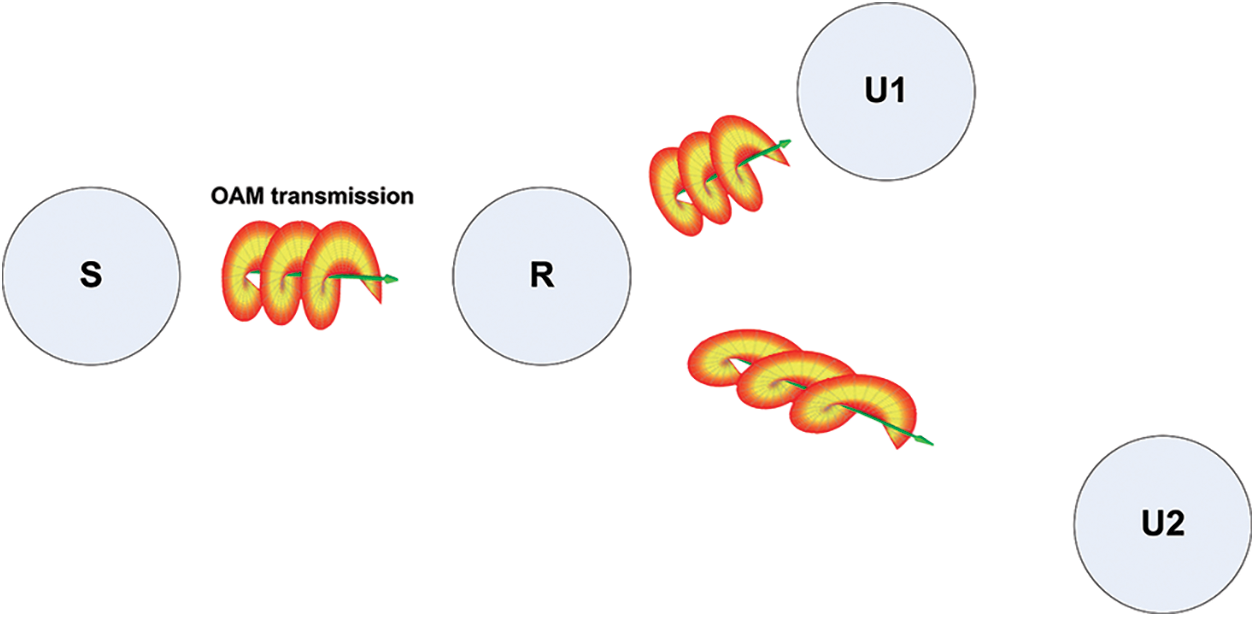
Figure 1: OAM-based cooperative NOMA network system model

We assume that the source always has sufficient information (i.e., it is saturated) to send to relays in all time slots. Due to path loss and shadowing, we assume that the source and destination are not directly connected.

The data rate is fixed at the value ϵ . If the channel capacity is greater than or equal to the data rate ϵ , the link can handle the transmission successfully. Retransmission occurs based on the acknowledgment (ACK) and negative ACK (NACK) mechanism; this mechanism happens between transmitters (S or R) and receivers (R or users). Each receiver broadcasts the ACK/NACK signal to the transmitters: R to S and users to R.

The channel state information at all receivers is assumed to be available. At time slot t , the corresponding link capacities for channels hsr and hru1,2 ( hru1,2 represents the channel coefficients of R to U1 link and R to U2 link, this notation is used in the rest of the paper wherever U1 and U2 have the same equation) are given by:

Csr=log(1+γsr(t)) (1)

Cru1,2=log(1+γru1,2(t)) (2)

where γsr(t)=Ptσ2|hsr(t)|2andγru1,2(t) = Ptσ2|hru1,2(t)|2 .

The channel gains |hsr(t)|2 and |hru1,2(t)|2 are exponentially distributed with the average θsr=E[|hsr(t)|2] and θru1,2=E[|hru1,2(t)|2], where θsr and θru1,2 denote average S to R channel gain and average R to users U1 and U2 channel gain, respectively, and E[.] is the expectation operator. γsr(t) and γru1,2(t) are also exponentially distributed with average γsr¯=Ptσ2θsr and γru1,2¯=Ptσ2θru1,2 . Thus, γsr and γru1,2 are the instantaneous Signal to Noise Ratio (SNR) values, while γsr¯ and γru1,2¯ are the average SNR values for channels hsr , hru1 and hru2 respectively.

The system throughput depends on the channel outage; hence we first describe the outage analysis of the cooperative NOMA network. In ordinary transmission networks, an outage occurs if the link capacity is less than the target data rate. Since NOMA is applied from R to users, the relay R needs to have the packets of the two users prior to applying NOMA. In the literature, this is done by two approaches: adding a buffer to R which lengthens the system delay waiting for the two packets to become available at R. The second approach is considering NOMA not applicable unless the link between S and R supports the transmission of the two packets simultaneously, so double transmission rises the outage probability of S to R link to (see [16,17]):

P(log(1+γsr)<2ϵ)=1−e−22ϵ−1γsr¯. (3)

On the other hand, for the R to U1 and U2 links, NOMA can be applied to transmit packets to the two users simultaneously. The superimposed NOMA symbol at R is given by

xr(t)=αxru1(t)+1−αxru2(t) (4)

where xru1(t) and xru2(t) are data for users U1 and U2 respectively, and α is the power allocation factor. Then the received signal at U1 and U2 is given by

y1,2(t)=αPthru1,2(t)xru1(t)+(1−α)Pthru1,2(t)xru2(t)+nu1,2(t) (5)

where nu1,2(t) is the AWGN of users U1 and U2 links. When NOMA is applied, the link capacity is not given by (2) but must include the interference within the superimposed symbol. In particular, NOMA depends on having different SNR levels among users. When γru1(t)>γru2(t) , the SNR to decode xru2(t) at U2 is given by

SINR(xru2(t))=(1−α)γru2(t)αγru2(t)+1 (6)

xru2(t) can also be decoded at U1 because U1 has higher SNR than U2. SIC is utilized at U1 to remove xru2(t) from the received signal, the required SNR to decode xru1(t) at U1 is given by

SNR(xru1(t))=αγru1(t) (7)

Similar to the procedures in [16,17], the condition for finding α that supports NOMA transmission to both U1 and U2 (i.e., log2(1+SINR(xru2(t)))≥ϵ and log2(1+SNR(xru1(t)))≥ϵ ) is given by

γru2(t)≥(2ϵ−1)γru1(t)γru1(t)−2ϵ(2ϵ−1) (8)

Equivalently, if γru2(t)>γru1(t) , NOMA condition becomes

γru1(t)≥(2ϵ−1)γru2(t)γru2(t)−2ϵ(2ϵ−1) (9)

The probability that (8) or (9) are satisfied to support NOMA is

P(v,w)=1γruv¯exp⁡(−(2ϵ−1)γruv¯+(22ϵ−2ϵ)γruw¯γruv¯.γruw¯)×∫2ϵ−1∞−xγruv¯−2ϵ(2ϵ−1)2γruw¯.xdx−γruw¯γruv¯+γruw¯exp⁡(−(2ϵ−1)(γruv¯+γruw¯)(22ϵ+2ϵ)γruv¯.γruw¯) (10)

where v,w=1,2 respectively if γru1(t)>γru2(t) , and v,w=2,1 otherwise.

2.2 OAM Wave Decomposition

OAM wave of order l has a complex amplitude that can be expressed in Bessel–Gauss form as:

u(r,∅)=exp(−r2/d2)Jl(krr)exp(jl∅) (11)

the exponential term ( exp(−r2/d2) ) is the Gaussian envelope, d denotes the width of the envelope. Jl is the lth order Bessel function of the first kind, r is the radial coordinate, ∅ is the azimuth and kr is a radial frequency [18].

The propagation of OAM wave in space is determined by the paraxial Helmholtz equation:

j∂u∂z+12ko(∂2u∂x2+∂2u∂y2)=0 (12)

where z is the propagation distance, ko=2π/λ denotes the vacuum wavenumber and λ represents the wavelength. Helmholtz wave equation can be analytically solved by well-known techniques such as Fourier transform [19]. As a result, the following general expression of the Bessel–Gauss wave in free propagation is derived:

u(r,∅,z)=G(rz,zL,krd)Jl(krr1+jzL)ejl∅ (13)

where L=πd2/λ denotes the Gaussian envelope Rayleigh distance, and the function G represents the propagation of the Gaussian envelope which does not rely on the OAM order l [20].

Fig. 2 shows the transversal spatial distributions of Bessel–Gaussian waves at different OAM orders. All distances in the figure are normalized to λ . In the figure, a change in the amplitude color from blue to yellow indicates an increase in the field intensity. The deep blue at the beam center indicates amplitude null, this amplitude null extends with the increase in OAM order. The phase fronts in the right–hand plots depict the plane which intersects the beam at z=5 from the transmitting circular antenna array. The rotational phase front of the OAM beams is clearly displayed for two cases OAM order =1 and OAM order =5 . The number of rotational phase fronts equals the OAM order.

Figure 2: The upper two images show the field spatial amplitude distribution (left). The phase fronts of OAM order = 1 (right). Similarly, OAM order = 5 is shown in the lower two images

3  Simulation Experiments Results

This section presents the simulation experiments results to justify the proposed OAM-based cooperative NOMA system analysis and design. In addition, this section provides performance comparisons between the proposed system and the available related solutions in [14,17]. In the simulations, we assume that the noise variance ( σ2 ) is normalized to unity and we follow [14,17] in assuming the data rate ϵ= 2 bps/Hz to make fair comparisons. It is worth mentioning that the values of the parameters are normalized to make it suitable for general applications.

Fig. 3 shows the impact of changing the OAM order on the proposed system throughput. In this experiment, the size of the receiving aperture is selected to match the maximum intensity radius of a certain OAM order (the impact of mismatched size and OAM order on the system throughput is shown in Fig. 4). A receiver consists of a sufficient number of antenna elements (e.g., short dipoles) distributed around a circular circumference (see [12]). It is obvious that the higher the OAM order is the better, especially at high SNR. For instance, at 5 dB (low SNR) the difference between the system throughput at OAM order = 1 and OAM order = 5 is almost 3 packets per time-slot, while this difference is enlarged to 4 packets per time-slot at 20 dB SNR. However, the number of practical OAM orders is limited due to three challenges: the complexity of the receiver, the decrement in the received power and the non-pure rotating phase of large number of OAM orders [12]. On the other hand, the number of users in NOMA technique is limited due to the complexity of SIC design [4].

Figure 3: The proposed OAM-based cooperative NOMA system throughput at different OAM orders

Figure 4: The impact of different receiving aperture sizes on the proposed OAM-based cooperative NOMA system throughput where OAM order = 5

As mentioned above, matching the receiving aperture to the maximum intensity radius of the OAM order maximizes the system throughput. In Fig. 4, OAM orders = 5, if a smaller receiving aperture size 2 is used, the system throughput degrades proportional to SNR, for example, the degradation is almost 3 packets per time-slot at 20 dB compared to using the optimal size i.e., 5.

As in [14], different percentages of the maximum received power (thresholds) have to be considered in order to achieve higher throughputs. Examples of different received power thresholds are shown in Fig. 5. The received power decreases as the OAM order increases. However, the received power decrement can be eased with the right receiver size, which boosts the system throughput. Because the throughput is the summation over all throughputs from every order with received power passing the threshold value.

Figure 5: Different percentages of the maximum received power (thresholds)

It can be observed that lowering the threshold makes the reception less impeded and allows higher OAM orders, therefore, higher throughput is achieved at lower thresholds. This is clearly shown in Fig. 6, the throughput at 10 dB SNR is 4 packets per time-slot higher at 20% threshold than at 90% threshold. The distinction between different thresholds is weekend at high SNR, for example, it is trimmed to 3 packets per time-slot at 20 dB SNR, because raising the SNR helps OAM orders pass the high threshold (i.e., 90%) which enhances the throughput at high thresholds.

Figure 6: The significance of reducing the received power threshold on the system throughput with 5 OAM orders

In [14], the cooperative OAM with 5 OAM orders is compared to the ordinary cooperative NOMA with 5 users. Fig. 7 shows a comparison between these two systems and the proposed OAM-based cooperative NOMA system. The results show the throughput superiority of the proposed system compared to two of the promising solutions for 5G applications. The proposed system almost doubles the throughput of the cooperative OAM which in turn outperforms the ordinary cooperative NOMA. It can be seen from the figure that the cooperative OAM has the highest throughput at very low SNR ( ≤ 3 dB), this is due to the requirements of NOMA conditions ((8) and (9)). It is worth noting that employing OAM with NOMA has a positive impact in making NOMA available for lower SNR values compared with ordinary NOMA, this is obvious in Fig. 8, which shows the impact of applying OAM with NOMA in reducing the outage probability of the proposed system in low SNR range ( ≤ 10 dB). The reason for this reduction in outage probability is the ability of OAM transmission to achieve a higher data rate and raises the value of (10) at lower SNR. Finally, as shown comprehensively in [14], the ability of cooperative relay to combat the divergence of high OAM orders by shortening the distance between source and destination, here we just show the positive impact of mitigating divergence on system throughput.

Figure 7: Throughput comparison among the proposed OAM-based cooperative NOMA, the cooperative OAM and the ordinary cooperative NOMA

Figure 8: Outage probability comparison between the proposed OAM-based cooperative NOMA and the ordinary cooperative NOMA

4  Conclusions

This paper proposes an OAM-based cooperative NOMA solution for future demanding applications such as tactile internet (the next generation of IoT). The throughput of the proposed system is proportional to the OAM orders and the number of users, higher OAM orders is suitable with larger size receiver and with cooperation solutions. The received power threshold has a noticeable impact on the system throughput especially at low SNR. In general, lower power received thresholds achieve higher throughputs. Furthermore, OAM transmission has a positive impact on NOMA by lowering its outage probability. As a result, the proposed OAM-based cooperative NOMA outperforms the separated using of OAM in cooperative OAM and NOMA in ordinary cooperative NOMA.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  J. G. Andrews, S. Buzzi, W. Choi, S. V. Hanly, A. Lozano et al., “What will 5G be?,” IEEE Journal on Selected Areas in Communications, vol. 32, no. 6, pp. 1065–1082, 2014. [Google Scholar]

 2.  Z. Ding, M. Peng and H. V. Poor, “Cooperative non-orthogonal multiple access in 5G systems,” IEEE Communications Letters, vol. 19, no. 8, pp. 1462–1465, 2015. [Google Scholar]

 3.  L. Lv, J. Chen and Q. Ni, “Cooperative non-orthogonal multiple access in cognitive radio,” IEEE Communications Letters, vol. 20, no. 10, pp. 2059–2062, 2016. [Google Scholar]

 4.  H. S. Ghazi and K. W. Wesołowski, “Improved detection in successive interference cancellation NOMA OFDM receiver,” IEEE Access, vol. 7, pp. 103325–103335, 2019. [Google Scholar]

 5.  M. Alkhawatrah, Y. Gong, O. Aldabbas and M. Hammoudeh, “Buffer-aided 5G cooperative networks: Considering the source delay,” in Proc. of the 3rd Int. Conf. on Future Networks and Distributed Systems (ICFNDS ’19), New York, NY, USA, Association for Computing Machinery, Article 13, pp. 1–6, 2019. [Google Scholar]

 6.  A. Bletsas, H. Shin and M. Win, “Cooperative communications with outage-optimal opportunistic relaying,” IEEE Transactions on Wireless Communications, vol. 6, no. 9, pp. 3450–3460, 2007. [Google Scholar]

 7.  A. Nosratinia, T. Hunter and A. Hedayat, “Cooperative communication in wireless networks,” IEEE Communications Magazine, vol. 42, no. 10, pp. 74–80, 2004. [Google Scholar]

 8.  A. Sendonaris, E. Erkip and B. Aazhang, “User cooperation diversity. part I. system description,” IEEE Transactions on Communications, vol. 51, no. 11, pp. 1927–1938, 2003. [Google Scholar]

 9.  Z. Ding, H. Dai and H. V. Poor, “Relay selection for cooperative NOMA,” IEEE Wireless Communications Letters, vol. 5, no. 4, pp. 416–419, 2016. [Google Scholar]

10. M. Alkhawatra and N. Qasem, “Improving and extending indoor connectivity using relay nodes for 60 GHz applications,” International Journal of Advanced Computer Science & Applications, vol. 51, no. 11, pp. 427–434, 2016. [Google Scholar]

11. B. Thidé, H. Then, J. Sjöholm, K. Palmer, J. Bergman et al., “Utilization of photon orbital angular momentum in the low-frequency radio domain,” Physical Review Letters, vol. 99, no. 8, pp. 087701-1–4, 2007. [Google Scholar]

12. S. M. Mohammadi, L. K. Daldorff, J. E. Bergman, R. L. Karlsson, B. Thidé et al., “Orbital angular momentum in radio—A system study,” IEEE Transactions on Antennas and Propagation, vol. 58, no. 2, pp. 565–572, 2010. [Google Scholar]

13. B. Mohammadi, J. Nourinia, C. Ghobadi, F. Alizadeh and M. Karamirad, “Wideband sub-wavelength orbital angular momentum reflectarray antenna,” in 5th Conf. on Knowledge-Based Engineering and Innovation (KBEI-2019), Tehran, Iran, pp. 869–873, 2019. [Google Scholar]

14. M. Alkhawatrah, A. Alamayreh and N. Qasem, “Cooperative relay networks based on the OAM technique for 5G applications,” Computer Systems Science & Engineering, in press. [Google Scholar]

15. Z. Wei, J. Guo, D. W. K. Ng and J. Yuan, “Fairness comparison of uplink NOMA and OMA,” in 2017 IEEE 85th Vehicular Technology Conf. (VTC Spring), Sydney, Australia, pp. 1–6, 2017. [Google Scholar]

16. M. Alkhawatrah, Y. Gong, G. Chen, S. Lambotharan and J. A. Chambers, “Buffer-aided relay selection for cooperative NOMA in the internet of things,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 5722–5731, 2019. [Google Scholar]

17. Q. Zhang, Z. Liang, Q. Li and J. Qin, “Buffer-aided non-orthogonal multiple access relaying systems in Rayleigh fading channels,” IEEE Transactions on Communications, vol. 65, no. 1, pp. 95–106, 2017. [Google Scholar]

18. J. Durnin, “Exact solutions for nondiffracting beams. I. The scalar theory,” Journal of the Optical Society of America A, vol. 4, no. 4, pp. 651–654, 1987. [Google Scholar]

19. D. Lahaye, J. Tang and K. Vuik, “Modern solvers for Helmholtz problems”. Birkhäuser, 2017. [Online]. Available: https://link.springer.com/book/10.1007/978-3-319-28832-1. [Google Scholar]

20. P. L. Greene and D. G. Hall, “Diffraction characteristics of the azimuthal Bessel-Gauss beam,” Journal of the Optical Society of America A, vol. 13, no. 5, pp. 962–966, 1996. [Google Scholar]