Portable and Efficient Implementation of CRYSTALS-Kyber Based on WebAssembly

1  Introduction

As the Internet of Things (IoT) era dawns, several heterogeneous devices are now connected to the Internet, and they need to protect transmitted secret information or privacy-sensitive data. Typically, an encryption algorithm such as advanced encryption standard (AES), a block cipher, is used to protect transmitted data from eavesdroppers. To share the key, used for encryption and decryption, between a transmitter and a receiver, current public key-based key transport (e.g., Rivest–Shamir–Adleman (RSA)-based key transport) or key agreement algorithm (e.g., Diffie–Hellman (DH) and elliptic curve DH (ECDH)) are widely used. However, with the rapid advancement of quantum computers capable of realizing Shor’s algorithm, currently used public key-based keying algorithms will no longer be secure. Thus, currently, National Institute of Standards and Technology (NIST) is conducting a competition for post-quantum cryptography (PQC) standard that is secure against quantum computers. NIST requires two types of PQC: quantum-resistant key encapsulation mechanism (KEM) for key establishment and quantum-resistant digital signature [1]. In July 2022, NIST selected the final standard algorithms: Crystals-Kyber [2] for KEM and Crystals-Dilithium [3], Falcon [4], and Sphincs+ [5] for Digital Signature Algorithm (DSA) and announced four round candidates. The reason for selecting Crystals-Kyber is its efficiency in terms of computation and the size of ciphertext and keys. Because Crystals-Kyber is the only algorithm for KEM standards, optimizing its performance in the web environment is crucial. As aforementioned, because many heterogeneous devices are used in the IoT environment, it is required to develop IoT applications that can efficiently run on any device. Therefore, the portability of IoT applications is becoming more important. Web browsers are the most representative platform for web applications running on IoT devices, and JavaScript, a cross-platform/browser language, is currently the most popular language for portable web applications. Until now, some studies have been conducted for developing portable Lattice-based PQC libraries based on Javascript for secure communication in the IoT web environment [6–8]. Although Javascript-based crypto libraries can be executed on any IoT device due to their portability, their performance is significantly lower than software based on native languages such as C/C++ and Assembly.

WebAssembly (Wasm), released in 2017, is a portable execution framework for developing high-performance web applications [9,10]. Wasm enables C/C++-based native codes to run on web applications. Namely, Wasm modules implemented with native languages can be loaded and used by Javascript applications in the web environment. Furthermore, with Wasm, multiple data of the same type can be processed with single instruction multiple data (SIMD) instructions. Recently, BoSun Park et al. presented a crypto library based on JavaScript and Wasm to provide portable, efficient, and secure communication in web-based IoT systems [11]. However, to date, there is no Wasm-based PQC library; thus, this study presents an optimized Crystals-Kyber-KEM library based on Wasm for both efficiency and portability in the web environment.

The contribution of this study can be summarized as follows.

•   Optimizing NTT-based Polynomial Multiplication using SIMD instructions available on Wasm Framework

We optimize number theoretic transform (NTT)-based polynomial multiplication, one of the most core operations in the Kyber algorithm, with SIMD intrinsic instructions available in Wasm. With a 128-bit Wasm SIMD register, it is possible to process eight coefficients because q is 3329, which is less than 212. Our parallel implementations of NTT conversion, point-wise multiplication, and inverse NTT conversion provide ×6.83, ×4.95, and ×7.99 of improved performance compared with the latest Javascript implementation from [8]. As far as we know, this is the first work optimizing NTT-based polynomial multiplication with Wasm SIMD functionality.

•   Presenting Efficient and Portable Crystals-Kyber Library based on Wasm Framework

We present the first optimized Crystals-Kyber library by fully utilizing the Wasm framework for efficient and portable secure communication in the web environment. We construct our Wasm module containing an NTT-based polynomial multiplication function, which is the most time-consuming operation, except for the secure has algorithm (SHA)-3-based hash function in Kyber. The rest of the Kyber operations are implemented with Javascript. Thus, our Kyber library is also an efficient and portable PQC KEM library in the web environment. On Google Chrome (resp. Firefox and Microsoft Edge), our Kyber library provides approximately ×4.02 (resp. ×4.32 and ×4.1), ×3.42 (resp. ×3.52 and ×3.44), and ×3.41 (resp. ×3.44 and ×3.38) better performance than the latest Javascript Kyber implementation [8] in terms of key generation, encapsulation, and decapsulation, respectively.

•   Presenting Optimized Wasm module implementation for Kyber-768 parameter for Representative three Browsers

We focus on optimizing Kyber-768, providing NIST security level 3. We measure the performance on three representative web browsers: Google Chrome, Firefox, and Microsoft Edge. Our experimental results on these three browsers can be useful when developing secure web applications using Crystals-Kyber on the three browsers.

The remainder of this paper is organized as follows. Section 2 describes some preliminaries about Crystals-Kyber, NTT-based polynomial multiplication, Kyber parameters, and Wasm. Section 3 describes previous Kyber implementations in the web environment. Section 4 presents the proposed parallel implementation methods for NTT-based polynomial multiplication. The experimental results are given in Section 5, and the conclusion is drawn in Section 6.

2  Preliminaries

This section describes the preliminary background of our works: the introduction of Kyber, NTT-based polynomial multiplication, Kyber parameters, Kyber operations, and Wasm/SIMD.

2.1 Crystals-Kyber

Crystals-Kyber (Kyber) is an indistinguishability under chosen-ciphertext attack-secure (IND-CCA2) KEM, and its security is based on the Module Ring-LWE problem [2]. The Kyber-KEM is constructed using the Kyber public key encryption (Kyber-PKE) using the Fujisaki–Okamoto (FO) transform. Kyber-PKE consists of three algorithms: key generation, encryption, and decryption. Except for the random sampling based on the hash function, the core operation of each Kyber-PKE algorithm is either matrix by vector multiplication or vector by vector multiplication. Note that each element of the matrix and vector is over Ring Rq = Zq[X]/(Xn + 1), where n and q are 256 and 3329, respectively. In the following algorithm description, bold upper-case letters (e.g., A) and bold lower-case letters (e.g., s) denote matrixes and vectors, respectively.

2.2 NTT-based Polynomial Multiplication

The major operation of matrix by vector multiplication and vector by vector multiplication is the polynomial multiplication over Rq. The naive polynomial multiplication method requires O(n2) complexity, where n is 256 in the case of Kyber. To accelerate the speed of polynomial multiplication over Rq, the NTT-based polynomial multiplication method is widely used in the context of LWE-based cryptosystems, including Kyber, because its complexity is O(nlogn) [12,13]. NTT-based polynomial multiplication consists of three steps: NTT conversion, component-wise (or point-wise) multiplication, and inverse NTT conversion. In other words, the multiplication of two polynomials f=∑i=0255⁡fiXi and g=∑i=0255⁡giXi in Rq is conducted in three steps.

•   Converting each polynomial into the NTT domain with Eq. (1):

f^←NTT(f)andg^←NTT(g), whereNTT(f)=(f0^+f1^X,  f0^+f3^X, …,  f254^+f255^X)with f2i^=∑j=0127⁡f2jζ(2i+1)j and f2i+1^=∑j=0127⁡f2j+1ζ(2i+1)j(ζis the 256−root of unity andζ(2i+1)jvalues are precomputed.). (1)

•   Conducting component-wise multiplication with Eq. (2):

h^=f^∘g^ whereh2i^+h2i+1^X=(f2i^ + f2i+1^X)(g2i^ + g2i+1^X)mod(X2−ζ2i+1)for i=0, …,  127. (2)

•   Applying inverse NTT conversion with Eq. (3):

fg=NTT−1(h^) (3)

For NTT conversion and inverse NTT conversion, typically the Cooley–Tukey (CT) method [14] and Gentleman–Sande (GS) method [15] are used, respectively.

2.3 Kyber Parameters

Table 1 shows the parameters of the Kyber algorithm. The degree n and prime q are fixed as 256 and 3329, respectively, among all security levels. k represents a security scaling factor, and it is the dimension of a matrix and vector such as A ∈ Rqk×k and s ∈ Rqk . η1  ,  η2 , du , and dv represent parameters to balance between the ciphertext size and failure probability in the process of central binomial distribution (CBDη), Compress, and Decompress. Kyber provides parameters for security levels 1, 3, and 5, which correspond to AES-128, AES-192, and AES-256 security levels, respectively.

2.4 Kyber-PKE and Kyber-KEM

Algorithms 1, 2, and 3 show the key generation, encryption, and decryption of Kyber-PKE, respectively. In these algorithms, extendable-output function (XOF) and pseudo-random function (PRF) mean an extendable output function and a pseudorandom function, respectively. The Kyber reference implementation uses secure hash algorithm and keccak (SHAKE)-128 and SHAKE-256 as an instantiation of XOF and PRF, respectively. Parse is a function used to convert randomly generated byte streams to NTT representations. CBD is a centered binomial distribution function. Encode and Decode are used for the serialization and deserialization of Kyber data, respectively. Compress and Decompress are used to reduce the size of a ciphertext. The details of these functions can be found in the specifications of Crystals-Kyber.

Algorithm 1 generates public and private key pairs (pk, sk). A public matrix A is generated based on the seed value ρ, and the elements in the matrix are converted into the NTT domain in step 2. The secret key vector s and error vector e are sampled through steps 4 to 5. Then, a public key vector is generated by computing t^←A^°s^+e^ in step 8 (Note that the computation is conducted in the NTT domain for efficiency).

Finally, a public key pk and a secret key sk are generated using the encoding function in steps 9 and 10. Note that to reduce the size of pk, ρ is appended in pk rather than containing the whole A. In other words, if a recipient receives pk, he/she can compute A from the ρ value.

Algorithm 2 generates ciphertext c from a message m using the public key pk. The generated ciphertext consists of two parts ( c1 , c2 ). Through steps 1–3, the public key factors t^ and A^ are recovered from pk. A random vector r, a random error vector e1, and an error polynomial e2 are sampled through steps 4–6. c1, the first part of the ciphertext, is generated through steps 8 to 9. Note that matrix by vector multiplication is computed in the NTT domain in step 8. c2, the second part of the ciphertext, is computed in steps 10 and 11. Vector by vector multiplication is also computed in the NTT domain in step 10.

Algorithm 3 recovers the message m from the ciphertext with the secret key sk. The original message m comes from c2 by computing step 4. In other words, the randomness is removed by subtracting NTT−1(s^T∘NTT(u)) from v.

As aforementioned, Kyber-KEM is constructed using Kyber-PKE, which consists of key generation, encapsulation, and decapsulation. For INC-CCA2 security, each algorithm of Kyber-KEM is different from the corresponding algorithm of Kyber-PKE. The most different part is between the decapsulation of Kyber-KEM and the decryption of Kyber-PKE. Namely, the decapsulation executes an additional process that encrypts the recovered message to check whether the generated ciphertext is the same as the received ciphertext. The detailed Kyber-KEM process can be found in the algorithm specification and supporting document [2].

2.5 WebAssembly and SIMD Programming

Since its release in 2017, Wasm has provided a portable execution framework for developing high-performance web applications [9,10]. Because Wasm enables C/C++-based native codes to run on web applications, Wasm modules with Javascript applications provide not only portability but also high performance in the web environment. Regarding the secure execution of Wasm-based modules, because Wasm provides a memory-safe, sandboxed execution environment inside JavaScript virtual machines, the used browser’s security policies are applied to them. Furthermore, with Wasm, it is possible to process multiple data in parallel in an SIMD manner. Namely, SIMD instructions in Wasm process several data units packed in a 128-bit register in parallel. When the element size is 8-bit, sixteen elements can be packed in a register. Similarly, eight (resp. four) and 16-bit (resp. 32-bit) data can be packed in a register. However, currently, Wasm supports only 128-bit SIMD instructions, whereas AVX2 [16] in typical CPUs provides a set of 256-bit registers. wasm_simd128.h defines several SIMD intrinsic functions.

Fig. 1 shows the process of building a Wasm module and using it in a web application. First, native code modules developed in C/C++ are compiled with Emscripten SDK, producing a Wasm module (.wasm extension). The Wasm module is a binary bytecode and consists of several standard sections such as type, import, and function. When the module is loaded into a web browser supporting Wasm, it verifies whether the module is valid, and the virtual bytecode is compiled into a machine code of the device (x86 or ARM) the browser is running on.

Figure 1: Wasm conversion process

Regarding crypto optimization using Wasm, in 2021, Bosun Park et al. presented a crypto library based on Wasm and Javascript for providing portable, efficient, and secure communication in Web-based IoT applications [11]. However, there is no research on optimizing the PQC algorithm using Wasm yet. Thus, we present an optimized Crystals-Kyber-KEM library based on Wasm for efficient and secure key establishment in the quantum computing era.

3  Related Works

Thus far, research on Kyber performance optimization has been focused on general-purpose CPUs (with AVX2 instructions) and ARM-based embedded processors (Cortex-M4, ARMv8-A series). However, there is little research on developing portable Lattice-based PQC libraries based on Javascript for secure web communication. Their goal has been to prove the feasibility of using Lattice-based cryptography in the web environment.

As a first step, in 2016, Yuan et al. presented a portable implementation of several Lattice-based cryptosystems (NTRU, NTRU-IEEE07, Regev’s LWE, LPR10-LWE, LP10 Ring-LWE, and LP11) based on Javascript on several web browsers (Google Chrome, Firefox, Opera, and Internet Explorer; Android and Tessel) [6]. They optimized the core parts of Lattice-based cryptosystems such as polynomial multiplication and discrete Gaussian sampling and measured the performance of key generation, encryption, and decryption on their target web browsers. Furthermore, notably, they analyzed the proportion of sub-operations constituting each key generation, encryption, and decryption. However, their target algorithms do not belong to the NIST PQC Round 3 finalist (Parameters used by NTRU implementation in [6] differ from those of NTRU in NIST PQC Round 3 finalist).

In 2019, Ye Yuan et al. presented Javascript implementations of five Lattice-based cryptosystems (Lizard [17], Ring-Lizard [18], Kyber [2], FrodoKem [19], and NewHope [20]) for providing a portable key exchange protocol in the web environment. They measured their Javascript implementations on several web browsers and analyzed the proportion of sub-operations (matrix multiplication, error sampling, NTT-based polynomial multiplication, and so on). In their implementation, Kyber and NewHope outperformed Lizard, Ring-Lizard, and Frodo. Among their target algorithms, only Kyber belongs to the NIST PQC Round 3 finalist. However, the Kyber parameters used in their implementation are not the same as those presented in Kyber’s final round specification.

In 2021, Anton Tutoveanu presented a Kyber implementation using the parameter presented in the NIST PQC Round 3 finalist based on Javascript and benchmarked the performance of the key establishment process using Kyber when a client received 150,000 bytes of encrypted data from a server [8]. They stated that the key establishment process using Kyber accounted for approximately 23% of the total transaction time.

Until now, several Lattice-based cryptosystems have been implemented using Javascript for portability. There is no research utilizing the latest Wasm technology. Thus, we use Wasm and take full advantage of SIMD instructions available with Wasm for not only portability but also high performance.

Regarding Lattice-based cryptosystems, several studies have been conducted for constructing cryptographic protocols or secure applications such as medical big data management systems [21], blind signature schemes for blockchain-enabled systems [22], and secure distributed healthcare service design [23].

4  Proposed Optimization Strategies of Crystals-Kyber

Our Kyber implementation is based on Wasm and takes full advantage of SIMD functionality in Wasm. First, we profile the performance of the latest Kyber Javascript implementation [8]. Our strategy is to identify the time-consuming parts of the Kyber Javascript implementation and then replace them with our proposed Wasm modules for both portability and high performance. In other words, our Kyber library is implemented with Javascript language for portability, and the time-consuming parts are implemented with Wasm modules for efficiency.

4.1 Performance Profiling

We have profiled each key generation, encryption, and decryption of the latest Kyber Javascript implementation. We have measured sub-operations constituting each key generation, encryption, and decryption using the performance.now() method, which can measure time by milliseconds. Fig. 2 shows the profiling results for Kyber key generation, encapsulation, and decapsulation. From the figure, the first two time-consuming parts are the generation of matrix A and hash functions (SHA-3-224, SHA-3-512, and SHAKE). Note that the matrix generation significantly uses SHA-3-related functions. Although the ratio of A ◦ s, the multiplication between a matrix and a vector, seems to be smaller than that of matrix generation and hash functions, the main reason for this is that the codes used for SHA-3 and its variants (SHAKE-128 and SHAKE-256) in [8] are not optimized. Profiling results from the other literature [24] show that the overhead of A ◦ s is larger than that of matrix generation. Furthermore, several CPUs and ARM-based MCUs (Cortex-A53) support a hardware accelerator of SHA hash function (SHA-1 and SHA-256) with a dedicated instruction set. Although SHA-3 is not currently supported yet, it is expected that upcoming CPUs/MCUs will support an SHA-3 hardware accelerator. Thus, in our implementation, we aim at optimizing the performance of NTT-based polynomial multiplication, which is the core operation when computing matrix by vector multiplication and vector by vector multiplication with SIMD intrinsic functions available in Wasm. Algorithms 1, 2, and 3 show the execution of NTT conversions, point-wise multiplication, and inverse NTT conversion.

Figure 2: Timing profile of kyber operation

4.2 SIMD Intrinsics on Wasm

Table 2 introduces Wasm intrinsic functions used to implement our parallel NTT-based polynomial multiplication. Wasm SIMD Intrinsic functions provide 128-bit vector registers and related arithmetic functionalities similar to Intel’s streaming SIMD extensions (SSE). However, Wasm SIMD is under development, so its support for SIMD is incomplete. Thus, a Wasm SIMD library to directly convert crypto software implemented with SSE extension intrinsic to a module using Wasm SIMD intrinsics is currently unavailable. Refer to [10] for the current limitations of Wasm SIMD.

4.3 Optimization of NTT-Based Polynomial Multiplication with Wasm SIMD

NTT-based polynomial multiplication consists of three steps: NTT conversion, component-wise (point-wise) multiplication, and inverse NTT conversion. NTT conversion step converts a polynomial a over Rq = Zq[X]/(X256 + 1) to 128 sub-polynomials over X2 − ζ. Two polynomials a and b over Rq need to be converted into the NTT domain. Point-wise multiplication computes multiplications between 128 sub-polynomials constituting a and 128 sub-polynomials constituting b. Finally, the sub-polynomials from point-wise multiplications are converted to a polynomial c over Rq. Because each coefficient in Kyber is stored in a 16-bit integer value, eight coefficients can be loaded in a 128-bit vector. Thus, our parallel version of each NTT conversion, point-wise multiplication, and inverse NTT conversion processes eight coefficients in parallel. In the following subsections, we describe the target codes (NTT conversion, point-wise multiplication, and inverse NTT conversion) and how to convert them to parallel codes with Wasm intrinsic functions.

4.3.1 Proposed Parallel NTT Conversion

Listing 1 shows the original ntt function that converts a polynomial over Rq to the NTT domain. Because a polynomial contains 256 coefficients, and each coefficient is less than q (=3329), int16_t r[256] is used to express a polynomial. This ntt function is an in-place version, which means that the intermediate results are updated to the input array r. In the ntt function, the zeta values are precomputed and stored in the global memory area (zetas is an array containing twiddle factor values over Rq = Zq[X]/(X256 + 1). Steps 12–14 are called Butterfly operations because the symmetric computations are related such as r[j + len] = r[j] − t and r[j] = r[j] + t. First, r[j + len] is multiplied by a twiddle factor zeta. Because two 16-bit words are multiplied, the result needs to be reduced over q. This reduction is conducted with Montgomery-based reduction. Note that fqmul(x, y) in the function multiplies x and y and then reduces the result of multiplication with the Montgomery reduction described in Listing 2. Then, t, the result of the reduction, is either added to or subtracted from r[j].

Listing 1: ntt Function for NTT domain conversion

We parallelize the internal computation of ntt with Wasm SIMD intrinsic functions (Wasm SIMD supports only 128-bit wide vector registers). Because each coefficient in a polynomial is less than q, which is approximately 12-bit, eight coefficients can be loaded in a vector register of Wasm SIMD. Namely, we process eight execution of for-loop simultaneously with Wasm SIMD. For efficiency, we unroll the nested for-loops in ntt for easy application of the SIMD technique.

Fig. 3 shows the overall structure of the proposed parallel NTT conversion process. For simplicity, we use a polynomial with 32 coefficients rather than 256 coefficients. First, eight coefficients are loaded into a vector with the wasm_v128_load() function. Note that the related twiddle factors are also loaded into a vector. Then, vector by vector multiplication is performed using two intrinsic functions: wasm_i32 × 4_extmul_low_i16 × 8() and wasm_i32 × 4_extmul_high_i16 × 8(). In other words, wasm_i32 × 4_extmul_low_i16 × 8() multiplies the lower 16-bit four lanes in the blue-colored vector and lower 16-bit four lanes in the green-colored vector, and the 32-bit four results are stored in the yellow-colored vector (low parts). Higher part multiplications are executed in the same way using wasm_i32 × 4_extmul_high_i16 × 8(), and the results are stored in the yellow-colored vector (high parts). Because each of the eight 32-bit results held in the two vectors is larger than q, it needs to be reduced. For efficient reduction, Montgomery reduction is applied.

Figure 3: The structure of proposed parallel NTT conversion

Listing 2 shows the reduction algorithms used for NTT-based polynomial multiplication. montgomery_reduce() reduces 32-bit data to a value less than q with simple arithmetics (two-word multiplications, one right shift, and one subtraction). Note that QINV and KYBER_Q are predefined values for the Montgomery reduction. In our parallel implementation, eight 32-bit results are reduced with our parallel implementation of the montgomery_reduce() function. It uses wasm_i16 × 8_mul() for eight computations of a ∗ QINV in step 5 and uses wasm_i32 × 4_extmul_low_i16 × 8() and wasm_i32 × 4_extmul_high_i16 × 8() for eight computations of t ∗ KYBER_Q in step 6. The subtraction and right shift in step 6 are executed with wasm_i32 × 4_sub() and wasm_i32 × 4_shr(). Finally, each of the reduced results held in the two vector registers is either added or subtracted with r[j] and then stored in r[j] and r[j + len], respectively. As the result of NTT conversion, a 255-th degree polynomial over Rq is converted into 128 1-th degree sub-polynomials.

Listing 2: ntt function for NTT domain conversion

4.3.2 Proposed Parallel Point-Wise Multiplication

Listing 3 shows the original poly_basemul_montgomery function that multiplies two polynomials (a and b) in the NTT domain in a point-wise multiplication manner. Each of a and b consists of 128 1-th degree sub-polynomials such as a =   (a255X+a254, …,  a3X+a2, a1X+a0) and b =   (b255X+b254, …,  b3X+b2, b1X+b0) . Point-wise multiplication computes c =   (c255X+c254, …,  c3X+c2, c1X+c0) , where (c2i+1X+c2i)=(a2i+1X+a2i)∘(b2i+1X+b2i) . Note that one point-wise multiplication calls five fqmul functions because c2i+1X=(a1⋅b0+a0⋅b1)X,  c2i=(a0⋅b0+a1⋅b1⋅ζ2i+1) , where X2=ζ2i+1 .

Listing 3: poly_basemul_montgomery function for point-wise multiplication

Fig. 4 shows the overall structure of the proposed parallel point-wise multiplication process. For simplicity, we use a polynomial with 32 coefficients rather than 256 coefficients. The proposed method computes eight point-wise multiplications in parallel. First, eight sub-polynomials of a (resp. b) are loaded into two vector registers v1 and v0 (resp. v3 and v2 ). Furthermore, coefficients with (resp. without) X are loaded into v3 and v1 (resp. v2 and v0 ) vector registers. Twiddle factors are also loaded into a temporary vector register vt . Then, v1 , v3 , and vt are multiplied with two fqmul executions and stored in a temporary register vlower . v0 and v2 are also multiplied with one fqmul execution, and the result is accumulated to vlower register. The coefficients in vlower are (e.g., ( c14 , c12 ,  … , c2 , c0 )) without X. The accumulation of two vector multiplication results (e.g., ( v1 and v2 , and v0 and v3 )) with two fqmul executions constructs coefficient c2i+1 (e.g., c15 , c13 ,  … , c3 , c1 )) with X. The main computation in the proposed parallel point-wise multiplication is fqmul. In our parallel fqmul implementation, first, eight coefficients of two vectors are multiplied with wasm_i32 × 4_extmul_low_i16 × 8() and wasm_i32 × 4_extmul_high_i16 × 8(). Then, the results of multiplications are reduced with Montgomery reduction, which is described in the proposed parallel NTT conversion.

Figure 4: The structure of proposed parallel point-wise multiplication

4.3.3 Proposed Parallel Inverse NTT Conversion

Listing 4 shows the original invntt function, which converts a polynomial (consisting of 128 1-th degree sub-polynomials) in the NTT domain to a polynomial over Rq. The structure of invntt is similar to that of ntt, except for its sequence of operations. The execution of addition and subtraction precedes multiplication with fqmul (the zeta value used in the multiplication is the inverse value of zeta in the ntt function). Because the result of addition may become larger than q, it needs to be reduced using the Barrett reduction method. The function for Barrett reduction is given in Listing 2, and it is related to two-word multiplications, one addition, one subtraction, and one right shift (v value is the precomputed value (1 << 26) and is determined at compile time). The result of Barrett reduction and the result of fqmul are stored in r[j] and r[j + len], respectively. Note that the final 256 coefficients (steps 17–21) need to be multiplied by f value (2−7 mod q) with fqmul because coefficients are doubled at each layer as the result of addition and subtraction.

Listing 4: invntt function for inverse NTT conversion

Fig. 5 shows the overall structure of the proposed parallel inverse NTT conversion process. For simplicity, we use a polynomial with 32 coefficients rather than 256 coefficients. Eight r[j] values and eight r[j + len] values are loaded into two vectors (vector1 and vector2), respectively. Then, vector1 and vector2 are added using wasm_i16 × 8_add(), and the results are reduced by our parallel Barrett reduction method. Our parallel implementation of Barrett reduction uses wasm_i32 × 4_extmul_low_i16 × 8() and wasm_i32 × 4_extmul_high_i16 × 8() to compute eight multiplications of v*a. Eight multiplications of t * = KYBER_Q are computed with wasm_i16 × 8_mul_low_i16 × 8(). The results of Barrett reduction are stored in their original memory locations r[j]. The results of (vector1–vector2) are multiplied with twiddle factors and then reduced by Montgomery reduction. The final results of the reduction are stored in their memory addresses r[j + len].

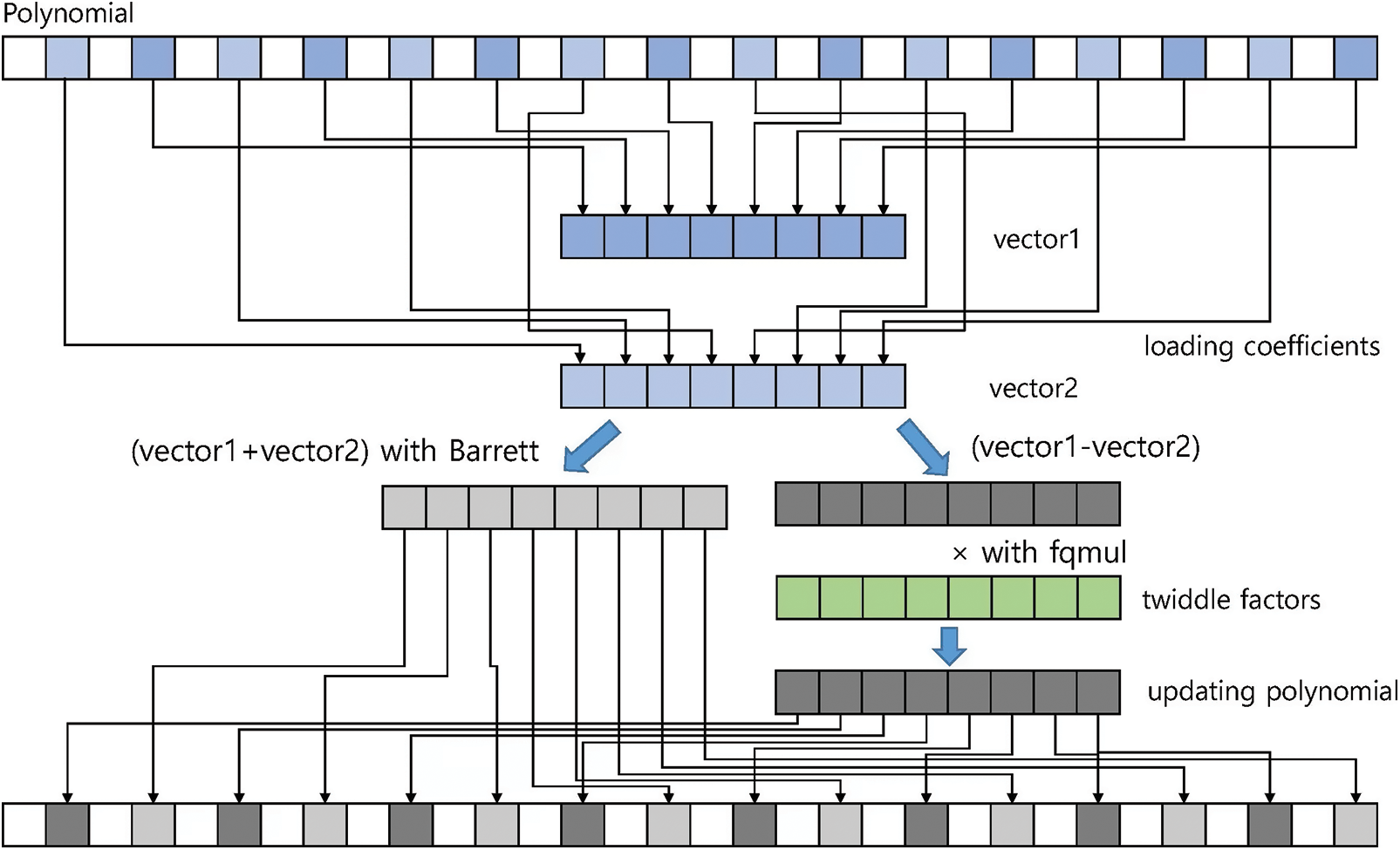
Figure 5: The structure of proposed parallel inverse NTT conversion

5  Performance Analysis

In this section, we analyze our proposed implementations and compare them with those of previous studies. For efficiency comparison, we measure the execution times and compare them with those of previous studies. Because our software is a web-based cryptographic library, it will run on web browsers on personal computers or smartphones. Thus, the code size is not a meaningful comparison factor. For performance analysis and comparison, we use three browsers: Google Chrome, Firefox, and Microsoft Edge. Table 3 shows the experimental environment for performance analysis.

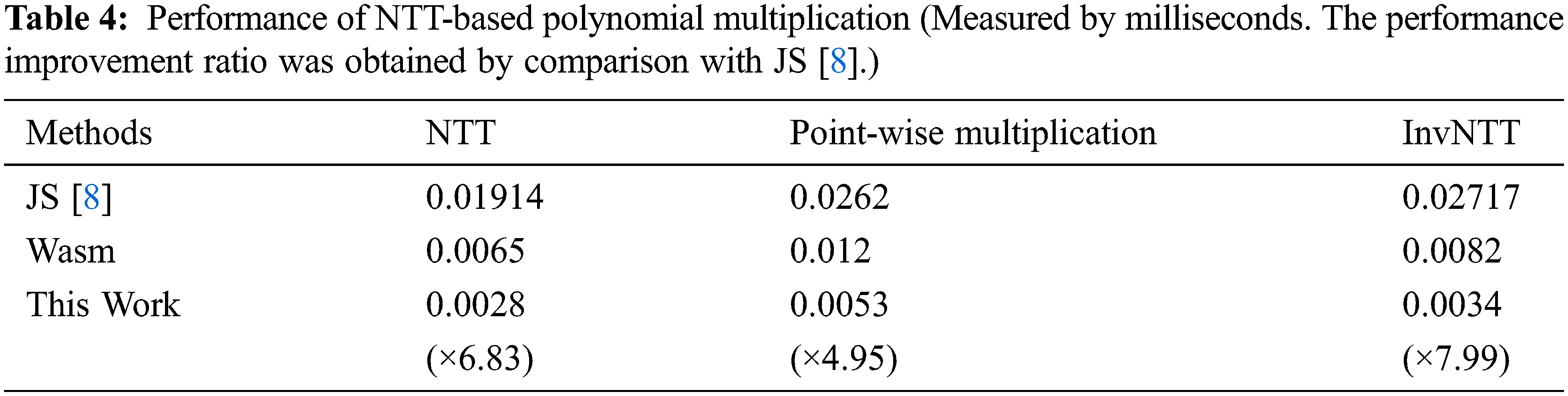
First, we analyze the performance of the proposed parallel implementation of NTT-based polynomial multiplication and compare it with the previous implementations. Table 4 compares the performance of the proposed implementation with the latest Crystals-Kyber Javascript implementation from [8]. In Table 4, Wasm means NTT-based polynomial multiplication steps implemented with only the C language using the Wasm framework. This Works means that each step in NTT-based multiplication is implemented with Wasm SIMD functionality. From the table, the proposed SIMD implementation outperforms the latest Javascript implementation from [8] by ×6.83, ×4.95, and ×7.99 in terms of NTT conversion, point-wise multiplication, and inverse NTT conversion. Compared with our naive Wasm implementation, our SIMD implementation provides ×2.24, ×2.344, and ×2.113 superior performance in terms of NTT conversion, point-wise multiplication, and inverse NTT conversion. Although we parallelize the internal process of NTT-based multiplication by eight data units, the performance improvement is less than eight times. This is because the overhead of data conversion between the Javascript and Wasm data types is large, as well as loading data to SIMD registers and storing them in memory, is significant.

We integrate the proposed parallel implementation of NTT-based polynomial multiplication into Crystals-Kyber software. Tables 5–7 compare our Kyber software with the latest Kyber Javascript implementation from [8] on Google Chrome, Firefox, and Microsoft Edge in terms of key generation, encapsulation, and decapsulation. For key generation (resp. encapsulation and decapsulation), our software provides ×4.02 (resp. ×3.42 and ×3.41), ×4.32 (resp. ×3.52 and ×3.44), and ×4.1 (resp. ×3.44 and ×3.38) improved performance on the three browsers, respectively. The proposed Kyber implementation based on Wasm SIMD outperformed the previous work.

6  Conclusion

In this study, we present the first implementation of Crystals-Kyber with Wasm in the web environment. Using the SIMD functionality of the Wasm framework, we parallelize NTT-based polynomial multiplication with intrinsic functions. Our optimized parallel implementation of NTT-based polynomial multiplication outperforms the previous Javascript NTT implementation by ×6.83, ×4.95, and ×7.99 in terms of NTT conversion, point-wise multiplication, and inverse NTT conversion, respectively. Based on the proposed parallel NTT-based multiplication, we propose a Crystals-Kyber Wasm module for providing security levels 1, 3, and 5. The proposed Crystals-Kyber module can be used by various web applications for key establishment processes in TLS v1.3, SSH (Secure Shell), IPSec IKE (Internet Key Exchange), and so on. Our future work is to design and implement a hybrid key exchange mode using Crystals-Kyber and classical ECDH, which are described in NIST 800-56C rev2 [25].

Funding Statement: This work was supported by Institute of Information & communications Technology Planning & Evaluation (IITP) grant funded by the Korea government (MSIT) (No.2022-0-01019, Development of eSIM security platform technology for edge devices to expand the eSIM ecosystem). This was partly supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC (Information Technology Research Center) support program (IITP-2022-RS-2022-00164800) supervised by the IITP (Institute for Information & Communications Technology Planning & Evaluation).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. NIST, “Nist post-quantum cryptography,” 2022. [Online]. Available: https://csrc.nist.gov/Projects/post-quantum-cryptography. [Google Scholar]

    2. P. Schwabe, R. Avanzi, J. Bos, L. Ducas, E. Kiltz et al., “Crystals-kyber,” 2021. [Online]. Available: https://pq-crystals.org/kyber/index.shtml. [Google Scholar]

    3. V. Lyubashevsky, L. Ducas, E. Kiltz, T. Lepoint, P. Schwabe et al., “Crystals-dillithium,” 2021. [Online]. Available: https://pq-crystals.org/dilithium/index.shtml. [Google Scholar]

    4. T. Prest, P. -A. Fouque, J. Hoffstein, P. Kirchner, V. Lyubashevsky et al., “Falcon,” 2021. [Online]. Available: https://falcon-sign.info. [Google Scholar]

    5. J. -P. Aumasson, D. J. Bernstein, W. Beullens, C. Dobraunig, M. Eichlseder et al., “Sphincs+,” 2021. [Online]. Available: https://sphincs.org/index.html. [Google Scholar]

    6. Y. Yuan, C. -M. Cheng, S. Kiyomoto, Y. Miyake and T. Takagi, “Portable implementation of lattice-based cryptography using javascript,” International Journal of Networking and Computing, vol. 6, no. 2, pp. 309–327, 2016. [Google Scholar]

    7. Y. Yuan, J. Xiao, K. Fukushima, S. Kiyomoto and T. Takagi, “Portable implementation of lattice-based cryptography using javascript,” Security and Communication Networks, vol. 2018, pp. 9846168:1–9846168:14, 2018. [Google Scholar]

    8. A. Tutoveanu, “Active implementation of end-to-end post-quantum encryption,” Cryptology ePrint Archive, Report 2021/356, 2021. [Online]. Available: https://eprint.iacr.org/2021/356. [Google Scholar]

    9. WebAssembly Community Group, “Webassembly,” 2022. [Online]. Available: https://webassembly.org. [Google Scholar]

  10. WebAssembly Community Group, “Porting simd code targeting webassembly,” 2022. [Online]. Available: https://emscripten.org/docs/porting/simd.html. [Google Scholar]

  11. J. S. BoSun Park and S. C. Seo, “Efficient implementation of a crypto library using web assembly,” MDPI Electronics, vol. 9, no. 11–1839, pp. 1–23, 2020. [Google Scholar]

  12. C. Agarwal and R. Burrus, “Fast convolution using fermat number transforms with applications to digital filtering,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 2, no. 22, pp. 87–97, 1974. [Google Scholar]

  13. G. Seiler, “Faster avx2 optimized ntt multiplication for ring-lwe lattice cryptography,” IACR Cryptol. ePrint Arch, 2021. [Online]. Available: https://eprint.iacr.org/2021/356. [Google Scholar]

  14. T. J. Cooley and J. W. Tukey, “An algorithm for the machine calculation of complex Fourier series,” Mathematic of Computation, vol. 19, no. 90, pp. 297–301, 1965. [Google Scholar]

  15. W. M. Gentleman and G. Sande, “Fast fourier transforms: For fun and profit,” in  Proc. AFIPS’66, New York, NY, USA: Association for Computing Machinery, pp. 563–578, 1966. [Google Scholar]

  16. Intel, “Intel haswell new instruction descriptions,” 2012. [Online]. Available: https://www.intel.com/content/www/us/en/develop/documentation/cpp-compiler-developer-guide-and-reference/top/compiler-reference/intrinsics/intrinsics-for-avx2.html. [Google Scholar]

  17. J. H. Cheon, D. H. Kim and Y. Song, “Lizard: Cut off the tail! practical post-quantum public-key encryption from lwe and lwr,” IACR Cryptol. ePrint Arch, 2016. [Online]. Available: https://eprint.iacr.org/2016/1126.pdf. [Google Scholar]

  18. J. H. Lee, D. Kim, H. Lee, Y. Lee and J. H. Cheon, “RLizard: Post-quantum key encapsulation mechanism for IoT devices,” IEEE ACCESS, vol. 7, pp. 2080–2091, 2018. [Google Scholar]

  19. E. Alkim, J. W. Bos, L. Ducas, P. Longa, I. Mironov et al., “Frodokem,” 2021. [Online]. Available: https://frodokem.org. [Google Scholar]

  20. E. Alkim, R. Avanzi, J. W. Bos, L. Ducas, A. d. l. Piedra et al., “Newhope,” 2021. [Online]. Available: https://newhopecrypto.org. [Google Scholar]

  21. C. Li, M. Dong, J. Li, G. Xu, X. -B. Chen et al., “Efficient medical big data management with keyword-searchable encryption in healthchain,” IEEE Systems Journal, vol. 16, no. 4. pp. 1–12, 2022. [Google Scholar]

  22. C. Li, Y. Tian, X. Chen, and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, no. 6, pp. 253–264, 2021. [Google Scholar]

  23. C. Li, M. Dong, J. Li, G. Xu, X. Chen et al., “Healthchain: Secure EMRs management and trading in distributed healthcare service system,” IEEE Internet of Things Journal, vol. 8, no. 9, pp. 7192–7202, 2020. [Google Scholar]

  24. P. Sanal, E. Karagoz, H. J. Seo, R. Azarderakhsh and M. Mozaffari-Kermani, “Kyber on arm64: Compact implementations of kyber on 64-bit arm cortex-A processors,” IACR Cryptol. ePrint Arch, 2021. [Online]. Available: https://eprint.iacr.org/2021/561. [Google Scholar]

  25. NIST, “Recommendation for key-derivation methods in key establishment schemes,” 2020. [Online]. Available: https://csrc.nist.gov/publications/detail/sp/800-56c/rev-2/final. [Google Scholar]