 Open Access
Open Access
ARTICLE
Influence of Wind Turbine Structural Parameters on Wind Shear and Tower Shadow Effect
1
School of Transportation and Municipal Engineering, Inner Mongolia Technical College of Construction, Hohhot, 010070, China
2
School of Mechanical Engineering, Inner Mongolia University of Technology, Hohhot, 010051, China
* Corresponding Author: Zhiguo Li. Email:
(This article belongs to the Special Issue: Wind Energy Development and Utilization)
Energy Engineering 2023, 120(2), 501-510. https://doi.org/10.32604/ee.2022.021423
Received 13 January 2022; Accepted 17 May 2022; Issue published 28 November 2022
Abstract
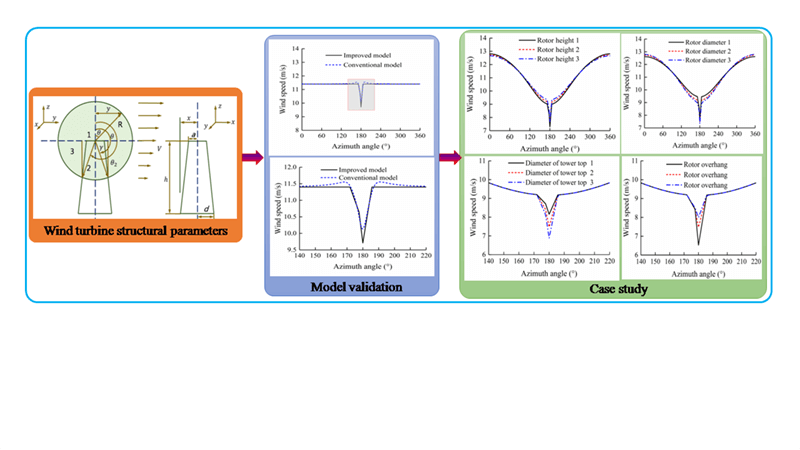
To overcome the problems of natural decreases in power quality, and to eliminate wind speed fluctuation due to wind shear and tower shadow effect arising from wind turbine structural parameters, an improved prediction model accounting for the dual effect of wind shear and tower shadow is, in this paper, built. Compared to the conventional prediction model, the proposed model contains a new constraint condition, which makes the disturbance term caused by the tower shadow effect always negative so that the prediction result is closer to the actual situation. Furthermore, wind turbine structural parameters such as hub height, rotor diameter, the diameter of the tower top, and rotor overhang on wind shear and tower shadow effect are also explored in detail. The results show that the wind shear effect became weaker with the increase in hub height. The hub height is independent of the tower shadow effect. The rotor diameter is positively correlated with the wind shear and tower shadow effect. The tower shadow effect is positively correlated with the diameter of the tower top and negatively correlated with the rotor overhang.Graphic Abstract
Keywords
Nomenclature
| wind speed at height | |
| wind speed at the height of rotor hub | |
| hub height | |
| vertical height from the ground | |
| wind shear coefficient related to surface roughness | |
| disturbance term of wind shear on wind speed | |
| azimuth angle | |
| critical azimuth angles | |
| local radius of blade | |
| wind speed at hub height | |
| spatial average wind speed | |
| tower top radius | |
| tower base radius | |
| distance from the blade element to the tower axis in the direction of | |
| the horizontal distance between the rotor centre and the tower centerline | |
| disturbance term for tower shadow on wind speed in Cartesian coordinate system | |
| disturbance term for tower shadow on wind speed in cylindrical coordinate system | |
| rotor radius | |
| equal to | |
| tower shadow on the wind speed written as a cylindrical coordinate, it is equal to |
Wind speed is an important factor affecting the output power of horizontal axial wind turbine (HAWT). In addition to the mutation and uncertainty of natural wind, the periodic fluctuation of wind speed through blade surfaces caused by wind shear and the tower shadow effect cannot be ignored. Therefore, accurately predicting the wind speed under the action of wind shear and tower shadow effect, and analyzing the influence of structural parameters such as hub height, rotor diameter, the diameter of the tower top, and rotor overhang on the wind speed, are of great significance for optimizing the structural size, weakening the power fluctuation of the wind turbine, and slowing down the effect of the power grid.
Extensive studies have been conducted on the wind shear and tower shadow effect for HAWT. Dolan et al. [1] established a comprehensive aerodynamic torque model for three-blades wind turbine considering wind shear and tower shadow effect and showed that wind shear caused the rotor power pulsation; the tower shadow effect was more significant than the wind shear effect. Emeksiz et al. [2] first studied the effect of rotor overhang on the disturbed wind speed using the wind data from Tokat Gaziosmanpaşa University Campus. The results showed that the rotor overhang was the most effective parameter affecting the tower shadow effect. Wen et al. [3] modified the widely used tower shadow effect model and found that the tower shadow effect mainly caused the power fluctuation, and the power loss arose from wind shear. Sintra et al. [4–6] used MATLAB/Simulink, TurbSim, and FAST to simulate a three-blades variable speed wind turbine system. The results showed that wind shear and tower shadow effect significantly affected the upstream wind speed of the hub. To reduce the harm of wind turbine power oscillation, therefore, a new method was proposed by Fu et al. [7] to simulate the wind shear and tower shadow effect during wind power generation. Due to the existing equivalent wind speed model not considering the power loss, a new calculation method of equivalent wind speed based on equivalent power was proposed in reference [8]. Tian et al. [9] proposed a new pitch control scheme for a three-blade wind turbine to reduce the periodic fluctuation of aerodynamic load and torque ripple caused by wind shear and tower shadow effect. Liu et al. [10] established aerodynamic correction models, including dynamic stall, wind shear, and tower shadow effect, to study the aerodynamic performance of a floating HAWT. The spatial and temporal distribution characteristics of wind speed were explored by analyzing the wind speed of each point on the swept area of the rotor [11]. Han [12] studied the effect of wind speed characteristics such as turbulence effect, wind shear, and tower shadow effect on the power oscillation for a large-scale HAWT. Kim et al. [13] presented universal correlations between wind speed and wind shear exponent using 3D sonic anemometers collected 3-axis wind speed components.
The above studies evaluate the wind shear and tower shadow effect of HAWT in detail. The disturbance term due to wind shear can be approximated by a third-order Taylor series in the references [1,6,7,9], and the study on the tower shadow effect is divided into two areas in the reference [3]. However, the disturbance term generated by the tower shadow effect is a little different from the actual situation. In fact, the blade elements with the local radius
The rest of the manuscript is organized as follows. In Section 2, the numerical models such as wind shear, tower shadow effect, and the dual effect are introduced to divide the swept area of the rotor into three areas. In Section 3, case analysis for testing the accuracy of the numerical model is conducted, and the influence of wind turbine structural parameters on wind shear and tower shadow effect are analyzed in detail. In Section 4, the conclusions and discussion are presented.
Wind shear coefficient is used to illustrate the wind speed distribution along the vertical direction. There is a large velocity gradient at different spanwise positions of the blade during the rotor rotation for a large-scale HAWT, as shown in Fig. 1. For megawatt-scale HAWT, the distribution difference of wind velocity in the vertical direction must be considered. Usually, the exponential model is usually used to express the wind shear effect [7]:
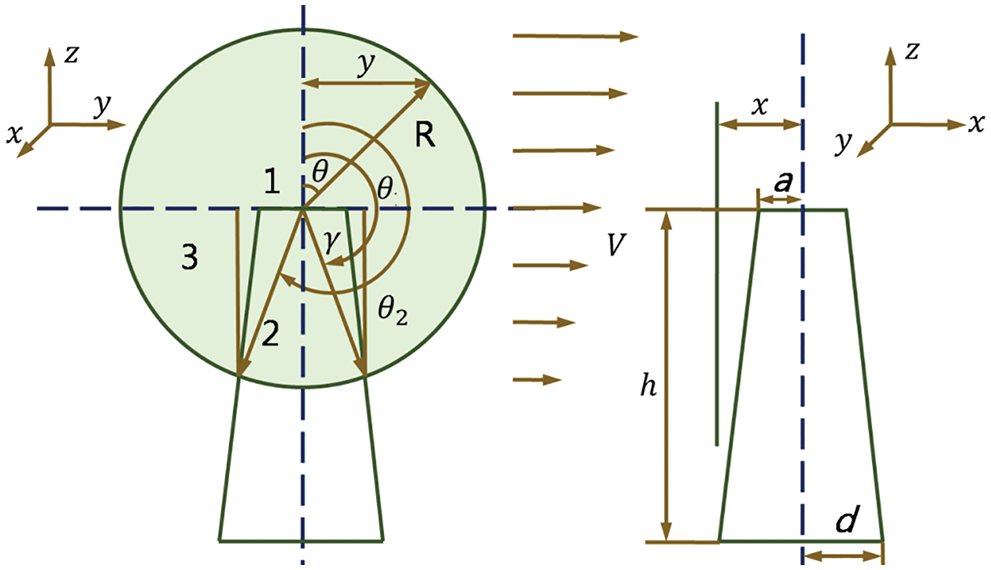
Figure 1: Wind turbine structural parameters
where
where
Tower shadow effect refers to the phenomenon that when the incoming wind flows through the tower, the spatial variation in the flowfield will affect the wind direction and reduce the inflow velocity in the upstream and downstream of the tower. The tower will cause fluctuations in the aerodynamic performance of the wind turbine due to interference with the airflow flowing through the blade. Meanwhile, the generator performance will be reduced subsequently. It is fully a negative effect for power quality and stability. According to the wind energy handbook [14], the velocity loss caused by the tower shadow effect for upwind wind turbines can be expressed as follows [14]:
where
According to Eq. (4), the constrained condition of the tower shadow effect is
In Eq. (5),
where
The wind speed fluctuation caused by wind shear and the tower shadow effect changes with rotor azimuth angle. The wind speed through the blade element significantly varies with different azimuth angles and spanwise positions. The dual effect of wind shear and tower shadow effect aggravates the periodic fluctuation of blade aerodynamic load. According to the blade azimuth angle
Area 1: The blade is located in the upper half swept area, and it is only subjected to wind shear effect. The mathematical model is created in the way of [3]:
Area 2: The blade is located in the lower half swept area, and its azimuth angle is between the critical azimuth angles
The calculation methods for critical azimuth
Area 3: The blade is located in the lower half swept area, but the blade azimuth angle is beyond the critical azimuth angles
To test the model accuracy in this study, the proposed model is used to calculate the wind speed at the blade tip for 5-MW HAWT from the National Renewable Energy Laboratory (NREL). The Gross properties chosen for the NREL 5-MW baseline wind turbine are listed in Table 1, and the details of blade section parameters are given in [17]. The calculation results are comprehensively compared with the conventional model. Compared to the conventional prediction model, the proposed model contains a new constraint condition of the blade elements with the local radius

Fig. 2 shows the variation trend of wind speed of blade tip with azimuth angle considering wind shear and tower shadow effect. Fig. 2a shows that the wind speed of the blade tip periodically fluctuates around 11.4 m/s, and reach to 12.7, 9.1 m/s respectively when the blade is located at the highest and lowest position, and the fluctuation range is about 3.6 m/s. Figs. 2b and 2c show a comparison of the wind speed of the blade tip under the tower shadow effect model in this paper with the conventional tower shadow effect model. According to the mathematical model of the tower shadow effect of upwind wind turbine (Eq. (4)), the constraint condition
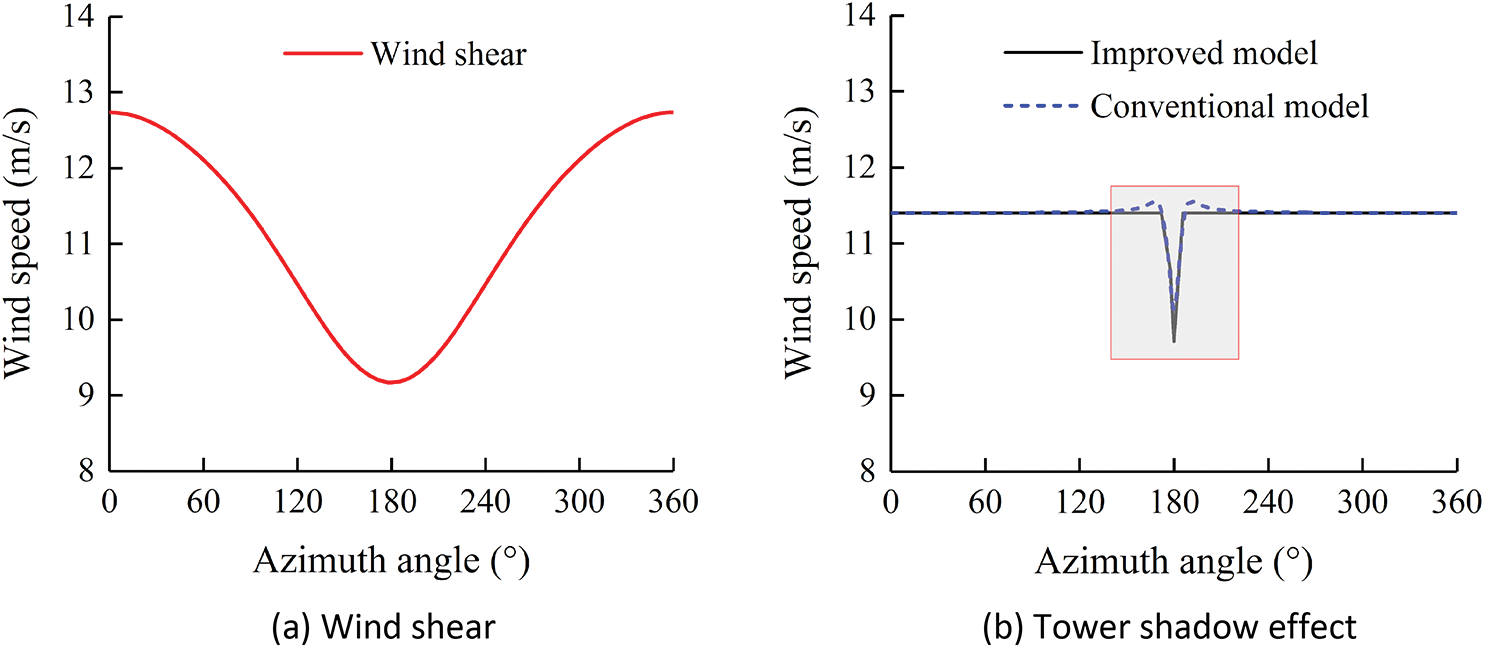
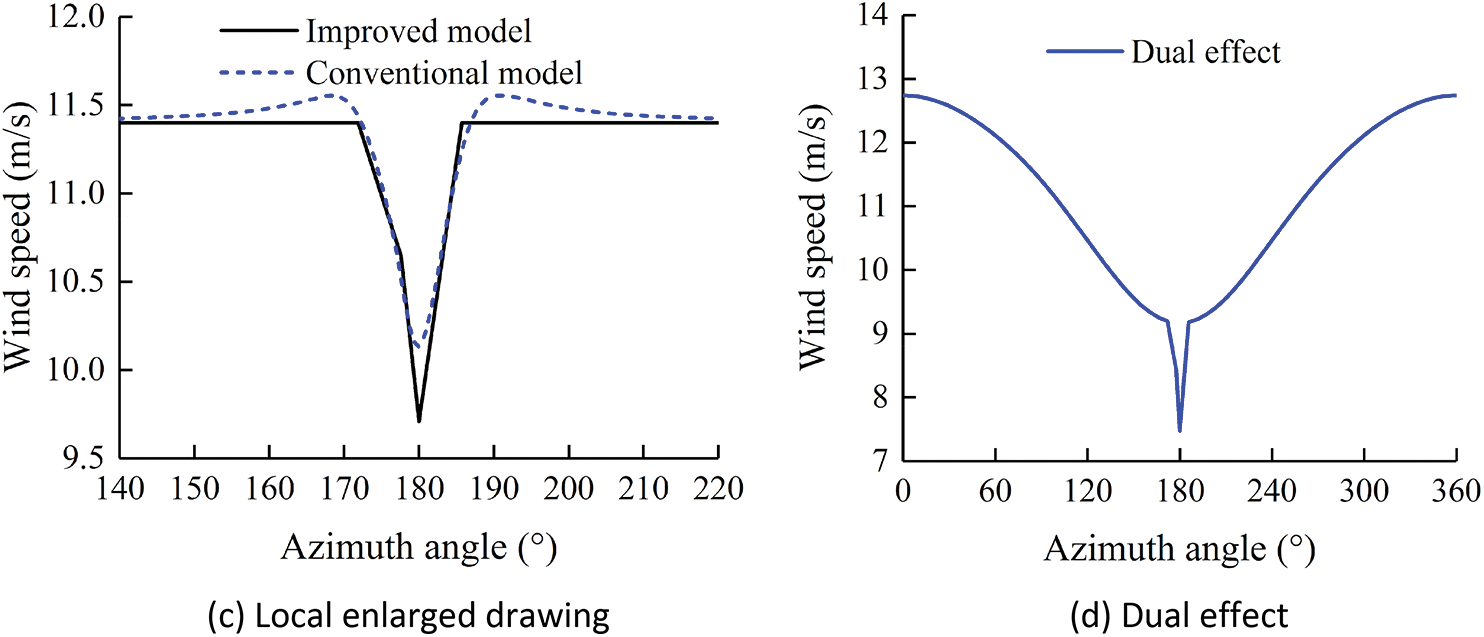
Figure 2: Wind speed of blade tip considering wind shear and tower shadow effect
To study the influence of structural parameters of a wind turbine such as hub height, rotor diameter, the diameter of tower top, and overhang on wind shear and tower shadow effect, wind speed of blade tip under different structural parameters are explored using the improved model. The detailed wind turbine structural parameters are shown in Table 2, and number 2 are the design parameters for a 5-MW baseline wind turbine.

Fig. 3a shows that the maximum wind speed of blade tip tends to decrease from 12.8 to 12.6 m/s with the increase of hub height. The minimum wind speed tends to increase from 7.2 to 7.6 m/s. It shows that the wind shear effect tends to decrease with the increase of hub height.
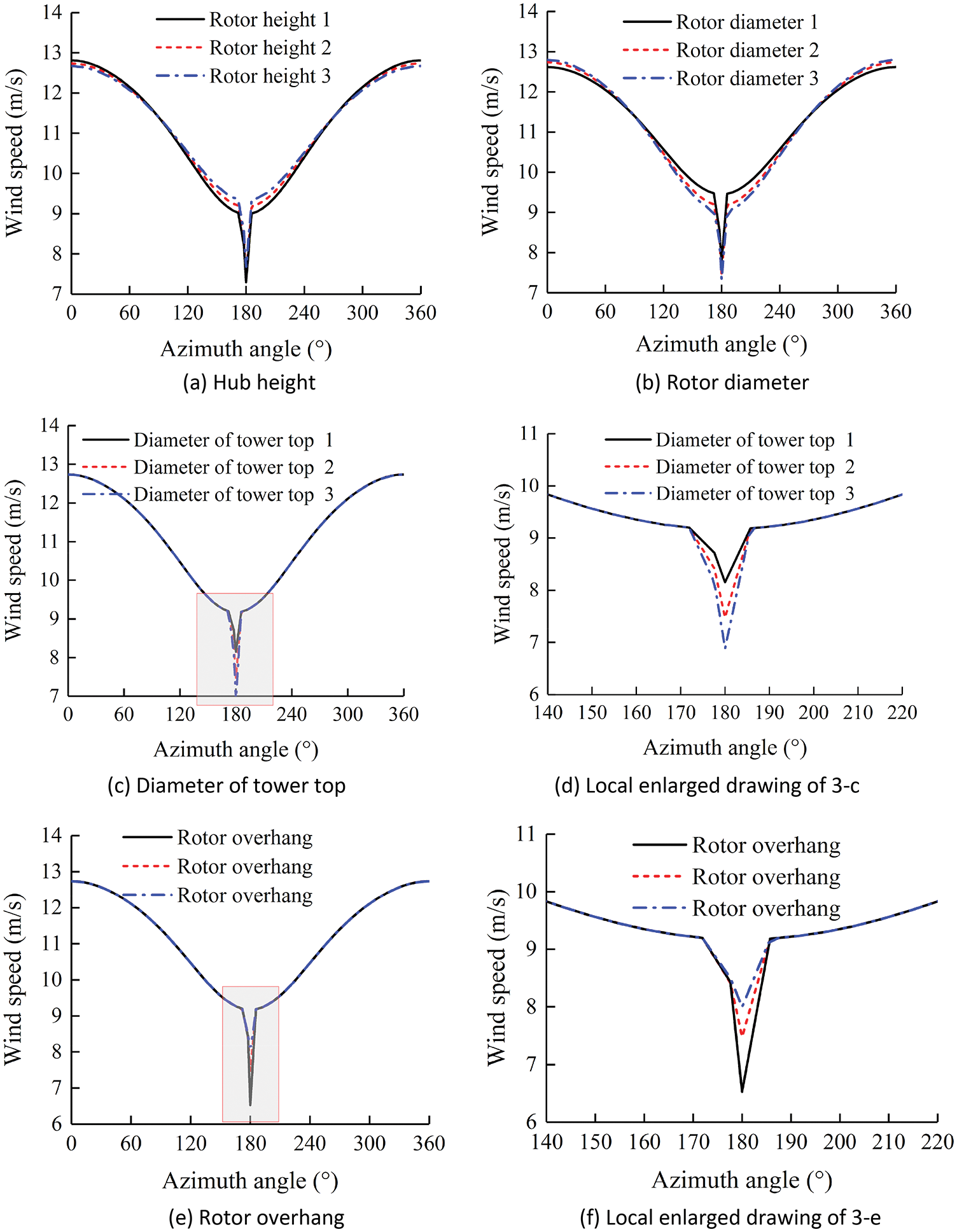
Figure 3: Wind speed of blade tip with different structural parameters
Fig. 3b shows the opposite trend compared with Fig. 3a. The larger the rotor diameter, the more significantater the difference between the maximum and minimum wind speed. This shows that the variation range of wind speed tends to increase with the rotor diameter increase. The rotor diameter is positively correlated with the wind shear and tower shadow effect.
Fig. 3c and its local enlarged drawing 3-d show that the diameter of the tower top slightly affects the wind speed of the blade tip beyond the critical azimuth angles of 175.5° and 184.5°, while the wind speed decreases sharply between the critical azimuth angles with the increase of top diameter. The speed drop caused by the change in tower top diameter is 1.3 m/s when the azimuth angle is 180°. It is shown that there is no correlation between the wind shear and the diameter of the tower top, and the tower shadow effect is positively correlated with the diameter of the tower top.
Fig. 3e shows the same variation trend as Fig. 3c when it is beyond the critical azimuth angle, indicating that the wind shear effect is independent of rotor overhang. However, within the critical azimuth angle, Fig. 3f shows the opposite trend to Fig. 3d, and the wind speed of the blade tip grows obviously with the increase of overhang. It indicates that the tower shadow effect is negatively correlated with the rotor overhang. The closer the rotor is to the tower, the more pronouncedious the tower shadow effect.
(1) An improved model accounting for the wind shear and tower shadow effect is established in the way of unified cylindrical coordinate using the fourth-order Taylor series, and the boundary of rotor swept area is further refined. Compared to the conventional model, the proposed model more realistically reflects the influence of the tower shadow effect on the incoming wind speed.
(2) Wind shear effect becomes weaker with the increase of hub height. It causes the maximum wind speed of the blade tip decreases, the minimum wind speed tends to increase, and the range of wind speed tends to decrease. The hub height is independent of the tower shadow effect.
(3) The larger the rotor diameter, the greater the difference between the maximum and minimum wind speed. The rotor diameter is positively correlated with the wind shear and tower shadow effect.
(4) Beyond the critical azimuth angles of 175.5° and 184.5°, the diameter of the tower top and rotor overhang does not affect the wind speed of the blade tip. Between the two critical azimuth angles, the wind speed decreases sharply with the increase in the diameter of the tower top but grows with the increase of rotor overhang. This is mainly because there is no correlation between wind shear and the diameter of the tower top, while the tower shadow effect is positively correlated with the diameter of the tower top, and negatively correlated with the rotor overhang.
This study focused on the relationship between wind turbine structural parameters with wind shear and the tower shadow effect. The future work will further analyze the influence of structural parameters on the rotor power and operation performance of wind turbines.
Data Availability: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Funding Statement: This work is funded by the National Natural Science Foundation of China (51866012).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Dolan, D. S. L., Lehn, P. W. (2006). Simulation model of wind turbine 3p torque oscillations due to wind shear and tower shadow. IEEE Transactions on Energy Conversion, 21(3), 717–724. DOI 10.1109/TEC.2006.874211. [Google Scholar] [CrossRef]
2. Emeksiz, C., Cetin, T. (2019). In case study: Investigation of tower shadow disturbance and wind shear variations effects on energy production, wind speed and power characteristics. Sustainable Energy Technologies and Assessments, 35(3), 148–159. DOI 10.1016/j.seta.2019.07.004. [Google Scholar] [CrossRef]
3. Wen, B., Wei, S., Wei, K., Yang, W. X., Chu, F. L. (2017). Power fluctuation and power loss of wind turbines due to wind shear and tower shadow. Frontiers of Mechanical Engineering, 12(3), 321–332. DOI 10.1007/s11465-017-0434-1. [Google Scholar] [CrossRef]
4. Sintra, H., Mendes, V., Melício, R. (2014). Modeling and simulation of wind shear and tower shadow on wind turbines. Procedia Technology, 17(17), 471–477. DOI 10.1016/j.protcy.2014.10.255. [Google Scholar] [CrossRef]
5. Mohammadi, E., Rasoulinezhad, R., Moschopoulos, G. (2020). Using a supercapacitor to mitigate battery microcycles due to wind shear and tower shadow effects in wind-diesel microgrids. IEEE Transactions on Smart Grid, 11(5), 3677–3689. DOI 10.1109/TSG.2020.2979140. [Google Scholar] [CrossRef]
6. Ayodele, T. R., Adekunle, S., Munda, J. L. (2020). Impact of wind shear and tower shadow on the small signal stability of power systems incorporating wind turbines. International Journal of Smart Grid and Clean Energy, 9(1), 52–60. [Google Scholar]
7. Fu, L., Wei, Y. D., Fang, S., Tian, G., Zhou, X. J. (2018). A wind energy generation replication method with wind shear and tower shadow effects. Advances in Mechanical Engineering, 10(3), 1–11. DOI 10.1177/1687814018759216. [Google Scholar] [CrossRef]
8. Liu, Y., Qiao, Y., Han, S., Tao, T., Munkhtuya, E. (2021). Rotor equivalent wind speed calculation method based on equivalent power considering wind shear and tower shadow. Renewable Energy, 172(15–16), 882–896. DOI 10.1016/j.renene.2021.03.089. [Google Scholar] [CrossRef]
9. Tian, W., Pan, W., Shao, Y., Xu, B., Liu, H. M. et al. (2019). Individual pitch control strategy for reducing aerodynamic loads and torque ripples. IEEJ Transactions on Electrical and Electronic Engineering, 14(3), 1–9. DOI 10.1002/tee.22984. [Google Scholar] [CrossRef]
10. Liu, L. Q., Xiao, C. S., Guo, Y. (2021). Study on aerodynamic characteristics of offshore floating horizontal axis wind turbine. Acta Energiae Solaris Sinica, 42(1), 294–301. [Google Scholar]
11. Yang, K., Wang, S. T., Kang, W. L. (2020). Pulsating wind speed model considering wind shear tower shadow effect. Journal of North China Electric Power University, 47(1), 63–69. [Google Scholar]
12. Han, B. (2018). Research on power and load optimization control method and technology of large wind turbine, pp. 1–50. Hunan, China: Hunan University. [Google Scholar]
13. Kim, D. Y., Kim, Y. H., Kim, B. S. (2021). Changes in wind turbine power characteristics and annual energy production due to atmospheric stability, turbulence intensity, and wind shear. Energy, 214(5), 119051. DOI 10.1016/j.energy.2020.119051. [Google Scholar] [CrossRef]
14. Burton, T., Sharpe, D., Nick, J., Ervin, B. (2005). Wind energy handbook, pp. 1–637. USA: John Wiley & Sons. [Google Scholar]
15. Kong, Y. G. (2013). Wind power generation technology and its MATLAB and bladed simulation, pp. 1–226. China: Electronic Industry Press. [Google Scholar]
16. International Electrotechnical Commission (2019). Wind energy generation systems–Part 1: Design requirements. IEC61400-1 International Standard Fourth edition, pp. 1–172. Geneva: International Electrotechnical Commission. [Google Scholar]
17. Jonkman, J., Butterfield, S., Musial, W., Scott, G. (2009). Definition of a 5-MW reference wind turbine for offshore system development [NERL/TP-500-38060], vol. 15, pp. 1–57. USA: National Renewable Energy Laboratory. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools