Nanoparticle Shape Effect on a Sodium–Alginate Based Cu–Nanofluid under a Transverse Magnetic Field

Nomenclature

1  Introduction

The basic idea of dispersing particles into liquids can be traced back to the published theoretical work of Maxwell [1]. The particles that had dimensions in the micrometer and millimeter range were considered in the study. However, particles in the order of millimeters or even micrometers cause problems of rapid settling, clogging, and abrasion [2]. The rapid development of nanotechnology makes the generation of nanometer–sized particles possible and eliminates problems arising from micrometer–sized particles. Nanofluids, first proposed by Choi [3], are a new class of heat transfer fluids that are superior to conventional micrometer–sized particles based fluids in terms of thermo–physical properties. The nanoparticles used in creating nanofluids include metals (gold, silver, copper), oxides (alumina, zirconia, silica, titania), and some other compounds (carbon nanotubes, silicon carbide, graphene). Buongiorno [4] developed an analytical model to explain the convective heat transfer in nanofluids. He considered seven slip mechanisms and concluded that Brownian diffusion and thermophoresis are the two most important slip mechanisms in nanofluids. Aly et al. [5] studied the effects of thermal radiation and suction/injection on the heat transfer flow of water based nanofluid past a vertical plate, and reported that a constant temperature was maintained on the plate. Moshizi et al. [6] considered mixed convection of Al2O3–water nanofluid inside a vertical micro–annulus with two different types of heat fluxes imposed at the walls. They noted that both temperature and concentration dependent buoyancy forces affect flow fields and nanoparticle migration. Sheikholeslami et al. [7] numerically investigated the magnetohydrodynamic (MHD) flow of CuO–water nanofluid flow in a porous semi annulus with constant heat flux. Sheikholeslami [8] numerically investigated the CuO–water nanofluid inside a porous channel in the presence of a magnetic field. They reported a significant enhancement in heat transfer rate with a corresponding rise in the Hartmann number. Kanimozhi et al. [9] evaluated the impact of coupled buoyancy and thermocapillary driven convection in a cylindrical porous annulus saturated with water based Ag–MgO hybrid nanofluid along with viscous dissipation effects. At varying levels of random motion of nanoparticles, a higher volume percentage resulted in a decreased heat transmission rate. Several researchers have extended heat transfer flow problems from Newtonian fluids to nanofluids using different nanoparticles such as Cu–water [10]; CNTs–water [11]; Al2O3–water/ethylene glycol [12]; Fe3O4–water [13]; TiO2–water [14]; MWCNTs–water [15].

Literature review revealed that most articles on nanofluids mainly focus on the impacts of nanoparticle dimensions, types, dispersibility of nanoparticles, and the base fluids. Some recent work suggests that the shapes of nanoparticles have a significant impact on the thermo–physical properties of nanofluids. Elias et al. [16] examined the effects of five types of nanoparticles shape (such as cylindrical, bricks, blades, spherical, and platelets) based nanofluids to improve the performance of a shell and tube heat exchanger. Boehmite alumina (γ–AlOOH) nanoparticles of different shapes were dispersed in ethylene glycol or water based nanofluids. They determined that cylindrically shaped nanoparticles showed a better heat transfer rate and higher entropy generation. Jeong et al. [17] investigated the viscosity and thermal conductivity of ZnO nanofluids with nanoparticle shapes of nearly rectangular and a sphere, under various volume concentrations of the nanoparticles, ranging from 0.05 to 5.0 vol.%. They reported that the viscosity and conductivity of ZnO nanofluid with rectangular shape nanoparticles was better than with sphere shape nanoparticles. Vanaki et al. [18] numerically studied the effects of different nanofluids on the thermal and flow fields through transversely wavy wall channels with different phase shifts between the upper and lower wavy walls. They found that the SiO2–EG nanofluid with platelets shape nanoparticles gave the highest heat transfer enhancement. The shape effects of nano–size particles in Cu–H2O nanofluid on entropy generation was analyzed by Ellahi et al. [19]. Their study concluded that platelets shape nanoparticles gained maximum temperature than brick and cylinder shape nanoparticles.

Monfared et al. [20] investigated the turbulent convection flow of boehmite–alumina incorporated with various shapes of nanoparticles inside a heat exchanger under entropy generation effects. They revealed that platelet shape nanoparticles led to a stronger frictional entropy generation rate. Dogonchi et al. [21] studied nanoparticle shape effects on water based CuO–nanofluid using CVFEM. The study concluded that platelet shape nanoparticles exhibit a strong heat transfer rate. Shakiba et al. [22] studied the mixed convection of MHD flow of nanofluid inside two vertical annulus under a radial magnetic field with respect to the suction or injection using the analytical solution method. The impact of Brownian motion and shape factor on the thermal state of CuO–water nanofluid was also considered. The highest overall rate of heat transfer was achieved in the case of platelet shape nanoparticles. Sheikholeslami et al. [23] performed a simulation using water based Fe3O4–nanofluids. Their results showed that platelet shape nanoparticles should be used to obtain the highest Nusselt number. Hosseinzadeh et al. [24] examined micropolar MHD fluid flow over a vertical plate where three different base fluids including water, ethylene glycol, and ethylene glycol/water (50%–50%) were used. Their findings indicated that for water-based fluids, the temperature profile of lamina–shaped nanoparticles was 38.09% higher than brick–shaped nanoparticles. MHD mixed convection water based MoS2–GO hybrid nanofluid flow through an upright cylinder with different shapes of nanoparticles was investigated by Chu et al. [25]. Their results showed that the blade–shaped nanoparticles of MoS2–GO hybrid nanofluid had the maximum temperature. Khashi’ie et al. [26] analyzed the effects of spherical, brick, and blade shape nanoparticles on Cu–Al2O3 water based nanofluid flow in respect of the two important of parameters of EMHD and thermal radiation. Their results indicated that the maximum heat transfer enhancement occured in the case of blade shape nanoparticles. Anwar et al. [27] examined the heat transfer rates of different shape nanoparticles in sodium alginate based MoS2–Co hybrid nanofluid. They used spherical, cylindrical, blade, platelet, and brick shape nanoparticles and found that maximum heat transfer rate occured in the case of blade shape nanoparticles. Shahsavar et al. [28] performed entropy generation analysis using boehmite–alumina nanofluid containing five different nanoparticles shapes (spherical, bricks, blades, cylindrical, and platelet). They reported that spherical shape nanoparticles had the minimum impact on entropy generation. Ganesh et al. [29] performed a numerical experiment through FEM on the convection of heat generating γ Al2O3–H2O nanofluid filled in a square cavity with multiple circular-, square-, and triangular-shaped obstacles. They found a higher heat transfer rate in the cavity with triangular obstacles. Cao et al. [30] remarked that the accompanying influence on the thermophoretic force and the type of the random motion of spherical carbon nanotubes, cylindrical graphene, and platelet alumina nanoparticles affects heat transfer and mass transfer rates. Xiu et al. [31] noted that because there are numerous platelet aluminium, cylindrical magnesium oxide, and titanium dioxide nanoparticles in the flow of water-based ternary hybrid nanofluids, heat transfer is significant even at the start of the fluid flow. Saleem et al. [32] discovered that the friction between the layers of a water–based ternary–hybrid nanofluid and the wall can be reduced by increasing the density of spherical nanoparticles.

In the above work, Newtonian fluids were taken as a base fluid. However, few researchers have considered non–Newtonian based nanofluids in their research. It is well recognized that non–Newtonian fluids are encountered in numerous transport processes such as central heating systems, molten polymers, and nuclear reactors [33]. Sodium alginate natural convection based Fe2O3–nanofluid with accretion/ablation was illustrated by Hussanan et al. [34]. The mixed convection ethylene glycol based nanofluids flow, together with the functional shape effects of nanoparticles was investigated by Memon et al. [35]. Hussanan et al. [36] highlighted the impacts of magnetic and non–magnetic nanoparticles on viscoplastic Casson-based mixture hybrid nanofluid. Kalaivanan et al. [37] investigated the influence of Arrhenius activation energy in heat and mass transfer of second–grade nanofluid flow and noted that the thickness of the boundary layer increased with non–dimensional activation energy. Influence of Arrhenius activation energy on the momentum, energy, and mass transport of a second-grade magneto nanofluid flow with elastic deformation effects was discovered by Kalaivanan et al. [38]. Hammachukiattikul et al. [39] discussed the heat transfer flow of viscoplastic Casson-based hybrid nanofluid with additional factors. These factors include radiation, heat source/sinks, and inclined Lorentz force. Ganesh et al. [40] investigated the thermal and hydraulic characteristics of a Casson-based MWCNT nanofluid inside a wavy square enclosure containing a circular–shaped obstacle. Ganesh et al. [41] explored the incompressible, two–dimensional, buoyancy driven convection flow of Casson-based MWCNT nanofluid in a square enclosure with a circular barrier and found that by increasing the MWCNT volume fraction along the wavy bottom wall, Casson parameter, Rayleigh number, and the heat transfer rate increased. To our knowledge, nanoparticle shape effects on non–Newtonian viscoplastic sodium alginate (SA) based Cu–nanofluid has not been explored yet. The purpose of this article is three–fold. Firstly, to formulate the SA based Cu–nanofluid flow over a stretching/shrinking sheet. Secondly, to analyze magnetic field and viscous dissipation effects. Finally, to solve the governing non–linear system numerically as well as analytically by using Runge–Kutta–Fehlberg (RKF) and MAPLE built–in differential equation solver, Dsolve, methods. Thermo-physical properties of Cu and SA are given in Table 1.

2  Formulation

The steady 2D flow of SA based Cu–nanofluids with five shapes of nanoparticles is considered over a stretching sheet having a sheet velocity assumed as uw(x)=bx , where b is a constant, as shown in Fig. 1. The x and y are taken along and normal to the sheet, respectively. It is also assumed that the temperature of the sheet is Tw(x)=T∞+Ax2 [42].

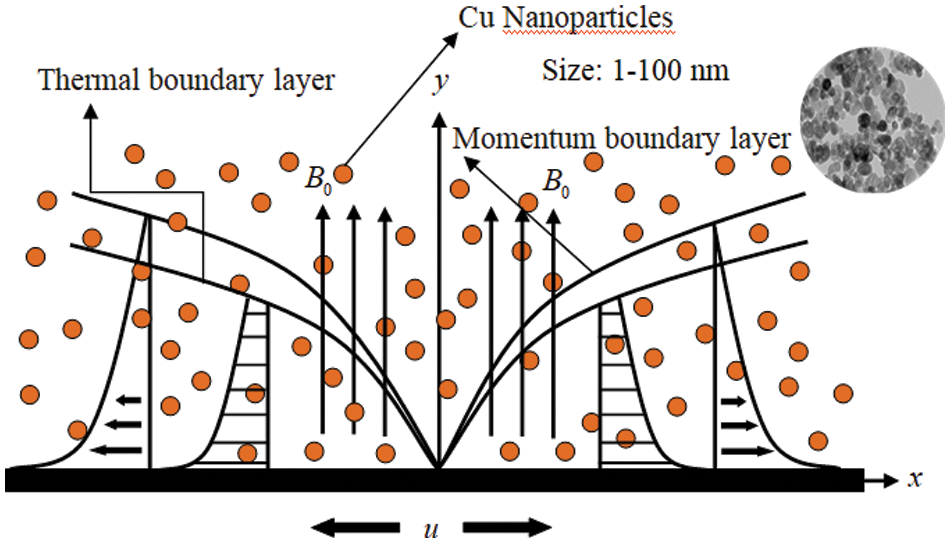
Figure 1: Stretching case (α>0)

The rheological behavior of Cu–nanofluid followed by [36,39] can be described in the form of continuity, momentum, and energy equations

∂u∂x+∂v∂y=0,  (1)

u∂u∂x+v∂u∂y=νNF(1+1γ)∂2u∂y2−σNFρNFB02u,  (2)

u∂T∂x+v∂T∂y=KNF(ρCp)NF∂2T∂y2−μNF(ρCp)NF(1+1γ)(∂u∂y)2,  (3)

where u and v are the components of velocity, γ is the viscoplastic parameter and B0 is the magnetic field. Other symbols and quantities are defined in the nomenclature. The boundary conditions are

u=αuw(x), v=0aty=0; u→0asy→∞,  (4)

T=Tw aty=0; T→T∞ asy→∞. (5)

The viscosity of SA based Cu–nanofluid with different shapes of nanoparticle, except spherical, is calculated from the following correlation:

μNF=(1+δ1ϕ+δ2ϕ2)μBF,  (6)

where the constants δ1 and δ2 are known as viscosity coefficients based on nanoparticle shapes as given by Timofeeva et al. [43], see Table 2.

In the case of spherical nanoparticle shape, viscosity of SA based Cu–nanofluid is

μNF=[1(1−ϕ)2.5]μBF. (7)

Pak et al. [44] introduced a correlation to predict the density of nanofluid, which is defined as

ρNF=[(1−ϕ)+ϕρNPρBF]ρBF. (8)

The electrical conductivity of SA based Cu–nanofluid given by Sheikholeslami [45] which is of the form

σNF=[1+3(σNPσBF−1)ϕ(σNPσBF+2)−(σNPσBF−1)ϕ]σBF. (9)

Many relationships proposed for the thermal conductivity of a two–phase mixture, in which Maxwell [1] developed a model for the thermal conductivity of a two–phase mixture based on thermal conductivity of base fluids, spherical particles and particle volume fraction. Hamilton et al. [46] expanded Maxwell model for non–spherical particle shapes. Their model allows calculating the effective thermal conductivity of a two–phase mixture under the empirical shape factor. This model is stated as

KNF=[KNP+(n−1)KBF+(n−1)(KNP−KBF)ϕKNP+(n−1)KBF−(KNP−KBF)ϕ]KBF,  (10)

where n= shape factor (for sphere n=3 , for cylinder n=6 ). Moreover, n=3ψ is empirical shape factor as given by Timofeeva et al. [43], see Table 3.

To simplify the Eqs. (2) and (3), following variables [11,39] are defined

η=ybνBF, u=bxFη(η), v=−bνBFF(η), θ(η)=T−T∞Tw−T∞. (11)

Using Eq. (11), governing Eqs. (2) and (3) are reduced as follows:

μNFμBFρBFρNF(1+1γ)Fηηη(η)+F(η)Fηη(η)−Fη2(η)−MρBFρNFσNFσBFFη(η)=0,  (12)

1PrKNFKBF(ρCp)BF(ρCp)NFθηη (η)+F(η)θη(η)−2Fη(η)θ(η)+μNFμBF(ρCp)BF(ρCp)NF(1+1γ)EcFηη2(η)=0,  (13)

where Fη(η) represents an ordinary derivative with respect to η , M2=σBFB02bρBF is the magnetic parameter, Pr=(ρCp)BFνBFKBF is the Prandtl number and Ec=b2A(Cp)BF=uw2(Tw−T∞)(Cp)BF is the Eckert number. The corresponding boundary conditions in the non–dimensional form are

F(η)=0, Fη(η)=α, θ(η)=1atη=0,  (14)

Fη(η)→0, θ(η)→0 asη→∞. (15)

3  Analytical Solutions

3.1 Momentum Equation Solution

The closed–form solution of Eq. (12) has been obtained by Chakrabarti et al. [47] can be written as

F(η)=αβ(1−exp⁡(−βη)),  (16)

where β=αε1+ε2 and

ε1=(γ1+γ)(11+δ1ϕ+δ2ϕ2)((1−ϕ)+ϕρNPρBF), ε2=M(γ1+γ)(11+δ1ϕ+δ2ϕ2)(1+3(σNPσBF−1)ϕ(σNPσBF+2)−(σNPσBF−1)ϕ).

The following closed–form solution for velocity is obtained

Fη(η)=αexp⁡[−(γ1+γ)(11+δ1ϕ+δ2ϕ2){α((1−ϕ)+ϕρNPρBF)+M(1+3(σNPσBF−1)ϕ(σNPσBF+2)−(σNPσBF−1)ϕ)}η],  (17)

Fηη(η) = α[(γ1+γ)(11+δ1ϕ+δ2ϕ2){α((1−ϕ)+ϕρNPρBF)+M(1+3(σNPσBF−1)ϕ(σNPσBF+2)−(σNPσBF−1)ϕ)}]×exp⁡[−(γ1+γ)(11+δ1ϕ+δ2ϕ2){α((1−ϕ)+ϕρNPρBF)+M(1+3(σNPσBF−1)ϕ(σNPσBF+2)−(σNPσBF−1)ϕ)}η]. (18)

3.2 Energy Equation Solution

By substituting F(η), Fη(η) and Fηη(η) in Eq. (13), we get

1Pr(KNFKBF)θηη (η)+(ρCp)NF(ρCp)BF[(αβ−αβe−βη)θη(η)−2αe−βηθ(η) ]+μNFμBF(1+1γ)Ec (−αβe−βη)2=0. (19)

Taking τ=e−βη , Eq. (19) turns

1PrKNFKBF[τθττ (τ)+θτ (τ)]−(ρCp)NF(ρCp)BF1β2[α(1−τ)θτ(τ)+2αθ(τ)]+μNFμBF(1+1γ)Ec α2τ=0,  (20)

and boundary conditions are

θ(τ=1)=1, θ(τ=0)=0. (21)

Closed–form solution of Eq. (21) with the help of MAPLE toolbox is obtained as

θ(τ)=[hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], ε4ε3τ)e−ε4ε3τ]C1+[hypergeometric([3], [ε3+ε4ε3], ε4ε3τ)τε4ε3e−ε4ε3τ]C2+12[ε5(ε3−ε4+2ε4τ)ε42],  (22)

where

ε3=KNFKBF1Pr, ε4=(ρCp)NF(ρCp)BFαβ2, ε5=μNFμBF(1+1γ)Ecα2

Z1=−12[ε5(ε3−ε4)ε42][hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], 0)]−1

Z2=[hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1eε4ε3−12[ε5(ε3+ε4)ε42][hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1eε4ε3+12[ε5(ε3−ε4)ε42][hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], ε4ε3)]×[hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1.

Using boundary conditions (21), we obtained

θ(τ)=−12[ε5(ε3−ε4)ε42][hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], ε4ε3τ)e−ε4ε3τ]×[hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], 0)]−1+12[ε5(ε3−ε4+2ε4τ)ε42]+[hypergeometric([3], [ε3+ε4ε3], ε4ε3τ)τε4ε3e−ε4ε3τ][hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1eε4ε3+[hypergeometric([3], [ε3+ε4ε3], ε4ε3τ)τε4ε3e−ε4ε3τ]×[−ε5(ε3+ε4)2ε42][hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1eε4ε3+[hypergeometric([3], [ε3+ε4ε3], ε4ε3τ)τε4ε3e−ε4ε3τ][hypergeometric([3], [ε3+ε4ε3], ε4ε3)]−1×12[ε5(ε3−ε4)2ε42][hypergeometric([3ε3−ε4ε3], [ε3−ε4ε3], ε4ε3)]. (23)

Note that above solution of temperature θ(τ) depends on τ ; in other words, θ(τ) is a function of τ . However, temperature depends on η . By substituting τ=e−βη in Eq. (23), we can find temperature solution with respect to η .

4  Runge–Kutta–Fehlberg (RKF) Method

The non–linear differential Eqs. (12) and (13) with the boundary conditions (14) and (15) have been solved numerically by the Runge–Kutta–Fehlberg (RKF) method using MAPLE software (Version 13) and analytically with the help of MAPLE built–in differential equation solver Dsolve. The system of differential equations consists of third–order velocity and second–order temperature equations are reduced in simultaneous ordinary differential equations. The step size Δy=0.001 and a convergence criterion of 10−6 are considered in the numerical computations. The asymptotic boundary conditions (15) are substituted by using a value of 12 for the similarity variable ηmax as

Fη(12)=0, θ(12)=0.

5  Graphical Results and Discussion

The effect of different physical parameters, namely, the viscoplastic parameter γ , magnetic parameter M, Eckert number Ec , Prandtl number Pr on velocity and temperature fields are shown in graphs. Figs. 2–5 describe the temperature field θ(η) variation at different values of viscoplastic parameter γ along a stretching sheet for SA based nanofluid when M>0 (in the presence of magnetic field) and α>0 (in case of stretching sheet), for different shapes of Cu nanoparticles such as bricks, cylinders, platelets, and blades respectively. It was noticed that temperature increased with increasing values of γ for bricks, cylinders, platelets, and blades shapes of Cu nanoparticles, respectively. To this end, increases in the values of γ led to decreases in yield stress which improved the temperature field. Figs. 6–9 show the influence of different values of Prandtl number Pr on the temperature field θ(η) for bricks, cylinders, platelets, and blades shapes of Cu nanoparticles when M>0 and α>0 . It was found that increases in Pr decreased the temperature of bricks, cylinders, platelets, and blades shapes of Cu nanoparticles. Physically, the increase in Pr number means that momentum diffusivity dominated over thermal diffusivity which caused the decrease in temperature field. Moreover, these figures show the comparison of temperature field θ(η) for four different types of base fluids such as water (Pr=6.2) , sodium alginate (Pr=6.45) , kerosene (Pr=21) and engine oil (Pr=6450) containing bricks, cylinders, platelets, and blades shapes of Cu nanoparticles. The temperature of water and sodium alginate-based Cu–nanofluids was noticed to be higher than kerosene and engine oil based Cu–nanofluids. The reason for this is that water and sodium alginate have better thermal conductivity than kerosene and engine oil-based fluids. Therefore, water and sodium alginate-based fluids raised the temperature θ(η) of the Cu–nanofluid.

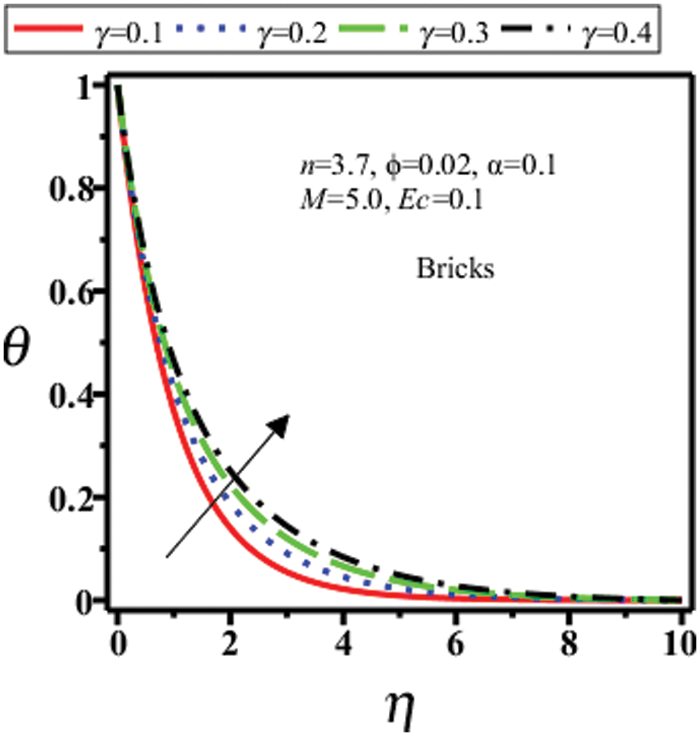
Figure 2: Temperature field of bricks shape nanoparticles for different γ

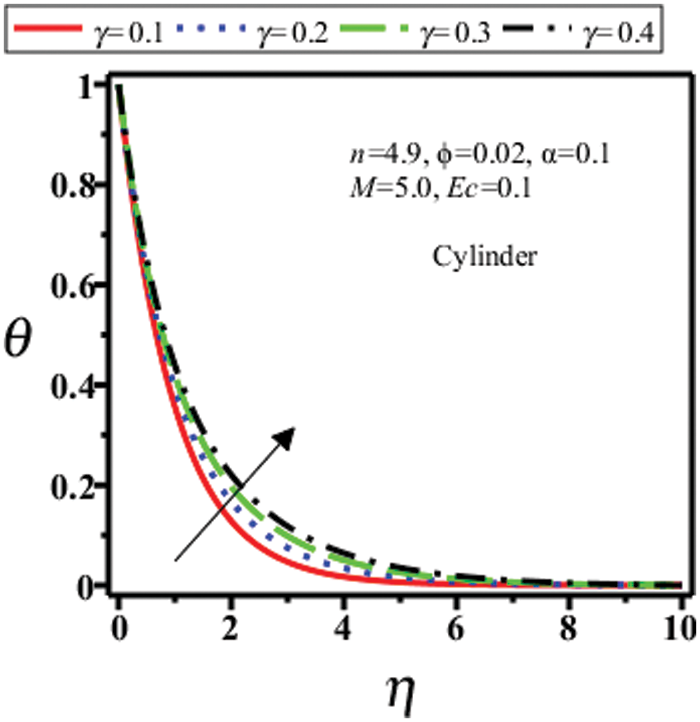
Figure 3: Temperature field of cylinder shape nanoparticles for different γ

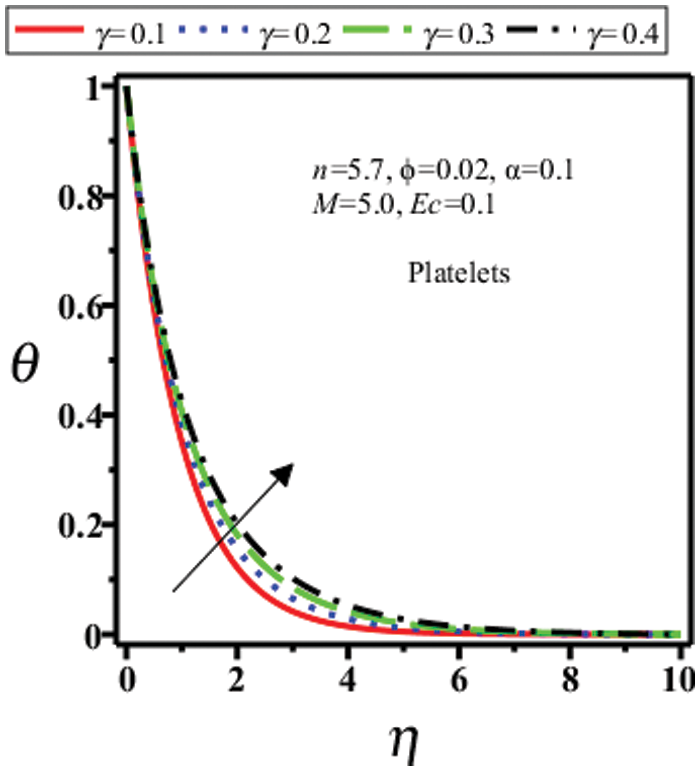
Figure 4: Temperature field of platelets shape nanoparticles for different γ

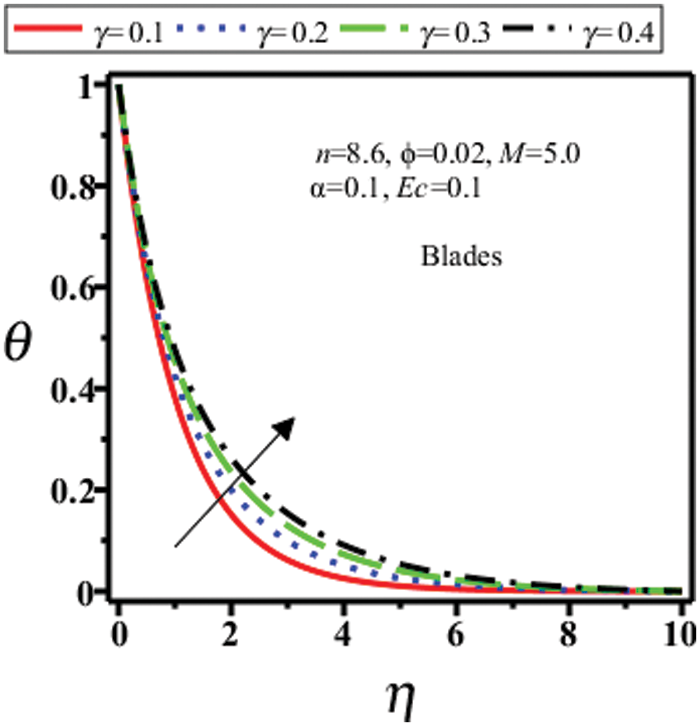
Figure 5: Temperature field of blades shape nanoparticles for different γ

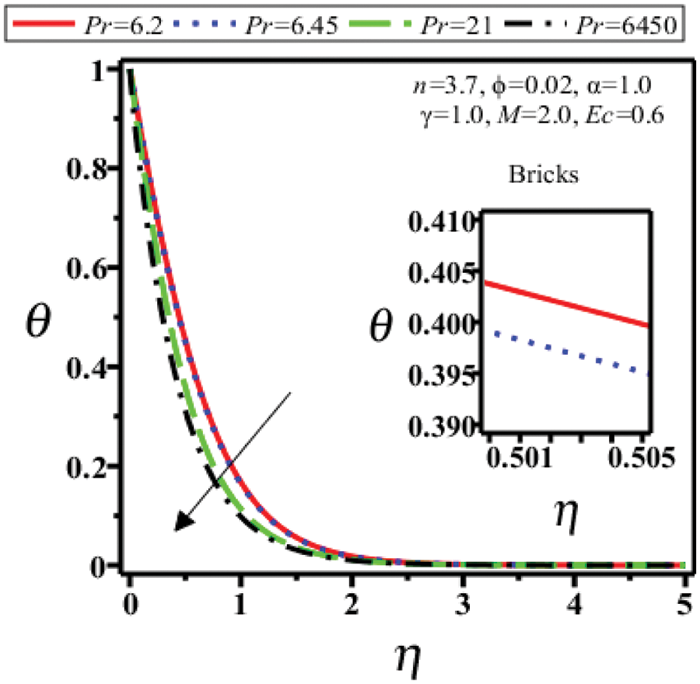
Figure 6: Temperature field of bricks shape nanoparticles for different Pr

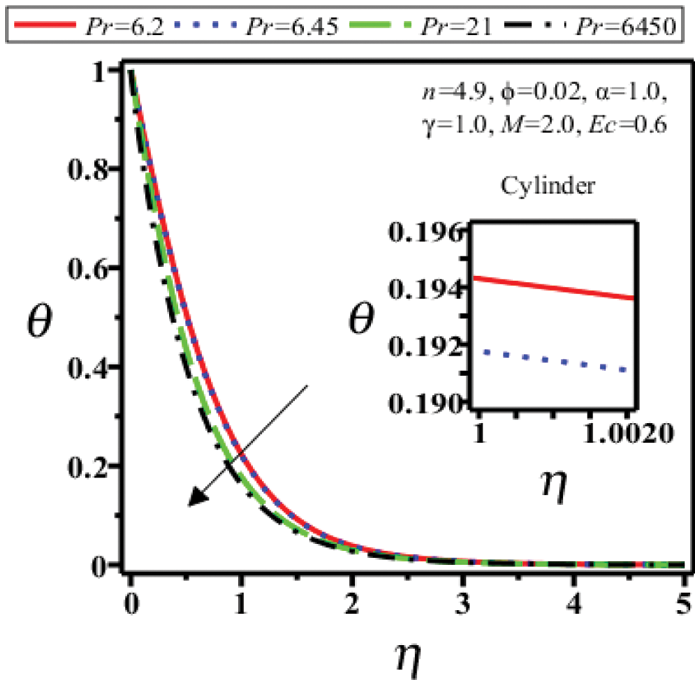
Figure 7: Temperature field of cylinder shape nanoparticles for different Pr

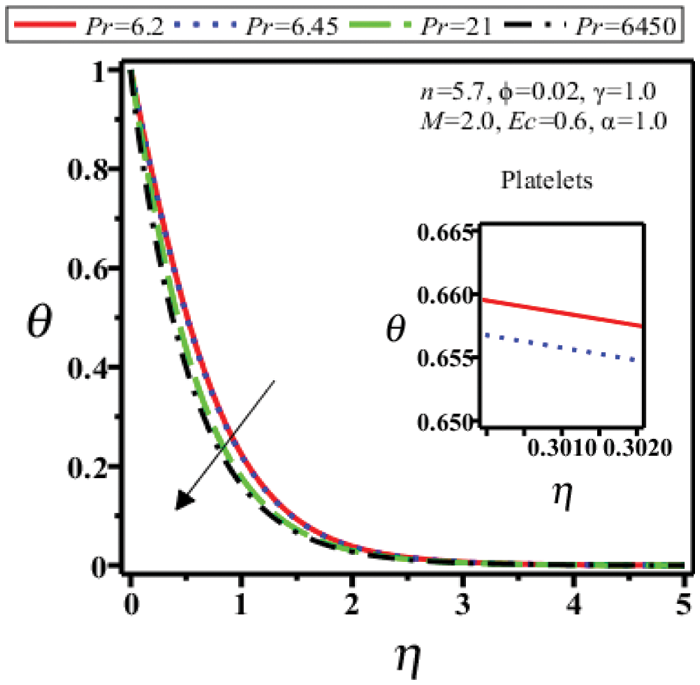
Figure 8: Temperature field of platelets shape nanoparticles for different Pr

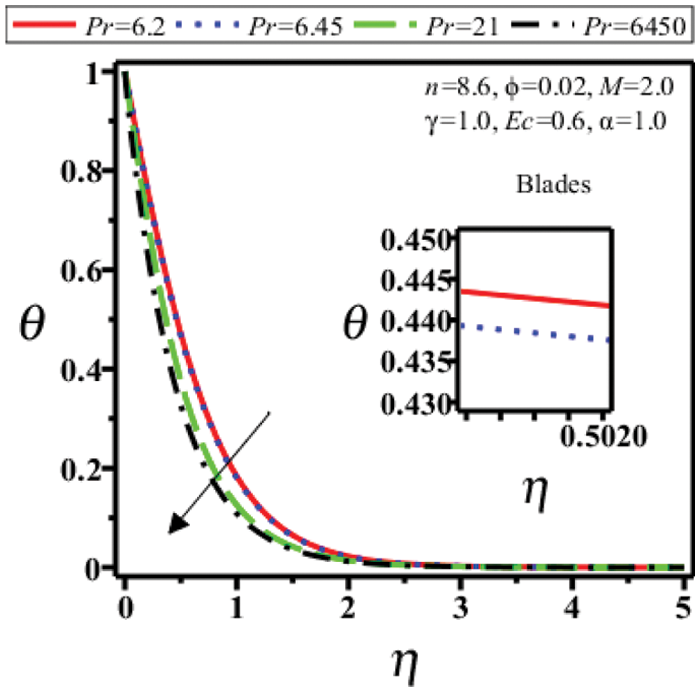
Figure 9: Temperature field of blades shape nanoparticles for different Pr

Figs. 10–13 show the temperature profile θ(η) for different values of Eckert number Ec for brick, cylinder, platelet, and blade shapes of Cu–nanoparticles respectively when M>0 and α>0 . It was observed that temperature increased for all shapes of nanoparticles respectively with increasing values of Ec . This was due to increases in Ec resulting in enhancement of the kinetic energy, as it is a well–known fact that temperature is defined as average kinetic energy. Moreover, the dissipative frictional forces between layers were enhanced with the increases in Ec and consequently, the temperature of the Cu–nanofluid rose. Velocity fields Fη(η) for different shapes of nanoparticles (bricks, cylinders, platelets, and blades) respectively for different values of viscoplastic parameter γ when M>0 and α>0 are shown in Figs. 14–17. It was observed that velocity field decreased for all nanoparticles with increasing values of γ . To this end, increases in values of γ led to reductions in yield stress, therefore the velocity field Fη(η) reduced. Figs. 18–21 present the variations in velocity profile Fη(η) with the variations in stretching sheet parameters α when M>0 for different shapes of nanoparticles. It was observed that the increases in the α increased the velocity field Fη(η) . Figs. 22–25 show the impact of different values of magnetic parameter M when α>0 on the velocity field Fη(η) for different shapes of nanoparticles (bricks, cylinders, platelets and blades), respectively. It was observed that increases in magnetic parameter M decreased the velocity field Fη(η) . Resultant resistive type forces due to enhancement of magnetic field strength, also called Lorentz forces with respect to the aligned magnetic field play a key factor in slowing the fluids motion. Hence, increasing values of M immediately cause an increase in drag force which decreases the velocity profile. To test the present numerical results, the results of velocity and temperature fields for Cu–nanofluid are compared with those obtained by Saleem et al. [48] in Figs. 26 and 27, for blade and platelet shapes nanoparticles when M=0 (n the absence of magnetic field) and γ→∞ (in case of Newtonian fluid), respectively. Both of these results for velocity and temperature fields of Cu–nanofluid are found in an excellent agreement.

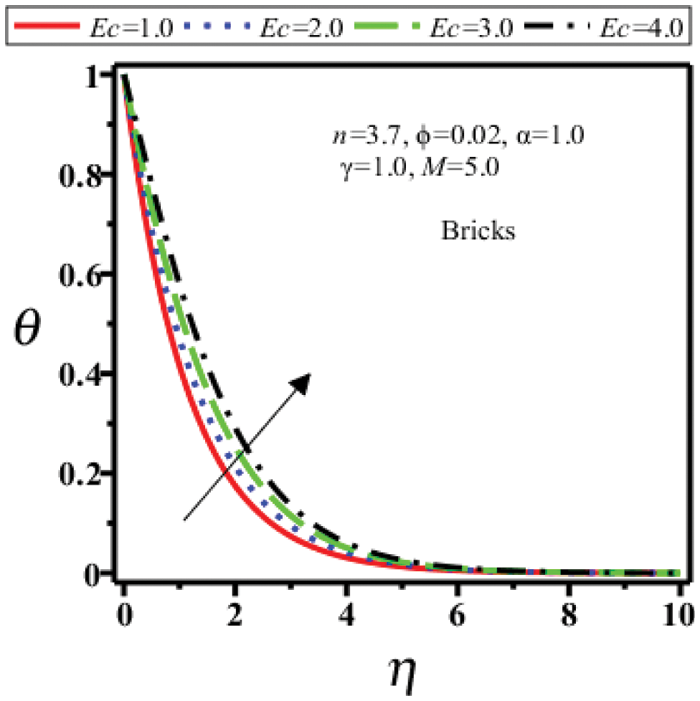
Figure 10: Temperature field of bricks shape nanoparticles for Ec

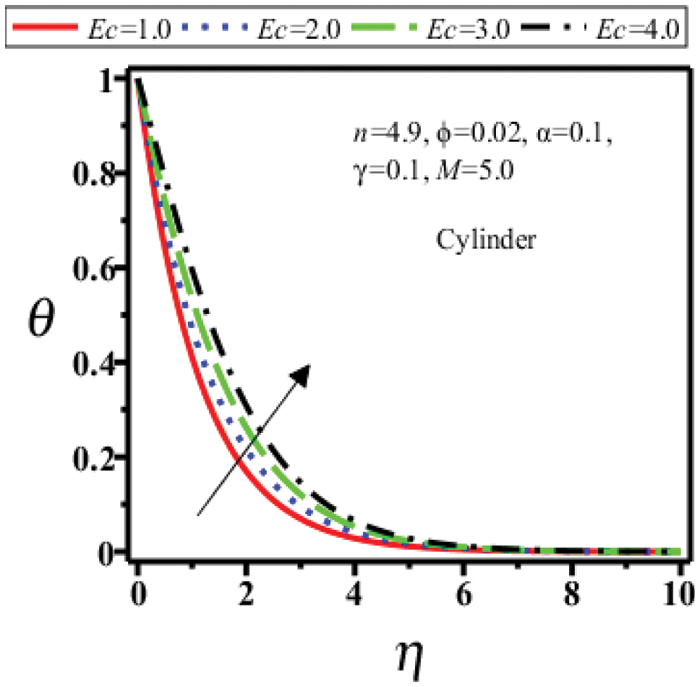
Figure 11: Temperature field of cylinder shape nanoparticles for Ec

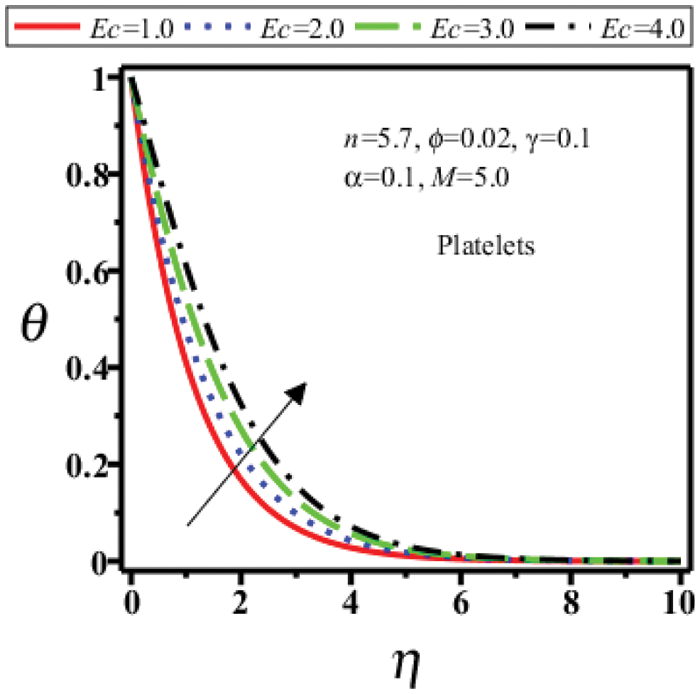
Figure 12: Temperature field of platelets shape nanoparticles for Ec

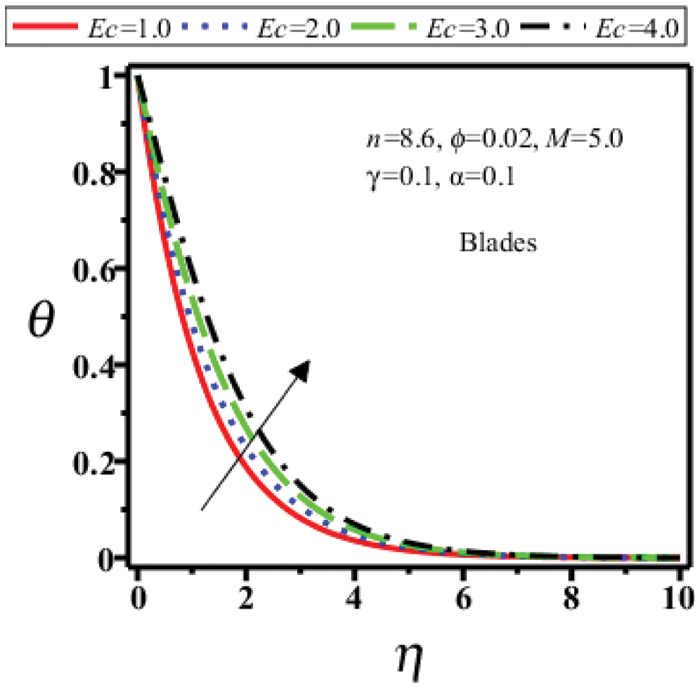
Figure 13: Temperature field of blades shape nanoparticles for Ec

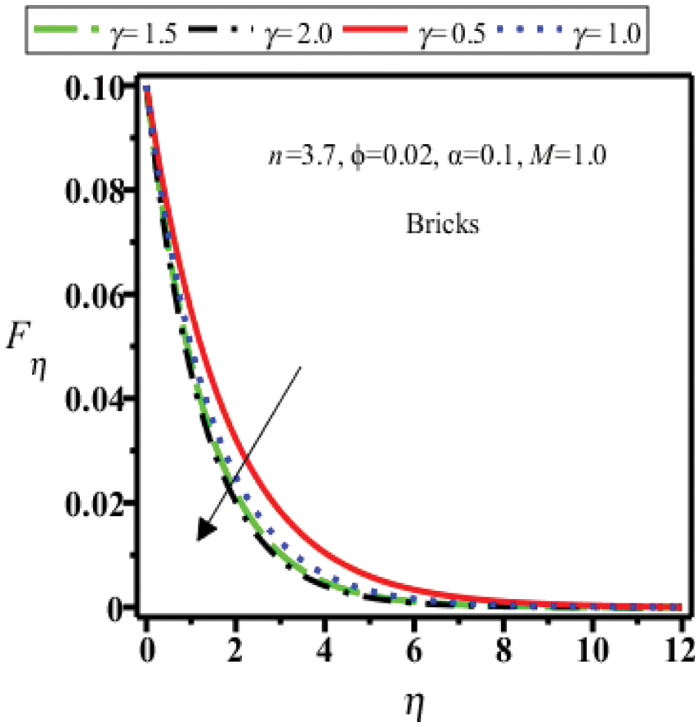
Figure 14: Velocity field of bricks shape nanoparticles for γ

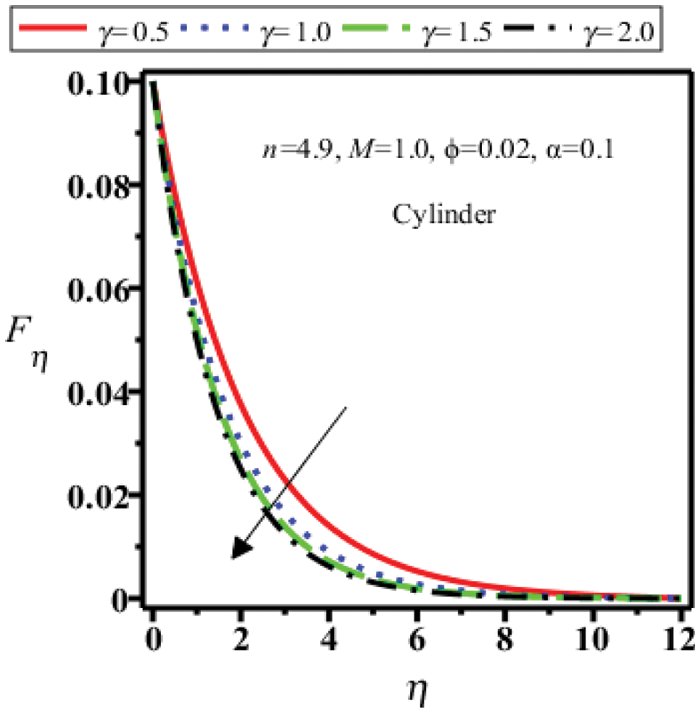
Figure 15: Velocity field of cylinder shape nanoparticles for γ

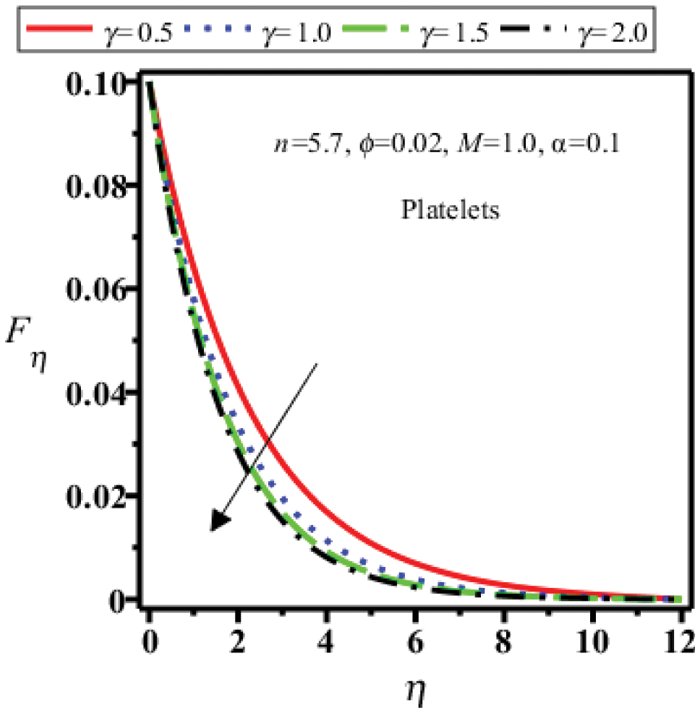
Figure 16: Velocity field of platelets shape nanoparticles for γ

Figure 17: Velocity field of blades shape nanoparticles for γ

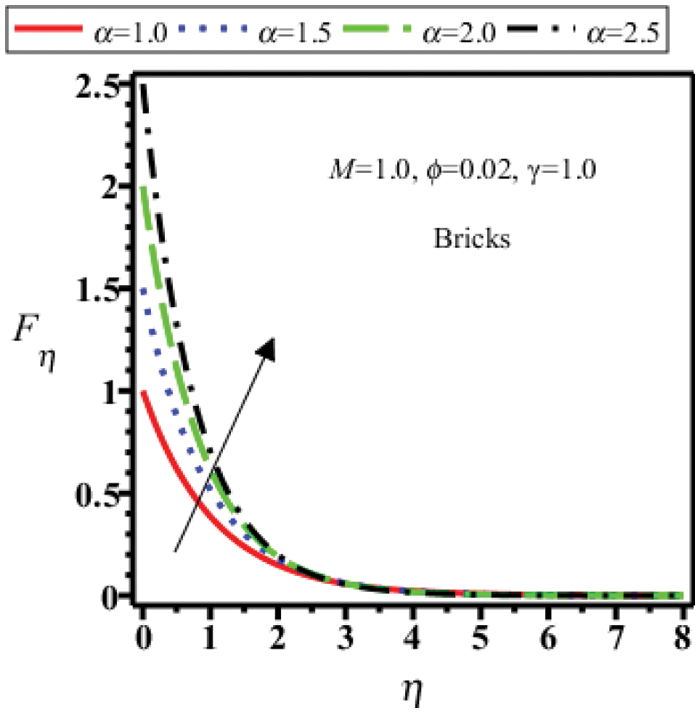
Figure 18: Velocity field of bricks shape nanoparticles for α

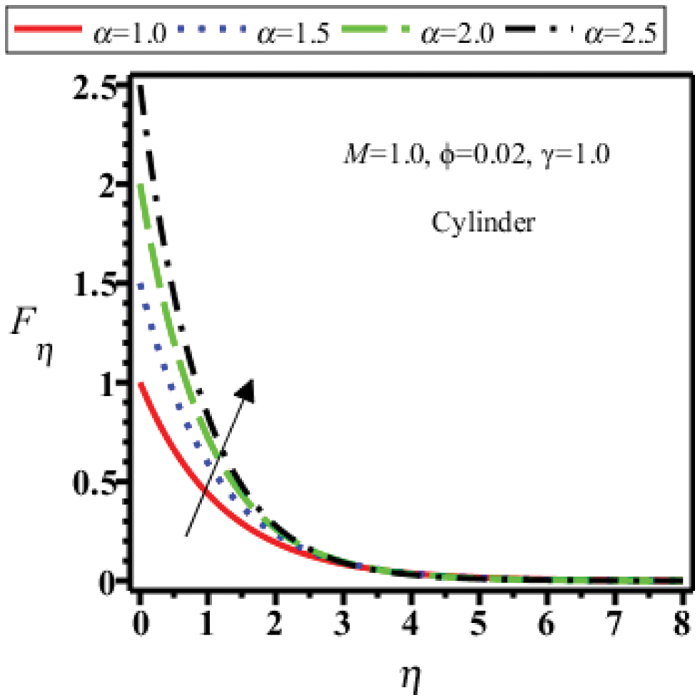
Figure 19: Velocity field of cylinder shape nanoparticles for α

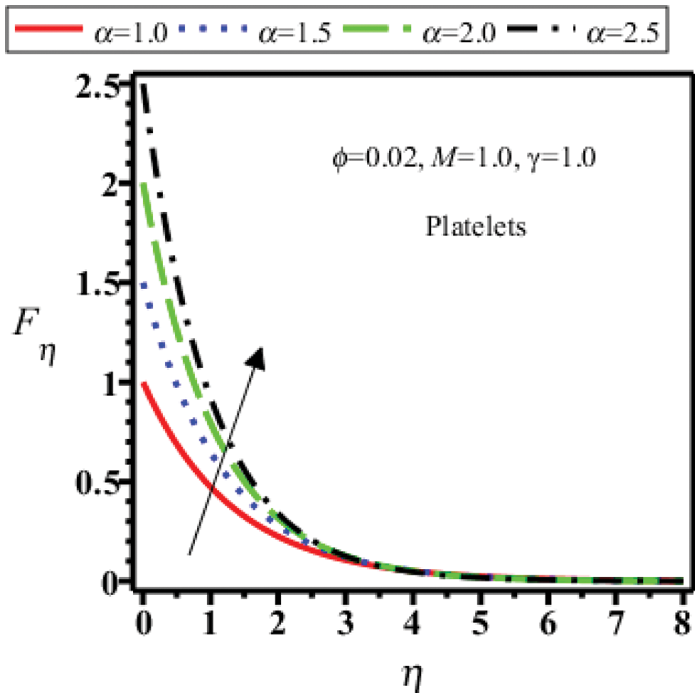
Figure 20: Velocity field of platelets shape nanoparticles for α

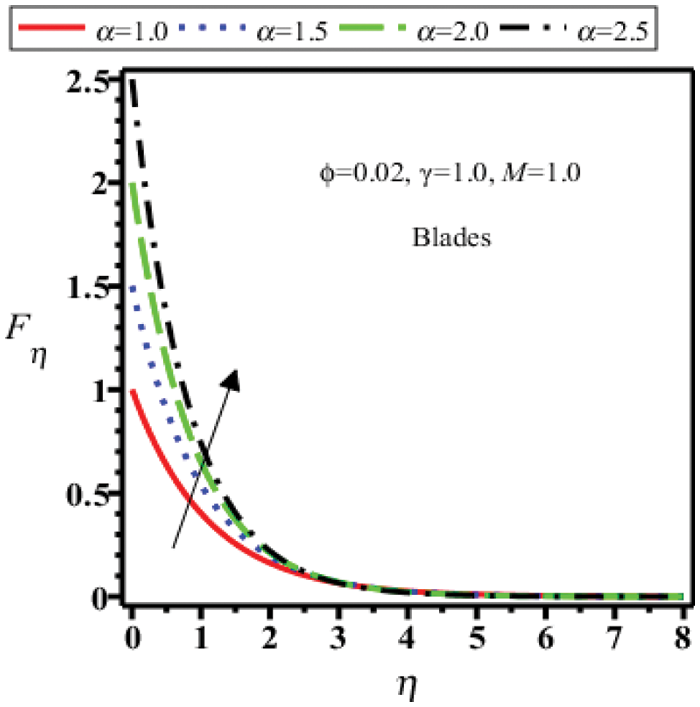
Figure 21: Velocity field of blades shape nanoparticles for α

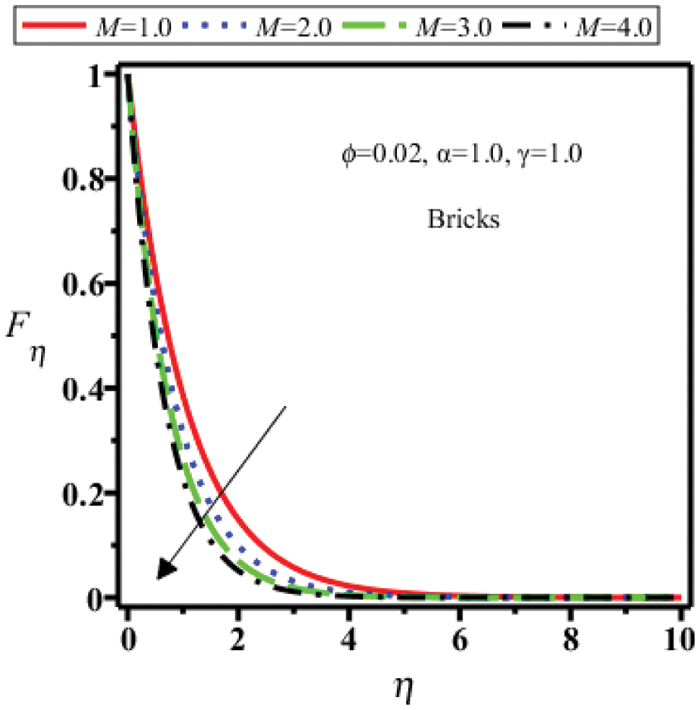
Figure 22: Velocity field of bricks shape nanoparticles for M

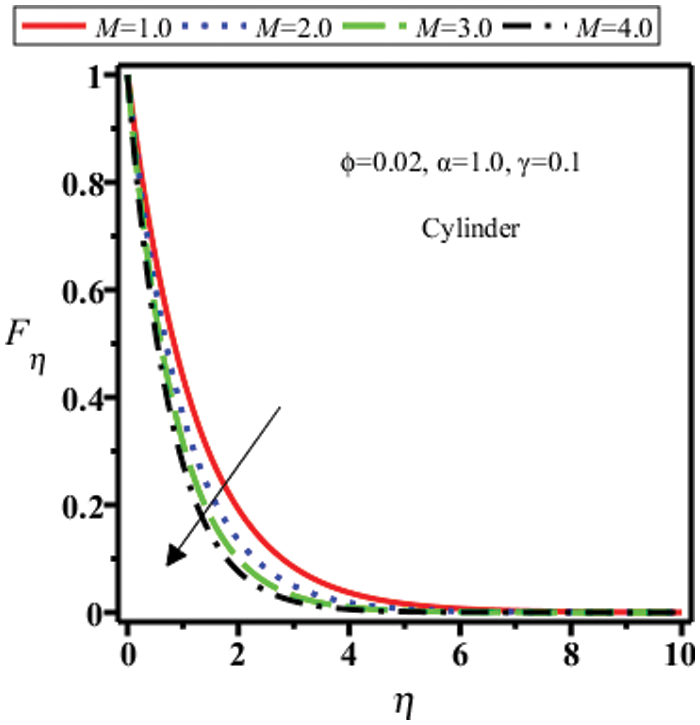
Figure 23: Velocity field of cylinder shape nanoparticles for M

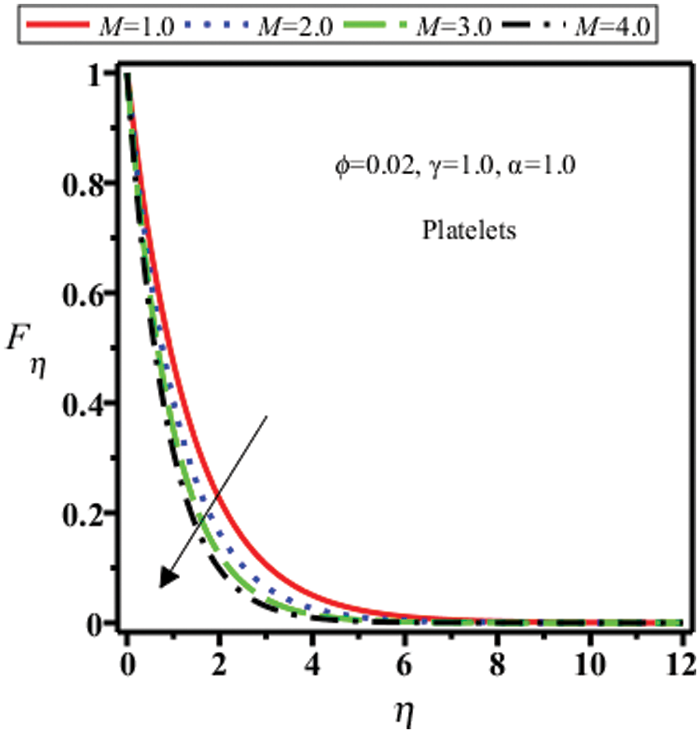
Figure 24: Velocity field of platelets shape nanoparticles for M

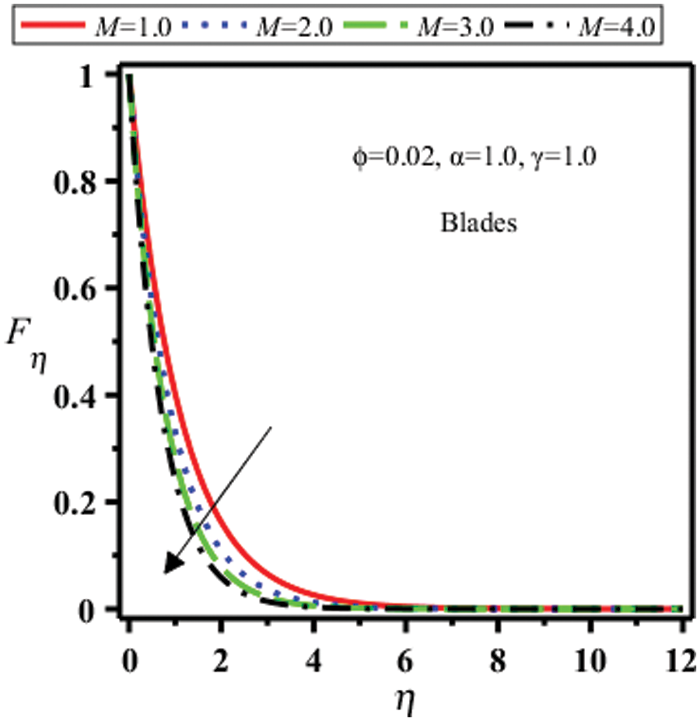
Figure 25: Velocity field of blades shape nanoparticles for M

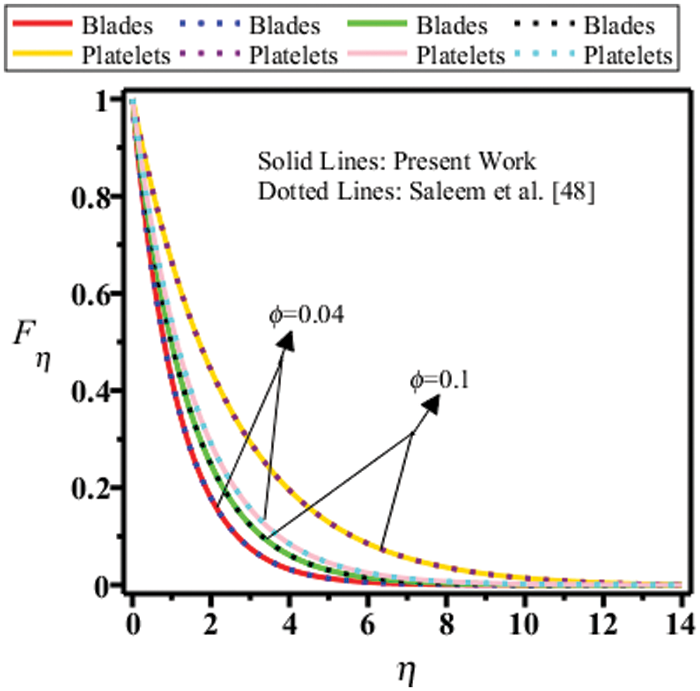
Figure 26: Comparison of velocity field of platelets shape and blade shape nanoparticles of present paper with Saleem et al. [48]

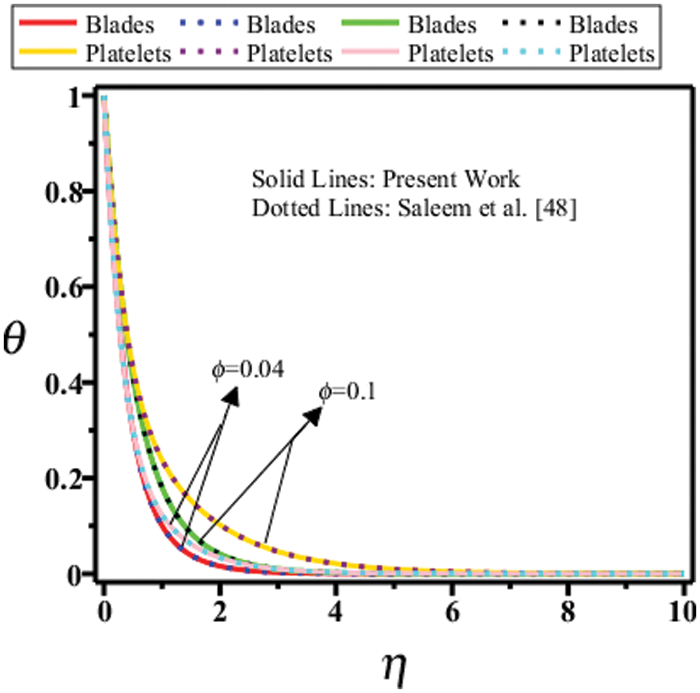
Figure 27: Comparison of temperature field of platelets shape and blade shape nanoparticles of present paper with Saleem et al. [48]

6  Conclusion

The present article examined nanoparticles shape effects on sodium alginate-based Cu–nanofluid over a stretching/shrinking sheet. The vital findings are

     i)  Velocity field decreases for all shapes of Cu nanoparticles for magnetic parameter and viscoplastic parameter.

    ii)  Velocity field increases for all shapes of Cu nanoparticles for stretching sheet parameter.

   iii)  Temperature field increases for different shape of Cu nanoparticles for viscoplastic parameter and Eckert number.

    iv)  Temperature field decreases for all shapes of Cu nanoparticles for Prandtl number.

    v)  The temperature of non–Newtonian sodium alginate-based Cu–nanofluids is higher than kerosene and engine-oil-based Cu–nanofluids.

Acknowledgement: The fourth author would like to thank University of Education, Lahore, Pakistan for the financial support.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Maxwell, J. C. (1873). Electricity and magnetism. Oxford, UK: Clarendon Press. [Google Scholar]

2. Wong, K. V., Castillo, M. J. (2010). Heat transfer mechanisms and clustering in nanofluids. Advances in Mechanical Engineering, 2, 1–9. https://doi.org/10.1155/2010/795478 [Google Scholar] [CrossRef]

3. Choi, S. U. S., Eastman, J. A. (1995). Enhancing thermal conductivity of fluids with nanoparticles. 1995 International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA. [Google Scholar]

4. Buongiorno, J. (2006). Convective transport in nanofluids. ASME Journal of Heat Transfer, 128, 240–250. https://doi.org/10.1115/1.2150834 [Google Scholar] [CrossRef]

5. Aly, E. H., Ebaid, A. (2016). Exact analysis for the effect of heat transfer on MHD and radiation marangoni boundary layer nanofluid flow past a surface embedded in a porous medium. Journal of Molecular Liquids, 215, 625–639. https://doi.org/10.1016/j.molliq.2015.12.108 [Google Scholar] [CrossRef]

6. Moshizi, S. A., Malvandi, A. (2016). Different modes of nanoparticle migration at mixed convection of Al2O3–water nanofluid inside a vertical microannulus in the presence of heat generation/absorption. Journal of Thermal Analysis and Calorimetry, 126, 1947–1962. https://doi.org/10.1007/s10973-016-5560-1 [Google Scholar] [CrossRef]

7. Sheikholeslami, M., Shehzad, S. A. (2017). Magnetohydrodynamic nanofluid convection in a porous enclosure considering heat flux boundary condition. International Journal of Heat and Mass Transfer, 106, 1261–1269. https://doi.org/10.1016/j.ijheatmasstransfer.2016.10.107 [Google Scholar] [CrossRef]

8. Sheikholeslami, M. (2018). Numerical investigation for CuO–H2O nanofluid flow in a porous channel with magnetic field using mesoscopic method. Journal of Molecular Liquids, 249, 739–746. https://doi.org/10.1016/j.molliq.2017.11.069 [Google Scholar] [CrossRef]

9. Kanimozhi, B., Muthtamilselvan, M., Al–Mdallal, Q. M., Abdalla, B. (2022). Coupled buoyancy and marangoni convection in a hybrid nanofluid–filled porous cylindrical annulus with a circular thin baffle. The European Physical Journal Special Topics, 231, 2645–2660. https://doi.org/10.1140/epjs/s11734-022-00594-7 [Google Scholar] [CrossRef]

10. Pandey, A. K., Kumar, M. (2017). Boundary layer flow and heat transfer analysis on Cu–water nanofluid flow over a stretching cylinder with slip. Alexandria Engineering Journal, 56(4), 671–677. https://doi.org/10.1016/j.aej.2017.01.017 [Google Scholar] [CrossRef]

11. Hussanan, A., Khan, I., Gorji, M. R., Khan, W. A. (2019). CNTs water–based nanofluid over a stretching sheet. BioNanoScience, 9, 21–29. https://doi.org/10.1007/s12668-018-0592-6 [Google Scholar] [CrossRef]

12. Ganesh, N. V., Al–Mdallal, Q. M., Fahel, S. A., Dadoa, S. (2019). Riga–plate flow of γ Al2O3–water/ethylene glycol with effective prandtl number impacts. Heliyon, 5, e01651. https://doi.org/10.1016/j.heliyon.2019.e01651 [Google Scholar] [PubMed] [CrossRef]

13. Pourhoseini, S. H., Aval, H. R., Naghizadeh, N. (2020). FHD and MHD effects of Fe3O4–water magnetic nanofluid on the enhancement of overall heat transfer coefficient of a heat exchanger. Physica Scripta, 95(4), 045705. https://doi.org/10.1088/1402-4896/ab6eb6 [Google Scholar] [CrossRef]

14. Kristiawan, B., Rifa’i, A. I., Enoki, K., Wijayanta, A. T., Miyazaki, T. (2020). Enhancing the thermal performance of TiO2/water nanofluids flowing in a helical microfin tube. Powder Technology, 376, 254–262. https://doi.org/10.1016/j.powtec.2020.08.020 [Google Scholar] [CrossRef]

15. Javadpour, R., Heris, S. Z., Mohammadfam, Y. (2021). Optimizing the effect of concentration and flow rate of water/MWCNTs nanofluid on the performance of a forced draft cross–flow cooling tower. Energy, 217, 119420. https://doi.org/10.1016/j.energy.2020.119420 [Google Scholar] [CrossRef]

16. Elias, M. M., Miqdad, M., Mahbubul, I. M., Saidur, R., Kamalisarvestani, M. et al. (2013). Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger. International Communications in Heat and Mass Transfer, 44, 93–99. https://doi.org/10.1016/j.icheatmasstransfer.2013.03.014 [Google Scholar] [CrossRef]

17. Jeong, J., Li, C., Kwon, Y., Lee, J., Kim, S. H. et al. (2013). Particle shape affect the viscosity and thermal conductivity of ZnO nanofluids. International Journal of Refrigeration, 36(8), 2233–2241. https://doi.org/10.1016/j.ijrefrig.2013.07.024 [Google Scholar] [CrossRef]

18. Vanaki, S. M., Mohammed, H. A., Abdollahi, A., Wahid, M. A. (2014). Effect of nanoparticle shapes on the heat transfer enhancement in a wavy channel with different phase shifts. Journal of Molecular Liquids, 196, 32–42. https://doi.org/10.1016/j.molliq.2014.03.001 [Google Scholar] [CrossRef]

19. Ellahi, R., Hassan, M., Zeeshan, A. (2015). Shape effects of nanosize particles in Cu–H2O nanofluid on entropy generation. International Journal of Heat and Mass Transfer, 81, 449–456. https://doi.org/10.1016/j.ijheatmasstransfer.2014.10.041 [Google Scholar] [CrossRef]

20. Monfared, M., Shahsavar, A., Bahrebar, M. R. (2019). Second law analysis of turbulent convection flow of boehmite alumina nanofluid inside a double–pipe heat exchanger considering various shapes for nanoparticle. Journal of Thermal Analysis and Calorimetry, 135, 1521–1532. https://doi.org/10.1007/s10973-018-7708-7 [Google Scholar] [CrossRef]

21. Dogonchi, A. S., Waqas, M., Ganji, D. D. (2019). Shape effects of copper–oxide (CuO) nanoparticles to determine the heat transfer filled in a partially heated rhombus enclosure: CVFEM approach. International Communications in Heat and Mass Transfer, 107, 14–23. https://doi.org/10.1016/j.icheatmasstransfer.2019.05.014 [Google Scholar] [CrossRef]

22. Shakiba, A., Rahimi, A. B. (2019). Nanofluid flow and MHD mixed convection inside a vertical annulus with moving walls and transpiration considering the effect of brownian motion and shape factor. Journal of Thermal Analysis and Calorimetry, 138(1), 501–515. https://doi.org/10.1007/s10973-019-08201-z [Google Scholar] [CrossRef]

23. Sheikholeslami, M., Shamlooei, M. (2017). Magnetic source influence on nanofluid flow in porous medium considering shape factor effect. Physics Letters A, 381(36), 3071–3078. https://doi.org/10.1016/j.physleta.2017.07.028 [Google Scholar] [CrossRef]

24. Hosseinzadeh, K., Roghani, S., Asadi, A., Mogharrebi, A., Ganji, D. D. (2021). Investigation of micropolar hybrid ferrofluid flow over a vertical plate by considering various base fluid and nanoparticle shape factor. International Journal of Numerical Methods for Heat & Fluid Flow, 31(1), 402–417. https://doi.org/10.1108/HFF-02-2020-0095 [Google Scholar] [CrossRef]

25. Chu, Y. M., Nisar, K. S., Khan, U., Daei Kasmaei, H., Malaver, M. et al. (2020). Mixed convection in MHD water–based molybdenum disulfide–graphene oxide hybrid nanofluid through an upright cylinder with shape factor. Water, 12(6), 1723. https://doi.org/10.3390/w12061723 [Google Scholar] [CrossRef]

26. Khashi’ie, N. S., Arifin, N. M., Sheremet, M., Pop, I. (2021). Shape factor effect of radiative Cu–Al2O3/H2O hybrid nanofluid flow towards an EMHD plate. Case Studies in Thermal Engineering, 26, 101199. https://doi.org/10.1016/j.csite.2021.101199 [Google Scholar] [CrossRef]

27. Anwar, T., Kumam, P., Thounthong, P. (2022). A comparative fractional study to evaluate thermal performance of NaAlg–MoS2–Co hybrid nanofluid subject to shape factor and dual ramped conditions. Alexandria Engineering Journal, 61(3), 2166–2187. https://doi.org/10.1016/j.aej.2021.06.085 [Google Scholar] [CrossRef]

28. Shahsavar, A., Farhadi, P., Yıldız, C., Moradi, M., Arıcı, M. (2022). Evaluation of entropy generation characteristics of boehmite–alumina nanofluid with different shapes of nanoparticles in a helical heat sink. International Journal of Mechanical Sciences, 225, 107338. https://doi.org/10.1016/j.ijmecsci.2022.107338 [Google Scholar] [CrossRef]

29. Ganesh, N. V., Javed, S., Al-Mdallal, Q. M., Kalaivanan, R., Chamkha, A. J. (2020). Numerical study of heat generating γ Al2O3–H2O nanofluid inside a square cavity with multiple obstacles of different shapes. Heliyon, 6(12), e05752. https://doi.org/10.1016/j.heliyon.2020.e05752 [Google Scholar] [PubMed] [CrossRef]

30. Cao, W., Animasaun, I. L., Yook, S. J., Oladipupo, V. A., Ji, X. (2022). Simulation of the dynamics of colloidal mixture of water with various nanoparticles at different levels of partial slip: Ternary–hybrid nanofluid. International Communications in Heat and Mass Transfer, 135, 106069. https://doi.org/10.1016/j.icheatmasstransfer.2022.106069 [Google Scholar] [CrossRef]

31. Xiu, W., Animasaun, I. L., Al–Mdallal, Q. M., Alzahrani, A. K., Muhammad, T. (2022). Dynamics of ternary–hybrid nanofluids due to dual stretching on wedge surfaces when volume of nanoparticles is small and large: Forced convection of water at different temperatures. International Communications in Heat and Mass Transfer, 137, 106241. https://doi.org/10.1016/j.icheatmasstransfer.2022.106241 [Google Scholar] [CrossRef]

32. Saleem, S., Animasaun, I. L., Yook, S. J., Al–Mdallal, Q. M., Shah, N. A. et al. (2022). Insight into the motion of water conveying three kinds of nanoparticles shapes on a horizontal surface: Significance of thermo–migration and brownian motion. Surfaces and Interfaces, 30, 101854. https://doi.org/10.1016/j.surfin.2022.101854 [Google Scholar] [CrossRef]

33. Yang, L., Du, K. (2020). A comprehensive review on the natural, forced, and mixed convection of non–Newtonian fluids (nanofluids) inside different cavities. Journal of Thermal Analysis and Calorimetry, 140, 2033–2054. https://doi.org/10.1007/s10973-019-08987-y [Google Scholar] [CrossRef]

34. Hussanan, A., Aman, S., Ismail, Z., Salleh, M. Z., Widodo, B. (2018). Unsteady natural convection of sodium alginate viscoplastic casson based nanofluid flow over a vertical plate with leading edge accretion/ablation. Journal of Advanced Research in Fluid Mechanics and Thermal Sciences, 45(1), 92–98. [Google Scholar]

35. Memon, I. Q., Abro, K. A., Solangi, M. A., Shaikh, A. A. (2021). Functional shape effects of nanoparticles on nanofluid suspended in ethylene glycol through mittage–leffler approach. Physica Scripta, 96, 025005. https://doi.org/10.1088/1402-4896/abd1b3 [Google Scholar] [CrossRef]

36. Hussanan, A., Qasim, M., Chen, Z. (2020). Heat transfer enhancement in sodium alginate based magnetic and non–magnetic nanoparticles mixture hybrid nanofluid. Physica A, 550, 123957. https://doi.org/10.1016/j.physa.2019.123957 [Google Scholar] [CrossRef]

37. Kalaivanan, R., Ganesh, N. V., Al-Mdallal, Q. M. (2020). An investigation on arrhenius activation energy of second grade nanofluid flow with active and passive control of nanomaterials. Case Studies in Thermal Engineering, 22, 100774. https://doi.org/10.1016/j.csite.2020.100774 [Google Scholar] [CrossRef]

38. Kalaivanan, R., Ganesh, N. V., Al-Mdallal, Q. M. (2021). Buoyancy driven flow of a second-grade nanofluid flow taking into account the arrhenius activation energy and elastic deformation: Models and numerical results. Fluid Dynamics and Materials Processing, 17(2), 319–32. https://doi.org/10.32604/fdmp.2021.012789 [Google Scholar] [CrossRef]

39. Hammachukiattikul, P., Govindaraju, M., Sohail, M., Vadivel, R., Gunasekaran, N. et al. (2022). Analytical study on sodium alginate based hybrid nanofluid flow through a shrinking/stretching sheet with radiation, heat source and inclined lorentz force effects. Fractal and Fractional, 6(2), 68. https://doi.org/10.3390/fractalfract6020068 [Google Scholar] [CrossRef]

40. Ganesh, N. V., Al-Mdallal, Q. M., Hirankumar, G., Kalaivanan, R., Chamkha, A. J. (2022). Buoyancy-driven convection of MWCNT–casson nanofluid in a wavy enclosure with a circular barrier and parallel hot/cold fins. Alexandria Engineering Journal, 61(4), 3249–3264. https://doi.org/10.1016/j.aej.2021.08.055 [Google Scholar] [CrossRef]

41. Ganesh, N. V., Al–Mdallal, Q. M., Öztop, H. F., Kalaivanan, R. (2022). Analysis of natural convection for a casson–based multiwall carbon nanotube nanofluid in a partially heated wavy enclosure with a circular obstacle in the presence of thermal radiation. Journal of Advanced Research, 39, 167–185. https://doi.org/10.1016/j.jare.2021.10.006 [Google Scholar] [PubMed] [CrossRef]

42. Afridi, M. I., Qasim, M., Shafie, S. (2017). Entropy generation in hydromagnetic boundary flow under the effects of frictional and joule heating: Exact solutions. The European Physical Journal Plus, 132, 404. https://doi.org/10.1140/epjp/i2017-11704-5 [Google Scholar] [CrossRef]

43. Timofeeva, E. V., Routbort, J. L., Singh, D. (2009). Particle shape effects on thermophysical properties of alumina nanofluids. Journal of Applied Physics, 106(1), 014304. https://doi.org/10.1063/1.3155999 [Google Scholar] [CrossRef]

44. Pak, B. C., Cho, Y. (1998). Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particle. Experimental Heat Transfer, 11, 151–170. https://doi.org/10.1080/08916159808946559 [Google Scholar] [CrossRef]

45. Sheikholeslami, M. (2017). Magnetohydrodynamic nanofluid forced convection in a porous lid driven cubic cavity using lattice boltzmann method. Journal of Molecular Liquids, 223, 555–565. https://doi.org/10.1016/j.molliq.2017.02.020 [Google Scholar] [CrossRef]

46. Hamilton, R., Crosser, O. (1962). Thermal conductivity of heterogeneous two–component systems. Industrial & Engineering Chemistry Fundamentals, 1(3), 187–191. https://doi.org/10.1021/i160003a005 [Google Scholar] [CrossRef]

47. Chakrabarti, A., Gupta, A. S. (1979). Hydromagnetic flow and heat transfer over a stretching sheet. Quarterly of Applied Mathematics, 37, 73–78. https://doi.org/10.1090/qam/99636 [Google Scholar] [CrossRef]

48. Saleem, S., Qasim, M., Alderremy, A., Noreen, S. (2020). Heat transfer enhancement using different shapes of Cu nanoparticles in the flow of water based nanofluid. Physica Scripta, 95(5), 055209. https://doi.org/10.1088/1402-4896/ab4ffd [Google Scholar] [CrossRef]