Wave Reflection by Rectangular Breakwaters for Coastal Protection

1  Introduction

One of the problems in the construction of coastal structures is their protection against wave action which may be partially reflected by changes in the seabed due to changes in depth. To reduce the impact of wave on coastal installations or natural shores, submerged obstacles are used [1–4], which act as wave reflectors and represent one of the most effective solutions to the problem of protecting the marine and coastal environment.

In order to comprehend the mechanisms of wave attenuation and dissipation better, several analytical, numerical, and experimental research on the hydrodynamic performance of various submerged structures have been carried out. Indeed, in 1993, Driscoll et al. [5] studied numerically and experimentally the harmonic evolution of linear monochromatic waves in a wave flume when propagating over a submerged impermeable rectangular obstacle. Davidson et al. [6] in 1996 proposed a novel non-dimensional parameter for analyzing wave reflection from rubble mound breakwaters, this parameter offers valuable insights into the wave interaction with such structures, aiding the understanding and design of breakwater systems. Later in 2001, Stamos et al. [7] carried out an experimental investigation to examine how rigid and flexible rectangular breakwater models, secured to the flume bottom at different immersion depths, impact the transmission, reflection, and energy dissipation of regular waves. They demonstrated that, generally speaking, the reflection due to the rigid model exceeds that of the flexible one. In 2008, Christou et al. [8] conducted a numerical analysis employing the Boundary Element Method (BEM) to accurately simulate the interaction between regular nonlinear waves with a submerged rectangular breakwater. An analytical second-order solution approach to effectively address the problem of wave propagation over a submerged rectangular structure was proposed by Lee et al. [9] in 2014. Recent studies in this field include those of Patil et al. [10], who used the Multi-Domain Boundary Element Method (MDBEM) to conduct a numerical analysis of the hydrodynamic performance of diverse types and forms submerged breakwaters. In addition, Kar et al. [11] in 2019 carried out a numerical study that relied on the boundary element method, this study aimed to investigate gravity wave transformation generated by a floating dock of finite size when it encountered sea bottom variations like trenches, breakwaters, and an appropriate combination of trenches and breakwaters. In 2020, Chanda et al. [12] investigated wave behavior and interaction with dynamic bottom topography, contributing to the understanding of wave dynamics in multi-layered fluid environments. The same authors [13] examined the impact of a porous seabed on wave diffusion, focusing on the interaction between waves and two vertically immersed thin porous plates. As well as Mahmoudof et al. [14] in 2021, they presented an experimental investigation of the reflection, transmission and dissipation of irregular waves on three forms of impermeable submerged breakwaters (rectangular breakwater, trapezoidal breakwater and U-form breakwater). In order to advance applied ocean research, the same authors [15] did a field experiment on wave reflection from the permeable rubble mound breakwater at Chabahar Port, by examining wave behavior in a practical port environment. In the same year, Fu et al. [16] investigated the wave dissipation performance of a submerged plate breakwater using the High-Order Finite-Difference Method (HOFDM). In 2022, Nguyen et al. [17] performed the experimental tests on three classes of breakwaters (hollow triangle, pile-rock, and semi-circular) in order to calculate the wave transmission, reflection, and dissipation coefficients.

In the ocean environment, the wave is usually accompanied by different currents that can be generated by winds, tides, river flows, etc. Therefore, the current’s presence must be considered when studying the behavior of the wave while it is interacting with submerged obstacles. This broad topic has been the subject of much research in maritime hydrodynamics, ocean engineering and other disciplines. Furthermore, due to the fact that the wave always accompanied by current, several numerical methods had been used to describe this interaction. In 2003, Ryu et al. [18] performed a numerical study based on the Boundary Element Method (BEM) of the nonlinear wave-uniform current interaction. Zhang et al. [19] in 2014 established a numerical model to study wave-current interaction. This model was formulated based on Reynolds-Averaged Navier-Stokes (RANS) equations with the k-ε turbulence closure scheme. Chang et al. [20] in 2016 simulated a combined wave-current flow in a truncated domain, used the Generation and Absorption Boundary Condition (GABC) of wave and current simultaneously. In 2016, Kim et al. [21] used the commercial software FLUENT to numerically explore the wave force on offshore substructures in the presence of a uniform current, they relied on the continuity and Navier-Stokes equations. Fan et al. [22] in 2018 applied the Generalized Finite Difference Method (GFDM) in combination with the Runge-Kutta method to study the wave propagation under the influence of current in inclined and horizontal bottom flumes. In 2019, Gholamipoor et al. [23] proposed a Meshless Method for simulating completely time-domain nonlinear wave-wave and wave-current interactions. To analyze the nonlinear wave resonance generated by the oscillations of two cylinders in a uniform current, a numerical study by the High-Order Finite Element Method (HOFEM) with an eight-node element was proposed by Huang et al. [24] in 2022.

In related to the same topic, many investigators have examined the influence of the current on the interaction between waves and submerged obstacles [25–30]. In 2015, Liang et al. [27] presented a numerical investigation employing a non-hydrostatic wave model to analyze wave transmission over dual submerged trapezoidal breakwaters in present of the current. Bai et al. [28] in 2017 studied the forces applied to a horizontal cylinder when a wave passes in the presence of a sheared current. The propagation of a nonlinear wave on a rectangular breakwater immersed on a flat seabed in presence of the current was investigated both numerically and experimentally by Chen et al. [29] in 2017. Naasse et al. [30] in 2019 analytically studied the wave-plate-current interaction taking on consideration the evanescent modes model, they examined the complex dynamics of this interaction by focusing on the impact of geometrical parameters. In 2021, Akarni et al. [31] numerically investigated the influence of the geometry of a totally immersed horizontal plate on the wave reflection in the presence of current.

In the context of the same subject matter, with a focus on enhancing the efficiency of the breakwater attenuator amid various occurring phenomena, this study was conducted to determine optimal breakwater dimensions capable of offering superior protection against the influences of waves and currents. This was achieved through the utilization of a computational framework. The framework entails a numerical representation of two closely spaced rectangular breakwaters affixed to the bottom of a wave flume, accounting for wave propagation when a uniform current is present. The model is founded upon the Boundary Element Method (BEM), and comprehensive numerical experiments are conducted to systematically explore the impact of both the current velocity and geometric parameters on the resulting reflection coefficient. A confrontation between our results and those of the experiment is presented to validate the proposed approach.

2  Problem Position

We assume a monochromatic incident wave of low amplitude a period T and wavelength λ propagating with the existence of a uniform horizontal velocity current Uc in a flat-bottom flume measuring length L and depth H .

A breakwater system fixed on the bottom of a wave flume consisting of two rectangular obstacles spaced at a distance d . The length and height of the left obstacle are l1 and h1 , respectively, and those of the right one are l2  and h2 . The whole system is related to a Cartesian coordinate system ( O, x, z ) such that the axis ( Oz ) is oriented upwards, the axis ( Ox ) is coincident with the free surface in the rest position (see Fig. 1).

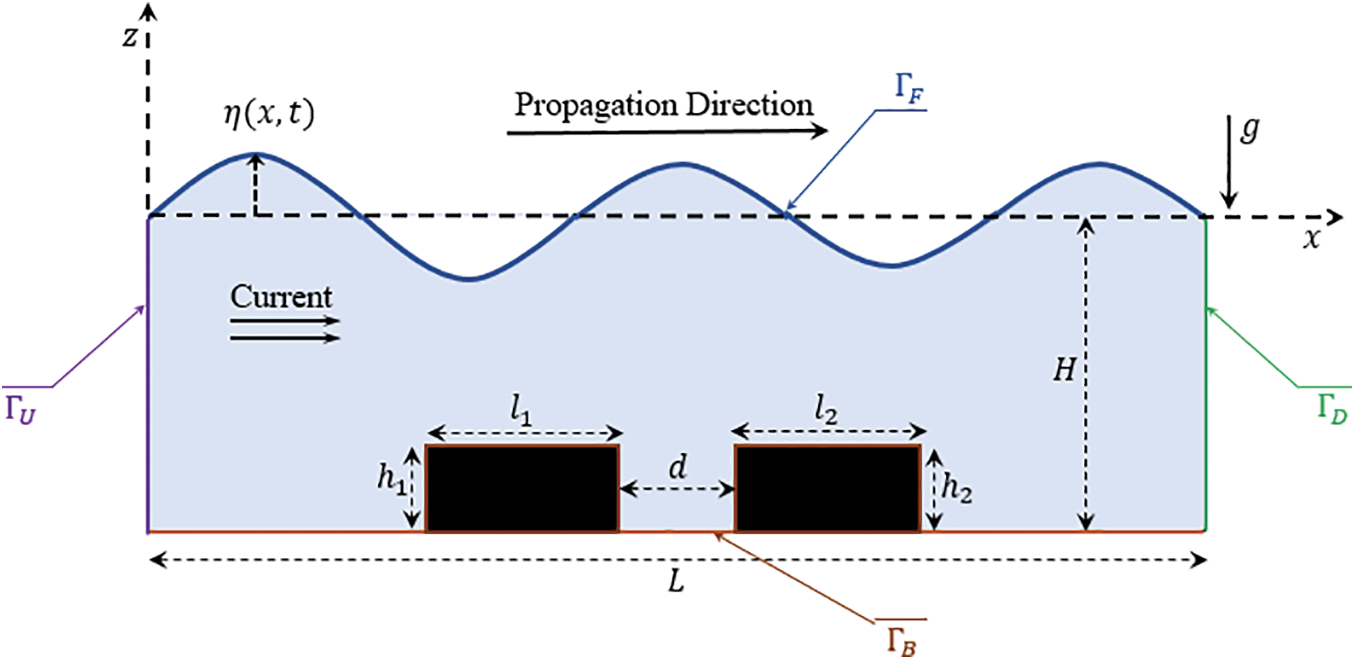
Figure 1: Descriptive schema of the study domain

The linear wave theory adopted in this work requires the following hypothesis, the flow is two-dimensional, periodic and irrotational. The surface tension is neglected and the fluid is assumed to be homogeneous, inviscid, heavy and incompressible. Furthermore this theory is based on the determination of velocity potential ϕ(x,z,t) and free surface elevation η(x,t) , which are believed to be complex and harmonic in terms of their time dependence.

The velocity potential ϕ(x,z,t) is a superposition of two potential functions ϕw(x,z,t) and ϕc(x) , respectively representing the potential generated by the wave and that generated by the current, where x and z denote spatial variables and t denotes time [18,30–32]:

ϕ(x,z,t)=ϕw(x,z,t)+ϕc(x) (1)

With:

{ϕc=Uc xϕw(x,z,t)=φw(x,z)eiωt  (2)

where g is the gravitational acceleration, i is the complex number and ω=2πT is the pulsation of the incident wave.

The velocity potential associated with the linear wave must verify the following equations [18]:

In the study domain D :

Δϕw=0 (3)

The impermeability condition at the bottom:

(∂ϕw∂z)z=−H=0          (4)

The kinematic condition at the free surface:

∂η∂t+Uc∂η∂x−(∂ϕw∂z)z=0=0 (5)

The dynamic condition at the free surface:

∂ϕw∂t+gη+12(Uc2+2Uc∂ϕw∂x)=0 (6)

3  Numerical Formulation

The basic idea of the integral formulation of the Boundary Element Method (BEM) is to transpose the internal problem to the boundary using Green’s identity. The application of Green’s second identity allows the wave velocity potential φw to be expressed in the following integral form:

c(p) φw(p)=∫Γ⁡[G(q,p)∂φw(q)∂n−φw(q)∂G(q,p)∂n]ds (7)

where p is the source point of coordinates (x,z) , q is the current point of the study domain of coordinates (x′,z′) and n is the exterior normal on the domain boundary Γ . The coefficient of the free term c(p) is determined by:

c(p)={ 0             p≡(x,z)∉DUΓ 12              p≡(x,z)∈Γ 1               p≡(x,z)∈D (8)

The Laplace equation in two dimensions is represented by the Green’s function G and its normal derivative ∂G∂n , which are defined by:

G=−12πln(r) and  ∂G∂n=−12πr∂r∂n (9)

where r=(x−x′)2+(z−z′)2 is the distance between p and q .

The domain boundary Γ is subdivided into N segments with N=∑i=14⁡Ni . The bottom boundary ΓB is subdivided into N1 elements, the downstream boundary ΓD into N2 elements, the free surface boundary ΓF into N3 elements and the upstream boundary ΓU into N4 elements (see Fig. 2).

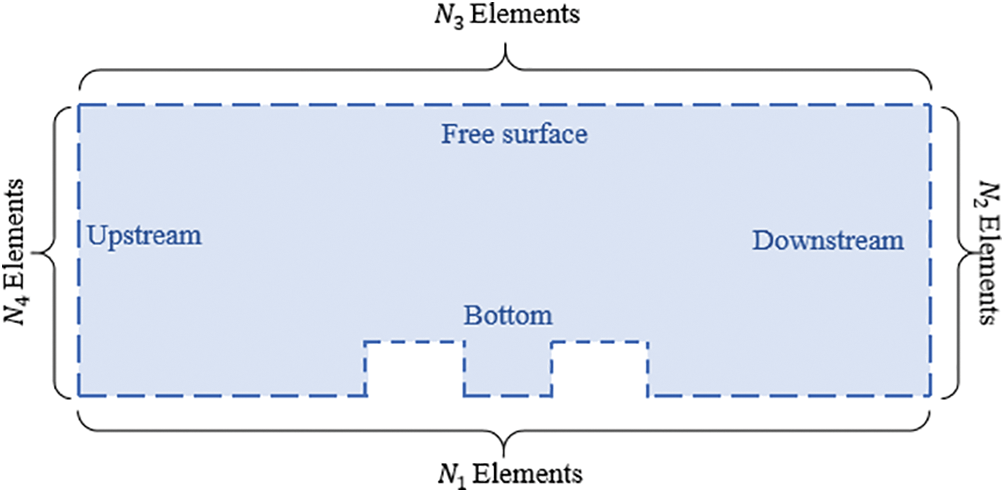
Figure 2: Domain discretization

Each segment has a length of Δl and a singularity is implied on each one for obtaining numerically the wave velocity potential φw and its normal derivative ∂φw∂n  on the whole of this boundary Γ . Then the integral on each segment can be given by applying a singularity located in the center of each segment, the calculation of the wave velocity potential φw on the domain boundary comes down to solving a matrix system.

ciφwi=∑j=1N⁡Eij∂φwj∂nj−Hijφwj (10)

The influence matrices H and E have the following explicit form:

•   For i≠j : Hij=∫(Δlj)∂G∂ndl and  Eij=∫(Δlj)⁡Gdl

•   For  i=j: Hij=2π  and  Eij=2(1−ln(Δlj))Δlj

As a result, the new matrix form of Eq. (10) is as follows:

{φw}=[A]{∂φw∂n} (11)

In this system the number of equations is inferior to the number of unknowns ( N equations with unknowns). The N supplementary equations are given by the following boundary conditions:

•   Boundary condition on ΓB

The bottom of the flume and the solid surfaces of the structures fixed on the bottom (i.e., the boundary ΓB are impermeable and are specified as solid walls (no fluid can penetrate them). The gradient of the unsteady wave velocity potential φw in the normal direction ( n ) of the boundary ΓB is null [18,31–32]:

∂φw∂n=0        on  ΓB  (12)

•   Boundary condition on ΓF

In the absence of current at the free surface, we can write [20]:

g∂φw∂z=−c02∂2φw∂x2 (13)

where c0=λT is the celerity of the incident wave when no current is present.

Using Eq. (13), the free-surface condition in the presence of uniform current can be written [31]:

∂φw∂n=∂φw∂z=ω c02(2Uck−ω)g(Uc2−c02)φw    on  ΓF (14)

•   Boundary condition on ΓD

Downstream, the wave is assumed to propagate without reflection, we can write:

φw=A Te−i k+xcosh(k+(z+H)) (15)

So we can deduce the downstream condition [31]:

  ∂φw∂n=∂φw∂x=−ik+φw         on  ΓD (16)

•   Boundary condition on ΓU

Upstream, when the wave encounters a change in depth, it is partly reflected and partly transmitted. We will have on the upstream boundary ΓU a superposition of two waves incident and reflected upstream:

φw=φwi+φwr (17)

Knowing that the potential and its normal derivative upstream are continuous, we can write:

φw=f(z)+R′f′(z)  (18)

∂φw∂n=−∂φw∂x=i[ k+f(z)− k−R′f′(z)] (19)

With f(z) and f′(z) are functions linked to the wave features as follows :

{ f(z)=A cosh(k+(z+H)) f′(z)=A cosh(k−(z+H)) (20)

The upstream condition can be rewritten as [31]:

∂φw∂n=i( k−+ k+)f(z)− ik−φw      on  ΓU (21)

With:

{A= ai g(ω−k+Uc)cosh(k+H)R′= ar g(ω+k−Uc)cosh(k−H)1AT= at g(ω−k+Uc)cosh(k+H)1A (22)

where ai , ar and at are respectively the amplitude of the incident wave, the reflected wave and the transmitted wave at the free surface in the presence of the current. Meanwhile, k+ and k− are the wavenumbers that represent the solutions of the following dispersion equations:

(ω±Uck∓)2=gk∓tanh(k∓H) (23)

Finally, the boundary conditions can be expressed as follows:

{∂φw∂n}=[B]{φw}+{SN} (24)

By injecting Eq. (24) into Eq. (11), the determination of the wave velocity potential φw is therefore reduced to solving the following system:

[C]{φh}={SN} (25)

The numerical solution of the Eq. (25) can be done in a classical way by the Gauss method. When applying the numerical method, the correlation Δlλ<19 must be respected, this correlation is also referred to by other authors [31,33,34].

•   Reflection coefficient R

The reflection coefficient R is defined as follows:

R=arai=(ω+k−Uc)cosh(k−H)(ω−k+Uc)cosh(k+H) R′ (26)

Since the reflection coefficient R is determined locally, we perform an arithmetic mean to express it globally.

4  Results and Discussions

4.1 Validation (Without Current Uc=0 )

In this part, the proposed numerical approach will be validated by a comparative study of its results with the experimental ones. In order to do that, we are interested on one hand in the experiment of Driscoll et al. [5] concerning a rectangular breakwater of length l=0.79 m and height h=0.38 m with a water depth H=0.5 m . On the other hand, to the experiment of Mordane et al. [35] based on the study of two breakwaters of the same height h=0.5 H and the same length l=2.27 h , spaced by a distance d=l with a water depth H=2.5 m .

The comparison concerns the variation of the reflection coefficient R with the dimensionless wavenumber kH in the first case (Fig. 3) and with the dimensionless wavenumber kh in the other case (Fig. 4). The comparative studies show a good agreement between our numerical results obtained by the BEM and the experimental ones.

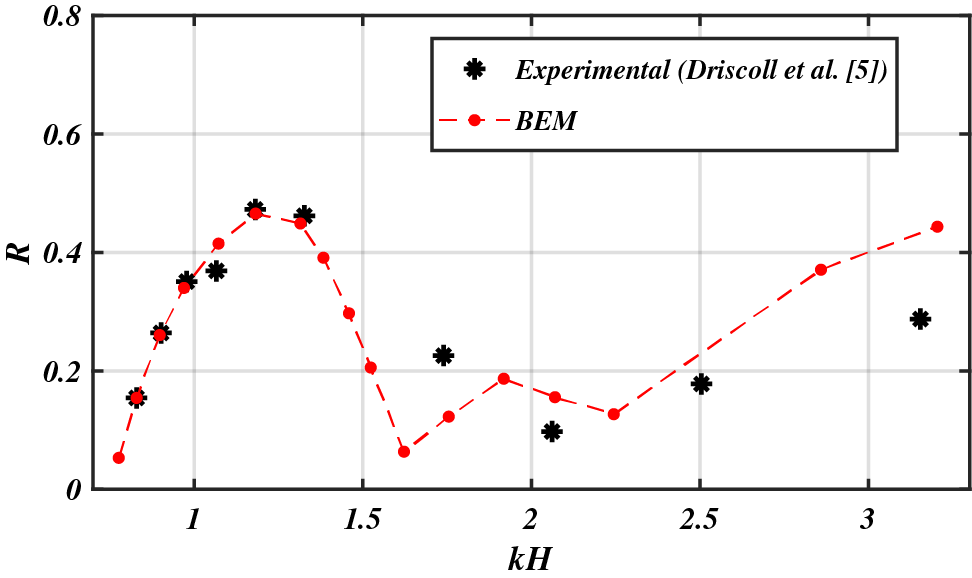
Figure 3: Comparative study of the variation of R vs. kH for rectangular breakwater

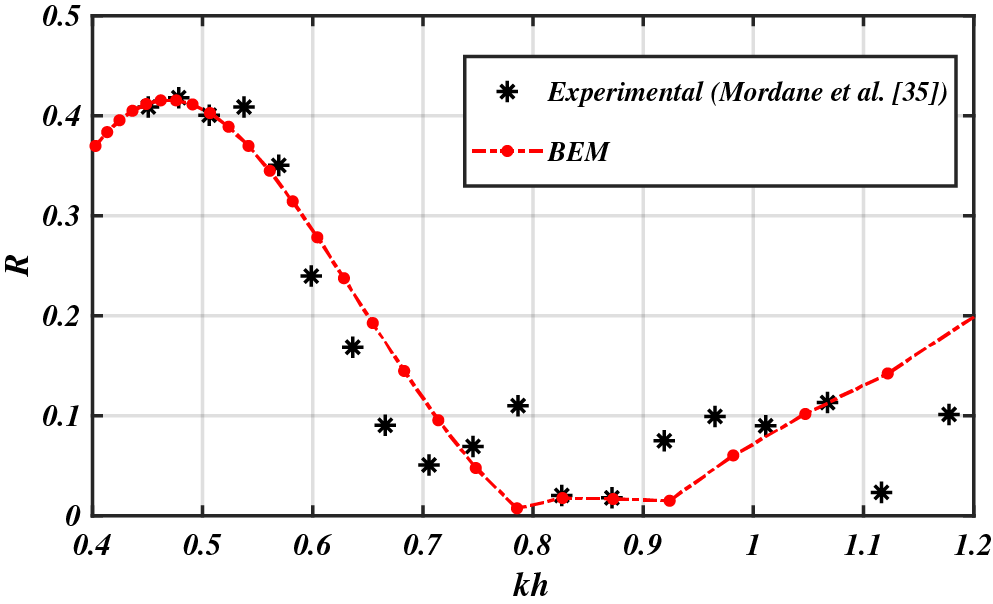
Figure 4: Comparative study of the variation of R vs. kh for two rectangular breakwaters

4.2 Wave-Rectangular Breakwaters-Current Interaction

4.2.1 Comparison between a Single and a Double Rectangular Breakwater

In this part, a comparison between a rectangular breakwater and an identical double rectangular one is presented in order to show the importance of using this type of geometry. The configurations are taking at the same height h=0.5 H with a length of (l=l1+l2+d) for the single breakwater and (l1=l2=1.5 H) for the double one spaced at a distance d=0.5 H (see Fig. 5). The variations of the reflection coefficient R are presented in Fig. 6 as a function of kH with a current velocity Uc=0.2 m/s .

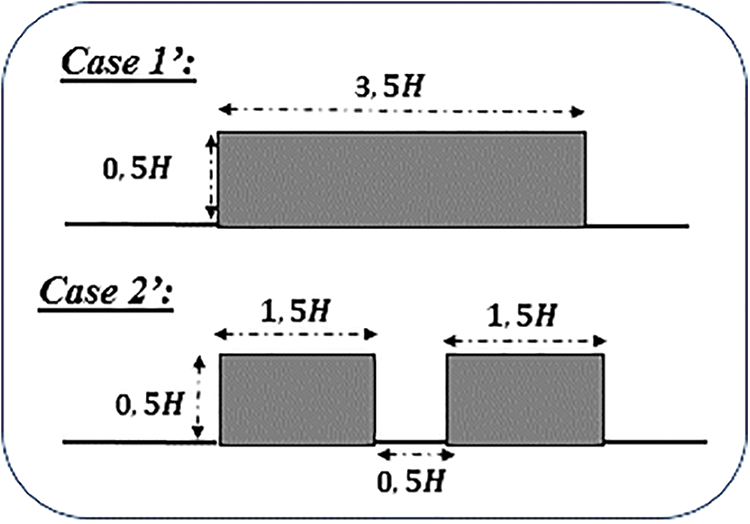
Figure 5: The different configurations

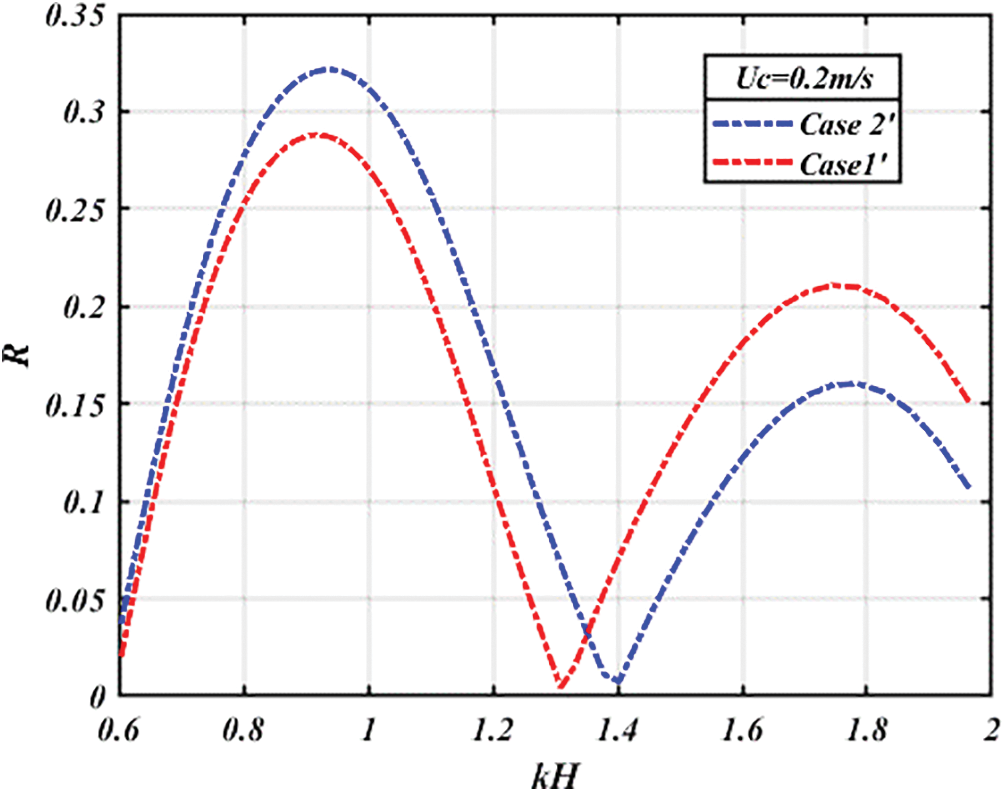
Figure 6: Variation of R vs. kH for Uc=0.2 m/s

The results of the comparative study show that the maximum reflection coefficient of the different configurations is around kH=0.9 . Knowing that a good wave attenuator corresponds to a higher maximum reflection coefficient and a wider reflection bung, therefore the single rectangular breakwater is the best wave attenuator compared to the double one in the zone of large wavenumbers k (the short waves). On the other hand in the zone of the small wavenumbers k (the long waves) the double rectangular breakwater is the best.

It is clear that in case 2’, a reflection superposition phenomenon occurs, involving both the first and second breakwaters. When short-wavelength waves encounter this scenario, they are unable to reach the second breakwater, leading to an overall reflection confined to the contribution of the first breakwater. Consequently, the maximum reflection coefficient in case 2’ is lower due to the shorter length of the breakwater, in contrast to case 1’.

Conversely, in the presence of long-wavelength waves, they are able to reach the second breakwater, leading to a combined effect of reflections from both breakwaters. This results in a higher maximum reflection coefficient in case 2’ compared to the first, attributed to the additive nature of the two reflections.

4.2.2 The Case of Two Identical Rectangular Breakwaters

This part is dedicated to the study of the influence of two identical rectangular breakwaters (of the same length l1=l2=1.25 H and the same height h1=h2=0.5 H ) spaced by a distance d=0.5 H on the propagation of a monochromatic incident wave with an amplitude of a=0.01 m , that is propagating in a wave flume characterized by a length of L=30 m and a depth of H=2.50 m , in the presence of the current. This study will focus on the effect of the current and the effects of the geometrical parameters on the reflection coefficient. All the figures below show the variation of the reflection coefficient R with the dimensionless wavenumber kH .

•   Effect of the current

Firstly, we are interested in studying the influence of the current velocity on the maximum value of the reflection coefficient and the width of the reflection band for different cases of the currents; without current, coplanar current and opposing current (Fig. 7).

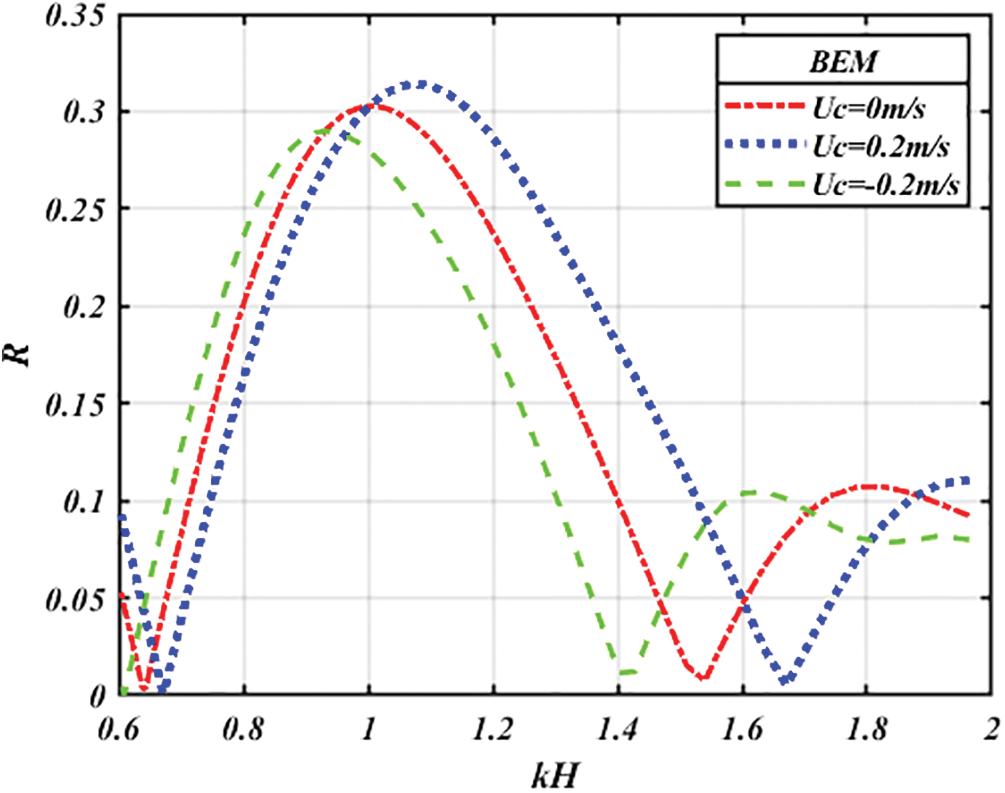
Figure 7: Variation of R vs. kH for Uc=0 m/s , Uc=0.2 m/s and Uc=−0.2 m/s

According to Fig. 7, we note that if the current is flowing in in the same direction to that of the incident wave ( Uc=0.2 m/s ) the reflection bandwidth and the maximum value of the reflection coefficient increase with a shift of the latter towards the large wavenumber k . In contrary, the opposite is observed if the current is flowing in the opposite direction to that of the incident wave Uc=−0.2 m/s ). This is because the incident wave is amplified by the current when they are in the same direction (coplanar current), which results in a stronger collision of the wave with the rectangular breakwaters leading to a higher reflection. Contrary to the case where the current and the incident wave are in opposite directions (opposing current), the latter is extinguished, leads to less reflection compared to the cases without current and coplanar current.

•   Effects of the geometrical parameters

In this part, we are interested in the effect of geometrical parameters on the reflection coefficient in the presence of current. These geometrical parameters are the length and height of two rectangular breakwaters and the spacing between them. Where calculations have been made in the presence of a current velocity Uc=±0.2 m/s .

•   Effect of the length of two rectangular breakwaters

We are interested in studying the effect of the length of two breakwaters on the reflection coefficient R for different values of each breakwater length (l = H, 1.25 H and 1.5 H). The curves in Fig. 8 show that in both cases coplanar current and opposing current, the maximum value of the reflection coefficient increases with the length of the rectangular breakwaters. This increase is accompanied by a shift of the maximum value of the reflection coefficient towards low wavenumbers k . On the other hand, the reflection bandwidth decreases. Regarding the current, we see the same effects observed in Fig. 7.

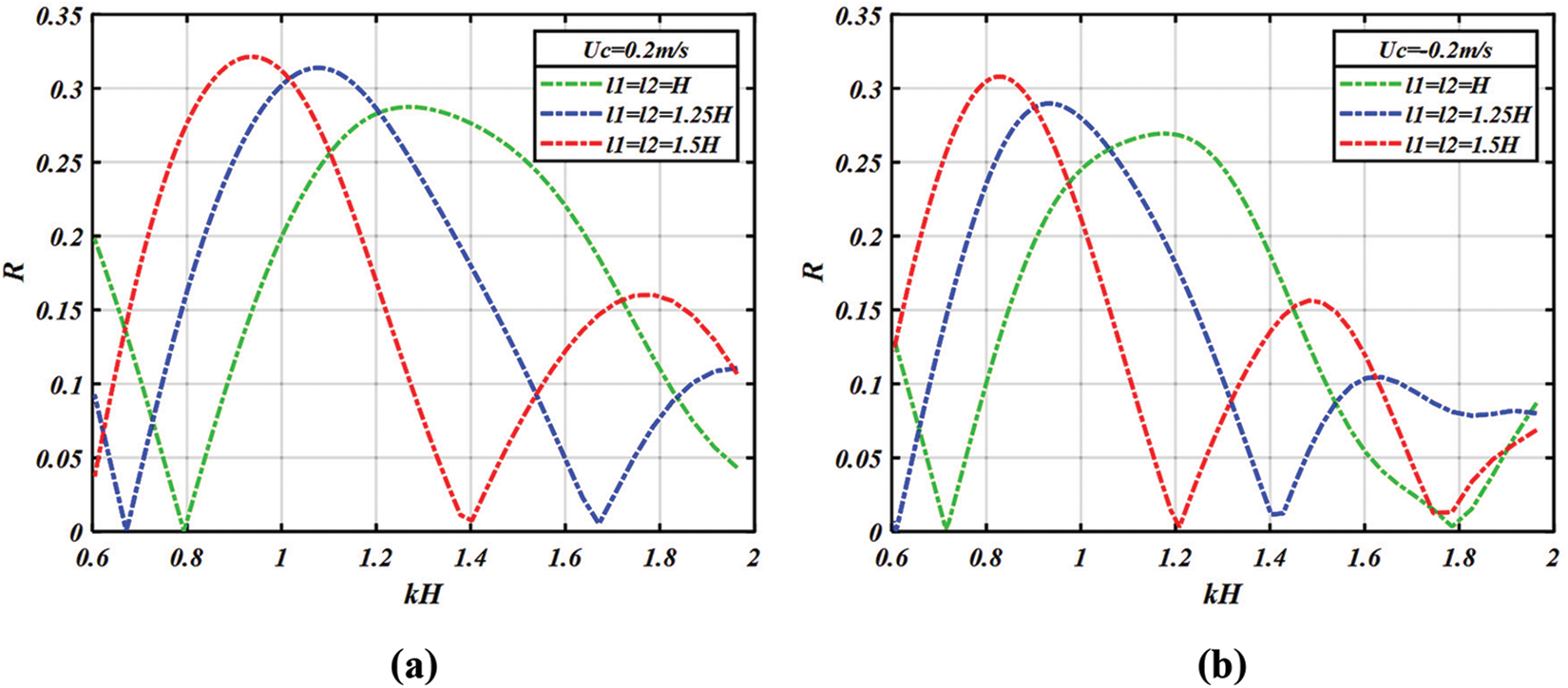
Figure 8: Variation of R vs. kH for (l1 = l2 = H, 1.25 H and 1.5 H). (a): Uc=0.2 m/s and (b): Uc=−0.2 m/s

•   Effect of the height of two rectangular breakwaters

We now present the effect of the height of two breakwaters on the reflection coefficient R for different heights of each breakwater (h = 0.25 H, 0.5 H and 0.75 H). Fig. 9 reveals that the maximum of the reflection coefficient increases with a shift to low wavenumbers k and the reflection bandwidth decreases when the height of the rectangular breakwaters increases. This is explained by the fact that when the height of two breakwaters increases (the rectangular breakwaters approach the free surface) the reflected wave will amplify which results in a higher maximum reflection coefficient leading to a greater reduction in wave dissipation.

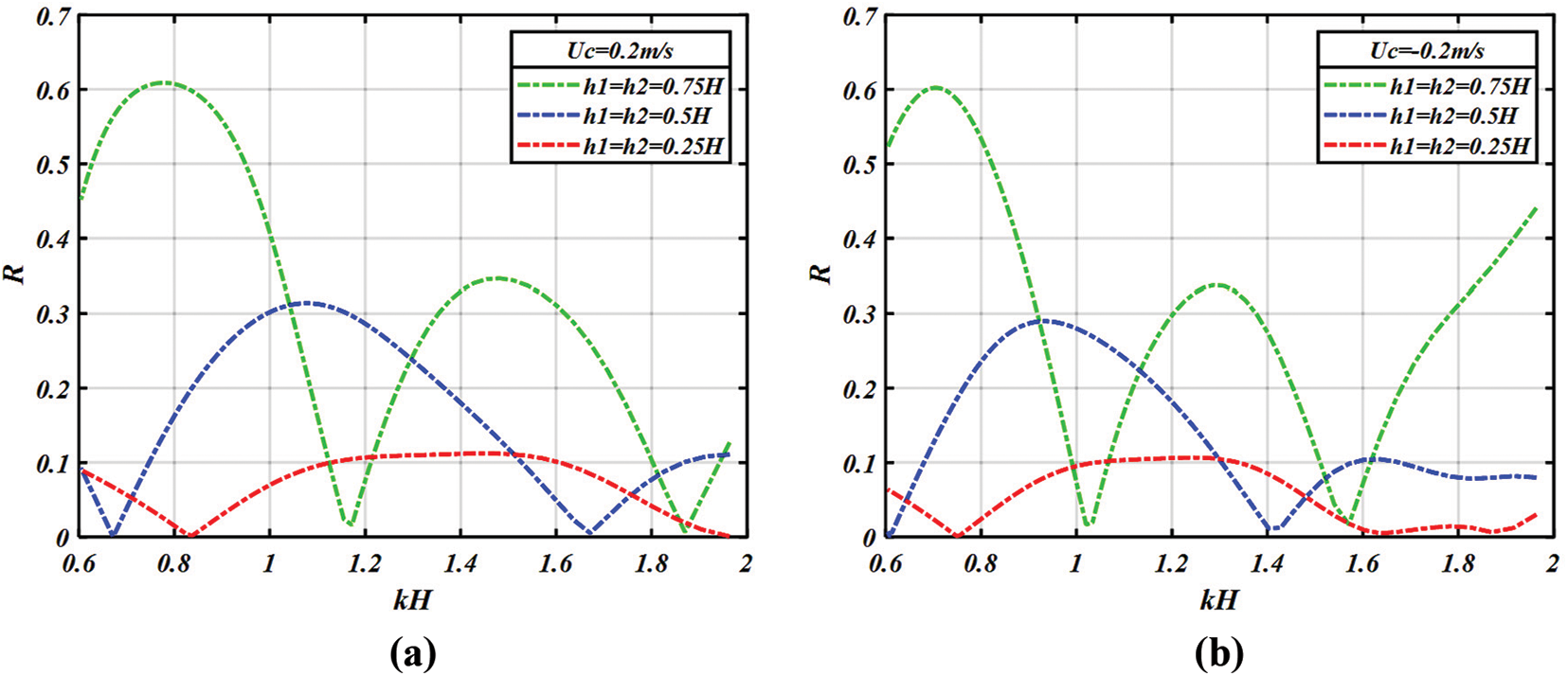
Figure 9: Variation of R vs. kH for ( h1=h2=0.25 H , 0.5 H and 0.75 H ). (a): Uc=0.2 m/s and (b): Uc=−0.2 m/s

•   Effect of the distance d

To study the influence of the spacing between the two breakwaters on the reflection coefficient in the presence of current, we depict the variations of this coefficient for different spacing (d = 0.5 H, 0.75 H and H). Based on the curves shown in Fig. 10, we notice that for the first band the maximum value of the reflection coefficient increases when the spacing between the two rectangular breakwaters d increases, unlike for the second band, the opposite is observed. Then the same thing happens periodically.

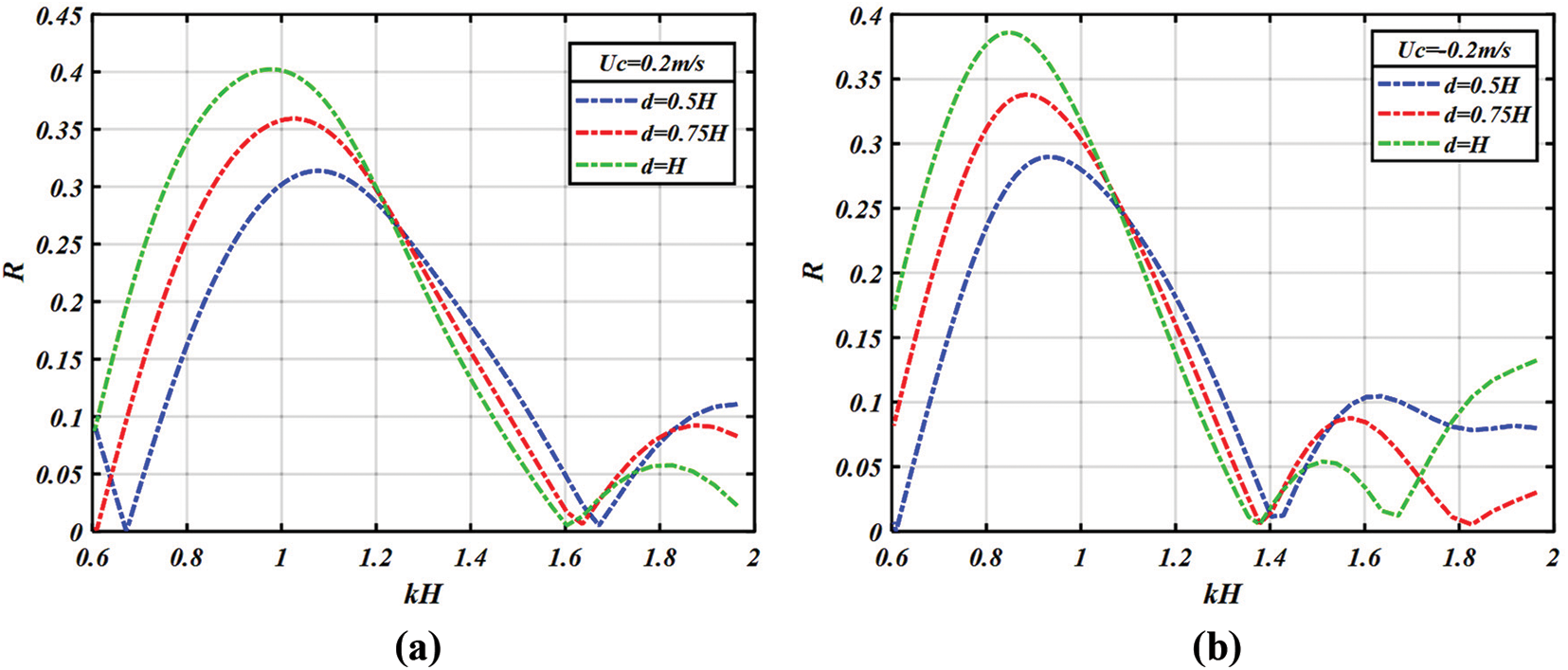
Figure 10: Variation of R vs. kH for (d = 0.5 H, 0.75 H and H). (a): Uc=0.2 m/s and (b): Uc=−0.2 m/s

4.2.3 The Case of Two Different Rectangular Breakwaters

In this part, we will present a comparison between different configurations by studying the variation of the reflection coefficient in the presence of a current velocity Uc=±0.2 m/s . The different configurations are shown Fig. 11 with a water depth H=2.50 m .

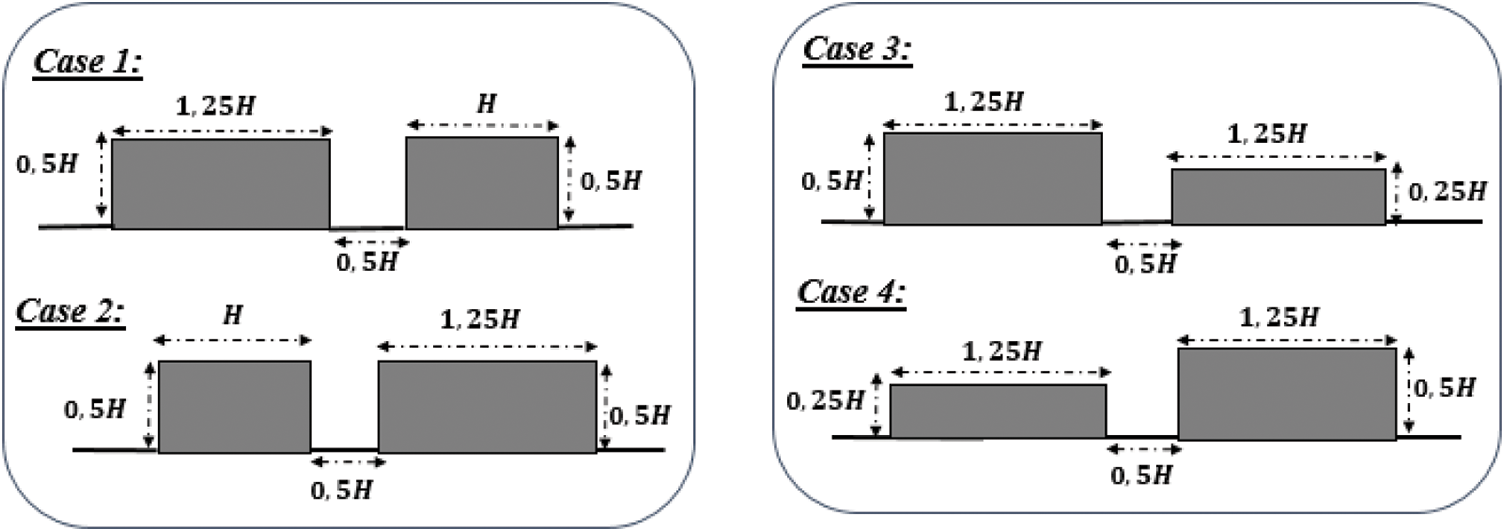
Figure 11: The different configurations

The curves illustrated in Fig. 12 show that whatever the position of two breakwaters of the same height with different lengths (Case 1 and Case 2) or of the same length with different heights (Case 3 and Case 4), the variation of the reflection remains practically unchanged.

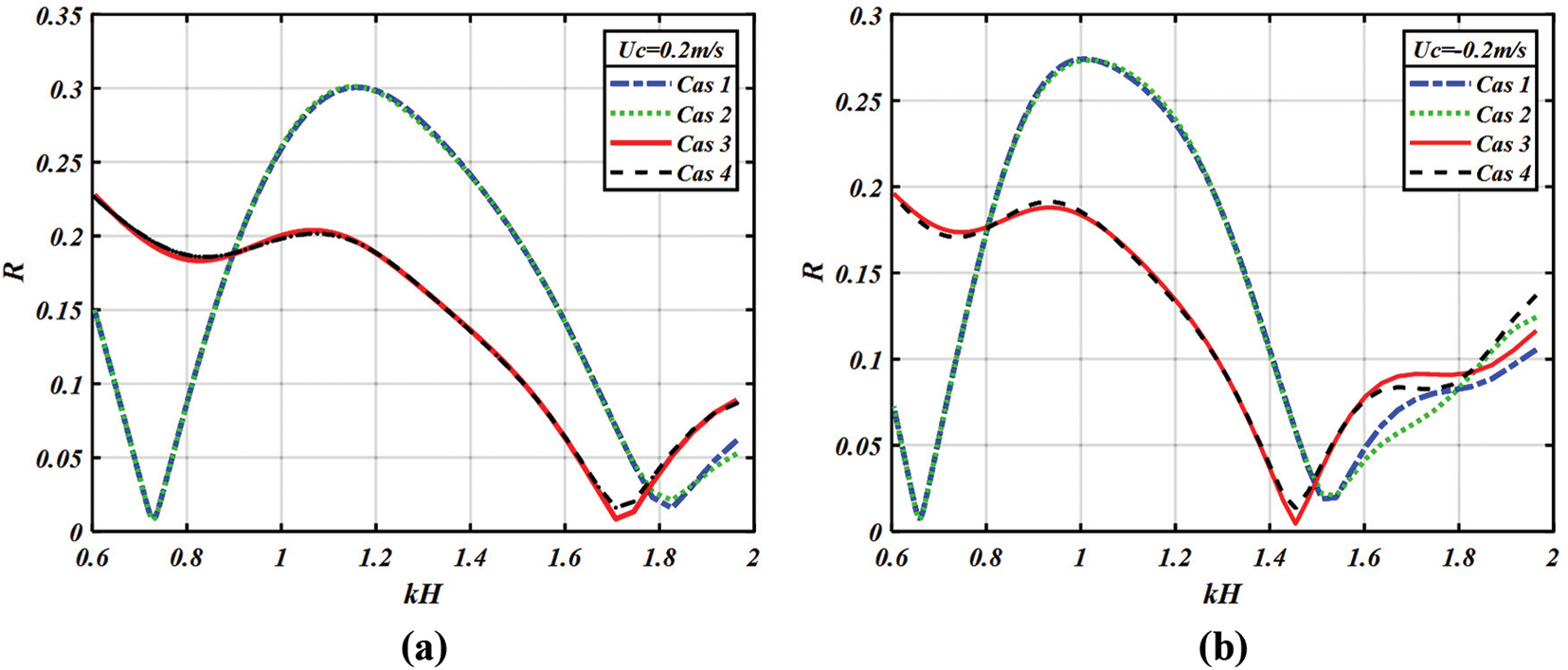
Figure 12: Variation of R vs. kH . (a): Uc=0.2 m/s and (b): Uc=−0.2 m/s

5  Conclusion

The current study focused on numerically investigating the interaction between waves and two rectangular breakwaters positioned at a certain distance from each other and fixed to the flat bottom of a wave flume. This investigation was carried out considering the presence of a uniform current. To validate the numerical approach based on the Boundary Element Method (BEM), a comparison with experimental results was conducted. The aim was to gain a better understanding of the mechanisms involved in wave attenuation and dissipation when the current is present, by studying the influence of the current velocity and the geometric parameters of the two rectangular breakwaters on the reflection bandwidth and the maximum reflection coefficient.

Based on our findings, we can conclude that the double rectangular breakwater provides better wave attenuation compared to a single breakwater, particularly for low wavenumbers. Furthermore, in the presence of a coplanar current, both the reflection bandwidth and the maximum reflection coefficient increase. Conversely, in the case of an opposing current, these parameters decrease. Additionally, as the length and height of two rectangular breakwaters and the spacing between them increase, the maximum reflection coefficient also increases, this implies an important reduction of the wave.

Acknowledgement: The authors do not have special thanks for this study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Conceptualization, H.A., H.M., L.E.A. and S.M.; methodology, H.A., H.M., L.E.A. and S.M.; software, H.A., H.M., L.E.A. and S.M.; validation, H.A., H.M., L.E.A. and S.M.; investigation, H.A., H.M., L.E.A. and S.M.; writing-original draft preparation, H.A., H.M., L.E.A. and S.M.; writing-review and editing, H.A., H.M., L.E.A. and S.M.; visualization, H.A., H.M., L.E.A. and S.M.; supervision, H.A., H.M., L.E.A. and S.M. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. El Aarabi, L., Mouakkir, L., Mordane, S. (2020). Numerical modeling of the wave-structure interaction using the boundary element method. software engineering perspectives in intelligent systems. Proceedings of 4th Computational Methods in Systems and Software, pp. 292–303. Cham: Springer International Publishing. [Google Scholar]

2. Shih, R. S., Weng, W. K., Li, C. Y. (2020). Characteristics of wave attenuation due to roughness of stepped obstacles. Ships and Offshore Structures, 15(6), 605–619. [Google Scholar]

3. Rey, V., Belzons, M., Guazzelli, E. (1992). Propagation of surface gravity waves over a rectangular submerged bar. Ships and Offshore Structures, 235, 453–479. [Google Scholar]

4. Romya, A. A., Moghazy, H. M., Iskander, M. M., Abdelrazek, A. M. (2022). Performance assessment of corrugated semi-circular breakwaters for coastal protection. Alexandria Engineering Journal, 61(5), 3587–3598. [Google Scholar]

5. Driscoll, A. M., Dalrymple, R. A., Grilli, S. T. (1993). Harmonic generation and transmission past a submerged rectangular obstacle. 23rd International Conference in Coastal Engineering, pp. 1142–1152. New York, USA: American Society of Civil Engineers. [Google Scholar]

6. Davidson, M. A., Bird, P. A. D., Bullock, G. N., Huntley, D. A. (1996). A new non-dimensional number for the analysis of wave reflection from rubble mound breakwaters. Coastal Engineering, 28(1–4), 93–120. [Google Scholar]

7. Stamos, D. G., Hajj, M. R. (2001). Reflection and transmission of waves over submerged breakwaters. Journal of Engineering Mechanics, 127(2), 99–105. [Google Scholar]

8. Christou, M., Swan, C., Gudmestad, O. (2008). The interaction of surface water waves with submerged breakwaters. Coastal Engineering, 55(12), 945–958. [Google Scholar]

9. Lee, J. F., Tu, L. F., Liu, C. C. (2014). Nonlinear wave evolution above rectangular submerged structures. Journal of Marine Science and Technology, 22(5), 531–541. [Google Scholar]

10. Patil, S. B., Karmakar, D. (2021). Performance evaluation of submerged breakwater using Multi-Domain Boundary Element Method. Applied Ocean Research, 114, 102760. [Google Scholar]

11. Kar, P., Sahoo, T., Behera, H. (2019). Effect of bragg scattering due to bottom undulation on a floating dock. Wave Motion, 90, 121–138. [Google Scholar]

12. Chanda, A., Bora, S. N. (2020). Propagation of oblique waves over a small undulating elastic bottom topography in a two-layer fluid flowing through a channel. International Journal of Applied Mechanics, 12(2), 2050023. [Google Scholar]

13. Chanda, A., Bora, S. N. (2020). Effect of a porous sea-bed on water wave scattering by two thin vertical submerged porous plates. European Journal of Mechanics-B/Fluids, 84, 250–261. [Google Scholar]

14. Mahmoudof, S. M., Hajivalie, F. (2021). Experimental study of hydraulic response of smooth submerged breakwaters to irregular waves. Oceanologia, 63(4), 448–462. [Google Scholar]

15. Mahmoudof, S. M., Eyhavand-Koohzadi, A., Bagheri, M. (2021). Field study of wave reflection from permeable rubble mound breakwater of Chabahar Port. Applied Ocean Research, 114, 102786. [Google Scholar]

16. Fu, D., Zhao, X., Wang, S., Yan, D. (2021). Numerical study on the wave dissipating performance of a submerged heaving plate breakwater. Ocean Engineering, 219, 108310. [Google Scholar]

17. Nguyen, N. M., Van, D. D., Le, D. T., Cong, S. D., Pham, N. T. et al. (2022). Wave reduction efficiency for three classes of breakwaters on the coastal Mekong Delta. Applied Ocean Research, 129, 103362. [Google Scholar]

18. Ryu, S., Kim, M., Lynett, P. J. (2003). Fully nonlinear wave-current interactions and kinematics by a BEM-based numerical wave tank. Computational Mechanics, 32(4), 336–346. [Google Scholar]

19. Zhang, J. S., Zhang, Y., Jeng, D. S., Liu, P. F., Zhang, C. (2014). Numerical simulation of wave--current interaction using a RANS solver. Ocean Engineering, 75, 157–164. [Google Scholar]

20. Chang, X., Akkerman, I., Huijsmans, R. H., Veldman, A. E. (2016). Generating and absorbing boundary conditions for combined wave-current simulations. Proceedings of the 12th International Conference on Hydrodynamics, Delft, Netherlands. [Google Scholar]

21. Kim, S. Y., Kim, K. M., Park, J. C., Jeon, G. M., Chun, H. H. (2016). Numerical simulation of wave and current interaction with a fixed offshore substructure. International Journal of naval Architecture and Ocean Engineering, 8(2), 188–197. [Google Scholar]

22. Fan, C. M., Chu, C. N., Šarler, B., Li, T. H. (2019). Numerical solutions of waves-current interactions by generalized finite difference method. Engineering Analysis with Boundary Elements, 100, 150–163. [Google Scholar]

23. Gholamipoor, M., Ghiasi, M. (2019). A meshless numerical wave tank for simulation of fully nonlinear wave--wave and wave--current interactions. Journal of Engineering Mathematics, 119(1), 115–133. [Google Scholar]

24. Huang, H. C., Yang, Y. F., Zhu, R. H., Wang, C. Z. (2022). Nonlinear wave resonance due to oscillations of twin cylinders in a uniform current. Applied Ocean Research, 121, 103096. [Google Scholar]

25. Shih, R. S., Li, C. Y., Weng, W. K. (2019). Wave-structure-current interactions over smooth and rough breakwaters. Ships and Offshore Structures, 17(1), 29–50. [Google Scholar]

26. Errifaiy, M., Naasse, S., Chahine, C. (2016). Analytical determination of the reflection coefficient by the evanescent modes model during the wave--current--horizontal plate interaction. Comptes Rendus Mécaniques, 344(7), 479–486. [Google Scholar]

27. Liang, B., Wu, G., Liu, F., Fan, H., Li, H. (2015). Numerical study of wave transmission over double submerged breakwaters using non-hydrostatic wave model. Oceanologia, 57(4), 308–317. [Google Scholar]

28. Bai, J., Ma, N., Gu, X. (2017). Study of interaction between wave-current and the horizontal cylinder located near the free surface. Applied Ocean Research, 67, 44–58. [Google Scholar]

29. Chen, L. F., Ning, D. Z., Teng, B., Zhao, M. (2017). Numerical and experimental investigation of nonlinear wave-current propagation over a submerged breakwater. Journal of Engineering Mechanics, 143(9), 04017061. [Google Scholar]

30. Naasse, S., Errifaiy, M., Chahine, C. (2019). Analytical study of the effect of the geometrical parameters during the interaction of regular wave-horizontal plate-current. Acta Oceanologica Sinica, 38(5), 10–20. [Google Scholar]

31. Akarni, H., El Aarabi, L., Mouakkir, L., Mordane, S. (2021). Numerical modeling of the wave-plate-current interaction by the Boundary Element Method. Fluids, 6(12), 435. [Google Scholar]

32. Ning, D. Z., Lin, H. X., Teng, B., Zou, Q. P. (2014). Higher harmonics induced by waves propagating over a submerged obstacle in the presence of uniform current. China Ocean Engineering, 28, 725–738. [Google Scholar]

33. Lee, J. J. (1971). Wave-induced oscillations in harbours of arbitrary geometry. Journal of Fluid Mechanics, 45(2), 375–394. [Google Scholar]

34. Dabsi, N. (1998). Modélisation numérique des oscillations induites dans un port sollicité par une houle incidente et étude du comportement d’un navire marré (Ph.D. Thesis). Hassan II University of Casablanca, Morocco. [Google Scholar]

35. Mordane, S. (2001). Contribution numérique à la résolution du problème d’interaction houle-obstacles (Ph.D. Thesis). Hassan II University of Casablanca, Morocco. [Google Scholar]