 Open Access
Open Access
REVIEW
State-of-the-Art Review on Seepage Instability and Water Inrush Mechanisms in Karst Collapse Columns
1 School of Civil Engineering, Henan Polytechnic University, Jiaozuo, 454003, China
2 School of Resources and Environment, Henan Polytechnic University, Jiaozuo, 454003, China
3 Henan Mine Water Disaster Prevention and Control and Water Resources Utilization Engineering Technology Research Center, Henan Polytechnic University, Jiaozuo, 454000, China
4 Collaborative Innovation Center of Coal Work Safety and Clean High Efficiency Utilization, Jiaozuo, 454000, China
* Corresponding Author: Cunhan Huang. Email:
Fluid Dynamics & Materials Processing 2025, 21(5), 1007-1028. https://doi.org/10.32604/fdmp.2025.062738
Received 26 December 2024; Accepted 15 April 2025; Issue published 30 May 2025
Abstract
Karst collapse columns typically appear unpredictably and without a uniform spatial arrangement, posing challenges for mining operations and water inrush risk assessment. As major structural pathways for mine water inrush, they are responsible for some of the most frequent and severe water-related disasters in coal mining. Understanding the mechanisms of water inrush in these collapse columns is therefore essential for effective disaster prevention and control, making it a key research priority. Additionally, investigating the developmental characteristics of collapse columns is crucial for analyzing seepage instability mechanisms. In such a context, this paper provides a comprehensive review of four critical aspects: (1) The development characteristics and hydrogeological properties of collapse columns; (2) Fluid-solid coupling mechanisms under mining-induced stress; (3) Non-Darcy seepage behavior in fractured rock masses; (4) Flow regime transitions and mass variation effects. Key findings highlight the role of flow-solid coupling in governing the seepage mechanisms of fractured rock masses within karst collapse columns. By synthesizing numerous studies on flow pattern transitions, this paper outlines the complete seepage process—from groundwater movement within the aquifer to its migration through the collapse column and eventual inflow into mine roadways or working faces—along with the associated transformations in flow patterns. Furthermore, the seepage characteristics and water inrush behaviors influenced by particle migration are examined through both experimental and numerical simulation approaches.Graphic Abstract
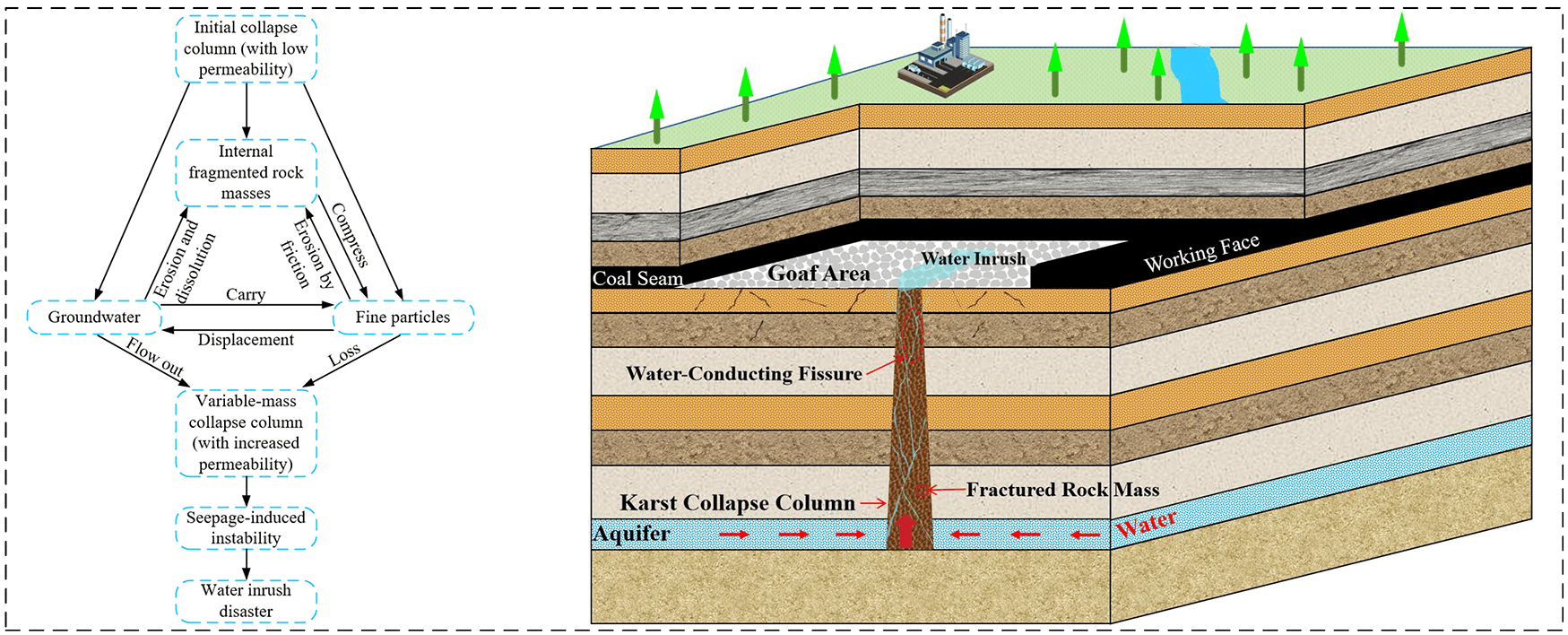
Keywords
As the most abundant fossil fuel globally, with proven reserves exceeding one trillion metric tons worldwide, coal remains a cornerstone of energy security and a stabilizing factor in energy portfolio optimization [1,2]. This conventional energy source has been fundamental to industrial development processes [3]. Current estimates indicate its continued dominance in global electricity generation, constituting approximately 40% of fuel sources [4]. During the energy transition phase, this conventional source is expected to remain vital in maintaining stable energy supplies.
However, mining operations in complex hydrogeological environments, particularly those involving deep coal-bearing strata, face escalating challenges from elevated stress levels, geothermal gradients, and hydraulic pressures exacerbated by intensive extraction activities [5]. These compounding factors render water inrushes a critical safety concern in modern mining systems (Fig. 1). Industrial observations confirm that hydrogeological connectivity and preferential flow pathways constitute fundamental prerequisites for such incidents [6]. Extraction-induced stress redistribution during longwall advancement significantly modifies the fracture network architecture of surrounding strata, critically altering their porosity-permeability relationships [7]. This geomechanical transformation, when coupled with hydraulic-mechanical interactions in fractured media containing weakly cemented geological discontinuities (e.g., collapse columns), facilitates preferential flow pathways. The unconsolidated nature of these structural fillings, characterized by low cohesion and fragmented particulates, demonstrates permeability characteristics highly sensitive to void ratio evolution, stress perturbations, and hydrodynamic forcing [8]. Such conditions may precipitate catastrophic flooding scenarios involving tunnel inundation, working face submersion, and large-scale waterlogging events with significant socioeconomic consequences.
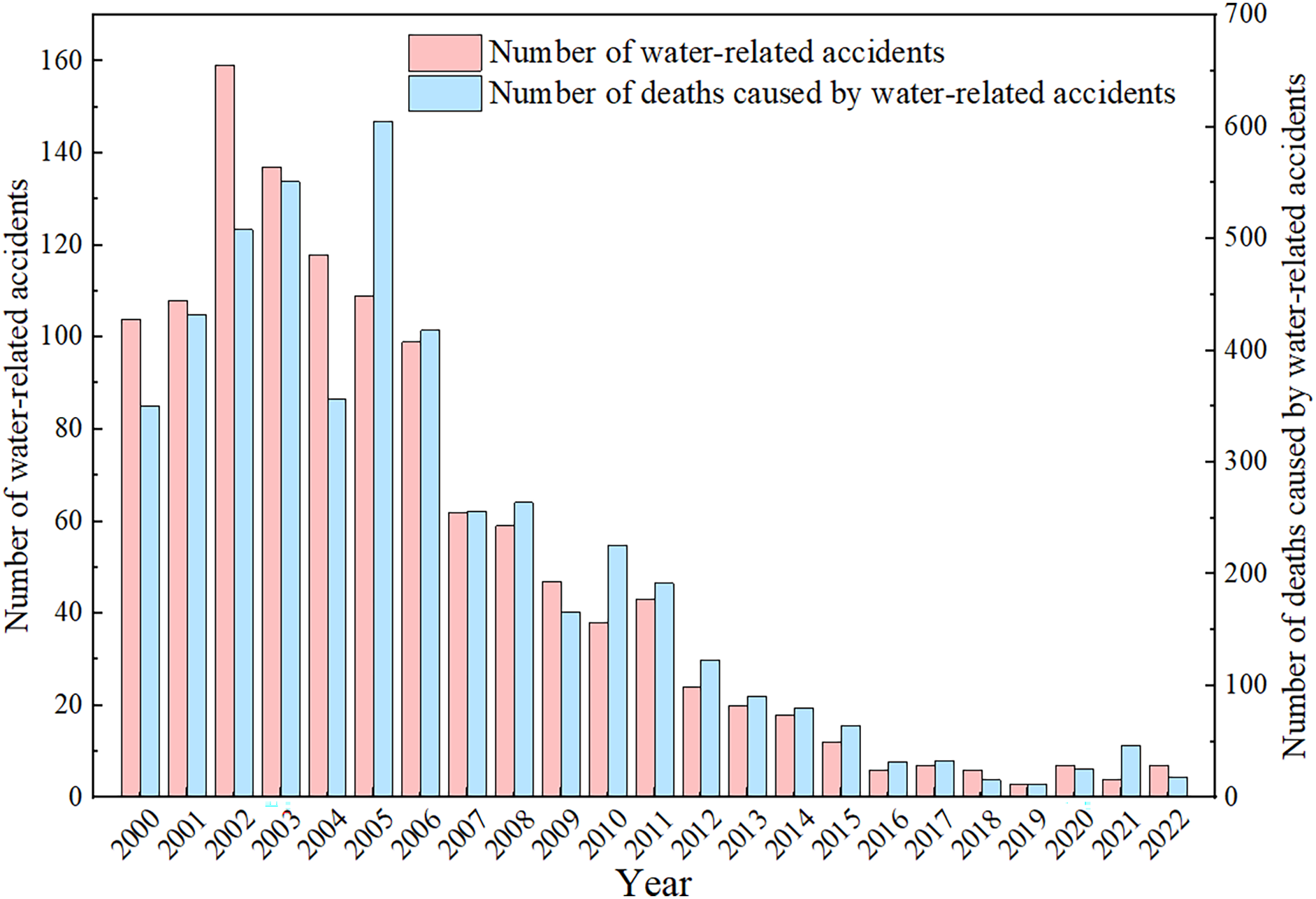
Figure 1: Number of mine water-related accidents and deaths from 2000 to 2022
Since the 1960s, large-scale coal resource exploitation has uncovered significant collapse column-related water hazards threatening mine safety [9]. Insufficient understanding of collapse column water inrush mechanisms has hindered the timely implementation of preventive measures, leading to recurring water-related incidents. Consequently, collapse column water inrush mechanisms have remained a critical research topic in rock mechanics and seepage mechanics, attracting sustained attention from academic and engineering communities. However, the complex interplay of hydrogeological factors involved in collapse column failure processes presents ongoing challenges for mechanistic understanding. This paper begins with a concise overview of collapse column development characteristics, formation mechanisms, and water-conducting properties. It then synthesizes advancements in fluid-solid coupling mechanisms, fractured rock seepage behaviors, flow regime transition processes, and variable-mass seepage theories to outline the state-of-the-art in collapse column water inrush mechanism research.
2 Basic Characteristics of Karst Collapse Columns
The structural attributes of collapse columns—irregular morphology, heterogeneous composition, complex formation processes, and hydraulic conductivity—offer critical insights into their seepage dynamics. These properties govern both groundwater flow patterns within the columns and hydraulic risk evolution during extraction activities. Systematic analysis of column characteristics enables accurate risk assessment of hydraulic hazards, informing science-driven mitigation strategies for safe mining operations. This section synthesizes current understanding of column morphology, internal architecture, genetic mechanisms, and fluid transport capabilities.
2.1 The Shape Characteristics of Karst Collapse Column
2.1.1 Planar Shape Characteristics of Karst Collapse Column
Karst collapse columns display varied cross-sectional geometries, predominantly elliptical or circular configurations [10]. These morphologies originate from groundwater dissolution along structural discontinuities followed by gravitational compaction. Elliptical forms exhibit major axis lengths spanning three orders of magnitude (10–1000 m), reflecting differential karstification intensity across geological settings. Geometric complexity emerges from synergistic effects of structural controls and lithological responses, including fracture network orientation and bedrock competency. Notably, individual collapse columns exhibit depth-dependent variations in cross-sectional geometry [11], primarily governed by progressive alterations in groundwater dissolution capacity and lithostatic stabilization.
2.1.2 Profile Shape Characteristics of Karst Collapse Column
Collapse columns in coal extraction operations typically display irregular profiles with serrated or undulating contours [12]. These morphologies originate from multi-phase geological processes involving bedrock fracturing, fluid-rock interactions, and structural deformation. Horizontal cross-sections frequently exhibit elliptical geometries, indicating radial expansion patterns during column evolution.
Stratigraphic configurations significantly influence collapse column morphology. In fractured competent strata, inverted conical geometries prevail (top diameter < base diameter) [13], developing through cavity propagation under sustained hydro-mechanical coupling. Gravitational compaction of overburden strata following cavity roof failure creates characteristic dip angles of 60°–80°, indicative of host rock mechanical integrity during structural collapse. Contrastingly, unconsolidated strata exhibit funnel-shaped collapse features (top diameter > base diameter) [14], where upward cavity migration dominates due to preferential groundwater erosion along weakly cemented zones. Reduced dip angles (40°–50°) in these systems correlate with diminished frictional resistance in poorly consolidated lithologies.
It is noteworthy that the collapse angle critically influences structural characteristics and seepage dynamics in karst columns. Empirical analyses reveal an inverse correlation between collapse angles and column cross-sectional areas [15]. Three typological classifications emerge: Type I (90°–85°), Type II (85°–81°), and Type III (<81°), based on angular discontinuities. Mechanistic modeling demonstrates optimal fracture development within 60°–90° angular domains [16], significantly compromising aquiclude integrity and elevating hydraulic risks.
2.1.3 The Central Axis of Karst Collapse Column
The central axis, defined by connecting cross-sectional centroids, serves as a key morphological indicator for karst collapse columns. Axis configuration types—vertical, inclined, curvilinear, and helical are classified according to structural alignment. These geometric patterns record polyphase evolutionary histories involving intermittent karstification and tectonic overprinting effects [17].
2.2 Internal Characteristics of Karst Collapse Column
The internal architecture of collapse columns exhibits discontinuous fabric characteristics, originating from gravitational reconfiguration of fragmented roof strata during structural failure. Angular lithic fragments ranging from meter-scale blocks to centimeter-sized debris demonstrate size-dependent geometric configurations [18,19]. Interstitial spaces within the fragmented mass contain unconsolidated infill materials including rock flour, carbonaceous particulates, and argillaceous matrices with limited cementation.
Collapse columns contain authigenic minerals deposited through prolonged hydrogeochemical processes. Iron oxides, carbonates, and clay minerals preferentially accumulate along fracture surfaces and intergranular voids. These secondary deposits increase structural heterogeneity by modifying pore architecture and cementation patterns. Hydraulic regimes dictate filling characteristics: columns experiencing active groundwater flow develop high-permeability fabrics through particle leaching, whereas stagnant systems preserve low-porosity lithologies [20].
2.3 The Genesis of Karst Collapse Column
Geological heterogeneity drives persisting debates regarding collapse column genesis, with current frameworks proposing four fundamental mechanisms: gravitational compaction, anhydrite dissolution, vacuum suction erosion, and hydrothermal alteration.
The gravitational compaction hypothesis proposes that collapse columns form through overburden subsidence into underlying karstified strata. Progressive cavity expansion induces downward migration of superjacent rock masses under lithostatic loading, ultimately creating columnar structures. This established theoretical framework has been extended through mechanical analyses of roof failure modes. Yang et al. [21] analyzed the stress distribution in the upper part of the roof of collapse column and introduced the concepts of pre-existing shear surfaces, sliding surfaces, and inter-layer detachment surfaces, along with the roles in the formation of collapse columns. Based on thin plate theory, Hu et al. [22] analyzed the stress conditions and failure mechanisms of cavern roofs, considering the weight of the overlying rock and soil as the load, and thus determined the ultimate load for the failure of cavern roofs.
The gypsum dissolution model explains collapse column formation through sequential geochemical processes: Hydration-driven expansion of anhydrite interbeds in Mid-Ordovician limestone induces mechanical fracturing during groundwater recharge events; Subsequent dissolution and transport of sulfates create interconnected void networks; Progressive roof collapse under lithostatic stress ultimately generates cylindrical structures [23].
The vacuolar erosion hypothesis conceptualizes collapse columns as semi-confined systems. Groundwater table fluctuations generate pressure differentials within these structures, creating lithostatic imbalances. Progressive roof failure occurs through synergistic gravitational loading and suction effects, ultimately forming columnar collapse features. Field evidence from specific mining contexts substantiates this failure mechanism [24].
The hydrothermal genesis hypothesis posits that collapse column formation correlates with subsurface fluid-rock interactions. Geothermal fluids chemically alter host rocks through dissolution and metasomatism, initiating karst void development. Progressive cavity enlargement coupled with sustained hydrothermal activity induces gravitational roof collapse, ultimately forming columnar structures.
In addition, other widely recognized theories on the formation mechanisms of karst collapse columns include: development of “inverse wedge-shaped” fractures in anticlines, “rock-water resonance”, dissolution cycle theory (seepage effect), liquefaction theory, and pressure differential theory, among others.
In conclusion, current research identifies four essential prerequisites for collapse column development: (1) soluble bedrock formations, (2) permeable hydrogeological networks, (3) active groundwater circulation, and (4) gravitational/tectonic loading. The multifactorial genesis theory (Fig. 2) demonstrates their formation through synergistic geological processes governed by interdependent factors and multi-stage evolution [9].
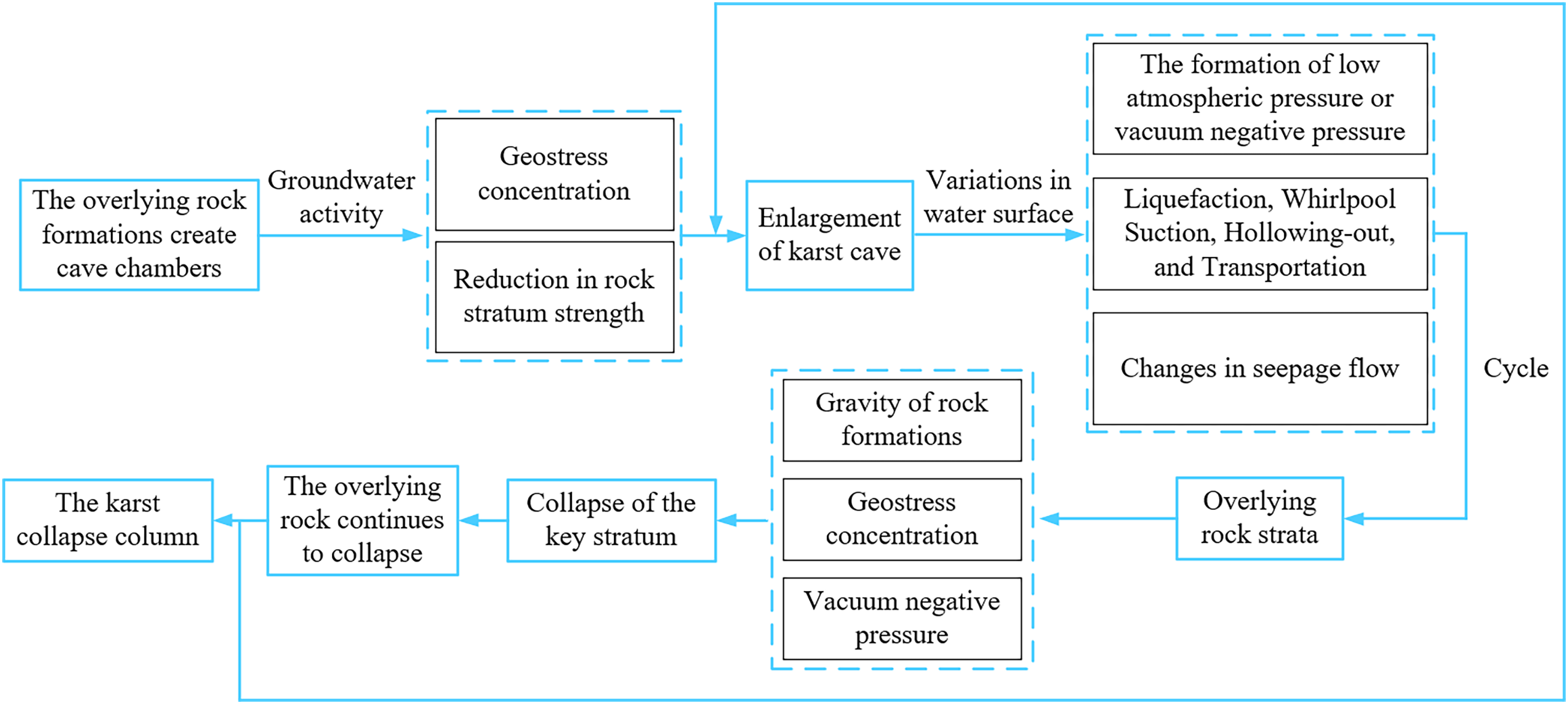
Figure 2: Comprehensive genetic model of formation mechanism of collapse column. Adapted with permission from Reference [9]. 2019, Yin S
2.4 The Water Inrush and Water Conductivity Properties of Collapse Columns
Multiple parameters govern the hydrodynamic characteristics of collapse columns. Systematic investigation of fluid breakthrough events and hydraulic transmission patterns enhances understanding of their impacts on fluid dynamics. This analytical approach enables mechanistic interpretation of subsurface flow processes.
Three principal components govern hydraulic breaching in collapse columns: source aquifers, fluid transmission pathways, and pressure differentials [25–27]. Aquifer productivity determines water availability, with soluble carbonate formations near structural zones posing elevated hydraulic risks due to enhanced groundwater mobility [28]. Three principal flow pathways emerge: (1) Column interiors with low-density fillings creating preferential conduits [29]; (2) Peripheral fracture networks susceptible to stress-induced connectivity; (3) Associated minor faults bridging hydraulically isolated zones [30]. Hydrodynamic drivers comprise confined aquifer pressure, recharge-discharge dynamics, and mining-induced stress redistribution. Elevated pressures (>5 MPa) in deep carbonate aquifers frequently exceed confining stratum thresholds [31]. Enhanced recharge rates accelerate groundwater flux through column structures, while excavation activities degrade hydraulic barriers through stress-path alterations [32].
Previous studies systematically analyzed the genetic conditions and spatial distribution patterns of karst collapse structures in stratigraphically complex coal basins [33]. Hydraulic classification identifies three distinct categories based on permeability: high-conductivity, moderate-conductivity, and aquiclude-type collapse columns. Temporal characteristics of water ingress events further differentiate these structures into instantaneous, progressive, and delayed failure modes.
Based on the overall filling characteristics and self-sealing water-blocking properties, Yang et al. [34] conducted extensive field and underground surveys of collapse columns, and divided the column into three sections from bottom to top: (1) gypsum breccia barrier layer, (2) argillaceous matrix seal, and (3) fragmentary cap reinforcement (Fig. 3). The basal gypsum breccia layer dissipates hydrodynamic energy through inter-block flow constriction, achieving permeability reduction via tortuous microchannel networks. Intermediate argillaceous seals demonstrate ultra-low permeability due to clay-dominated mineralogy and cohesive cementation, forming persistent hydraulic barriers. Superjacent breccia layers exhibit permeability anisotropy controlled by particle gradation, primarily enhancing structural confinement of underlying seals.
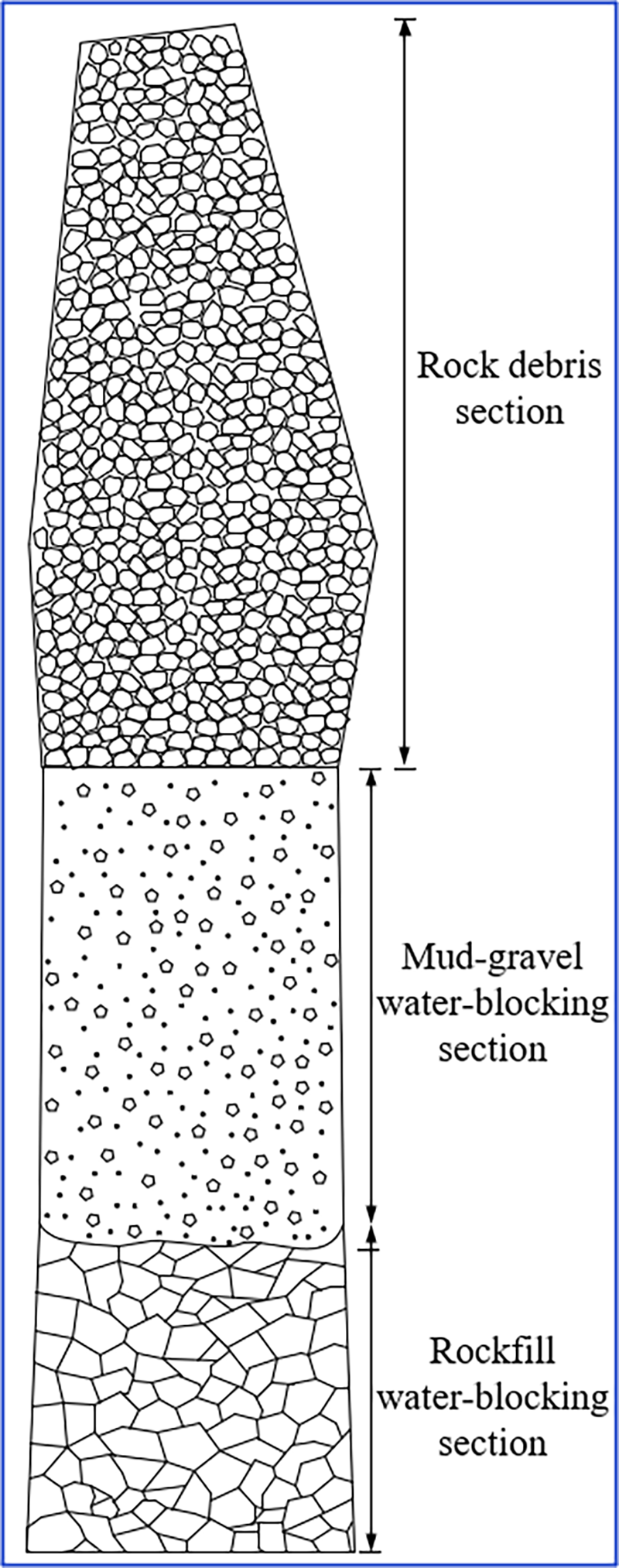
Figure 3: Collapse column macro-structural model
As mentioned above, extensive research has elucidated the morphological configuration, internal architecture, genetic mechanisms, and hydraulic properties of collapse columns. These investigations establish fundamental frameworks for analyzing their seepage dynamics while revealing critical formation processes. As preferential pathways for groundwater flow, collapse columns exhibit structural complexity and fill heterogeneity that significantly modulate seepage behavior. In order to more accurately predict and assess the impact of collapse columns on groundwater flow, further investigation into the seepage and water inrush mechanisms is necessary. Subsequent sections critically evaluate four pivotal research domains in collapse column hydromechanics: flow-solid coupling mechanism, seepage mechanism of fractured rock masses, flow regime transition mechanism, and characteristics of variable mass seepage, in order to outline the overall situation of research in this field.
3 The Fluid-Solid Coupling Mechanism and Seepage Characteristics of Karst Collapse Column
Mining-induced fractured zones (including surrounding rock damage, fault breccias, and collapse columns) constitute porous geological structures with complex seepage networks [35,36]. These systems exhibit hydromechanical behavior fundamentally controlled by rock-fluid interactions. The intensified fluid-solid coupling under excavation disturbances represents the key dynamic driver of water inrush events. Deciphering this coupling mechanism provides critical insights into seepage instability within collapse columns. This section systematically reviews advances in hydromechanical coupling theory and fractured media seepage dynamics.
3.1 The Fluid-Solid Coupling Mechanism of Karst Collapse Column
Classical seepage theory typically assumes rigid behavior in porous media like rock masses, where fluid pressure variations induce no structural deformation. In mining engineering practice, however, hydraulic instabilities primarily arise from dynamic interactions between fluid flow and rock deformation. Seepage forces exert dual mechanical effects on fractures: normal pressure altering stress distribution and tangential drag modifying flow pathways. Stress-dependent fracture aperture variations reciprocally regulate permeability coefficients and flow velocities. This interdependent fluid-stress system governs the hydro-mechanical coupling mechanisms during collapse column water inrushes. Explicit consideration of seepage-stress coupling proves essential for predicting and mitigating hydraulic hazards in fractured formations.
The foundational work on poromechanics originated with Terzaghi, who established the effective stress principle by conceptualizing fluid flow in deforming porous media as a coupled system. His one-dimensional consolidation model [37] remains a cornerstone in geomechanics. Building on this framework, Biot formulated the first three-dimensional consolidation theory through rigorous analysis of porous media deformation and pore pressure interactions. Key assumptions included incompressible Darcy flow and isotropic linear elastic behavior [38]. Subsequent extensions incorporated anisotropic media and dynamic loading conditions [39–42], significantly broadening the theory’s applicability. While these theoretical advances provide essential frameworks, field-scale geological complexities necessitate ongoing experimental validation to enhance model fidelity.
Li et al. [43] developed a nonlinear hydromechanical model for non-Darcy flow in saturated fractured media based on porous media effective stress theory, quantifying parameter-dependent system responses. Their analysis of pressurized fracture networks revealed bifurcation phenomena in coupled stress-seepage fields under non-Darcy flow regimes. Li et al. [44] designed a specialized shear-flow coupling apparatus to examine fracture network evolution under multifactor loading, experimental data demonstrated triphasic permeability-porosity evolution (initiation, acceleration, stabilization) during progressive shear displacement.
Recent advances in numerical modeling have facilitated high-resolution analysis of multiphysics coupling mechanisms in geological systems. For instance, Zhang et al. [45] employed FLAC3D to simulate stress-permeability interactions under coupled conditions, demonstrating how elevated pore pressure accelerates rock strength degradation. Building on fractured media seepage theory, Yao et al. [46] developed a dynamic fluid-solid coupling model incorporating particulate transport effects (Fig. 4), validated through COMSOL-based simulations of permeability evolution in heterogeneous formations.
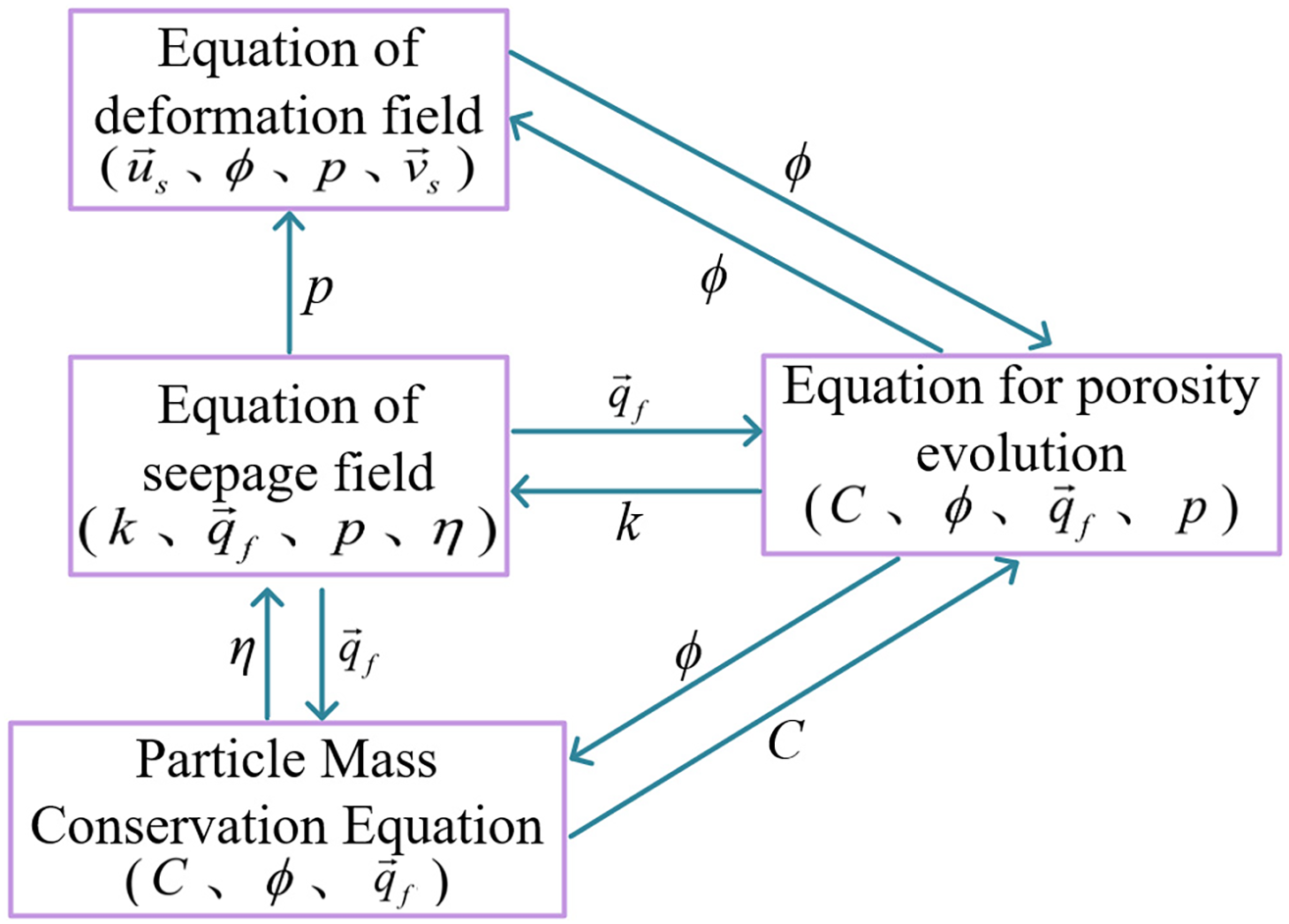
Figure 4: Coupling relationship between model equations. Adapted with permission from Reference [46]. 2014, Yao B
In the Fig. 4,
Extensive investigations of fluid-rock coupling mechanisms in geological formations have advanced substantially since the mid-20th century. Research methodologies combining theoretical frameworks, experimental simulations, and computational modeling have yielded critical insights into porous media hydrodynamics. Systematic investigations across multiple disciplines have established fundamental principles governing fluid transport through karst collapse columns.
3.2 Seepage Mechanism in Fractured Rock Mass
Fluid-solid coupling analysis reveals dynamic interplays between stress fields and seepage systems. Fractured rock masses exhibit distinctive structural configurations characterized by irregular geometries, angular discontinuities, stochastic fracture networks, and elevated porosity. These structural properties impart pronounced nonlinearity to stress-seepage interactions. Such nonlinear behavior governs both mechanical responses and hydrodynamic evolution patterns within geological media. Collapse column fill materials demonstrate reduced mechanical strength, enhanced pore connectivity, and accelerated fluid transmission compared to intact rock matrices. These structural heterogeneities drive flow regime transitions from Darcy-type to inertial-dominated dynamics. Recent investigations combine theoretical modeling with experimental validation to elucidate non-Darcy flow mechanisms in porous media systems.
Analyzing seepage behavior in fractured media under high-pressure groundwater advances understanding of collapse column water inrush mechanisms. Researchers have developed multiple theoretical models to characterize these processes. Darcy’s pioneering 1856 study established fundamental principles for flow through porous media, demonstrating a linear relationship between hydraulic gradient and velocity under low-permeability conditions. Subsequent investigations demonstrated non-Darcy flow behavior in heterogeneous media with high porosity and large particle sizes, where velocity and pressure gradient exhibit nonlinear correlations [47]. Elevated flow velocities and Reynolds numbers characterize such systems, particularly in complex fracture networks within collapse columns.
Prior research [48] systematically categorizes nonlinear phenomena in geohydraulic systems into six distinct classes: (1) Free-surface seepage dynamics, (2) non-Darcy flow characteristics, (3) variably saturated media behavior, (4) multiphase flow interactions, (5) heterogeneous media transport, (6) multiphysics coupling effects (fluid-solid-thermal-chemical interactions). Fractured media hydrology in collapse columns typically involves multiple interrelated phenomena from this classification framework. Current understanding of nonlinear flow dynamics in fractured systems remains limited compared to conventional Darcy flow models, no comprehensive theoretical framework currently exists to fully characterize these complex flow regimes. Two empirical models dominate current research applications: The power-law relationship and the quadratic resistance formulation [49,50]. Subsequent studies [51] have established specific application criteria for these models, as detailed in Table 1.
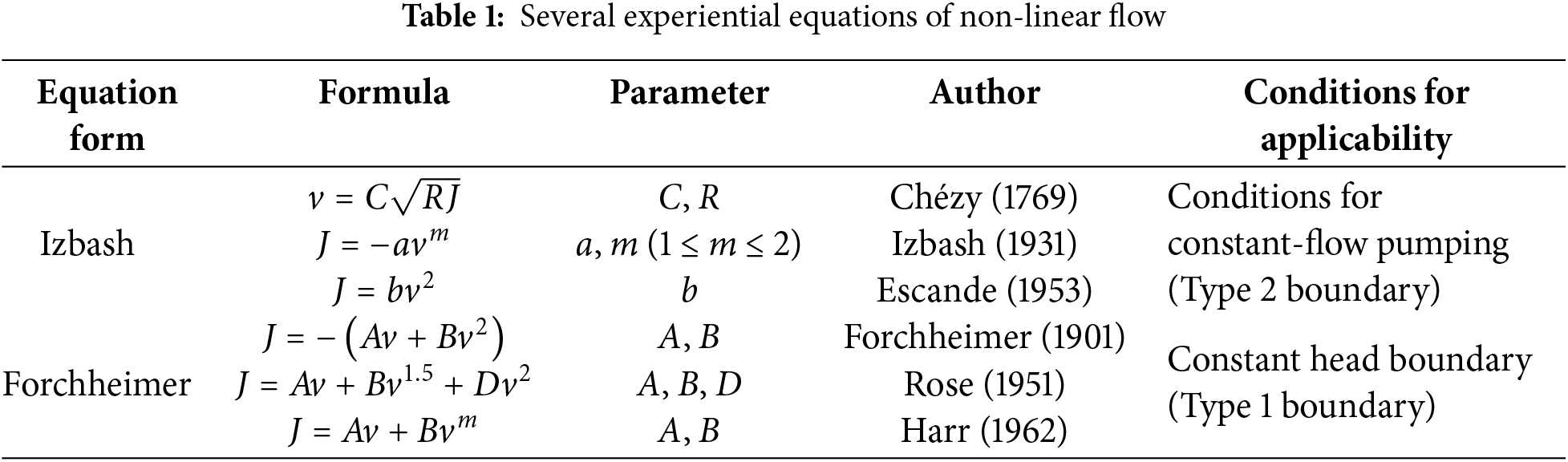
Since its formulation in 1901, the Forchheimer equation has undergone extensive permeability experiments confirming its effectiveness in modeling nonlinear seepage behavior at high Reynolds numbers [52–54]. The equation’s widespread adoption stems from its two physically meaningful terms representing viscous and inertial forces during fluid motion [55,56]. Viscous forces originate from internal fluid friction caused by velocity gradients, dominating laminar flow regimes characterized by orderly, parallel fluid layers [57]. Inertial forces reflect fluid mass resistance to acceleration changes, predominating in turbulent regimes marked by chaotic vortices and random velocity fluctuations [58]. The equation’s unique capacity to integrate both force components enables comprehensive description of non-Darcy flow across velocity ranges [59–61]. This dual-mechanism integration has motivated extensive research on empirical determinations of coefficients A and B within the equation framework [62,63].
In 1952, Sabri Ergun established a seminal empirical model for pressure gradients in granular beds through gas permeation experiments, correlating porosity and particle geometry with hydraulic resistance [64].
In the equation, n represents the porosity of the porous medium; d denotes the average particle diameter size within the porous medium; g stands for the gravitational acceleration; u represents the kinematic viscosity coefficient.
This formulation quantitatively links hydraulic parameters with porous media characteristics [65–68]. Subsequent advancements include Irmay’s 1964 nonlinear adaptation for unconsolidated media [69,70]:
Macdonald’s team [71] further refined the model through comprehensive seepage analyses of glass beads and granular materials across porosity ranges (0.33–0.92):
Comparative analysis reveals key variations in coefficients A and B across formulations, attributable to differing particle morphology and size distributions in experimental media [72–75]. This variability presents critical challenges in parameter selection for practical applications of the Forchheimer law.
Recent investigations [76–78] have advanced quantitative methods for determining viscous (kv) and inertial (ki) permeability coefficients in the Forchheimer equation, establishing the relationship ki = β · kvα/2. High-pressure gradient tests demonstrate nonlinear reductions in these coefficients with increasing porosity and rock mass heterogeneity. Enhanced computational models incorporating fracture tortuosity now enable improved prediction of permeability evolution and hydrodynamic instability risks in geologically vulnerable zones.
In addition, controlled seepage experiments under varying axial loads [79], particle gradation configurations [80], and initial void ratios have revealed permeability evolution patterns in fractured media. These investigations confirm the prevalence of Forchheimer-type flow over traditional Darcy flow regimes [81–84]. A non-Darcy flow model derived from the Forchheimer equation has been developed to simulate hydraulic fracture propagation in mining contexts [35]. Comparative experimental and analytical studies demonstrate that permeability degradation in porous reservoirs primarily stems from elastoplastic deformation bands, with thicker strata exhibiting enhanced transverse band formation sensitivity [85]. Fractal-derived nonlinear flow formulations incorporating clay interactions and particle migration effects have further advanced fractured media characterization, with experimental validation confirming model-predicted critical pressure gradients [86]. Confined compression-permeability testing has quantified particle size distribution evolution, introducing relative fracture rate as a key parameter linking porosity-permeability relationships in saturated fractured systems [87]. These studies have laid the theoretical foundation for the application of the Forchheimer equation in mine water inrushes associated with collapse columns.
The Izbash equation, an empirical formula derived from experimental data (Table 1), characterizes flow regimes through its exponent values. With exponent m = 1 matching Darcy’s law for linear flow and m = 2 aligning with Forchheimer’s turbulence model, the coefficient quantifies deviations from linear seepage behavior [88–90]. Extensive research has focused on parameterizing coefficients a and m. Experimental studies demonstrate that during laminar flow, coefficient a shows positive correlation with non-Darcy factor E, while transitional flows reveal inverse correlation patterns [91]. Systematic investigations of fractured media under high confinement reveal pressure-dependent nonlinearity: coefficient a exhibits threshold-limited growth, while m converges toward unity (0.55 → 1.10), indicating reduced flow complexity at elevated pressures [92].
In summary, current research on non-Darcy flow in fractured media has undergone extensive investigation. Experimental validation remains critical for seepage theory development, with empirical studies being widely implemented due to their methodological transparency. Geological discontinuities associated with mining operations frequently exhibit complex fluid transport behaviors, particularly in zones susceptible to hydraulic instability. These structural features demonstrate characteristic non-Darcy flow patterns requiring specialized analysis. Through integrated theoretical and experimental approaches, researchers have substantially advanced understanding of fluid migration mechanisms in fractured systems. These advancements establish fundamental principles for hydraulic risk mitigation in subsurface engineering applications.
4 Disaster-Causing Mechanism of Flow Transition in Collapse Column
Non-Darcy flow in fractured media establishes the physical basis for hydraulic state transitions. Critical seepage velocities induce permeability transformations as flow regimes shift from laminar to turbulent. This flow transition mechanism connects microscopic seepage behavior with macroscopic hydraulic disasters, governing the complete progression of water inrush events. Water inrush events during mining operations predominantly result from coupled excavation-induced stress redistribution and high-pressure hydraulic forces, triggering abrupt groundwater migration from aquifers into subsurface voids. During this process, groundwater migration evolves through sequential stages: fine-pore aquifer movement → fracture-dominated conduit flow → terminal convergence in mining cavities, with distinct flow regime transitions. Characterizing fluid flow regimes and analyzing their transition mechanisms provide critical insights for assessing water inrush risks in collapse columns and predicting discharge magnitudes.
Chilton et al. [93] established the Reynolds number as a critical parameter for characterizing non-Darcy flow regimes (Eq. (4)). This dimensionless quantity quantifies the ratio of inertial to viscous forces in fluid systems.
In the equation, Re represents the Reynolds number; ρ is the fluid density; v is the seepage velocity; d is the diameter of the medium particles; and u is the dynamic viscosity coefficient.
Experimental evidence indicates Darcy’s law governs laminar flow when 1 < Re < 10, demonstrating linear velocity-gradient correlation. Beyond this threshold, transitional flow regimes emerge with distinct non-Darcy characteristics [94]. Subsequent experimental work by BASAK systematically categorized porous media flow into three regimes: low-velocity non-Darcy flow, Darcy flow, and high-velocity non-Darcy flow [95], as illustrated in Fig. 5.
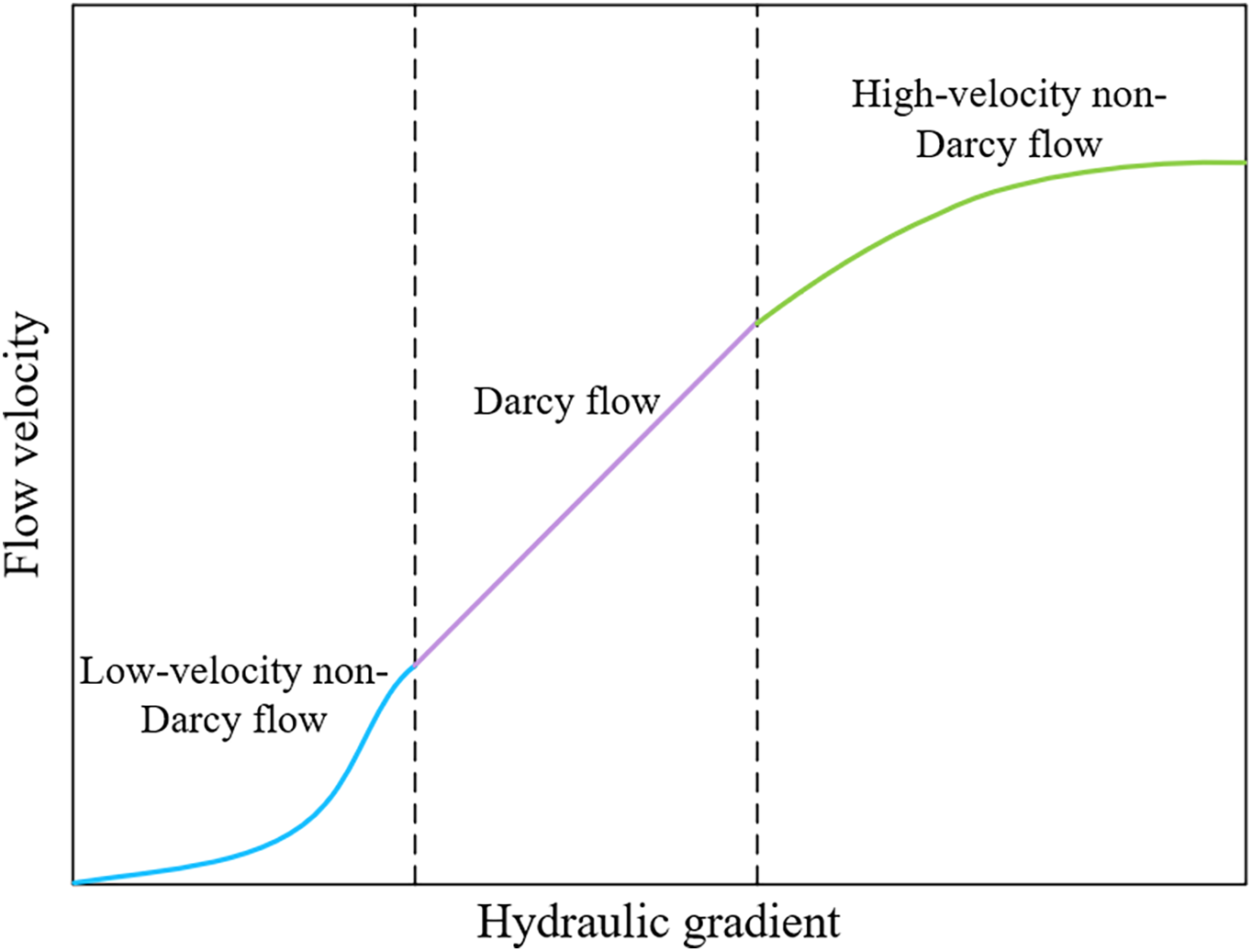
Figure 5: Hydraulic gradient-seepage velocity relationship curve
The flow regime transition in collapse columns depends significantly on granular characteristics and void geometry within infill materials. Recent experimental investigations have demonstrated nonlinear flow behavior in granular media under extreme hydraulic gradients (>500) [96]. A specialized testing apparatus was designed to simulate fracture networks using spherical analogs, with systematic measurements conducted across six uniform particle sizes. Three characteristic flow regimes were identified through gradient-controlled experiments: linear laminar flow, nonlinear transitional flow, and fully developed turbulence. Threshold analysis revealed transitional flow initiation occurring at hydraulic gradients exceeding 145.
Contemporary analyses of collapse column hydrodynamics typically integrate three distinct flow regimes. Fluid migration progresses sequentially from Darcy laminar flow in aquifer formations to nonlinear flow dynamics within fractured media, ultimately achieving turbulent flow conditions in mining voids. Initial aquifer flows obey Darcy’s law with velocity proportional to hydraulic gradients. Structural degradation in collapse columns induces porosity amplification, triggering nonlinear flow patterns where inertial forces dominate. Terminal flow phases exhibit full turbulence requiring Navier-Stokes formulations for accurate characterization.
The Navier-Stokes equations govern viscous fluid motion by modeling velocity and pressure field variations through conservation principles of mass, momentum, and energy. While fundamental for classical fluid dynamics, these equations prove inadequate for characterizing fluid transport through fractured geological media.
In the equation, the subscript “NS” refers to the Navier-Stokes flow field; FNS represents the body force; v is the velocity; ρ is the fluid density; and η is the hydrodynamic viscosity coefficient.
Previous analyses have established the limitations of conventional models in addressing nonlinear flow through fractured systems. While the Forchheimer formulation captures non-Darcy behavior, its omission of viscous stress components prevents accurate characterization of interfacial resistance effects at fracture-pore boundaries, particularly underestimating pressure gradients in low-velocity regimes. Given the critical role of fractured zones in flow regime transitions within geological structures, improved mathematical representations of porous media transport become essential. By integrating viscous shear components from Navier-Stokes theory with Darcy’s framework, researchers developed an enhanced hydrodynamic model [97–99]:
In the equation, the subscript “B” denotes the Brinkman flow field; k is the permeability; and I represents the identity matrix.
The integration of Darcy, Navier-Stokes, and Brinkman equations has gained significant traction in developing multi-regime fluid models to investigate water inrush mechanisms in karst collapse columns. Recent investigations [100] examine non-linear flow patterns within fracture networks under mining disturbances, developing a stress-independent computational framework through coupled finite element/volume methods. Fig. 6 demonstrates the hydrodynamic transition from viscous to inertial dominance during fluid migration through rock discontinuities. High-velocity flows exhibit rapid pathway convergence with pronounced directional reorganization, while turbulent vortices at structural interfaces illustrate momentum redistribution mechanisms governing inrush dynamics.
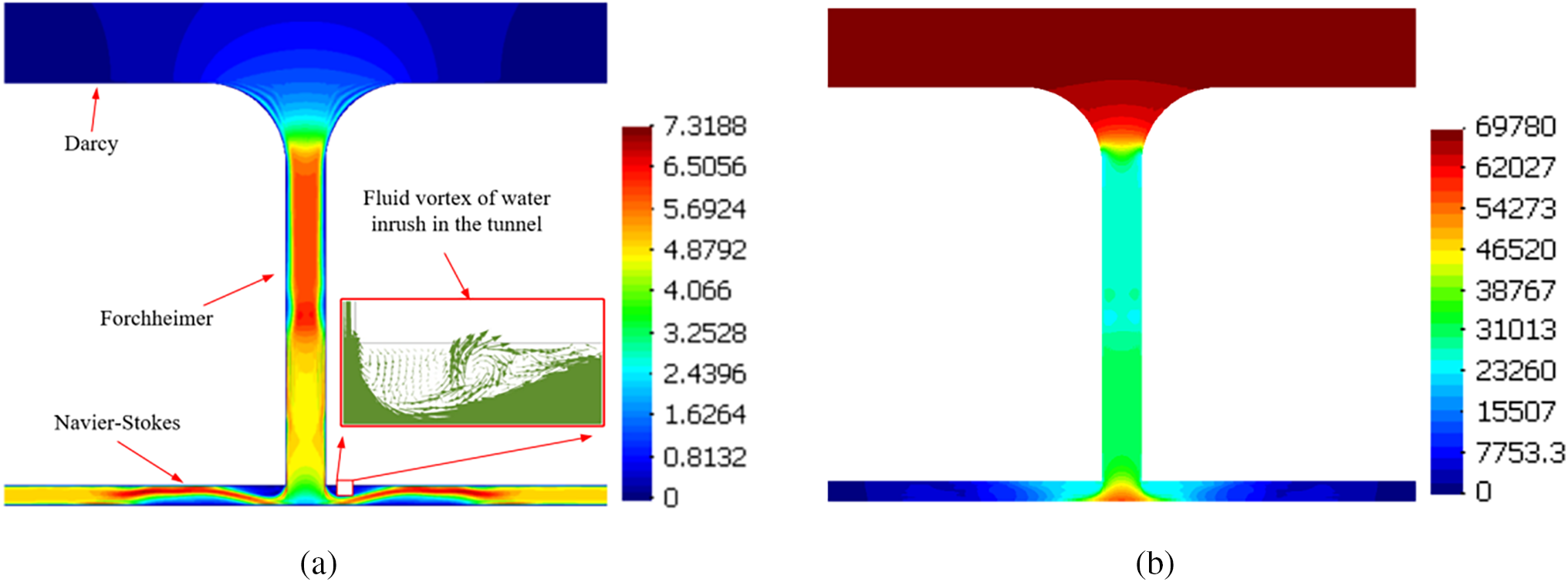
Figure 6: Space-time distribution of the flow velocity and pressure of water inrush. (a) Velocity distribution cloud map (t = 300 s); (b) Pressure distribution cloud map (t = 300 s). Adapted with permission from Reference [100]. 2015, Shi W
Furthermore, Wu et al. [101] established a six-stage vertical division of collapse columns from bottom to top (Fig. 7), corresponding to evolutionary states during six consecutive time intervals. The upper region above each stage interface follows Forchheimer-modified Brinkman equations for porous media, while the lower region below the interface adheres to Navier-Stokes turbulence equations. COMSOL simulations systematically investigated the complete transition process from non-Darcy high-velocity flow to Navier-Stokes turbulent flow during seepage-induced water inrush. Results demonstrate gradual expansion of turbulence equation-dominated zones with diminishing porous media regions, accompanied by progressively increasing flow velocities. Over sufficient time duration, the entire collapse column transitions to turbulent flow, intensifying water inrush velocities and hydrodynamic risks through complete flow regime conversion.
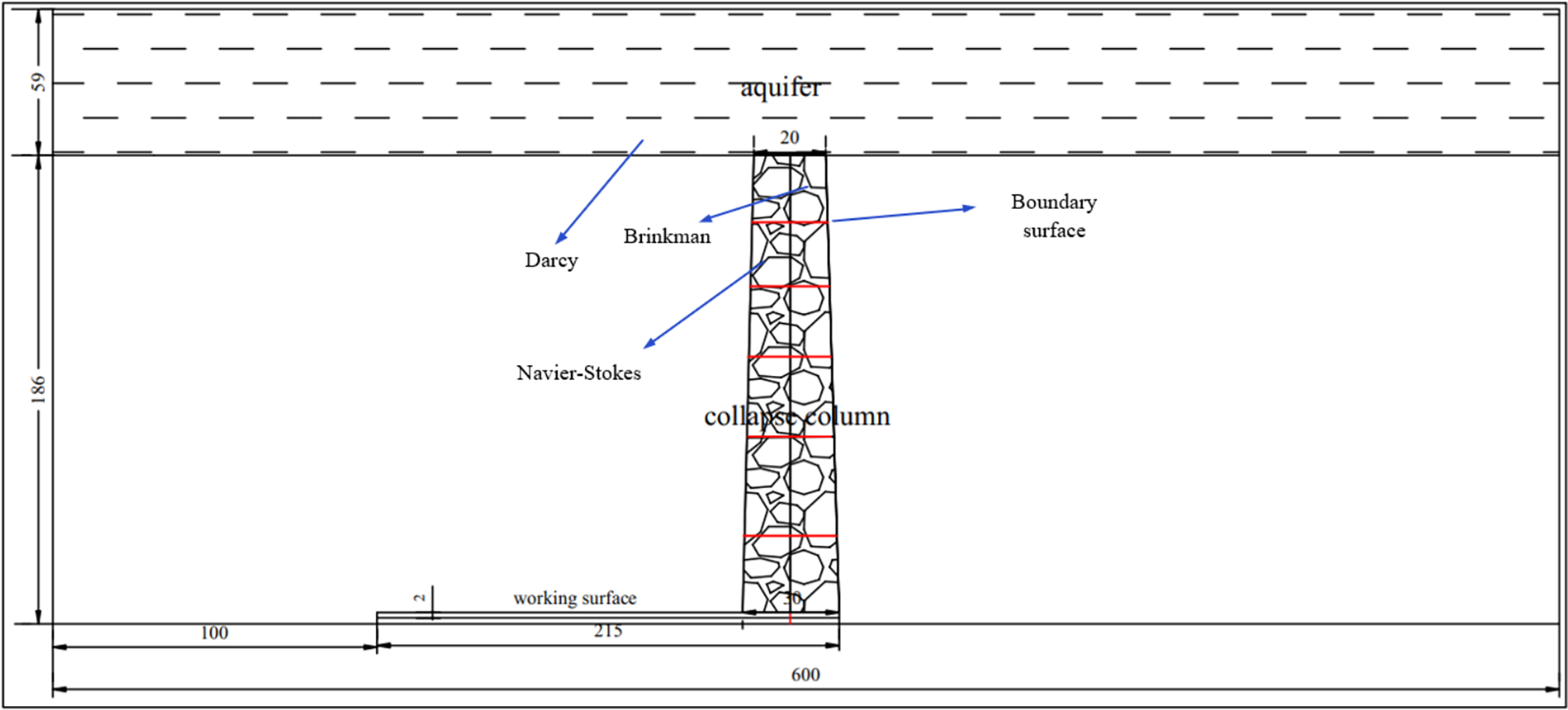
Figure 7: Numerical simulation of different time steps of water inrush in collapse column
Recent investigations into flow regime transitions within collapse columns have received significant research attention. Instrumentation constraints have limited experimental studies compared to theoretical and numerical approaches in this domain. Current experimental efforts predominantly examine fractured media seepage characteristics, simulating hydromechanical behaviors within mining-induced fracture networks. Numerical simulations enable visualization of groundwater migration pathways from aquifers through collapse columns to underground excavations. These computational tools facilitate parametric analysis of hydrogeological conditions, including initial hydraulic pressure, porosity distribution, and collapse column morphology. Such simulations provide critical insights into flow regime evolution and its role in water inrush mechanisms.
5 Variable-Mass Seepage Mechanism in Collapse Column
The dynamic coupling of flow regime transitions and structural evolution in collapse columns presents a pivotal scientific challenge in water inrush mechanisms. Hydrodynamic analysis demonstrates spatiotemporal evolution patterns, while particulate migration introduces complex feedback within these geological structures. Continuous particle transport drives architectural modification through mass variation effects, concurrently inducing temporal permeability evolution in seepage pathways.
Mining disturbances trigger biphasic mechanical responses: rigid block displacement precedes contact zone comminution under progressive loading. Fragmentation-derived particulates redistribute through fluid transport, dynamically altering pore-fracture network hydraulics. The synergy between fluid dynamics and structural disintegration facilitates catastrophic flow transformation via coupled seepage-stress-damage interactions [46]. This multiscale interaction framework provides systematic understanding of critical transition conditions in water inrush phenomena.
Under groundwater action, the internal filling material of the collapse column undergoes continuous dissolution, erosion, and abrasion processes, leading to the gradual development of microstructural features such as solution pores and fractures along structural planes. These physicochemical processes alter the micro-porous structure of the rock, thereby inducing significant changes in macroscopic seepage parameters. When compressive fragmentation between rock blocks combines with the migration and loss of fine particles transported by water flow [53], the permeability of the collapse column exhibits distinct stochastic and time-dependent characteristics. The dynamic evolution process can be divided into five stages (Fig. 8): Initial phase, infiltration phase, fragmentation phase, feedback phase and critical phase.
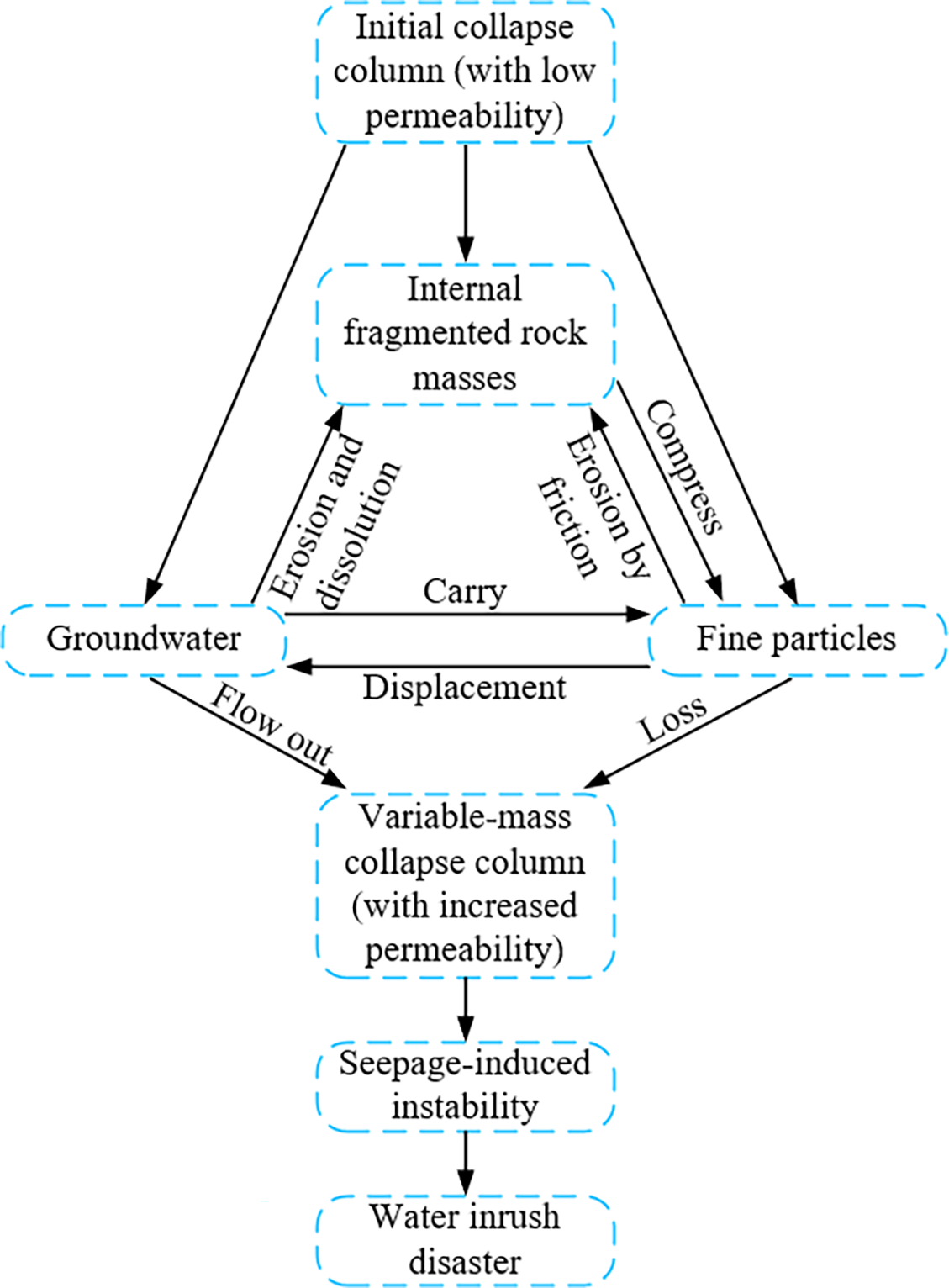
Figure 8: Mechanism of permeability variation in collapse columns
Current research on particulate migration in fractured media primarily utilizes standardized cylindrical specimens (50 mm × 100 mm) composed of graded particles and cementitious materials. Using combined experimental and theoretical approaches, Wang et al. [102] investigated time-dependent fine particle migration and loss mechanisms in mining-induced fractured zones under groundwater erosion. They developed metrics for mass loss rate and particle migration rate based on total mass change observations. Zhang et al. [103] designed a geostress-coupled experimental system to study water-mud inrush phenomena, identifying particle migration within fractured zones as the primary triggering mechanism. Their work further proposed a permeability evolution model for fault fractured zones.
The variable-mass seepage behavior in collapse columns is significantly influenced by filling material properties, including particle size distribution and cementation strength. In columns with poorly sorted fillings (such as gravel-silt mixtures), fine particles are readily eroded under seepage forces, resulting in continuous material removal and permeability enhancement. Zhang et al. [104] characterized three distinct phases during particle-loss-induced water breakthroughs: initial seepage, catastrophic instability, and pipe-flow eruption. Zhang and Cao et al. [105,106] fabricated graded specimens simulating mining-induced fractured zones and conducted mass change seepage experiments under varying axial displacements, confining pressures, and pore water pressures. The experimental results revealed particle migration patterns, pore structure instability mechanisms, and time-dependent flow velocity characteristics, and proposed a triaxial stress-dependent permeability evolution model (Fig. 9).
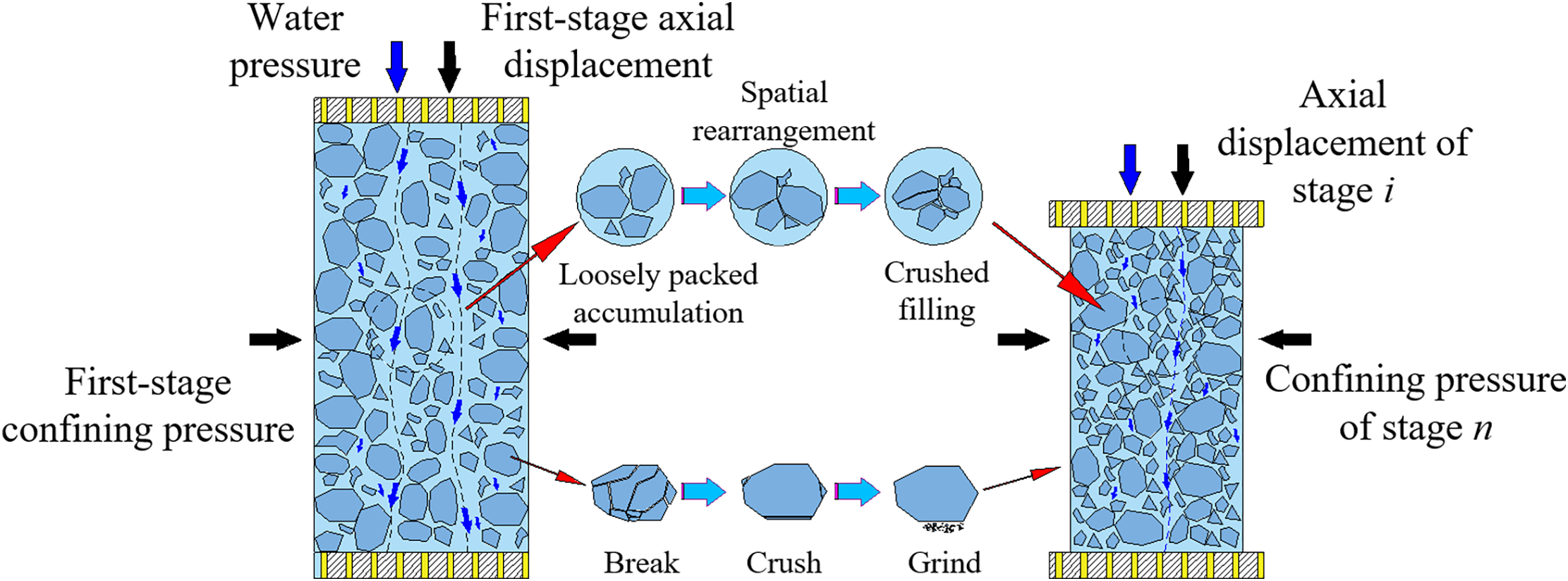
Figure 9: Physical model of permeability evolution in fractured rock mass under triaxial stress. Reprinted with permission from Reference [105]. 2022, Zhang S
In addition, extensive research has been conducted on collapse column seepage mechanisms through theoretical analysis and numerical modeling. Yao et al. [107] proposed a dual porosity framework composed of matrix porosity and fracture networks as a viable approach for studying rock mass seepage characteristics, as illustrated in Fig. 10a. Rock mechanics studies indicate that rock masses undergo three deformation phases under loading: (1) Elastic deformation phase: reversible aperture changes occur in fractures without structural damage. (2) Yield phase: progressive microcracking initiates when loads exceed yield strength, leading to irreversible structural alterations. (3) Post-peak phase: catastrophic failure occurs with significant increases in fracture connectivity and permeability, as shown in Fig. 10b.
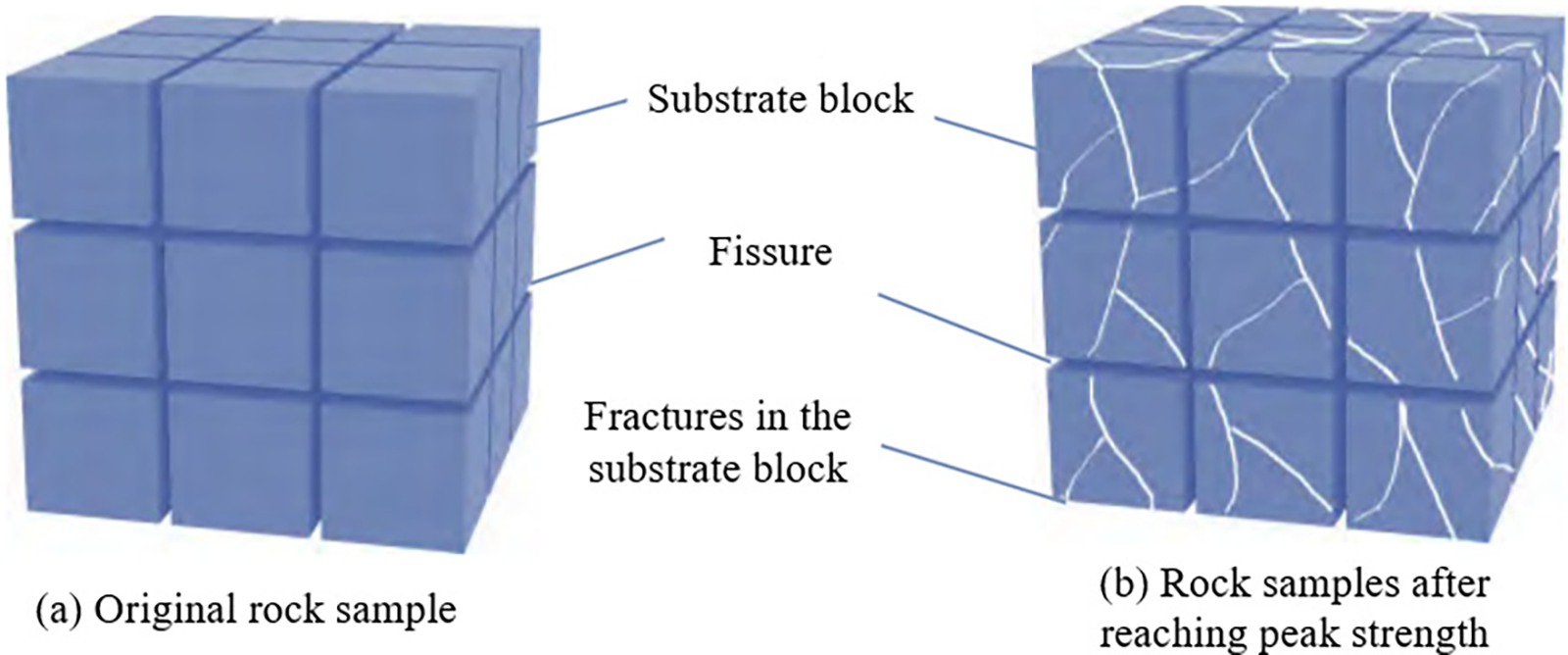
Figure 10: Geometric model of rock damage-seepage. Reprinted with permission from Reference [107]. 2023, Yao B
Cao et al. [10] developed a particle mass conservation equation, seepage field equation, and porosity-permeability relationship, incorporating the heterogeneous distribution of fractured rock masses within collapse columns. The study identified three distinct water inrush stages under groundwater erosion: initial steady-state flow, rapid acceleration, and stabilized seepage (Fig. 11).
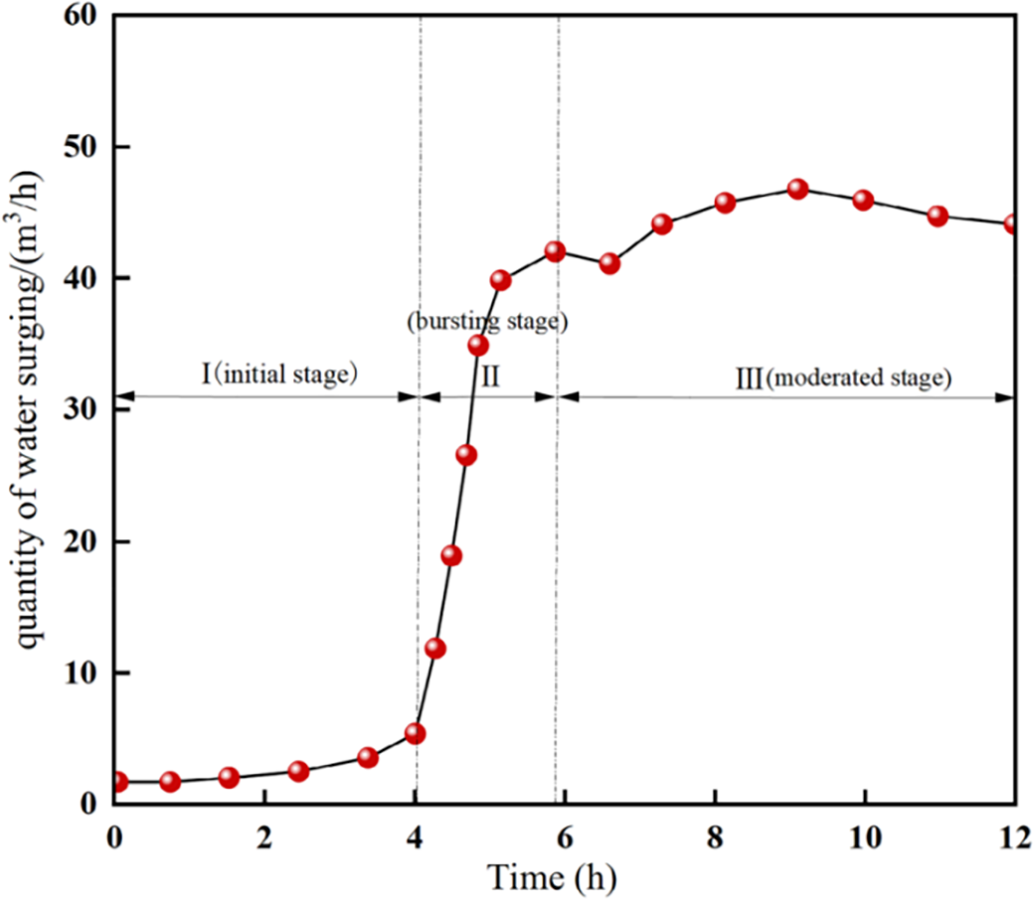
Figure 11: Variation curve of inflow water volume in the collapse column
In summary, particle migration-induced mass loss in collapse columns and its effects on seepage behavior have been comprehensively studied through experimental, theoretical, and numerical approaches. Seepage experiments primarily utilize triaxial seepage testing systems to characterize flow behavior in fractured samples under varying grain size distributions, confining pressures, axial stresses, and initial porosities. Combined theoretical and numerical modeling provides insights into particle transport pathways within collapse columns and the formation mechanisms of breakthrough channels under groundwater flow. Additionally, numerical simulations enable parametric studies of water inrush mechanisms under conditions such as different homogeneity levels, skeleton-to-matrix mass ratios, and column dimensions.
6 Conclusions and Suggestions for Further Research
The investigation into karst collapse columns and their associated water inrush mechanisms has yielded critical advancements in understanding their morphological complexity, hydrogeological behavior, and dynamic interactions under mining-induced stresses. While significant progress has been made in characterizing the fluid-solid coupling mechanisms and non-Darcy seepage behaviors within fractured rock masses, several unresolved challenges persist. The genesis of collapse columns remains debated, with existing theories often constrained to specific geological contexts, highlighting the need for a unified framework that accounts for multi-factor interactions such as dissolution, tectonic forces, and groundwater dynamics. Experimental studies, though foundational, face limitations in capturing the full spectrum of multi-field coupling effect-particularly under high stress, high temperature, and high hydraulic pressure-which dominate deep mining environments. Furthermore, while numerical models have effectively simulated flow regime transitions from Darcy laminar to turbulent flow, experimental validation of these transitions at critical interfaces (e.g., aquifer-collapse column-tunnel systems) remains sparse, limiting the practical application of theoretical insights.
The dynamic evolution of permeability due to particle migration and mass loss within collapse columns introduces additional complexity. Although theoretical and numerical studies have delineated erosion-seepage coupling mechanisms, direct observation of particle migration paths and pore structure evolution under real-world conditions remains technically challenging. This gap underscores the necessity for advanced experimental systems capable of integrating triaxial stress, fluid flow, and real-time imaging to bridge theoretical predictions with empirical validation. Future research should prioritize interdisciplinary approaches that combine geomechanical modeling, high-resolution monitoring technologies, and field-scale validation to address the stochastic nature of collapse column development and refine risk assessment frameworks. By enhancing predictive accuracy and developing targeted prevention strategies, such efforts will mitigate water inrush disasters, ensuring safer and more sustainable mining practices in hydrogeologically vulnerable regions.
Acknowledgement: Not applicable.
Funding Statement: This research is supported by the Natural Science Foundation of Henan Province (242300421246, 222300420007, 232300421134), the National Natural Science Foundation of China (52004082, 52174073, 52274079, 42402255), the Science and Technology Project of Henan Province (232102321098), Zhongyuan Science and Technology Innovation Leading Talent Program (244200510005), the Program for Science & Technology Innovation Talents in Universities of Henan Province (24HASTIT021), the Program for the Scientific and Technological Innovation Team in Universities of Henan Province (23IRTSTHN005), and the National Postdoctoral Researchers Program Foundation of China (GZC20230709).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Zhengzheng Cao, Shuaiyang Zhang; data collection: Cunhan Huang; analysis and interpretation of results: Feng Du, Zhenhua Li, Shuren Wang; graphics and curves: Wenqiang Wang, Minglei Zhai; draft manuscript preparation: Shuaiyang Zhang. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data and models generated or used during the study appear in the submitted article.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. Hower JC, Finkelman RB, Eble CF, Arnold BJ. Understanding coal quality and the critical importance of comprehensive coal analyses. Int J Coal Geol. 2022;263(II):104120. doi:10.1016/j.coal.2022.104120. [Google Scholar] [CrossRef]
2. Amir Raza M, Karim A, Aman MM, Al-Khasawneh MA, Faheem M. Global progress towards the coal: tracking coal reserves, coal prices, electricity from coal, carbon emissions and coal phase-out. Gondwana Res. 2025;139:43–72. doi:10.1016/j.gr.2024.11.007. [Google Scholar] [CrossRef]
3. Wang G, Ren S, Pang Y, Qu S, Zheng D. Development achievements of Chinese coal industry during the 13th five-year plan period and implementation path of “dual carbon target ”. Coal Sci Technol. 2021;49(9):1–8. doi:10.13199/j.cnki.cst.2021.09.001. [Google Scholar] [CrossRef]
4. Park JH, Lee YJ, Jin MH, Park SJ, Lee DW, Bae JS, et al. Enhancement of slurryability and heating value of coal water slurry (CWS) by torrefaction treatment of low rank coal (LRC). Fuel. 2017;203:607–17. doi:10.1016/j.fuel.2017.03.016. [Google Scholar] [CrossRef]
5. Khanal M, Qu Q, Zhu Y, Xie J, Zhu W, Hou T, et al. Characterization of overburden deformation and subsidence behavior in a kilometer deep longwall mine. Minerals. 2022;12(5):543. doi:10.3390/min12050543. [Google Scholar] [CrossRef]
6. Liu W, Zhao J, Kong D. A quantitative method for water inrush risk from fractured rocks based on nonlinear seepage theories. J China Coal Soc. 2024;49(11):4520–41. doi:10.13225/j.cnki.jccs.2023.1391. [Google Scholar] [CrossRef]
7. Li J. Study on separated layer water burst mechanism for weakly cemented giant thick glutenite. Coal Sci Technol. 2024;52(2):209–18. doi:10.12438/cst.2023-1681. [Google Scholar] [CrossRef]
8. Ma D, Li Q, Zhang J, Liu Y, Hou W. Pore structure characterization and nonlinear seepage characteristics of rock mass in fault fracture zones. J China Coal Soc. 2023;48(2):666–77. doi:10.13225/j.cnki.jccs.S022.1678. [Google Scholar] [CrossRef]
9. Yin S, Lian H, Liu D, Yin H. 70 years of investigation on Karst collapse column in North China Coalfield: cause of origin, mechanism and prevention. Coal Sci Technol. 2019;47(11):1–29. doi:10.13199/j.cnki.cst.2019.11.001. [Google Scholar] [CrossRef]
10. Cao Z, Zhang S, Li Z, Du F, Huang C, Wang W. Numerical research on disastrous mechanism of seepage instability of karst collapse column considering variable mass effect. Sci Rep. 2024;14(1):13900. doi:10.1038/s41598-024-63344-w. [Google Scholar] [PubMed] [CrossRef]
11. Li X, Wang L. Analysis and prediction of development characteristics of collapse column in Liyazhuang mine field. Coal Min Mod. 2023;32(2):75–8,83. doi:10.13606/j.cnki.37-1205/td.2023.02.006. [Google Scholar] [CrossRef]
12. Zhao J, Guo M, Li W. Morphological and fabric characteristics of Karst collapse pillars in Xishan coalfield. J China Coal Soc. 2020;45(7):2389–98. doi:10.13225/j.cnki.jccs.dz20.0443. [Google Scholar] [CrossRef]
13. Ding T, Wang M, Liu M, Zhu C, Wen D, Chen X. Technology of accurately constructing collapse column water plugging plug in laminated multi branch horizontal wells. Coal Sci Technol. 2022;50(7):244–51. doi:10.13199/j.cnki.cst.2020-0936. [Google Scholar] [CrossRef]
14. Jiang X. Formation mechanism of collapse pillar dark structures in Huainan Coalfield. China Min Mag. 2024;33(S2):296–300. doi:10.12075/j.issn.1004-4051.20241414. [Google Scholar] [CrossRef]
15. Zhao J, Wang J, Yang G, Guo M. Pillar wall angles of karst collapse pillars in the Xishan coalfield: characteristics and implications. Coal Geol Explor. 2024;52(9):23–30. doi:10.12363/issn.1001-198. [Google Scholar] [CrossRef]
16. Li A, Li Y, Liu C, Ji Y, Wang F, Liu Y, et al. Water inrush mechanism and engineering application of concealed collapse column in coal seam floor. Coal Sci Technol. 2024;52(S2):142–52. doi:10.12438/cst.2022-1364. [Google Scholar] [CrossRef]
17. Kelsall PC, Case JB, Chabannes CR. Evaluation of excavation-induced changes in rock permeability. Int J Rock Mech Min Sci Geomech Abstr. 1984;21(3):123–35. doi:10.1016/0148-9062(84)91530-4. [Google Scholar] [CrossRef]
18. Guo Q. Analysis of developmental regularity and major controlling factors of collapse columns in xiqu coal field. Coal Technol. 2023;42(12):22–6. doi:10.13301/j.cnki.ct.2023.12.005. [Google Scholar] [CrossRef]
19. Li D, Lin Z, Yang D. The law of water inrush disaster of collapse column considering the influence of fillings activation. Saf Coal Mines. 2023;54(5):113–20. doi:10.13347/j.cnki.mkaq.2023.05.017. [Google Scholar] [CrossRef]
20. Liu J, Shen H, Xi J, Li Q, Zhao J, Li M. Improving the prediction accuracy of coalfield collapse column via diffraction wave imaging. J China Coal Soc. 2021;47(9):3442–50. doi:10.13225/j.cnki.jccs.2021.1235. [Google Scholar] [CrossRef]
21. Yang W, Zhou Z. Analysis of rock mass structure of Karst collapse column. J Huainan Min Inst. 1997;17(2):1–7. [Google Scholar]
22. Hu B, Song X. Deep Karst cave and collapse column formation mechanism in Huaibei Coalfield. Coal Geol China. 1997;9(2):47–9. [Google Scholar]
23. Zhang M, Yin S. Forming process of subsided column in coalfields of North China. Coal Geol Explor. 2007;2007(6):26–9. [Google Scholar]
24. Hou E, Xia Y, Fan H, Jv T. Cause analysis and prediction of mine collapse column. Northwest Geol. 1994;27(2):18–22. [Google Scholar]
25. Qian Z, Lu C, Gong Q, Wu X, Wang B. Mechanism and application of high pressure grouting in karst collapse column with vein-like water channel. Coal Sci Technol. 2024;2024:1–12. [Google Scholar]
26. Atanacković N, Štrbački J, Živanović V, Davidović J, Gardijan S, Stojadinović S. Hydrochemistry-based statistical model for sourcing groundwater inrush into underground mining works: a case study in eastern serbia. Mine Water Environ. 2024;43(2):313–25. doi:10.1007/s10230-024-00986-2. [Google Scholar] [CrossRef]
27. Mugova E, Molaba L, Wolkersdorfer C. Understanding the mechanisms and implications of the first flush in mine pools: insights from field studies in Europe’s deepest metal mine and analogue modelling. Mine Water Environ. 2024;43(1):73–86. doi:10.1007/s10230-024-00969-3. [Google Scholar] [CrossRef]
28. Li P. Hazard source effect and location experiment of concealed water disaster in coal seam floor. Coal Geol Explor. 2021;49(4):178–84. doi:10.3969/j.issn.1001-1986.2021.04.021. [Google Scholar] [CrossRef]
29. Tian G. Comprehensive exploration technology for development characteristics of large-scale water-flowing collapse column. Coal Eng. 2021;53(6):63–7. [Google Scholar]
30. Zhang J, Sun N, Liu Z, Qi Z. Electromagnetic methods in the detection of water hazards in coal mines: a review. Coal Geol Explor. 2023;51(2):301–16. doi:10.12363/issn.1001-1986.22.12.0962. [Google Scholar] [CrossRef]
31. Li Z, Zheng S, Shi Z, Wang Y. Prevention and control technology of goaf water hazard in unauthorized mining areas of extremely soft and medium-thick coal seams. Coal Geol Explor. 2021;49(6):167–74. doi:10.3969/j.issn.1001-1986.2021.06.020. [Google Scholar] [CrossRef]
32. Zhang H, Zhai X, Wu J, Shen S. Study of collapse column water inrush under fluid-solid coupling effect of coal seam mining in deep. J Mining Strata Control Eng. 2017;22(5):102–5. doi:10.13532/j.cnki.cn11-3677/td.2017.05.026. [Google Scholar] [CrossRef]
33. Zhang B, Chen Z. Distribution of karstic collapse columns of North-China type coal field and its hydrogeologic significance. J Liaoning Tech Univ. 1996;3:44–7. [Google Scholar]
34. Yang W, Zhou Z, Li Z. Analysis of the filling characteristics of karstic collapse pillars and its reactivation-induced water-conducting. Carsol Sin. 2001;4:34–8. [Google Scholar]
35. Yang T, Chen S, Zhu W, Meng Z, Gao Y. Water inrush mechanism in mines and nonlinear flow model for fractured rocks. Chin J Rock Mech Eng. 2008;27(7):1411–6. [Google Scholar]
36. Ihm M, Lee H. Analysis of geological factors for risk assessment in deep rock excavation in South Korea. Tunn Undergr Sp. 2021;31(4):211–20. [Google Scholar]
37. Terzaghi K. Theoretical soil mechanics. New York, NY, USA: Wiley; 1943. [Google Scholar]
38. Biot M. Theory of elasticity and consolidation for a porous anisotropic solid. J Appl Phys. 1954;26(2):182. doi:10.1063/1.1721956. [Google Scholar] [CrossRef]
39. Biot M. Mechanics of deformation and acoustic propagation in porous media. J Appl Phys. 1962;33(4):1482. doi:10.1063/1.1728759. [Google Scholar] [CrossRef]
40. Fagbemi S, Tahmasebi P. Coupling pore network and finite element methods for rapid modelling of deformation. J Fluid Mech. 2020;897:A20. doi:10.1017/jfm.2020.381. [Google Scholar] [CrossRef]
41. Studeník O, Isoz M, Šourek M, Kočí P. OpenHFDIB-DEM: an extension to OpenFOAM for CFD-DEM simulations with arbitrary particle shapes. SoftwareX. 2024;27(2):101871. doi:10.1016/j.softx.2024.101871. [Google Scholar] [CrossRef]
42. Zamani M, Knez D. Experimental investigation on the relationship between biot’s coefficient and hydrostatic stress for enhanced oil recovery projects. Energies. 2023;16(13):4999. doi:10.3390/en16134999. [Google Scholar] [CrossRef]
43. Li S, Chen Z, Miao X, Mao X. Bifurcation of fluid-solid coupling flow in broken rock. J China Coal Soc. 2008;7:754–9. [Google Scholar]
44. Li Q, Ma D, Zhang J, Liu Y, Hou WT. Mining-induced shear deformation and permeability evolution law of crushed rock mass in fault zone. Coal Geol Explor. 2023;51(8):150–60. doi:10.12363/issn.1001-1986.23.01.0022. [Google Scholar] [CrossRef]
45. Zhang C, Song W, Li T, Fu J, Li Y. Study on stress seepage coupling model and numerical simulation of fractured rock mass. J Mining Saf Eng. 2020;38(6):1220–30. doi:10.13545/j.cnki.jmse.2020.0267. [Google Scholar] [CrossRef]
46. Yao B, Mao X, Wei J, Wang D. Study on coupled fluid-solid model for collapse columns considering the effect of particle transport. J China Univ Min Technol. 2014;43(1):30–5. doi:10.13247/j.cnki.jcumt.000007. [Google Scholar] [CrossRef]
47. López J, Toledo M, Moran R. A unified view of nonlinear resistance formulas for seepage flow in coarse granular media. Water. 2021;13(14):1967. doi:10.3390/w13141967. [Google Scholar] [CrossRef]
48. Chai J. Nonlinear problems in rock and soil mass hydraulics. Rock Soil Mech. 2003;S2:159–62. doi:10.16285/j.rsm.2003.s2.036. [Google Scholar] [CrossRef]
49. Yang T, Shi W, Li S, Yang X, Yang B. State of the art and trends of water-inrush mechanism of nonlinear flow in fractured rock mass. J China Coal Soc. 2016;41(7):1598–609. doi:10.13225/j.cnki.jccs.2016.0336. [Google Scholar] [CrossRef]
50. Elsanoose A, Abobaker E, Khan F, Rahman M, Aborig A, Butt S. Characterization of a non-darcy flow and development of new correlation of non-darcy coefficient. Energies. 2022;15(20):7616. doi:10.3390/en15207616. [Google Scholar] [CrossRef]
51. Moutsopoulos K, Tsihrintzis V. Approximate analytical solutions of the Forchheimer equation. J Hydrol. 2005;309(1–4):93–103. doi:10.1016/j.jhydrol.2004.11.014. [Google Scholar] [CrossRef]
52. Li Z, Wan J, Zhan H, Cheng X, Chang W. Particle size distribution on Forchheimer flow and transition of flow regimes in porous media. J Hydrol. 2019;574(3):1–11. doi:10.1016/j.jhydrol.2019.04.026. [Google Scholar] [CrossRef]
53. Huang C, Zhang S, Gao Y, Wu S, Zhou Y, Sun H, et al. Triaxial permeability test of fault fractured tuff based on Talbot theory. J Cent South Univ Technol. 2022;53(8):3092–103. doi: 10.11817/j.issn.1672-7207.2022.08.026. [Google Scholar] [CrossRef]
54. Aguilar-Madera C, Flores-Cano J, Matías-Pérez V, Briones-Carrillo J, Velasco-Tapia F. Computing the permeability and Forchheimer tensor of porous rocks via closure problems and digital images. Adv Water Resour. 2020;142(3):103616. doi:10.1016/j.advwatres.2020.103616. [Google Scholar] [CrossRef]
55. Lenci A, Zeighami F, Di Federico V. Effective Forchheimer coefficient for layered porous media. Transp Porous Media. 2022;144(2):459–80. doi:10.1007/s11242-022-01815-2. [Google Scholar] [CrossRef]
56. Takeuchi Y, Takeuchi J, Izumi T, Fujihara M. Two-dimensional numerical analysis of non-Darcy flow using the lattice Boltzmann method: pore-scale heterogeneous effects. J Fluids Eng. 2021;143(6):061401. doi:10.1115/1.4049689. [Google Scholar] [CrossRef]
57. Xiong F, Jiang Q, Chen S, Hu X. Modeling of coupled Darcy—forchheimer flow in fractured porous media and its engineering application. Chin J Geotech Eng. 2021;43(11):2037–45. doi:10.11779/CJGE202111010. [Google Scholar] [CrossRef]
58. Zhou X, Sheng J, Ye Z, Luo W, Huang S, Cheng A. Effects of geometrical feature on Forchheimer-flow behavior through rough-walled rock fractures. Chin J Geotech Eng. 2021;43(11):2075–83. doi:10.11779/CJGE202111014. [Google Scholar] [CrossRef]
59. Winter R, Valsamidou A, Class H, Flemisch B. A study on Darcy versus Forchheimer models for flow through heterogeneous landfills including macropores. Water. 2022;14(4):546. doi:10.3390/w14040546. [Google Scholar] [CrossRef]
60. Singh K, Camulli H, Bradley J. Sediment size effects on non-Darcy flow: insights from Izbash equation and Forchheimer inertial coefficient analysis. Hydrogeol J. 2024;32(7):1853–71. doi:10.1007/s10040-024-02823-w. [Google Scholar] [CrossRef]
61. Houben G, Batelaan O, Birk S, Kacimov A. The force of Forchheimer-the contributions of Philipp Forchheimer to groundwater hydrology. Hydrol Sci J. 2025;70(3):1–20. doi:10.1080/02626667.2024.2438337. [Google Scholar] [CrossRef]
62. Banerjee A, Jagupilla S, Pasupuleti S, Annavarapu C. Alternative relationships to enhance the applicability of nonlinear filtration models in porous media. Acta Geophy. 2023;71(4):1787–99. doi:10.1007/s11600-022-00950-0. [Google Scholar] [CrossRef]
63. Abed Meften G, Ali A, Al-Ghafri K, Awrejcewicz J, Bazighifan O. Nonlinear stability and linear instability of double-diffusive convection in a rotating with LTNE effects and symmetric properties: brinkmann-forchheimer model. Symmetry. 2022;14(3):565. doi:10.3390/sym14030565. [Google Scholar] [CrossRef]
64. Ergun S, Orning A. Fluid flow through randomly packed columns and fluidized beds. Ind Eng Chem. 1952;41(6):1179–84. doi:10.1021/ie50474a011. [Google Scholar] [CrossRef]
65. Alvarado-Rodríguez C, Díaz-Damacillo L, Plaza E, Sigalotti L. Smoothed particle hydrodynamics simulations of porous medium flow using Ergun’s fixed-bed equation. Water. 2023;15(13):2358. doi:10.3390/w15132358. [Google Scholar] [CrossRef]
66. Graciano-Uribe J, Pujol T, Puig-Bargués J, Duran-Ros M, Arbat G, Ramírez de Cartagena F. Assessment of different pressure drop-flow rate equations in a pressurized porous media filter for irrigation systems. Water. 2021;13(16):2179. doi:10.3390/w13162179. [Google Scholar] [CrossRef]
67. Díaz-Damacillo L, Alvarado-Rodríguez C, Sigalotti L, Vargas C. Performance of ergun’s equation in simulations of heterogeneous porous medium flow with smoothed-particle hydrodynamics. Water. 2024;16(19):2801. doi:10.3390/w16192801. [Google Scholar] [CrossRef]
68. Marchelli F, Di Felice R. An experimental assessment of fluid-solid drag models based on the pressure drop in bidisperse fixed beds. Int J Multiphase Flow. 2023;166:104513. doi:10.1016/j.ijmultiphaseflow.2023.104513. [Google Scholar] [CrossRef]
69. Irmay S. Theoretical models of flow through porous media, RILEM Symp. Transfer of Water in porous media, Paris. Bull RILEM. 1964;29(45):37–43. [Google Scholar]
70. Rao P, Murmu B, Agarwal S. A comparison of porous structures on the performance of slider bearing with surface roughness in micropolar fluid film lubrication. Therm Sci. 2019;23(3 Part B):1813–24. doi:10.2298/TSCI170825304R. [Google Scholar] [CrossRef]
71. Macdonald I, El-Sayed M, Mow K, Dullien F. Flow through porous media-the Ergun equation revisited. Ind Eng Chem Fundam. 1979;18(3):199–208. doi:10.1021/i160071a001. [Google Scholar] [CrossRef]
72. Franchi F, Straughan B. Continuous dependence and decay for the Forchheimer equations. 2003;459(2040):3195–202. doi:10.1098/rspa.2003.1169. [Google Scholar] [CrossRef]
73. Pažanin I, Radulović M. On the forchheimer—extended darcy—brinkman flow through a thin fracture. Z Angew Math Mech. 2024;104(3):e202300541. doi:10.1002/zamm.202300541. [Google Scholar] [CrossRef]
74. Arianfar A, Ramezanzadeh A, Khalili M. Numerical study of nonlinear fluid flow behavior in natural fractures adjacent to porous medium. J Pet Sci Eng. 2021;204(3):108710. doi:10.1016/j.petrol.2021.108710. [Google Scholar] [CrossRef]
75. PLeão T. Flow stability and permeability in a nonrandom porous medium analog. Phys Fluids. 2024;36(10):1–10. doi:10.1063/5.0222094. [Google Scholar] [CrossRef]
76. Zhou J, Chen Y, Wang L, Bayani Cardenas M. Universal relationship between viscous and inertial permeability of geologic porous media. Geophys Res Lett. 2019;46(3):1441–8. doi:10.1029/2018GL081413. [Google Scholar] [CrossRef]
77. Zhang S, Qiao W, Wu Y, Fan Z, Zhang L. Experimental study on seepage characteristics of microfracture with different aperture. Sci Rep. 2020;10(1):5452. doi:10.1038/s41598-020-62350-y. [Google Scholar] [PubMed] [CrossRef]
78. Ma D, Li Q, Cai K, Zhang J, Li Z, Hou W, et al. Understanding water inrush hazard of weak geological structure in deep mine engineering: a seepage-induced erosion model considering tortuosity. J Cent South Univ. 2023;30(2):517–29. doi:10.1007/s11771-023-5261-4. [Google Scholar] [CrossRef]
79. Sun W, Tian D, Ma C, Xue Y, Yang C, Zhu K. Deformations and seepage-induced erosion of fractured rocks in fault under confined settings. Coal Geol Explor. 2024;53(1):193–203. doi:10.12363/issn.1001-1986.24.05.0333. [Google Scholar] [CrossRef]
80. Huang Z, Wang Z, Gu Q, Zhang X, Xu H, Wu Y, et al. Characterizing seepage behavior of weakly cemented filling fault fracture zone. J China Coal Soc. 2025;2025:1–14. [Google Scholar]
81. Das T, Dhar A. Effect of leakage on confined non-Darcian aquifer considering storage in semipervious layers. Adv Water Resour. 2023;182(4):104565. doi:10.1016/j.advwatres.2023.104565. [Google Scholar] [CrossRef]
82. Pandey S, Sharma P. Experimental study on non-Darcian flow through a single artificial fracture for different fracture apertures and surface roughness. J Hydroinf. 2023;25(6):2460–78. doi:10.2166/hydro.2023.143. [Google Scholar] [CrossRef]
83. Spiridonov D, Vasilyeva M. Non-local multi-continuum method (NLMC) for Darcy—Forchheimer flow in fractured media. J Comput Appl Math. 2024;438(12):115574. doi:10.1016/j.cam.2023.115574. [Google Scholar] [CrossRef]
84. Gunda S, Giammarini A, Ramírez-Torres A, Natarajan S, Barrera O, Grillo A. Fractionalization of Forchheimer’s correction to Darcy’s law in porous media in large deformations. Math Mech Solids. 2025;30(4):809–49. doi:10.1177/10812865241252577. [Google Scholar] [CrossRef]
85. Kozhevnikov E, Turbakov M, Riabokon E, Gladkikh E, Guzev M, Qi C, et al. The mechanism of porous reservoir permeability deterioration due to pore pressure decrease. Adv Geo-Energy Res. 2024;13(2):96–105. doi:10.46690/ager.2024.08.04. [Google Scholar] [CrossRef]
86. Liu W, Zhao J, Huo Z, Yang C, Han M, Wu H, et al. Study on a mathematical model and experiments for nonlinear seepage in complex crushed rocks with mud-rock slurry. Coal Sci Technol. 2023;52(5):46–59. doi:10.12438/cst.2023-1152. [Google Scholar] [CrossRef]
87. Yu B, Pan S, Wei J, Yue L, Guo J. Particle crushing and permeability evolution of saturated broken rock under compaction. J Mining Saf Eng. 2020;37(3):632–8. doi:10.13545/j.cnki.jmse.2020.03.023. [Google Scholar] [CrossRef]
88. Zhang Y, Chai J, Cao C, Xu Z. Investigating Izbash’s law on characterizing nonlinear flow in self-affine fractures. J Pet Sci Eng. 2022;215:110603. doi:10.1016/j.petrol.2022.110603. [Google Scholar] [CrossRef]
89. Sedghi-Asl M, Afrasiabi B, Rahimi H. New correlations for non-Darcy flow in porous media. Acta Mech. 2023;234(10):4559–72. doi:10.1007/s00707-023-03586-3. [Google Scholar] [CrossRef]
90. Banerjee A, Pasupuleti S, Singh M, Dutta S, Kumar G. Modelling of flow through porous media over the complete flow regime. Transp Porous Media. 2019;129(1):1–23. doi:10.1007/s11242-019-01274-2. [Google Scholar] [CrossRef]
91. Xing K, Ma L, Qian J, Ma H, Deng Y. Experimental and numerical study on the Izbash equation coefficients in rough single fractures. Phys Fluids. 2023;35(12):126603. doi:10.1063/5.0176467. [Google Scholar] [CrossRef]
92. Li W, Zhou J, He X, Chen Y, Zhou C. Nonlinear flow characteristics of broken granite subjected to confining pressures. Rock Soil Mech. 2017;38(S1):140–50. doi:10.16285/j.rsm.2017.S1.016. [Google Scholar] [CrossRef]
93. Chilton T, Colburn A. Pressure drop in packed tubes. Ind Eng Chem. 1931;23(8):913–9. doi:10.1021/ie50260a016. [Google Scholar] [CrossRef]
94. Sharifabad N. Impact of sedimentary structure and grain-size heterogeneity on Darcy to non-Darcy flow characteristics: a quantitative analysis of Forchheimer and Izbash parameters from pore-scale porous media [master’s thesis]. Kent, OH, USA: Kent State University; 2024. [Google Scholar]
95. Basak P. Non-Darcy flow and its implications to seepage problems. J Irrig Drain Div. 1977;103(4):459–73. doi:10.1061/JRCEA4.0001172. [Google Scholar] [CrossRef]
96. Yang B, Xu Z, Yang T, Yang X, Shi W. Experimental study of non-linear water flow through unconsolidated porous media under condition of high hydraulic gradient. Rock Soil Mech. 2018;39(11):4017–24. doi:10.16285/j.rsm.2017.0643. [Google Scholar] [CrossRef]
97. Brinkman H. A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles. Appl Sci Res. 1949;1(1):27–34. doi:10.1007/BF02120313. [Google Scholar] [CrossRef]
98. de Paulo Ferreira L, de Oliveira T, Surmas R, da Silva M, Peçanha R. Brinkman equation in reactive flow: contribution of each term in carbonate acidification simulations. Adv Water Resour. 2020;144(2):103696. doi:10.1016/j.advwatres.2020.103696. [Google Scholar] [CrossRef]
99. Konopka T, Carvalho M. Two-phase flow in heterogeneous porous media based on Brinkman and Darcy models. Comput Geotech. 2025;29(1):1–14. doi:10.1007/s10596-024-10333-7. [Google Scholar] [CrossRef]
100. Shi W, Yang T, Liu H, Yang B, Yang X, Zhou Y. Non-Darcy flow model and numerical simulation for water-inrush in fractured rock mass. Chin J Rock Mech Eng. 2015;35(3):446–55. doi:10.13722/j.cnki.jrme.2015.0389. [Google Scholar] [CrossRef]
101. Wu Y, Cao Z, Li Z, Du F, Wang W, Zhai M, et al. Seepage evolution characteristics and water inrush mechanism in collapse column under mining influence. Sci Rep. 2024;14(1):5862. doi:10.1038/s41598-024-54180-z. [Google Scholar] [PubMed] [CrossRef]
102. Wang L, Kong H, Qiu C, Xu B. Time-varying characteristics on migration and loss of fine particles in fractured mudstone under water flow scour. Arab J Geosci. 2019;12(5):1–12. doi:10.1007/s12517-019-4286-3. [Google Scholar] [CrossRef]
103. Zhang Q, Chen W, Yuan J, Liu Q, Rong C. Experimental study on evolution characteristics of water and mud inrush in fault fractured zone. Rock Soil Mech. 2019;41(6):1911–22,1932. doi:10.16285/j.rsm.2019.1527. [Google Scholar] [CrossRef]
104. Zhang T, Zhang X, Pang M, Liu N, Zhang S, Gao H. Effect of particle loss on the pore structure and emergent behavior of karst column fills. J China Coal Soc. 2021;46(10):3245–54. doi:10.13225/j.cnki.jccs.2020.1110. [Google Scholar] [CrossRef]
105. Zhang S. Research on mechanism and prevention technology of water-rich fault permeation disaster in deeply buried high-speed railway tunnel [dissertation]. Beijing, China: University of Science and Technology Beijing; 2022. 10.26945/d.cnki.gbjku.2022.000303. [Google Scholar] [CrossRef]
106. Cao Z, Zhang S, Du F, Ma D, Li Z, Huang C, et al. Water inrush mechanism and variable mass seepage of karst collapse columns based on a nonlinear coupling mechanical model. Mine Water Environ. 2025;164(1):1–16. doi:10.1007/s10230-025-01041-4. [Google Scholar] [CrossRef]
107. Yao B, Li S, Du F, Li Z, Zhang B, Cao Z, et al. Mechanical model of deformation-seepage-erosion for Karst collapse column water inrush and its application. J China Coal Soc. 2023;49(5):2212–21. doi:10.13225/j.cnki.jccs.2023.0394. [Google Scholar] [CrossRef]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools