Nanofluid Flow across a Moving Plate under Blasius-Rayleigh-Stokes (BRS) Variable Transport Fluid Characteristics

1  Introduction

Nanofluids (NFs), which are suspensions of nanoparticles (NPs) in base fluids, are commonly used to enhance thermal and mechanical properties. Understanding the flow of nanofluids over moving plates is crucial for developing effective engineering solutions. Due to the time and location dependence of parameters like thermal conductivity, viscosity, and density, the flow characteristics of nanofluids can exhibit unsteady behavior. Accurately modeling nanofluid flow considering these varying parameters is essential. Nanofluids find applications in various industries, such as heat exchangers, microfluidics, electronic cooling systems, and aeronautical engineering. For example, they are used in the electronics sector to improve heat transfer and reduce the temperatures of electronic equipment. In the aircraft industry, where engines and power plants experience high temperatures and thermal stresses, nanofluids are utilized in cooling systems.

Accurate modeling of nanofluid flow over moving plates is crucial for optimization purposes. By understanding the dynamic behavior of nanofluids, engineers can design more efficient and reliable cooling systems capable of withstanding significant thermal stresses and temperature gradients. The study of nanofluid flow over moving plates holds both theoretical and practical value. The Blasius-Rayleigh-Stokes (BRS) flow, which describes the unsteady flow of a viscous fluid over a flat plate, is of interest to experts in technology, engineering, science, production, and invention. Boundary layers, which are thin fluid layers near the plate that experience viscous forces, are formed in this flow. The BRS flow is named after Heinrich Blasius, Lord Rayleigh, and George Gabriel Stokes, who made significant contributions to our understanding of this phenomenon. In addition to its fundamental importance in fluid mechanics, the BRS flow finds applications in aeronautical engineering, chemical engineering, and materials research, particularly in the design of heat exchangers and cooling systems involving fluid flow over flat plates.

In 1997, Todd [1] developed a time-dependent flow class via a moving surface created by a slot with a specific accretion or ablation rate. He presented an innovative sequence of reactions employing the BRS variable to lower the controlling PDEs to a similar condition. Therefore, Ramesh et al. [2] thoroughly examined a various fluid dynamics problems with nanofluids. Qin et al. [3] used Cattaneo-Christov theory to include the magnetohydrodynamic BRS flow of a hybrid NF with silver and magnesium oxide NPs and water moving past a stretching sheet with ablation or accretion, melting heat, chemical reaction, viscous dissipation, and Stefan blowing. They asserted that the retardation effect occurs due to a more accurate assessment of the magnetic and volume fraction parameters, resulting in a rise in liquid speed. In addition, as the Stefan blowing parameter is estimated more precisely, the thickness and velocity of the fluid improve. Using the BRS variable, Ishaq et al. [4] analyzed the uneven flow of a nanoliquid toward an isothermal magnetized plate emerging from a stirring slot. Al-Nuwairan et al. [5] assessed the BRS flow over a plate using a computational technique that accounted for magnetic fields and nonlinear thermal radiation. MWCNT is more susceptible to the effects of a magnetic field than SWCNT. Kumar et al. [6] analyzed the hybrid nanofluid flow of synchronized Blasius and Rayleigh-Stokes fluids in a synchronized magnetic field. Lu et al. [7] explored the time-dependent flow of a viscous-based liquid motivated via pedesis and Lugwig-Soret diffusion based on the movement of the moving slot using the Blasius-Rayleigh-Stokes variable. Fang et al. [8] determined the thermal transport features of boundary layer (BL) flow. Khan et al. [9] examined the influence of non-Fourier heat flux through the relevance of hybrid nanoparticles across a plate in an unstable Blasius-Rayleigh-Stokes flow. It has been discovered that hybrid nanoparticles raise the temperature while decreasing velocity. In addition, friction factor increases of up to 1.4399 percent and a heat transfer rate increase of up to 1.123 percent have been detected. Jiang et al. [10] explored the role of Stefan driving through the Cattaneo-Christov features of the BRS flow of hybrid nanofluids and found that the damping effect increases the liquid velocity for more significant amounts of the magnetic property and volume fraction term. The articles [11–15] contain additional research utilizing the Blasius–Rayleigh–Stoke attribute and [16–21] for nanofluids.

In the past few years, the investigation of BL mobility and heat transport in the thin liquid film via a stretching sheet has fascinated many due to its wide range of food processing, continuous casting, and chemical processing equipment. Considering this characteristic, Crane [22] was the first to explore Newtonian fluid’s constant two-dimensional BL motions due to a linearly stretched sheet. McCormack et al. [23] investigated how an elastic flat sheet’s deformation affected a liquid’s two-dimensional motion. Due to its practical applicability, the stretching sheet problem has involved various researchers over the past four decades, including Wang [24,25] and Andersson et al. [26,27]. Prasad et al. [28] considered temperature-dependent viscosity through the mobility and heat transport of a nanoliquid passing a flat sheet. Prasad et al. [29] reported convective boundary conditions and temperature-dependent fluid characteristics of a magnetohydrodynamic liquid’s mixed convective motion and heat transport via a variable-thickness elastic sheet. Prasad et al. [30,31] explored the influence of varying fluid characteristics and a transverse magnetic field on a non-Newtonian’s motion, energy, and concentration transfer in the presence of combined temperature and species concentration effects.

Nanofluids, an innovation of research groups in the growing field of nanotechnology, leverage materials’ thermal properties to recover a liquid’s thermal conductivity. Choi [32] proposed the word “nanofluids,” which considerably boosted the heat transfer performance of diverse fluids. The suggested model is based entirely on nanoparticle distribution, such as metals, polymers, and non-metals in a particular base liquid such as water or other fluids. The improved thermal behavior of nanofluids may set the framework for a significant revolution in heat transfer acceleration, which is crucial for a range of manufacturing sectors involving nuclear power, computing, biotechnology, and agriculture. A circumstance evolved because of extensive and rapid heat transference in different equipment for more effective and increased thermal control. The current examination suggests and scrutinizes a new category of uneven BL via a stretching surface in response to Todd’s [1] examination of a novel family of time-dependent boundary layers. To the best of the author’s awareness, no study has until now investigated the Blasius–Rayleigh–Stokes flow of nanoliquid with variable fluid properties. The impact of temperature-dependent transport characteristics on unsteady BRS nanofluid flow and heat transport via a moving plate generated by a moving slot is investigated, and the obtained results are compared to the findings reported in the literature by Grubka et al. [33], Ali [34], and Chen [35]. Several new mass, momentum, and heat transfer features of this flow pattern will be looked at and studied.

2  Formulation

It is to be anticipated that an incompressible nanofluid with varying liquid properties would flow in two dimensions in a time-dependent manner through a permeable, movable plate that coincides with the y = 0 plane (Fig. 1). The x-axis coincides with the principal flow direction, and the y-axis is perpendicular to the plate’s motion. The fluid is at a standstill. The plate stretching speed is Uw and the slot moving speed will be given in the following. The x-axis runs along the sheet stretching direction and the y-axis is perpendicular to it. Under these assumptions and using the standard BL estimation, the governing equations of momentum, mass, and heat transfer for the unsteady flow issue under consideration with changing liquid characteristics (i.e., fluid viscosity and thermal conductivity) may be written as follows. Todd [1] provided the governing continuity, velocity, energy, and mass equations for an unsteady flow condition with variable fluid parameters.

∂u∂x+∂v∂y=0,(1)

∂u∂t+u∂u∂x+v∂u∂y=1ρ∞∂∂y(μ∂u∂y),(2)

(∂T∂t+u∂T∂x+v∂T∂y)=1ρ∞cp∂∂y(k(T)∂T∂y)+ε(DB(C)∂C∂y∂T∂y+DTT∞(∂T∂y)2),(3)

(∂C∂t+u∂C∂x+v∂C∂y)=∂∂y(DB(C)∂T∂y)+DTT∞∂2T∂y2(4)

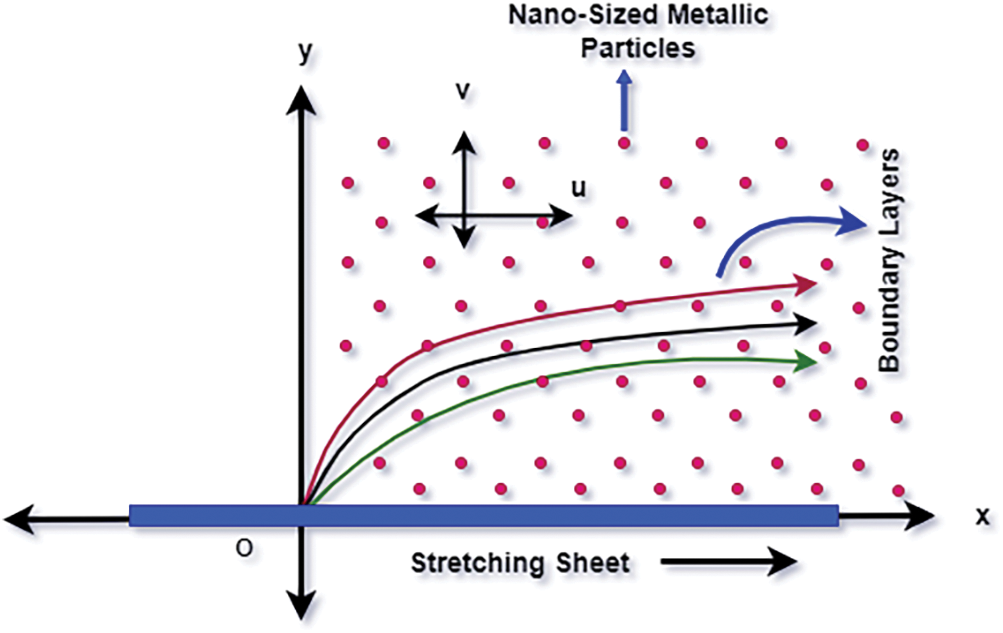
Figure 1: Systematic diagram of the problem

Variable viscosity µ varies as an inverse function of temperature defined as

1μ=1μ∞[1+δ(T−T∞)],i.e.,1μ=δ(T−Tr),(5)

wherea=δμ∞ andTr=T∞−1δ.(6)

Here both a and Tr are constants, which depends on δ, generally, a<0 corresponds to gases and a>0 to liquid. T∞ and µ∞ are the constant values for temperature and the coefficient of viscosity away from the sheet. Temperature conditional thermal conductivity and diffusivity are defined as:

1ρ∞Cpk(T)=α∞(=k∞ρ∞Cp)(1+ε1(T−T∞Tw−T∞))andDB(C)=DB∞(1+ε2(C−C∞Cw−C∞)),(7)

where ε1 and ε2 are the erratic thermal conductivity and erratic diffusivity parameter, respectively. The impact of these small parameters is to enhance the thermal as well as species distribution thickness, respectively.

Substituting Eqs. (5)–(7) in Eqs. (2)–(4), we find:

∂u∂t + u∂u∂x + v∂u∂y=1ρ∞∂∂y(µ∞1+δ(T−T∞)∂u∂y),(8)

ρCp(∂T∂t+u∂T∂x)+(ρCpv−k∞εΔT∂T∂y)∂T∂y=(k∞(1+ε1ΔT(T−T∞)))∂2T∂y2+ε(DB∞(1+ε2ΔC(C−C∞))∂C∂y∂T∂y+DTT∞(∂T∂y)2)(9)

(∂C∂t+u∂C∂x)+(v−DB∞ε2ΔC∂C∂y)∂C∂y=(DB∞(1+ε2ΔC(C−C∞)))∂2C∂y2+DTT∞∂2T∂y2(10)

The impact of the small parameters, namely, ε1 and ε2 is to enhance the thermal as well as species distribution thickness, respectively. The associated BCs are (Todd [1]):

u=uw,v=0,T=TwC=Cwaty=0,u→0,T→T∞,C→C∞asy→∞,(11)

Since the unsteady flow is a generalized case of a steady flow. Todd [1] generalized the Blasius and Rayleigh-Stokes variables to get similar equations for the boundary layer flow of viscous fluid over a moving surface termed as Blasius Rayleigh- Stokes variable which is represented as:

η=y/cos⁡αν∞t+sin⁡α(ν∞x/uw)(12)

This variable depicts that the slot at Y = 0 is moving with a constant speed −uwcot⁡α. To obtain similarity solutions for the system of Eqs. (8)–(10), we introduce the following similarity variables.

ψ(x,y,t)=uwcos⁡αν∞t+sin⁡α(ν∞x/uw)f(η),θ(η)=T−T∞/Tw−T∞,ϕ(η)=C−C∞/Cw−C∞(13)

Considering u=∂ψ/∂yandv=−∂ψ/∂x

Using Eqs. (12), (13), we obtain the following equation:

(f″/(1−θ/θr))′+(1/2)ηcos⁡αf″+(1/2)sin⁡αff″=0(14)

[1+ε1θ]θ″+ε1θ′2+(Pr2)(ηcos⁡α+sin⁡αf)θ′+Nb(1+ε2ϕ)θ′ϕ′+Ntθ′2=0,(15)

[1+ε2ϕ]ϕ″+ε1φ′2+(Le2)(ηcos⁡α+sin⁡αf)φ′+NtNbtθ″=0,(16)

f′(η)=1,f(η)=0,θ(η)=1,ϕ(η)=1atη=0,f′(η)→0,θ(η)→0,ϕ(η)→0asη→∞(17)

Here θr=Tr−T∞Tw−T∞=−1δ(Tw−T∞),Le=ν∞DB∞,Pr=ν∞α∞,Nb=τDB∞(Cw−C∞)v∞. and ,Nt=τDT(Tw−T∞)T∞v∞ are erratic viscosity factor, Lewis number, Prandtl number, Brownian factor and Thermophoresis factor, respectively.

It is important to note that as γ→0, specifically when μ=μ∞ (a constant), θr tends towards infinity. The polarity of varies depending on the state of matter, θr with a negative value for liquids and a positive value for gases. The reason for this is that, typically, the viscosity of a liquid tends to decrease as the temperature rises, whereas for gases, it tends to increase. The chosen reference temperatures for the correlations have proven to be highly valuable for a wide range of applications. When the value of θr is large or the difference between T∞ and Tw is small, it may be feasible to ignore the effects of fluctuating viscosity on the flow.

2.1 The Engineering Quantities of Interest

The article focuses on analyzing the behavior of the nanofluid by examining the skin friction coefficient, local Nusselt number, and local Sherwood number. These parameters are defined as follows:

Cfx=τw(x)/(ρ∞uw2/2)

Nux=xqw1/k∞(Tw−T∞)(18)

Shx=xqw2/D∞(Cw−C∞)

τw(x)=μ∞(∂u/∂y)aty=0

qw1(x)=−k∞(∂T/∂y)aty=0(19)

qw2(x)=−D∞(∂C/∂y)aty=0

Using (13) and (19) in Eq. (18), the following dimensionless form of the skin friction, local Nusselt number and the local Sherwood number are obtained.

Rex1/2Cf=γ∞sin⁡α+τAcos⁡αf″(0)Rex1/2Nux=−K∞sin⁡α+τAcos⁡αθ′(0)Rex1/2Shx=−D∞sin⁡α+τAcos⁡αφ′(0)(20)

where the expression of local Reynolds number is Rex=−U∞x1λ∞.

3  Numerical Procedure

Eqs. (14)–(17) represent a system of coupled ODEs, with orders ranging from second to third. These equations exhibit a notable degree of nonlinearity. The Keller-Box method, a highly influential numerical technique, has been adopted due to the impracticality of finding an exact analytical solution for the entire set of Eqs. (14)–(17). This method utilizes a second-order finite difference scheme. The given coupled boundary value problem (14) to (17) is of third order in f and second order in θ and ϕ. By applying the method of superposition and assuming f=f1,f′=f2,f″=f3,θ=θ1,θ′=θ2,ϕ=ϕ1andϕ′=ϕ2, the problem has been transformed into a system of seven simultaneous ordinary differential equations of first order for five unknowns. In order to solve this system of equations, it is necessary to have a total of seven initial conditions. However, we currently only have two initial conditions, f(0),f′(0)onf, one initial condition θ(0)onθ, and one initial condition ϕ(0)onϕ. The values of f′(η),θ(η)andϕ(η) are known at η=∞, while the initial conditions for f″(0),θ′(0)andϕ′(0)are unspecified. A numerical Keller-Box scheme is used in this approach, which incorporates two boundary conditions to determine two unknown initial conditions as η=0. The process of selecting η∞ involves starting with an initial guess value and solving the boundary value problem using specific parameters. This allows us to obtain the values of f″(0),θ′(0)andϕ′(0). The initial approximation for the variables is as follows: f3(0)=α0andθ2(0)=β0andϕ2(0)=γ0. Let α,βandγ represent the accurate values of f3(0),θ2(0)andϕ2(0), respectively. The resultant system of five ordinary differential equations is integrated using the fourth-order Runge-Kutta method. The values of f3(0),θ2(0)andϕ2(0) are denoted. The solution process is iterated using a larger value of η∞. This is done until two consecutive values of f″(0),θ′(0)andϕ′(0) differ only after the desired digit that represents the limit of the boundary along η. The final value of η∞ is selected as the suitable value for the given set of terms. The problem has been successfully resolved by employing the Keller-Box technique, a second-order finite difference scheme. The process of obtaining numerical solutions involves four steps. These steps are as follows:

1.    Convert Eqs. (14) and (17) into a system of first-order equations.

2.    Express the difference equations using central differences.

3.    Apply Newton’s technique to linearize the algebraic equations and represent them in matrix-vector form.

4.    Solve the linear system using the block tri-diagonal elimination technique.

In order to perform numerical calculations, it has been determined that a uniform step size of Δη=0.01 is sufficient. Additionally, the solutions are obtained with an error tolerance of 10−6 in all cases. In order to assess the effectiveness of the current method, we analyze the skin friction and wall temperature gradient by comparing them to previously reported results. These comparisons can be found in Table 1.

4  Results and Discussion

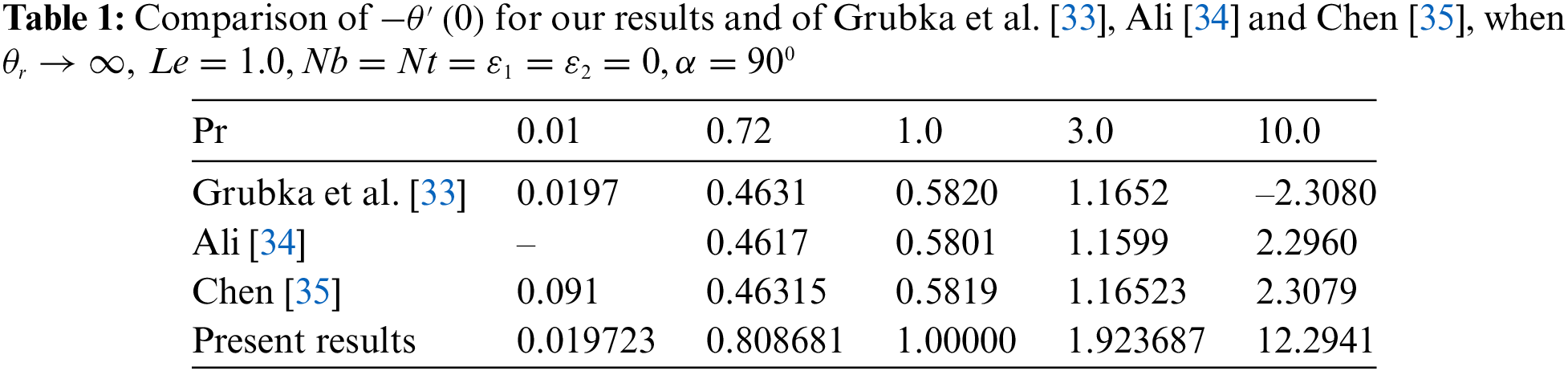
The figures and tables presented in the text (Figs. 2–5 and Tables 2–4) demonstrate the use of a numerical approach known as the Keller-Box technique. This technique is widely regarded as accurate in providing solutions for the Nusselt number, skin friction, and Sherwood number.

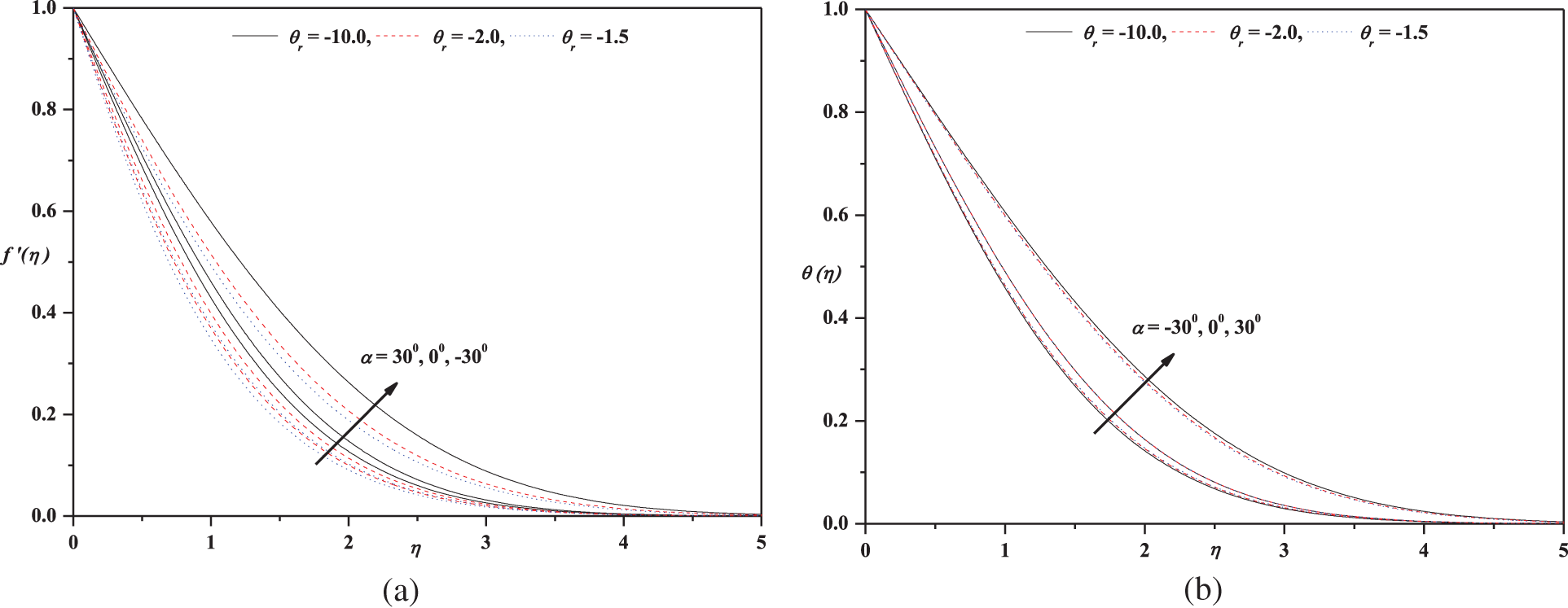
Figure 2: (a) Horizontal velocity profile for different values of θr and α with Pr = 1 Le = 0.22, Nt = 0.5, Nb = 0.5, ε1 = 0.1, ε2 = 0.1. (b) Temperature profile for different values of θr and α with Pr = 1.0 Le = 0.96, Nt = 0.5, Nb = 0.5, ε1 = 0.1, ε2 = 0.1

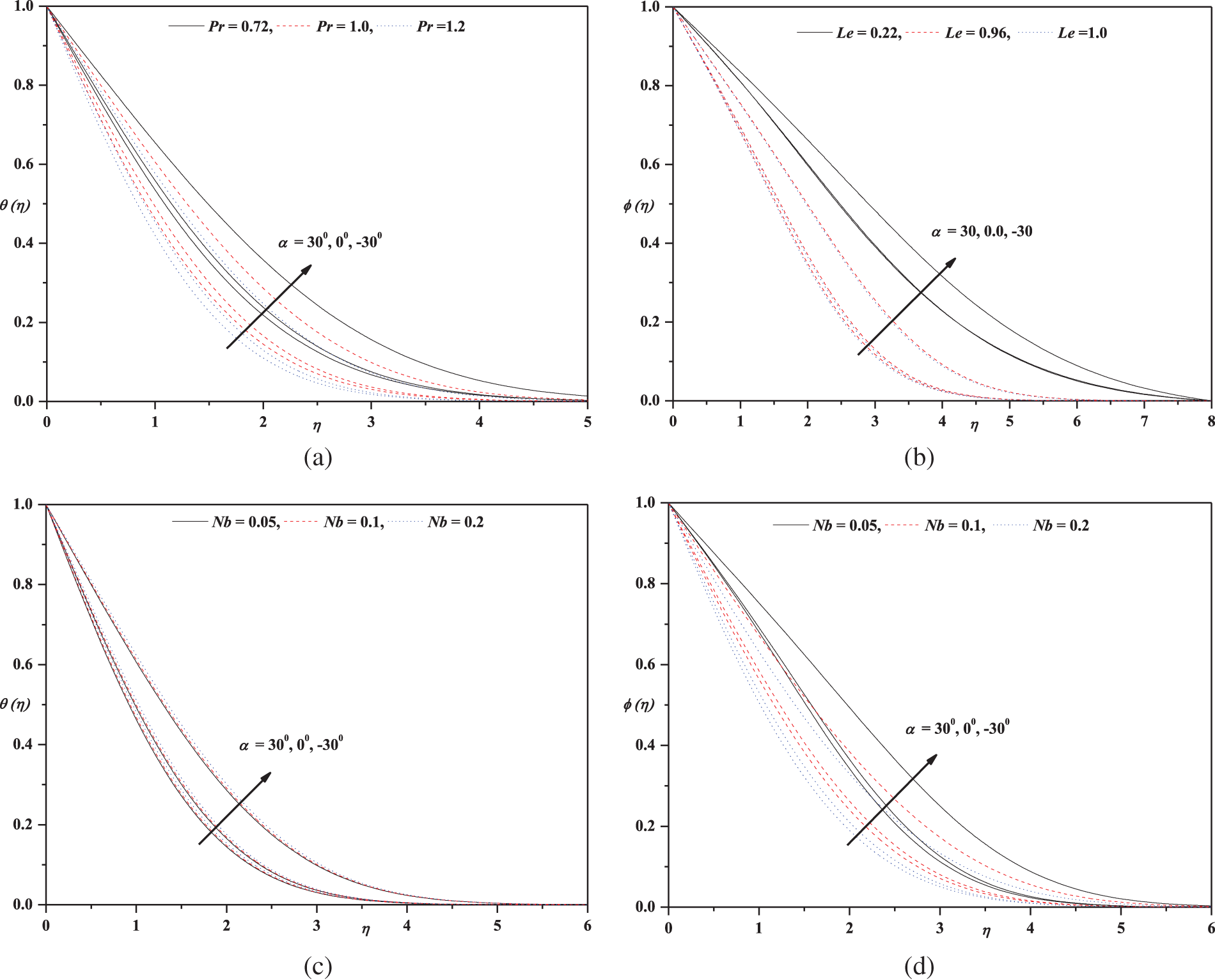
Figure 3: (a) Temperature profile for different values of Pr and α with θr = −5.0 Le = 1.0, Nt = 0.5, Nb = 0.5, ε1 = 0.1, ε2 = 0.1. (b) Concentration profile for different values of Le and α with θr = −5.0 Pr = 1.0, Nt = 0.5, Nb = 0.5, ε1 = 0.1, ε2 = 0.1. (c) Temperature profile for different values of Nb and α with θr = −5.0 Le = 1.0, Nt = 0.5, Pr = 1.0, ε1 = 0.1, ε2 = 0.1. (d) Concentration profile for different values of Nb and α with θr = −5.0 Le = 1.0, Nt = 0.5, Pr = 1.0, ε1 = 0.1, ε2 = 0.1

Figure 4: (a) Temperature profile for different values of Nt and α with θr = −5.0 Le = 1.0, Nb = 0.5, Pr = 1.0, ε1 = 0.1, ε2 = 0.1. (b) Concentration profile for different values of Nt and α with θr = −5.0 Le = 1.0, Nb = 0.5, Pr = 1.0, ε1 = 0.1, ε2 = 0.1

Figure 5: (a) Temperature profile for different values of ε1 and α with θr = −5.0 Le = 1.0, Pr = 1.0, Nt = 0.5, Nb = 0.5, ε2 = 0.1. (b) Concentration profile for different values of ε2 and α with θr = −5.0 Le = 1.0, Pr = 1.0, Nt = 0.5, Nb = 0.5, ε1 = 0.1

The purpose of Figs. 2a, 2b is to illustrate the influence of selected terms of θr and α on f′(η) with varying values. It is essential to illustrate in Fig. 2a that rising values of θr via f′(η) with corresponding varying values of α=30,0.0,−30 results in depleting function of nanofluid velocity (f′(η)). Similarly, Fig. 2b expresses the effect of moving slot parameter α=30,0.0,−30 and different values of θr on θ(η), the boundary layer thickness ascribed to θ(η)experienced a depletion in the nanofluid motion consequently upon the augmentation of θr. As Pr is inversely proportional to thermal conductivity, the Prandtl number conveys a decline in θ(η) with an elevation of the Prandtl number and in alignment with a corresponding increase/decrease of α seen in Fig. 3a. Hence, a higher fall on the thermal boundary layer (BL) thickness for θ(η) through elevation of Prandtl number is observed. It is important to display that Fig. 3b shows the rising values of Lewis number on ϕ(η) by definition. The ratio between heat and mass diffusivity is the Lewis number; Given the elevation of the Lewis number, the mass diffusivity increases and, as a result ϕ(η) depletes with an enriched asymptotically behavior of α. Fig. 3c elucidates the impact of Nb on θ(η) with the effect of the moving slot parameter α=30,0.0,−30. It is factual through Fig. 3c that rising values of Nb upswing θ(η) with synchronized growing effect of moving slot parameter within the BL thickness due to the tendency in thermal disparity. At the same time, the reverse implication is perceived for ϕ(η) in Fig. 3d with the simultaneous growing effect of Nb. and α=30,0.0,−30 vis-a-vis Fig. 3c. Fig. 4a displays the effect of Nt on θ(η) with varying moving slot parameters. It is discovered from Fig. 4a that increasing values of Nt implies the larger difference between ambient temperature and wall temperature and hence produces a synchronized growing varied α temperature distribution.

Furthermore, Fig. 4b demonstrates the effect of Nt on ϕ(η) with varying moving slot parameters. It is found from Fig. 4b that increasing values of Nt generates a robust sequential concentration distribution growth with αdisparity. Figs. 5a and 5b shows the impact of enhanced thermal and concentration distribution thickness for ε1 and ε2 on θ(η) and ϕ(η), respectively. As ε1 and ε2 has direct impact on thermal conductivity and diffusivity of the fluid, it is reported in Figs. 5a and 5b that higher values of ε1 and ε2 elevates temperature and concentration distributions lead to the enhanced and concentration boundary layer thickness.

Table 2 captures the computation of f″(0) and θ′(0) for the selected parameter of θr and α through Le=Pr=1.0,Nb=Nt=0.5,ε1=ε2=0.1. It is quite evident from the table that (f″(0)) and (θ′(0)) are empowered by rising values of θr and α invariably influencing the thermal conductivity of the NF. More so, in Table 3, the numerical output of θ′(0) for varying values of α,Pr,Nb,Nt,ε1 keeping other variables of θr=−0.5,Le=1.0,ε2=0.1 constant. It is clear from the table that (θ′(0)) escalates with the growing values of α,Pr,Nb,Nt,ε1 enriching the thermal conductivity of the nanoliquid. In Table 4, demonstrated the numerical output of ϕ′(0) for varying values of Nb,Nt,ε2,Pr, where θr=−0.5,Pr=1.0,ε1=0.1 are constant values. It is obvious from the table that Sherwood number (ϕ′(0)) rises through the larger values of Nb,Nt,ε2,Pr, enriching the species distribution of the nanofluid.

5  Conclusions

The time-dependent BRS flow of nanofluid over a moving surface incorporating Brownian motion, moving slot effect, and thermophoretic diffusion are investigated in this scientific paper. The following is a summary of the results using the Keller-Box method:

➤   The Prandtl number and Lewis number are important dimensionless parameters in fluid mechanics that characterize the relative magnitudes of momentum and thermal diffusivities in a fluid. The depletion of and distributions with increasing moving slot parameter implies that the transport properties of the fluid are changing, affecting the flow characteristics near the moving plate.

➤   The enhancement of on and with varying values tends to a downswing of nanofluid velocity and temperature distributions, suggesting that the nanofluid’s thermal and mass transport properties are affected by the flow over the moving plate. The variation in influences the rate of heat transfer and mass transfer in the nanofluid.

➤   The Nb variable is a dimensionless parameter that characterizes the thermophoretic diffusion of NPs in the NF. An increase in the moving slot term elevates the Nb variable, indicating that the transport of nanoparticles is affected by the flow over the moving plate. This, in turn, has a reverse effect on the distribution.

➤   The Nt factor is a dimensionless parameter that characterizes the effect of the thermal conductivity of the NF on the temperature distribution. The increase in the Nt factor with a progressive parameter of the moving slot indicates that the thermal conductivity of the nanofluid is affected by the flow over the moving plate.

➤   The Sherwood number, Nusselt number, and Skin friction coefficient are important dimensionless parameters that characterize the mass transfer, heat transfer, and frictional forces in the fluid, respectively. The increase in these parameters with growing values suggests that the flow over the moving plate affects the nanofluid’s thermal and mass transfer properties. These parameters are also known to influence the thermal conductivity of the nanoliquid, which can have significant implications for industrial applications.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design, data collection, analysis and interpretation of results, draft manuscript preparation: H. Vaidya, K. V. Prasad, F. Mebarek-Oudina, R. Choudhari, N. Z. Basha and S. Kalal. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data are available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Todd, L. (1997). A family of laminar boundary layers along a semi-infinite flat plate. Fluid Dynamics Research, 19, 235–249. [Google Scholar]

2. Ramesh, K., Mebarek-Oudina, F., Souayeh, B. (2023). Mathematical modelling of fluid dynamics and nanofluids. Boca Raton: CRC Press. https://doi.org/10.1201/9781003299608 [Google Scholar] [CrossRef]

3. Qin, L., Ahmad, S., Khan, M. N., Ahammad, N. A., Gamaoun, F. et al. (2022). Thermal and solutal transport analysis of Blasius-Rayleigh–Stokes flow of hybrid nanofluid with convective boundary conditions. Accepted for publication in Waves in Random and Complex Media. [Google Scholar]

4. Ishaq, A., Ahmad, A. (2021). Blasius-Rayleigh–Stokes flow of nanofluid past an isothermal magnetized surface. Advances in Mechanical Engineering, 13(10), 1–12. [Google Scholar]

5. Al-Nuwairan, M., Souayeh, B. (2021). Blasius-Rayleigh–Stokes flow over a semi-infinite plate by considering carbon nanotubes. Microsystem Technology, 27, 2001–2008. [Google Scholar]

6. Kumar, K. G., Lokesh, H. J., Shehzad, S. A., Ambreen, T. (2019). On analysis of Blasius and Rayleigh-Stokes hybrid nanofluid flow under aligned magnetic field. Journal of Thermal Analysis and Calorimetry, 139(3), 2119–2127. [Google Scholar]

7. Lu, D., Mumtaz, S., Farooq, U., Ahmad, A. (2019). Analysis of unsteady flow and heat transfer of nanofluid using Blasius-Rayleigh–Stokes variable. Coatings, 9(3), 211. [Google Scholar]

8. Fang, T., Zhang, J., Yao, S. (2010). A new family of unsteady boundary layers over a stretching surface. Applied Mathematics and Computation, 217, 3747–3755. [Google Scholar]

9. Khan, U., Zaib, A., Ishak, A., Bakar, S. A. (2021). Time-dependent Blasius-Rayleigh–Stokes flow conveying hybrid nanofluid and heat transfer induced by non-Fourier heat flux and transitive magnetic field. Case Studies in Thermal Engineering, 26, 101151. [Google Scholar]

10. Jiang, Y., Zhang, J., Abdeljawad, T., Ahmad, S., Khan, M. N. et al. (2022). Blasius-Rayleigh–Stokes flow of hybrid nanomaterial liquid past a stretching surface with generalized Fourier’s and Fick’s Law. Nanomaterials, 12, 439. [Google Scholar] [PubMed]

11. Ahmad, A., Khan, R. (2019). A new family of unsteady boundary layer flow over a magnetized plate. Journal of Magnetics, 24, 75–80. [Google Scholar]

12. Na, T. (1994). Boundary layer flow of Reiner-Philippoff fluids. International Journal of Nonlinear Mechanics, 29, 871–877. [Google Scholar]

13. Reddy, M. G., Rani, M. S., Kumar, K. G., Prasannakumar, B. C., Chamkha, A. J. (2020). Cattaneo-Christov heat flux model on Blasius-Rayleigh–Stokes flow through a transitive magnetic field and Joule heating. Physica A: Statistical Mechanics and its Applications, 548, 123991. [Google Scholar]

14. Ahmad, A. (2016). Flow of Reiner Philippoff based nanofluid past a stretching sheet. Journal of Molecular Liquids, 219, 643–646. [Google Scholar]

15. Mabood, F., Khan, W. A. (2020). A computational study of unsteady radiative magnetohydrodynamic Blasius and Sakiadis flow with leading-edge accretion (ablation). Heat Transfer, 49, 1355–1373. [Google Scholar]

16. Ramesh, K., Mebarek-Oudina, F., Ismail, A. I., Jaiswal, B. R., Warke, A. S. et al. (2023). Computational analysis on radiative non-Newtonian Carreau nanofluid flow in a microchannel under the magnetic properties. Sciencia Iranica, 30(2), 376–390. [Google Scholar]

17. Mebarek-Oudina, F., Preeti, Sabu, A. S., Vaidya, H., Lewis, R. W. et al. (2024). Hydromagnetic flow of magnetite-water nano-fluid utilizing adapted Buongiorno model. International Journal of Modern Physics B, 38(1), 2450003. https://doi.org/10.1142/S0217979224500036 [Google Scholar] [CrossRef]

18. Mebarek-Oudina, F., Dharmaiah, G., Balamurugan, K. S., Ismail, A. I., Saxena, H. (2023). The role of quadratic-linearly radiating heat source with carreau nanofluid and exponential space-dependent past a cone and a wedge: A medical engineering application and renewable energy. Journal of Computational Biophysics and Chemistry, 22(8), 997–1011. https://doi.org/10.1142/S2737416523420073 [Google Scholar] [CrossRef]

19. Zubair, T., Usman, M., Hamid, M., Sohail, M., Nazir, U. et al. (2021). Computational analysis of radiative Williamson hybrid nanofluid comprising variable thermal conductivity. Japanese Journal of Applied Physics, 60, 87004. https://doi.org/10.35848/1347-4065/ac1388 [Google Scholar] [CrossRef]

20. Sohail, M., El-Zahar, E. R., Mousa, A. A., Nazir, U., Althobaiti, S. et al. (2022). Finite element analysis for ternary hybrid nanoparticles on thermal enhancement in pseudo-plastic liquid through porous stretching sheet. Scientific Reports, 12(1), 9219. [Google Scholar] [PubMed]

21. Naseem, T., Shahzad, A., Sohail, M., Askar, S. (2023). Axisymmetric flow and heat transfer in TiO2/H2O nanofluid over a porous stretching-sheet with slip boundary conditions via a reliable computational strategy. Energies, 16(2), 681. [Google Scholar]

22. Crane, L. J. (1970). Flow past a stretching plane. Journal of Applied Mathematics and Physics, 21, 645–647. [Google Scholar]

23. McCormack, P. D., Crane, L. J. (1973). Physical fluid dynamics. New York: Academic Press. [Google Scholar]

24. Wang, C. Y. (1988). Fluid flow due to a stretching cylinder. Physics of Fluids, 31, 466–468. [Google Scholar]

25. Wang, C. Y. (1988). Stretching a surface in a rotating fluid. Journal of Applied Mathematics and Physics (ZAMP), 39, 177–185. [Google Scholar]

26. Anderson, H. I., Hansen, O. R., Holmedal, B. (1994). Diffusion of a chemically reactive species from a stretching sheet. International Journal of Heat and Mass Transfer, 37, 659–664. [Google Scholar]

27. Andersson, H. I., Aarseth, J. B., Dandapat, B. S. (2000). Heat transfer in a liquid film on an unsteady stretching surface. International Journal Heat and Mass Transfer, 43, 69–74. [Google Scholar]

28. Prasad, K. V., Vajravelu, K., Vaidya, H., Gorder, R. A. V. (2017). MHD flow and heat transfer in a nanofluid over a slender elastic sheet with variable thickness. Results in Physics, 7, 1462–1474. [Google Scholar]

29. Prasad, K. V., Vajravelu, K., Vaidya, H., Basha, N. Z., Umesh, V. (2018). Thermal and species concentration of MHD Casson fluid at a vertical sheet in the presence variable fluid properties. Ain Shams Engineering Journal, 9, 1763–1779. [Google Scholar]

30. Vaidya, H., Prasad, K. V., Vajravelu, K., Vishwanatha, U. B. (2019). Buongiorno model for MHD nanofluid flow between rotating parallel plates in the presence of variable liquid properties. Journal of Nanofluids, 8, 399–406. [Google Scholar]

31. Prasad, K. V., Vaidya, H., Mebarek-Oudina, F., Ramadan, K. M., Khan, M. I. et al. (2022). Peristaltic activity in blood flow of Casson nanoliquid with irreversibility aspects in vertical non-uniform channel. Journal of the Indian Chemical Society, 99(8), 100617. https://doi.org/10.1016/j.jics.2022.100617 [Google Scholar] [CrossRef]

32. Choi, S. U. S. (1995). Enhancing thermal conductivity of fluids with nanoparticles. ASME International Mechanical Engineering Congress & Exposition, 66, 99–105. [Google Scholar]

33. Grubka, L. G., Bobba, K. M. (1985). Heat transfer characteristics of a continuous stretching surface with variable temperature. Journal of Heat Transfer, 107, 248–250. [Google Scholar]

34. Ali, M. E. (1994). Heat transfer characteristics of a continuous stretching surface. Heat and Mass Transfer, 29, 227–234. [Google Scholar]

35. Chen, C. H. (1988). Laminar mixed convection adjacent to vertical continuously stretching sheets. Heat and Mass Transfer, 33, 471–476. [Google Scholar]