Adaptive Fuzzy Logic Despeckling in Non-Subsampled Contourlet Transformed Ultrasound Pictures

1  Introduction

Medical images are increasingly being used for diagnostic purposes, posing preservation, image enhancement, analysis, and transmission problems. Medical acoustic imaging, in particular, is widely used due to its safety, non-invasiveness, utilizes non-ionizing radiation, and inexpensive cost. Even though photo quality in ultrasound B-mode has markedly enhanced in recent times. The main shortcoming in ultrasound imaging is poor image quality due to the minor variations in acoustic impedance and backscattered echo signals of distinct soft tissues called speckles [1]. Speckle noise reduces image contrast and distorts image features, making registration and segmentation more difficult.

Moreover, poor image quality makes it difficult for the physician to diagnose and classify the different regions in the image using computer-based systems [2,3]. Hence, speckle filtering is an essential step in the pre-processing process of ultrasound images. However, the speckle noise may include crucial diagnostic information in other cases, and removing it too much might obstruct medical analysis. Therefore, researchers developed various approaches for speckle reduction [4–6]. These methods use the local statistics of images for speckle reduction and perform well in uniform regions but fail to reduce noise in lines, textures, and edges. Therefore, many partial differential equation-based methods were proposed [7,8]. Even though these techniques are more effective at speckle removal and edge-preserving, over smoothening and fine details in the image may still be lost. However, these diffusion-based iterative approaches have difficulty distinguishing the signal from the image noise. Therefore, multi-scale analyses have been proposed [9,10]. Some real-time application of ultrasound is used in healthcare for various purposes, including obstetric sonography, diagnostic testing, blood supply assessment, and directed surgeries. These photos were taken on a real-time basis and did not contain any ionizing radiation. Ultrasound imaging is a cost-effective, accessible, and easy imaging technique. They are, nevertheless, susceptible to disturbances during capture and processing. Visual clarity is harmed by noise because it obscures image features and reduces sharpness. In ultrasound imaging, the most common noise is exponential noise, often known as speckle. While these techniques effectively remove the noises and enhance the edges, facing an artificial appearance of an image may appear in the reconstructed image.

2  Related Works

Krissian et al. [11] developed a speckle reduction filter using a matrix diffusion scheme. They use the larger window to estimate coefficient and speckle scale function variation. This method is an iterative process and achieves smooth images after despeckling, and during iterations, it removes the essential structural details. Pizurica et al. [12] used a non-homomorphic filtering scheme, in which it filters the transformed coefficients by the generalized likelihood (GenLike) method based on the likelihood ratio of local neighbors. Coupe et al. [13] anticipated a despeckling filter by Bayesian formulation to adapt a non-local mean filter (OBNLM). Automatic tuning of filter parameters needs for despeckling. Bhuiyan et al. [14] offered a despeckling filter based on a distribution modeling of noise and signal from which the noise-free signal estimate using Maximum a Posteriori Probability (MAP). Farzana et al. [15] presented a speckle reduction filter for iteratively estimating filtering parameters. It uses homogeneity metrics by modifying the bilateral filter with image denoising. Cunha et al. [16] evaluated the Nonsubsampled Contourlet Transform (NSCT) on images affected by additive noise. In terms of image enhancement, this approach outperforms the undecimated wavelet transform.

Fuzzy logic-based many despeckling filters have been proposed [17–20] for synthetic aperture radar and ultrasound images. Fuzzy edges and weights of each pixel compute from the local squared window. The main limitation is its iterative process; this estimation of filtering parameters is complex. A modified despeckling filter developed by Guo et al. [21] comprised two stages: the first step determines the maximum likelihood estimator noise-free pixel. Then, restore the details using a non-local means algorithm. The main drawback is optimizing the filtering parameter in the maximum likelihood estimator. A noise filter based on discrete topological derivatives proposes by Nedumaran et al. [22]. This technique is capable of reducing speckle noise and improving image quality. Tsakalakis et al. [23] designed a despeckling filter by combining spatial and frequency domain signals derived from the multi- transducer. The primary disadvantage is reconstructing images collected from the multiple sensors, necessitating an image registration process. Jai Jaganath Babu et al. [24] anticipated a despeckling method related to the adaptive binary morphological operations applied on NSCT coefficients with a good edge preservation index. Still, the contrast of the denoised image is low. Singh et al. [25] developed a method by combining directional smoothing filter and wavelet thresholding by the modified Bayesshrinkage rule. This method removes the speckle noise very well. Leal et al. [26] proposed a new orthonormal wavelet relation for image denoising. Different wavelets were analyzed and performed better in edge preservation and speckle reduction. Jain et al. [27] employed a rule-based thresholding technique applied to noisy transformed images for speckle reduction.

This article proposes a novel denoising filter based on the Nonsubsampled Contourlet Transform (NSCT) and directional derivative of the transformed noisy ultrasound images. Integrates adaptiveness into two phases; in the first stage, fuzzy is applied on directional the difference features derived from NSCT coefficients to classify the regions in the transform domain. Then, the appropriate filters are applied to the classified areas using a weighted average filter to distinguish the edges and noise in the second stage. The projected algorithm is widely studied and compared with previous denoising filters on different images like standard images, simulated images, and clinical ultrasound images.

We organized this paper as follows: We cover the theoretical basis in Section 2. In Section 3, the noise model, multi-scale transform, fuzzy logic model, direction difference features fuzzy inference, and present the design of the weighted average filter. Then, Section 4 describes quantifying the outcomes of the experiments selected for the study. Finally, we conclude this study in Section 5.

3  Theoretical Backgrounds

It makes many attempts to reduce speckle noise in ultrasound pictures, which only reduces or eliminates noise and dilutes the essential features. Moreover, the techniques cannot discriminate the edge information and noises, causing sharp and weak edges to be suppressed and assuming them as noise. As a result, a method needs to reduce speckles ultimately and effectively preserve the edges and retain fine superior points in the image. The Viola-Jones technique is a method described in [28–30] for detection purposes, as the detection framework checks for features such as the total of image pixels within rectangular sections. It is highly sophisticated because it involves well over one rectangle characteristic within the approach, although it is simple to apply with a limited dataset. It can also help to minimize or remove distortion in real-world images. However, our technique is designed specifically for medical images, such as ultrasound images. Therefore, we’re taking steps to improve medical image quality by reducing distortion in ultrasound images. In this article, based on the parameters extracted from NSCT transformed noisy image, fuzzy logic is applied to directional features to define each class. The proposed technique’s filtering stage adapts suitable filtering methods that classify the regions to preserve details, sharp and weak edges.

3.1 Modeling of Speckle Noise

In an ultrasound picture, speckle noise displays a granular texture, and it is due to constructive and destructive ultrasound waves with objects from sub-resolution scatters [31]. The presence of speckle noise can explain using statistical and probabilistic approaches. Assume the ultrasound picture is distorted in size by multiplicative and additive noise. The noisy image before logarithmic compression described as,

R(a,b)=I(a,b)×n(a,b)+η(a,b) (1)

I(a, b) is the true image. It acknowledges that additive noise (sensor noise) has less influence than multiplicative noise due to coherent interference. Eq. (1) simplifies to

R(a,b)=I(a,b)×n(a,b) (2)

Arsenault et al. [30] demonstrated that the speckle noise is approximately correlated with Gaussian noise when the image transforms logarithmically. By applying the logarithmic transformation, we can rewrite Eq. (2) as,

R′(a,b)= log [I(a,b)]+log [n(a,b)] (3)

NSCT uses despeckling in ultrasound images. When compared with contourlet transform, it observes that the NSCT is entirely shifting invariant, multi-scale, and multi-direction.

We develop NSCT by combining the Non-subsampled Directional Filter Banks (NSDFB) and Non-subsampled Pyramid (NSP) to provide multi-scale properties and variable angles. For example, let Rj be the input image at j level. Then, NSP uses two non-sampling filters, H0 and H1, to separate the input image Rj into lowpass subband Rj0 and highpass subband Rj1 .

 Rji=Hi∗Rj (4)

* is the convolution operator. The highpass subband is Rj1 decomposed into multiple directional subbands by NSDFB. Ukequ and Yj,k is the equivalent filter for the process mentioned above. The output of NSDFB Yjk is,

Yjk=Ukequ∗Rj1,where k=1,2,3…2lj (5)

The above process works on the low-pass sub-band Rj0 by setting

Rj+1=Rj (6)

Then, the ‘max-flat’ and ‘dmaxflat7’ filters implement NSP and NSDFB [31]. Assume G0, G1 and Vkequ be the reconstruction filters of H0, H1and Ukequ respectively, for reconstruction.

R^j=G0∗R^j0+G1∗R^j1 (7)

R^j0=R^j+1 (8)

R^j1=∑k=12lj⁡Vkequ∗Yjk, where j=1,2,3….J (9)

The input image may then restore using the above process, which is carried out iteratively from the jth to the 1st level. The primary objective of this study is to use adaptive fuzzy logic filtering with a directional difference to denoise each directional subband.

3.2 Fuzzy Logic Model

The speckle noise influences the image pixels in ultrasound imaging and classifies regions as homogeneous, detail, or edge. So defined class has its distinct characteristics and varied membership function. As a result, we need to categorize each transformed coefficient in each directional subband as a suitable reasoning approach. As a result, we use fuzzy logic to classify each directional subband’s noisy coefficient into three classes based on the degree of membership function. There are two stages in the method proposed, i.e., detection and filtering. First, the image parameter directional difference was used in the detection stage to classify each level of transformed coefficient in each directional subband for detection [32]. Then, three different filters are used on the defined classes to improve the visual quality and eliminate speckle noise.

3.2.1 Directional Difference Features

This stage’s primary goal is to separate the noisy coefficients into homogeneous picture structures or edges. The neighbor reflects the features of every coefficient in the converted noisy picture. Directional Differences (DD) between altered coefficients and it identifies the neighbors to find the attributes of each coefficient in the transformed noisy image. The lesser the differential value, the more regular or homogeneous the noise coefficient is. The bigger the differential value, the more likely the noisy factor is to be considered an edge. Finally, the direction flow depicted in Fig. 1 provides the most data about the image’s morphological characteristics.

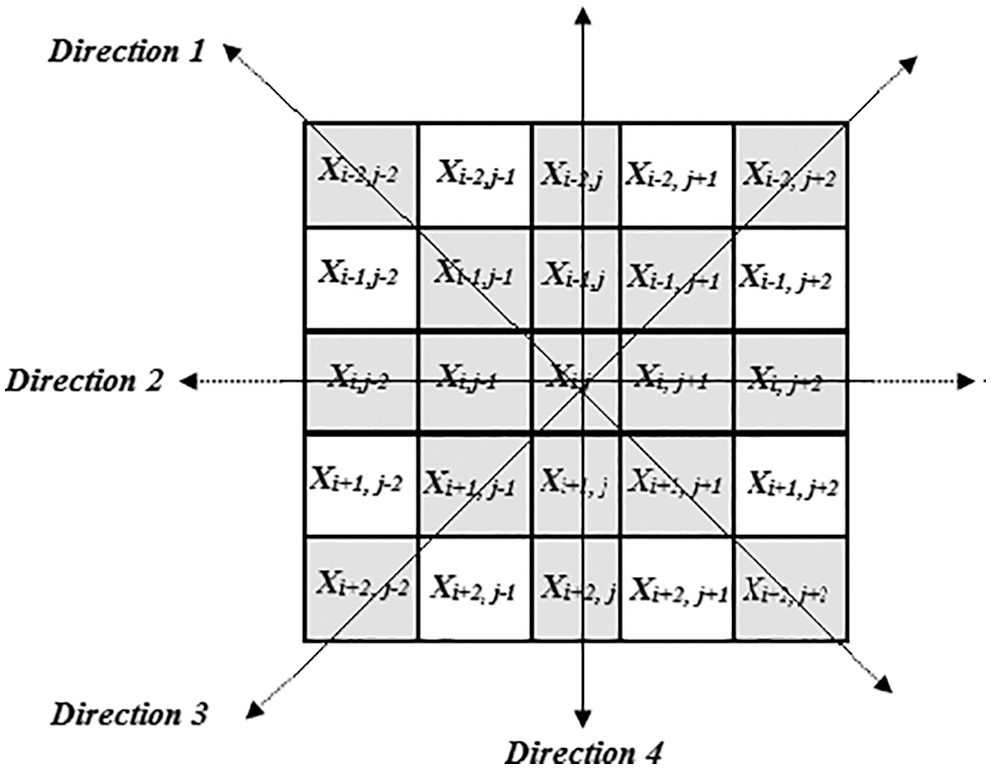
Figure 1: Sliding window with four directions

We represent the coefficient and coordinates in each direction. The absolute deviation with all coefficients in every direction presents in the chosen size frame. Then average values of all differences [32] in each direction have been seen in Eq. (10).

Dl=14∑x∈Dl⁡|x−xi,j| (10)

where, l=1,2,3,4

Above Eq. (10), these average difference values map into the fuzzy domain in each direction. As noise spreads over the transformed image, it cannot eliminate noise in the image filtering process. As a result, the Gaussian membership function integrates directional difference features into the fuzzy domain and defines Eq. (11).

μmi(Dl)=e(−(Dl−ci)22σi2) (11)

Eq. (11) is the membership function of different classes with mean and variance and denotes other regions defined in the method. The graphical representation of the membership function for the various courses depicts in Fig. 2.

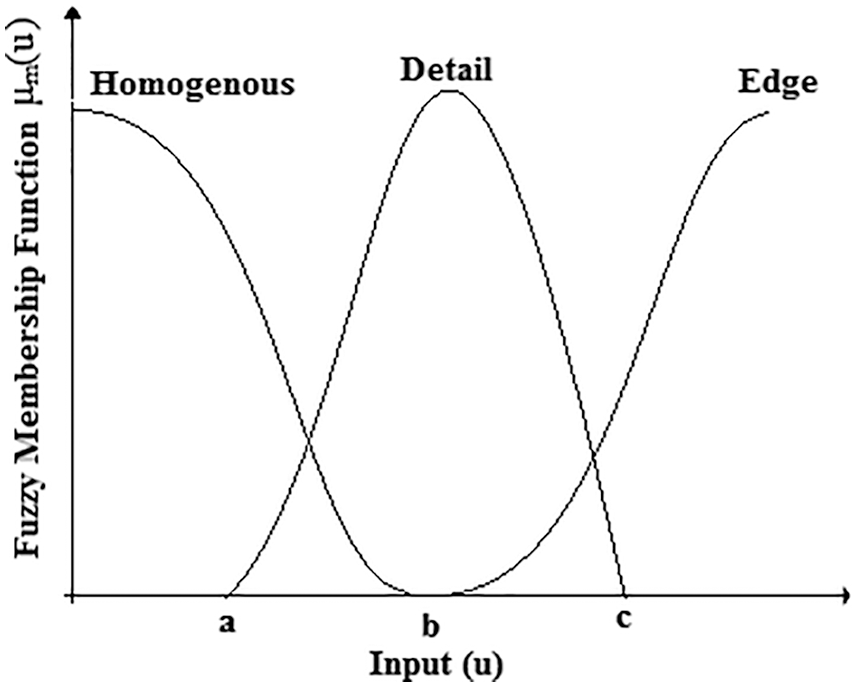
Figure 2: Gaussian membership functions with different class

We obtain a, b, and c values using Eq. (12) to classify different regions.

μmi(Dl)={homogenous,u<bdetail,u≥a andu≤cedges,u>b (12)

The coefficients with lower directional difference values belong to the uniform region. We choose the minimum value of the directional difference from XθL(x,y) to set point ‘a’. Coefficients with maximum directional difference value are considered edges. We determine the threshold ‘c’ by defining edge defined class. Edges are distinguished efficiently by gradient operation and computed from XθL(x,y) . To set the point ‘c,’ the maximum value of the directional difference is chosen. Finally, the average weight of ‘a’, ‘c,’ and ‘b’ values is selected.

Eqs. (13)–(17) gives the threshold calculation equations for each direction.

al=min[Rl],  where l=1,2,3,4 (13)

Rl=DD[XθL(a,b)]W×W (14)

cl=peak[Rl′] (15)

Rl′=DD[grad(XθL(a,b)]W×W (16)

bl=average[al,cl]   (17)

As a result, thresholds a, b, and c values noisy coefficients combine into different classes stated and adaptively varied in each direction based on the quantity of noise present in the ultrasound picture. Tab. 1 comprises thresholds for natural and accurate ultrasound images in different directions, and we depict them graphically in Fig. 3.

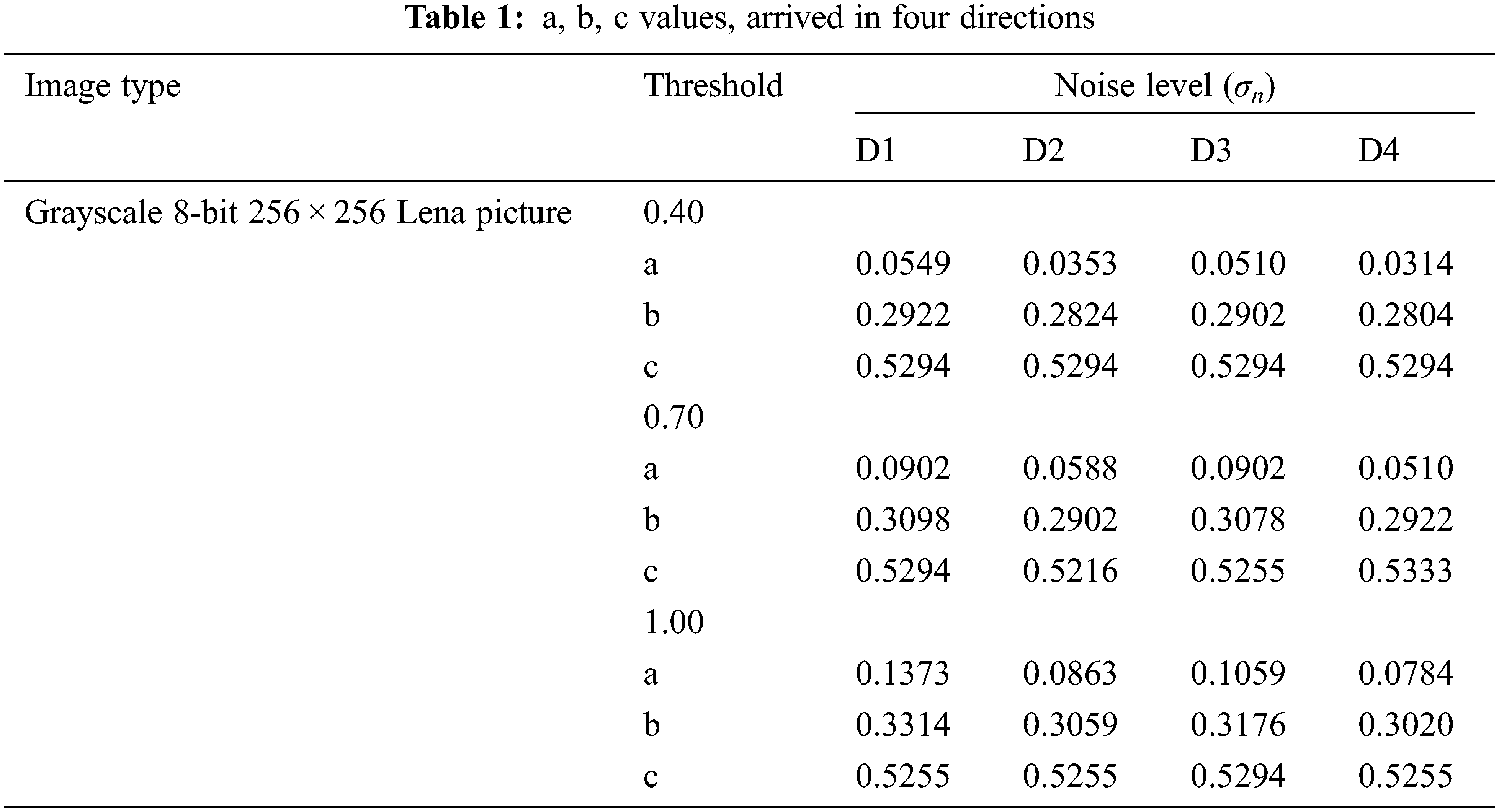
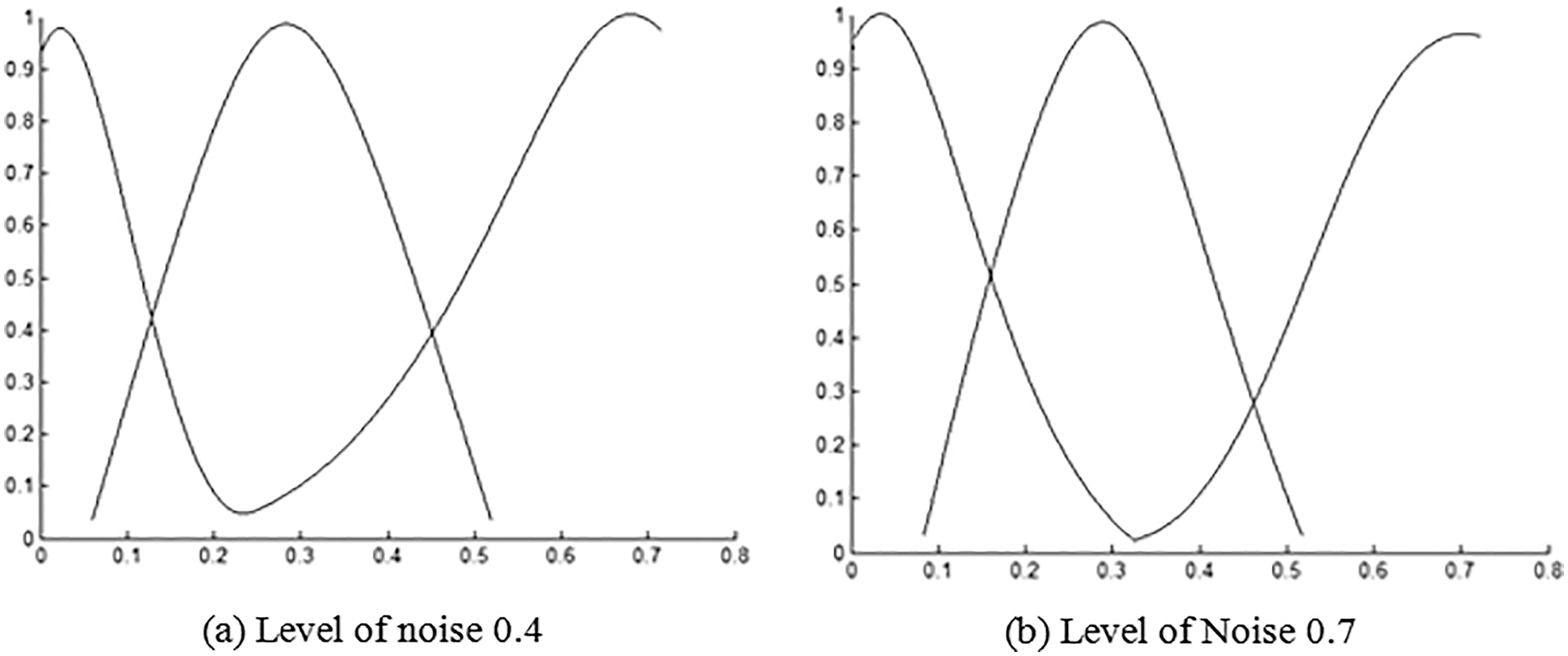
Figure 3: Membership function for Lena image and ultrasound image1

3.2.2 Fuzzy Inference for Defining Class

We frame fuzzy rules to define noisy coefficients as detail, edge, and homogenous. ‘Large’ and ‘Small’ represent the connection level in each class. For the classification of each coefficient in three different classes, six rules are framed based on directional differences, as given below.

Rule 1: Ifμm1(D1)islargeandIfμm1(D2)islargeand

Ifμm1(D3)islargeandIfμm1(D4)islargethen noisycoefficientinhomogenousclass

Rule 2: Ifμm2(D1)islargeandIfμm2(D2)islargeand

Ifμm2(D3)islargeandIfμm2(D4)islargethen noisycoefficientindetailclass

Rule 3: Ifμm3(D1)islargeandIfμm3(D2)islargeand

Ifμm3(D3)islargeandIfμm3(D4)islargethen noisycoefficientinedgeclass

Rule 4: If(μm1(D1)islargeandIfμm1(D3)islarge)or

If(μm2(D1)islargeandIfμm2(D3))islargeor

If(μm3(D1)islargeandIfμm3(D3)islarge)thennoisycoefficientin detailclass

Rule 5: If(μm1(D2)islargeandIfμm1(D4)islarge)or

If(μm2(D2)islargeandIfμm2(D4)islarge)

If(μm3(D2)islargeandIfμm3(D4)islarge)then noisycoefficientindetailclass

Rule 6: (Ifμm1(D1)islargeandμm2(D1)islargeandμm3(D1))islarge)

or(Ifμm1(D2)islargeandμm2(D2)islargeandμm3(D2))islarge)

or(Ifμm1(D3)islargeandμm2(D3)islargeandμm3(D3))islarge)

or(Ifμm1(D4)islargeandμm2(D4)islargeandμm3(D4))islarge)

then noisycoefficientinedgeclass

These rules may use to easily differentiate all distinct classes of coefficients and perform effective fuzzy inference.

3.3 Speckle Denoising Filters

Let R′(a, b) be the log-transformed picture. Then, employing NSCT on R′(a, b) for ‘’L’’ scales and ‘’θ’’ directions per scale, the transformed picture obtains when it comes to scale and direction is X(s, L, θ).

Where, θ=2L,L=2,3,4,….

In defining three different classes, each coefficient is X(s, L, θ) is mapped based on directional features. In the reasoning step, each coefficient is examined and classified as homogeneous, detailed, and edge regions. A suitable filter is necessary for denoising, removing the noise without altering the image’s structural information. As a result, appropriate filters apply to the defined classes.

3.3.1 Homogeneous Class

For the homogenous class region, for every scale ‘L’ and every direction ‘θ,’ a simple mean filter of size (2K + 1) × (2K + 1) is enough because nearby pixels are more correlated, and it is suitable to average them together by preserving details and suppressing noise away, and we define it by Eq. (18),

FθL(a,b)=1(2K+1)2∑r=−KK⁡  ∑p=−KK⁡XθL(a+r,b+p) (18)

where, K=1,2….is an integer

3.3.2 Detail Class

Fine details carry some helpful information, and if preserved, it cannot apply a mean filter on the coefficients classified as detail region X(s, L, θ). One of the non-linear and order static filters, the median filter, can preserve edges and retains desirable information for analysis given below in Eq. (19)

FθL(a,b)=median(XθL(a+r,b+p)), where−K≤(r,p)≤K (19)

3.3.3 Edge Class

In this class, we define the transformed coefficients with maximum directional difference value as edges, and there is a chance of having noise or sharp edges. Therefore, an adaptive weighted average filter must preserve essential details in a transformed image by suppressing noise, given in Eq. (20). Based on the observation, we assign higher and lower weights for edges and noise, respectively—the weight wθL(x,y) function is given in Eq. (21).

FθL(a,b)=∑r=−KK⁡∑s=−KK⁡wθL(r,p)× XθL(a+r,b+p)∑r=−KK⁡∑p=−KK⁡         wθL(r,p) (20)

wθL(a,b)=mθL(a,b)× z(a,b) (21)

where z(a, b) and mθL(a,b) are the similarities defined in [33] based on amplitude and spatial.

mθL(a,b)=exp(−(XθL(a,b)−XθL(a+r,b+p)δ)2) (22)

z(a,b)=exp(−(r2+p2(2K+1)2)) (23)

where XθL(a,b) and XθL(a+r,b+p) is coefficient to be altered based on its neighboring coefficient defined (2K + 1) × (2K + 1) of square window size,  r,p∈[−K to K ] . δ=C×σ^n , tuning parameter (′C′) and noise variance (σ^n) . It must select the tuning value ‘C’ specifically to filter and preserve essential details effectively. ‘C’ is estimated using the Structural Similarity Index Measure (SSIM), and it defines as:

ρ=SSIM(n+1)−SSIM(n)SSIM(n) (24)

Fig. 4 shows the plot between ′C′ and ′ρ′ for different noise levels, 0.4 and 0.7. We choose the Copt value when difference value approaches below zero.

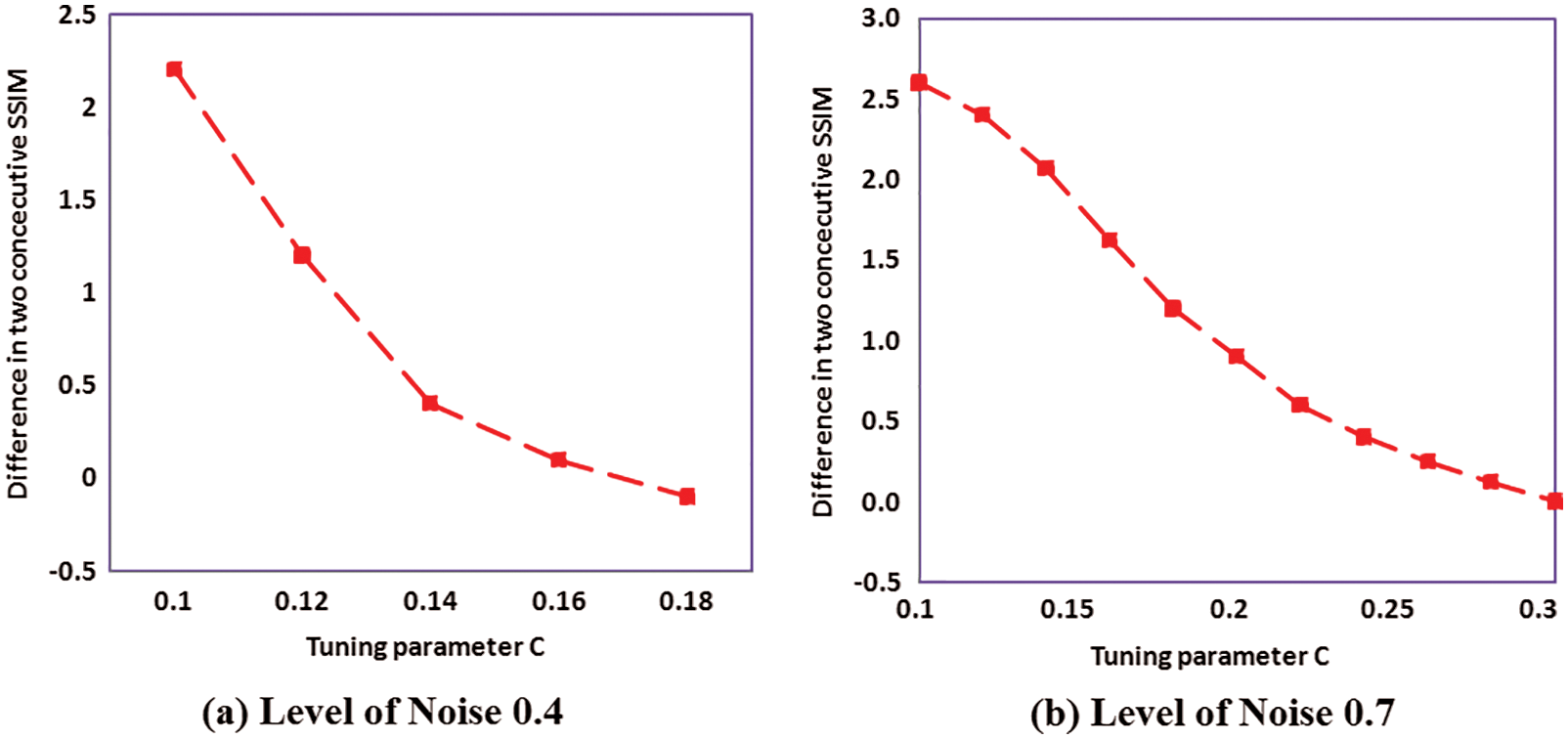
Figure 4: Tuning parameter plot for standard image

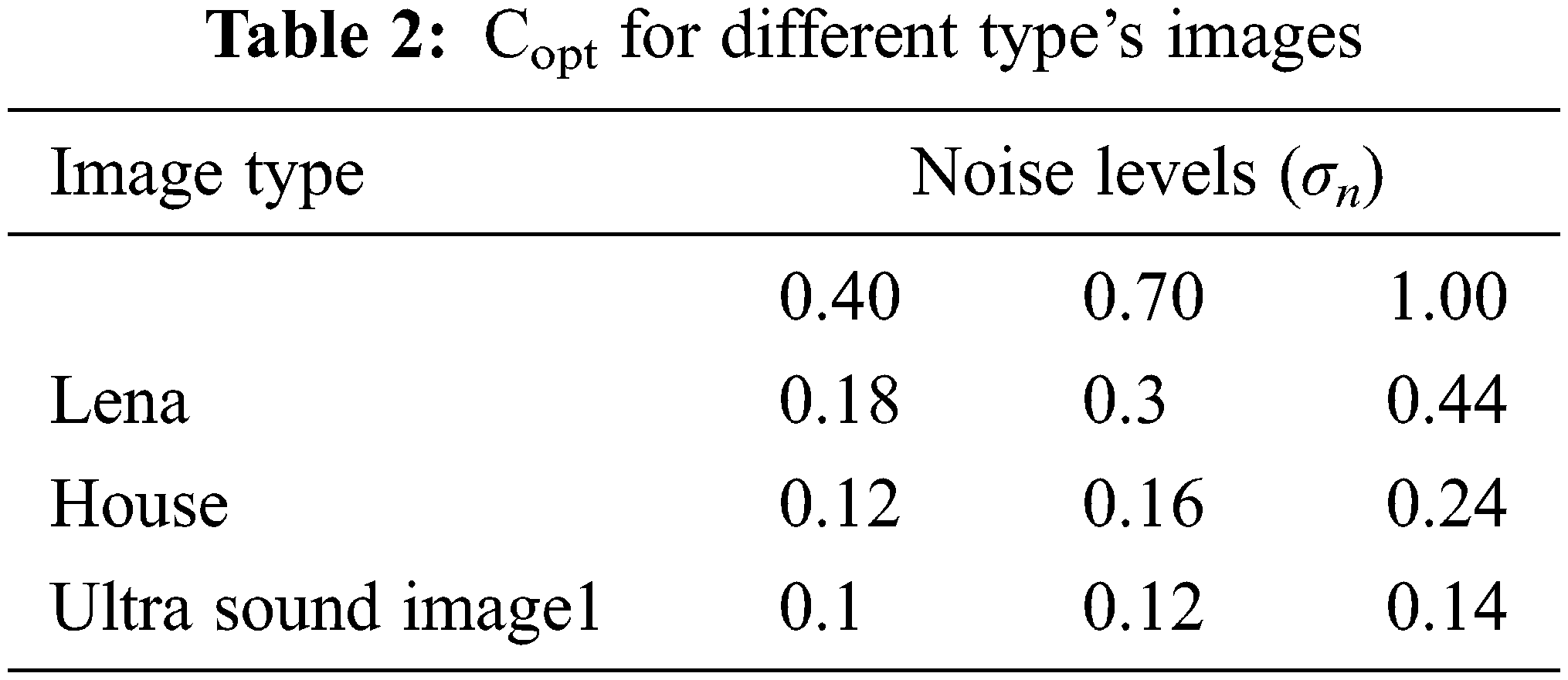
Tab. 2 shows the optimal ′C′ value for standard and real images with varied noise standard deviations. As a result, the weights applied by the proposed weighted averaging filter differ depending on the picture type and the quantity of noise distorting the image.

Apply inverse NSCT on FθL(a,b) to get F^(L,θ) and apply exponential transform on F^(L,θ) to get filtered image F^′(a,b). Perform relative difference in SSIM, ρ using Eq. (24). Check for the stopping condition; if ρ(n + 1) − ρ(n) < 0 , then C = Copt else choose another C value and repeat steps from 6 to 8.

4  Results and Discussions

All despeckling filters apply to all types of ultrasound images and analyze with other speckle reduction techniques. In this study, a speckled image obtains as defined in [34]. The quality of the denoised images evaluates using the standard metrics signal-to-noise ratio (SNR) and edge preservation (EPI) performance. To study structural similarity (SSIM) and use the quantity of filtering in the simulated pictures (USDAI). The investigational results of existing methods are obtained based on the filter parameters defined in the article. The filtered outputs of various processes for a standard noisy Lena picture with a standard deviation of 0.75 depicts in Fig. 5. With the use of existing despeckling filters, it is clear that the projected adaptive fuzzy filter with a directional difference as features efficiently eliminates speckle noise while maintaining finer details and edges in an image [35–37].

Figure 5: Denoised images of various despeckling filters. (a) Standard image (b) Noisy lena picture with standard deviation 0.75. Despeckled picture using (c) GenLike [11] (d) SNIG [12] (e) ABF [13] (f) ATMAV [17] (g) Morphological operator on NSCT [19] (h) Proposed adaptive Fuzzy on NSCT

The difference between speckled and despeckled images is obtained from the existing methods to validate the proposed method qualitatively to preserve fine details and edges. We depict the results in Fig. 6. It clearly shows that the GenLike procedure smoothens more points and edges while SNIG despeckling is very poor. In the ATMAV method, achieve smoothening in the denoised image. The morphological operator on the NSCT method filters more noise but has low contrast [38–42]. While comparing visually with other methods, the proposed denoising filter with a directional difference as a feature achieves better retention of fine details in the denoised picture.

Figure 6: Level of noise eliminated from standard picture (a) GenLike, (b) SNIG, (c) ABF (d) ATMAV (e) Morphological operator on NSCT (f) Proposed adaptive Fuzzy on NSCT

The performance of the proposed technique analyzes quantitatively by a standard edge preservation index (β) metric. We use this metric to investigate the ability of the method to preserve sharp and weak edges. We list the values of β for various despeckling methods in Tab. 3. The table list that the β value of the suggested speckle reduction scheme is more significant than other existing speckle reduction filters. It shows proposed method has good edge preservation. The edge preservation index defines as,

β=∑⁡(ΔZ−ΔZ¯)×(ΔZ^−ΔZ^¯)∑⁡(ΔZ−ΔZ¯)2∑⁡(ΔZ^−ΔZ^¯)2 (25)

Accordingly, using the 3 × 3 typical Laplacian function, ΔZ and ΔZ^ are the highpass filtration outputs of ΔZ¯ and ΔZ^¯ , accordingly. ΔZ and ΔZ^ are the average intensities of Z and Z^, accordingly. The range of β value is [0–1].

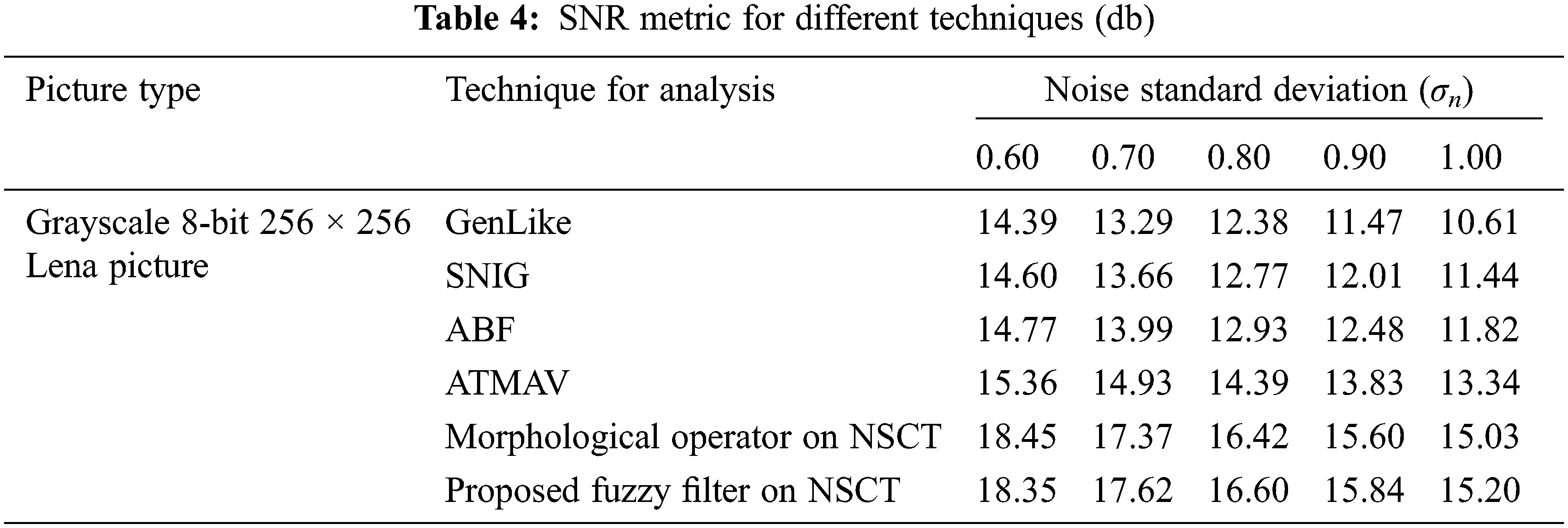
We use Signal to Noise Ratio (SNR) to analyze quantitatively for various despeckling methods, and it is defined by,

SNR=10log10⁡(σIσD) (26)

where A denotes noise-free image variance I(x, y) and σD, the difference in noise-free and denoised image variance, i.e., D=I(x,y)−F^′(x,y) , whereF^′(x,y) , represents filtered images. Finally, we list SNR values of the various despeckling method used in this study for comparison in Tab. 4. It is observed from the table that the developed despeckling algorithm on the directional difference on NSCT outperforms well in all other methods.

We evaluated the performance of the suggested despeckling scheme with authentic ultrasound images. First, we removed the natural speckle noise from online ultrasound pictures, http://www.telin.rug.ac.be/sanja/ [12]. A comparison of the proposed technique on authentic ultrasound images depict in Fig. 8. The figure shows that an adaptive fuzzy filter with a directional difference as a feature outperforms others in eliminating speckle noise and retains essential elements of an ultrasound picture. On the other side, the ATMAV [17] method smoothens the image more and fails to preserve crucial structures. In the case of [19], based on the parameters chosen, filters with less noise depicts clearly in Fig. 7.

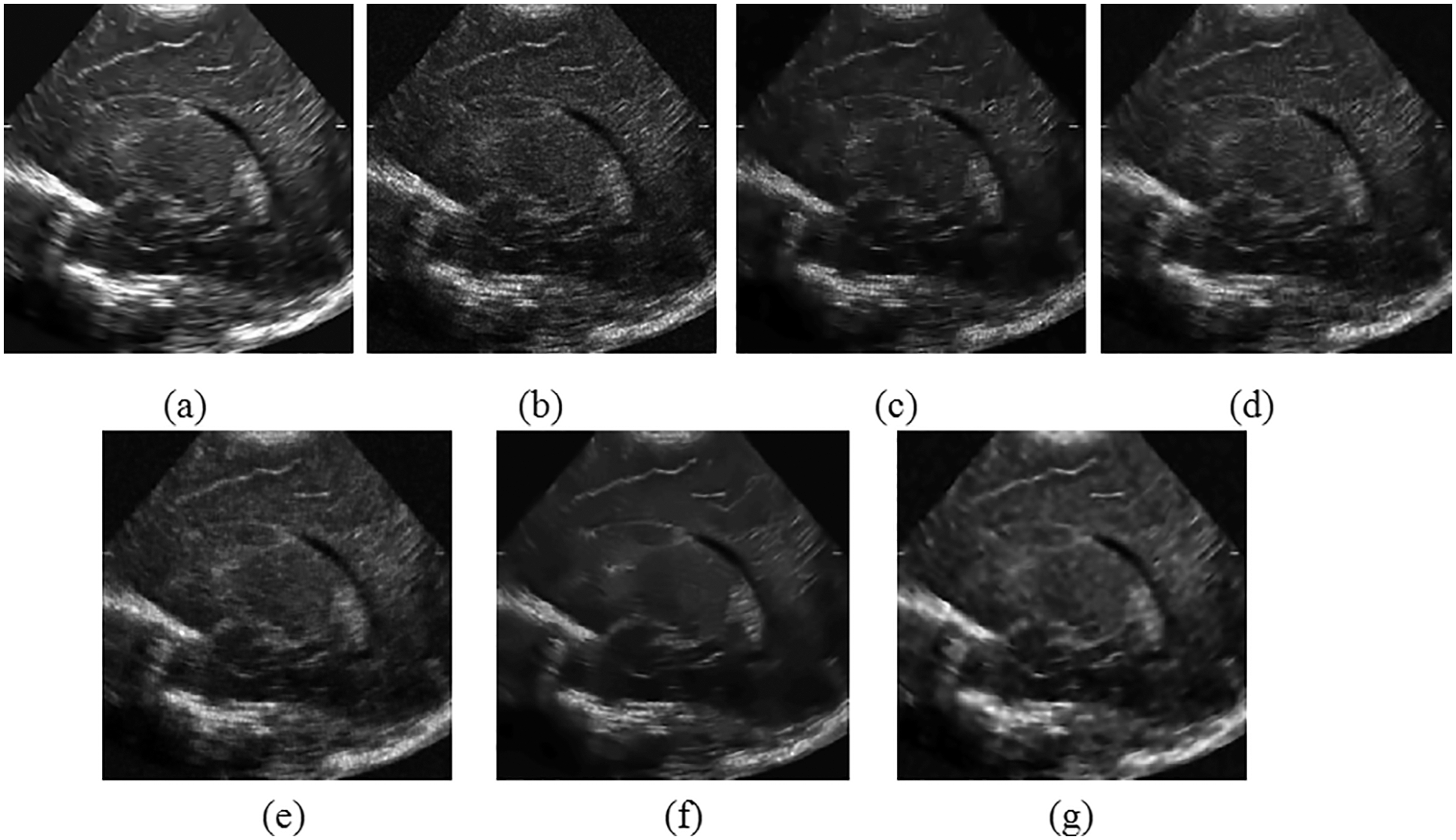
Figure 7: Denoised image of various speckle reduction filters (a) noise free ultrasound picture (b) noisy picture (c) GenLike (d) SNIG (e) ATMAV (f) morphological operator on NSCT (g) NSCT method

Figure 8: Level of noise eliminated ultrasound picture (a) GenLike, (b) SNIG, (c) ATMAV (d) Morphological operator on NSCT (e) NSCT suggested method

The difference between noisy and denoised images obtained to evaluate the various despeckling techniques to preserve fine details is shown in Fig. 8. The developed despeckling algorithm on the directional difference from the difference image has retained all the essential features in the actual ultrasound image. SNIG [12] method filters noise and crucial details in the image, clearly shown in the figure. The morphological operator on NSCT [17] filters more information in the image than noise.

The case of authentic ultrasound images with the denoised image of different despeckling filtering and Noise level removed ultrasound picture depicted in Figs. 7 and 8. As a consequence, hiding the essential elements of the ultrasound image. On the other side, the suggested methodology benefits from denoising the speckle surrounding the lesions in an ultrasound picture while filtering less in the lesion structure, retaining the information features of the lesions in the ultrasound medical image.

5  Conclusions

We take an adaptive fuzzy logic filter with a directional difference as a feature for defining membership function on NSCT as proposed in this article. In the formulated technique, adaptiveness integrates into two stages. We classify image regions at the first stage by applying the membership function [35,36] to the directional difference obtained from the NSCT noisy images. Then, the system adaptively selects the better-suited filter for the specific image region, resulting in significant speckle reduction and enhanced image structural features. We use the structural similarity measure as a tuning parameter, dependent on the kind of picture and the amount of noise contained in the images. The advanced despeckling method has better edge preservation with two degrees of adaptiveness compared to the existing techniques. A study of different despeckling ways on standard, simulated and actual ultrasound pictures. Investigatory results demonstrated that the suggested scheme outperforms previous approaches in noise isolation on homogeneous regions and can preserve boundaries and tiny features in denoised images. Furthermore, our approach has better retention in textures and sharp edges for the actual ultrasound picture than the existing methods. Experiments were conducted on Field II simulated image and the outcomes achieved are improved than the other approaches. The proposed technique outperforms well than other current techniques quantitatively as well as qualitatively.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  V. Dutt and J. F. Greenleaf, “Adaptive speckle reduction filter for log-compressed B-scan images,” IEEE Transactions on Medical Imaging, vol. 15, no. 6, pp. 802–813, 1996. [Google Scholar]

 2.  K. Z. Abd-Elmoniem, A. -M. Youssef and Y. M. Kadah, “Real-time speckle reduction and coherence enhancement in ultrasound imaging via nonlinear anisotropic diffusion,” IEEE Transactions on Biomedical Engineering, vol. 49, no. 9, pp. 997–1014, 2002. [Google Scholar]

 3.  S. Karthikeyan, T. Manikandan, V. Nandalal, J. L. Mazher Iqbal and J. J. Babu, “A survey on despeckling filters for speckle noise removal in ultrasound images,” in 2019 3rd Int. Conf. on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, pp. 605–609, 2019. [Google Scholar]

 4.  J. -S. Lee, “Digital image enhancement and noise filtering by use of local statistics,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-2, no. 2, pp. 165–168, 1980. [Google Scholar]

 5.  V. S. Frost, J. A. Stiles, K. S. Shanmugan and J. C. Holtzman, “A model for radar images and its application to adaptive digital filtering of multiplicative noise,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-4, no. 2, pp. 157–166, 1982. [Google Scholar]

 6.  D. T. Kuan, A. A. Sawchuk, T. C. Strand and P. Chavel, “Adaptive noise smoothing filter for images with signal-dependent noise,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-7, no. 2, pp. 165–177, 1985. [Google Scholar]

 7.  P. Perona and J. Malik, “Scale-space and edge detection using anisotropic diffusion,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 12, no. 7, pp. 629–639, 1990. [Google Scholar]

 8.  Y. Yu and S. T. Acton, “Speckle reducing anisotropic diffusion,” IEEE Transactions on Image Processing, vol. 11, no. 11, pp. 1260–1270, 2002. [Google Scholar]

 9.  A. Achim, A. Bezerianos and P. Tsakalides, “Novel Bayesian multiscale method for speckle removal in medical ultrasound images,” IEEE Transactions on Medical Imaging, vol. 20, no. 8, pp. 772–783, 2001. [Google Scholar]

10. Y. Yue, M. M. Croitoru, A. Bidani, J. B. Zwischenberger and J. W. Clark, “Nonlinear multiscale wavelet diffusion for speckle suppression and edge enhancement in ultrasound images,” IEEE Transactions on Medical Imaging, vol. 25, no. 3, pp. 297–311, 2006. [Google Scholar]

11. K. Krissian, C. Westin, R. Kikinis and K. G. Vosburgh, “Oriented speckle reducing anisotropic diffusion,” IEEE Transactions on Image Processing, vol. 16, no. 5, pp. 1412–1424, 2007. [Google Scholar]

12. A. Pizurica, W. Philips, I. Lemahieu and M. Acheroy, “A versatile wavelet domain noise filtration technique for medical imaging,” IEEE Transactions on Medical Imaging, vol. 22, no. 3, pp. 323–331, 2003. [Google Scholar]

13. P. Coupe, P. Hellier, C. Kervrann and C. Barillot, “Nonlocal means-based speckle filtering for ultrasound images,” IEEE Transactions on Image Processing, vol. 18, no. 10, pp. 2221–2229, 2009. [Google Scholar]

14. M. I. H. Bhuiyan, M. O. Ahmad and M. N. S. Swamy, “Spatially adaptive thresholding in wavelet domain for despeckling of ultrasound images,” IET Image Processing, vol. 3, no. 3, pp. 147–162, 2009. [Google Scholar]

15. E. Farzana, M. Tanzid, K. M. Mohsin, M. I. H. Bhuiyan and S. Hossain, “Adaptive bilateral filtering for despeckling of medical ultrasound images,” in TENCON 2010–2010 IEEE Region 10 Conf., Japan, pp. 1728–1733, 2010. [Google Scholar]

16. A. L. Da Cunha, J. Zhou and M. N. Do, “The nonsubsampled contourlet transform: Theory, design, and applications,” IEEE Transactions on Image Processing, vol. 15, no. 10, pp. 3089–3101, 2006. [Google Scholar]

17. C. Hua and T. Jinwen, “Speckle reduction of synthetic aperture radar images based on fuzzy logic,” in 2009 First Int. Workshop on Education Technology and Computer Science, Wuhan, China, pp. 933–937, 2009. [Google Scholar]

18. Y. Zhang, H. D. Cheng, J. Tian, J. Huang and X. Tang, “Fractional subpixel diffusion and fuzzy logic approach of ultrasound images,” Pattern Recognition, vol. 43, no. 8, pp. 2962–2970, 2010. [Google Scholar]

19. H. K. Kwan, “fuzzy filters for noise reduction in images,” In: M. Nachtegael, D. Van der Weken, E. E. Kerre, D. Van De Ville. (eds) in Fuzzy Filters for Image Processing. Studies in Fuzziness and Soft Computing, Springer, Berlin, Heidelberg, vol 122, pp. 25–53, 2003. [Google Scholar]

20. H. K. Kwan and Y. Cai, “Fuzzy filters for image filtering,” in The 2002 45th Midwest Symp. on Circuits and Systems, 2002. MWSCAS-2002, Tulsa, OK, USA, pp. III–672, 2002. [Google Scholar]

21. Y. Guo, Y. Wang and T. Hou, “Speckle filtering of ultrasonic images using a modified non local-based algorithm,” Biomedical Signal Processing and Control, vol. 6, no. 2, pp. 129–138, 2011. [Google Scholar]

22. D. Nedumaran, R. Sivakumar, V. Sekar and K. M. Gayathri, “Speckle noise reduction in ultrasound biomedical b-scan images using discrete topological derivative,” Ultrasound in Medicine and Biology, vol. 38, no. 2, pp. 276–286, 2012. [Google Scholar]

23. M. Tsakalakis and N. G. Bourbakis, “Ultrasound image despeckling/Denoising based on a novel multi-transducer architecture,” in 2014 IEEE Int. Conf. on Bioinformatics and Bioengineering, Boca Raton, FL, USA, pp. 62–68, 2014. [Google Scholar]

24. J. Jai Jaganath Babu and G. F. Sudha, “Nonsubsampled contourlet transform based image denoising in ultrasound thyroid images using adaptive binary morphological operations,” IET Computer Vision, vol. 8, no. 6, pp. 718–728, 2014. [Google Scholar]

25. P. Singh and R. Shree, “A new SAR image despeckling using directional smoothing filter and method noise thresholding,” Engineering Science and Technology, an International Journal, vol. 21, no. 4, pp. 589–610, 2018. [Google Scholar]

26. A. S. Leal and H. M. Paiva, “A new wavelet family for speckle noise reduction in medical ultrasound images,” Measurement, vol. 140, pp. 572–581, 2019. [Google Scholar]

27. L. Jain and P. Singh, “A novel wavelet thresholding rule for speckle reduction from ultrasound images,” Journal of King Saud University-Computer and Information sciences, 2020. [Google Scholar]

28. U. Masud, T. Saeed, H. M. Malaikah, F. U. Islam and G. Abbas, “Smart assistive system for visually impaired people obstruction avoidance through object detection and classification,” IEEE Access, vol. 10, pp. 13428–13441, 2022. [Google Scholar]

29. D. L. Donoho, “De-noising by soft-thresholding,” IEEE Transactions on Information Theory, vol. 41, no. 3, pp. 613–627, 1995. [Google Scholar]

30. H. H. Arsenault and G. April, “Properties of speckle integrated with a finite aperture and logarithmically transformed,” Journal of the Optical Society of America, vol. 66, no. 11, pp. 1160–1163, 1976. [Google Scholar]

31. J. M. Mejía Muñoz, H. de Jes´us Ochoa Dom´ınguez, L. Ortega M´aynez, O. O. Vergara Villegas, V. G. Cruz Sánchez et al., “SAR image denoising using the non-subsampled contourlet transform and morphological operators,” in 9th Mexican Int. Conf. on Artificial Intelligence, Mexico, pp. 337–347, 2010. [Google Scholar]

32. C. -C. Kang and W. -J. Wang, “Fuzzy reasoning-based directional median filter design,” Signal Processing, vol. 89, no. 3, pp. 344–351, 2009. [Google Scholar]

33. L. Jun, C. Guangmeng and H. Bo, “Image denoising based on fuzzy in wavelet domain,” in 2005 Instrumentation and Measurement Technology Conf., Ottawa, Canada, pp. 2019–2023, 2005. [Google Scholar]

34. J. A. Jensen and N. B. Svendsen, “Calculation of pressure fields from arbitrarily shaped, apodized, and excited ultrasound transducers,” IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 39, no. 2, pp. 262–267, 1992. [Google Scholar]

35. X. R. Zhang, X. Chen, W. Sun and X. Z. He, “Vehicle re-identification model based on optimized densenet121 with joint loss,” Computers, Materials and Continua, vol. 67, no. 3, pp. 3933–3948, 2021. [Google Scholar]

36. W. Sun, G. C. Zhang, X. R. Zhang, X. Zhang and N. N. Ge, “Fine-grained vehicle type classification using lightweight convolutional neural network with feature optimization and joint learning strategy,” Multimedia Tools and Applications, vol. 80, no. 20, pp. 30803–30816, 2021. [Google Scholar]

37. S. Arun and K. Sudharson. “DEFECT: Discover and eradicate fool around node in emergency network using combinatorial techniques.” Journal of Ambient Intelligence and Humanized Computing, pp. 1–12, 2020. https://doi.org/10.1007/s12652-020-02606-7. [Google Scholar]

38. N. Partheeban, K. Sudharson and P. J. Sathish Kumar, “SPEC-serial property based encryption for cloud,” International Journal of Pharmacy & Technology, vol. 8, no. 4, pp. 23702–23710, 2016. [Google Scholar]

39. K. Sudharson, A. M. Ali and N. Partheeban, “NUITECH–Natural user interface technique foremulating computer hardware,” International Journal of Pharmacy & Technology, vol. 8, no. 4, pp. 23598–23606, 2016. [Google Scholar]

40. K. Sudharson and V. Parthipan, “A Survey on ATTACK–Anti terrorism technique for adhoc using clustering and knowledge extraction,” in Advances in Computer Science and Information Technology. Computer Science and Engineering. CCSIT 2012. Lecture Notes of the Institute for Computer Sciences, Social Informatics and Telecommunications Engineering, Springer, Berlin, Heidelberg, vol 85, pp. 508–514, 2012. [Google Scholar]

41. K. Sudharson and V. Parthipan, “SOPE: Self-organized protocol for evaluating trust in MANET using eigen trust algorithm,” in 2011 3rd Int. Conf. on Electronics Computer Technology, Kanyakumari, India, pp. 155–159, 2011. [Google Scholar]

42. K. Sudharson, M. Akshaya, M. Lokeswari and K. Gopika, “Secure authentication scheme using CEEK technique for trusted environment,” in 2022 Int. Mobile and Embedded Technology Conf. (MECON), Noida, India, pp. 66–71, 2022. [Google Scholar]