Scale Invariant Feature Transform with Crow Optimization for Breast Cancer Detection

1  Introduction

In the medical image processing field, many medical images are taken from medical firms. The data was accessed successfully to manage and access these medical images based on some parameters [1]. The retrieval of images from the large medical data set is done based on the feature information and its similarities [2]. The content-based image retrieving model extracts more features of mammographic images from the different datasets. This system is liable in various fields such as commercial advertisement, military application, medical image processing, and scientific patent management system [3]. Retrieval or classification of images from many databases is a difficult task in the current image classification model. This efficient and effective method of analysis, classifying, describing, identifying, and similarity measures in the database [4–6] are gaussian functions.

The essential component of the content-based image retrieval (CBIR) system is extracting image features and representing them in feature vector format. In the CBIR system, image retrieval is based on the query image, and the featured vector is calculated for the image-based query. This query image vector is evaluated with the feature vector values saved in the database. Then the system gets the similarity of the image from the database based on minimum distance or highly matching feature vector values in the database. Therefore, feature extraction of the image plays a vital role in retrieving the image [7–10]. The CBIR system needs the minimum cost of time and minimum storage requirements to get more accurate. It should be performing the operations like rotation, scaling, illumination, and transformation of the image [11].

Many research works have been done, and applying these techniques will be inaccurate for detecting the similarity of images from the large data set. Therefore, to improve the detection of the similarity of images and reduce the average computing time, this paper proposed an optimized classification of crow search optimization algorithms with a deep belief network (CSO-DBN). In this proposed work, features are extracted using SIFT and proper and efficient implementation of dimensionality reduction of features using the crow search optimization algorithm is used. The contribution of this work is as follows:

•   Implementing retrieval of similar images based on the optimized concept of the crow search optimization algorithm.

•   To improve accuracy, pre-processing of this work implements the Kalman filter and by using SIFT algorithm for extracting features of the image.

•   For retrieving the similarity image or actual image using Euclidean distance metric measures.

The article’s organization is given as follows: the Section 2 reviews traditional works, the Section 3 provides the proposed model for image retrieval, the Section 4 discusses the experimental outcome, and the last Section finally concludes the work with future ideology.

2  Literature Survey

Recently the development of technology and the increase in usage of multimedia, smartphones, and digital cameras gathering, the graphical format of data from various areas or databases are stored securely. This similar retrieval of images helps physicians diagnose disease within the minimum time requirement [12–14]. The basic need for the recovery of images from the data set is searching for query images based on the concept of similarity of semantic features. In the internet world, many search engines have retrieved the images based on textual elements of the image [15–17]. The user submits the query image through some keyword or text entered for searching the similarity of the appearance. This text or keywords perform the matching process in the database and retrieve the relevant information. It does not retrieve irrelevant information [18–21].

This paper proposed [22] retrieval of images using labels and annotations, which does not satisfy the user’s query of the textual information. Therefore, it is challenging, and researchers should focus on it and retrieve the similarity of images based on the content image retrieval based on the content of mid-level descriptors. This automatic generation of descriptors of lower-level image features is determined in the clinical-based embodiments developed [23]. This methodology implements three steps of a process lower-level feature extraction, med-level feature extraction, and med-level feature vectors, which are used in the online-based retrieval of images. Here, the query image is also applied in the concept of mid-level descriptors [24].

This paper [25] presented a technique for retrieving the image by applying the deeper pre-trained Convolutional neural network (CNN) model. This CNN model extracts the class-specific descriptors and patient-specific descriptors for determining the tumor. This process was done by implementing the model and training it with a binary breast classifier [26]. This paper proposed two-feature extraction of the descriptors of the mammographic image. This type of descriptor is used texture features and classifies the image [27] as benign–malignant, usual, and abnormal classifications. Table 1 shows the survey on CBIR in the mammographic image.

3  Proposed CSO-DBN Methodology

This proposed work CSO-DBN contains two phases, namely online and offline. The framework of the proposed work is given in Fig. 1. In the offline phase, preprocessing work removes noise and pectoral muscles. The online image with the offline database image is virtually connected to preprocessing step. The Kalman filter is used for preprocessing the data. Further, SIFT extracts essential features and optimizes the proposed ideology.

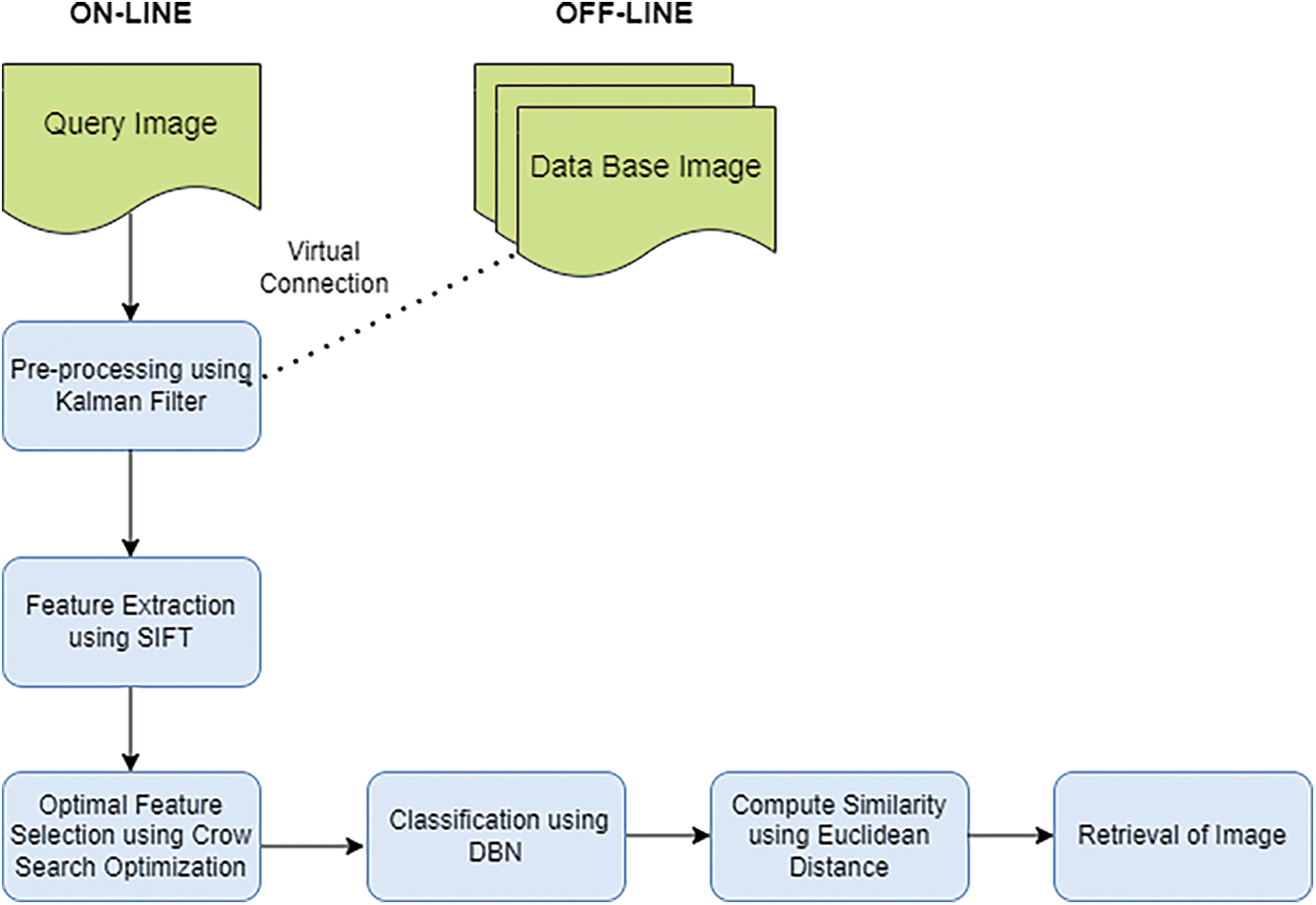
Figure 1: Framework of K-SIFT-CSOIFC

3.1 Pre-Processing

For diagnosing, mammographic images are challenging to identify. Therefore, pre-processing is needed. In this work, pre-processing work removes noise and pectoral muscles. At the posterior upper margin, thick muscles are present. This muscle is fan-shaped and appears like triangular opacity. The estimation of density in mammography is less. This helps to process specified regions by applying the detection technique. Fig. 2. show that pre-processing.

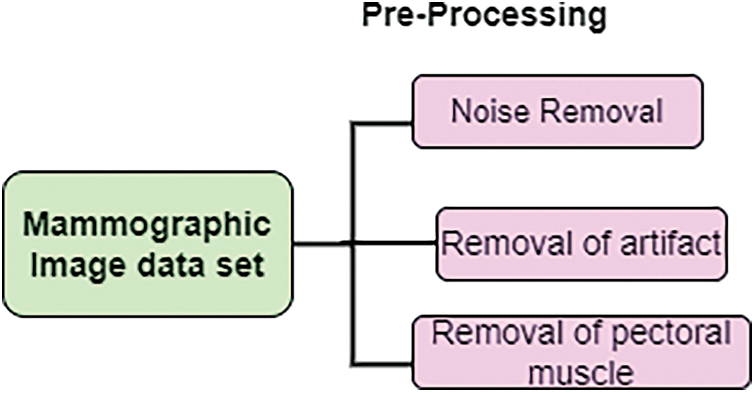
Figure 2: Pre-processing

3.1.1 Noise Removal

The primary purpose of applying the Kalman filter is to identify the inaccurate rates and noise in the mammographic image. This filter is based on the concept of mathematical approach, which is then neighbor data as a linear system with Gaussian errors to update continuously. This filter updates the value of the best current value of the neighbor. The pixel value of the mammographic image is spatially dependent on the value of the neighbor pixel of the image, and it is represented, and its mathematical model is:

mimg(a,b)=∑(p,q)∈N⁡∑m(p,q)x(a−p)+(b−q)+u(a,b) (1)

where denotes the neighboring pixel range value of the mammographic image, which is used to evaluate the linear sum. Indicates the coordinate value of the image, which represents the noise, and the importance of noise in the image is zero mean when the absolute pixel value of the image is selected. Removal of noises in the mammographic image by adding additive noise and blurred noise. Then the original image is represented by:

mimg(l)=Bmimg(k−1)+u(k) (2)

Here, mimg(l)=[mimg0(l),immg1(l),…, mimgn(l)]T

3.1.2 Removal of Artifact

To effectively retrieve mammographic images from the large dataset, removing the artifact is necessary. Since artifacts affect numerous mammographic images, such as; labels, scratches, tags, scanning, and opaque marker artifact, in this work removal of label artifact procedure is given below:

3.1.3 Removal of the Pectoral Muscle

The pectoral muscle of a mammogram image is a very thick and fan-like shape that presents as triangular opacity. It reduces the bias of mammographic estimate density and detects the lesion in the image. The procedure for removing pectoral muscle is given below:

3.2 Feature Extraction

The feature extraction purpose is to decrease the time of retrieval in the image dataset. This increases the result outcome and accuracy. Feature extraction derives attribute subset from the original attribute. This paper extracts feature shapes using SIFT. Scale-invariant features transform (SIFT) is a technique for detecting and describing the image’s local features. This SIFT is based on scaling, illumination, and rotation.

Step 1: To detect the location and scale of the input mammographic image from various views of the same input image. This can be implemented by using the function of scale-space efficiently. This scale space is based on the concept of Gaussian function. Now the scale space of the ime is defined by:

LS(x,y,σ)=Ga(x,y,σ)∗I(x,y) (3)

where, Ga(x,y,σ) is the Gaussian function for scale of the image, I(x,y) is the input image and ∗ is a convolution operator. To detect the location of stable key point in the scale-space is done by evaluating the difference between two images with the m times scale value. Then the Gaussian difference DG(x,y,σ) is defined as:

DG(x,y,σ)=LS(x,y,mσ)−LS(x,y,σ) (4)

For detecting the local minima and maxima of DG(x,y,σ) , in which each point is compared with 8 neighbors in the same scale value and 9 × 2 neighboring pixels in scale value of before and after.

Step 2: For the key point localization of the input image the magnitude and direction of neighborhood pixels. It removes the low contrast extreme value. To identify the orientation of the image in the region of the key point. This cancels the orientation and makes it rotation invariant.

Step 3: Generate feature vector value. For 128 key points generate the SIFT vector and it is clear from the geometric transformation of the image like rotation and changes in scale values.

3.3 Optimal Feature Selection Using Crow Search Optimization

Crows are intelligent birds that can recognize the faces and where they store food. A flock of crows has similarities in their behavior pattern. In acquiring the food, it follows one another. In implementing the optimized algorithm, crow search for food is considered search space (environment) for the best feasible solution (i.e., environment’s position). The best food source is regarded as a global solution. The quality of the food source represents the fitness function of the program. This crow search optimization algorithm is determined by two main factors: diversion and intensification. The parametric control is Balancing these two factors is Awareness Probability (AP). In implementing the search space, the unexplored area must be visited using diversification. Similarly, searching for the best region using intensification is done to find the best solution.

For considering the dataset, a crow encoding process is needed. For that, the value of each particle is encoded into a sequence string of sets of fundamental importance. For ‘m’ data points, forming a C cluster by combining cluster centers as the string is denoted as every single crow. If data dimensions d, then the length of each is capped words. Randomly generate the initial population, representing the vector for various cluster centers. It can be depicted in Fig. 3.

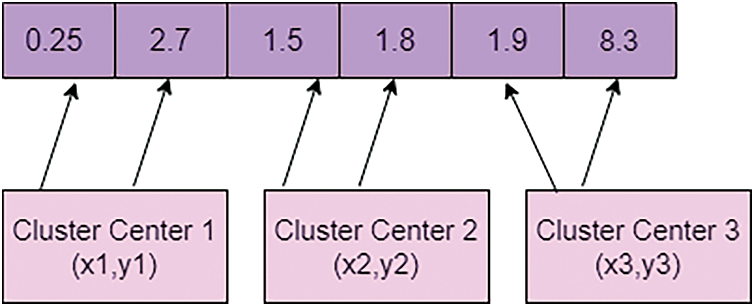
Figure 3: Encoding the value of crow

Fig. 3 is a representation of the encoding value of crow from the initial population. Let be the size of the people and represent that crow’s position at the iteration. One of the best characteristics of the crow is memorizing the hiding places and best position crow. The pseudo-code for crow search optimization is described below:

The above pseudocode of crow search optimization described calculating the fitness function of crow. Select the crow and crow. Evaluate the fitness function of crow and crow, and it is compared with the probability of awareness (AP), and if it is the high new position of crow is generated by using:

posmci,t+1=posmci,t+rndi. follmci,t.(memmcj,t−posmci,t) , if rndi≥APmcj,t (7)

If the probability of awareness (AP) is low, then to make fool the follower crow i choose the random position and aware of its follower. New position of crow is checked and updated by its position.

3.4 Classification Using Deep Belief Network (DBN)

DBN is the undirected connection between layers, and it is also called Restricted Boltzmann Machines (RBM). RBM has various layers, including DBN and trained the network based on the unsupervised training process. In this proposed work, the structure of DBN contains one visible layer and multiple hidden layers. The visible nodes are, and the hidden layer nodes are in the visible layer. The features of the visual and hidden layer are and. The bias of visible nodes is, and the preferences of a remote node are. In the RBM, the connection between the visible layer and hidden layers is restricted. To transmit the input data to the hidden layer, the RBM layer communicates with previous and subsequent layers [34].To transform input data from visible to hidden layers, use a sigmoid function with the RBM learning rule. The framework of DBN with RBM is shown in Fig. 4.

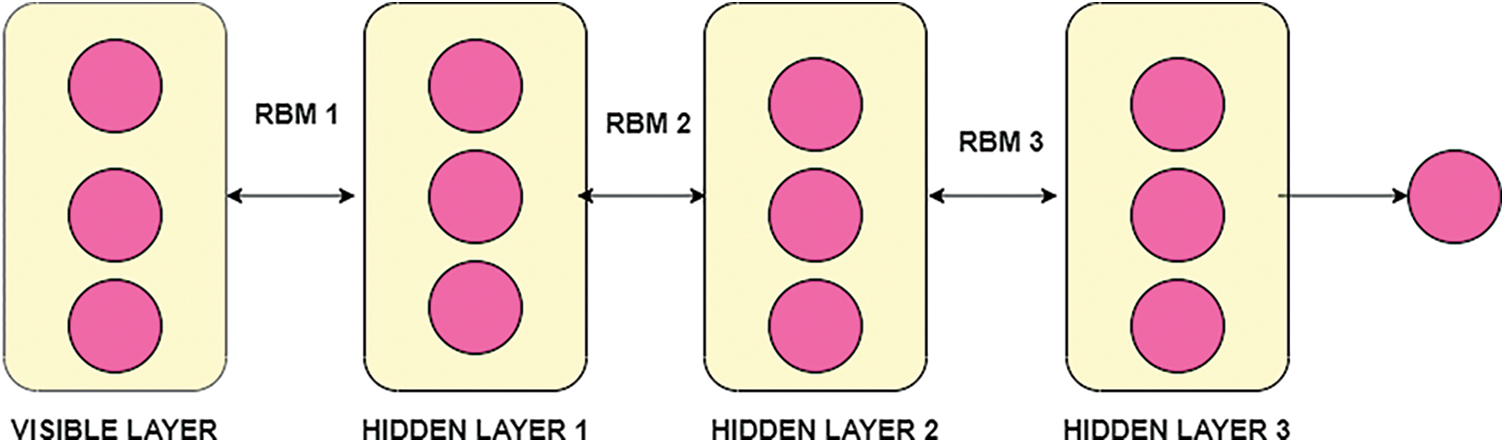
Figure 4: Framework of DBN with RBM

In the Fig. 4, DBN with stacked RBM, in the visible layer then the training process of classifier DBN is based on the RBM associated with learning rule. In the training process which includes parameters of weight between layers, neuron states along with bias value. Similarly weight of previous layer with next layer helps the transmission of layer. Applying the sigmoid function is given as:

P(sigi=1)=11+exp(−bii−∑j⁡sigjwtij) (8)

Initialized, the bias and synaptic weight value for all neurons in the RBM is given. Training the input neurons in the visible layer consists of positive and negative phases. In the positive step, it transforms the data from the visible layer to the hidden layer and, for the negative phase, converts the data from the hidden layer to the visual layer. The activation function for individual positive and negative steps is evaluated using Eqs. (9) and (10).

P(vii=1|hi)=sigm(−vbii−∑j⁡hijwtij) (9)

P(hii=1|vi)=sigm(−hbi−∑j⁡hijwtij) (10)

Comparing the DBN model this proposed work optimized the weights of parametric values until it reaches the maximum number of epochs. In the training process all parametric values are optimized by using Eq. (11).

update(wtij+η2×(positive(Edij)−negative(Edij)) (11)

where,

positive(Edij) -Positive statistics of edge Edij=p(hij=1|vi)

negative(Edij) -Positive statistics of edge Edij=p(vij=1|hi)

η -learning rate

The process mentioned above is used for the training of one RBM. Repeat the same process until all RBMs are get trained. The feature classification of the mammographic image using the crow search optimization with a deep belief network produces the efficiency in detecting mammographic images from the large data set.

The preprocessing step filters the noise from the input image and pectoral image. These techniques improve feature extraction and feature classification more accurately. Optimization-based extraction is used to select the relevant and optimal features, leading to improved accuracy. As a whole, the proposed deep belief network in retrieving the mammographic image is an efficient way. Some real-time prediction strategy is discussed in the article.

3.5 Calculating Similarity Measure

For the query mammographic image retrieval from the large dataset, Euclidean distance metric measures are used. The formula foe Euclidean distance metric measure is:

Ed=∑i=1n⁡(xi−yi)2 (12)

where, xi is the training image in the large data set and yi is the query image. The value of minimum distance value signifies an query exactly for matching image in the large data set.

4  Result and Discussion

4.1 Data Set Description

The extraction and classification techniques are performed in MATLAB R2018a. The data collection for this proposed work is a publicly available dataset: Mammographic Image Analysis Society (MIAS)/Mini-MIAS and Digital Database for Screening Mammography (DDSM)/CBIS-DDSM. The MIAS database is digitized at 50 micron-pixel edge but reduced to a 200-micron pixel edge and clipped each image with pixels. The CBIS-DDSM dataset is provided in 16-bit DICOM format with a resolution of 3131 × 5295 pixels. Fig. 5 shows that sample data image from the MIAS and mini MIAS dataset.

Figure 5: Sample data image from MIAS and mini MIAS data set

Figs. 5a and 5b shows data from the MIAS data set and Fig. 5c shows data from the mini MIAS data set. Fig. 6 shows the sample data image from the CBIS-DDSM dataset.

Figure 6: Sample data image from CBIS-DDSMdata set

In Fig. 6 shows that data from CBIS-DDSM data set.

4.2 Performance of Parametric Measures

These parametric metric measures are computed and assessed to retrieve the similarity of the image from the extensive data set in the effectiveness of this proposed work CSO-DBN. This proposed work is compared with existing algorithms of SVM, Naïve Bayesian classifier (NB), butterfly optimization algorithm (BOA), and Crow Search optimization algorithm (CSO).

sensitivity=TPTP+FN (13)

Specificity=TNTN+FP (14)

Accuracy=TP+TNTP+TN+FP+FN (15)

Sensitivity is a statistical performance metric measure and it is also called as TP rate. It is the proportion of similar mammographic image is recognized in the data set. Specificity is also termed TN rate. It recognized the dissimilar mammographic image. Accuracy precise the mammographic images are categorized accurately.

Precision

It is called positive predictive value (PPV). It evaluates true positive for all positive values by using

Precision=TPTP+FP (16)

Recall

It evaluates true negatives for all negative values by using

Recall=TPTP+FN (17)

In calculating the F-Score by combining the recall and precision to its value. The maximum value of F-Score is 1 and minimum score is 0. In the MCC is the correlation coefficient value between −1 & +1. Table 2 shows that parametric measures of sensitivity and specificity.

From the Table 2 for the sensitivity rate CSO-DBN algorithm is better than SVM (81.4%) and NB (84.2%), BOA (88.81%), CSO (91.68%) and similarly, CSO-DBNoutperforms other algorithms with specificity of 96.8%. Fig. 7 shows that accuracy rate of various techniques used.

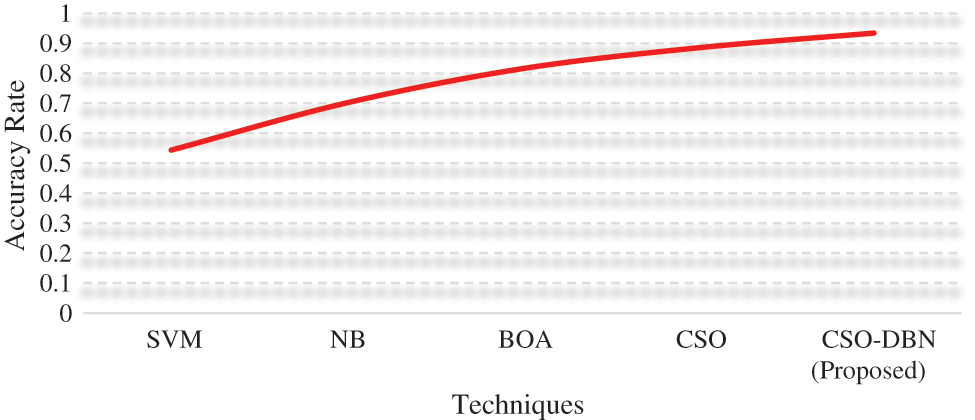
Figure 7: Accuracy rate

From the Fig. 7. Proposed work CSO-DBN has an accuracy of 0.9344 whereas SVM (0.5434), NB (0.7014), BOA (0.8156), and CSO (0.8852). The highest accuracy rate is achieved by our proposed work CSO-DBN. Fig. 8 shows that graphical representations of FRR and MCC for various algorithms.

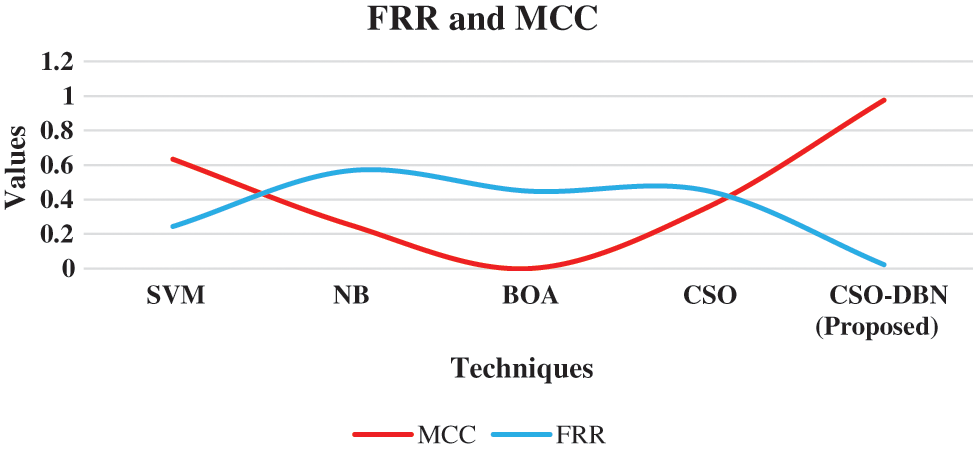
Figure 8: Graphical representation of the MCC and FRR

From the Fig. 8, the FRR and MCC are executed in various techniques. Proposed work CSO-DBN attained the value of 0.976 in MCC and 0.0226 in FRR. The value of MCC for SVM 0.634, NB 0.252, BOA 0.334, CSO 0.352 are observed. The observed value for FRR are SVM 0.244, NB 0.568, BOA 0.449, CSO 0.452 respectively. Table 3 shows that metric measures of precision, recall and F-Score.

The precision value of proposed work CSO-DBN has achieved better percentage of 86.32%. In the recall rate of CSO-DBNgot 91.62% compared with SVM, NB, BOA, and CSO. The CSO-DBNalgorithm outperforms with an F-score of 95.34%. In applying the Kalman filter for removing the noise in the mammographic image and PSNR value (‘Peak Signal to Noise Ratio’) is evaluated to observe the quality of the image by using:

PSNR=1M×N∑i=0M−1⁡∑j=0N−1⁡[mh(i,j)−nk(i,j)]2 (21)

where M and N denotes the number of rows and columns respectively. nk(i,j) denotes the noisy image and mh(i,j) , denotes the monochrome image. Fig. 9. PSNR values of various algorithm.

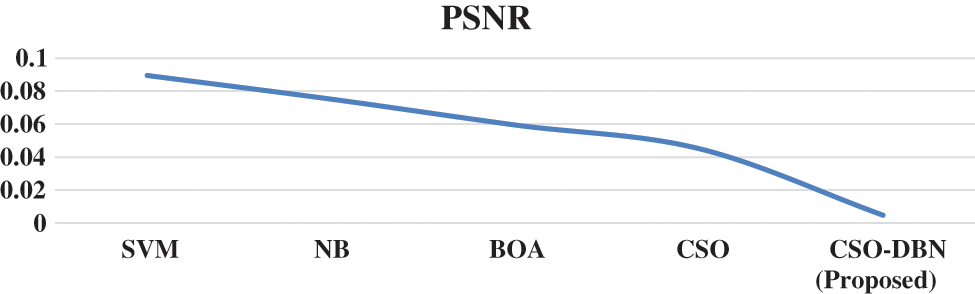
Figure 9: PSNR Rate for various techniques

Observation of Fig. 9 shows that our proposed work CSO-DBN attained best result. The average computation time for various techniques is given in the Fig. 10.

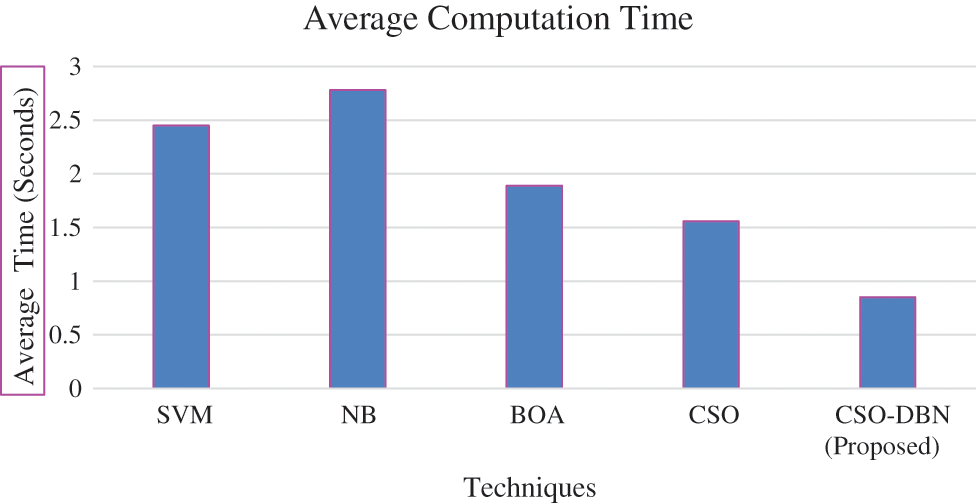
Figure 10: Average computation time

From the Fig. 10 observed that average computation time of proposed work produces minimum compared it with other existing techniques. The proposed work CSO-DBN is used for feature selection and it is compared with other existing algorithms of SVM, NB, BOA, CSO in terms of average fitness, best fitness, mean, standard deviation and worst fitness. The parameter values for fitness function are 0.99 and 0.01. Table 4 shows that metric measures of feature selection.

The results of the proposed CSO-DBN algorithm in this Table 4 shows that the better result when compared it with other existing techniques. SVM, NB, BOA, CSO algorithms are used for selecting the features from best fitness to worst fitness. The proposed algorithm CSO-DBN outperforms other existing algorithms and the best fitness value is 0.1036, worst fitness value is 0.2103 and average fitness value is 0.2015.

5  Conclusion

This paper demonstrated Virtual Mammography Image Retrieval Using an Optimized feature selection with a classifier. Data are collected from the publicly available dataset (MIAS)/Mini-MIAS and Digital Database for Screening Mammography (DDSM)/CBIS-DDSM. In the pre-processing phase Kalman filter is used to remove noise, and for the feature extraction SIFT algorithm is implemented. The accurate and efficient retrieval of the mammographic image from the large dataset is done. The most relevant features are selected using an optimized crow search algorithm and classified using a deep belief network. The accuracy rate of proposed work CSO-DBN is 0.9344 whereas SVM (0.5434), NB (0.7014), BOA (0.8156), and CSO (0.8852). Our proposed work outperforms better results in metric performance measures of error rate, computation time, MCC, and FRR. In the future, this work may extend up implementing the classification by using various optimization techniques.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare no conflict of interest regarding the publication of the paper.

References

1. R. Dhaya, “Analysis of adaptive image retrieval by transition kalman filter approach based on intensity parameter,” Journal of Innovative Image Processing (JIIP), vol. 3, no. 1, pp. 7–20, 2021. [Google Scholar]

2. S. Jenifer Rayen and R. Subhashini, “An efficient mammogram image retrieval system usingan optimized classifier,” Neural Processing Letters, vol. 53, no. 4, pp. 2467–2484, 2021. [Google Scholar]

3. R. C. Gonzalez and R. E. Woods, Digital image processing, 3rd ed., Upper Saddle River, NJ, USA: Prentice-Hall, 2007. [Google Scholar]

4. D. H. Hubel and T. N. Wiesel, “Receptive fields of single neurones in the cat’s striate cortex,” Journal of Physiology, vol. 148, no. 3, pp. 574–591, 2000. [Google Scholar]

5. S. Zeng, R. Huang, H. Wang and Z. Kang, “Image retrieval using spatio grams of colors quantized by gaussian Mixture Models,” Neuro Computing, vol. 171, pp. 673–684, 2016. [Google Scholar]

6. R. Datta, D. Joshi, J. Li and J. Z. Wang, “Image retrieval: Ideas, influences, and trends of the new age,” ACM Comput Survey, vol. 40, no. 2, pp. 1–60, 2008. [Google Scholar]

7. S. L. Michael, S. Nice, D. Chababe and J. Ramsesh, “Content based multimedia information retrieval: State of the art and challenges,” ACM Transactions on Multimedia Computation Communication Application, vol. 2, no. 1, pp. 1–19, 2006. [Google Scholar]

8. H. Farhidzadeh, D. B. Goldgof, L. O. Hall, R. A. Gatenby and R. J. Gillies, “Texture feature analysis to predict metastaticand necrotic soft tissue sarcomas,” in Proc. IEEE Int. Conf. on Systems, Man, and Cybernetics (SMC), Prague, Czech Republic, pp. 2798–2802, 2015. [Google Scholar]

9. H. Farhidzadeh, J. Y. Kim, J. G. Scott, D. B. Goldg, L. O. Hall et al., “Classification of progression free survival with nasopharyn geal carcinoma tumors,” in SPIE Medical Imaging, Int. Society for Optics and Photonics, California, United States, pp. 97851–97859, 2016. [Google Scholar]

10. D. Giveki, M. A. Soltanshahi and G. A. Montazer, “A new image feature descriptor for content based image retrieval using scale invariant feature transform and local derivative pattern,” Optik, vol. 131, pp. 242–254, 2017. [Google Scholar]

11. D. Zhang, M. M. Islam and G. Lu, “A review on automaticimage annotation techniques,” Pattern Recognition, vol. 45, no. 1, pp. 346–362, 2012. [Google Scholar]

12. Y. Liu, D. Zhang, G. Lu and W. Y. Ma, “A survey of content based image retrieval with high level semantics,” Pattern Recognition, vol. 40, no. 1, pp. 262–282, 2007. [Google Scholar]

13. T. Khalil, M. U. Akram, H. Raja, A. Jameel and I. Basit, “Detection of glaucoma using cup to disc ratio from spectral domain optical coherence tomography images,” IEEE Access, vol. 6, pp. 4560–4576, 2018. [Google Scholar]

14. S. Yang, L. Li, S. Wang, W. Zhang, Q. Huang et al., “SkeletonNet: A hybrid network with a skeleton-embedding process for multiview image representation learning,” IEEE Transactions on Multimedia, vol. 1, no. 1, pp. 2916–2929, 2019. [Google Scholar]

15. W. Zhao, L. Yan and Y. Zhang, “Geometric constrained multi view image matching method based on semi-globaloptimization,” Geo Spatial Information Science, vol. 21, no. 2, pp. 115–126, 2018. [Google Scholar]

16. W. Zhou, H. Li and Q. Tian, “Recent advance in content basedimage retrieval: A literature survey,” International Journal of Computer and Electrical Engineering, vol. 31, no. 7, pp. 1–8, 2017. [Google Scholar]

17. A. Amelio, “A new axiomatic methodology for the imagesimilarity,” Applied Soft Computing, vol. 81, no. 4, pp. 105474–105485, 2019. [Google Scholar]

18. C. Celik and H. S. Bilge, “Content based image retrieval withsparse representations and local feature descriptors: A comparative study,” Pattern Recognition, vol. 68, no. 3, pp. 1–13, 2017. [Google Scholar]

19. T. Khalil, M. Usman Akram, S. Khalid and A. Jameel, “Improved automated detection of glaucoma from fundusimage using hybrid structural and textural features,” IET Image Processing, vol. 11, no. 9, pp. 693–700, 2017. [Google Scholar]

20. L. Amelio, R. Jankovi and A. Amelio, “A new dissimilaritymeasure for clustering with application to dermoscopicimages,” in Proc. 9th Int. Conf. on Information, Intelligence, Systems and Applications(IISA), Zakynthos, Greece, pp. 1–8, 2018. [Google Scholar]

21. Q. Li, X. Richeng, H. Zhao, X. Lili and X. Shan, “Computer aided diagnosis of mammographicmasses using local geometric constraint image retrieval,” Optik, vol. 171, pp. 754–767, 2018. [Google Scholar]

22. Z. Zhou, M. Qutaish, Z. Han, R. M. Schur, Y. Liu et al., “MRI detection of breastcancer micrometastases with a fibronectin targeting contrast agent,” National Communication, vol. 6, pp. 7984–7994, 2015. [Google Scholar]

23. X. Jun, L. Xiang, Q. Liu, H. Gilmore, W. Jianzhong et al., “Stacked sparse autoencoder(SSAE) for nuclei detection on breast cancer histopathology images,” IEEE Transaction Medical Imaging, vol. 35, no. 1, pp. 119–130, 2016. [Google Scholar]

24. E. M. Nejad, L. S. Affendey, R. B. Latip, I. B. Ishak and R. Banaeeyan, “Transferred semantic scores for scalable retrieval of histopathological breast cancer images,” International Journal of Multimedia Information Retrieval, vol. 7, pp. 1–9, 2015. [Google Scholar]

25. M. Azimzadeh, M. Rahaie, N. Nasirizadeh, K. Ashtari and H. NaderiManesh, “An electro chemical nano bio sensor for plasma miRNA-155 based on graphene oxide and gold nanorod, for early detectionof breast cancer,” Biosensors Bioelectronics, vol. 77, pp. 99–106, 2016. [Google Scholar] [PubMed]

26. A. A. Shastri, D. Tamrakar and K. Ahuja, “Density wise two stagemammogram classification using texture exploiting descriptors,” Expert Systems With Applications, vol. 99, pp. 71–82, 2018. [Google Scholar]

27. M. Zhu, Q. LV, H. Huang, C. Sun and D. Pang, “Identification of a four long non coding RNA signaturein predicting breast cancer survival,” Oncology Letters, vol. 19, pp. 221–228, 2020. [Google Scholar] [PubMed]

28. S. Dutta, S. Ghatak, A. Sarkar, R. Pal and R. Roy, “Cancer prediction based on fuzzy inference system,” in Proc.3rd Int. Conf. on Smart Innovations in Communication and Computational Sciences (ICSICCS), Ayodhya, India, pp. 27–28, 2020. [Google Scholar]

29. C. L. Chowdhary and D. P. Acharjya, “Segmentation and feature extraction in medical imaging: A systematic review,” Procedia Computer Science, vol. 167, pp. 26–36, 2020. [Google Scholar]

30. V. Prakash Singh, S. Srivastavaand and R. Srivastava, “Automated and effective content basedimage retrieval for digital mammography,” Journal of X-Ray Science and Technology, vol. 26, no. 1, pp. 29–49, 2018. [Google Scholar]

31. G. E. Hinton, S. Osindero and Y. W. Teh, “A fast learning algorithm for deep belief nets,” Neural Computation, vol. 18, no. 7, pp. 1527–1554, 2006. [Google Scholar] [PubMed]

32. M. Lakshmitha and A. Abdul Hayum, “SVM based approach of detectionand classification of tumors inmammography,” International Journal of Engineering Applied Sciences and Technology, vol. 5, no. 1, pp. 436–440, 2020. [Google Scholar]

33. S. Arora and S. Singh, “Butterfly optimization algorithm: Anovel approach for global optimization,” Soft Computing, vol. 23, no. 3, pp. 715–734, 2019. [Google Scholar]

34. S. Parvathavarthini, V. Karthikeyani and S. Shanthi, “Breast cancer detection using crow search optimization based intuitionistic fuzzy clustering with neighborhood attraction,” Asian Pacific Journal of Cancer Prevention, vol. 20, no. 1, pp. 157–165, 2019. [Google Scholar]