A Low-Cost and High-Performance Cryptosystem Using Tripling-Oriented Elliptic Curve

1  Introduction

Elliptic curve cryptosystem (ECC) is a relatively new family of public key cryptosystems whose security level depends on the difficulty of solving the discrete logarithm problem for elliptic curves (EC). ECC is immune to many cryptanalysis attacks and can provide an equivalent level of security to that of other types of public key cryptosystems using much shorter key sizes. This ECC feature results in saving the time and resources required for cryptographic operations. Hence, ECC is attractive for newly introduced security applications requiring high-performance crypto processors, such as cryptocurrencies and multimedia applications [1].

However, the current implementation of ECC operations has several limitations that reduce its utility for modern security applications. The significant drawbacks of the current ECC implementation are the time consumption and high costs or resources-consumptions. These problems limit the ECC’s ability to meet the requirements of modern security applications [2–5].

Many ECC implementations use the affine coordinates that require performing the modular inversion operation. However, this operation consumes a longer time and causes an extra delay for ECC point operations [2]. Additionally, the sequential design pattern adopted in most ECC implementations increases the time delay for encryption and decryption processes [3]. Furthermore, current ECC implementations use standard EC forms with relatively high computational complexity, thus negatively impacting performance [4]. Moreover, hardware implementation for ECCs require dedicated resources and might be expensive for many applications [5–7].

These problems hinder ECC from fulfilling the performance requirements for modern applications and make it an expensive option for applications with limited resources.

Many studies have attempted to solve the problem of the time-consuming inversion operation using projective coordinate systems [2]. However, projective coordinates eliminate inversion operations, but they cause more multiplication operations, imposing limitations regarding ECC speed, particularly when using sequential design patterns [3].

Researchers used inherited parallelism in ECC computations using parallel hardware design patterns to implement cryptographic operations. This optimized the ECC performance level compared to sequential design implementations [4,5]. However, such designs cost additional resources and consume extra hardware components and computational power [4–6].

It should also be noted that most previous studies focused on the standard form of EC, which has higher level of computational complexity, and may deepen the time delay problem. Conversely, the newly introduced forms of EC with lower computational complexity have not been widely investigated [7]. Therefore, using such forms of ECs can reduce the Galois Field (GF) calculations required to perform ECC point operations. This makes them attractive and helpful in developing high-speed ECCs.

National Institute of Standards and Technology (NIST) has recommended some EC forms that have lower computational complexity, such as Montgomery and 3DIK curves [8].

Although few studies investigated the performance level of the different EC alternatives, most of these works used the hardware implementations of ECC, which are considered expensive and requires extra hardware resources precisely when adopting the parallel design patterns [9–11].

Software implementation for ECC has emerged as a cost effective solution, which can be supported by parallel design implementation to boost cryptosystem performance [12,13].

Recent studies have investigated parallel software implementations for relatively new forms of ECs, such as the Montgomery curve, which achieved promising improvement on the performance level [14]. Therefore, this motivates more studies to explore potential enhancements that could be achieved on the speed (performance) of ECC using other EC forms, which have less computational complexity.

This study addresses significant research problems represented by the long-time delay and hence low-performance level for ECC. Additionally, this study proposes an efficient, low-cost software implementation for ECC to address the issue of costly resources required for hardware-based ECC.

The main aims of this research are to improve ECC cryptographic operations’ speed by solving the time-delay-related issues and to develop an efficient, low-cost software-based ECC.

Therefore, to achieve the aims above, this study presents a parallel software implementation for ECC using a new form called tripling-oriented (3DIK) EC. In addition to using parallel design patterns, the factors affecting the performance, such as the projective coordinates and the scalar multiplication algorithms are also explored. This study seeks to understand the best ECC design and implementation choices and develop a high-performance cryptosystem that consumes the least resources and computational power.

This article discusses, in great details, the development stages of the proposed high-speed 3DIK ECC. The promising implementation results show that the proposed cryptosystem achieves high performance.

The following section elaborates on the motivation behind the current research work.

2  Research Motivation

Many recently emerged applications, such as multimedia and wireless sensors, require a high-performance and low-cost cryptosystem that can provide security services and satisfy performance and resource constraints. Unfortunately, the current cryptosystems, including usual ECC implementations, suffer from time delay and resource consumption issues and thus have limited ability to serve modern applications.

Therefore, developing a high-performance and cost effective ECC has become an urgent and pressing requirement for modern applications nowadays. Moreover, ECC is used for many purposes, including digital signatures and key exchange, which are incorporated into many information security systems and TLS protocols. Therefore, improving the performance and reducing the cost of ECC will positively impact many modern applications. This motivated the current study and encourages researchers to investigate several ways to enhance the performance of ECC.

The current research develops better understanding of the impact of the different factors affecting the ECC performance, such as projective coordinate systems, scalar multiplication algorithms, and the use of parallel design. This enables a tune-up of these significant factors to accomplish higher performance and lead to the development of high-speed ECC.

3  Background

Since the development of EC cryptography in 1985, several EC forms have been proposed, one of which is the tripling-oriented curve (3DIK) [15]. The 3DIK, is suitable for security applications requiring high-speed due to its relatively low computational complexity compared to the standard EC form. The 3DIK curve equation over the prime field GF (p) is defined as follows:

y2=x3+3a(x+1)2, where the value of ‘a’ is predefined, and a(4a−9)≠0, x, y, a are elements of the finite field.

ECC is based on the EC discrete logarithm problem, which is considered more challenging to solve than the various factorization and general discrete logarithm problems used in other cryptosystems. Therefore, ECC can provide a comparable level of security with shorter key sizes. This feature reduces storage and transmission requirements and considerably improves the performance of the cryptosystem. The increased performance and the lower resource consumption represent the primary benefits of ECC compared with other public key cryptosystems [1].

The EC can be defined using either a prime (GF(p)) or a binary (GF(2m)) finite field.

ECC comprises multiple layers of computations, as shown in Fig. 1. Note that the lower level of computations includes finite field arithmetic, particularly modular addition, subtraction, multiplication, and division operations.

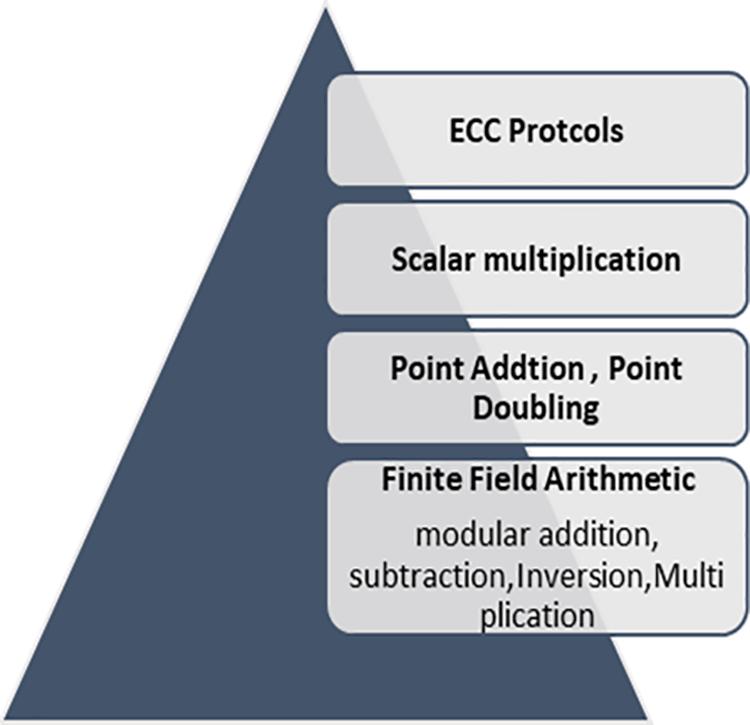
Figure 1: The elliptic curve cryptography hierarchy

However, the latter requires calculating the multiplicative inverse, which is the most time-consuming operation. The basic building blocks for the upper level of computations are point doubling and addition. The next level includes The scalar multiplication operation as depicted in Fig. 1. It is considered the major operation in ECC encryption. Finally, ECC protocols represent the top of the hierarchy and use the lower computational levels to perform cryptographic protocols such as key exchange and digital signatures, among others [1,14–16].

The scalar multiplication algorithm performs either one or both point operations in each iteration. The point addition operation adds two different points, G and Q to obtain another EC point, R. The point addition can be calculated by computing the coordinates (x3, y3) of the resulting point, asfollows [1]:

G(x1, y1)+Q(x2,y2)=R(x3,y3), where x1≠x2

The slope (M) = y2−y1x2−x1

x3=M2−x1−x2

y3=M(x1−x3)−y1

Alternatively, the point doubling operation adds the point to itself (Q = G) and can be calculated as follows [1]:

G(x1, y1)+G(x1,y1)=R(x3,y3), where x1≠0

The Tripling-oriented slope m=3x2+6a(x+1)2y

x3=M2−2x1

y3=M(x1−x3)−y1

It is worth noting that the EC form does not affect the point addition calculations because it does not rely on the EC form. In contrast, point doubling calculation changes according to the EC form and the use of coordinate systems since it requires deriving the slope equation from the EC equation [3–5].

The points on an EC can be represented using different types of coordinate systems. The standard coordinates are the affine coordinates P(x, y). Alternatively, projective coordinates can improve the performance of ECC computations because of their ability to avoid time-consuming inversion operations. It should be noted here that the use of certain projection system plays a vital role in determining the complexity level of ECC computations and thus represents a significant factor that should be considered when designing an efficient cryptosystem [1,3–7].

Three main algorithms were used to perform scalar multiplication: the Montgomery ladder, NAF, and Binary left to right (LTR). Scalar multiplication algorithms vary in speed and security levels[15–17]. Therefore, this study investigates their characteristics to determine the most efficient algorithm for developing high-speed ECC.

Furthermore, using parallel design to implement ECC operations is another important factor in improving cryptosystem performance [4–6,13]. This factor will also be considered in this study to achieve the maximum gain in performance.

4  Literature Review

Many studies have been conducted to improve the performance of ECC. However, most previous studies investigated the main elements that could improve the ECC performance, such as using a specific EC form, projective coordinates, parallel and concurrent elliptic curve computations, and efficient scalar multiplication techniques. These factors impact the ECC performance and should be considered when developing a high-speed cryptosystem.

Conversely, some studies have focused on improving the security level of ECC from certain types of attacks, such as simple time attacks (STA).

This section summarizes the most important studies that explored several ways to improve ECC’s performance and security.

According to the infrastructure used to implement cryptographic computations, studies related to ECC implementations can be categorized into hardware and software-based implementations.

Numerous studies on the hardware implementation of ECC exist, where some employed sequential implementations while others used parallel hardware implementations to improve performance. Researchers in [4] and [5] proposed several parallel hardware architectures for ECC point doubling and addition, respectively. Interestingly, both used the projective coordinates to eliminate the modular inversion operation. Researchers also employed parallel hardware implementation to use the inherent parallelism in ECC computations, which boosts the speed of ECC computations. The authors of [10], using various projective coordinates, presented concurrent data flows for the tripling-oriented (3DIK) ECC calculations over GF (P). Researchers have built an optimal parallel data flow that takes advantage of the highest degree of parallelism. According to this study, the 3DIK curve is an efficient choice for constructing a high-speed EC crypto-processor, particularly when used with appropriate projection and parallel design. In [6], researchers explored the different parallel design choices for Binary Edward ECC over GF(p), which led to considerable improvement in the performance, but with consuming extra hardware resources. Similar studies were conducted in [9] and [18] to investigate the impact of parallel hardware designs and projective coordinate factors on Montgomery and Edward ECCs, respectively. It has been proven that using these two factors is vital in enhancing the ECC performance. The Montgomery and 3DIK forms of EC perform better than others since they require less finite field operations and better use of parallel design implementations.

Other studies that used parallel hardware implementations further implemented the upper level of computations, represented by points doubling and addition, in parallel to optimize the performance level. For example, in [19], researchers used a modified Right to Left (RL) binary algorithm to implement point doubling and addition operations in parallel. In contrast, in [20], researchers used the NAF algorithm for the same purpose. Although both studies successfully improved the performance level, they require extra hardware resources.

The main disadvantage of hardware implementations is that they require separate crypto-processor and hardware components, significantly increasing the cost of designing and implementing the cryptosystem. Therefore, many security applications, particularly those with limited resources, find hardware implementation of ECC to be an expensive and complicated choice, becoming even worse when using parallel design patterns.

However, software implementation for ECC has lower development costs, is easier to upgrade, and is more adaptable. The following is a brief overview of previous studies that used software implementation to develop ECC.

The study published in [21] introduced a sequential software implementation of ECC using the standard Weierstrass form over GF(p). This study investigated the use of projective and affine coordinate systems. It has been shown that Jacobean and mixed coordinates can eliminate the costly modular inversion operation. The study evaluated all EC operations on the different coordinate systems using a 256-bit key size. Therefore, this study’s experimental results show that the time required to perform scalar multiplication using projective coordinates require only 5.037 milliseconds. Another study published in [6] presented a software implementation for ECC Diffie–Hellman, Encryption, and Decryption using the GMP library, which supports large integers. The C software used Lopez–Dahab coordinates to avoid the affine coordinates’ inversion.

In [22], researchers presented software implementation for ElGamal ECC over GF(P). The study fully described the ElGamal ECC’s essential phases and used the NAF algorithm for scalar multiplication. The general Weierstrass EC equation and affine coordinates for the point representation were adopted in this study. The authors in [17] suggested a new ECC that prevents the need for the mapping procedure used in previous studies. This result was accomplished by constructing the mapping technique using ASCII values for each character rather than a specific algorithm, enabling the encryption process to run faster. The study published in [23] provided detailed software implementation for ECC, which can encrypt and decrypt text and images. The main advantage of such a study is that it presents significant technical details about developing software-based ECC. Therefore, this could be useful for researchers and organizations that work on manufacturing-efficient cryptosystems.

The study in [24] explained how to create a software-based ECC using Java over the prime and binary fields. The study used the SunEC provider to implement key pair creation, exchange, and ECDSA. Another study [25] employed the Java Development Kit version 1.2 to develop the EC Digital Signature Algorithm. Different key sizes were applied to test the proposed cryptosystem. Additionally, the experimental results showed that generating 256-bit key pairs takes 13.6 milliseconds, while the digital signing takes 13.7 milliseconds. However, the signature validation process takes a similar time as the signing process. Other researchers examined the performance of Java implementation of EC operations on both standard and finite fields [26]. According to this study, the Java BigInteger class is more efficient for software implementations of EC operations in the GF(p) than GF(2n). The study reported in [27] proposed a Java implementation of the EC with an integrated encryption scheme over both finite fields. Another study [28] provided a performance evaluation of software implementations ECC encryption and decryption over GF(p) than GF(2n) using different key sizes that vary between 228-bits and 1864-bits. The results showed that the GF(p) is faster than the GF(2n), making it better for software implementations. In [29], the authors demonstrated a simple software ECC. The cryptosystem encrypts data sent between client and server applications using Java socket programming. In another technical, applied study published in [30], the authors developed an email encryption and decryption system using ECC.

The authors of [31] surveyed the scalar multiplication algorithms commonly used to perform ECC point operations. The execution time, the hamming weight of the scalar k, the number of doubling operations, and the required precomputation were compared. It has been concluded that the addition and subtraction method is more efficient than the binary scalar technique since it uses the (NAF), which has less hamming weight. It is worth noting that NAF uses a table of pre-computed points; the window technique is ideal for less limited memory. This study showed that the NAF algorithm has the shortest execution time compared with other algorithms. Furthermore, the results proved that the prime field is more efficient for software implementations than the binary field; scalar multiplication over the prime field is faster.

Notably, a parallel software implementation for ECC operating in a multithreading environment was introduced in [13]. The suggested parallel ECC uses Karatsuba and Montgomery algorithms for point multiplication. Additionally, the GF(p) was faster than the GF(2n). Therefore, this study supports the use of GF(p) for ECC software implementations.

It can be noted that most previous studies concentrated on sequential software implementation for ECC computations and only investigated one scalar multiplication method per suggested ECC implementation. Unfortunately, the sequential implementation limits the cryptosystem speed and exposes it to the risk of side-channel attacks such as STA. Moreover, they considered the standard form of EC and affine coordinates; however, it turns out that using other EC alternatives can lead to lower computational complexity levels and hence better performance. Another disadvantage of previous studies is that they rarely provide comprehensive performance analysis and testing for their proposed ECC software implementation to demonstrate its efficiency.

Notably, a promising study has been recently published in [14]. The authors proposed parallel software implementations for the Montgomery ECC over GF(p). Additionally, different factors were used to improve the cryptosystem performance, such as a projective coordinate system and parallel design. Furthermore, experimental results showed that using light EC forms such as Montgomery and an efficient scalar multiplication algorithm could greatly improve ECC performance. This finding motivated this study to investigate other EC forms with low computations, particularly the recently introduced tripling-oriented EC form.

This study explores the performance of 3DIK ECC when implemented with the support of a projective coordinate system and parallel design. The Java multithreading technique was used to realize parallel processing of EC computations. Projective coordinates were used to avoid the time consumption modular division operation. Additionally, several scalar multiplication algorithms were used to implement ECC operations. Finally, a comprehensive performance analysis was performed using the different scalar algorithms.

This study aims to determine the best options for all factors affecting ECC performance and align them to develop a high-speed cryptosystem.

The next sections provide the detailed design and software implementation for 3DIK ECC and testing and performance analysis.

5  The Cryptosystem Design

This section presents the EC equations and methods used to implement the cryptosystem. Additionally, the parallel computational schemes, which are required for parallel software implementations, are presented in this section.

The study used the recently introduced form of EC, the tripling-oriented curve (3DIK), presented in [32]. As mentioned previously, this form of EC is selected since it has relatively low computational complexity. Furthermore, EC point calculations are performed using projective coordinates instead of the affine form to avoid the modular inversion operation. Three types of projective coordinates were examined in this study, and finally, the one that gave the best performance was selected for developing the proposed high-speed ECC.

This study employs the Java multithreading technique to implement ECC computations in parallel by using the inherent parallelism in ECC computations to obtain higher performance levels. Researchers examined the use of almost all possible parallel designs and eventually selected the one that scored the best performance results.

This experimental study evaluates the ECC performance using the major scalar multiplication algorithms: the binary method, the NAF algorithm, and the Montgomery ladder algorithm. The results show that the cryptosystem performance varies significantly based on the used scalar multiplication algorithm.

The following section presents the calculations of the 3DIK point doubling and addition using the three projection systems.

5.1 ECC Computations

This section introduces the reader to the ECC points doubling and addition computations using projective coordinates. In [10], the 3DIK ECC computations were performed using projective coordinates to improve the performance by avoiding the time-consuming inversion operation. Then, the authors used hardware components to design and implement the encryption processes. This study adopts a similar methodology to perform ECC computations using projective coordinates. However, the current research investigates the parallel software implementation of ECC computations using the multithreading technique.

The tripling-oriented ECC point doubling computations with homogenous projection can be performed using the following equations:

X3=2YZ[(3X2+6aZ(X+Z))2−8XY2Z](1)

Y3=[(3X2+6aZ(X+Z))∗[12XY2Z−(3X2+6aZ(X+Z))2]−8Y4Z2](2)

Z3=8Y3Z3(3)

Point doubling computations using the Lopez–Dahap coordinates can be performed as follows:

X3=Z(3X2+6aZ(X+Z))2−8XY2(4)

Y3=2YZ(3X2+6aZ(X+Z))∗[12XY2−Z(3X2+6aZ(X+Z))2]−16Y5(5)

Z3=4Y2Z(6)

Eventually, the Jacobean coordinate system uses the following equations to compute the tripling-oriented point doubling operation:

X3=(3X2+6aZ2(X+Z2))2−8XY2(7)

Y3=(3X2+6aZ2(X+Z2))∗[12XY2−(3X2+6aZ2(X+Z2))2]−8Y4(8)

Z3=2YZ(9)

It should be recalled here that point addition computations do not vary with the change in EC form.

The following section presents the parallel computational designs for ECC point doubling and addition.

5.2 Parallel Computational Designs

This section presents the parallel designs used to implement ECC computations.

Based on the experiments conducted here, the design with four parallel multiplication (PM) operations achieves the least time delay for the 3DIK ECC point doubling with the three projections.

This study develops high-speed ECC and thus focuses on the parallel design that achieves the least number of multiplication cycles since it requires less time to perform EC point computations.

The sequential ECC design was also implemented in this research to prove the possible improvement in the performance level, which can be gained using the parallel design implementation.

Tables 1–3 present the modular arithmetic computations required to perform the tripling-oriented ECC point doubling using the three projective coordinate systems. Table 1 presents the computations required to calculate point doubling Eqs. (1)–(3) for a homogenous projection. The table shows the levels of computations required to perform point doubling. The computation levels can be categorized as multiplication or addition. Additionally, the table shows the parallel computations performed at each level. The proposed computational scheme uses four parallel multiplications. Note that the computations at a certain level cannot be performed until the results of the previous level are received. For example, the modular multiplication (M12) at level 7 can only be performed after finalizing the addition (A3) at level 6.

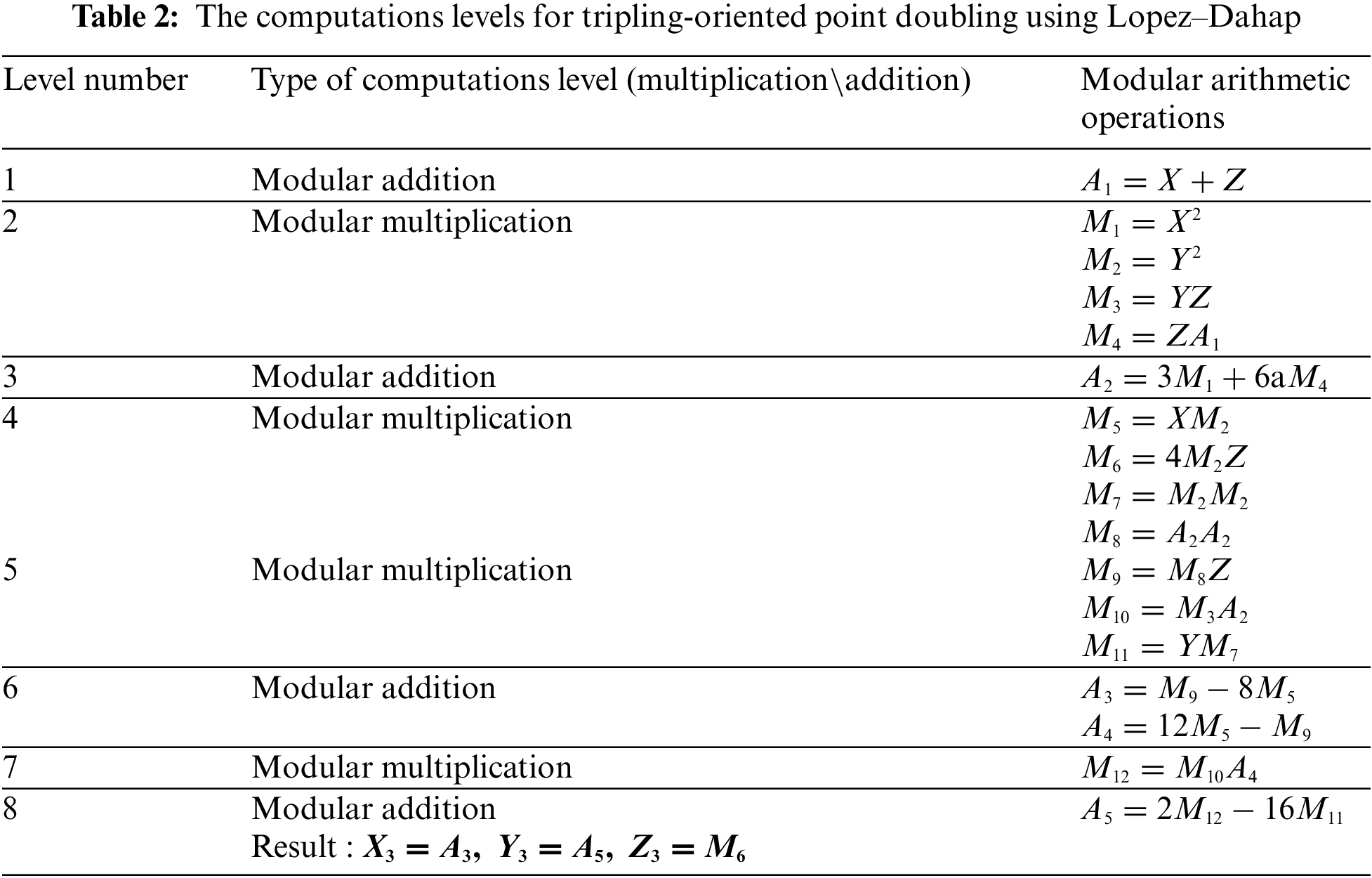
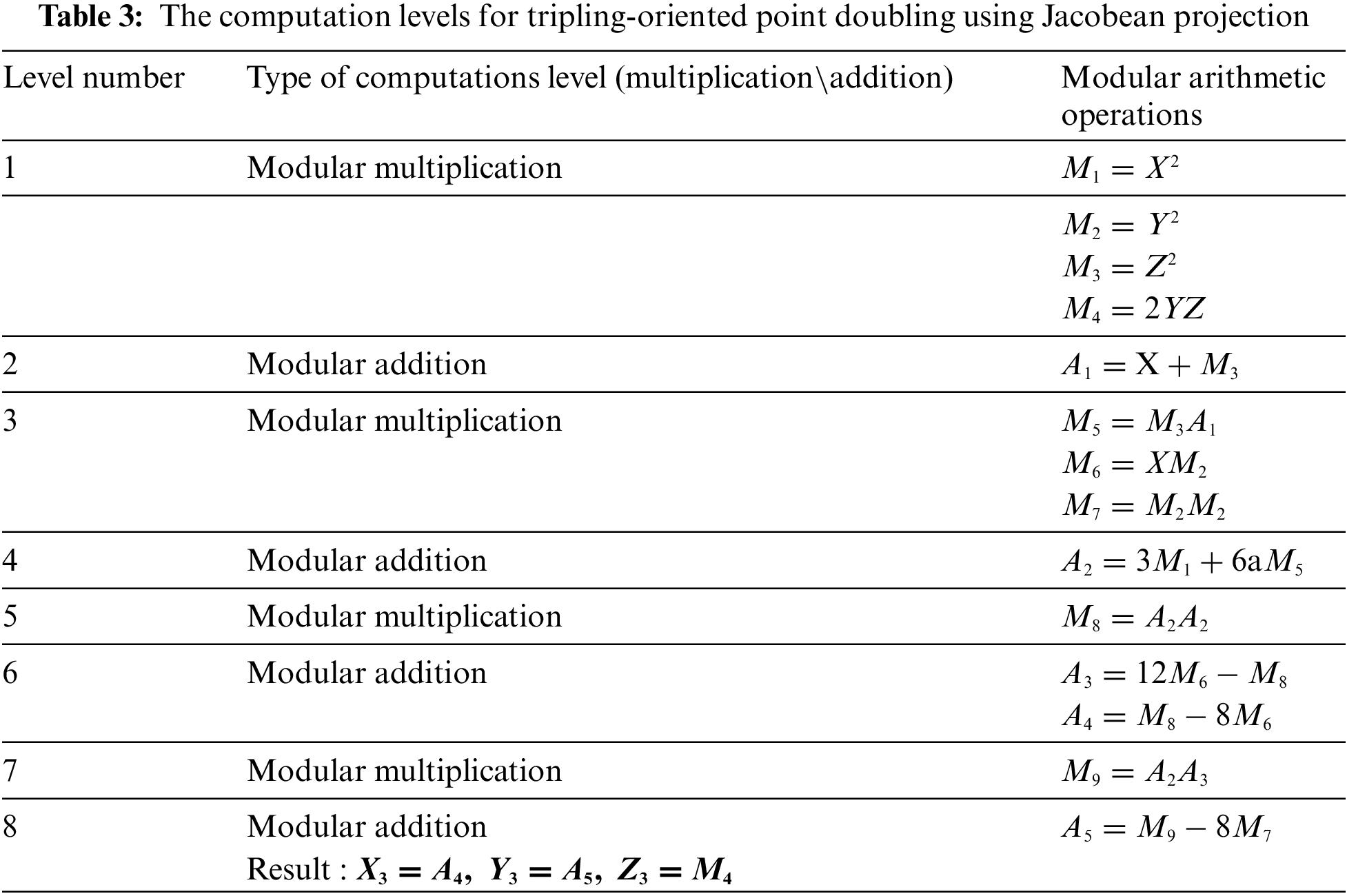
Similar computations for Lopez–Dahap Eqs. (4)–(5) and Jacobean Eqs. (7) and (8) are presented in Tables 2 and 3, respectively.

To provide a deeper insight into the parallel implementation of ECC, this study introduces the computational design schemes for ECC point operations that illustrate how the modular arithmetic of the 3IDK curve is executed using the 4-PM design. Those designs are implemented later using the Java multithreading to measure the actual performance level.

Figs. 2–4 show the computational designs for the tripling-oriented ECC point doubling computations using the three projective coordinate systems.

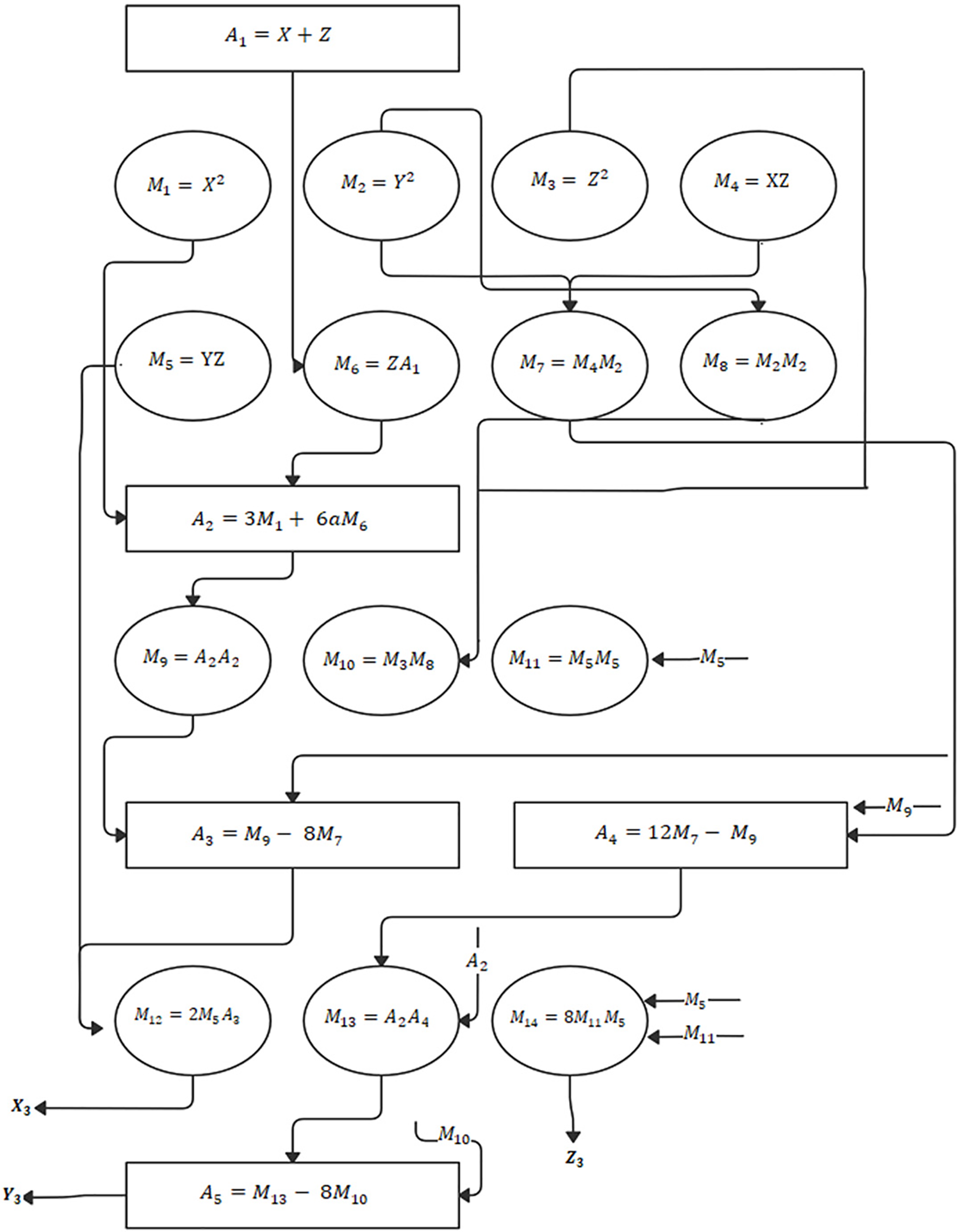
Figure 2: Computational design for 3DIK point doubling using homogenous projection

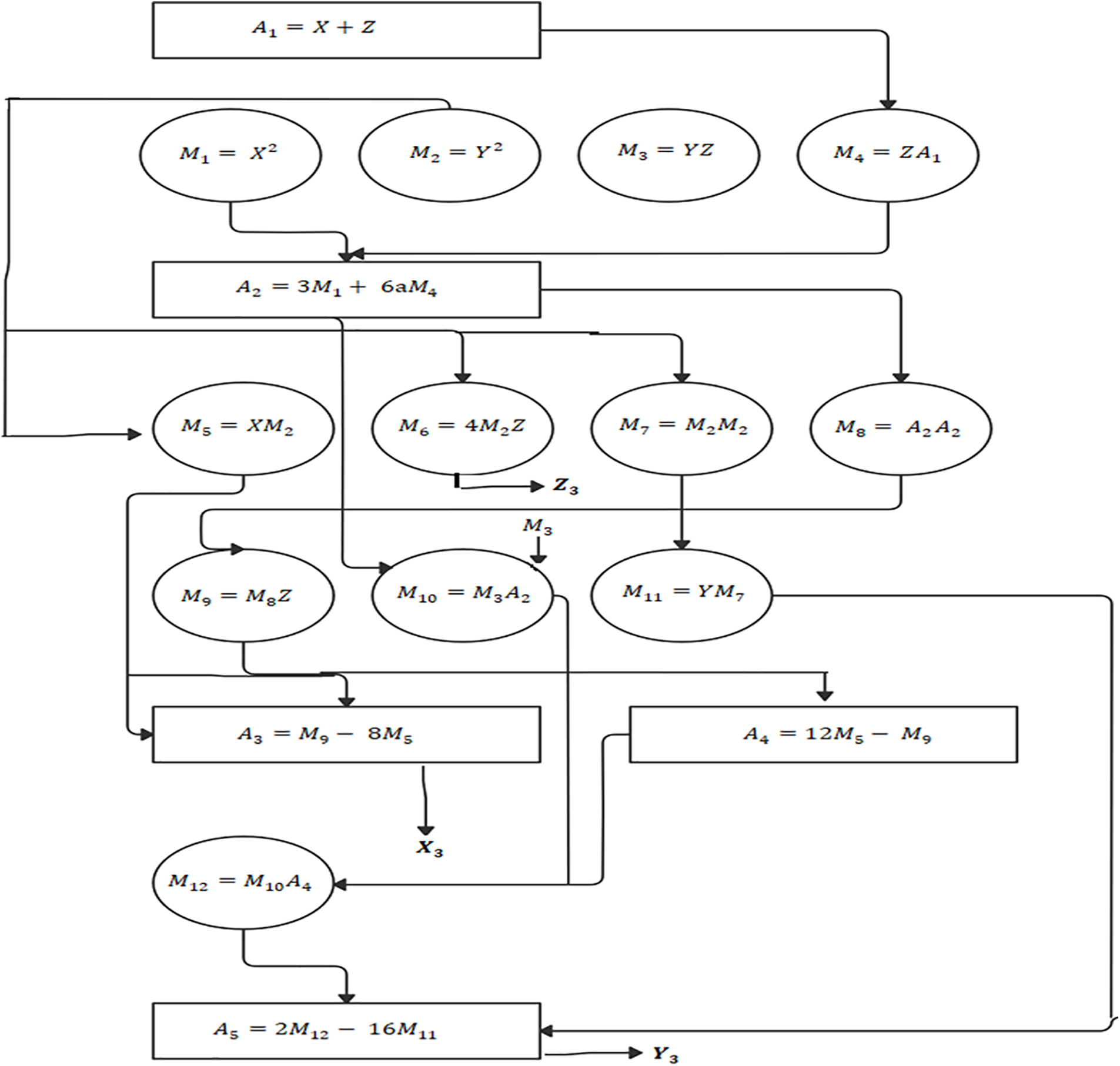
Figure 3: Computational design for 3DIK point doubling using Lopez–Dahap projection

Figure 4: Computational design for 3DIK point doubling using Jacobean projection

It can be observed that the Jacobian projection presented in Fig. 4 requires less number of multiplications; therefore, it may achieve the shortest time delay when using the sequential design implementation. Conversely, the homogenous projection requires the largest number of finite field multiplication operations, making it expensive for sequential implementation of the 3DIK ECC.

Note that parallel ECC designs depicted in Figs. 2–4 utilizes the inherited parallelism in ECC computations by implementing multiple finite field operations in each level of computations in parallel.

It can be observed from the parallel computational designs presented in Figs. 2–4, that all projections consume a similar number of multiplication cycles when implemented in parallel.

However, the software implementations for presented ECC designs should be performed carefully to evaluate the performance more accurately and to determine the ECC design that achieves the highest speed for cryptographic operations

The next section presents the software implementation procedures for the 3DIK ECC.

6  Equations Software Implementation

The software implementation of the proposed parallel and high-speed GF(P) ECC using the 3DIK curve is illustrated in this section.

The Java BigInteger class was used for programming the prime field since it can support calculations with much greater integers, often 256 bits, which cannot be performed using regular primitive data types. Additionally, this class provides many useful built-in methods for implementing finite field operations.

In the proposed software implementation for ECC operations, two Java classes were created: EllipticCurve and Point classes. The point class represents the EC point and has three attributes for each projective point coordinates X, Y, and Z. and nine operations to set and get these attributes.

The EllipticCurve class has six attributes and ten operations, where the attributes handle the domain parameters, which are the following:

  i.   a: the 3 DIK’s EC coefficient.

 ii.   P: the prime number (the modulus).

iii.   n: the cyclic subgroup order.

iv.   h: the cofactor, the number of cyclic subgroups in the EC group.

 v.   orderE: the EC order.

vi.   basePoint: the generator point for ECC calculations.

The operations of the EllipticCurve class perform the EC computations and relevant cryptographic operations, which are as follows:

  i.   EllipticCurve(): constructor to initialize the EC object and the domain parameters.

 ii.   PointDoubling() : perform the 3DIK point doubling computations.

iii.   PointAddition(): perform the ECC point addition computations.

iv.   scalarMultplication(): perform the point multiplication computations using the scalar multiplication algorithm.

 v.   Encryption(): return the cipher points after encryption.

vi.   Decryption(): return the decipher points after decryption.

vii.  selectPrivatekey(): return the private key randomly selected from a range starting from 3 to the cyclic subgroup order n.

viii. computePublic_key (): return the public point key by invoking a call to the scalar multiplication method and passing the private key and the base point.

ix.   + isInverse(): checks if the two points passed in the parameters are negation of each other.

The sequential implementation of ECC point operations is simple and only executes one operation per level of computation. Conversely, the parallel software implementation of point operations reflects the parallel designs provided in section V and performs the cryptosystem computations in parallel. The Java multithreading technology was employed to perform multiple field operations in each computation cycle for point doubling and point addition operations to accomplish this operation. Therefore, the Java thread can execute many operations simultaneously and separately to reduce the execution time for ECC point operations. Three key methods from the Java thread class were used as follows:

  i.   Run (): This method is used to act on a Java thread.

 ii.   start (): This function is responsible for initiating the thread’s execution of the GF(p) operation.

iii.   join (): This function waits until it receives the results of a GF(p) operation within a particular Java thread.

As mentioned earlier, more descriptions of the methods can be found in [14].

The proposed implementation assigns one Java thread for each finite field operation. A maximum of four threads are executed at each computation level. Java codes are inserted within the Run method’s bracket.

At the next implementation stage, several threads are programmed at each level of computation in ECC point operations. The proposed ECC designs in section V for point doubling and addition operations illustrate the number of threads required per computation cycle.

In the proposed multithreaded implementation of ECC, each thread calls for the joint method at the end of every computation level. Therefore, this ensures that the thread has completed its computations before starting the next computation levels. Other ECC point computation levels were performed in parallel using a similar approach. Overall, 16 Java threads were established to construct the Tripling-Oriented point doubling using the Homogeneous Projective system.

This study examined the implementation of ECC scalar multiplication using three well-known algorithms, which are as follows:

  i.   The Montgomery ladder,

 ii.   The NAF, and

iii.   The Binary (RL) method.

The experimental investigation presented in this study determines the fastest algorithm that achieves the shortest time delay for ECC encryption and decryption processes.

Experimental results confirmed expectations and found that the NAF algorithm requires executing fewer EC point operations. This result is expected since it has a lower hamming wait than the other algorithms. Specifically, NAF algorithms require a few point addition operations because of their signed binary representation. The LTR Binary method is faster than the Montgomery ladder algorithm because it requires approximately half the number of point operations. In contrast, the Montgomery algorithm requires executing both point doubling and addition operations for every scanned binary bit in the scalar K.

Furthermore, the encryption and decryption functions are parts of the EllipticCurve class. Here, the encryption function gathers the message and the other party’s public key as inputs and produces a cipher array of points for each char in the message. Alternatively, the decryption function takes the cipher array of points and the private key and reproduces the plaintext’s mapped points.

Complete details about the proposed ECC’s software implementation and source code are placed in [33] They are made available so researchers can use them in future studies and improvement.

A client server application has been developed and made available on the web as a proof of concept. The application allows testing of the encryption and decryption processes for the proposed 3DIK ECC. Additionally, the application is supported with instructions and GUIs to guide the user through the steps to be followed to perform encryption and decryption processes [33].

7  Results and Discussions

7.1 Experimental Environment

This experimental study used a Dell PC (Intel(R) Core(TM) i7-4770 CPU @ 3.40 GHz, 4 GB RAM) and the Windows 7 operating system to test the proposed ECC implementations. Additionally, the code used Java version 1.8 and the Eclipse IDE tool.

The Java command System.nanoTime was used to get the current time in Nanosecond (ns) to calculate the running time for proposed ECC implementations and to obtain precise results. The code segment below shows the technique for calculating the running time for any Java code segment. At the beginning of the program execution, the startTime variable of type long is declared to hold the time. In contrast, the endTime is displayed at the end of the execution to save the system time after finalizing a specific task. Finally, the duration is calculated by subtracting the start time from the end time.

7.2 Theoretical Speedup Using Amdahl’s Law

This section estimates the enhancement achieved in the ECC performance using the proposed parallel design.

Programs that perform parallel processing have some instructions that need to be executed sequentially, limiting the program’s speed. Therefore, adding more parallel processors or multithreading may not result in the expected improvement level. Amdahl’s law can be used to predict the theoretical speedup of the parallel execution when using multiple processors [34]. Amdahl’s law can be expressed as

S(n)=1S+Pn

where:

S (n) is the theoretical speedup.

S is the fraction of the program that is executed sequentially.

P is the fraction of the program that is performed in parallel.

n is the number of CPU threads.

The execution time of the different parts to perform the computations of Amdahl’s law, parallelizable and non-parallelizable parts of ECC computations, should be analyzed. Furthermore, Tables 4 and 5 present the non-parallelizable and parallelizable parts of the 3DIK ECC operations, respectively.

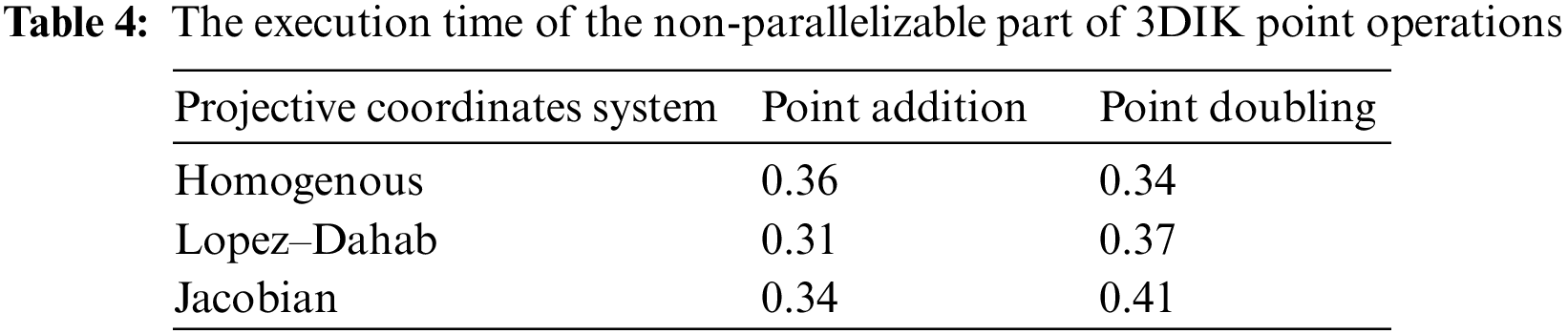
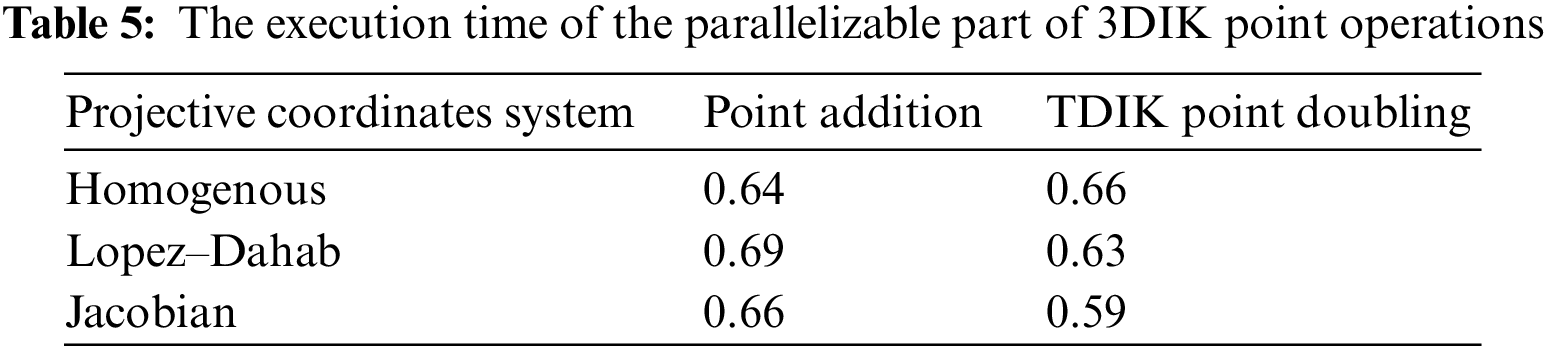
It can be observed from Tables 4 and 5 that the time consumed by the part of the computation that can be implemented in parallel in Table 5 is greater than that of the non-parallelizable computations in Table 4. Therefore, this motivates the use of parallel implementation since it will save considerable time for those parallelizable computations.

The execution time of the program with parallelization factors of N (N Threads) would be

T(N)=S+(1−S)N

where N is the number of threads required to implement the parallel computations.

Note that s is the execution time of the non-parallelizable part of the operation; N = 4 and 5 for point doubling and point addition, respectively. Table 6 shows the program’s execution time with parallelization factors of N.

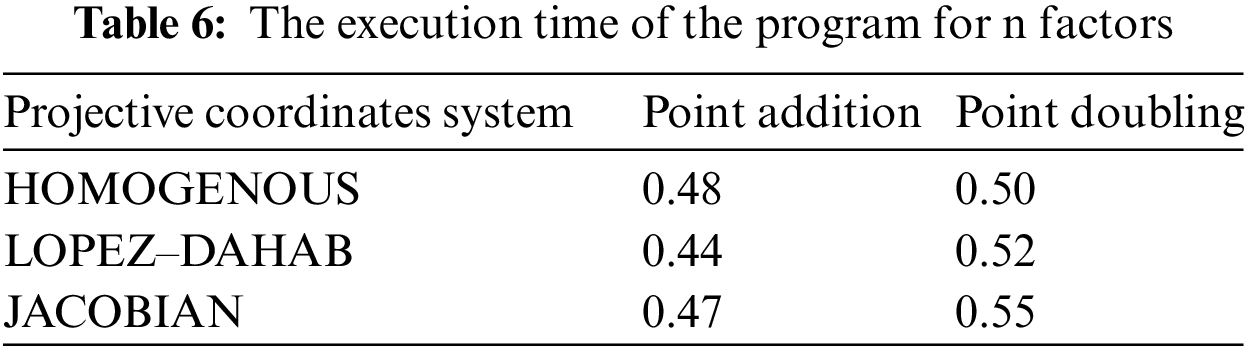
It can be observed from Table 6 that the use of parallel threads significantly decreases the time delay for ECC point operations. The best-expected execution time for point doubling is achieved using homogenous projection. In contrast, the least time delay for point addition is performed using Lopez–Dahab coordinates.

Eventually, the theoretical speedup results, which can be calculated using the following formula, are presented in Table 7.

S(n)=1T(N)

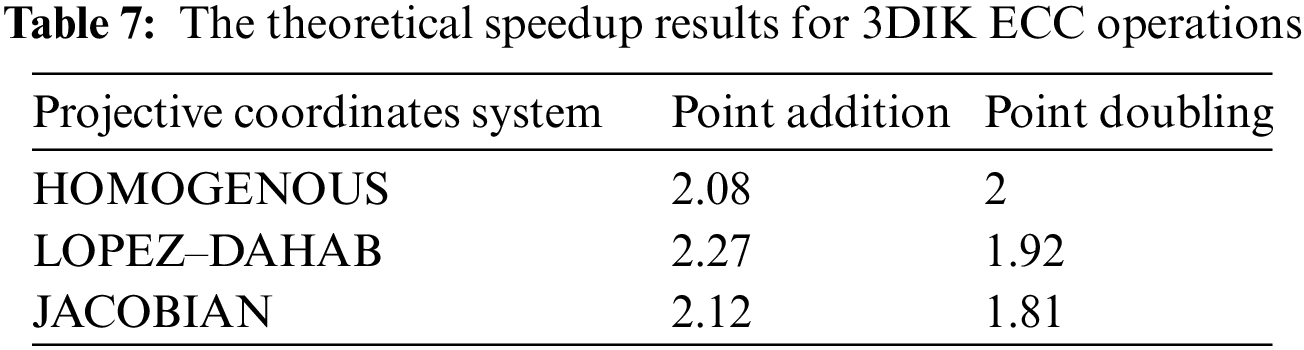
It can be observed from the theoretical speed up results presented in Table 7 that the proposed parallel implementation will speed up the EEC operations two times faster than the sequential implementation. Consequently, it will improve the ECC performance. For example, the best-expected speedup for point doubling, which is the dominant operation in ECC, is achieved using a homogenous projection. In contrast, the Lopez–Dahab coordinates achieved the best speedup for the point addition operation. This is expected since homogenous and Lopez–Dahab projections achieved the best parallel execution time for point doubling and addition operations, respectively.

The following section presents the experimental performance results of the proposed 3DIK ECC.

7.3 Experimental Results

This section discusses the results and outcomes obtained from this study and compares several implementations and algorithms for tripling-oriented ECC over GF (p) using different projective coordinates. Additionally, a performance comparison between the proposed high-speed ECC and private key cryptosystems such as AES and 3DES, and comparisons with previous studies, are presented to show how the proposed ECC can optimize the performance level and close the gap in terms of speed between public and private key cryptosystems.

The performance of ECC encryption and decryption can be evaluated through the time delay of the scalar multiplication process (ECSM). Here, three main methods were used to perform ECSM: Binary (LTR), NAF, and Montgomery ladder algorithms.

Table 8 compares the time consumption for 3DIK point doubling when operated using sequential and parallel designs for the three projective coordinate systems.

Table 8 reveals that the parallel ECC implementation shortens the time delay for the 3DIK point doubling operation compared with the corresponding sequential implementation. This improvement is because the parallel implementation can perform up to five parallel fields of arithmetic computations, multiplications, and additions, per each cycle of computations. Knowing that the time consumed by one cycle of computations is equivalent to the time of one field arithmetic operation, it can be realized that parallel ECC implementation greatly enhances the performance level for point operations. For example, the usual sequential ECC implementation requires 14 multiplication (M) operations to perform a point doubling. In contrast, the parallel ECC implementation needs only five cycles of computations, equivalent to the time consumed by 4-M operations. Furthermore, Table 10 shows that the time consumed by the sequential ECC is 443493 nanoseconds, whereas it requires only 217900 nanoseconds for the corresponding parallel ECC. This supports the fact that parallel implementation of ECC computations positively impacts the performance level.

Table 9 shows a performance improvement percentage for each parallel ECC operation with each projection.

Table 9 shows that the best-reported improvement percentage is 203% and was achieved using the homogenous projection. This indicates that using parallel ECC implementation for homogenous projection is an effective solution when there is a need to speed up cryptographic operations. The speedup percentage presented in Table 9 aims to understand better possible enhancements achieved by the parallel ECC implementation for each type of projective coordinate.

This study investigates the performance of the main scaler multiplication algorithms to determine which one is the most efficient choice when a high-speed ECC is required. Table 10 presents a comparison in terms of time delays between the sequential and parallel ECC implementations using the three scalar multiplication algorithms; Montgomery ladder, NAF, and Binary (LRT) method.

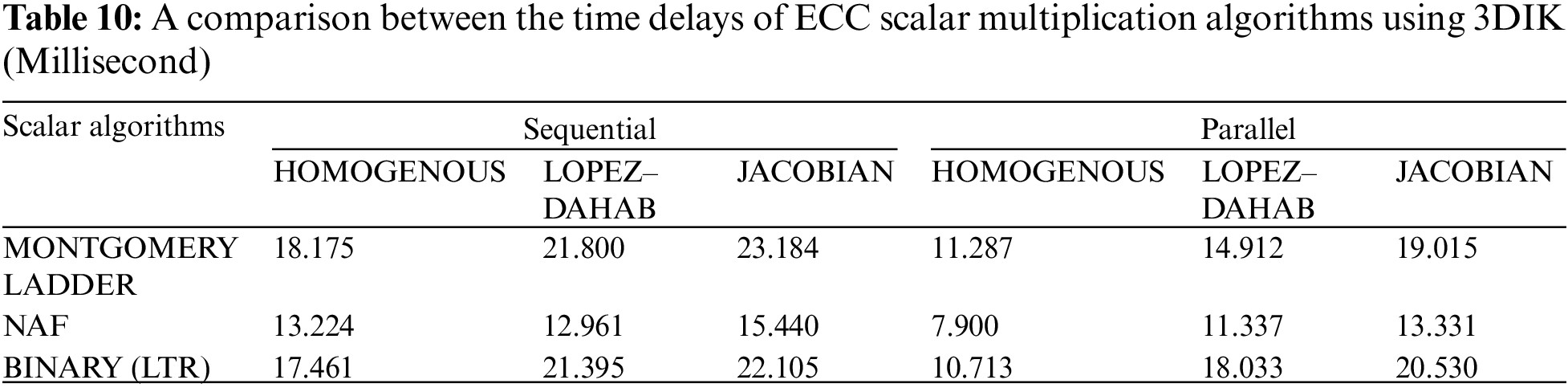
It can be observed from Table 10 that the NAF algorithm achieved the least time consumption (7.900 ms) for 3DIK ECC encryption when applied using a parallel (multithreaded) design and homogenous projection. Furthermore, the NAF algorithm achieved the shortest time delay (12.961 ms) for the sequential ECC implementation when used with Lopez–Dahab coordinates. It should be noted here that the NAF algorithm has a low humming wait, which means that NAF requires performing fewer point operations, particularly point addition, to compute the outputs of ECC scalar multiplication compared with other algorithms. Accordingly, this is the main reason for its improved performance level.

Regarding the performance level, the Binary (LTR) and Montgomery ladder algorithms achieved second and third places. Note that LRT requires less number of point addition operations compared to the Montgomery ladder method, and thus it achieved a shorter time delay for scalar multiplication.

Table 11 compares with the previously published studies to prove the accomplished improvement in the performance level of ECC. Therefore, only software implementations of ECC are considered to make reasonable and accurate comparisons. It should be stated here that there are insufficient published studies that present detailed performance analyses for software implementation of ECC, especially for the newly introduced curves.

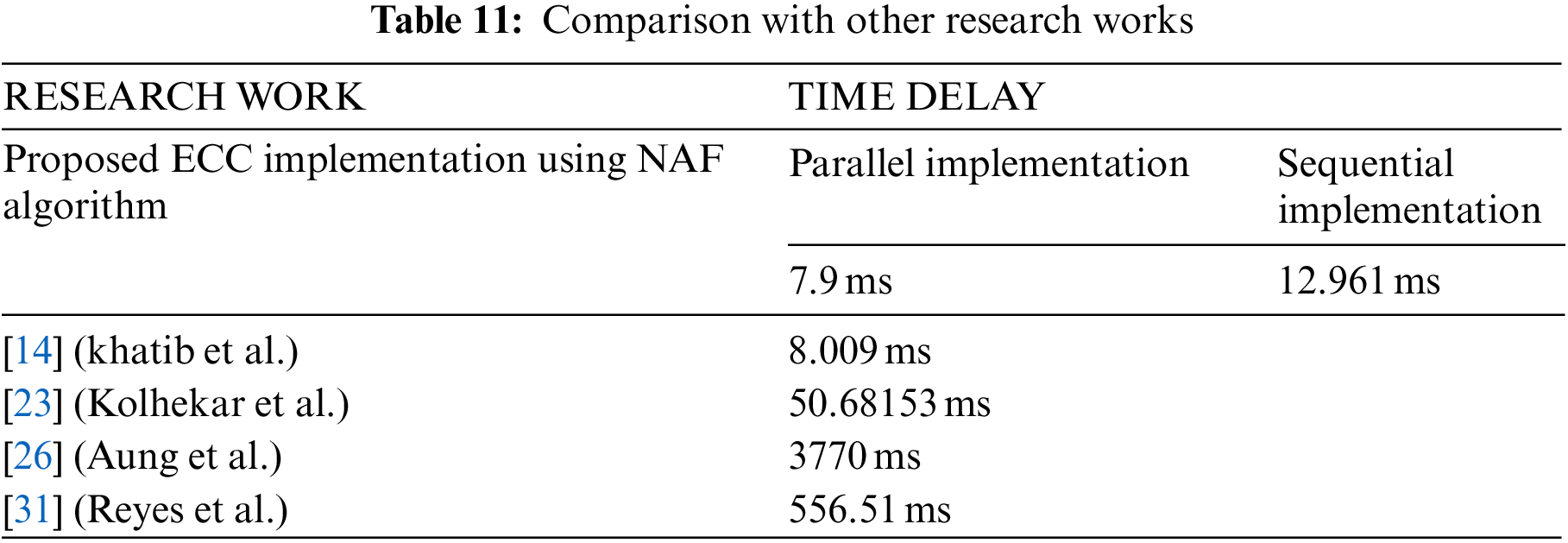
Table 11 shows the time delay of the encryption operations for the recently developed software implementations of ECC. Additionally, it can be observed that the performance of the proposed parallel cryptosystem implementation for the tripling-oriented curve overcomes the other counterparts.

The significant factors that played an essential role in optimizing the performance level are the parallel multithreaded implementation, the application of projective coordinates, the use of an EC form with low computational complexity, and final implementation of scalar multiplication using the fast NAF algorithm. All these factors are adopted in the proposed ECC implementation, making it an efficient solution for applications that need high-speed ECC.

Fig. 5 shows the results of the running time of all scalar multiplication algorithms on the tripling-oriented curve using sequential and parallel implementations. The results indicate that NAF with the parallel implementation and the use of homologous projection takes the least time compared to the other implementations. Conversely, the sequential ECC implementation using the Montgomery ladder and Jacobin projection consumes the most extended (worst) time delay.

Figure 5: The time-delay for ECSM algorithms using 3DIK curve

Fig. 6 shows a comparison regarding time delays (in milliseconds) between the symmetric and Public Key cryptosystems. This comparison highlights the improvement that can be achieved using the proposed cryptosystem concerning minimizing the difference in the time delay between the two types of cryptoalgorithms. It can be observed from the results presented in Fig. 6 that parallel implementation significantly improves the 3DIK ECC performance compared with the sequential implementation. Additionally, it reduces the time delay difference between the EC cryptosystem and AES. However, the AES’s performance still overcomes the parallel 3DIK ECC, which is expected since symmetric ciphers are generally faster than asymmetric ciphers Therefore, to provide a better insight into the resource consumption of the proposed ECCs, the below the charts depicted in Figs. 7 and 8 show a comparison based on CPU usage and memory consumption between the AES, the sequential, and the parallel implementation of a homogeneous tripling-oriented ECC.

Figure 6: A comparison between symmetric and public-key cryptosystems

Figure 7: A comparison based on CPU utilization between symmetric and public-key cryptosystems

Figure 8: A comparison in terms of memory consumption between AES and proposed public-key cryptosystems

8  Conclusion

This study presents in great detail, the main development stages of a high-speed EC cryptosystem that has become a pressing requirement for modern security applications. Therefore, to achieve the desired improvement, several factors affecting the ECC performance were explored, including the use of several projective coordinate systems, lightweight form of EC, fast algorithms to implement the scalar multiplication, and the parallel software implementation of ECC operations. The experimental results showed that the performance of the proposed multithreaded parallel software implementation for projective 3DIK ECC overcomes other sequential ECC implementations. Moreover, results showed that using the NAF algorithm and homogenous coordinates with the 4-PM design achieves the highest performance level. These results are augmented by the fact that parallel implementation can considerably reduce the time delay for ECC computations. Additionally, the tripling-oriented EC form has less computational complexity. Furthermore, the NAF algorithm has a relatively low hamming weight compared with other scalar multiplication methods. Moreover, projective coordinates’ use also reduce the time complexity by avoiding the costly inversion operation.

Compared to previous hardware implementations, the proposed software-based cryptosystem does not require dedicated hardware; thus, it needs fewer resources. It is also considered more flexible and can be easily integrated into other systems.

As a future study direction, researchers may investigate using newly emerged types of projective coordinate systems, such as extended Jacobean coordinates, which may lead to lower complexity levels for ECC point operations and better performance. Additionally, using state-of-the-art hardware multipliers and adders along with parallel design may play a significant role in optimizing the performance level of ECC.

Acknowledgement: Authors acknowledge the support from Imam Mohammad Ibn Saud Islamic University (IMISIU) for this research.

Funding Statement: Authors thank the Deanship of Scientific Research at IMSIU for funding and supporting this work through Graduate Student Research Support Program.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Paar and J. Pelzl, “Elliptic curve cryptosystem,” in Understanding Cryptography: A Textbook for Students and Practitioners, 2nd ed., Berlin, Germany: Springer Science & Business Media, 2010. [Google Scholar]

2. T. Lange, “A note on López-Dahab coordinates,” IACR Cryptol. ePrint Arch, vol. 2004, no. 1, pp. 323, 2004. [Google Scholar]

3. M. Al-khatib, A. Jaafar, Z. Zukarnain and M. Rushdan, “On the design of projective binary Edwards elliptic curves over GF (p) benefiting from mapping elliptic curves computations to variable degree of parallel design,” International Journal on Computer Science and Engineering, vol. 3, no. 4, pp. 1697–1712, 2011. [Google Scholar]

4. Q. AlHaija, A. Jaafar and M. Alkhatib, “Choices on designing GF (p) elliptic curve coprocessor benefiting from mapping homogeneous curves in parallel multiplications,” International Journal on Computer Science and Engineering, vol. 3, no. 2, pp. 467–480, 2011. [Google Scholar]

5. M. Alkhatib, Q. Al-Haijaa and A. Jaafar, “Hardware architecture & designs for projective elliptic curves point addition operation using variable levels of parallelism,” International Review on Computers and Software, vol. 6, no. 2, pp. 237–243, 2011. [Google Scholar]

6. M. AlKhatib, Q. Al-Haija and R. Mahmud, “Performance evaluation of projective binary Edwards elliptic curve computations with parallel architectures,” The Journal of Information Assurance and Security (JIAS), vol. 6, no. 1, pp. 001–009, 2011. [Google Scholar]

7. G. M. de Dormale and J. Quisquater, “High-speed hardware implementations of elliptic curve cryptography: A survey,” The Journal of Systems Architecture (JSA), vol. 53, no. 2–3, pp. 72–84, 2007. [Google Scholar]

8. L. Chen, D. Moody, A. Regenscheid and K. Randall, “Recommendations for discrete logarithm-based cryptography: Elliptic curve domain parameters,” The NIST Special Publication, vol. 1, pp. 800–186, 2019. [Google Scholar]

9. M. AlKhatib, A. Jaafar, Z. Zuriati and M. Rushdan, “Hardware designs and architectures for projective montgomery ECC over GF (p) benefiting from mapping elliptic curve computations to different degrees of parallelism,” in International Review on Computers and Software (IRECOS), vol. 6, no. 6, pp. 1059–1070, 2011. [Google Scholar]

10. M. AlKhatib and A. AlSalem, “Efficient hardware implementations for tripling oriented elliptic curve crypto-system,” The International Review on Computers and Software (IRECOS), vol. 9, no. 4, pp. 609–617, 2014. [Google Scholar]

11. L. Tawalbeh and Q. Abu AlHaija, “Speeding up elliptic curve cryptography computations by adopting Edwards curves over GF (P),” International Journal of Security (IJS), Malays., vol. 3, no. 4, pp. 1–19, 2009. [Google Scholar]

12. A. Sghaier, “Software implementation of ECC using GMP library,” in Int. Conf. on Automation, Control Engineering and Computer Science, Tunisia, 2016. [Google Scholar]

13. U. S. Kanniah and A. Samsudin, “Multithreading elliptic curve cryptosystems,” in IEEE Int. Conf. on Telecommunications and Malaysia Int. Conf. on Communications, Penang, Malaysia, 2007. [Google Scholar]

14. M. AlKhatib and W. Saif, “Improved software implementation for montgomery elliptic curve cryptosystem,” The CMC-Computers, Materials & Continua (CMC), vol. 70, no. 3, pp. 4847–4865, 2022. [Google Scholar]

15. V. Miller, “Uses of elliptic curves in cryptography,” Lecture Notes in Computer Science Book Series, vol. 218, pp. 417–426, 1986. [Google Scholar]

16. N. Koblitz, “Elliptic curve cryptosystems,” Mathematics of Computation (MCOM), vol. 48, no. 177, pp. 203–209, 1987. [Google Scholar]

17. L. D. Singh and K. M. Singh, “Implementation of text encryption using elliptic curve cryptography,” in Eleventh Int. Multi-Conf. on Information Processing, India, 2015. [Google Scholar]

18. M. AlKhatib, A. Jaafar, Z. Zuriati and M. Rushdan, “Trade-off between area and speed for projective edwards elliptic curves cryptosystem over GF (p) using parallel hardware designs and architectures,” International Review on Computers and Software (IRECOS), vol. 6, no. 4, pp. 163–173, 2011. [Google Scholar]

19. M. AlKhatib, “High-speed and secure elliptic curve cryptosystem for multimedia applications,” International Journal of Advanced Computer Science and Applications (IJACSA), vol. 11, no. 9, pp. 117–129, 2020. [Google Scholar]

20. M. Alkhatib, A. Jaafar, M. Said and Z. Zukarnain, “Parallelizing GF (p) montgomery elliptic curve cryptosystem operations to improve security and performance,” Advanced Materials Research, vol. 622–623, pp. 1906–1911, 2012. [Google Scholar]

21. L. Setiadi, A. I. Kistijantoro and A. Miyaji, “Elliptic curve cryptography: Algorithms and implementation analysis over coordinate systems,” in 2nd Int. Conf. on Advanced Informatics: Concepts, Theory and Applications (ICAICTA), Chonburi, 2015. [Google Scholar]

22. M. Saikia and D. Boruah, “Implementation of ElGamal elliptic curve cryptography over prime field using C,” in IEEE Int. Conf. on Information Communication and Embedded Systems (ICICES), India, 2014. [Google Scholar]

23. M. Kolhekar and A. Jadhav, “Implementation of elliptic curve cryptography on text and image,” International Journal of Enterprise Computing and Business Systems (IJECBS), vol. 1, no. 2, pp. 2230–8849, 2011. [Google Scholar]

24. V. G. Martínez and L. H. Encinas, “Implementing ECC with java standard, 7th ed.,” International Journal of Computer Science and Artificial Intelligence, vol. 3, no. 4, pp. 134–142, 2013. [Google Scholar]

25. Y. Kortesniemi, “Implementing elliptic curve cryptosystems in Java 1.2,” in Third Nordic Workshop on Secure IT Systems, Trondheim, Norway, 1998. [Google Scholar]

26. T. M. Aung and N. N. Hla, “Implementation of elliptic curve arithmetic operations for prime field and binary field using java BigInteger class,” International Journal of Engineering Research and Technology, vol. 6, no. 8, pp. 2278–0181, 2018. [Google Scholar]

27. V. Gayoso, L. Hernandez and C. Sanchez, “A java implementation of the elliptic curve integrated encryption scheme,” in Int. Conf. on Security & Management, USA, 2010. [Google Scholar]

28. A. Kaurand and V. G. Luthra, “Java implementation and arithmetic performance evaluation of elliptic curve cryptography using MATLAB,” International Journal of Engineering Research & Technology (IJERT), vol. 2, no. 6, pp. 2695–2699, 2013. [Google Scholar]

29. S. Gupta and S. Vashisht, “Implementation of ECC using socket programming in java,” The International Organization of Scientific Research Journal of Computer Engineering (IOSR-JCE), vol. 16, no. 4, pp. 65–68, 2014. [Google Scholar]

30. A. Mitra, S. Chakrabarty and P. Mitra, “Elliptic curve cryptosystem for email encryption,” The International Journal of Computer and Communication Technology, vol. 1, no. 4, pp. 230–235, 2010. [Google Scholar]

31. C. Reyes and A. V. Castillo, “A performance comparison of elliptic curve scalar multiplication algorithms on smartphones,” in the 23rd Int. Conf. on Electronics, Communications and Computing, Mexico, 2013. [Google Scholar]

32. C. Doche, T. Icart and D. R. Kohel, “Efficient scalar nultiplication by isogeny decompositions,” International Workshop on Public Key Cryptography, vol. 3958, pp. 191–206, 2006. [Google Scholar]

33. M. AlKhatib and W. Saif, in TriplingOrientedDIK Cryptosystem, Source Code, version 1.0, 2022. [Online]. Available: https://github.com/WafaSaif/TriplingOrientedDIKCryptosystem [Google Scholar]

34. D. P. Rodgers, “Improvements in multiprocessor system design,” ACM SIGARCH Computer Architecture News, vol. 13, no. 3, pp. 225–231, 1985. [Google Scholar]