Two-Layer Information Granulation: Mapping-Equivalence Neighborhood Rough Set and Its Attribute Reduction

1  Introduction

In rough set theory [1–5], the whole sample is called the universe. The universe can be divided into several subsets of samples by indistinguishable relations between the samples, this is a process known as information granulation, and the divided subsets of samples are called information granules. The information granules are the basic units of the universe, and any concept in the universe can be approximated by the concatenation of information granules. This approach simulates the human learning and reasoning process and is widely valued as it is easy to understand and generalize. Unfortunately, the classical rough set model based on indistinguishable relation is only suitable for dealing with discrete data, but not directly for continuous data, which is widely available in real applications. To extend the application of rough sets [6,7], Hu et al. [8] proposed the neighborhood rough set based on the concept of δ-neighborhood in the metric space. The core of the neighborhood rough set model is the neighborhood relation. The composition of the neighborhood information granules is defined by the neighborhood relation. The process of constructing all the neighborhood information granules in the universe is called neighborhood information granulation, which can also be abbreviated as information granulation. Therefore, different information granulation processes and results are determined by different neighborhood relations. Then different neighborhood rough set models are generated.

Attribute reduction [9–12], as a feature selection technique [13,14], is one of the core research directions in rough sets. The exhaustive algorithm [15,16] and the heuristic algorithm [17,18] are two commonly used mechanisms for deriving attribute reduction. Compared with exhaustive algorithm, heuristic algorithm based on the greedy search strategy is more favored by many scholars because of its fast speed advantage. In heuristic algorithm, multiple iterations are required, the unselected attributes need to be evaluated separately in each iteration, and information granulation is performed in each evaluation. Unfortunately, the neighborhood information granulation is exceptionally time-consuming, resulting in low efficient in attribute reduction. Therefore, how to accelerate attribute reduction is a subject that worth discussing. This has been noted by relevant scholars, and some valuable acceleration strategies have been proposed [19–21]. These strategies can be generally defined as two types: one is to reduce the frequency of information granulation during iteration [22,23]; the other is to accelerate the process of information granulation [24,25]. The research in this paper focuses on the latter, exploring ways to further improve the speed of information granulation from neighborhood relations, then accelerate the process of attribute reduction.

Most of the existing studies on neighborhood relations focus on issues such as the distribution and differences of samples in the universe, with little consideration of the impact on the efficiency of information granulation. For example, Hu et al. [26] introduced the k-nearest-neighbor relation, which addressed the problem of uneven distribution of samples in the universe and proposed the k-nearest-neighbor rough set. Wang et al. [27] integrated and analyzed the δ-neighborhood relation [8] and the k-nearest-neighbor relation, proposed the k-nearest neighborhood relation, and induced the k-nearest neighborhood rough set. Yang et al. [28] considered that it is not enough to define the binary relation between samples only by distances, the label information between samples is also should be considered, so the pseudo-label neighborhood relation and pseudo-label neighborhood rough set are proposed. Zhou et al. [29] regarded that all existing neighborhood relations need to specify a parameter in advance, but it is a challenge to select unified and optimal parameters before learning for all different types of datasets. To fill such gap, the adaptive GAP neighborhood relation [29] was proposed, and the GAP neighborhood rough set was generated. Yang et al. [30] further improved the formula for calculating the distances between samples by using the distance metric learning (DMN), then a novel neighborhood rough set model based on DMN is proposed. Ba et al. [31] reinterpreted information granulation from a multigranulation view, and the Triple-G multigranulation rough set model was proposed by combining the granular ball relation [32], GAP neighborhood relation, and δ-neighborhood relation.

Although the above neighborhood relations significantly improve the performance of neighborhood rough sets, but the process of their information granulations is still not efficient. Therefore, to further improve the efficiency of information granulation, based on the divide-and-conquer strategy, a two-layer information granulation neighborhood rough set model is proposed, which is called the mapping-equivalence neighborhood rough set model. Two kinds of binary relations are used for the two-layer information granulation. The first layer of information granulation is based on our proposed mapping-equivalence relation, which aims to divide the universe into multiple sub-universes as shown in Fig. 1. The δ-neighborhood relation is used for the second layer of information granulation, which aims to perform neighborhood information granulation as shown in Fig. 2. In this paper, the δ-neighborhood relation is chosen because the value of δ can be set to obtain different results of information granulations. This model can be described below:

(1)   Construct a mapping relation to generate a discrete mapping sample for each continuous sample. In Fig. 1, xi (1 ≤ i ≤ n) represents continuous samples, and xi′ represents discrete mapping samples.

(2)   According to the mapping-equivalence relation, divide the universe into mutually independent mapping-equivalence classes.

(3)   Establish mapping-equivalence relation between the continuous samples according to the equivalence relation of the mapping samples.

(4)   Treat each mapping-equivalence class as a sub-universe, and perform neighborhood information granulation. In Fig. 2, δ(xi) (1 ≤ i ≤ n) represents the neighborhood information granules represented by xi.

(5)   Merge all neighborhood information granules to complete the final information granulation.

Figure 1: The first layer of information granulation

Figure 2: The second layer of information granulation

To further understand the whole process of two-layer information granulation more conveniently, a relevant illustration is given in Fig. 3. It is seen that the two-layer information granulation is more in line with the idea of divide-and-conquer in big data analysis than the single-layer information granulation which works directly on the raw dataset (universe). The raw dataset (universe) can be divided into multiple subdatasets (sub-universes) reasonably by the first layer of information granulation; the second layer of information granulation is performed on each divided subdataset (sub-universe) separately. Finally, all the information granules are merged to make up the final information granulation results. The universe with a large amount of data can reasonably be divided into several sub-universes to perform information granulation separately in this model. Thus, this model has higher efficiency of information granulation than other single-layer information granulation models. The higher the efficiency of information granulation, the less time consumption in each iteration of attribute reduction, and thus can accelerate attribute reduction.

Figure 3: Comparisons of different information granulation strategies

The remainder of this paper is organized as follows. In Section 2, we review the neighborhood rough set and discuss related concepts of reduct. In Section 3, we propose a two-layer information granulation strategy, from which the mapping-equivalence neighborhood rough set model is generated. Section 4 compares the proposed model with four commonly used models and gives experimental analyses to verify the effectiveness of the proposed model. Section 5 concludes the whole paper.

2  Preliminary Knowledge

This section will review some basic concepts of the neighborhood rough set and gives the definition of reduct.

Given a neighborhood decision system, it can be represented as NDS = <U, AT, d>, in which U is a nonempty and finite set of samples, called the universe; AT is the set of condition attributes; d is a decision attribute. ∀x ∊ U, d(x) denotes the decision attribute value of x, ∀a ∊ AT, a(x) denotes its value over condition attribute a. ∀x, y ∊ U, if d(x) = d(y), then x and y satisfy the indistinguishable relation over d, referred to as INDd = {(x, y) ∊ U × U | d(x) = d(y)}. We can divide the U into decision classes by INDd, denoted as U/INDd = {X1, X2, …, Xq}, and generally abbreviated as U/d. If Xi ∊ U/d, then Xi is generally called the ith decision class. If sample x ∊ Xi, then Xi can be denoted by [x]d. In a neighborhood rough set, the relation between two samples is determined by their distance. If the distance is less than a certain threshold, we can say that the two samples satisfy the neighborhood relation. The formal definition of the neighborhood relation is as follows.

Definition 1 [8] Given an NDS, δ is a given neighborhood radius, ∀A ⊆ AT, the neighborhood relation determined by A is defined as

δA={(x,y)∈U×U|dA(x,y)≤δ},(1)

where dA(x, y) is the distance between x and y over A. By δA, the neighborhood of x over A is defined as

δA(x)={y∈U|(x,y)∈δA},(2)

or

δA(x)={y∈U|dA(x,y)≤δ},(3)

which is also called the neighborhood granule of x.

Definition 2 [8] Given an NDS, δ is a given neighborhood radius, U/d = {X1, X2, …, Xq}, ∀A ⊆ AT, Xi ∊ U/d, the lower and upper approximations of Xi are defined as

N_Aδ(Xi)={x∈U|δA(x)⊆Xi},(4)

N¯Aδ(Xi)={x∈U|δA(x)∩Xi≠∅}.(5)

N_Aδ(Xi) denotes the union of all neighborhood granules that can be contained by Xi, N¯Aδ(Xi) denotes the union of neighborhood granules that contain some elements in Xi.

To measure the contribution of condition attributes to the classification, many scholars have proposed multiple measures [33–36]. Among them, the approximation quality (AQ) [34] and the neighborhood mutual information (NMI) [35] are two commonly used measures, their formal definitions are given below.

Definition 3 [34] Given an NDS, δ is a given neighborhood radius, U/d = {X1, X2, …, Xq}, ∀A ⊆ AT, the approximation quality (AQ) is defined as

AQδ(A)=|∪i=1qN_Aδ(Xi)||U|,(6)

where |⋅| represents the cardinality of set ⋅.

Definition 4 [35] Given an NDS, δ is a given neighborhood radius, ∀A ⊆ AT, the neighborhood mutual information (NMI) about A and d is defined as

NMIδ(A:d)=−1|U|∑x∈Ulog⁡|δA(x)|⋅|[x]d||U|⋅|δA(x)∩[x]d|.(7)

If A refers to a subset of AT, both AQ and NMI can be used to measure the contribution of A to the classification, the greater the value of the measure, the greater the contribution of A.

Reduct is a special subset of AT with no weaker classification performance than AT. The process of acquiring a reduct is called attribute reduction, in which redundant attributes can be removed to obtain simplified decision rules.

Definition 5 Given an NDS, a measure ρ, ∀A ⊆ AT, if the following conditions are satisfied

(1)   ρ(A) ≥ ρ(AT),

(2)   ∀a ∊ A, ρ(A − a) < ρ(A),

then A is called a reduct.

Based on the Def. 5, we can see that the reduct does not decrease the distinguishability of the system, and there are no redundant attributes in the reduct.

3  Mapping-Equivalence Neighborhood Rough Set Model

This section will describe the construction process of the mapping-equivalence neighborhood rough set model in detail. Because there are two layers of information granulation, it will be divided into two subsections for discussion. Subsection 3.1 discusses the mapping-equivalence relation. Subsection 3.2, the mapping-equivalence neighborhood rough set model is proposed, and then several related concepts concerning attribute reduction are also given.

3.1 Mapping-Equivalence Relation

The first step in establishing the mapping-equivalence relation is to establish a mapping relation. Establishing the mapping relation depends on the relative distances between the samples and the center of each decision class. First of all, we will give the definition of the center of decision class.

Definition 6 Given an NDS, U/d = {X1, X2, …, Xq}, ∀Xi ∊ U/d, the center of Xi is defined as

dci=1|Xi|∑x∈Xix.(8)

∀x ∊ U, its mapping sample is defined as x′=(i,j), where i=argmin{∪i=1qd(x,dci)}, j = argmax{∪j=1qd(x,dcj)}, 1 ≤ i, j ≤ q. That is, i represents the sequence number of the decision class closest to x, and j represents the sequence number of the decision class farthest from x.

All mapping samples are combined to form U′. ∀A ⊆ AT, if the mapping relation is established over A, then x′ can be specially recorded as xA′, and U′ can be registered as UA′. After all samples are mapped, the following mapping-equivalence relation can be defined.

Definition 7 Given an NDS, ∀A ⊆ AT, the mapping-equivalence relation is represented as

INDAME={(x,y)∈U×U|xA′=yA′}.(9)

Obviously, the mapping-equivalence relation is transitive. That is, ∀x, y, z ∊ U, if x and y satisfy the mapping-equivalence relation, y and z also satisfy the mapping-equivalence relation, then x and z satisfy the mapping-equivalence relation. After the mapping-equivalence relation is defined, the universe can be granulated according to this mapping-equivalence relation, which is recorded as U/INDAME={X1ME,X2ME,…,XkME}. The samples that satisfy the mapping-equivalence relation are in the same mapping-equivalence class, and XiME represents the ith mapping-equivalence class. If a certain sample is used as a representative, the mapping-equivalence class can be expressed as follows.

Definition 8 Given an NDS, ∀A ⊆ AT, INDAME, ∀x ∊ U, the mapping-equivalence class determined by x is

[x]AME={y∈U|(x,y)∈INDAME},(10)

or

[x]AME={y∈U|yA′=xA′}.(11)

It is not difficult to draw the following conclusions:

(1)   [x]AME≠∅, because x ∊ [x]AME;

(2)   [x]AME=[y]AME, if y ∊ [x]AME.

Assuming that there are n samples in U, the time complexity to calculate the center of the decision class is O(n), and the time complexity from U to U′ is also O(n). Because the mapping-equivalence relation is transitive and the samples which satisfy the mapping-equivalence relation are in the same mapping-equivalence class, the time complexity of information granulation according to the mapping-equivalence relation is O(nlogn). In summary, the time complexity of the first layer of information granulation is O(nlogn).

3.2 Mapping-Equivalence Neighborhood Rough Set

After the first layer of information granulation is completed, the universe has been divided into multiple disjoint mapping-equivalence classes. If each mapping-equivalence class is regarded as a sub-universe, the second layer of information granulation is naturally induced.

Definition 9 Given an NDS, δ is a given neighborhood radius, ∀A ⊆ AT, the mapping-equivalence neighborhood relation (ME-neighborhood relation) determined by A is defined as

δAME={(x,y)∈I N DAME|dA(x,y)≤δ},(12)

∀XiME∈U/INDAME, if x∈XiME, then the mapping-equivalence neighborhood of x over A is defined as

δAME(x)={y∈XiME|(x,y)∈δAME},(13)

or

δAME(x)={y∈XiME|dA(x,y)≤δ}.(14)

At this point, the proposed mapping-equivalence neighborhood rough set model completes the information granulation. Algorithm 1 presents this process in detail. Steps 1 to 12 of the algorithm are the first layer of information granulation. Through the analysis at the end of Subsection 3.1, we know that the time complexity is O(nlogn), n is the number of samples in the universe. Steps 13 to 19 are the second layer of information granulation. Suppose that step 12 divides the universe into k mapping-equivalence classes, and each mapping-equivalence class contains nk samples on average. Then the time complexity of Steps 13 to 19 is k∗O((nk)2). Therefore, the overall time complexity of Algorithm 1 is O(nlogn) + k∗O((nk)2).

After the information granulation is completed, the corresponding information granules can be obtained. Similar to the traditional neighborhood rough set model, this model also has the following definitions.

Definition 10 Given an NDS, δ is a given neighborhood radius, U/d = {X1, X2, …, Xq}, ∀A ⊆ AT, ∀Xi ∊ U/d, the lower and upper approximations of Xi based on the ME-neighborhood relation are defined as

N_AME(Xi)={x∈U|δAME(x)⊆Xi},(15)

N¯AME(Xi)={x∈U|δAME(x)∩Xi≠∅}.(16)

Definition 11 Given an NDS, δ is a given neighborhood radius, U/d = {X1, X2, …, Xq}, ∀A ⊆ AT, ∀Xi ∊ U/d, the ME- approximation quality (AQ) is defined as

AQME(A)=|∪i=1qN_AME(Xi)||U|.(17)

Definition 12 Given an NDS, δ is a given neighborhood radius, ∀A ⊆ AT, the ME-neighborhood mutual information about A and d is defined as

NMIME(A:d)=−1|U|∑x∈Ulog⁡|δAME(x)|⋅|[x]d||U|⋅|δAME(x)∩[x]d|.(18)

So far, the mapping-equivalence neighborhood rough set model has been constructed. To more accurately test the acceleration effect of the new proposed model on information granulation and attribute reduction, the forward greedy attribute reduction algorithm is adopted as one of the classical heuristics. A detailed description of the algorithm is given in Algorithm 2.

4  Experiments

4.1 Description of the Datasets

To verify the effectiveness of the proposed strategy, 9 UCI datasets were selected to conduct the experiments. The basic information of the datasets is described in Table 1, in which “Sample” represents the cardinality of the universe, “Attribute” represents the number of all condition attributes, and “Class” represents the number of decision classes. It is worth mentioning that some datasets contain training samples and test samples, which we have merged, and some datasets have multiple decision attributes, which we only take the first one.

4.2 Experimental Comparisons

In this subsection, the mapping-equivalence neighborhood rough set (MENRS) is compared with other neighborhood rough sets. Because the δ-neighborhood relation is used in proposed model, some neighborhood rough set models based on δ-neighborhood relation are selected, including the k-nearest neighborhood rough set (KNRS) [27], pseudo-label neighborhood rough set (PLNRS) [28], Triple-G multigranulation rough set (TMGRS) [31] and δ-neighborhood rough set (DNRS) [8]. The KNRS, PLNRS and TMGRS were introduced in Section 1, the DNRS was reviewed in Section 2. AQ and NMI will be employed as the measures for searching reducts. It should be noted that NMI cannot be applied to TMGRS because TMGRS does not have a definite neighborhood relation, so TMGRS is only involved in the comparison experiments using AQ as the measure.

Both experiments are implemented by using MATLAB R2020b and conducted on a laptop with Intel Intel(R) Core(TM) i7–8750H CPU @ 2.20 GHz 2.21 GHz and 8 GB memory. To facilitate unified processing, all datasets are normalized to [0,1] in advance. Taking into account that when the value of δ is large, all the rough set model reduction results tend to be homogeneous. Therefore, to facilitate experimental comparison, 10 different δ (0.03, 0.06, …, 0.3) have been selected. The 5-fold cross-validation strategy will be used to ensure the reliability of the experimental results. In the tables, the data with better performance will be bolded for easy observation.

4.2.1 Comparisons of Time Consumption

In this subsection, we will take note of the time consumption of five rough set models for the two measures considered in this paper. Detailed results are recorded in Figs. 4 and 5. The abscissa is the selected 10 different δ, and the ordinate is the time consumption of the attribute reduction. Taking a closer inspection and comparison, we can conclude the following.

(1)   With the increase of δ, the time consumption of attribute reduction also tends to increase. This is reflected in almost all datasets. The larger the δ, the more condition attributes need to be selected, so the number of iterations of the algorithm increases and the time consumption increases.

(2)   MENRS does allow for faster information granulation. In almost all datasets, MENRS has obvious advantages in terms of time consumption. Further observation of Car (ID: 3), Waveform (ID: 8) and Yeast (ID: 9) shows that MENRS has more obvious advantages on datasets with larger amounts of data and more decision classes. Conversely, on a dataset with a smaller amount of data and fewer decision classes, the advantage of MENRS is less obvious. This is mainly because when the total number of samples is large, MENRS can effectively divide the universe into mapping-equivalence classes with a smaller total number of samples, so the efficiency is higher. The more decision classes, the more mapping-equivalence classes obtained by the first layer information granulation of MENRS, and the smaller the total number of samples in a single mapping-equivalence class, so the information granulation is faster.

Figure 4: Time consumption by using AQ

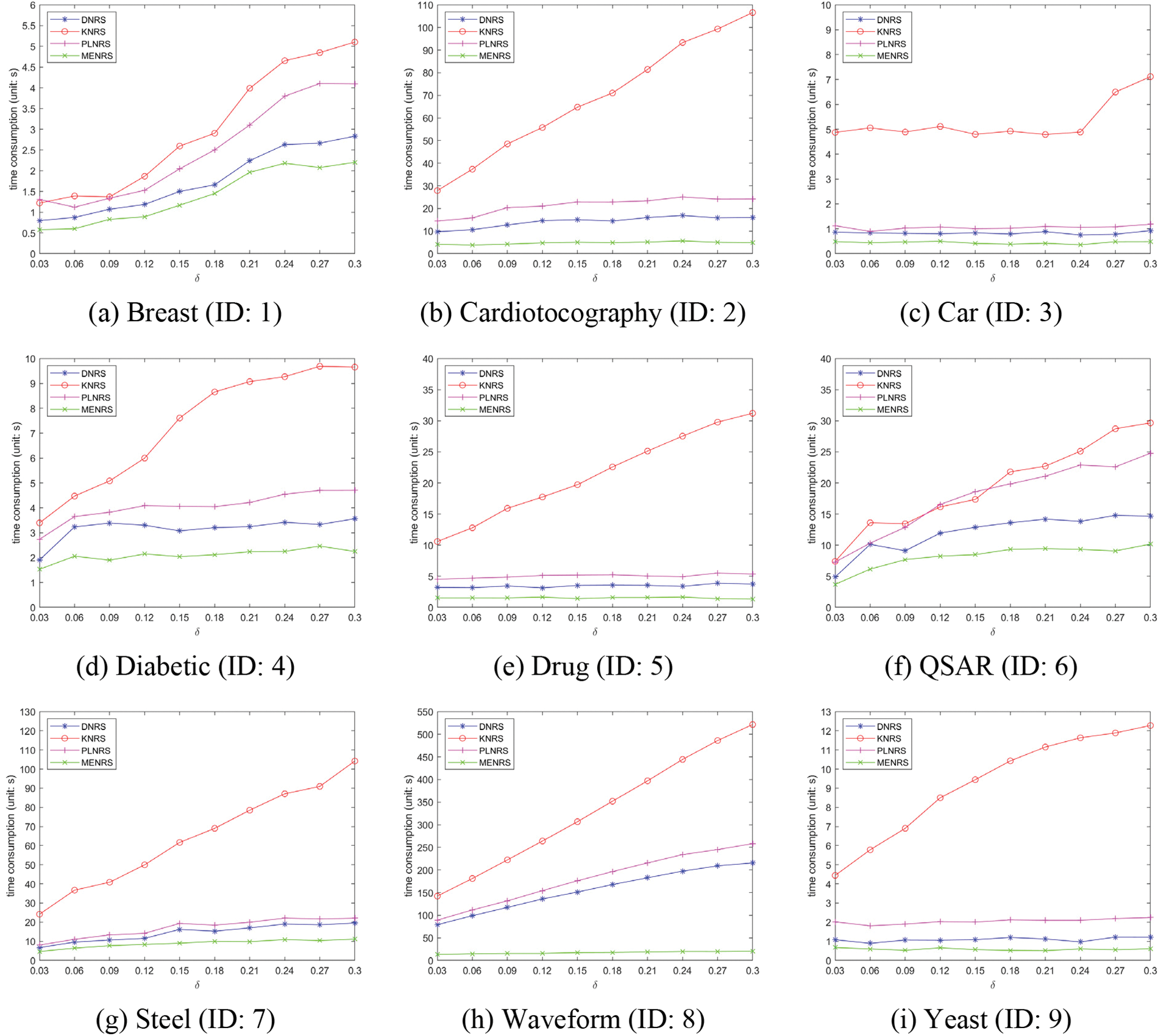
Figure 5: Time consumption by using NMI

4.2.2 Comparisons of Classification Accuracy

In this subsection, we will take the reducts from the five neighborhood rough sets respectively, use the CART [37] classifier and the KNN (K = 5) [38] classifier for classification. The column AQ represents the classification accuracy of the reducts obtained with the AQ as the measure, and the column NMI represents the classification accuracy of the reducts obtained with the NMI as the measure. 10 δ values were used to obtain the reducts and classifications respectively, and the final result was averaged. Detailed comparison results are reported in Tables 2 and 3.

Taking a close observation of Table 2, it can be drawn that the classification performance of the reducts taken from the five models is comparable. Across the 9 datasets, the models do not differ much in performance. For example, on dataset Breast (ID: 1), PLNRS and MENRS perform best, and on datasets such as Diabetic (ID: 4) and Yeast (ID: 9), DNRS, KNRS and TMGRS are better. This is because although the neighborhood rough sets are different, the condition attributes selected based on the attribute reduction algorithm are similar, so the obtained reducts are not much different. Looking at Table 3, the same conclusion as that of Table 2 can be drawn. Therefore, it can be concluded that MENRS performs well and is not weaker than other neighborhood rough sets in terms of classification accuracy.

4.2.3 Comparisons of Information Granulation Results

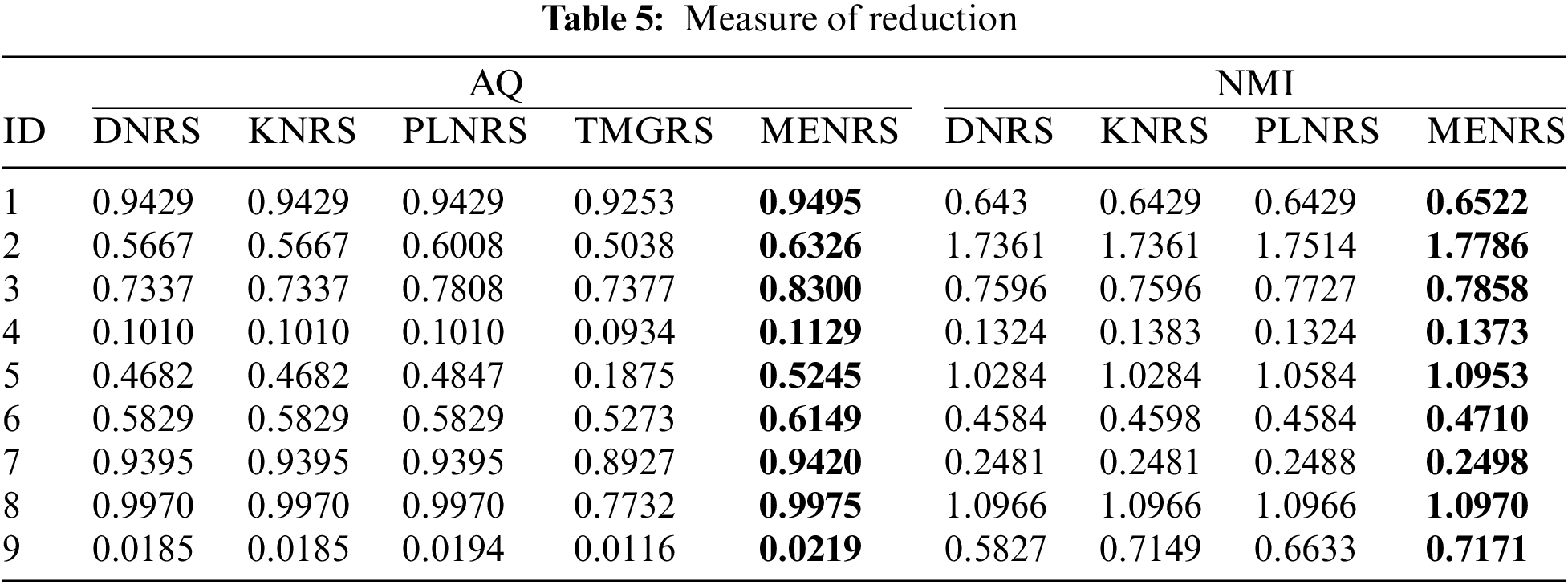
In this subsection, we will use the five neighborhood rough sets for information granulation of the universe separately and use two measures, AQ and NMI, to evaluate the results of information granulation. The AQ column represents the results obtained by using AQ as the measure, and the NMI column represents the results measured by NMI. When δ is small, the neighborhood members of the sample may be few, which is inconvenient for reflecting the differences between the models. Therefore, for convenience of observation, take the maximum value of 0.3 among the 10 δ for comparison.

Table 4 is the results of the information granulation on the raw data, that is, the universe before attribute reduction. With a careful investigation of Table 4, it is not difficult to observe that information granulation in MENRS is more likely to reduce system uncertainty, and it performs the best in almost all datasets, followed by PLNRS, DNRS, KNRS and TMGRS. Take Cardiotocography (ID: 2) as an example, using AQ as a measure, MENRS = 0.6326, PLNRS = 0.6008, DNRS = KNRS = 0.5667, TMGRS = 0.5031. This is because the first layer of information granulation of MENRS divides the more similar samples into the same mapping-equivalence class. Therefore, in the second layer of information granulation, the samples in the neighborhood granule are more relevant. The pseudo-label strategy of PLNRS also screens the samples, but the pseudo-labels are generated by clustering, the clustering results are unstable, and the relations between samples are also unstable. Therefore, the quality of its information granulation is weaker than MENRS, but better than that of DNRS, KNRS and TMGRS.

Table 5 is the results of the information granulation on the universe after attribute reduction. With a careful investigation of Table 5, it is not difficult to observe that information granulation in MENRS is more likely to reduce system uncertainty, performing optimally in almost all datasets, followed by PLNRS, and then DNRS, KNRS and TMGRS in that order, which is consistent with the observations in Table 4. Combining Tables 4 and 5, we can draw the conclusion that MENRS can better information granulation than other neighborhood rough set models.

5  Conclusions

In the field of neighborhood rough set research, the speed of attribute reduction is largely influenced by the efficiency of information granulation. The way of information granulation was determined by neighborhood relations. Therefore, a new research has been done on neighborhood relations and the mapping-equivalence neighborhood rough set model is generated.

The main contributions of this paper are as follows: first, the mapping-equivalence relation is proposed, which is established between continuous data. Second, the two-layer information granulation strategy is proposed and generates the mapping-equivalence neighborhood relation by combining the existing neighborhood relations. Finally, the mapping-equivalence neighborhood rough set model is naturally deduced from the mapping-equivalence neighborhood relation, which provides a new thinking for the expansion of neighborhood rough set models. The experimental results demonstrate the effectiveness of the proposed model.

Albeit the good performance of the proposed model, we acknowledge its limitations which motivate our more investigations in this direction. First, when the amount of data is relatively small, the advantages of the proposed model are not very obvious. Besides, the second layer of information granulation in this paper only uses the δ-neighborhood relation, while do not take other neighborhood relations into consideration. Finally, there are some more intensive studies that were not conducted. Thus, the following topics deserve further research:

(1)   Improve the mapping-equivalence relation for better information granulatio n performance.

(2)   Enhance the extensibility of the proposed model by using other neighborhood relations.

(3)   Extend two-layer information granulation strategy to multiple layers should also be explored.

Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 62006099, 62076111), and the Key Laboratory of Oceanographic Big Data Mining & Application of Zhejiang Province (No. OBDMA202104).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Z. Pawlak, “Rough sets,” International Journal of Computer & Information Sciences, vol. 11, pp. 341–356, 1982. [Google Scholar]

2. D. Q. Miao, Q. G. Duan, H. Y. Zhang and N. Jiao, “Rough set based hybrid algorithm for text classification,” Expert Systems with Applications, vol. 36, no. 5, pp. 9168–9174, 2009. [Google Scholar]

3. L. Ezhilarasi, A. P. Shanthi and V. Uma Maheswari, “Rough set based rule approximation and application on uncertain datasets,” Intelligent Automation & Soft Computing, vol. 26, no. 3, pp. 465–478, 2020. [Google Scholar]

4. W. T. Li and W. H. Xu, “Double-quantitative decision-theoretic rough set,” Information Sciences, vol. 316, pp. 54–67, 2015. [Google Scholar]

5. B. J. Fan, E. C. C. Tsang, W. H. Xu and J. H. Yu, “Double-quantitative rough fuzzy set based decisions: A logical operations method,” Information Sciences, vol. 378, pp. 264–281, 2017. [Google Scholar]

6. X. Zhang, J. G. Luo, X. M. Sun and J. C. Xie, “Optimal reservoir flood operation using a decomposition-based multi-objective evolutionary algorithm,” Engineering Optimization, vol. 51, no. 1, pp. 42–62, 2019. [Google Scholar]

7. K. H. Yuan, W. H. Xu, W. T. Li and W. P. Ding, “An incremental learning mechanism for object classification based on progressive fuzzy three-way concept,” Information Sciences, vol. 584, pp. 127–147, 2022. [Google Scholar]

8. Q. H. Hu, D. R. Yu and Z. X. Xie, “Numerical attribute reduction based on neighborhood granulation and rough approximation,” Journal of Software, vol. 19, no. 3, pp. 640–649, 2008. [Google Scholar]

9. Y. Y. Yang, D. G. Chen and H. Wang, “Active sample selection based incremental algorithm for attribute reduction with rough sets,” IEEE Transactions on Fuzzy Systems, vol. 25, no. 4, pp. 825–838, 2017. [Google Scholar]

10. E. C. C. Tsang, D. G. Chen, D. S. Yeung, X. Z. Wang and J. W. T. Lee, “Attributes reduction using fuzzy rough sets,” IEEE Transactions on Fuzzy Systems, vol. 16, no. 5, pp. 1130–1141, 2008. [Google Scholar]

11. M. Hu, E. C. C. Tsang, Y. T. Guo and W. H. Xu, “Fast and robust attribute reduction based on the separability in fuzzy decision systems,” IEEE Transactions on Cybernetics, vol. 52, no. 6, pp. 5559–5572, 2022. [Google Scholar] [PubMed]

12. H. R. Ju, W. P. Ding, Z. Q. Shi, J. S. Huang, J. Yang et al., “Attribute reduction with personalized information granularity of nearest mutual neighbors,” Information Sciences, vol. 613, pp. 114–138, 2022. [Google Scholar]

13. U. Kanimozhi and D. Manjula, “An intelligent incremental filtering feature selection and clustering algorithm for effective classification,” Intelligent Automation & Soft Computing, vol. 24, no. 4, pp. 701–709, 2018. [Google Scholar]

14. B. B. Sang, H. M. Chen, L. Yang, T. R. Li and W. H. Xu, “Incremental feature selection using a conditional entropy based on fuzzy dominance neighborhood rough sets,” IEEE Transactions on Fuzzy Systems, vol. 30, no. 6, pp. 1683–1697, 2022. [Google Scholar]

15. Y. Y. Yao and Y. Zhao, “Discernibility matrix simplification for constructing attribute reducts,” Information Sciences, vol. 179, no. 7, pp. 867–882, 2009. [Google Scholar]

16. X. B. Yang, Y. S. Qi, X. N. Song and J. Y. Yang, “Test cost sensitive multigranulation rough set: Model and minimal cost selection,” Information Sciences, vol. 250, pp. 184–199, 2013. [Google Scholar]

17. X. Y. Zhang, H. Yao, Z. Y. Lv and D. Q. Miao, “Class-specific information measures and attribute reducts for hierarchy and systematicness,” Information Sciences, vol. 563, pp. 196–225, 2021. [Google Scholar]

18. W. S. Du and B. Q. Hu, “A fast heuristic attribute reduction approach to ordered decision systems,” European Journal of Operational Research, vol. 264, no. 2, pp. 440–452, 2018. [Google Scholar]

19. Y. Chen, X. B. Yang, J. H. Li, P. X. Wang and Y. H. Qian, “Fusing attribute reduction accelerators,” Information Sciences, vol. 587, pp. 354–370, 2022. [Google Scholar]

20. Z. H. Jiang, X. B. Yang, H. L. Yu, D. Liu, P. X. Wang et al., “Accelerator for multi-granularity attribute reduction,” Knowledge-Based Systems, vol. 177, pp. 145–158, 2019. [Google Scholar]

21. Z. H. Jiang, K. Y. Liu, X. B. Yang, H. L. Yu, H. Fujita et al., “Accelerator for supervised neighborhood based attribute reduction,” International Journal of Approximate Reasoning, vol. 119, pp. 122–150, 2020. [Google Scholar]

22. Y. Chen, K. Y. Liu, J. J. Song, H. Fujita, X. B. Yang et al., “Attribute group for attribute reduction,” Information Sciences, vol. 535, pp. 64–80, 2020. [Google Scholar]

23. X. S. Rao, X. B. Yang, X. Yang, X. J. Chen, D. Liu et al., “Quickly calculating reduct: An attribute relationship based approach,” Knowledge-Based Systems, vol. 200, pp. 106014, 2020. [Google Scholar]

24. Y. Liu, W. L. Huang, Y. L. Jiang and Z. Y. Zeng, “Quick attribute reduct algorithm for neighborhood rough set model,” Information Sciences, vol. 271, pp. 65–81, 2014. [Google Scholar]

25. Z. Chen, K. Y. Liu, X. B. Yang and H. Fujita, “Random sampling accelerator for attribute reduction,” International Journal of Approximate Reasoning, vol. 140, pp. 75–91, 2022. [Google Scholar]

26. Q. H. Hu, J. F. Liu and D. R. Yu, “Mixed feature selection based on granulation and approximation,” Knowledge-Based Systems, vol. 21, no. 4, pp. 294–304, 2008. [Google Scholar]

27. C. Z. Wang, Y. P. Shi, X. D. Fan and M. W. Shao, “Attribute reduction based on k-nearest neighborhood rough sets,” International Journal of Approximate Reasoning, vol. 106, pp. 18–31, 2019. [Google Scholar]

28. X. B. Yang, S. C. Liang, H. L. Yu, S. Gao and Y. H. Qian, “Pseudo-label neighborhood rough set: Measures and attribute reductions,” International Journal of Approximate Reasoning, vol. 105, pp. 112–129, 2019. [Google Scholar]

29. P. Zhou, X. G. Hu, P. P. Li and X. D. Wu, “Online streaming feature selection using adapted neighborhood rough set,” Information Sciences, vol. 481, pp. 258–279, 2019. [Google Scholar]

30. X. L. Yang, H. M. Chen, T. R. Li, J. H. Wan and B. B. Sang, “Neighborhood rough sets with distance metric learning for feature selection,” Knowledge-Based Systems, vol. 224, pp. 107076, 2021. [Google Scholar]

31. J. Ba, K. Y. Liu, H. R. Ju, S. P. Xu, T. H. Xu et al., “Triple‐G: A new MGRS and attribute reduction,” International Journal of Machine Learning and Cybernetics, vol. 13, pp. 337–356, 2022. [Google Scholar]

32. S. Y. Xia, Y. S. Liu, X. Ding, G. Y. Wang, H. Yu et al., “Granular ball computing classifiers for efficient, scalable and robust learning,” Information Sciences, vol. 483, pp. 136–152, 2019. [Google Scholar]

33. Y. B. Wang, X. J. Chen and K. Dong, “Attribute reduction via local conditional entropy,” International Journal of Machine Learning and Cybernetics, vol. 10, pp. 3619–3634, 2019. [Google Scholar]

34. Q. H. Hu, D. R. Yu, J. F. Liu and C. X. Wu, “Neighborhood rough set based heterogeneous feature subset selection,” Information Sciences, vol. 178, no. 18, pp. 3577–3594, 2008. [Google Scholar]

35. Q. H. Hu, L. Zhang, D. Zhang, W. Pan, S. An et al., “Measuring relevance between discrete and continuous features based on neighborhood mutual information,” Expert Systems with Applications, vol. 38, no. 9, pp. 10737–10750, 2011. [Google Scholar]

36. Q. Wan, J. H. Li, L. Wei and T. Qian, “Optimal granule level selection: A granule description accuracy viewpoint,” International Journal of Approximate Reasoning, vol. 116, pp. 85–105, 2020. [Google Scholar]

37. C. Iorio, M. Aria, A. D’Ambrosio and R. Siciliano, “Informative trees by visual pruning,” Expert Systems with Applications, vol. 127, pp. 228–240, 2019. [Google Scholar]

38. S. C. Zhang, X. L. Li, M. Zong, X. F. Zhu and R. L. Wang, “Efficient kNN classification with different numbers of nearest neighbors,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 5, pp. 1774–1785, 2018. [Google Scholar] [PubMed]