Novel Apodized Fiber Bragg Grating Applied for Medical Sensors: Performance Investigation

1  Introduction

Fiber Bragg Gratings (FBGs) is a fiber with a core refractive index induced with periodic variation in the direction of the fiber axis for a length called grating length. A specific wavelength is reflected back due to this periodic grating and it is known as Bragg wavelength (λB). The periodicity (Λ), modulation of the index (Δn) and length (L) of the grating determines and manages the optical properties of FBG [1–4]. The advantages of these grating-based sensors are their resistance to EMI, lightweight, robustness, compact size, stability, remote sensing ability, easy fabrication, installation and maintenance [5,6]. This enables their implementation in various areas of the optical field such as structural health monitoring, medical applications, measurement of temperature and strain in aerospace, as lasers, as buffers, as filters, as multiplexers [7–12], heat transfer application [13] and sewer corrosion [14]. Uniform FBG has a main lobe corresponding to Bragg wavelength in addition to the presence of many side lobes. The occurrence of these side lobes affects the peak resonance detection, making it undesirable characteristics for sensing applications. Apodization is the technique that can be applied to reduce or eliminate these side lobes. Various articles [15–23] suggested implementing the existing functions or proposed novel apodization functions for the improvement of sensing characteristics, strain and temperature measurement, dispersion compensation, structural health monitoring, etc. In a few literatures, sensitivity enhancement has been achieved by using coating materials [24,25]. In the earlier stage, metals and their compounds having high thermal expansion coefficients, were used to amplify temperature sensitivity [26–29]. Due to the complex fabrication process and residual stress, this method was not widely applicable. Later, the utilization of polymer with high thermal expansion and thermo optic coefficient has been researched to enhance the sensitivity. Various works on different polymers such as polydimethylsiloxane, polyvinyl alcohol, polycarbonate, polymethylmethacrylate and polystyrene have been reported [30–43]. The variant of grating, known as Bragg Fibers, is implemented to enhance sensing applications [44–46]. The light propagated in the cladding region is measured for sensing the measure. The application of artificial intelligence improves the performance of the sensor in health care which makes it a promising future in sensor technology [47–49]. In this work, a novel apodization function is proposed to enhance the sensing characteristics and to maximize the usage of FBG as a vital sign sensor, which measures pulse as strain and temperature. Enhancement in wavelength shift in the sensing signal is also measured. Improvement in sensitivity is reported using polydimethylsiloxane coating. Table 1 shows the comparison between the existing and the proposed apodization functions for various applications.

The organization of the present work is as follows: Section 2 gives the principle of operation and the coupled mode theory of uniform FBG, the functions of various existing apodization profiles and properties of coating materials considered for the proposed apodization function. Section 3 deals with the results and discussion. Section 4 summarizes the conclusion, followed by references.

2  Theoretical Background

2.1 Principle of Uniform Fiber Bragg Grating (UFBG)

The refractive index variation of the Fiber Bragg Grating with periodic variation along its axis is given as

n(z)=ncore+Δncos⁡(2πzΛ)(1)

where ncore is the refractive index of the core region, z is the direction of propagation, Λ is the grating periodicity, Δn is the refractive index modulation. Bragg wavelength (λB), is given as

λB=2neffΛ(2)

where neff is the core effective refractive index. Using couple mode theory, the reflectivity of uniform grating FBG is given as

R(L,λB)=k2sinh2⁡(sL)Δβ2sinh2⁡(sL)+s2cosh2⁡(sL)(3)

where k is the coefficient of coupling, Δβ is the detuning wave vector and is given as β-(Π/Λ) and s2 = k2–β2. k, the coupling coefficient is represented as

k=πΔnλMp(4)

where Mp is part of the power contained in fiber core. β is the propagation constant and given as 2π ncore/λ. At centre wavelength, maximum reflectivity happens as Δβ = 0.

Rmax(L,λB)=tanh2⁡(kL)(5)

The strain-based shift in Bragg wavelength is given as

ΔλB=λB(1−pe)Δε(6)

pe=neff2[p11 − vf(p11+p12)]/2(7)

where pe is the effective photoelastic coefficient, neff is the effective refractive index and vf is the Poisson ratio. p11 and p12 are Pockel’s piezo coefficients for strain optic tensor. For silica, p11 = 0.121, p12 = 0.27 and vf = 0.17.

The wavelength shift due to the change in temperature is given as

ΔλB=λB(αf+αn)ΔT(8)

where αf is thermal expansion coefficient and αn is thermo optic coefficient and its corresponding values are 5.5 × 10–7 1k and 8.3 × 10–61ks, respectively. The sensitivity of bragg wavelength for both temperature and strain can be represented as

ΔλB=λB[(1−pe)Δε+(αf+αn)ΔT](9)

Fig. 1 shows the diagrammatic representation of the working of FBG.

Figure 1: Theory of FBG

2.2 Coupled Mode Theory

The propagation of electromagnetic waves inside the fiber core can be represented using coupled mode theory (CMT). The electric field distribution in forward and backward propagating waves can be defined by equations as shown below, respectively.

Ea(z,t)=A(z)ei(ωt−βz)(10)

Eb(z,t)=B(z)ei(ωt+βz)(11)

where A(z) and B(z) are complex amplitudes and are described as

dA(z)dz=ikB(z)e−2iΔβz(12)

dB(z)dz=−ik∗A(z)e2iΔβz(13)

For 0 ≤ z ≤ L. By applying boundary conditions B(0) = Bo and A(L) = AL and solving for closed form solutions,

a(z)=A(z)e−iβz(14)

b(z)=B(z)eiβz(15)

Scattering matrix is used to express the reflected and transmitted wave as

[a(0)b(L)]=[S11S12S21S22][a(L)b(0)](16)

Substituting values of a(0) and b(L) from Eqs. (14) and (15) results in

S11=S22=iSe−iβ0L−Δβsinh⁡(SL)+iScosh(SL)(17)

S12=kk∗S21e2iβ0L=ksinh(SL)−Δβsinh⁡(SL)+iScosh(SL)(18)

To obtain the general solution of coupled mode equation, an effective method known as the Transfer matrix method (T-matrix) has been used, in which a single grating is subdivided into a series of separate gratings (N) of uniform type and described aa s square 2 * 2 matrix. This provides greater flexibility and the precision is based on the number of sections, N. The T-matrix is described as

[a(0)b(0)]=[T11T12T21T22][a(L)b(L)](19)

where,

T11=T∗22=Δβsinh⁡(SL)+iScosh(SL)iSe−iβ0L(20)

T12=T∗21=ksinh(SL)iSe−iβ0L(21)

The reflectivity of FBG is expressed as

R=|T21T11|2(22)

2.3 Existing Apodization Functions

The apodization functions considered for comparison of performance evaluation are listed in this section. Apodization functions are chosen from the literature [15–21].

1.    Uniform

g(x)=1for0≤x≤L(23)

2.    Gaussian

g(x)=exp⁡(−ln2(2(x−(L2)0.5L)2)for0≤x≤L(24)

3.    Barthan

g(x)=0.62--0.48(xL−0.5)+0.38cos⁡(xL−0.5)for 0≤x≤L(25)

4.    Sine

g(x)=sin⁡(πxL)for 0≤x≤L(26)

5.    Welch

g(x)=1--[(x−L2)2/(L2)2]for 0≤x≤L(27)

6.    Cones

g(x)={1−[(x−L2)2/(L2)2]}2for 0≤x≤L(28)

7.    Hamming

g(x)=0.54--0.46cos⁡(2πxL)for 0≤x≤L(29)

8.    Blackman

g(x)=0.42--0.5cos⁡(2πxL)+0.08cos⁡(4πxL)for 0≤x≤L(30)

9.    Nutall

g(x)=0.3635819--0.48917755(2πxL)+0.1365996(4πxL)-- 0.0106411(6πxL)for 0≤x≤L(31)

10.   Bessel [17]

g(x)=J0[cos⁡(3xL)]8[cos⁡(2xL−1)]4for 0≤x≤L(32)

J0-Bessel function of the first kind of zero order and L is the grating length.

2.4 Proposed Apodization Function

In this work, we propose a new apodization function for better sensor characteristics and reflectivity level. The above mentioned characteristics can be attained by using a compact transform which results in narrow bandwidth with high resolution. The strategy to make a transform compact is to increase the power of the exponent or multiply with the increasing functions. The former one is implemented to optimize the apodization function, maximizing its usage as a sensor. The proposed apodization function is given in Eq. (33).

g(x)={1−[(x−L2)2/(L2)2]}4for 0≤x≤L(33)

where L is the grating length. The performance of the existing and proposed apodization functions can be analyzed based on side lobe reflectivity level (MSL), sensitivity, side lobe suppression ratio (SLSR), quality parameter and detection accuracy [16].

Sensitivity=Changeinpeakresonancereflectivitychangeinrefractiveindex(34)

Detection Accuracy=ResonancepeakwavelenthFWHM(35)

Quality Parameter=SensitivityFWHM(36)

The schematic representation of the proposed novel apodized FBG based sensor system is shown in Fig. 2. It embodies source, FBG based sensor, circulator, data acquisition system and Optical interrogator. FBG interrogator and PC are used to measure the reflected signal to determine the measurand. The measurement of applied temperature and strain are given as a shift in peak wavelength.

Figure 2: Schematic diagram of sensing system

2.5 Optical Characteristics of Coating Materials

The coating on uniform FBG enhances its sensitivity. The schematic diagram of UFBG with coating is shown in Fig. 3. Polymer based materials such as Poly-dimethylsiloxane (PDMS), Polycarbonate (PC) and Polymethyl methacrylate (PMMA) have been considered for coating on FBG to enhance sensitivity. These polymers are safe on human skin and can be used directly for non-invasive measurements using FBG on human beings. These materials also have good mechanical and temperature stability. The optical properties of these materials are given in Table 2. Though all materials are safe on human skin, due to its high thermal expansion and thermo optic coefficient, PDMS is considered and performance is analyzed in enhancing the sensitivity of the proposed apodization function. The advantages of PDMS are its low cost, high thermal stability, low electrical conductivity, transparency in optical characteristics, high durability and oxidative stability, less toxicity and biocompatibility [41–43]. Sylgard 184 type of PDMS is regarded for analysis.

Figure 3: Schematic diagram of UFBG with coating

3  Results and Discussion

Using Opti-Grating software, simulations to investigate the optical properties of various existing apodization functions with the proposed apodization function are evaluated by considering a single mode fiber (silica) with 1.46 as refractive index of core and 1.45 as refractive index of cladding. The center wavelength of 1550 nm is considered. The length of the grating has been varied from 1 mm to 15 mm and index depth is varied from 1 × 10–4 to 2.5 × 10–4 for performance evaluation. Fig. 4 exhibits the profile of all the existing apodizations studied and the proposed novel apodization function. Compared to other existing functions, the proposed apodization provides better truncation at both the ends of the grating length which effectively reduces the side lobe levels and narrows the bandwidth.

Figure 4: Profile of various apodizations (a) Uniform (b) Gaussian (c) Barthan (d) Sine (e) Welch (f) Cones (g) Hamming (h) Blackman (i) Nutall (j) Bessel (k) Proposed

An increase in the reflectivity level of the main lobe, for varying grating length with Δn = 0.0001 and index modulation with grating length 10 mm, is shown in Figs. 5a and 5b. In uniform FBG, peak resonance level increases by 99.5% and 96.54%, respectively, for increasing index change and grating length. The proposed apodization function shows 88.4% and 98.28% increase in reflectivity level of peak resonance for increasing index change and grating length, respectively.

Figure 5: Mainlobe reflectivity level for existing and proposed Apodization for (a) Varying Grating length (b) Varying Index Change

Figs. 6a shows the increasing reflectivity level of the left side lobe and 6b shows the reflectivity of the right-side lobe for increasing modulation index. Figs. 7a and 7b show the reflectivity of the left and right-side lobes for increasing grating length. The non-linearity in the side lobe reflectivity level is due to the mismatch between the scattered light and the spacing of the high refractive zone.

Figure 6: Reflectivity level for increasing modulation index (a) Left-side lobe (b) Right-side lobe

Figure 7: Reflectivity level for increasing grating length (a) Left-side lobe (b) Right-side lobe

In cones apodization function, left and right-side lobe levels increase by 22.84% and 22.43%, respectively, for increasing index change and by 63.02% and 71.04%, respectively, for increasing grating length. Likewise, for Gaussian function, left and right-side lobe level increases by 29.67% and 22.04%, respectively, for increasing index change and by 59.19% and 66.55% respectively for increasing grating length. The proposed apodization function shows 22.39% and 22.92% increase in the left and right-side lobe reflectivity levels, respectively, for increasing index modulation and 68.15% and 74.56% increase in left and right-side lobe reflectivity levels respectively for increasing grating length.

Table 3 shows the optical properties of various apodization profiles. The Least FWHM of 0.06 nm is given by Gaussian, Hamming and Blackman apodizations. Better detection accuracy is obtained by narrow FWHM. The second lowest FWHM of 0.07 nm is achieved by the proposed apodization function, which is 41.67% lesser than the FWHM of UFBG. The proposed novel apodized function has a side lobe level of −34.6852 dB which is nearer to Gaussian and shows 148% reduction compared to UFBG. A side lobe suppression ratio of −30.3563 dB which is 71.16% more compared to UFBG has been attained by the proposed apodization function.

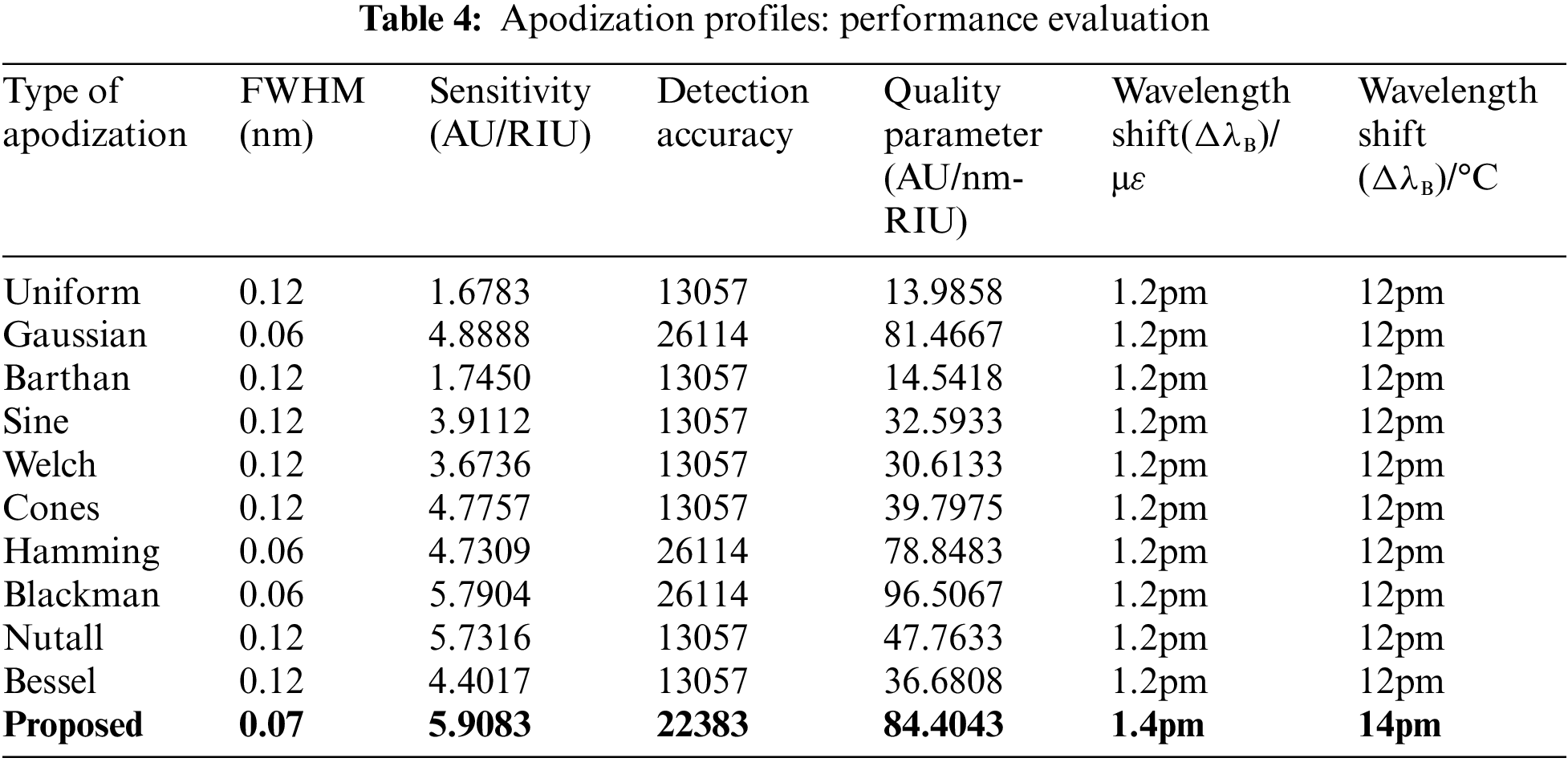
Table 4 shows evaluation parameters considered for the comparison of existing and proposed apodization function. The proposed novel apodization results in a greater sensitivity of 5.9083 AU/RIU and the Uniform apodization has lower sensitivity (1.6783 AU/RIU). The sensitivity of the proposed apodization function increases by 3.52 times, compared to UFBG. The proposed novel apodization function has a detection accuracy of 22383 which is 71.42% more compared to UFBG. The Blackman apodization has the peak quality parameter of 96.5067 AU/nm-RIU. The quality parameter of 84.4043 AU/nm-RIU has been achieved by the proposed system which makes it 503% more than UFBG. Evaluations have been carried out for Δn = 0.0001 and L = 10 mm. The comparison between the UFBG and the proposed apodization function is tabulated in Table 5.

Induced periodic refractive index modulation along the fiber core is given as

Δn(z)=Δn0(1+f(z)vcos[2ΠzΛ+φ(z)])(37)

where f(z) is apodization profile function, v is fringe visibility of index change, φ(z) is grating chirp and Δn0 is the averaged index change. Eq. (37) explains the dependence of effective modulation on the apodization profile. This dependence is responsible for the shift in the wavelength, as Bragg shift depends on the effective refractive index from Eq. (2). The proposed novel apodization function has an increased wavelength shift for the applied temperature and strain based on this. Wavelength shift for the strain applied is shown in Fig. 8a. The strain was applied in steps of 50 με. The proposed novel apodization function achieves a shift of 1.4 pm/με. Change in Bragg wavelength relating to varying temperature (steps of 10°C) is shown in Fig. 8b. The proposed apodization function achieves a wavelength shift of 14 pm/°C (Table 4).

Figure 8: Shift in wavelength for (a) Variation in strain (b) Variation in temperature

Optimization of grating length (L) and index modulation (Δn) is essential to determine the maximum reflectivity of peak resonance. To achieve 100% reflectivity, a proper selection of ‘L’ and ‘Δn’ should be made. In this study, simulation was performed for various values of index modulation and the grating length and observations are tabulated as shown in Table 6. Fig. 9 shows the graphical representation of Table 6. Reflectivity level of the left and right-side lobes for various index modulations and grating lengths, are shown in Fig. 10. The optimized values are calculated as L = 15 mm and Δn = 0.00025, in which the reflectivity level of peak resonance is 100% and the reflectivity level of the left and right-side lobes are −23.5077 dB and −23.5921 dB, for the proposed apodization function.

Figure 9: Main lobe reflectivity vs. index modulation and grating length

Figure 10: Side lobe reflectivity vs. Index modulation and grating length (a) Left-side lobe (b) Right-side lobe

Sensitivity enhancement with PDMS coating for varying thickness is shown in Fig. 11. The temperature sensitivity is 72 pm/°C, which is 5.14 times higher than that of the proposed apodized FBG without coating and 6 times higher than UFBG without coating. The negative thermal expansion coefficient develops a blue shift in the wavelength for increasing temperatures. There exists a non-linearity in the wavelength shift from 50°C–70°C based on the thickness of the PDMS coating. As the present study focuses on the temperature measurement of human beings, the coating thickness does not show any effect on temperature sensitivity. Strain sensitivity does not show any change and is linear with increasing strain. The wavelength shift is 1.2 pm/με and shows a red shift.

Figure 11: Sensitivity variation for different coating thickness of PDMS (a) Varying temperature (b) Varying strain

4  Conclusion

Apodization functions are implemented to enhance the performance of sensors by suppressing side lobes and making FHWM narrower. The proposed novel apodization is manifested to have suitable performance parameters to implement it as a sensor in the field of medicine. Narrow FWHM, highest sensitivity (3.52 times more compared to UFBG) and detection accuracy (71.42% more than UFBG), make it a preferable solution for sensing employment. Enhancement in sensitivity as 1.4 pm/με and 14 pm/°C is shown by the proposed novel apodization for strain and temperature measurement respectively. With optimization, maximum reflectivity of 100% has been achieved for 15 mm of grating length and index modulation of 0.00025 for the proposed apodization function. Enhancement in temperature sensitivity of 72 pm/°C was achieved by using PDMS coating, which is 5.14 times greater than the proposed apodization without coating, enabling its implementation for monitoring vital signals in human beings.

Author Contribution Statement: Ramya Arumugam: Conceptualization, Methodology, Validation, Original Draft Preparation. Ramamoorthy Kumar: Conceptualization, Supervision, Editing and Review. Samiappan Dhanalakshmi: Conceptualization, Supervision, Editing and Review. Khin Wee Lai: Editing and Review. Lei Jiao: Editing and Review. Xiang Wu: Editing and Review.

Funding Statement: This work was supported in part by Universiti Malaya, and ACU UK under Project No. IF063–2021.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  Kashyap, R. (2010). Fiber bragg gratings. Elsevier, USA, Academic Press. [Google Scholar]

 2.  Yu, Q., Zhang, Y., Dong, Y., Li, Y. P., Wang, C. et al. (2012). Study on optical fiber bragg grating temperature sensors for human body temperature monitoring. 2012 Symposium on Photonics and Optoelectronics, pp. 1–4. Shanghai, China, IEEE. [Google Scholar]

 3.  Liu, L., Zhang, H., Zhao, Q., Liu, Y., Li, F. (2007). Temperature-independent FBG pressure sensor with high sensitivity. Optical Fiber Technology, 13(1), 78–80. DOI 10.1016/j.yofte.2006.09.001. [Google Scholar] [CrossRef]

 4.  Campanella, C. E., Cuccovillo, A., Campanella, C., Yurt, A., Passaro, V. M. (2018). Fibre bragg grating based strain sensors: Review of technology and applications. Sensors, 18(9), 3115. DOI 10.3390/s18093115. [Google Scholar] [CrossRef]

 5.  Othonos, A., Kalli, K. (2000). Fiber bragg gratings: Fundamentals and applications in telecommunications and sensing. Physics Today, 53(5), 61. DOI 10.1063/1.883086. [Google Scholar] [CrossRef]

 6.  Nicolas, M. J., Sullivan, R. W., Richards, W. L. (2016). Large scale applications using FBG sensors: Determination of in-flight loads and shape of a composite aircraft wing. Aerospace, 3(3), 18. DOI 10.3390/aerospace3030018. [Google Scholar] [CrossRef]

 7.  Lecourt, J. B., Duterte, C., Narbonneau, F., Kinet, D., Hernandez, Y. et al. (2012). All-normal dispersion, all-fibered PM laser mode-locked by SESAM. Optics Express, 20(11), 11918–11923. DOI 10.1364/OE.20.011918. [Google Scholar] [CrossRef]

 8.  Keshk, M. M., Ashry, I. A., Aly, M. H., Okaz, A. M. (2007). Analysis of different fiber bragg gratings for use in a multi-wavelength erbium doped fiber laser. 2007 National Radio Science Conference, pp. 1–13. Cairo, Egypt, IEEE. [Google Scholar]

 9.  Ashry, I., Shalaby, H. M. (2010). All-optical variable delay buffer for next generation optical networks. 2010 12th International Conference on Transparent Optical Networks, pp. 1–3. Munich, Germany, IEEE. [Google Scholar]

10. Ashry, I., Shalaby, H. M. (2010). Tunable fabry-perot interferometer based on fiber bragg gratings. 2010 17th International Conference on Telecommunications, pp. 534–537. Doha, Qatar, IEEE. [Google Scholar]

11. Orr, P., Niewczas, P. (2011). High-speed, solid state, interferometric interrogator and multiplexer for fiber bragg grating sensors. Journal of Lightwave Technology, 29(22), 3387–3392. DOI 10.1109/JLT.2011.2169044. [Google Scholar] [CrossRef]

12. Goncalves, A. F., Ferreira, L. A., Araujo, F. M. M., Mendes, P. M., Correia, J. H. (2010). A smart skin PVC foil based on FBG sensors for monitoring strain and temperature. IEEE Transactions on Industrial Electronics, 58(7), 2728–2735. DOI 10.1109/TIE.2010.2057233. [Google Scholar] [CrossRef]

13. Chakravartula, V., Rakshit, S., Dhanalakshmi, S., Kumar, R., Narayanamoorthi, R. (2021). Linear temperature distribution sensor using FBG in liquids—Local heat transfer examination application. IEEE Sensors Journal, 21(15), 16651–16658. DOI 10.1109/JSEN.2021.3078731. [Google Scholar] [CrossRef]

14. Raju, B., Kumar, R., Dhanalakshmi, S., Dooly, G., Duraibabu, D. B. (2021). Review of fiber optical sensors and its importance in sewer corrosion factor analysis. Chemosensors, 9(6), 118. DOI 10.3390/chemosensors9060118. [Google Scholar] [CrossRef]

15. Adel Naguib, B., Maher Ata, M., Alzalabani, M. M., Yousif, B. B. (2021). Performance evaluation and enhancement of apodized fiber bragg grating for dispersion compensation. AIP Advances, 11, 015231. DOI 10.1063/5.0026190. [Google Scholar] [CrossRef]

16. Maiti, S., Singh, V. (2020). Performance analysis of apodized fiber bragg gratings for sensing applications. Silicon, 14, 1–7. [Google Scholar]

17. Ashry, I., Elrashidi, A., Mahros, A., Alhaddad, M., Elleithy, K. (2014April). Investigating the performance of apodized fiber bragg gratings for sensing applications. Proceedings of the 2014 Zone 1 Conference of the American Society for Engineering Education, pp. 1–5. Indianapolis, Indiana, USA, IEEE. [Google Scholar]

18. Mohammed, N. A., Ali, T. A., Aly, M. H. (2014). Evaluation and performance enhancement for accurate FBG temperature sensor measurement with different apodization profiles in single and quasidistributed DWDM systems. Optics and Lasers in Engineering, 55, 22–34. DOI 10.1016/j.optlaseng.2013.10.013. [Google Scholar] [CrossRef]

19. Dwivedi, K. M., Trivedi, G., Khijwania, S. K. (2020). Theoretical study and optimization of apodized fiber bragg grating for single and quasi-distributed structural health monitoring applications. 2020 30th International Conference Radioelektronika (RADIOELEKTRONIKA), pp. 1–6. Bratislava, Slovakia, IEEE. [Google Scholar]

20. Ashik T, J., Kachare, N., Kumar, D. S. (2017). Analysis of simultaneous measurement of temperature and strain using different combinations of FBG. LET THERE BE LIGHT: Reflections of a Congress on Light, 1849(1), 020031. [Google Scholar]

21. Ugale, S., Mishra, V. (2010). Fiber bragg grating modeling, characterization and optimization with different index profiles. International Journal of Engineering Science and Technology, 2(9), 4463–4468. [Google Scholar]

22. Jiang, S. C., Wang, J., Sui, Q. M., Ye, Q. L., Wang, L. J. (2015). Study of three-component FBG vibration sensor for simultaneous measurement of vibration, temperature, and verticality. Journal of Sensors, 38, 2865. [Google Scholar]

23. Arumugam, R., Kumar, R., Dhanalakshmi, S. (2022). Optimization and performance evaluation of apodization function for fiber bragg grating as vital sign sensor. Kuala Lumpur International Conference on Biomedical Engineering, pp. 341–350. Springer, Cham. [Google Scholar]

24. Chakravartula, V., Samiappan, D., Kumar, R. (2020). Sensitivity enhancement analysis due to different coating materials of fibre bragg grating-based depth sensor for underwater applications. Optical and Quantum Electronics, 52 (1), 1–15. DOI 10.1007/s11082-019-2144-x. [Google Scholar] [CrossRef]

25. Samiappan, D., Kesarikiran, A. V. S., Chakravartula, V. (2020). Enhancing sensitivity of fiber bragg grating-based temperature sensors through teflon coating. Wireless Personal Communications, 110(2), 593–604. DOI 10.1007/s11277-019-06744-w. [Google Scholar] [CrossRef]

26. Gupta, S., Mizunami, T., Yamao, T., Shimomura, T. (1996). Fiber bragg grating cryogenic temperature sensors. Applied Optics, 35(25), 5202–5205. DOI 10.1364/AO.35.005202. [Google Scholar] [CrossRef]

27. Lupi, C., Felli, F., Ippoliti, L., Caponero, M. A., Ciotti, M. et al. (2005). Metal coating for enhancing the sensitivity of fibre bragg grating sensors at cryogenic temperature. Smart Materials and Structures, 14(6), N71–N76. DOI 10.1088/0964-1726/14/6/N02. [Google Scholar] [CrossRef]

28. Jung, J., Nam, H., Lee, B., Byun, J. O., Kim, N. S. (1999). Fiber bragg grating temperature sensor with controllable sensitivity. Applied Optics, 38(13), 2752–2754. DOI 10.1364/AO.38.002752. [Google Scholar] [CrossRef]

29. Lin, G. C., Wang, L., Yang, C. C., Shin, M. C., Chuang, T. J. (1998). Thermal performance of metal-clad fiber bragg grating sensor. IEEE Photonics Technology Letters, 10(3), 406–408. DOI 10.1109/68.661425. [Google Scholar] [CrossRef]

30. Rong, Q., Sun, H., Qiao, X., Zhang, J., Hu, M. et al. (2012). A miniature fiber—Optic temperature sensor based on a fabry–Perot interferometer. Journal of Optics, 14(4), 045002. DOI 10.1088/2040-8978/14/4/045002. [Google Scholar] [CrossRef]

31. Sampath, U., Kim, D., Kim, H., Song, M. (2018). Cryogenic temperature sensor based on fresnel reflection from a polymer-coated facet of optical fiber. IEEE Sensor Journal, 18(9), 3640–3644. DOI 10.1109/JSEN.2018.2813303. [Google Scholar] [CrossRef]

32. Romano, I. H., Hernández, D. M., Hernández, C. M., Hernandez, D. M., Villatoro, J. (2015). Highly sensitive temperature sensor based on a polymer-coated microfiber interferometer. IEEE Photonics Technology Letters, 27(24), 2591–2594. DOI 10.1109/LPT.2015.2478790. [Google Scholar] [CrossRef]

33. Estella, J., Vicente, P. D., Echeverria, J. C., Garrido, J. J. (2010). A Fibre-optic humidity sensor based on a porous silica xerogel film as the sensing element. Sensors and Actuators B, 149(1), 122–128. DOI 10.1016/j.snb.2010.06.012. [Google Scholar] [CrossRef]

34. Zhang, Y., Wang, F., Liu, Z., Duan, Z., Cui, W. et al. (2017). Fiber-optic anemometer based on single-walled carbon nanotube coated tilted fiber bragg grating. Optics Express, 25(2), 24521–24530. DOI 10.1364/OE.25.024521. [Google Scholar] [CrossRef]

35. Wong, W. C., Chan, C. C., Chen, L. H., Li, T., Lee, K. X. et al. (2012). Polyvinyl alcohol coated photonic crystal optical fiber sensor for humidity measurement. Sensors and Actuators B, 174, 563–569. DOI 10.1016/j.snb.2012.07.032. [Google Scholar] [CrossRef]

36. Muto, S., Suzuki, O., Amano, T., Morisawa, M. A. (2003). Plastic optical fibre sensor for real-time humidity monitoring. Measurement Science and Technology, 14(6), 746–750. DOI 10.1088/0957-0233/14/6/306. [Google Scholar] [CrossRef]

37. Salunkhe, T. T., Choi, H. W., Park, S. J., Kim, J. H., Kim, I. T. (2020). High sensitivity temperature sensor based on fresnel reflection with thermosensitive polymer: Control of morphology and coating thickness. Japanese Journal of Applied Physics, 59, SGGG06. DOI 10.7567/1347-4065/ab5c7d. [Google Scholar] [CrossRef]

38. El-Amassi, D. M., Taya1, S. A., Vigneswaran, D. (2018). Temperature sensor utilizing a ternary photonic crystal with a polymer layer sandwiched between Si and SiO2 layers. Journal of Theoretical and Applied Physics, 12(4), 293–298. DOI 10.1007/s40094-018-0308-x. [Google Scholar] [CrossRef]

39. Esposito, F., Zotti, A., Palumbo, G., Zuppolini, S., Consales, M. et al. (2018). Liquefied petroleum gas monitoring system based on polystyrene coated long period grating. Sensors, 18(5), 1435. DOI 10.3390/s18051435. [Google Scholar] [CrossRef]

40. Zhang, Z., Zhao, P., Lin, P., Sun, F. (2006). Thermo-optic coefficients of polymers for optical waveguide applications. Polymer, 47(14), 4893–4896. DOI 10.1016/j.polymer.2006.05.035. [Google Scholar] [CrossRef]

41. Fendinger, N. J. (2000). Polydimethylsiloxane (PDMSEnvironmental fate and effects. In: Organosilicon chemistry IV: From molecules to materials, pp. 626–638. DOI 10.1002/9783527619917. [Google Scholar] [CrossRef]

42. Turek, I., Tarjanyi, N., Martincek, I., Kacik, D. (2014). Effect of mechanical stress on optical properties of polydimethylsiloxane. Optical Materials, 36(5), 965–970. DOI 10.1016/j.optmat.2013.12.049. [Google Scholar] [CrossRef]

43. Nedoma, J., Fajkus, M., Vasinek, V. (2016). Influence of PDMS encapsulation on the sensitivity and frequency range of fiber-optic interferometer. Optical Materials and Biomaterials in Security and Defence Systems Technology XIII, pp. 99940P.1–99940P.7. SPIE. [Google Scholar]

44. Arumugam, R., Ramamoorthy, K., Samiappan, D. (2021). Study of various structures of bragg fibers based on modal analysis. ICOL-2019, pp. 271–274. Springer, Singapore. [Google Scholar]

45. Yeh, P., Yariv, A. (1978). Theory of bragg fiber. Journal of Optical Society of America, 68(9), 1196–1201. DOI 10.1364/JOSA.68.001196. [Google Scholar] [CrossRef]

46. Guo, S., Albin, S., Rogowski, R. S. (2004). Comparative analysis of bragg fibers. Optics Express, 12(1), 198–207. DOI 10.1364/OPEX.12.000198. [Google Scholar] [CrossRef]

47. Teo, K., Yong, C. W., Muhamad, F., Mohafez, H., Hasikin, K. et al. (2021). The promise for reducing healthcare cost with predictive model: An analysis with quantized evaluation metric on readmission. Journal of Healthcare Engineering, 2021. DOI 10.1155/2021/9208138. [Google Scholar] [CrossRef]

48. Yeoh, P. S. Q., Lai, K. W., Goh, S. L., Hasikin, K., Hum, Y. C. et al. (2021). Emergence of deep learning in knee osteoarthritis diagnosis. Computational Intelligence and Neuroscience, 2021. DOI 10.1155/2021/4931437. [Google Scholar] [CrossRef]

49. Miotto, R., Wang, F., Wang, S., Jiang, X., Dudley, J. T. (2018). Deep learning for healthcare: Review, opportunities and challenges. Briefings in Bioinformatics, 19(6), 1236–1246. DOI 10.1093/bib/bbx044. [Google Scholar] [CrossRef]