Efficient Power Control for UAV Based on Trajectory and Game Theory

1  Introduction

Rapid changes in mobile internet have also made it difficult for mobile wireless networks to be designed well, especially when it comes to delivering very high data speeds with very little time delay. This is especially the case because of the rapid changes in mobile internet. According to a recent report by the International Telecommunication Union (ITU), the amount of data that is transmitted through cellular networks is expected to increase 10,000 times over the course of the next five years in comparison to 2010. The ultra-dense network (UDN) strategy ought to have the ability to accommodate the requirements of an increasing volume of data flow [1,2]. The network coverage can be successfully expanded, and the overall throughput may be increased, by utilising flexible deployment and the establishment of several small cell base stations (SBSs) with low transmit power [3]. The majority of the research that is being done on UDNs right now is geared toward enhancing the functionality of terrestrial heterogeneous cellular networks. This is accomplished through the management of components such as user association in heterogeneous ultra-dense scenarios, Wi-Fi, and energy-efficient frequency reuse in heterogeneous small cell networks [4,5].

In recent years, networking and communication between UAVs have been quite popular due to the fact that they are highly speedy and may be employed in a variety of various ways. There is the potential for a great deal of success to result from combining the usage of UAVs and UDNs [6,7]. It is simple to employ UAVs as an alternative to the conventional land-based infrastructure in order to deliver wireless services to customers in any location. Another prospective usage for these devices is as base stations (BSs) in public gathering places like stadiums and campuses where there is no existing cellular infrastructure [8,9]. When users are located in various areas and are unable to communicate with one another in a direct manner, flying relays may be utilised. UAVs have the potential to assist in ensuring a smooth transition for users who are relocating. The majority of the time, line of sight (LOS) communication links, also known as “nearly line of sight” links, can be created by manoeuvring UAVs in a variety of different ways. As a direct consequence of this, the functionality of the system can be significantly enhanced. UAVs have the potential to either transport energy sources for wireless nodes or act as energy sources for wireless nodes themselves, so extending the lifespan of the network. Cable charging is incompatible with certain software platforms and networks, including the IoT and wireless sensor networks [10,11].

The IoT will be a significant contributor to the development of successful wireless networks and the subsequent generation of mobile communications [12]. Recent advancements in the installation of the Internet of Things have resulted in a substantial rise in the volume of information that is being shared [13]. Communication systems need to have greater room, quicker speeds, faster arrival times, and less energy consumption in order for the internet to be a successful venture [14]. IoT applications and advances must also overcome significant challenges that have never been encountered before because of energy restrictions of wireless devices. For the Internet of Things to become more widespread, it will need to find a solution to one of its most significant challenges: how to make use of renewable energy (IoT). Wireless Power Transfer (WPT) technology might be a good approach to deliver sustainable energy and overcome the energy bottleneck that the Internet of Things is experiencing [15]. Soon, more wireless devices will make use of WPT technology, which will reduce the amount of battery power they require. Numerous technologies, including as electric cars and medical devices that are implanted in the body, use wireless power transmission to provide power to their components. UAV, which stands in contrast to typical wireless networks, makes it possible for Internet of Things devices to freely move around, collect data, share services, and obtain power [16,17]. In a hypothetical scenario, high-altitude UAV navigation may also deliver all the power that wireless devices require in a more expedient and adaptable manner [18,19]. The UAV was able to assist WPT in improving the functionality of IoT-UDN by dynamically switching between different power sources.

This research project investigates how the Internet of Things (IoT) system allocates its resources and how unmanned aerial vehicles (UAVs) can assist in wirelessly powering the IoT. In order to investigate how resources are distributed among UAV nodes and wireless IoT devices, a non-cooperative game theory was utilised. To collect energy for Internet of Things nodes, drones are deployed. This is the solution that has been suggested. When wireless power transmission is utilised to power wireless nodes, drones are employed as a floating power source to power the drones themselves. The resources are going to be split between the drones and the wireless nodes. The method of game theory is applied to locate the Nash equilibrium and discover a solution to this problem. Unmanned Aerial Vehicles (UAVs) utilise Nash Equilibrium to determine the most efficient way to distribute their power sources, which enables them to transmit electricity without the usage of wires.

The most significant takeaways from the research are as follows:

1.    IoT wireless power can be generated by UAVs; even just one UAV with a large number of wireless nodes is sufficient. Drones utilise wireless power transfer technology for the purpose of harvesting wireless nodes. The data transmission process is powered by the energy that is collected by wireless nodes.

2.    A simulation of the process by which wireless local area network (WLAN) nodes and UAVs must share resources might be carried out with the help of a competitive game of power control. In the made-up game, the drone has perfect control over its source of energy transfer, and the wireless node has perfect control over its source of information transfer.

3.    Ground sensors that have a lot of internet of things capabilities are being looked at as a solution to the problem of non-cooperative power control game theory.

4.    The game of power control has reached a point of Nash equilibrium at this point. In addition, it has been demonstrated that the game that has been proposed and its Nash do in fact exist and are one of a kind.

5.    An iterative power control strategy is a good fit for the unmanned aerial vehicle situation, as well as its Sigmoid and Spiral trajectories, which are presented in this study.

6.    The findings of the simulation indicate that the method of the proposed algorithm is beneficial.

The rest parts of the text are organised as follows: In Section 2, we discuss the overall system model as well as the construction process for games. In order to demonstrate, in a mathematical sense, that the proposed equations in Section 3 are accurate, game theory was utilised. Information pertaining to the algorithm is presented in Section 4 of the aforementioned document. New concepts for the green transmission algorithm were conceived as a direct result of the simulation results and the throughput performance, which are covered in Section 5. The most important findings of the study and a conclusion are outlined in the 6th section.

2  System Model and Game Formulation

As a result of their mobility, unmanned aerial vehicles (UAVs) offer advantages that cannot be matched by conventional infrastructures on the ground, which are rooted in one location. The manner in which and the timing of any changes made to UDNs will be significantly influenced by UAVs. UAVs, sometimes famous as drones, are depicted functioning as mobile energy generators in Fig. 1. Additionally, unmanned aerial vehicles (UAVs) have the ability to transport a source of energy or even provide that source of energy themselves, so extending the network’s operational lifetime. The IoT and sensor networks are required to be employed in situations when cable charging is not a possibility.

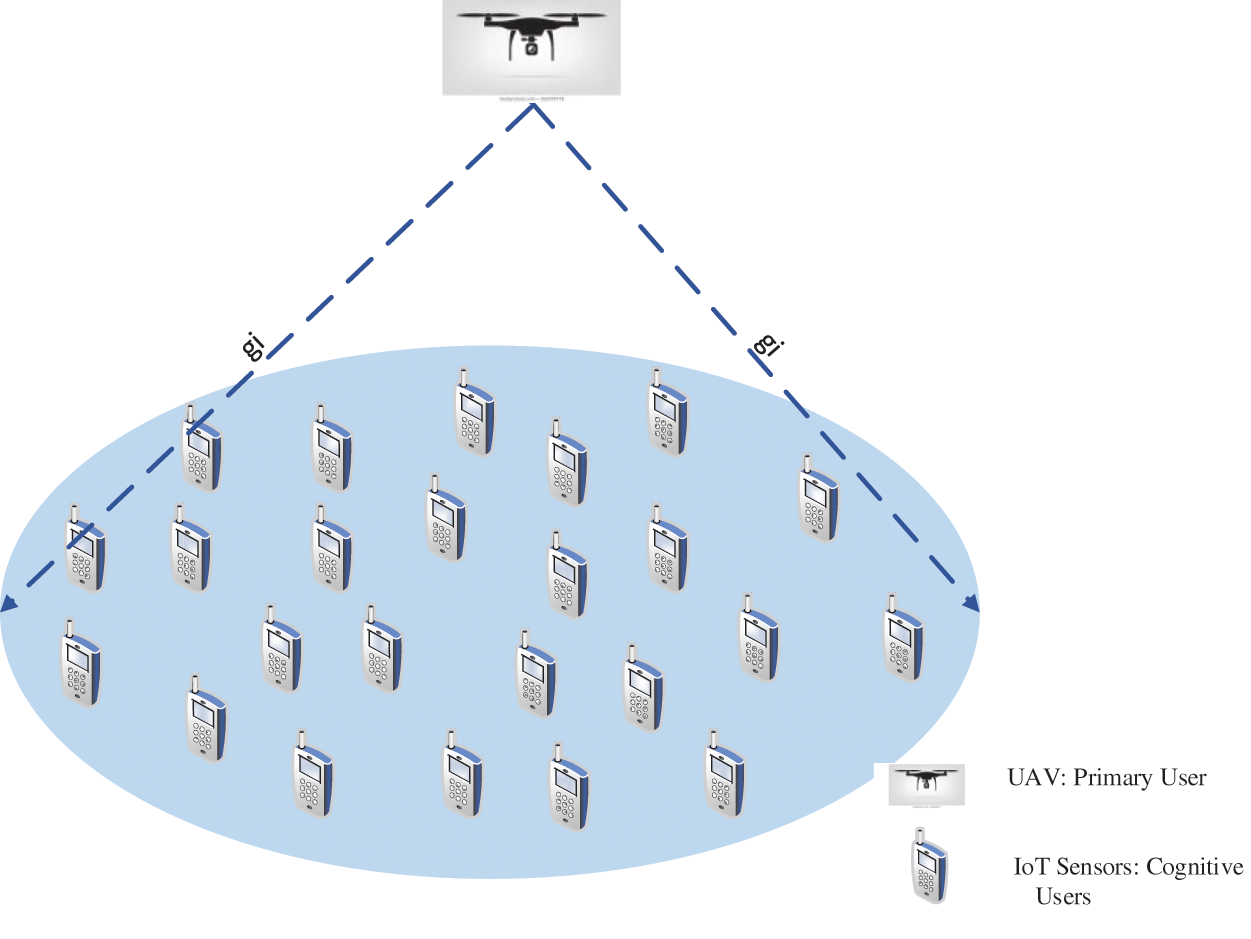
Figure 1: System model of UAV supported IoT energy transfer

UDNs typically consist of sensor nodes, communication nodes that are used for device-to-device (D2D) and machine-to-machine (M2M) connections, and other wireless nodes that are dispersed throughout a large region. It is difficult to reduce energy consumption while keeping networks operational for an extended period of time due to the fact that batteries continue to be the primary source of power for many networks. It is possible to spend a significant amount of time and resources in order to regularly recharge or replace the battery packs in large nodes [10]. It is necessary for the unmanned aerial vehicle (UAV) to be able to hover close to the wireless nodes for it to be able to transfer data and charge them. We searched for the most efficient method of putting the system’s resources to use to wirelessly transmit data and power to the IoT. The IoT nodes that are a part of our complex systems transmit data to the UAVs that are powered by those same nodes. Wireless nodes have the potential to be powered by moving sources like UAVs or drones. Drones have the ability to collect any and all data transmitted by wireless nodes. In this particular research project, wireless nodes throughout the IoT ecosystem were powered by drones.

In this article, we take a look at the most significant aspects of UAV-based wireless communication, which is based on UAV-drones and IoT nodes that are located on the ground. The three-dimensional (3D) position of the unmanned aerial vehicle’s (UAV) trajectory design is shown as q(t)=[x(t),y(t),H(t)]T∈R3 at each time t. This is accomplished within the allotted amount of time, T. For the time being, it is assumed that the final time and the initial time are equivalent because it is believed that the UAV is always in the same location t(0)=0,t(N)=T. Since the parameter for the δt elemental time slot length has been added, the horizon time T is divided into M time slots and now be written as T=Mδt. This was previously not possible. It was agreed, with the use of an elemental duration, that the unmanned aerial vehicles (UAVs) and ground nodes would remain in the same location during each time frame. One further technique to illustrate the location of the UAV in 3D during time slot m is as follows:

q[m]=[x(m),y(m),H(m)]T,m=1,2,…,M(1)

We determine the route of the unmanned aerial vehicle (UAV) by taking into consideration its position {q[m]}m=1M, speed {v[m]}m=1M and acceleration {acc[m]}m=1M. The horizontal location q[m]=[x[m],y[m]]T, m=1,…,M where M can be used to show where the unmanned aerial vehicle (UAV) is on its trajectory in the m th time slot for the fixed height of the UAV at H, where M is the last time slot at the end of the trajectory. This can be done by suppose that the height of the UAV remains constant throughout the trajectory.

Most of the time, a UAV’s path is set by the following time intervals:

q[m+1]=q[m]+v[m]δt+0.5acc[m]δt2,m=0,1,2,…,M(2)

v[m+1]=v[m]+acc[m]δt,m=0,1,2,…,M(3)

Maximum speed (Vmax), and the fastest speed that is allowed (acc[m]=0), trajectory constraints of the UAV are shown below:

||q[m+1]−q[m]||≤Vmaxδt,m=0,1,2,…,M(4)

In this case, q[0]=[x[0],y[0]]T stands for where the UAV starts in the horizontal plane.

Communication between aircraft and ground stations is different because the line of sight (LoS) is most probably to spread out in a three-dimensional space [20]. So, the environment has a bigger effect on the amount of LoS than was thought before. However, the effects of propagation blockage [21] like building blockage still exist for the complete channel models. So, large-scale Rayleigh and free-space fading models are the best for ATG channels. The distance between ground nodes and UAVs can be written as for each elemental time slot: (x,y,H), and represented as:

Ri=di2+H2(5)

Here, at t xi,yi, the i th ground node is found, and its horizontal distance from the UAV is calculated as di=(x−xi)2+(y−yi)2. Here’s a simple way to explain how the i th ground node and the UAV lost their route [22]:

L(Ri)=10log(4πfcRic)α(6)

Here α>2 and the carrier frequency fc can be used to describe the speed of light in metres per second c, (Hz). As an alternative, [23] gives the chance for a Line of Sight:

PLoS=11+aexp⁡(−b(arctan⁡(Hdi)−a))(7)

They are written as aandb. In other words, PNLoS=1−PLoS.

When a UAV is linked to its ground nodes, the path loss expression is:

PL(Ri)=L(Ri)+ηLoSPLoS+ηNLoSPNLoS(8)

In this case, the average extra losses for LoS and non-line of sight (NLoS) are given by ηLoS and ηNLoS, respectively.

Los is thought to be the most important model for free-space path loss [24]. Here’s how to figure out the channel gain for time slot t, defined as:

gi(t)=β0ρ2Ri−α(t)(9)

Actually, Ri(t)=(x−xi)2+(y−yi)2+H2 and the path loss exponent given by Reduction Factor ρ, the channel power gain at the reference distance, and the β0 value can be used to figure out the distance between the UAV and the IoT nodes on the ground. Power gain from IoT on the ground to UAV is given as gi [25].

The drone’s power is used to send data from a wireless node to a drone. Using the power source of a wireless contract, data can be sent, and generate revenue. All IoT nodes in a protected zone are in the same class and use the same channel to talk to each other [26] can utilizing signal to interference ratio (SIR) to imply the income based on the data transmission, it can be displayed as control level relating to data transmission:

γi(pi)=pi(t)gi(t)∑j≠iNpj(t)gj(t)+σi2(t)≥Γi,i=1,2,,3,…,n(10)

where, Γi and σi2 stand for the SIR threshold and the Gaussian noise power, respectively. [27,28] Since the denominator of Eq. (10) is noise, we can replace it with the user’s and other users’ transmission powers to get Eq. (1) and could be done as Ii(p−i):

γi(pi,p−i)=pi(t)gi(t)Ii(p−i)=pi(t)gi(t)∑j≠iNpj(t)gj(t)+σi2(t)(11)

Except for the ith node, interference is shown by −i and is based on how much power all users send.

Cognitive IoTs make it illegal to cause more interference than is allowed by the interference temperature, interference temperature limit is expressed as:

∑i=1Npig0i≤ITL(12)

In the non-cooperative game theory power allocation approach for spectrum sharing, the amount of power each node uses are lowered to meet the predefined requirements for SIR to find the target and to give communication systems a maximum amount of interference they can handle. Using the non-cooperative game theory, IoT nodes that are connected to the system can work in a Nash game in a way that maximises their own utility. There is no doubt that the Nash equilibrium exists and is the only one of its kind. Because of what we found, we’ve made an iterative power allocation method with low processing costs and shown that fast convergence is important in games with multiple nodes. Due to a predetermined SIR need for target identification and a maximum interference tolerance limit, this work can’t reach its main goal, which is to reduce each node’s power consumption and make the best use of transmission power. This is why game theory is seen as a good mathematical tool that considers the rational and self-interested actions of the players. Nodes often compete against each other to win a reward, and they choose a strategy based on how well they can send information.

The way players interact in the non-cooperative power allocation game can be thought of in the following ways:

Φ=[N,{Pi},{Ui(.)}](13)

The integers N={1,2,…,N}, represent the player’s index set of IoT nodes. To get the most out of the game, each player must do the right thing to transfer power. For Set i, Pimax is the transmission power strategy, while Pi=[0,Pimax] is the strategy for consumers. In the utility function for user i, it is shown that each person who is connected to the network wants to maximise their own utility. In non-cooperative game theory, you have to figure out the optimal utility function. You can figure out the utility function for user i by using the number of bits of information received per joule of energy [29]:

Ui(pi,p−i)=LRf(γi)Mpi(14)

In cognitive networks, information is sent from transmitters to receivers using M bit frames or packets of data. With a data rate of L<M bits/sec and the transmission efficiency function f(γ), a bit/sec rate of R bits/sec is used f(γ). A function called f(γ), which has a value ranging from 0 to 1 (i.e., f(γ)∈[0,1]), affects the SIR that is found in the channel f(γ). You can see how much power you’ve sent out by using the power pi. Fig. 2 shows how the efficiency curve changes when the tuning factor z is changed and make the proposed function more efficient than others.

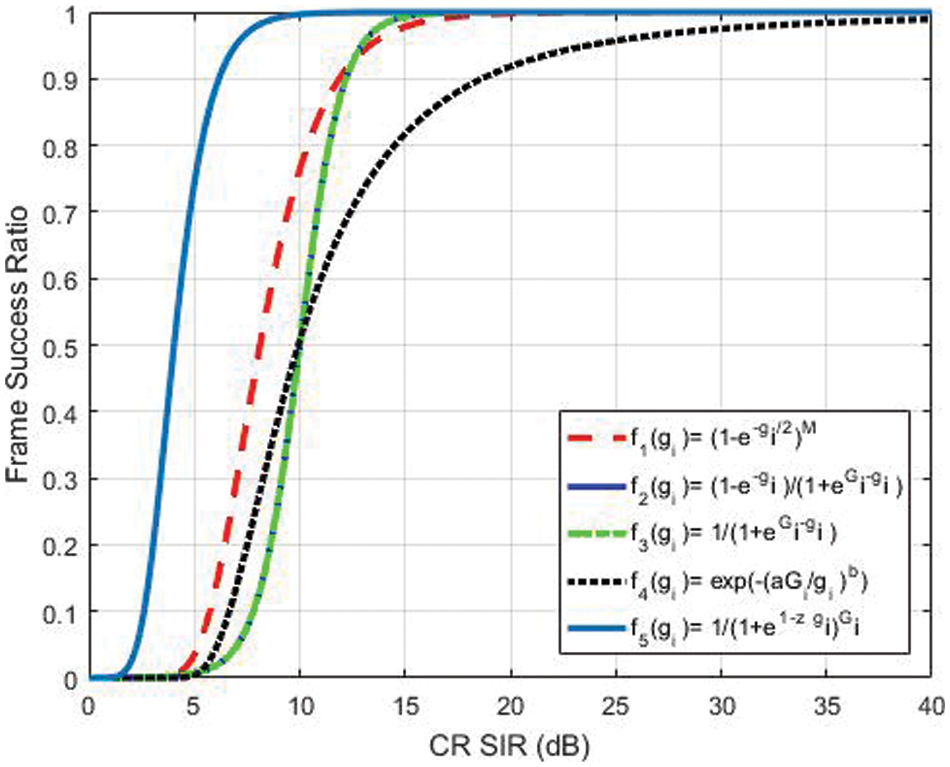
Figure 2: Proposed efficiency function (f5) compared to functions in [30–32] and [33]

Furthermore, the user’s transmission power and pricing function have been considered to improve efficiency even more. Also included, as shown below, are a sigmoid efficiency function as a fraction of exponential power ratio power multiplied by tuning factor (z) and total power to target SIR:

f(γi)=1(1+exp(1−zsiri))Γi(15)

Fig. 3 presents how the proposed utility can be made more efficient by tuning factor vs. others in the literature. The decrease in value of the parameter z results in an increase in utility and a decrease in the transmitting power, but it also results in a decrease in target of SIR pertaining to the system. Furthermore, the primary system can transmit the tuning factor z with the help of cognitive networks for adjusting the targeted SIR based on interference. When the sum of interference is about to reach the limit of interference temperature, a lower value of z is sent by the primary system. Eq. (14) can be used to show the utility function for the i th cognitive node.

Ui=LRMpi1(1+exp(1−zsiri))Γibitjoule(16)

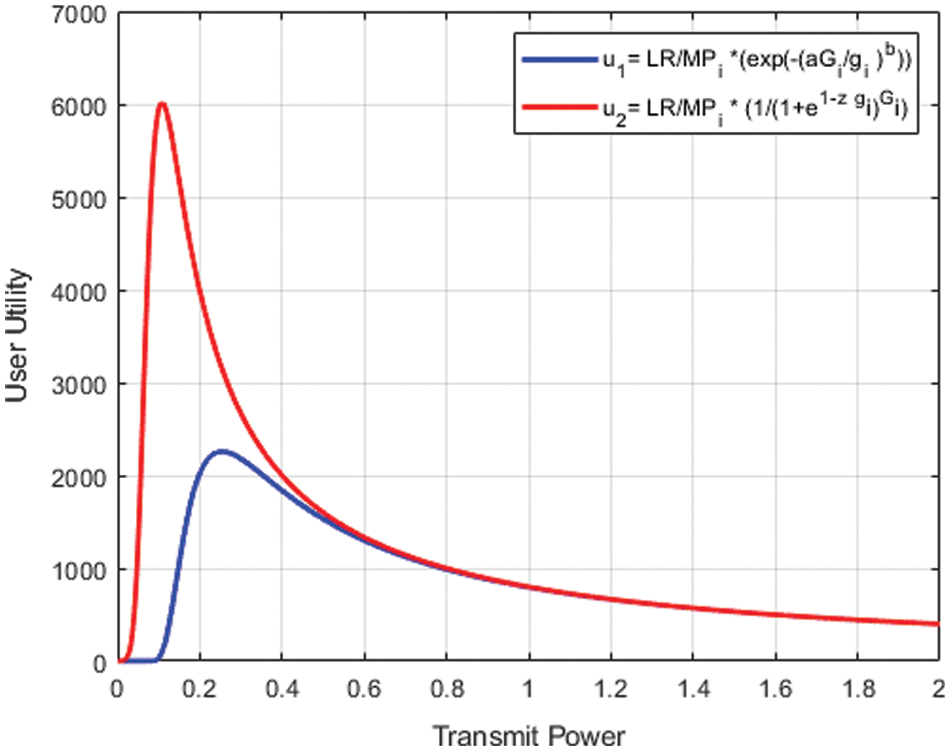
Figure 3: Proposed utility u2 compared to u1 [30]

Power control that doesn’t work with other nodes hurts them and costs them money. This makes the Nash equilibrium less effective than it should be. The pricing idea was put in place to get users to use as many network resources as possible. Here’s how a power-control game based on prices works when players don’t work together:

Φc=[N,{Pi},{Uic(.)}c](17)

where, Uic(.) means the utility function employing pricing and it is shown like this:

Uic(pi,p−i)=Ui(pi,p−1)−Ci(pi,p−1)(18)

Therefore, the proposed pricing function is detailed as:

Ci(pi,p−i)=cpiexp(piα)(19)

One of our ideas for improving system performance is to change the way prices work so that CRs are rewarded for making better use of system resources. This design participates by influencing the next taken a toll for clients who are most remote from the base station and utilize more power.

So, instead of the usual linear way of pricing transmission power, we use an exponential power function. Pricing functions for the power strategy [0, 1] have probably been completed numerically, with power transferred by different users covering a range from minimum to maximum. If the transmission power is low and the network is close, it’s easier to get lower prices.

If the transmission power is high and the network is far away, it’s harder. So, the pricing system for this paper can be summed up as follows:

UiC(pi,p−i)=LRMpi1(1+exp(1−zsiri))Γi−cpiexp(piα)(20)

In this case, the price factor is shown by the c and α. Playing the suggested green non-cooperative power control with price has led to the following:

EE−NGPAP:maxpi∈PiUiC(pi,p−i)=LRMpi1(1+exp⁡(1−zsiri))Γi−cpiexp⁡(piα)(21)

3  Existence and Uniqueness of Nash Equilibrium

In this part, a mathematical illustration related to the individuality and existence is given in the next section [34]:

Definition 3.1: Nash equilibrium in the EE-NGPAP method can be described as the power vector, e.g., Pi=[pi,….,pi], no participant can improve the utility function, Ui(pi,p−i), independently modifying its personal approach form, i.e.,.,pi. In mathematical terms, Nash equilibrium is presented as follows:

Ui(pi,p−i)≥Uj(pi,p−i),∀pi∈Pi,^∀i∈N(22)

3.1 Nash Equilibrium Existence

The Nash equilibrium in the suggested method gives a stable and predictable results where numerous CRs with opposing activities contribute and go to a position where no contributor can request to set its own method form. To emphasize NE’s being exist, the below theorem is suggested:

Theorem 3.1: The Nash equilibrium is appeared in EE-NGPAP=[N,{Pi},{Ui(.)}], if it meets the subsequent conditions ∀i∈N:

1)   The profile action approach (i.e.,pi) is a compact, convex, and nonempty subset.

2)   The function of utility Ui(pi,p−i) is a concave and continuous function over strategy set of the players.

Proof: It can be obtained by proving that both the criteria provided in Theorem 3.1 are satisfied by EE-NGPAP. It is corroborated by the following evidence:

1)   As every cognitive uses a strategy outline well-defined by optimal and minimal power as given in Eq. (15), the first condition is promptly satisfied.

2)   For proving that the second criterion is also satisfied, the given utility function based on variable pricing must be shown to be concave in pi,∀i∈N.

Definition 3.2: Based on [35] Super Modular definition 5, The utility function Ui(pi,p−i) characterised by the convex set Pi^ is concave in Pi only in case, the surplus function’s second derivative is greater than 0 [35,36].

To show this condition is true, the Equations: ∂2uip∂2pic>0, be required to solve ∀i. Therefore, the next Lemma need to be fulfilled.

Lemma 3.1: The utility function based on pricing provided in Eq. (20) is concave in pi,∀i∈N.

Considering that both the criteria are given in Theorem 3.1 are satisfied, the recommended EE-NPGP is a concave n-player game having one or more NE in it.

3.2 Nash Equilibrium Uniqueness

The approach defines of the players consists of the recommender concave and continuous application function accordingly, NE is present in EE-NGPAP. However, a question can also rise at this juncture obviously: Is the existence of the NE unique? the distinctiveness of NE may be tested as follows:

Definition 3.3: An alternative NE definition is the best response strategy which can be defined as per the following:

BR(p−i)={pic∈P^i:uic(pic,p−ic)≥uic(p→ic,p−ic),∀p→ic∈P^i}(23)

Additionally, the best approach for reaction is a set consist of exactly a single maximum point that will increase the objective function, which is mathematically formulated as follows:

pi=argmaxpi∈PiUic(pi,p−i)(24)

Likewise, the second derivative has been demonstrated to be bigger than zero, which means that the maximum point is the optimal unique point.

Theorem 3.2: The NE of the EE-NGPAP game is [N,{Pi},{Ui(.)}] which is unique.

Proof: The key feature of the uniqueness of NE is to confirm that a typical function is the best approach for response. For the suggested game, EE-NGPAP  =  [N,{Pi},{Ui(.)}], which is the best response given by the ith user Regarding others’ power approach.

To prove the uniqueness of NE, the function for the most suitable response must be a regular function and be required to have the following traits as well [37]:

1)   Positivity: BR(p−i)>0.

2)   Monotonicity: given p≥p^, then BR(p−i)≥BR(p~−i).

3)   Scalability: given, for all ε>1, then εBR(p−i)>BR(εp−i).

Furthermore, it’s been proven in [38] that if a fixed point from Eq. (21) satisfies the traits as stated previously, so the BR(P-i) proceeds towards a fixed point. For this reason, based on [38], a fixed point in Eq. (21) meets the positivity, monotonicity and scalability under the particular conditions stated in theorem 3.1.

Finally, a standard function should be utilized as the most excellent reaction function. Hence, the proposed non-cooperative has as it been an only one NE solution that fulfils the prove of the uniqueness of the Nash Equilibrium.

4  Proposed EE-NGPAP Algorithm

In order to locate the point at which the model proposed in this article is in a state of equilibrium, an iterative distributed technique of power allocation is applied. To locate the Nash Equilibrium, point for the model that has been provided, the suggested algorithm approach requires that each cognitive node decide on its own what the ideal transmission power SIR value is at each time step. It is believed that EE-NGPAP is the ideal protocol for this paradigm due to the fact that each IoT node just needs to know how to send to all of the other nodes. It is not necessary for it to have any knowledge of the system. A distributed process with pseudo-code can be used to describe the iterative power allocation and pricing method. This method assumes a unique Nash equilibrium with the proposed model.

Nevertheless, we assume that each cognitive node updates it’s transmit power at time instances ti={ti1,ti2,….}, and tik<ti(k+1), in addition, we suppose the strategy set of power of the i th IoT node is Pi=[Pimin,Pimax]. For this reason, we set an infinity small quantity ε and (ε>0) then by considering the proposed algorithm as in Eq. (21) generates sequence of powers as thus:

_________________________________________________________________________________________________________________________________________

EE-NGPAP

I.     Initialize vector of transmit power p=[p10,p20,p30,…,pN0] randomly at time t0, besides other parameters including: H,α,ρ,β0,V, σ2, Pimax, Γi, Pricing factors (c&n) and Tuning factor (z).

II.     Initialize UAV’s Trajectory

          a)  Sigmoid

          b)  Spiral

III.     Inner Iteration:

          For all i∈N at time instant tk;

           a)  Update gi(tk) using Eq. (9)

           b)  Update γi(tk) using Eq. (10)

           c)  Given pi(tk−1), consider the best response of power strategy ri(tk) based on ri(tk)=argmaxpi∈PiuiC(pi,p−i(tk−1))

           d) Assign the transmit power as pi(tk)=min(ri(tk),pimax)

IV.     Convergence Step:

         If ‖p(tk)−p(tk−1)‖≤ε, declare Nash equilibrium and stop iteration as p(tk);

         Else: k=k+1 and go to step IV

V.     Exit Inner Iteration (Best Response (BR) Iteration)

VI.     End

_________________________________________________________________________________________________________________________________________

Actually, ri(tk) is utilized as the agent of the rest of the most excellent transmit powers that match to the i th IoT nodes. Typically, this is possible to gained only if the objective function is actualized with EE-NGPAP calculation over the time instant k. Likewise, the proposed method is depending on power allocation utilizing pricing function. Therefore, the computational complexity straightforwardly based on the number of users and the accessible channels can caused in O(log(N)).

5  Simulation Results & Discussion

To set up the simulation environment, the MATLAB software was utilised. The suggested algorithm was put to the test in an area that was 1,000×1,000m2 in size, the IoT equal to 20×20 nodes were dispersed in a random pattern across the region, and the greatest distance that could exist between the UAV and the nodes was 100 m. One may draw parallels between these low-power nodes and sensor nodes, which are able to store significant amounts of data and transfer enormous amounts of that data. In spite of this, it is generally believed that these nodes do not have a reliable source of power. Table 1, below outlines the configurations that have been created for the associated system.

This regulation cannot be broken in any way, shape, or form. The spiral trajectory is depicted in Fig. 4, in which blue colour refer to the default nodes, that can be interpreted as a spiral path with IoT sensor nodes scattered all over the place to demonstrate the system model. In this particular instance, the default colour for the nodes is blue. Furthermore, sigmoid trajectory is demonstrating in Fig. 5 in which yellow colour refer to the default nodes. However, in order to fulfil their contractual duties and generate the most money feasible, drones are required to transmit power to wireless nodes. As the game progresses, the drones will be required to transfer an increasing amount of electricity in order to fulfil the terms of their cell phone contracts and earn more money. In addition, spiral, sigmoid paths and a power-management game are utilised to transport energy to nodes at the precise moment that it is required.

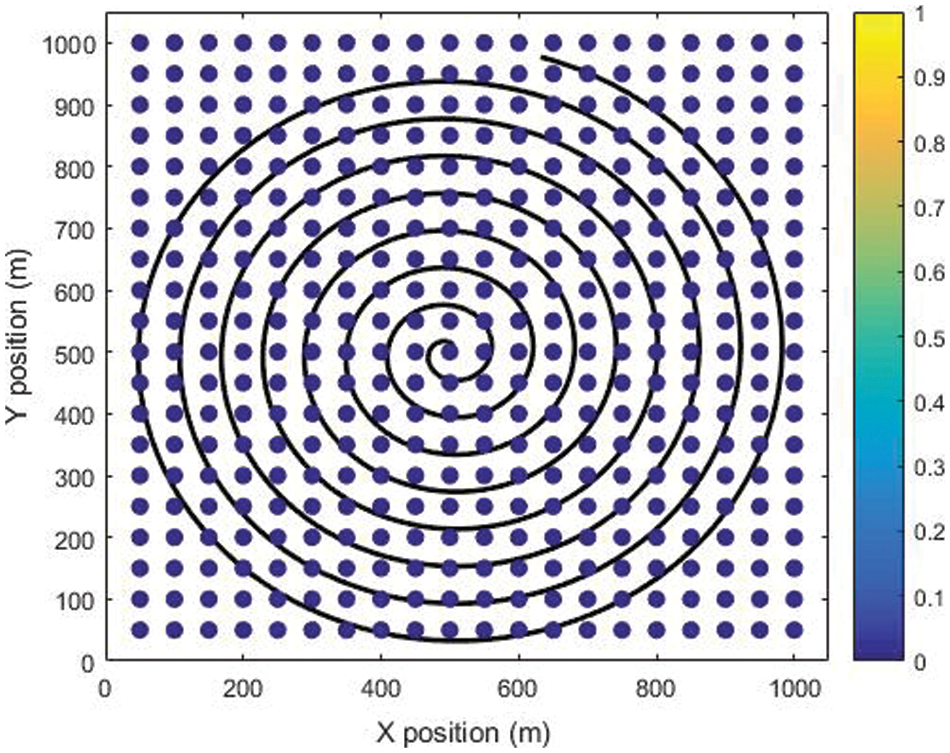
Figure 4: Spiral trajectory UAV scenario based dense IoT sensors

Figure 5: Sigmoid trajectory UAV scenario based dense IoT sensors

It has been determined that a maximum flight speed of 50m/s, can be anticipated without a reduction in generality. The findings were compared using Fig. 6 with height, as well as Fig. 7 with 100 m height, in order to demonstrate the benefits of a common mathematical procedure that is referred to as “multi-decision.” The results of sigmoid and without effects of game theory are displayed in Fig. 6 as subfigures of (a), (c), and (e), while the results obtained without using game theory with spiral trajectory are displayed in Fig. 6 as subfigures (b), (d), and (f). Further, The results of sigmoid and with effects of game theory are displayed in Fig. 7 as subfigures of (a), (c), and (e), and the results obtained with using game theory with spiral trajectory are displayed in Fig. 7 as subfigures (b), (d), and (f). In addition to this, we fly for many typical amounts of time at predetermined hovering speeds. The amount of time spent flying is indicated in seconds on average here. We can note from Figs. 6 & 7, the flight speed was 200s,300s , and 400s respectively in Sub-Fig. (a) & (b), Sub-Fig. (c) & (d), and Sub-Fig. (e) & (f).

Figure 6: UAV sigmoid & spiral trajectories without game of different flying time for H = 100 m

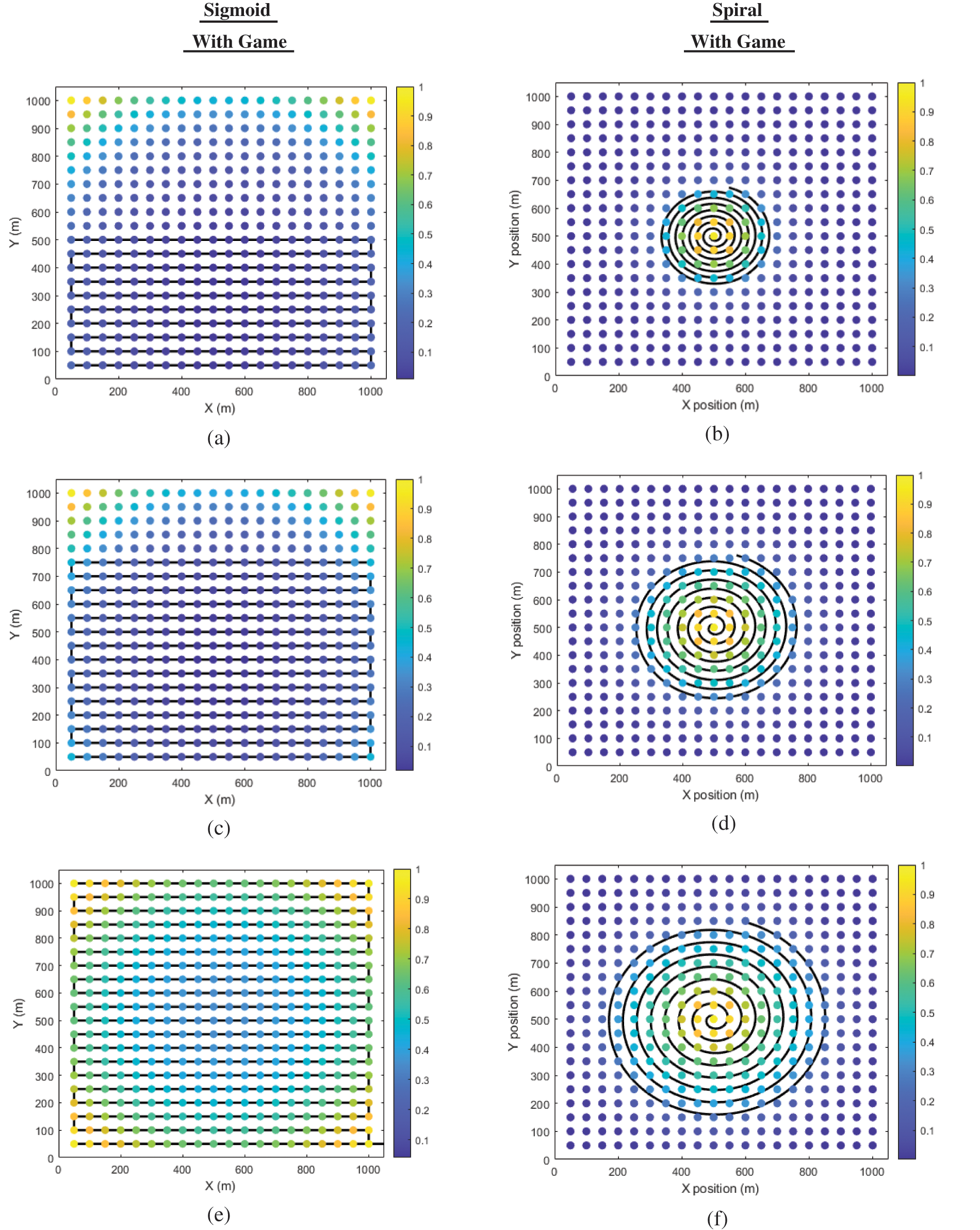
Figure 7: UAV sigmoid & spiral trajectories with game of different flying time for H = 100 m

The discount factor influences the best policies for wireless nodes when utilizing Nash equilibrium among players, which our approach represents as an IoT node, at a height of 100 metres and with multiple average flying times as ft=200s, ft=300s, and ft=400s, as shown in Fig. 6 as well as in Fig. 7. These figures showing in what way the discount factor influences the best policies for wireless nodes when applying Nash equilibrium between players. The correct responses are f, b, d, and c. It is expected that over time, the cost of transporting drones will increase, which will result in an increase in the price of each individual drone unit that is supplied. Drones need more power to carry energy through the air since wireless power transmission is inefficient and the distances it must cover are so great. The costs of transmitting power are going to significantly increase as a direct consequence of all these issues. UAVs will cause an increase in the cost of conveyed power units whenever there is a significant demand for wireless power. A game demonstrates that Figs. 7a, 7c, 7e and 7f are the most effective ways to connect IoT nodes. In addition, Fig. 6 with its subfigures for both trajectories shows lack in distributed power and save energy for long time since all used wants to use more power in selfish manner and no control for them to manage and distribute it fairly between them. So, use game theory for both trajectories in Fig. 7 solve the issues of power consumption and losing with few numbers of users and the most effective trajectory was sigmoid as shown in Fig. 7 with its subfigures (a), (c) and (e) since it covers a large numbers of ground IoT sensors and wide land on the ground. Also, Fig. 7, subfigure (f) which is represent spiral trajectory with 400 s flying time it shows an effective case for the UAV with spiral hovering.

Hence, we assumed that all nodes belonging to the same category are the same so that consumers would have an easier time comprehending the simulations we created. Figs. 6 and 7 are presented below. By lingering for longer, drones increase the amount of energy they use to convey information, which in turn increases the amount of energy they use. Even as energy unit prices are transferred over time by increasing hover time. IoT contracts are getting stronger as a result of drones increasing the level of wireless power delivery by increasing their average flight time to meet more wireless contract requirements. This is demonstrated in Fig. 7 with its sub-figures (e) and (f), separately. If the IoT node is able to generate more energy on its own, it will be able to transfer data for a longer period of time.

6  Conclusion

The EE-NGPAP algorithm which stands for non-cooperative game theory power allocation with pricing, was proposed as a method for controlling power in cognitive UAV networks with two trajectories (Sigmoid and Spiral) that contain IoT wireless nodes by the authors of this paper. In addition to this, a new energy harvesting function was proposed and simulations as well as mathematical arguments were utilised to demonstrate that the Nash equilibrium does in fact exist and is distinct from any other equilibrium. The simulations demonstrated that the method of non-cooperative power control was superior to other ways in terms of its ability to save energy. The recommended approach to energy collecting requires only 4 iterations to achieve NE, which makes it a more attractive option for potential enhancements to IoT technology in the near future. More research needs to be done on the concept of employing an unmanned aerial vehicle (UAV) as a moveable source of energy so that it can be put to use in the not-too-distant future. The application of machine learning in unmanned aerial vehicle (UAV) communications will be the subject of one of our next research projects.

Funding Statement: The authors are grateful to the Taif University Researchers Supporting Project number (TURSP-2020/36), Taif University, Taif, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Mukhlif, K. A. B. Noordin, A. M. Mansoor and Z. M. Kasirun, “Green transmission for C-RAN based on SWIPT in 5G: A review,” Wireless Networks, vol. 25, no. 5, pp. 2621–2649, 2019. [Google Scholar]

 2.  N. Bhushan, J. Li, D. Malladi, R. Gilmore, D. Brenner et al., “Network densification: The dominant theme for wireless evolution into 5G,” IEEE Communications Magazine, Article, vol. 52, no. 2, pp. 82–89, 2014. [Google Scholar]

 3.  M. Kamel, W. Hamouda and A. Youssef, “Ultra-dense networks: A survey,” IEEE Communications Surveys & Tutorials, vol. 18, no. 4, pp. 2522–2545, 2016. [Google Scholar]

 4.  L. Y. Su, C. Y. Yang and C. L. I, “Energy and spectral efficient frequency reuse of ultra dense networks,” IEEE Transactions on Wireless Communications, vol. 15, no. 8, pp. 5384–5398, 2016. [Google Scholar]

 5.  S. Samarakoon, M. Bennis, W. Saad, M. Debbah and M. Latva-Aho, “Ultra dense small cell networks: Turning density into energy efficiency,” IEEE Journal on Selected Areas in Communications, vol. 34, no. 5, pp. 1267–1280, 2016. [Google Scholar]

 6.  Y. Zeng, R. Zhang and T. J. Lim, “Wireless communications with unmanned aerial vehicles: Opportunities and challenges,” IEEE Communications Magazine, vol. 54, no. 5, pp. 36–42, 2016. [Google Scholar]

 7.  R. Alroobaea, R. Arul, S. Rubaiee, F. S. Alharithi, U. Tariq et al., “AI-Assisted bio-inspired algorithm for secure IoT communication networks,” Cluster Computing, vol. 25, no. 3, pp. 1805–1816, 2022. [Google Scholar]

 8.  F. Yang, J. Song, W. Xiong and X. Cui, “UAV-Based collaborative electronic reconnaissance network for 6G,” Wireless Communications and Mobile Computing, vol. 2021, Article ID 5827665, pp. 7, 2021. https://doi.org/10.1155/2021/5827665. [Google Scholar]

 9.  A. Anwar, I. U. Haq, I. A. Mian, F. Shah, R. Alroobaea et al., “Applying real-time dynamic scaffolding techniques during tutoring sessions using intelligent tutoring systems,” Mobile Information Systems, vol. 2022, Article ID 6006467, pp. 9, 2022. https://doi.org/10.1155/2022/6006467. [Google Scholar]

10. H. C. Wang, G. R. Ding, F. F. Gao, J. Chen, J. L. Wang et al., “Power control in UAV-supported ultra dense networks: Communications, caching, and energy transfer,” IEEE Communications Magazine, vol. 56, no. 6, pp. 28–34, 2018. [Google Scholar]

11. J. Niu, R. Alroobaea, A. M. Baqasah and L. Kansal, “Implementation of network information security monitoring system based on adaptive deep detection.” Journal of Intelligent Systems, vol. 31, no. 1, pp. 454–465, 2022. [Google Scholar]

12. H. Yu and Y. B. Zikria, “Cognitive radio networks for internet of things and wireless sensor networks,” Sensors, vol. 20, no. 18, pp. 5288 2020. [Google Scholar]

13. C. Lee, G. Jang, N. -N. Dao, D. S. Lakew, C. Lee et al., “Competitive game theoretic clustering-based multiple UAV-assisted NB-IoT systems,” Electronics, vol. 10, no. 3, pp. 356, 2021. [Google Scholar]

14. A. Majeed, R. Bhana and S. Parvez, “Retracted: Controlling energy consumption by internet of things (IoT) applications,” Journal of Fundamental and Applied Sciences, vol. 10, no. 4S, pp. 608–611, 2018. [Google Scholar]

15. S. Y. R. Hui, W. X. Zhong and C. K. Lee, “A critical review of recent progress in mid-range wireless power transfer,” IEEE Transactions on Power Electronics, vol. 29, no. 9, pp. 4500–4511, 2014. [Google Scholar]

16. Z. Zhang, H. L. Pang, A. Georgiadis and C. Cecati, “Wireless power transfer-an overview,”, IEEE Transactions on Industrial Electronics, vol. 66, no. 2, pp. 1044–1058, 2019. [Google Scholar]

17. S. Y. Lien, K. C. Chen and Y. H. Lin, “Toward ubiquitous massive accesses in 3GPP machine-to-machine communications,” IEEE Communications Magazine, vol. 49, no. 4, pp. 66–74, 2011. [Google Scholar]

18. B. Liu, H. Xu and X. Zhou, “Resource allocation in unmanned aerial vehicle (UAV)-assisted wireless-powered internet of things,” Sensors, vol. 19, no. 8, pp. 1908, 2019. [Google Scholar]

19. F. Mukhlif, J. O. Hodonu-Wusu, K. A. Bin Noordin and Z. M. Kasirun, “Major trends in device to device communications research: A bibliometric analysis,” in 2018 IEEE Student Conf. on Research and Development (SCOReD), Malaysia, pp. 1–6, 2018. [Google Scholar]

20. R. I. Bor-Yaliniz, A. El-Keyi and H. Yanikomeroglu, “Efficient 3-D placement of an aerial base station in next generation cellular networks,” in 2016 IEEE Int. Conf. on Communications, New York, pp. 985–989, 2016. [Google Scholar]

21. A. Al-Hourani, S. Kandeepan and A. Jamalipour, “Modeling air-to-ground path loss for low altitude platforms in urban environments,” in 2014 IEEE Global Communications Conf., New York, pp. 2898–2904, 2014. [Google Scholar]

22. M. Mozaffari, W. Saad, M. Bennis and M. Debbah, “Efficient deployment of multiple unmanned aerial vehicles for optimal wireless coverage,” IEEE Communications Letters, vol. 20, no. 8, pp. 1647–1650, 2016. [Google Scholar]

23. A. Al-Hourani, S. Kandeepan and S. Lardner, “Optimal LAP altitude for maximum coverage,” IEEE Wireless Communications Letters, vol. 3, no. 6, pp. 569–572, 2014. [Google Scholar]

24. J. Xu, Y. Zeng and R. Zhang, “UAV-Enabled wireless power transfer: Trajectory design and energy optimization,” IEEE Transactions on Wireless Communications, vol. 17, no. 8, pp. 5092–5106, 2018. [Google Scholar]

25. L. D. Nguyen, A. Kortun and T. Q. Duong, “An introduction of real-time embedded optimisation programming for UAV systems under disaster communication,” EAI Endorsed Transactions on Industrial Networks and Intelligent Systems, vol. 5, no. 17, pp. e5, 2018. [Google Scholar]

26. F. Mukhlif, K. A. Bin Noordin and O. B. Abdulghafoor, “Energy harvesting technique for efficient wireless cognitive sensor networks based on SWIPT game theory,” KSII Transactions on Internet and Information Systems (TIIS), vol. 14, no. 6, pp. 2709–2734, 2020. [Google Scholar]

27. F. Mukhlif, N. Ithnin, O. B. Abdulghafoor, F. Alotaibi and N. S. Alotaibi, “Game theory-based IoT efficient power control in cognitive UAV,” CMC-Computers, Matrials and Continua, vol. 72, no. 1, pp. 1561–1578, 2022. [Google Scholar]

28. F. Mukhlif, K. A. Bin Noordin, O. B. Abdulghafoor and T. Izam, “Green communication for cognitive radio networks based on game and utility-pricing theories,” Plos One, vol. 15, no. 8, pp. 21, 2020. [Google Scholar]

29. D. Goodman and N. Mandayam, “Power control for wireless data,” IEEE Personal Communications, vol. 7, no. 2, pp. 48–54, 2000. [Google Scholar]

30. Y. A. Al-Gumaei, K. A. Noordin, A. W. Reza and K. Dimyati, “A novel utility function for energy-efficient power control game in cognitive radio networks,” Plos One, vol. 10, no. 8, p. e0135137, 2015. [Google Scholar]

31. X. Z. Xie, H. L. Yang, A. V. Vasilakos and L. He, “Fair power control using game theory with pricing scheme in cognitive radio networks,” Journal of Communications and Networks, vol. 16, no. 2, pp. 183–192, 2014. [Google Scholar]

32. Y. H. Kuo, J. H. Yang and J. Chen, “Efficient swarm intelligent algorithm for power control game in cognitive radio networks,” Iet Communications, vol. 7, no. 11, pp. 1089–1098, 2013. [Google Scholar]

33. X. D. Zhang, Y. F. Zhang, Y. H. Shi, L. Zhao and C. R. Zou, “Power control algorithm in cognitive radio system based on modified shuffled frog leaping algorithm,” AEU-International Journal of Electronics and Communications, vol. 66, no. 6, pp. 448–454, 2012. [Google Scholar]

34. J. O. Neel, J. H. Reed and R. P. Gilles, “Convergence of cognitive radio networks,” in 2004 IEEE Wireless Communications and Networking Conf. (IEEE Cat. No. 04TH8733), Atlanta, GA, USA, vol. 4, pp. 2250–2255, 2004. [Google Scholar]

35. C. U. Saraydar, N. B. Mandayam and D. J. Goodman, “Efficient power control via pricing in wireless data networks,” IEEE Transactions on Communications, vol. 50, no. 2, pp. 291–303, 2002. [Google Scholar]

36. J. S. Pang, G. Scutari, D. P. Palomar and F. Facchinei, “Design of cognitive radio systems under temperature-interference constraints: A variational inequality approach,” IEEE Transactions on Signal Processing, vol. 58, no. 6, pp. 3251–3271, 2010. [Google Scholar]

37. R. D. Yates, “A framework for uplink power-control in cellular radio systems,” IEEE Journal on Selected Areas in Communications, vol. 13, no. 7, pp. 1341–1347, 1995. [Google Scholar]

38. S. Koskie and Z. Gajic, “A nash game algorithm for SIR-based power control in 3G wireless CDMA networks,” IEEE ACM Transactions on Networking, vol. 13, no. 5, pp. 1017–1026, 2005. [Google Scholar]