NOMA with Adaptive Transmit Power Using Intelligent Reflecting Surfaces

1  Introduction

Intelligent Reflecting Surfaces (IRS) are a good candidate for sixth generation 6G networks [1–3]. IRS phases are adjusted so that reflections have a zero-phase at all users [4–7]. IRS has been suggested for optical communications [8–10] and Millimeter Wave (mmWave) systems [11,12]. Experimental results of IRS have been presented in [13–15]. A practical implementation of IRS can be found in [16,17] were phase shifts can be continuous or quantized. Machine learning algorithms can be used to optimize the performance of IRS [18,19]. A real time cutting model using finite element was proposed in [20]. A fast and accurate tissue simulation model was discussed in [21]. Device to Device (D2D) communications for the fifth generation and beyond was studied in [22].

IRS can be used to reflect the transmitted signal to NOMA users. The source combines of symbols of K NOMA users. This signal is reflected by RIS toward K users. The weakest user detects its signal and considers the rest of signals as noise. The strongest user detects weakest user signal. Then, it removes it and continue the detection process of remaining users that are ranked from the weakest to the strongest one. IRS was implemented when the transmitter has a fixed transmit power in [1–19]. In all previous studies [1–19], IRS were implemented with fixed transmit power and previous results are not valid when the power of the secondary source is adaptive. In CRN, secondary nodes are allowed to transmit over the same band as primary users since they adapt their power to minimize the generated interference. In this paper, we derive the throughput of NOMA using IRS and adaptive transmit power.

In this article, we propose to:

–   Compute the throughput of CRN using NOMA and IRS where the secondary source has an adaptive power. Each secondary NOMA user has a given set of reflectors.

–   We derive the statistics of Signal to Noise Ratio (SNR) as well as Signal to Interference plus Noise Ratio (SINR). We study the effects of primary interference. CRN-NOMA using IRS offers 7, 13, 20 dB gain versus CRN-NOMA without IRS for N = 8, 16, 32 reflectors.

–   Two algorithms are discussed to rank the NOMA users.

Next section gives the throughput when there are two users. Section 3 generalizes the results to CRN-NOMA with K users. Section 4 discusses the obtained results. The paper is concluded in last section.

2  CRN-NOMA with Two Users

Fig. 1 depicts the network model with two secondary users, a Source (SS), a Primary Receiver and Transmitter and PR and PT. SS adapts its power to have a small interference at PR. We consider Rayleigh channels. Let λak be the channel from SS to k-th reflector of IRS. λ = 1/dSS, IRSple dX, Y is the distance from X to Y and ple is the path loss exponent. We can write ak = cke−j Φk where ck = |ak|.

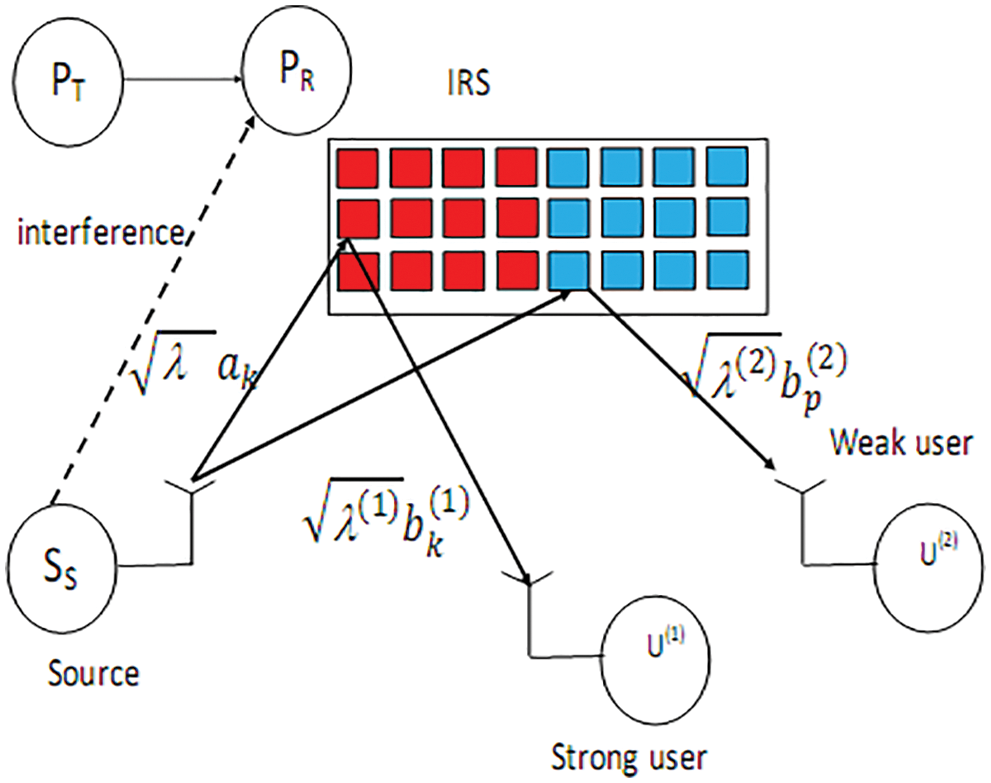
Figure 1: A network with two users

Let λ(i)bk(i) be the channel from k-th reflector to i-th user U(i). λ(i)= 1/dIRS,U(i)ple . We can write bk(i)=ek(i)e−jfk(i) where ek(i)=|bk(i)| . Let I(i) be the set of reflector’s of U(i). The phase of k-th reflector dedicated to U(i) in set I(i) given by

vk(i)=fk(i)+Φk, (1)

The transmitted symbol by SS is written as

s=po1s(1)+po2s(2), (2)

where s(i) is the symbol of U(i), poi is the power of U(i), po1 + po2 = 1 and 1 > po2 > po1 > 0.

The signal at U(i) given by

r(i)=sλλ(i)ESS∑k∈I(i)⁡akbk(i)ejvk(i)+n(i), (3)

n(i) is an additive Gaussian r.v. with variance N0 and ESS is SS symbol energy defined as

ESS=min(Emax,I|gSSPR|2) (4)

Emax is the maximum symbol energy, I is the interference threshold and gSSPR is channel coefficient between SS and PR. SS verifies interference constraints as

ESS|gSSPR|2≤I, (5)

Using (1), we obtain

r(i)=A(i)λλ(i)ESS[po1s(1)+po2s(2)]+n(i), (6)

where

A(i)=∑k∈I(i)⁡ckek(i), (7)

Weak user U(2) estimates s(2) with SINR

Γ(2)=po2B(2)po1B(2)+N0, (8)

where

B(i)=[A(i)]2λλ(i)ESS,. (9)

The probability of an outage event at U(2) is given by

Poutage(2)(x)=PB(2)(N0xpo2−po1x) (10)

where the Cumulative Distribution Function (CDF) of B(i) , PB(i)(x) , is provided in Appendix A. U(1) detects s(2) as po2>po1 with SINR

Γ(1)→(2)=po2B(1)po1B(1)+N0, (11)

Then U(1) removes s(2) and demodulates s(1) with SNR

Γ(1)→(1)=po1B(1)N0, (12)

The probability of an outage event at U(1) is computed as

Poutage(1)(x)=P(min[Γ(1)→(1),Γ(1)→(2)]≤x)=PB(1)(max[N0xpo1,N0xpo2−po1x]) (13)

The Packet Error Probability (PEP) of U(i) is given by

PEP(i)(po1,po2)≤Poutage(i)(W0), (14)

where

W0=∫0+∞⁡1−[1−SEP(w)]Ldw, (15)

L is packet length and

SEP(w)=2(1−1M)erfc(3wM−1), (16)

The throughput of U(i) is given by

Thr(i)(po1,po2)=log2(M)[1−PEP(i)(po1,po2)], (17)

The total throughput (TThr) is given by

TThr(po1,po2)=Thr(1)(po1,po2)+Thr(2)(po1,po2) (18)

We maximize the total throughput as follows

TThrmaximized=max0<po1<po2<1TThr(po1,po2) (19)

3  CRN-NOMA with K Users

3.1 Ranking Using Average Gains

The network model is depicted in Fig. 2. It contains PT, PR, SS and K secondary NOMA users. U(i) has the i-th maximum average channel gain between SS and NOMA users. Let P be defined as

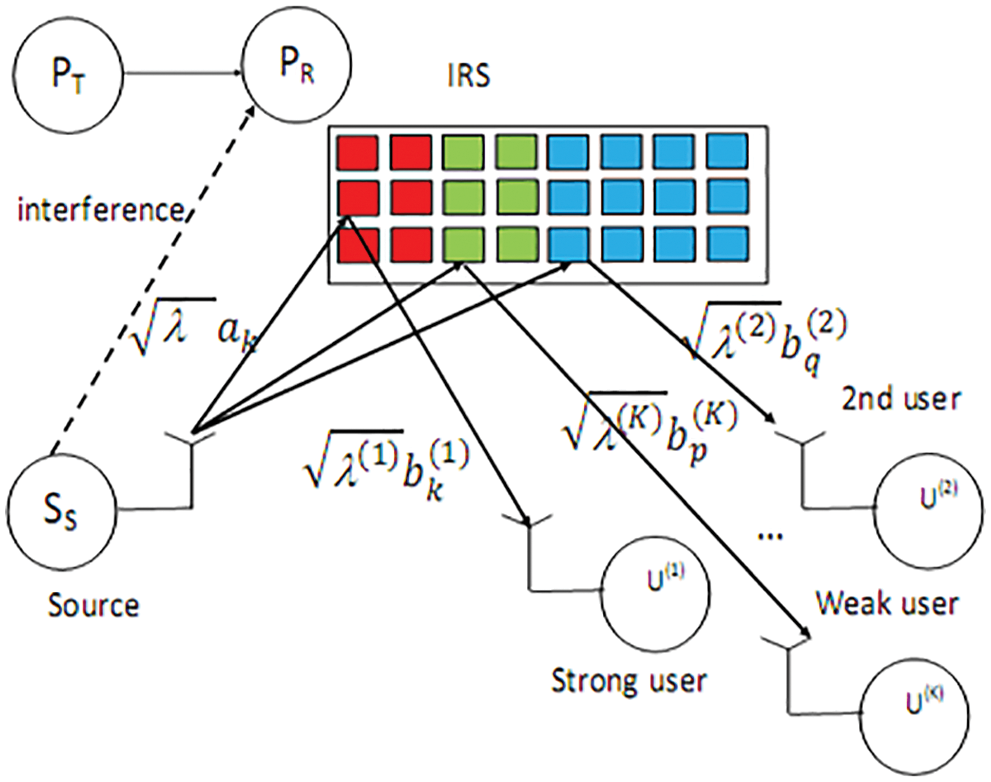
Figure 2: A network with K users

P=∑j=1K⁡N(j), (20)

N(j) is the number of IRS reflectors of U(j).

NOMA symbol is written as

s=∑i=1K⁡pois(i), (21)

where po1 + po2 = 1 and 1>po2>po1 > 0.

∑i=1K⁡poi=1 (22)

The received signal at U(i) is written as

r(i)=A(i)λλ(i)ESS[∑i=1K⁡pois(i)]+n(i), (23)

U(i) detects sK as poK > poi with SINR

Γ(i)→(K)=poKB(i)B(i)∑l=1K−1⁡pol+N0, (24)

Then U(i) performs Successive Interference Cancelation (SIC), removes sK to detect sK−1 with SINR

Γ(i)→(K−1)=poK−1B(i)B(i)∑l=1K−2⁡pol+N0, (25)

U(i) detects sp with SINR

Γ(i)→(p)=popB(i)B(i)∑l=1p−1⁡pol+N0, (26)

The probability of an outage event at U(i) is computed as

Poutage(i)(x)=P(Γ(i)→(K)≤x,…,Γ(i)→(i)≤x)=PB(i)(max1≤p≤K[N0xpop−x∑l=1p−1⁡pol]), (27)

The PEP at U(i) is equal to

PEP(i)(po1,…,poK)≤Poutage(i)(W0), (28)

where W0 is defined in (15)

The throughput of U(i) is given by

Thr(i)(po1,…,poK)=log2(M)[1−PEP(i)(po1,…,poK)], (29)

The total throughput (TThr) is given by

TThr(po1,…,poK)=∑i=1K⁡Thr(i)(po1,…,poK), (30)

We maximize the total throughput as follows

TThrmaximized=max0<po1<…<poK<1TThr(po1,…,poK). (31)

3.2 Ranking Using Instantaneous Gains

Let Ui(1) be the strongest user with largest instantaneous channel gain B(i):

Bi(1)=max1≤p≤KB(p), (32)

Let Ui(K) be the weakest user :

Bi(K)=min1≤p≤KB(p), (33)

Let Ui(q) be q-th ranked user:

Bi(q)=q−th−max1≤p≤KB(p), (34)

The CDF of Bi(q) is given by

PBi(q)(x)=∑j=1q⁡∑m1,m2,…,mj−1⁡∏l=1j−1⁡[1−PB(ml)(x)]∑mj,…,mN⁡∏p=jK⁡PB(mp)(x) (35)

where 1 ≤ mi ≤ N for i = 1,…,N. m1¹m_2 ¹… mN, mq < mq + 1<…< mK and PB^(i)(x) is given in Appendix A.

The PEP and throughput can be computed as Section 3.1 where we have to replace PB(q)(x) by PBi(q)(x) given in (35).

4  Effects of Primary Interference

The SINR is computed as

Γ(i)→(p)=popB(i)B(i)∑l=1p−1⁡pol+N0+IPT,i, (36)

The probability of an outage at U(i) is computed as

Poutage(i)(x)=∫0+∞⁡PB(i)(max1≤p≤K[(N0+y)xpop−x∑l=1p−1⁡pol])pIPT,i(y)dy, (37)

where

pIPT,i(y)=e−yIPT,i¯IPT,i¯ (38)

IPT,i¯ is the average interference. The PEP and throughput are computed using (37).

5  Numerical Results

Fig. 3 shows the total throughput for CRN-NOMA for K = 2, for I = 1 16 Quadrature Amplitude Modulation (QAM), dIRSU(i) = 1,1.5 i = 1,2 Packet length is L = 200.. IRS allows 6, 12, 18 dB vs. CRN-NOMA without IRS for N = 8, 16, 32.

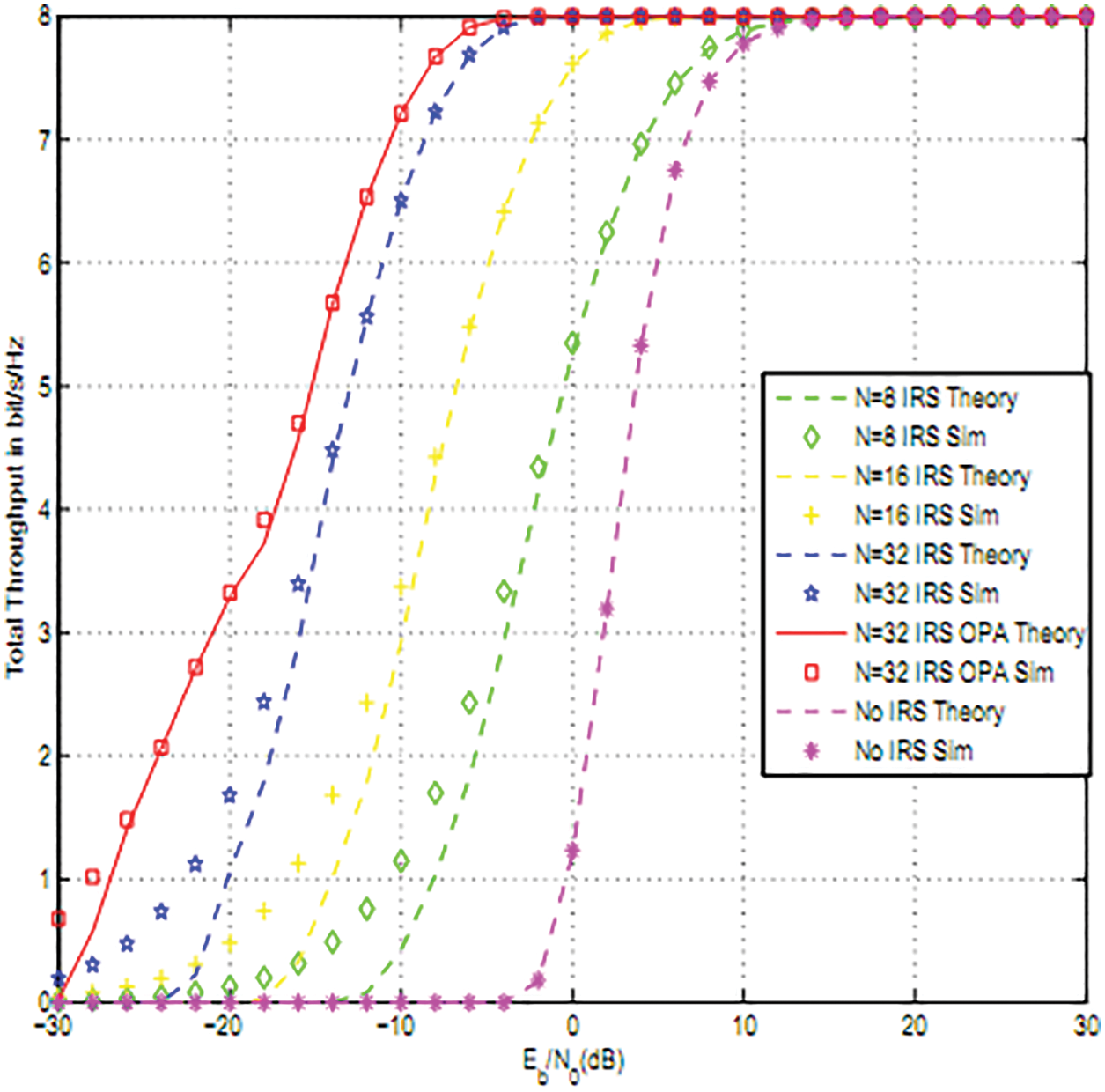
Figure 3: Total throughput for 2 users for 16QAM

Fig. 4 shows the throughput for different values of I, 16QAM modulation and N = 8 reflectors. As I increases as the throughput improves since SS can increase its power while verifying interference constraints.

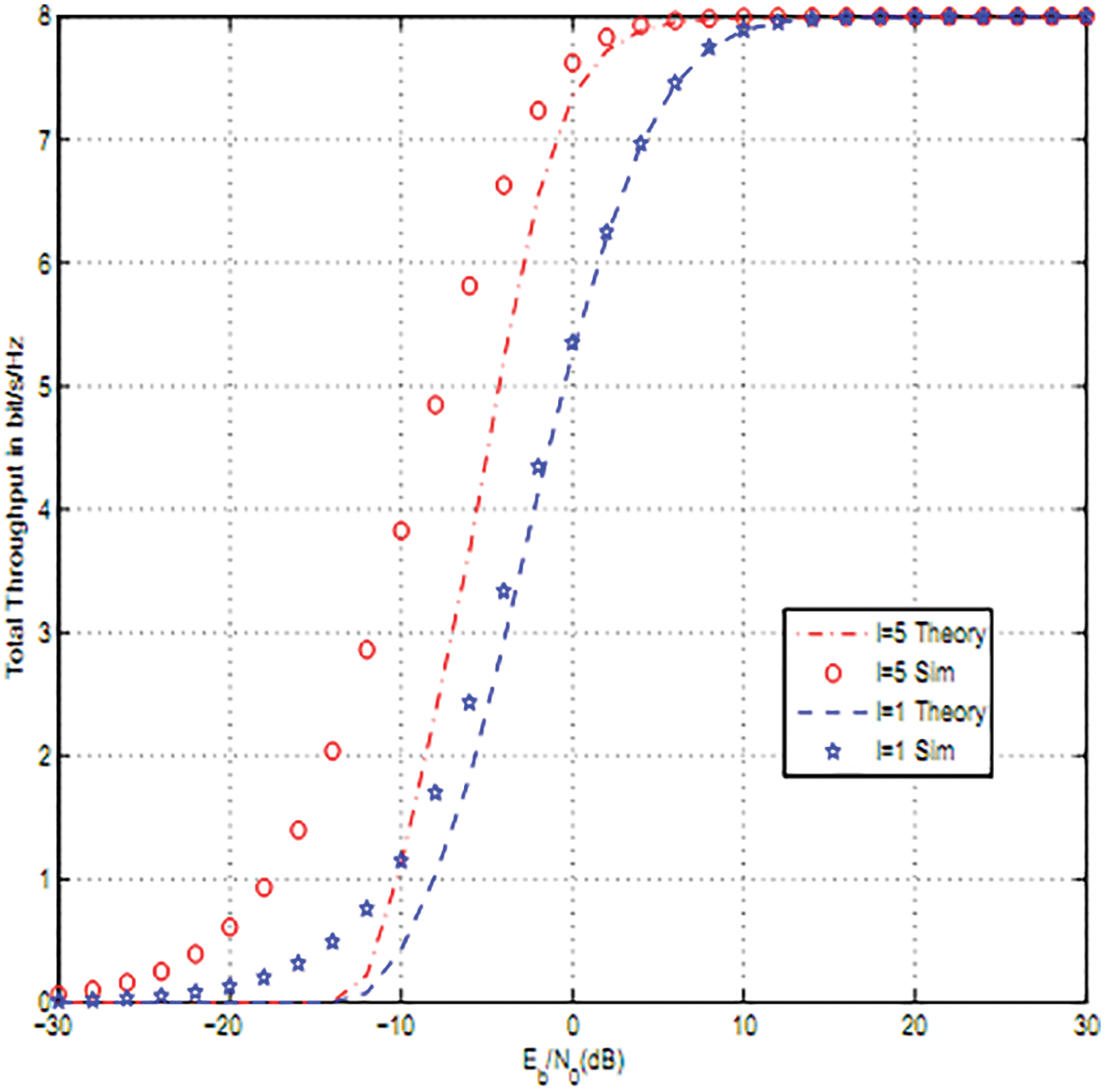
Figure 4: Effect of interference threshold I: 2 users, 16QAM and N = 8 reflectors

Fig. 5 shows that NOMA with IRS for N = 64 offers better performance than Orthogonal Multiple Access (OMA) and NOMA without IRS for 16QAM and two users. At high average SNR, the throughput of OMA is half that of NOMA.

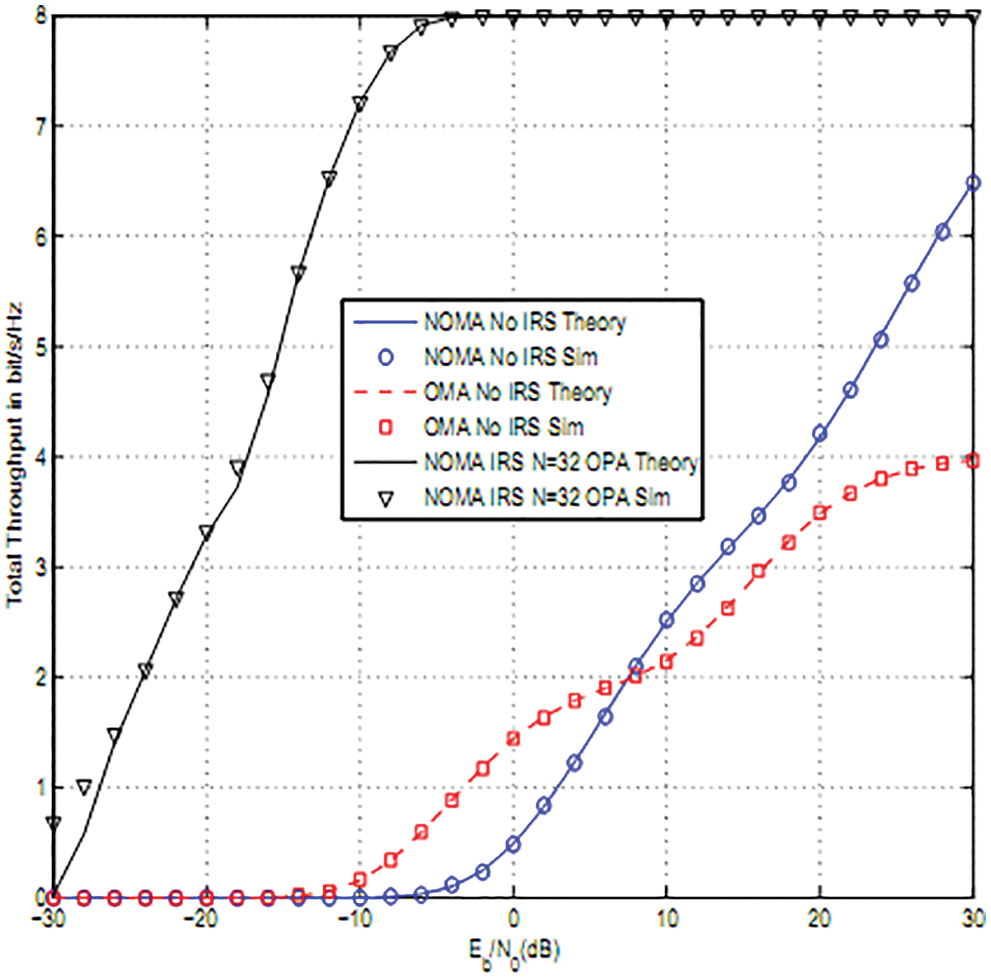
Figure 5: OMA and NOMA performance comparison

Fig. 6 depicts the effects of primary interference when there are two users, N = 8, 16 reflectors per user for 16QAM Modulation. The parameters are dPTU(i) = 1,0.9, 0.5,0.6. We notice that the performance degrades as PT is close to NOMA users since there is more interference.

Figure 6: Effects of primary interference on Total throughput of NOMA: 2 users, 16QAM modulation and N = 16

Fig. 7 depicts the total throughput for 16-QAM modulations for two users and N = 8, 16 reflectors. Ranking using instantaneous channel gains offers the best throughput.

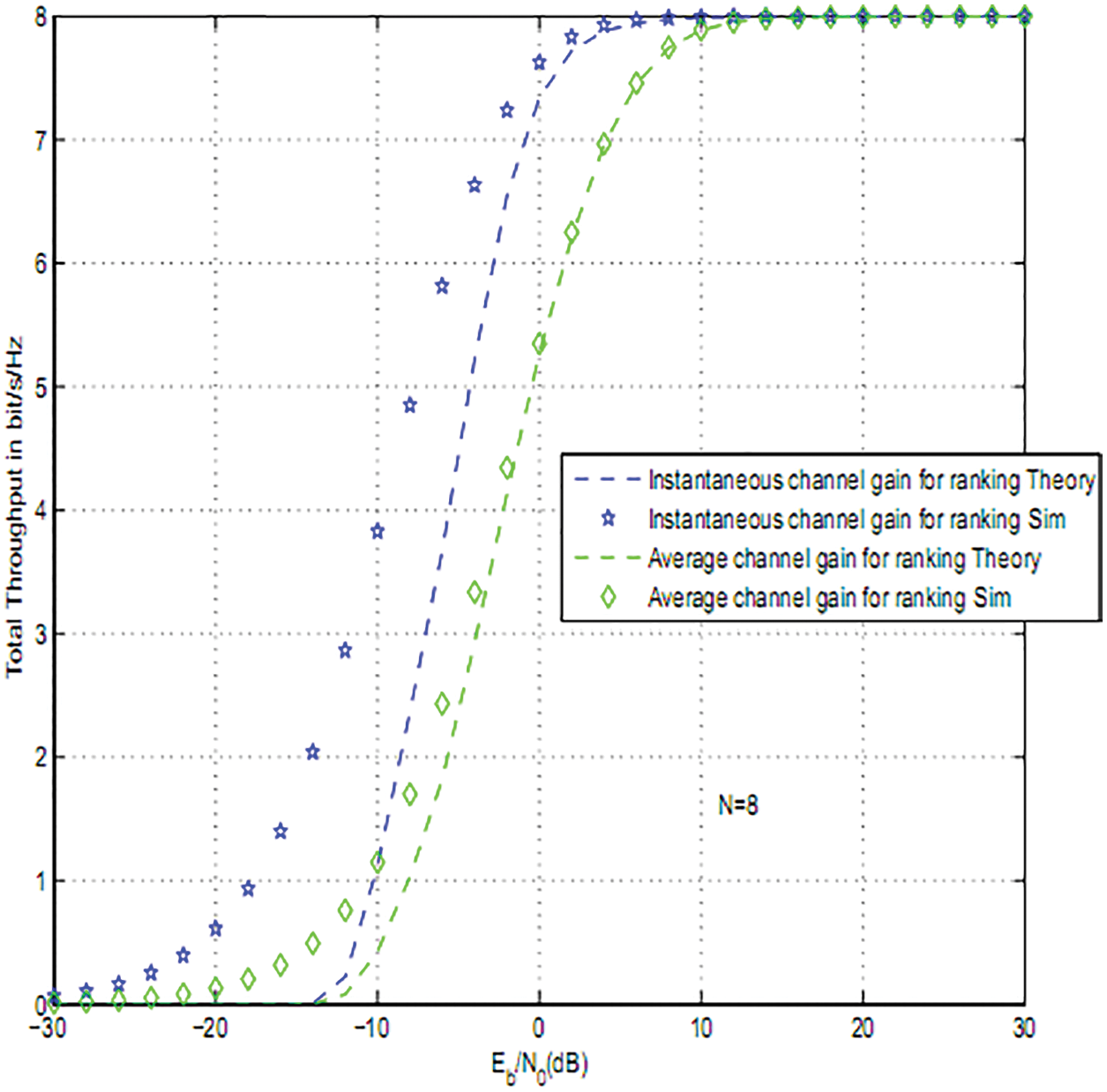
Figure 7: Secondary throughput for 16QAM modulation and different ranking strategies: N = 8

6  Conclusions

In this article, we computed the PEP and throughput of NOMA with adaptive transmit power and IRS. IRS are deployed to enhance data reception at all users. CRN-NOMA using IRS offers 7, 13, 20 dB gain vs. the absence of IRS for N = 8, 16, 32. We have also derived the SNR and SINR statistics.

Funding Statement: The authors extend their appreciation to the Deanship of Scientific Research at Saudi Electronic University for funding this research work through the Project Number 8093.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Ying, Z. Gao, S. Lyu, Y. Wu, H. Wang et al., “GMD-Based hybrid beamforming for large reconfigurable intelligent surface assisted millimeter-wave massive MIMO,” IEEE Access, vol. 8, no. 2, pp. 19530–19539, 2020. [Google Scholar]

 2.  L. Yang, W. Guo and I. Ansari, “Mixed dual-hop FSO-RF communication systems through reconfigurable intelligent surface,” IEEE Communications Letters, vol. 24, no. 7, pp. 1558–1562, 2020. [Google Scholar]

 3.  B. Di, H. Zhang, L. Li, L. Song, Y. Li et al., “Practical hybrid beamforming with finite-resolution phase shifters for reconfigurable intelligent surface based multi-user communications,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4565–4570, 2020. [Google Scholar]

 4.  Q. Nadeem, A. Kammoun, A. Chaaban, M. Debbah and M. Alouini, “Asymptotic max-min SINR analysis of reconfigurable intelligent surface assisted MISO systems,” IEEE Transactions on Wireless Communications, vol. 19, no. 12, pp. 7748–7764, 2020. [Google Scholar]

 5.  W. Zhao, G. Wang, S. Atapattu, T. Tsiftsis and C. Tellambura, “Is backscatter link stronger than direct link in reconfigurable intelligent surface-assisted system?,” IEEE Communications Letters, vol. 24, no. 6, pp. 1342–1346, 2020. [Google Scholar]

 6.  S. Li, B. Duo, X. Yuan, Y. Liang and M. Renzo, “Reconfigurable intelligent surface assisted UAV communication: Joint trajectory design and passive beamforming,” IEEE Wireless Communications Letters, vol. 9, no. 5, pp. 716–720, 2020. [Google Scholar]

 7.  L. Dai, B. Wang, M. Wang, X. Yang, J. Tan et al., “Reconfigurable intelligent surface-based wireless communications: Antenna design, prototyping and experimental results,” IEEE Access, vol. 8, no. 3, pp. 45913–45923, 2020. [Google Scholar]

 8.  S. Hua and Y. Shi, “Reconfigurable intelligent surface for green edge inference in machine learning,” in 2019 IEEE Globecom Workshops (GC Wkshps), vol. 2, no. 3, pp. 10–15, 2019. [Google Scholar]

 9.  C. Huang, G. Alexandropoulos, C. Yuen and M. Debbah, “Indoor signal focusing with deep learning designed reconfigurable intelligent surfaces,” in IEEE 20th Int. Workshop on Signal Processing Advances in Wireless Communications (SPAWC), vol. 3, no. 4, pp. 11–14, 2019. [Google Scholar]

10. E. Basar, M. Renzo, J. Rosny, M. Debbah, M. S. Alouini et al., “Wireless communications through reconfigurable intelligent surfaces,” IEEE Access, vol. 7, no. 2, pp. 116753–116773, 2019. [Google Scholar]

11. H. Zhang, B. Di, L. Song and Z. Han, “Reconfigurable intelligent surfaces assisted communications with limited phase shifts: How many phase shifts are enough?,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4498–4502, 2020. [Google Scholar]

12. M. Renzo, “6G wireless: Wireless networks empowered by reconfigurable intelligent surfaces,” in 25th Asia-Pacific Conf. on Communications (APCC), vol. 1, no. 1, pp. 12–13, 2019. [Google Scholar]

13. E. Basar, “Reconfigurable intelligent surface-based index modulation: A new beyond MIMO paradigm for 6G,” IEEE Transactions on Communications, vol. 68, no. 5, pp. 3187–3196, 2020. [Google Scholar]

14. Q. Wu and R. Zhang, “Towards smart and reconfigurable environment: Intelligent reflecting surface aided wireless network,” IEEE Communications Magazine, vol. 58, no. 1, pp. 106–112, 2020. [Google Scholar]

15. C. Huang, A. Zappone, G. Alexandropoulos, M. Debbah and C. Yuen, “Reconfigurable intelligent surfaces for energy efficiency in wireless communication,” IEEE Transactions on Wireless Communications, vol. 18, no. 8, pp. 4157–4170, 2019. [Google Scholar]

16. G. C. Alexandropoulos and E. Vlachos, “A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation,” in ICASSP 2020–2020 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Spain, Barcelona, vol. 1, no. 1, pp. 9175–9179, May 4–8, 2020. [Google Scholar]

17. H. Guo, Y. Liang, J. Chen and E. Larsson, “Weighted sum-rate maximization for reconfigurable intelligent surface aided wireless networks,” IEEE Transactions on Wireless Communications, vol. 19, no. 5, pp. 3064–3076, 2020. [Google Scholar]

18. V. Thirumavalavan and T. Jayaraman, “BER analysis of reconfigurable intelligent surface assisted downlink power domain NOMA system,” in 2020 Int. Conf. on COMmunication Systems and NETworkS (COMSNETS), Bangalore, India, vol. 1, no. 2, pp. 519–522, January 7–11, 2020. [Google Scholar]

19. C. Pradhan, A. Li, L. Song, B. Vucetic and Y. Li, “Hybrid precoding design for reconfigurable intelligent surface aided mmwave communication systems,” IEEE Wireless Communications Letters, vol. 9, no. 7, pp. 1041–1045, 2020. [Google Scholar]

20. X. R. Zhang, W. Z. Zhang, W. Sun, H. L. Wu, A. G. Song et al., “A Real-time cutting model based on finit element and order reduction,” Computer System Science and Engineering, vol. 43, no. 1, pp. 1–15, 2022. [Google Scholar]

21. X. R. Zhang, H. L. Wu, A. G. Song and S. K. Jha, “A fast and accurate tissue simulation model based on point primitive method,” Intelligent Automation and Soft Computing, vol. 27, no. 3, pp. 873–889, 2021. [Google Scholar]

22. M. S. M. Gismalla, A. I. Azmi, M. R. Bin Salim, M. Faiz, F. Iqbal et al. “Survey on device to device (D2D) communication for 5GB/6G networks: Concept, applications, challenges, and future directions,” IEEE Access, vol. 10, no. 1, pp. 30792–30821, 2022. [Google Scholar]

Appendix A: CDF of B(i)

The variance and mean of A(i) are σA2=N(1−π216) and mA = Nπ/4 . B(i) is equal to

B(i)=[A(i)]2λλ(i)ESS (39)

We deduce

PB(i)(x)=P(B(i)≤x|I|gSSPR|2<Emax)P(I|gSSPR|2<Emax)

+P(B(i)≤x|T|gSSPR|2>Emax)P(I|gSSPR|2>Emax), (40)

where

P(I|gSSPR|2<Emax)=e−IλSSPREmax, (41)

where λSSPR = E(|gSSPR|2), E(.) is the expectation operation and gSSPR is the channel coefficient between SS and PR. When I/|gSSPR|2>Emax, we have

B(i)=Emax[A(i)]2λλ(i) (42)

and

P(B(i)≤x|I|gSSPR|2>Emax)=1−Q0.5(mAσA,xEmaxλλ(i)σA2), (43)

where Qm(.,.) is the Generalized Marcum Q-function.

When I/|gSSPR|2<Emax , ESS=I|gSSPR|2 and we have

P(B(i)≤x|I|gSSPR|2<Emax)=∫IEmax+∞⁡1−Q0.5(mAσA,xyEmaxIλλ(i)σA2)e−ySSPR1λSSPRdy (44)

PB(i)(x) is computed using (40),(41) and (43),(44).