Optimal Operation of Distributed Generations Considering Demand Response in a Microgrid Using GWO Algorithm

1  Introduction

Along with developing thermal and electrical energy resources as distributed generation resources in microgrids, several methods with different purposes have been proposed to integrate these resources. Using energy management leads to consumption reduction over periods, and consequently, in addition to the appropriate load curve, it reduces the operation and planning cost [1,2]. The purpose of the Energy Management System (EMS) is to realize the best use of units to produce electric and heat power in the microgrid, the best program for the scheduling storage system and proper demand management and proper purchase and sale from the electric grid. There are several methods to establish the most suitable demand management program.

It has been shown in [3] that using energy management and reducing energy consumption in different time intervals, in addition to modifying the load curve, has caused a reduction in the cost of operation and planning. The primary purpose of the above reference is to realize the best use of distributed generation resources to generate power and heat in the microgrid. Intelligent algorithms were used in [4], to determine the best storage system schedule, proper demand management and accurate purchase and sale from the power grid. The results indicated that the use of algorithms and energy management of resources had a significant effect on cost reduction. To execute energy management in demand response programs have been used [5]. Demand response programs in the short-term lead to a decrease in peak demand, and are provided for a short period. In [6], demand response programs are based on encouragement and time-based programs, and the effect of each method in reducing the cost of operation is evaluated. In [7], price-based decentralized control is used for EMS. In decentralized control, each microgrid is controlled by a controller. Decentralized control is a possible solution for many controls and energy management problems in microgrids. It has been proved in [8] that, since the price of electricity varies depending on various times and places, receiving the electricity price at a fixed rate from the customers puts the electricity companies at risk, since they face a variable electricity price in the wholesale market. The authors in [9] believe that applying the actual price of electricity to consumers will increase efficiency. Therefore, the initial idea of this dynamic pricing was to apply the actual price of electricity to the consumers. On the hand, applying the time-varying tariffs, whether in the restructured power system or the traditional systems, improves the load consumption curve and reduces the load during periods of high demand. In [10], time-of-use response programs were used for microgrid energy management. This method encourages the customers to improve their electricity consumption patterns (consumption in periods of low demand, and reducing consumption in periods of high demand) through the change in electricity prices at different times of the day. Most customers do not have enough time and equipment to respond to these instantaneous changes. Therefore, it seems more logical to use several time intervals a day to apply different electricity tariffs to this group of consumers. The electricity tariff is determined in [11], as different prices for different time intervals of a day. The tariff is usually considered as the average cost of power generation and transmission in each time interval.

In this paper, the optimum operation of distributed generation resources in a microgrid has been performed through GWO to reduce operating costs. The algorithm should choose the most suitable capacity for energy generation by the resources according to the amount of electrical and thermal energy requested by subscribers at every hour and the energy price for that hour, so that the cost is minimized in the system.

2  The Studied System

The studied microgrid consisted of distributed thermal and electrical generation resources as well as storage which was connected to the national electricity network and could exchange electrical energy with it. A scheme of the studied grid is shown in Fig. 1.

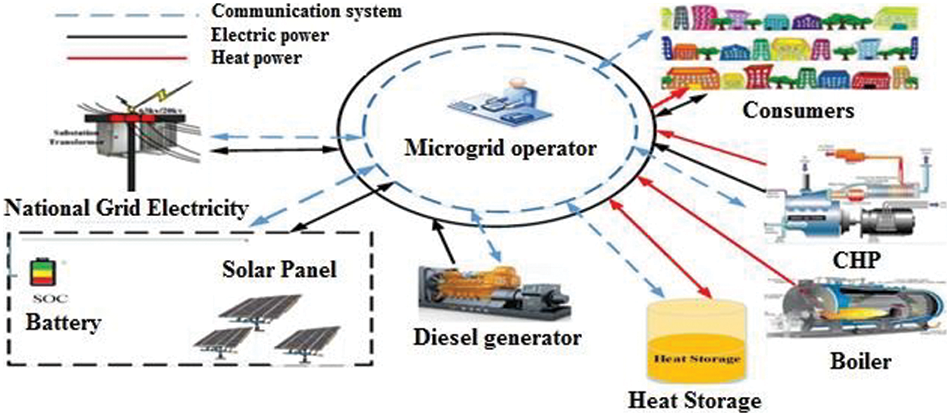
Figure 1: The studied microgrid

In the studied microgrid, distributed electrical generation resources such as solar panels and diesel generators with battery storage and boiler thermal resources with thermal storage were used. Also, in this microgrid, the CHP unit is used for the combined generation of thermal and electric energy. Electric energy transmission trajectories are plotted with black lines, and thermal transfer trajectories are plotted with red ones. In addition, the information transfer between the resources and the control center is plotted with a blue dashed line. The amount of solar radiation is shown in Fig. 2.

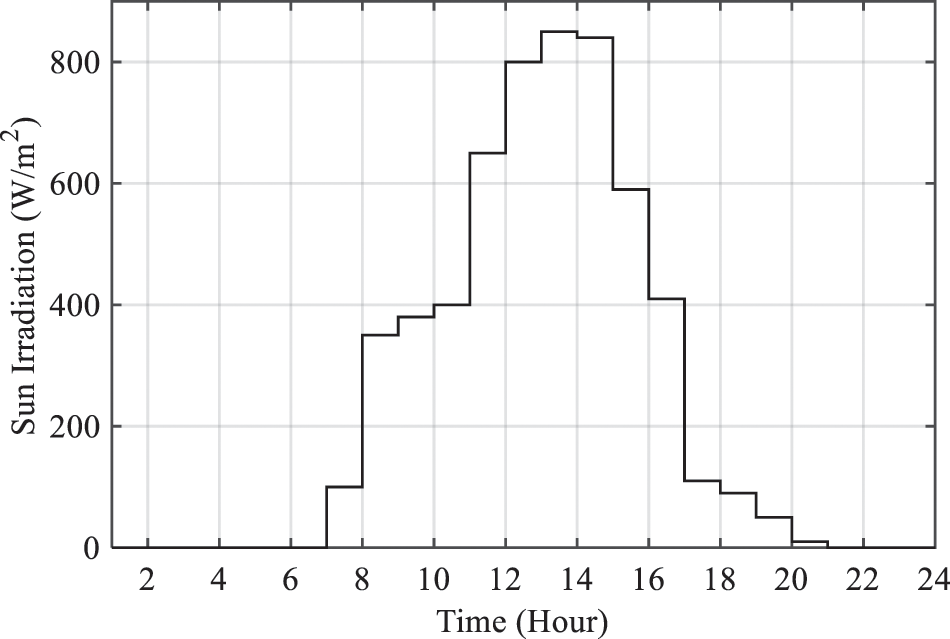
Figure 2: Intensity of solar radiation [12]

The amount of electrical and thermal energy demanded by subscribers in the 24-hour study is shown in Fig. 3.

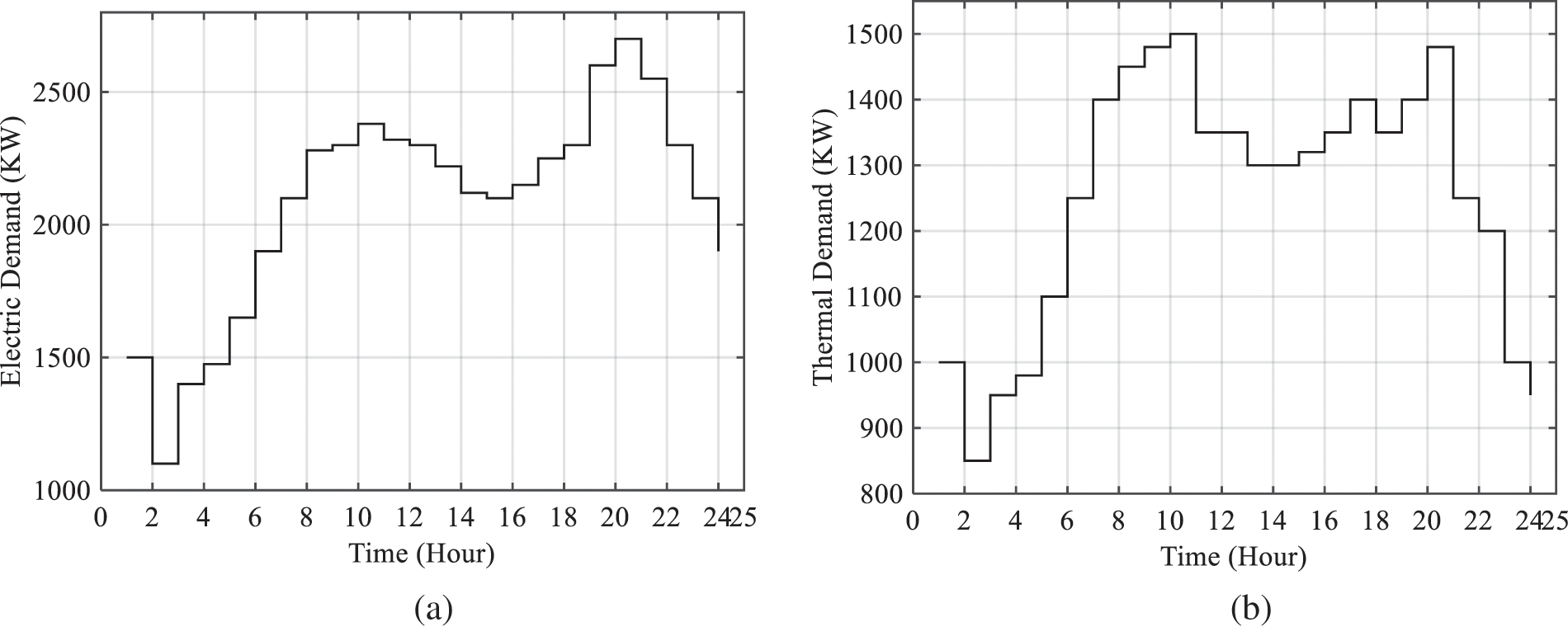
Figure 3: Amount of demanded electrical (a) and thermal energy (b) [12]

The energy price in the market in the 24-h study is shown in Fig. 4. The maximum and minimum energy price in this microgrid are about 13 cents/kWh and 6 cents/kWh, respectively. In periods of high demand, the energy price is increased in periods of low demand, the energy price has a minimum price, so subscribers are encouraged to reduce consumption in periods of high demand and postpone their consumption to periods of low demand.

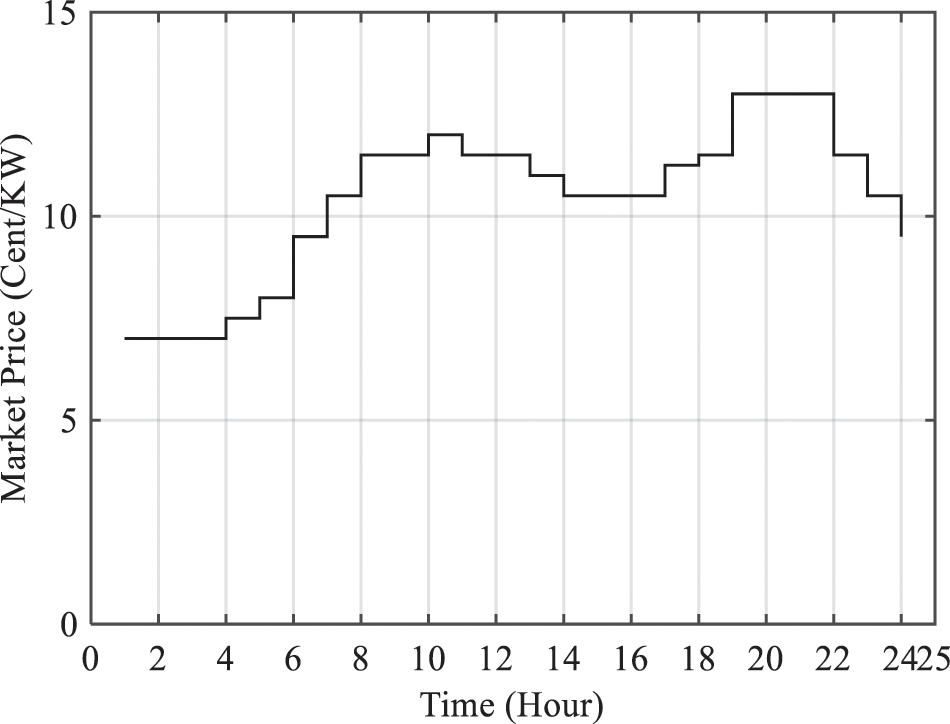
Figure 4: Electricity price in the market [12]

3  Objective Function and Restrictions

The proposed function to have an optimum operation is expressed in Eq. (1). The objective function indicates the operating costs that should be minimized during the planning process. Based on this equation, the operating costs are equal to the total cost of generation (including total variable cost and startup cost) and the cost of implementing demand response programs [13].

Objective Function=∑t=124(∑i=1G(CLDGi,t+SCLDGi,t)+PLi,t×ρLt+∑j=1nCCHPj,t+CSPLt)(1)

where t is the time operator, CLDGi,t and SCLDGi,t are the cost of electric energy generation and the cost of turning off/on the distributed generation, respectively and PLi,t is the amount of contributed electric power of demands in the demand response program, and ρLt is the reward paid due to consumption reduction. CCHPj,t, and CSPLt are the cost of electric energy generation of combined heat and power (CHP) and the cost of energy generation of solar parking lots (SPL), respectively. The restrictions of the problem are:

Power balance restriction: the total power of generation units must meet the demand.

In a grid-connected state, the amount of purchased and sold power is added to the generation units to supply the demand [13].

PeDemand(t)+PeCharge(t)=PeNet(t)+∑i=1N  DGPeDG(i,t)+Pedcharge(t),(2)

PthDemand(t)+Pthcharge(t)=∑i=1N  DGPthDG(i,t)+Pthdcharge(t)(3)

Minimum and maximum generation restriction: The generation unit in the microgrid has its operating limitations.

PeMin(i)≤PeDG(i,t)≤PeMax(i),(4)

PthMin(j)≤PthDG(j,t)≤PthMax(j)(5)

4  GWO Algorithm

Gray wolves are usually social animals, living and hunting in packs of 5–12. The pack leaders, also known as alpha, are an alpha male and an alpha female. Alpha is mainly responsible for deciding about how to hunt, where to sleep, when to wake up, etc. Decisions of alpha are ordered to the pack. The second in command in the gray wolf pack hierarchy is beta. Beta is an obedient wolf who helps the alpha in decision-making or other pack tasks. The beta wolf must respect the alpha, but it gives orders to the lower-ranking wolves. The lowest ranking is related to the gray wolf or omega. The main hunting phase of the gray wolf is divided into three parts: searching, running, and approaching the prey, chasing, encircling, exhausting the prey until it stops moving, and finally attacking the prey.

To mathematically model the encircling behavior, the following equations are proposed [14]:

D→=|C→.X→p(t)−X→(t)|(6)

X→(t+1)=X→p(t)−A→.D→(7)

where t is the current iteration, A→ and C→ are the coefficient vectors, X→p is the position vector of the prey, and X→ is the position vector of the gray wolf. The vectors A→ and C→ are calculated as follows:

A→=2a→. r→1−a→(8)

C→=2. r→2(9)

where components α→ of {\displaystyle {\vec {a}}} are linearly decreased from 2 to 0 throughout, for iterations and r→1 {\displaystyle r_{1}}, r→2 {\displaystyle r_{2}} are random vectors in [0, 1]. The hunt is guided by the alpha. The beta and delta might also participate in hunting occasionally. Therefore, we save the first three best solutions obtained so far and oblige the other search agents (including the omegas) to update their positions according to the position of the best search agent. The following formulas are proposed in this regard [14–18]:

D→α=|C→1.X→α−X→| ,    D→β=|C→2.X→β−X→|(10)

D→δ=|C→3.X→δ−X→|

X→1=X→α−A→1.(D→α)  ,  X→2=X→β−A→2.(D→β)(11)

X→(t+1)=X→1+X→2+X→33(12)

To mathematically model approaching the prey, we decrease the value of {\displaystyle {\vec {a}}} a→. The fluctuation range of {\displaystyle {\vec {A}}} A→ is also decreased by{\displaystyle {\vec {a}}} a→. In other words, A→ {\displaystyle {\vec {A}}} is a random value in the interval [−a,a] where a is decreased from 2 to 0 throughout, for iterations. When random values of {\displaystyle {\vec {A}}} A→ are in [–1, 1], the next position of a search agent can be in any position between its current position and the position of the prey. Gray wolves mostly search according to the position of the alpha, beta, and delta. They diverge from each other to search for prey and converge to attack prey. {\displaystyle {\vec {A}}} Another component of GWO that favors exploration is {\displaystyle {\vec {C}}} C→ which contains random values in [0, 2]. This component provides random weights for prey to stochastically emphasize (C→ > 1) or de-emphasize (C→ < 1) the effect of prey in defining the distance in Eq. (10). This assists GWO to show more random behavior throughout optimization, favoring exploration and local optima avoidance. It is worth mentioning here that C→ is not linearly decreased in contrast to A→. For iterations, alpha, beta, and delta wolves estimate the probable position of the prey. Each candidate solution updates its distance from the prey. The parameter a is decreased from 2 to 0 to emphasize exploration and exploitation, respectively. Candidate solutions tend to diverge from the prey when {\displaystyle |{\vec {A}}| > 1}A→>1 and converge towards the prey when {\displaystyle |{\vec {A}}| < 1}A→<1. Finally, the GWO algorithm is terminated by satisfying an end criterion[19–42].

5  Simulation Results and Analysis

A suitable program for the optimal operation of distributed generation resources and electrical and thermal storage in the microgrid, based on real-time pricing, has been presented. Energy management of resources and electrical and thermal storage was performed using a cost-reduction approach. The GWO algorithm was used for energy management in the microgrid. The algorithm found the optimal variables in such a way that the cost was minimized in the microgrid. The parameters of the proposed GWO are given in Table 1.

Simulations have been performed in two scenarios. In the first one, the energy management was just performed on resources and electrical storage. In contrast, the second scenario, energy management of resources and the combined electrical and thermal storages was simultaneously performed in the microgrid. To verify the results obtained from the simulation, a comparison has been made between the GWO results, and the results obtained from Particle Swarm Optimization (PSO) algorithm, Genetic Algorithm (GA), harmony search (HS), and Artificial Bee Colony (ABC).

5.1 First Scenario

In the first part of the simulations, the energy management of the resources and electrical storage in the microgrid was done by considering the demand response program to reduce the operating cost through the proposed GWO algorithm. Therefore, it was assumed that there was no control over the thermal resources, the required thermal energy of the subscribers was supplied by the boiler without any restrictions, and CHP only produced electrical energy. Also, there was no thermal energy storage in the system. The convergence process of the GWO algorithm in the optimization process is shown in Fig. 5.

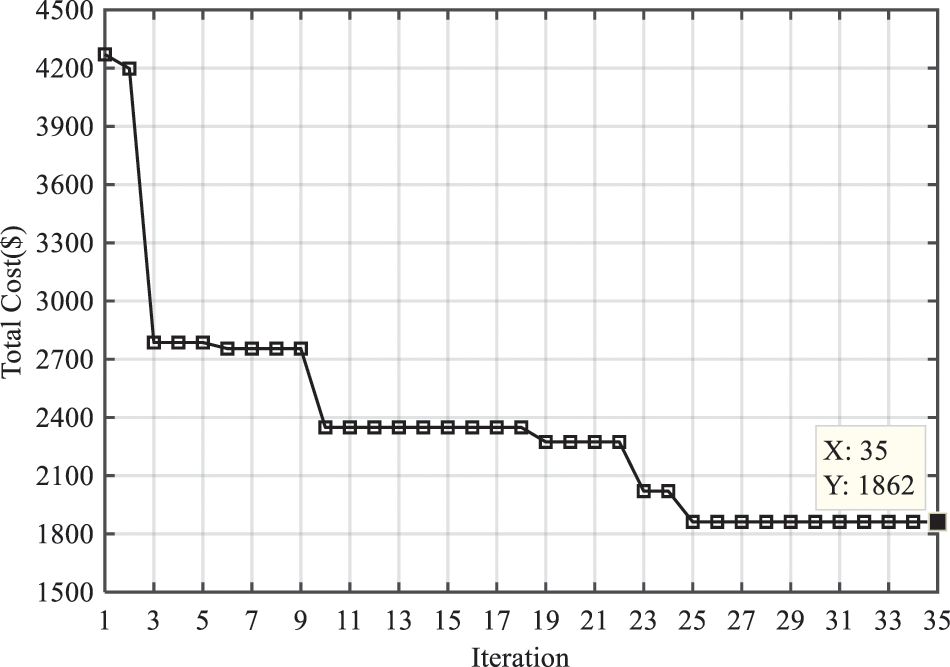
Figure 5: Convergence of GWO algorithm in electrical resources management

The energy supply cost without considering the demand response program was $2673, while after optimization through the proposed GWO algorithm, the amount of $1862 was obtained. The GWO algorithm converged to its final value after 25 iterations. In Table 2, the values of the best, the worst, and the average response, as well as the standard deviation for 20 iterations of running the PSO, GA, HS, (ABC) as well as the proposed GWO, are given.

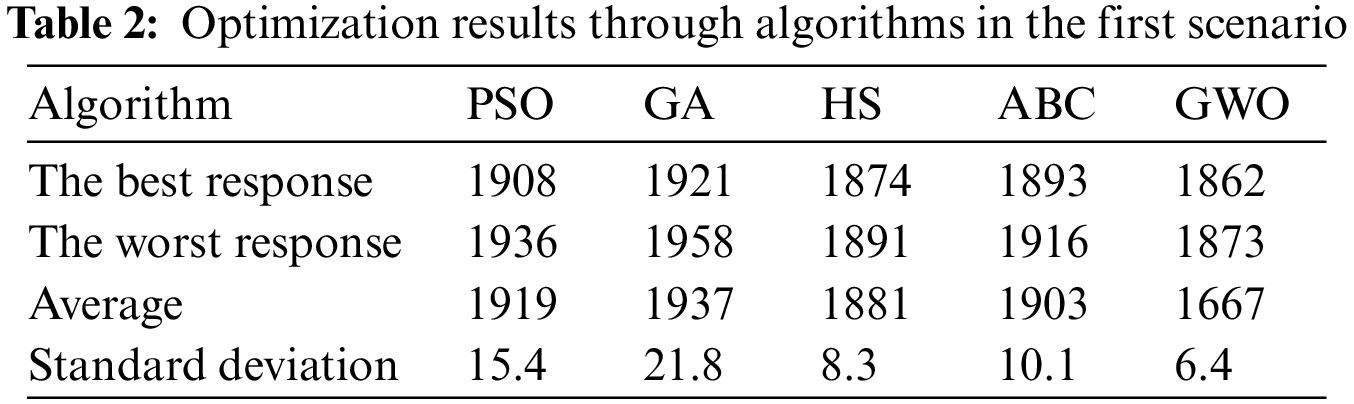
The best responses for the PSO, GA, HS, ABC, and GWO algorithms were obtained as $1908, $1921, $1874, $1893, and $1862, respectively. On the other hand, the low value of standard deviation for the proposed GWO algorithm indicated its higher efficiency, and because if the optimization algorithm has immediate responses to each other in different iterations, then the standard deviation would be at its minimum value. The power generated by the diesel generator, CHP, solar panel, and battery storage in the 24-hour study is shown in Fig. 6 after optimization.

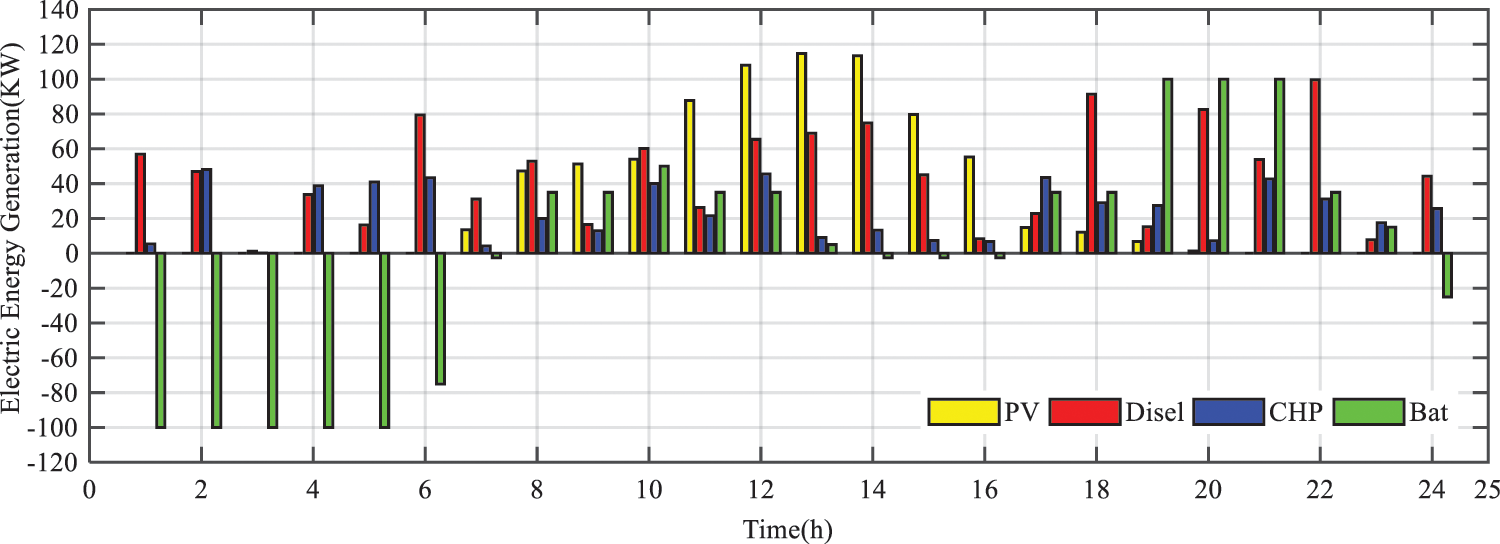
Figure 6: The transmitted electrical energy with the power grid

According to Fig. 6, most of the battery storage has been performed from 1:00 a.m. through 6:00 a.m., and most battery discharges occurred from 7:00 p.m. to 9:00 p.m. Batteries play a vital role in supply shifting and reducing costs in demand response programs. The amount of electrical energy transmitted to the nationwide electric network at the time of study is shown in Fig. 7. As illustrated in Fig. 7, the presence of the distributed generation of electrical resources has caused the received electrical energy from the grid to be negative in periods of high demand meaning that the electricity is being sold to the network. Selling electrical energy in periods of high demand, has made a sufficient profit for the microgrid operator, through which the energy supply costs in the microgrid become minimum. For instance, at 10:00 a.m., a profit of about $48.3 was made due to selling electrical energy.

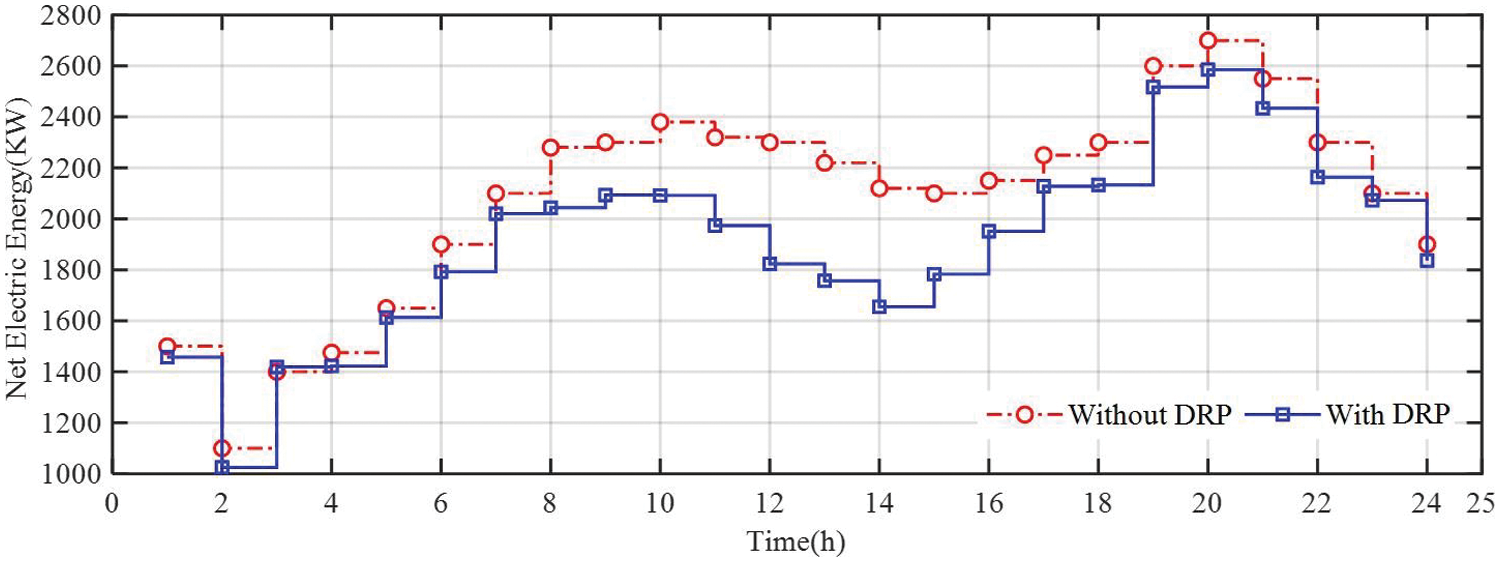
Figure 7: Electrical energy transmitted to the nationwide electric network

The thermal energy produced by the boiler is shown in Fig. 8.

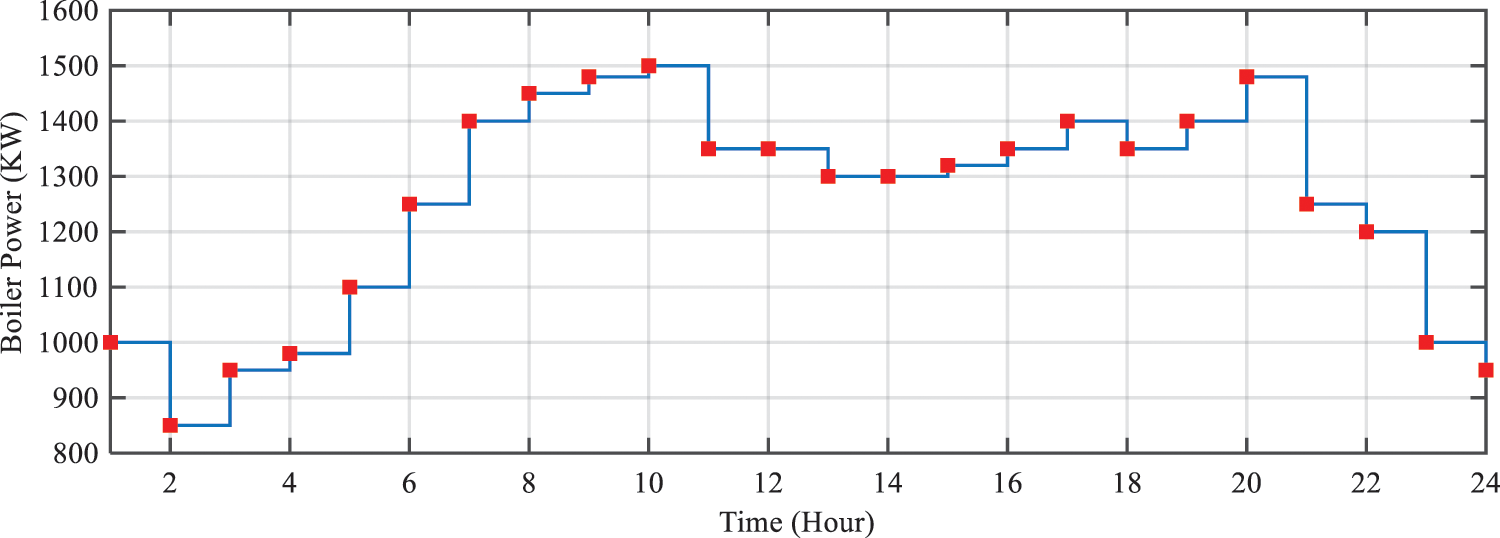
Figure 8: Thermal energy generated by the boiler

It is worth mentioning that, due to a lack of thermal resources management, the produced thermal energy profile by the boiler is precisely similar to the thermal energy needed by the consumers.

5.2 Second Scenario

To minimize the energy supply cost in the microgrids, it is required that the demand response program (DRP) be performed considering thermal and electrical resources at the same time because both terms are almost equally effective in the total cost of the microgrid. In the third scenario, thermal and electrical energy management in the microgrid is simultaneously performed using the GWO algorithm. Energy management of diesel generators, solar panels and battery storage as the electrical resources, and boiler with thermal storage has been performed as the thermal distributed generation resources. Finally, CHP has been carried out as the combined heat and power resources in the microgrid. The convergence process of the GWO algorithm in the problem of optimum energy management of thermal and electrical resources in the microgrid is shown in Fig. 9.

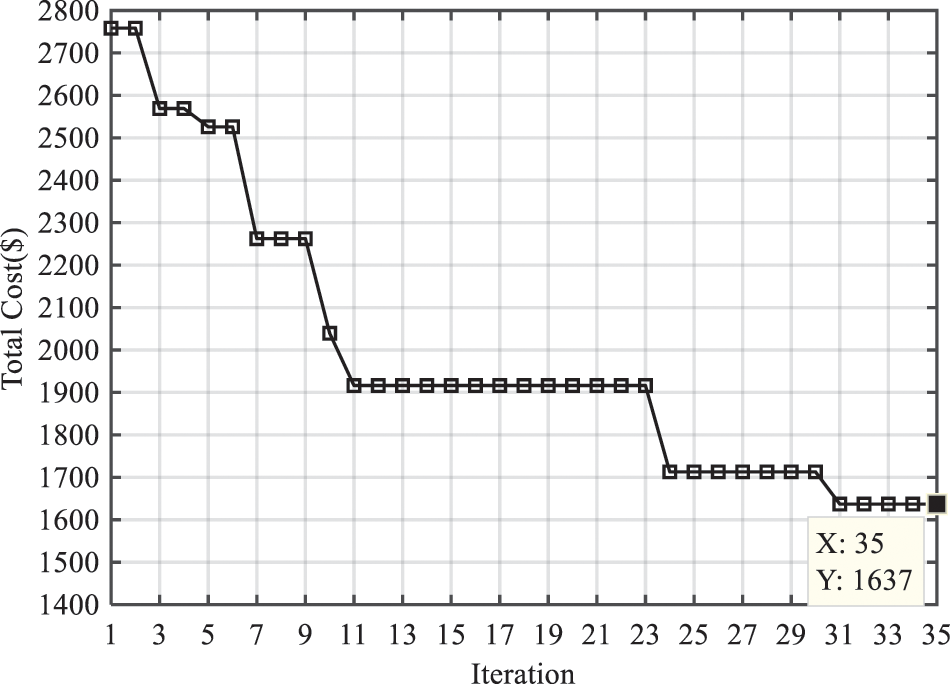
Figure 9: Convergence of GWO in thermal and electrical resources management

The cost of the microgrid after optimum management of the combined heat and power through the GWO algorithm was determined as $1637. The GWO algorithm converged to its minimum value after 31 iterations. Like the two previous scenarios, optimization algorithms were performed for 20 runs, the results of which are given in Table 3.

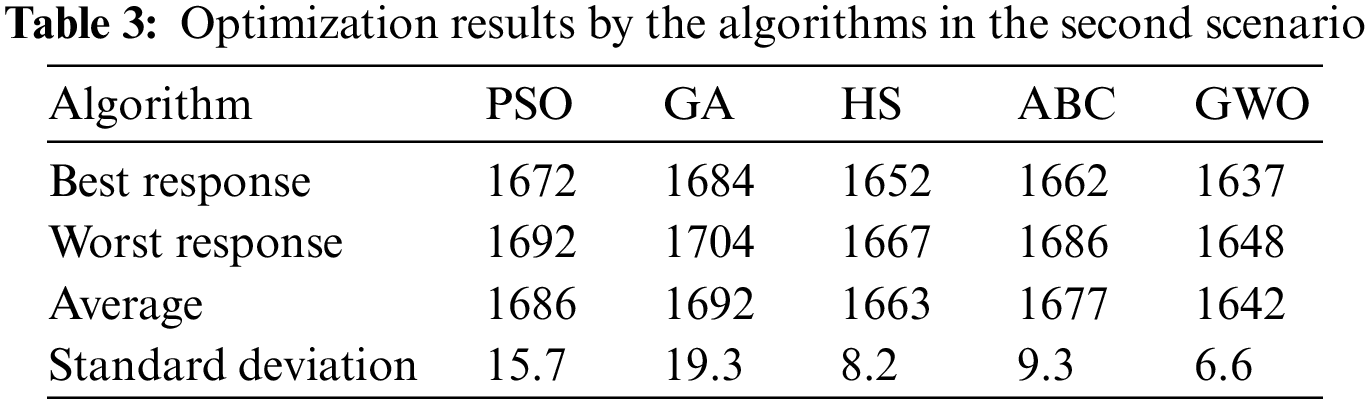
The optimization results in the third scenario indicated that the best response in the case of optimization through algorithms of PSO, GA, HS, ABC, and GWO had been calculated as $1672, $1684, $1652, $1662, and $1637, respectively. The slight difference between the obtained responses after 20 iterations of the GWO algorithm led to a standard deviation of 6.6, which is less than the value obtained through other algorithms. In the continuation of the procedure of the performed simulations, the amount of power generated by the electrical resources, and the amount of power generated by the thermal resources during a day in the case of optimization through GWO are shown in Figs. 10 and 11, respectively.

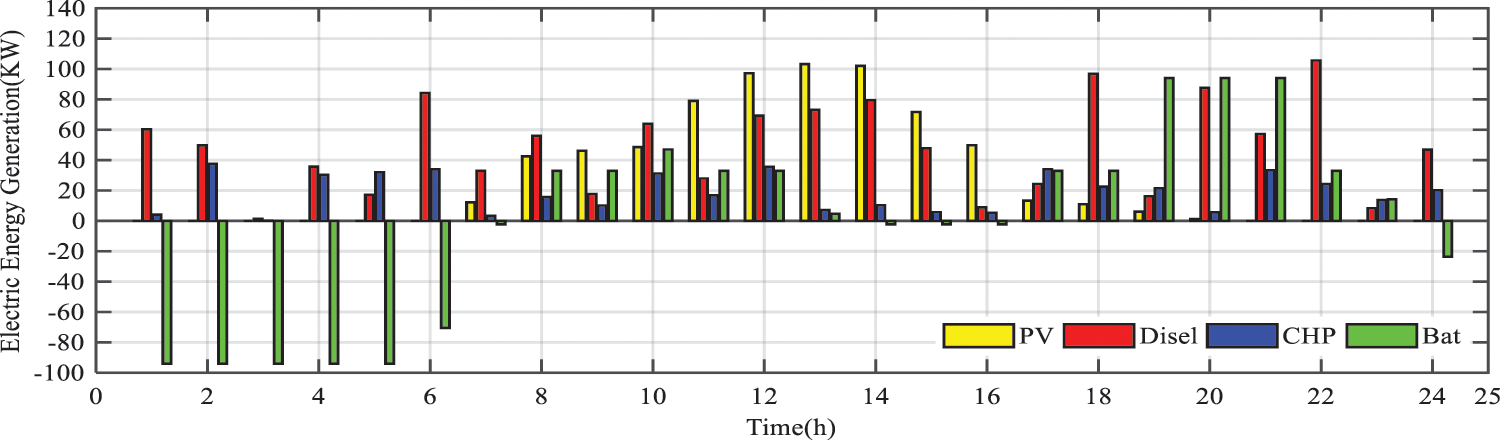
Figure 10: Electrical resource contribution in supplying the required energy

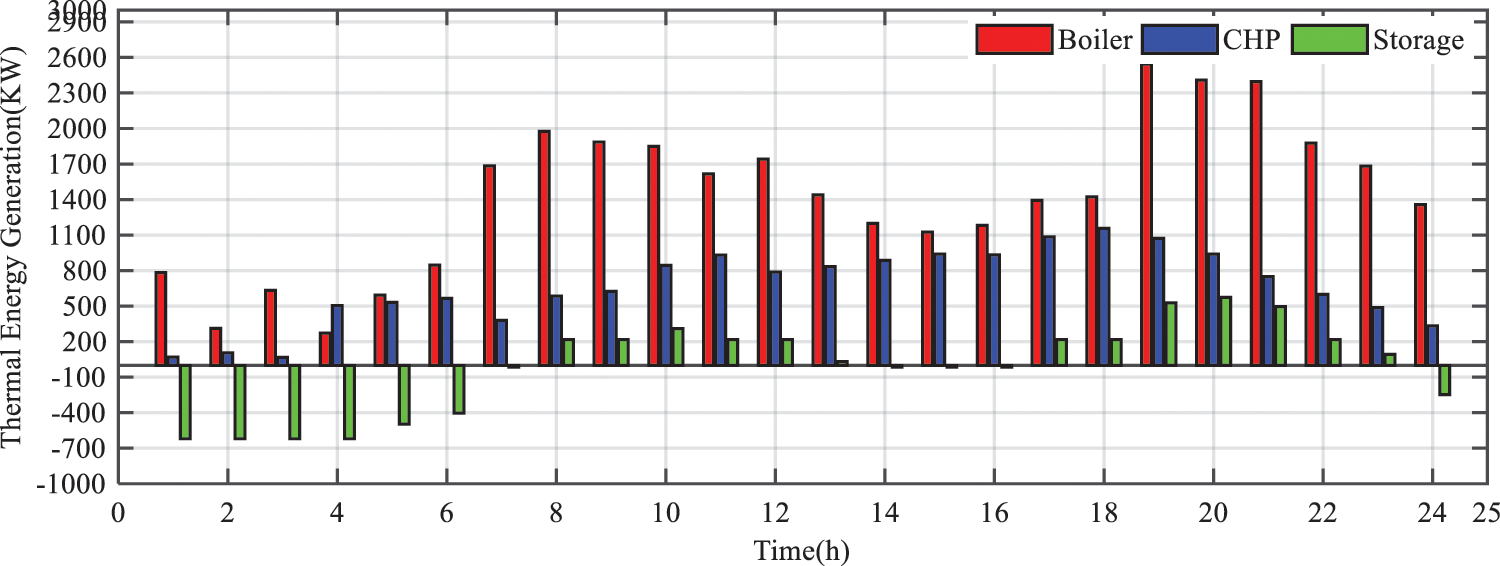
Figure 11: Thermal resource contribution in supplying the required energy in microgrid

Like the previous scenarios, to minimize the energy supply cost in the microgrid, energy storage depends on the low price of electricity and the periods of low demand in the microgrid. During these periods, the storage units store thermal and electrical energy at their maximum capacity, so that they can respond to the demand during periods of high demand. Other electrical and thermal resources also contribute to the energy required by the consumers, depending on the costs and price of the electricity in each period of demand. The amount of electrical energy transmitted with the nationwide electric network for the 24-hour study is shown in Fig. 12. Like the first scenario, electrical energy purchased in the early hours of the day is just for charging the batteries, so that it can make a profit through selling the stored electrical energy in the periods of high demand.

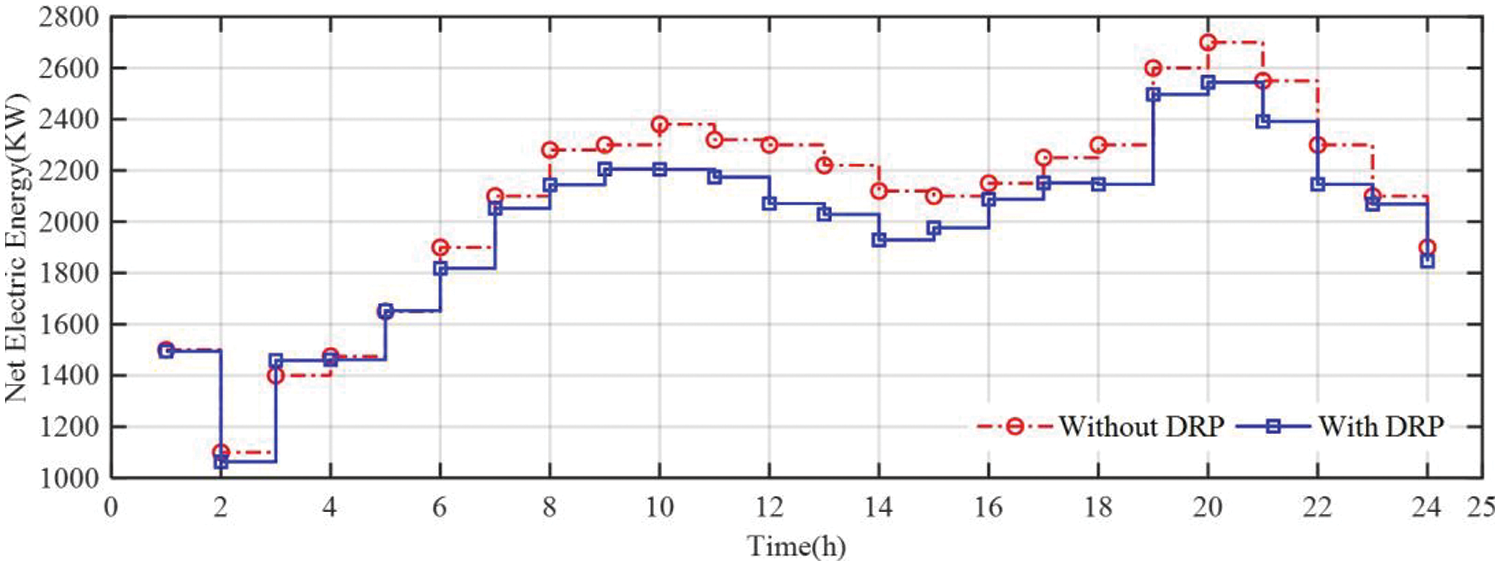
Figure 12: Transmitted electrical energy to the nationwide electric network

6  Conclusion

In this paper, based on real-time pricing and to reduce the energy supply cost in the microgrid through the GWO algorithm, the optimal operation of distributed generation resources and combined electrical and thermal storages in the microgrid was carried out. The studies were separately conducted in two scenarios. In the first part of the simulations, the energy management of resources and electric storage in the microgrid was done by considering the demand response program through the GWO algorithm, and there was no control of the heat resources. The total energy cost, after performing optimal energy management through the proposed GWO algorithm, in the first scenario, was decreased by about 30% compared to the primary conditions. In the second part of the simulations, to minimize the energy supply costs in the interested microgrids, the demand response program was carried out considering thermal and electrical sources at the same time. The total energy cost, after performing optimal energy management through the proposed GWO algorithm, in the second scenario, was decreased by about 30% compared to the primary conditions. Therefore, to have the minimum cost of energy supply in the microgrid, it is suitable to perform simultaneous management. On the other hand, comparing the results of the proposed GWO algorithm with some other optimization algorithms showed the high efficiency and accuracy of the GWO algorithm.

Funding Statement: This work was supported in part by an International Research Partnership “Electrical Engineering—Thai French Research Center (EE-TFRC)” under the project framework of the Lorraine Université d’Excellence (LUE) in cooperation between Université de Lorraine and King Mongkut’s University of Technology North Bangkok and in part by the National Research Council of Thailand (NRCT) under Senior Research Scholar Program under Grant No. N42A640328.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Ou, Y. Wei-Wei and K. Young-Bae, “Development of optimal energy management for a residential fuel cell hybrid power system with heat recovery,” Energy, vol. 219, no. 1, pp. 119499, 2021. [Google Scholar]

2. W. Violante, A. C. Claudio, A. T. Michele and F. Giuseppe, “An energy management system for isolated microgrids with thermal energy resources,” IEEE Transactions on Smart Grid, vol. 11, no. 4, pp. 2880–2891, 2020. [Google Scholar]

3. H. Mehrjerdi and E. Rakhshani, “Optimal operation of hybrid electrical and thermal energy storage systems under uncertain loading condition,” Applied Thermal Engineering, vol. 160, pp. 114094, 2019. [Google Scholar]

4. S. E. Ahmadi and N. Rezaei, “A new isolated renewable based multi microgrid optimal energy management system considering uncertainty and demand response,” International Journal of Electrical Power and Energy Systems, vol. 118, pp. 105760, 2020. [Google Scholar]

5. V. Sohrabi, S. Ghassemzadeh and S. Tohidi, “Energy management in hybrid microgrid with considering multiple power market and real time demand response,” Energy, vol. 174, no. 1, pp. 10–23, 2019. [Google Scholar]

6. H. Mehrjerdi and R. Hemmati, “Energy and uncertainty management through domestic demand response in the residential building,” Energy, vol. 192, pp. 116647, 2020. [Google Scholar]

7. H. Belaidi and Z. Rabiai, “Decentralized energy management system enhancement for smart grid,” Optimizing and Measuring Smart Grid Operation and Control, vol. 1, no. 1, pp. 156–169, 2021. [Google Scholar]

8. Z. Liang, B. Desong, Z. Xiaohu, S. Di, D. Ruisheng et al., “Optimal energy management for commercial buildings considering comprehensive comfort levels in a retail electricity market,” Applied Energy, vol. 236, no. 1, pp. 916–926, 2019. [Google Scholar]

9. A. Pallante, L. Adacher, M. Botticelli, S. Pizzuti, G. Comodi et al., “Decision support methodologies and day-ahead optimization for smart building energy management in a dynamic pricing scenario,” Energy and Buildings, vol. 216, no. 2, pp. 109963, 2020. [Google Scholar]

10. P. Firouzmakan, R. Hooshmand, M. Bornapour and A. Khodabakhshian, “A comprehensive stochastic energy management system of micro-CHP units, renewable energy sources and storage systems in microgrids considering demand response programs,” Renewable and Sustainable Energy Reviews, vol. 108, no. 1, pp. 355–368, 2019. [Google Scholar]

11. F. Luo, K. Weicong, R. Gianluca and Y. D. Zhao, “Optimal home energy management system with demand charge tariff and appliance operational dependencies,” IEEE Transactions on Smart Grid, vol. 11, no. 1, pp. 4–14, 2019. [Google Scholar]

12. H. Hosseinnia and B. Tousi, “Optimal operation of DG-based micro grid (MG) by considering demand response program (DRP),” Electric Power Systems Research, vol. 167, pp. 252–260, 2019. [Google Scholar]

13. S. Dorahaki, R. Dashti and H. R. Shaker, “Optimal energy management in the smart microgrid considering the electrical energy storage system and the demand-side energy efficiency program,” Journal of Energy Storage, vol. 28, pp. 101229, 2020. [Google Scholar]

14. A. Kaveh and Z. Pooya, “Improved GWO algorithm for optimal design of truss structures,” Engineering with Computers, vol. 34, no. 4, pp. 685–707, 2018. [Google Scholar]

15. A. Ibrahim, S. Mirjalili, M. El-Said, S. Ghoneim, M. Al-Harthi et al., “Wind speed ensemble forecasting based on deep learning using adaptive dynamic optimization algorithm,” IEEE Access, vol. 9, no. 1, pp. 125787–125804, 2021. [Google Scholar]

16. A. A. Salamai, E. -S. M. El-kenawy and A. Ibrahim, “Dynamic voting classifier for risk identification in supply chain 4.0,” Computers Materials & Continua, vol. 69, no. 3, pp. 3749–3766, 2021. [Google Scholar]

17. A. X. R. Irudayaraj, N. I. A. Wahab, M. Premkumar, M. A. M. Radzi, N. B. Sulaiman et al., “Renewable sources-based automatic load frequency control of interconnected systems using chaotic atom search optimization,” Applied Soft Computing, vol. 119, pp. 108574, 2022. [Google Scholar]

18. M. Premkumar, P. Jangir, C. Kumar, S. D. T. Sundarsingh Jebaseelan, H. H. Alhelou et al., “Constraint estimation in three-diode solar photovoltaic model using Gaussian and Cauchy mutation-based hunger games search optimizer and enhanced Newton–Raphson method,” IET Renewable Power Generation, vol. 16, no. 8, pp. 1733–1772, 2022. [Google Scholar]

19. Q. Zhang, C. Xin, F. Shen, Y. Gong, Y. Zi et al., “Human body IoT systems based on triboelectrification effect: Energy harvesting, sensing, interfacing and communication,” Energy & Environmental Science, vol. 9, pp. 1–34, 2022. [Google Scholar]

20. Q. Zhang, Z. Liu, X. Jiang, Y. Peng, C. Zhu et al., “Experimental investigation on performance improvement of cantilever piezoelectric energy harvesters via escapement mechanism from extremely low-frequency excitations,” Sustainable Energy Technologies and Assessments, vol. 53, pp. 102591, 2022. [Google Scholar]

21. W. Zhang, Z. Zheng and H. Liu, “A novel droop control method to achieve maximum power output of photovoltaic for parallel inverter system,” CSEE Journal of Power and Energy Systems, vol. 1, pp. 1–9, 2021. [Google Scholar]

22. L. Lin, C. Chen, B. Wei, H. Li, J. Shi et al., “Residential electricity load scenario prediction based on transferable flow generation model,” Journal of Electrical Engineering & Technology, vol. 85, pp. 1–11, 2022. [Google Scholar]

23. G. Luo, Q. Yuan, J. Li, S. Wang and F. Yang, “Artificial intelligence powered mobile networks: From cognition to decision,” IEEE Network, vol. 36, no. 3, pp. 136–144, 2022. [Google Scholar]

24. Y. Feng, B. Zhang, Y. Liu, Z. Niu, Y. Fan et al., “A D-band manifold triplexer with high isolation utilizing novel waveguide dual-mode filters,” IEEE Transactions on Terahertz Science and Technology, vol. 6, pp. 1–4, 2022. [Google Scholar]

25. B. Dai, B. Zhang, Z. Niu, Y. Feng, Y. Liu et al., “A novel ultrawideband branch waveguide coupler with low amplitude imbalance,” IEEE Transactions on Microwave Theory and Techniques, vol. 70, no. 8, pp. 1–9, 2022. [Google Scholar]

26. Y. Xi, W. Jiang, K. Wei, T. Hong, T. Cheng et al., “Wideband RCS reduction of microstrip antenna array using coding metasurface with low Q resonators and fast optimization method,” IEEE Antennas and Wireless Propagation Letters, vol. 21, no. 4, pp. 656–660, 2022. [Google Scholar]

27. T. Hong, S. Guo, W. Jiang and S. Gong, “Highly selective frequency selective surface with ultrawideband rejection,” IEEE Transactions on Antennas and Propagation, vol. 70, no. 5, pp. 3459–3468, 2022. [Google Scholar]

28. K. Xu, X. Weng, J. Li, Y. Guo, R. Wu et al., “60-GHz Third-order on-chip bandpass filter using GaAs pHEMT technology,” Semiconductor Science and Technology, vol. 37, no. 5, pp. 55004, 2022. [Google Scholar]

29. Y. Liu, K. Xu, J. Li, Y. Guo, A. Zhang et al., “Millimeter-vave e-plane waveguide bandpass filters based on spoof surface plasmon polaritons,” IEEE Transactions on Microwave Theory and Techniques, vol. 70, no. 10, pp. 4399–4409, 2022. [Google Scholar]

30. K. Xu, Y. Guo, Y. Liu, X. Deng, Q. Chen et al., “60-GHz compact dual-mode on-chip bandpass filter using GaAs technology,” IEEE Electron Device Letters, vol. 42, no. 8, pp. 1120–1123, 2021. [Google Scholar]

31. K. Liu, Z. Yang, W. Wei, B. Gao, D. Xin et al., “Novel detection approach for thermal defects: Study on its feasibility and application to vehicle cables,” High Voltage, vol. 2022, pp. 1–10, 2022. [Google Scholar]

32. A. Li, D. Spano, J. Krivochiza, S. Domouchtsidis, C. G. Tsinos et al., “A tutorial on interference exploitation via symbol-level precoding: Overview, state-of-the-art and future directions,” IEEE Communications Surveys & Tutorials, vol. 22, no. 2, pp. 796–839, 2020. [Google Scholar]

33. A. Li, C. Masouros, A. L. Swindlehurst and W. Yu, “1-bit massive MIMO transmission: Embracing interference with symbol-level precoding,” IEEE Communications Magazine, vol. 59, no. 5, pp. 121–127, 2021. [Google Scholar]

34. J. Hu, C. Ye, Y. Ding, J. Tang and S. Liu, “A distributed MPC to exploit reactive power V2G for real-time voltage regulation in distribution networks,” IEEE Transactions on Smart Grid, vol. 13, no. 1, pp. 576–588, 2021. [Google Scholar]

35. C. Lu, H. Zhou, L. Li, A. Yang, C. Xu et al., “Split-core magnetoelectric current sensor and wireless current measurement application,” Measurement: Journal of the International Measurement Confederation, vol. 188, pp. 110527, 2022. [Google Scholar]

36. Y. Zhang, X. Shi, H. Zhang, Y. Cao and V. Terzija, “Review on deep learning applications in frequency analysis and control of modern power system,” International Journal of Electrical Power & Energy Systems, vol. 136, pp. 107744, 2022. [Google Scholar]

37. X. Xu, D. Niu, L. Peng, S. Zheng and J. Qiu, “Hierarchical multi-objective optimal planning model of active distribution network considering distributed generation and demand-side response,” Sustainable Energy Technologies and Assessments, vol. 53, pp. 102438, 2022. [Google Scholar]

38. H. Li, K. Hou, X. Xu, H. Jia, L. Zhu et al., “Probabilistic energy flow calculation for regional integrated energy system considering cross-system failures,” Applied Energy, vol. 308, pp. 118326, 2022. [Google Scholar]

39. H. Wang, K. Hou, J. Zhao, X. Yu, H. Jia et al., “Planning-oriented resilience assessment and enhancement of integrated electricity-gas system considering multi-type natural disasters,” Applied Energy, vol. 315, pp. 118824, 2022. [Google Scholar]

40. K. Ma, X. Hu, Z. Yue, Y. Wang, J. Yang et al., “Voltage regulation with electric taxi based on dynamic game strategy,” IEEE Transactions on Vehicular Technology, vol. 71, no. 3, pp. 2413–2426, 2022. [Google Scholar]

41. K. Ma, Z. Li, P. Liu, J. Yang, Y. Geng et al., “Reliability-constrained throughput optimization of industrial wireless sensor networks with energy harvesting relay,” IEEE Internet of Things Journal, vol. 8, no. 17, pp. 13343–13354, 2021. [Google Scholar]

42. F. Guo, W. Zhou, Q. Lu and C. Zhang, “Path extension similarity link prediction method based on matrix algebra in directed networks,” Computer Communications, vol. 187, pp. 83–92, 2022. [Google Scholar]