A PSO Improved with Imbalanced Mutation and Task Rescheduling for Task Offloading in End-Edge-Cloud Computing

1  Introduction

Nowadays, users use various end devices for processing their request tasks with a wide variety of requirements. For example, smartphones are used by many people for entertainment in most of their waking hours; more and more vehicles with different levels of intelligence are running on the roads; Internet-of-things (IoT) devices can be seen almost everywhere. Due to the small physical sizes, most end devices have very limited capacities of the resource and battery, and cannot satisfy all user requests alone. Therefore, to be better able to serve their users, many service providers exploit end-edge-cloud cooperative computing (E2C), by combining both benefits of edge and cloud computing [1,2].

Cloud computing is to provide abundant computing and storage resources [3]. But cloud computing usually has low-bandwidth and high-latency networks, because it generally uses a wide area network (e.g., Internet) shared by varied users for the data transfer. Edge computing is to place some servers close to end devices, and thus provides high-bandwidth and low-latency network services [4]. While, an edge computing center takes up very little space, and thus is equipped with only a few servers. E2C makes end devices, edge computing, and cloud computing cooperate, for meeting the requirements of both delay-sensitive and resource-intensive applications. Thus, E2C has attracted much attention from both academia and industry.

While, how to make E2C resources cooperate well is challenging work for improving resource efficiency and service quality [5]. Task offloading is one of the efficient ways to address the challenge, which is to decide which and how many resources are allocated for every task in E2C. In recent years, many works focused on the task offloading of E2C [6], but they have some issues that should be addressed before their applications. For example, some works ignored the task or resource heterogeneity, which may result in resource inefficiencies. Several works didn’t consider to exploited local device resources for task processing, even though many modern devices are equipped with a fair resource amount, leading to resource waste. Many existing offloading methods exploited only one kind of heuristic or meta-heuristic algorithm, without exploiting the complementary advantages of different kinds of algorithms for performance improvement. Some existing works have proposed hybrid heuristic offloading algorithms. But these works just sequentially performed two or more algorithms, which leads to a low combination performance. Thus, this work tries to design a hybrid heuristic algorithm with an efficient combination approach, to improve service quality and resource efficiency by increasing resource cooperativity in E2C.

This paper first formulates the task offloading problem of E2C as a Binary Non-Linear Programming (BNLP), where the optimization objective is the task acceptance ratio. Then, to provide task offloading solutions in polynomial time, this paper designs a hybrid heuristic algorithm by integrating a mutation operator of the evolutionary algorithm and a heuristic task scheduling algorithm into Particle Swarm Optimization (PSO). To further improve the algorithm performance, this paper designs an imbalanced mutating scheme to improve the particle density near the global optimal position. In addition, this paper proposes to reschedule rejected tasks by a heuristic algorithm for improving the solution quality. To evaluate the performance of our proposed algorithm, this paper conducts extensive simulated experiments, where environment parameters are set referring to related works and reality. Experiment results show that our proposed algorithm performs better than ten of the classical and up-to-data algorithms in optimizing the accepted ratio. In brief, the contributions of this paper are as follows.

•    The task offloading problem is formulated in binary non-linear programming (BNLP) for E2C, concerning the cooperation of devices, edge servers, and the cloud, to optimize the accept ratio.

•    A hybrid meta-heuristic algorithm for solving the offloading problem, by integrating the evolutionary strategy of Genetic Algorithm (GA) into PSO. And to further improve the performance of the algorithm, the hybrid algorithm exploits an imbalance mutation operator and the task rescheduling approach for generating better offspring and improving the solution quality, respectively.

•    Extensive simulated experiments are conducted, where simulation parameters are set referring to recent related works and reality. Experiment results confirm the performance of the proposed hybrid offloading algorithm.

In the follows, this paper discusses related works in Section 2. In Section 3, this paper presents the problem formulation and illustrates the proposed hybrid heuristic offloading algorithm in Section 4. Then, this paper details the performance evaluation in Section 5. At last, this paper concludes in Section 6.

2  Related Works

With smart devices increasingly popular, E2C is applied to various fields of both academia and industry. To improve service quality and resource efficiency in E2C environments, several works studied the task offloading problem.

Sang et al. [7] proposed a heuristic offloading algorithm to improve the cooperativeness of EECC resources, by offloading tasks to the cloud at first. This helps to improve overall user satisfaction but negatively affects the overall performance. Wang et al. [8] presented the fastest response first (FRFOA) and a load balance offloading algorithm (LBOA). FRFOA offloads the task to the ES such that the response time is minimum, every time. LBOA assigns the task to the ES where the ES can satisfy the requirements of the greatest number of tasks at every time. These above approaches are heuristic-based solutions, which generally provide solutions with limited performance because they only exploit local search strategies.

Therefore, some works aim at better offloading solutions by meta-heuristics with global search abilities. Wang et al. [9] and Gao et al. [10] applied PSO with the same solution representation method as this paper. To improve the exploration ability of PSO, Gao et al. [10] used the Lévy Flight movement pattern for particle position updates. Wang et al. [11] used GA with the same optimization objectives as this paper. Chakraborty et al. [12] employed GA to reduce the energy consumption of task executions with latency constraints. Yadav et al. [13] used multiobjective grey wolf optimization (MOGWO) technique for computation offloading in fog computing, to improve energy consumption and computational time. Xu et al. [14] employed Multi-strategy collaboration-Tunicate Swarm Optimization Algorithm (M-TSA) which is the standard TSA improved by a memory learning strategy, the Levy flight strategy, and an adaptive dynamic weighting strategy, for seeking a solution with an optimized weighted sum of the time delay and the energy consumption for E2C systems. These works used only one kind of meta-heuristics, without exploiting the complementarity of different kinds of meta-heuristics for better performance.

Bali et al. [15] used NSGA-II to optimize the energy and queue delay for offloading data on edge and cloud servers. Hussain et al. [16] replaced the chromosome with its better offspring generated by the crossover operator for each individual, which is similar to the behavior of the population evolution in PSO. Nwogbaga et al. [17] performed a mutation operator for each individual at the end of every iteration for PSO to improve the diversity and avoid premature convergence. Farsi et al. [18] sequentially employed GA and PSO for the population evolution. Zhang et al. [19] presented a dynamic selection mechanism for combining multiple meta-heuristics by selecting offspring generated by these meta-heuristics for the next generation. All of the above works just performed two or more meta-heuristics separately, which leads to a very improved performance.

The difference between our work and the above works is twofold. First, this work integrates heuristic task ordering and heuristic task rescheduling approaches into PSO. Secondly, this work not only combines the mutation operator of GA in PSO but also exploits imbalanced mutation concerning the resource heterogeneity of E2C, which is hardly considered by related works for designing meta-heuristics or hybrid meta-heuristics.

3  Problem Statement

In the considered E2C environment, as shown in Fig. 1, there are various end devices, multiple edge servers (ES), and a cloud that provides sufficient cloud servers (CS). In the E2C, users launch various request tasks by these devices. For each device, the tasks that it launches can be processed locally if it has enough resources for satisfying the requirements of these tasks. But, most of the time, devices aren’t able to meet the requirements of their users’ tasks, especially devices without any computing resources, such as environmental sensors. Therefore, some tasks are offloaded to ES for their processing. In this case, the input data need to be transferred from the device to the ES, which requires that a task can be offloaded to ES only if the device has a network connection with the ES. Generally, an ES provides a local area network (LAN) for devices, e.g., 5G and Wifi, and thus has limited coverage and can only provide services for devices in its coverage. When users have many request tasks, and devices and ES cannot afford these tasks, delay-insensitive tasks can be offloaded to the cloud that provides services over WAN and can cover all devices. The cloud provides resources in the form of CS for processing offloaded tasks. The task offloading is to decide the computing node (local device, ES, or CS) by which every task is processed.

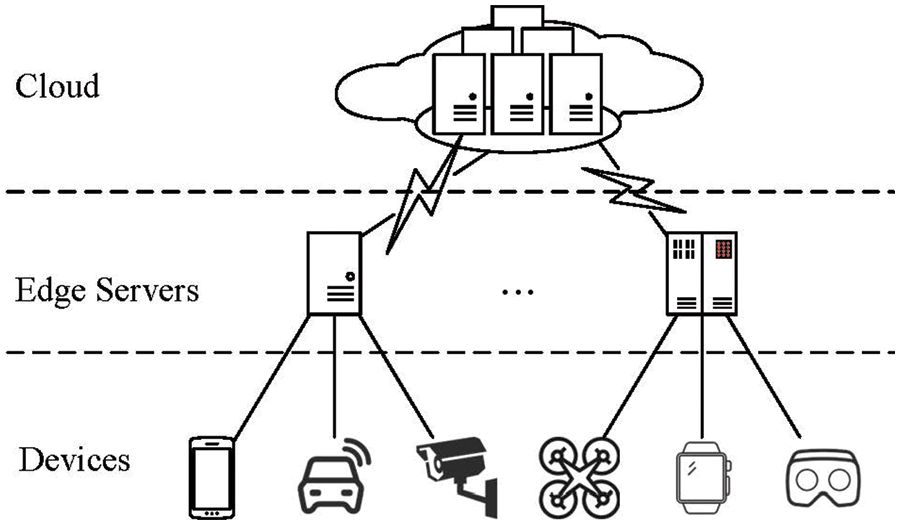
Figure 1: The architecture of end-edge-cloud computing

3.1 System Model

E2C consists of D+E+V computing nodes, D devices (ni, 1≤i≤D), E ES (ni, D+1≤i≤D+E), and V CS (ni, D+E+1≤i≤D+E+V). For node ni, the computing capacity is gi, and it provides bi network data transfer rate. Binary constants, ai,j, 1≤i≤D, D+1≤j≤D+E, are used to represent the coverage of ES, where ai,j=1 if device ni is covered by ES nj, and ai,j=0 if not. Then, for a task of ni, the data transfer rate is bi,j=ai,j⋅bj when it is offloaded to ES nj, where the data transfer rate can be easily calculated by the signal power and Gaussian noise of the network [20].

There are T tasks (tk, 1≤k≤T) requested from these D devices. This paper uses binary constants, mi,k, 1≤i≤D, 1≤k≤T, to indicate the relationships between tasks and devices, where mi,k=1 if tk is launched by ni, and mi,k=0, otherwise. For task tk, the computing size, i.e., the amount of required computing resources, is ck, and the amount of the input data is pk. The deadline of tk is dk, i.e., the finish time of its processing must be not later than dk. This paper focuses on the hard deadline requirement and leaves the consideration of the soft deadline constraint as one of future works. This is to say, if the deadline of a task can be met, it will be accepted and processed in E2C. Otherwise, the task is rejected, as there is no profit from processing the task. Without loss of generality, this paper assumes that dk≤dk+1,1≤k≤T−1.

For formulating the task offloading problem of E2C, binary variables are defined to represent the offloading decisions as Eq. (1).

xi,k={1,tkis decided to be processed byni0,otherwise,1≤i≤D+E+V,1≤k≤T(1)

3.2 Task Processing Model

For a task, there are three cases for its processing: (i) the task is processed locally using its device resources; (ii) the task is offloaded to an ES covering its device; (iii) the task is offloaded to a CS. Next, this paper illustrates the task processing in these three cases, respectively.

3.2.1 Task Processing Locally

In the first case, there is no transmission delay, because the data are stored locally as they are collected by the device according to the environment and the user behavior. Then, the processing time of the task is its computing time. While, the task can be started only when the computing resource is available, which is the time that the device completes all of its tasks that are processed before the task. Intending to maximize the accepted ratio which is the ratio between the accepted task number and the total task number, Earliest Deadline First (EDF) has proven that it provides the optimal solution. Thus, for establishing the optimization problem of task offloading, this paper deduces the finish time of every task by executing tasks with the order of EDF for each device. Therefore, the finish time of tasks processed locally can be calculated by Eq. (2). Where ck'/gi is the computing time of tk′ processed by ni and ∑k'=1kxi,k'⋅ck'/gi is the accumulative computing time of tasks including tk and tasks having earlier deadlines than tk in ni. For each task processed locally, it can be only processed in its device and thus Eq. (3) holds.

fkL=∑i=1D(mi,k⋅∑k′=1k(xi,k′⋅ck′/gi)),1≤k≤T(2)

xi,k≤mi,k,1≤i≤D,1≤k≤T(3)

3.2.2 Task Processing in Edge Servers

When a task is offloaded to an ES, the processing time consists of the input data transfer and the computing latencies. In this paper, this paper ignores the time consumed by the output data transfer, as the computing result are generally much less than the input data for a task.

For the task tk that is offloaded to ES ni (D+1≤i≤D+E), the input data transfer consumes pk/∑j=1D(mj,k⋅bj,i) time, where ∑j=1D(mj,k⋅bj,i) is the data transfer rate between the device that launches tk and the ES, and the computing latency is ck/gi. To avoid performance interference, the data transfers of different tasks offloaded to an ES are performed sequentially. Thus, with the EDF processing order, the complete time of the data transfer for the task tk when it is offloaded to an ES can be calculated by Eq. (4).

fkE_NET=∑i=D+1D+E(xi,k⋅∑k′=1k(xi,k′⋅pk′∑j=1D(mj,k′⋅bj,i))),1≤k≤T(4)

For a task offloaded to an ES, except the computing resource is available, its computing requires the finish of the input data transmission. Therefore, the finish time of a task on an ES can be achieved by Eq. (5), where max1≤k′<k{ xi,k′⋅fk′E } is the finish time of the task that is processed before tk.

fkE=∑i=D+1D+E(xi,k⋅(max{ fkE_NET,max1≤k′<k{ xi,k′⋅fk′E } }+ckgi)),1≤k≤T(5)

For each task, it can be only offloaded to the ES that has a network connection with its device. Thus, Eq. (6) needs to be met.

xi,k≤∑i′=1D(mi′,k⋅ai,i′),D+1≤i≤D+E,1≤k≤T(6)

3.2.3 Task Processing in the Cloud

For tasks offloaded to the cloud for their processing, similar to ES, the processes include data transfers and computing. Referring to Eqs. (4) and (5), the finish time of a task can be got when it is offloaded to a CS by Eqs. (7) and (8).

fkC_NET=∑i=D+E+1D+E+V(xi,k⋅∑k′=1k(xi,k′⋅pk′bi)),1≤k≤T(7)

fkC=∑i=D+E+1D+E+V(xi,k⋅(max{ fkC_NET,max1≤k′<k{ xi,k′⋅fk′C } }+ckgi)),1≤k≤T(8)

3.2.4 Summary

Summarizing the above processing model in three cases, the finish time of all tasks in D2C can be achieved, given a task offloading decision, from Eq. (9).

fk=fkD+fkE+fkC,1≤k≤T(9)

For each task, it is processed by only one computing node, when it is accepted. Then, Eq. (10) is satisfied for all tasks. ∑i=1D+E+Vxi,k is 1 for the accepted task, and equals 0 if tk is rejected due to the deadline violation.

∑i=1D+E+Vxi,k≤1,1≤k≤T(10)

3.3 Problem Model

This work considers the optimization objective as the acceptance ratio for the task offloading in E2C, with the deadline constraints. Therefore, the offloading problem can be formulated as the optimization model as follows.

Maximizing ∑k=1T∑i=1D+E+Vxi,kT(11)

Subject to deadline constraints, Eq. (12) and Eqs. (1)–(10).

fk≤dk,1≤k≤T(12)

As the total task number (T) is fixed, the optimization objective is identical to maximizing the number of accepted tasks (∑k=1T∑i=1D+E+Vxi,k). Decision variables are xi,k, 1≤i≤D+E+V, 1≤k≤T, which all are binary, making the offloading problem binary non-linear programming (BNLP). This problem can be solved by some existing tools, e.g., lp_solve [21] and Optimization Toolbox of MathWorks, Inc. [22]. These tools take exponential complexities, not applicable for middle-to-large scale optimization problems. Therefore, in the next section, this paper proposes a polynomial algorithm based on PSO.

4  PSO with Imbalanced Mutation and Task Rescheduling

In this section, this paper solves the task offloading problem for E2C, based on PSO. PSO iteratively moves particles toward their personal best positions and the global best position, for evolving the population consisting of multiple particles. PSO has a fast convergence speed, and can provide a good solution with small population size, and thus has lower time complexity than many evolutionary algorithms, e.g., genetic algorithm (GA). In addition, there are very few parameters needed to be set when applying PSO. So PSO has been applied for solving combinatorial optimization problems in many fields, e.g., unmanned aerial vehicle path planning [23], electrical power systems [24], and network topology optimization [25]. As shown in the previous section, the task offloading problem for E2C is also a kind of combinatorial optimization problem, and thus, this paper considers exploiting PSO for solving the task offloading problem.

But PSO has some deficiencies needed to be concerned to achieve better solutions. The main one is easily trapping into local optima. Therefore, this paper applies the mutation operator of GA to help particles in escaping from local optima by increasing the randomness of some movements, like the work of Nwogbaga et al. [17]. Different from this work, this paper takes into account the capacity heterogeneity of resources and proposes an imbalanced mutation operator, which will be illustrated in Section 4.3. Beyond this, to further improve the acceptance ratio and the resource efficiency, this paper adds the task rescheduling approach in each offloading solution derived from particles, by rescheduling the rejected tasks from their original assigned nodes to others, which is stated inSection 4.4.

4.1 Algorithm Framework

Now, this paper details the proposed task offloading algorithm, PSO improved with imbalanced mutation and task rescheduling (PIMR), as shown in Fig. 2. In PIMR, a particle position indicates a task assignment solution, i.e., decisions of the computing nodes that tasks are assigned to. Then, with a task execution order on each node, an offloading solution can be achieved from a particle position. To improve the performance of the offloading solution derived from a particle, PIMR reschedules rejected tasks, as illustrated in Section 4.4. The mapping between task offloading solutions and particle positions are elaborated in Section 4.2. The fitness of every particle/position is the accepted number when applying the corresponding offloading solution, which is shown in Eq. (13)

vl.k(t)=ω⋅vl.k(t)+c1⋅r1⋅(pbl.k−pl.k(t−1))+c2⋅r2⋅(gbk−pl.k(t−1))(13)

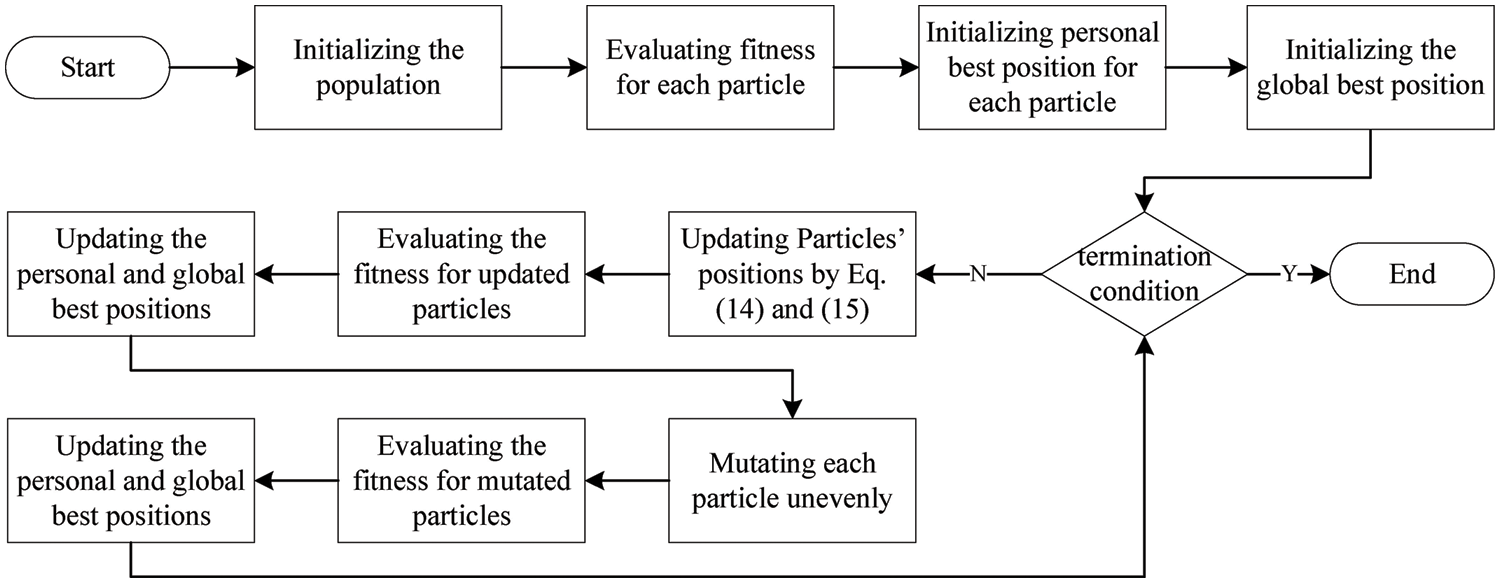
Figure 2: The flow chart of PIMR

As shown in Fig. 2, at first, PIMR initializes a population consisting of multiple particles, where each position in every dimension is randomly set for these particles. After the population initialization, the fitness of every particle is evaluated by transforming the position into a task offloading with task rescheduling. Then, PIMR records the personal best position as the current position for each particle and the global best position as the best position with the best fitness of particles. After this, PIMR iteratively evolves the population by updating the position of each particle as followings, where each iteration can be divided into two phases.

In the first phase, for each particle, the position is updated, as done by PSO, by Eqs. (14) and (15). Vl(t)=[vl,1(t),…,vl,k(t),…,vl,T(t)] is the velocity of the lth particle at the tth iteration. Pl(t)=[pl,1(t),…,pl,i(t),…,pl,T(t)] is the position of the lth particle at the tth iteration. ω is the inertia weight of particles. c1 and c2 are the acceleration coefficients of PSO. r1 and r2 are two random values ranging from 0 to 1. PBl=[pbl,1,…,pbl,i,…,pbl,T] is the personal best position of the lth particle. GB=[gb1,…,gbk,…,gbT] is the global best position of all particles.

vl.k(t)=ω⋅vl.k(t)+c1⋅r1⋅(pbl.k−pl.k(t−1))+c2⋅r2⋅(gbk−pl.k(t−1))(14)

pl.k(t)=pl.k(t−1)+vl.k(t)(15)

After the particle updates its position, its fitness is evaluated. The personal best position will be updated as the updated position if the updated position has better fitness, and the same action is performed on the global best position.

In the second phase of each iteration, PIMR performs the imbalanced mutation operator on each particle with the mutation probability, to increase the population diversity, combining the advantage of GA and concerning the resource heterogeneity. The details of the imbalanced mutation operator are presented in Section 4.3. After performing the mutation for a particle, its personal best position and the global best position are updated as done in the first phase.

4.2 Solution Representation

In PIMR, a particle position is indicating a task offloading solution. There is a one-to-one relationship between the dimensions of particle positions and tasks. And the position on a dimension represents the computing node that the corresponding task is scheduled to. Then, the range of a position on a dimension is the number of candidate computing nodes that the corresponding task can be processed on, which includes the task’s device, ES with connections with the device, and CS. Now, a task assignment solution can be got from every particle position.

For example, there are 2 devices (d1 and d2), 3 ES (e1, e2 and e3), and 1 CS (c1 and c2) in an E2C. Each device launches one task, where d1 and d2 launch t1 and t2, respectively. d1 has network connection with e1, and d1 has connections with e2 and e3. Then, t1 can be scheduled to d1, e1, c1 and c2 for its processing and these computing nodes are numbered as 1–4, respectively. t2 can be scheduled to d2, e2, e3, c1 and c2, numbered as 1-5. In this E2C environment, the dimensions are 2 in each particle position, which corresponds to these two tasks. The value ranges of these two dimensions are 1–4 and 1–5, respectively, and the value of a dimension is the no. of the computing node that the corresponding task is assigned to.

Given a task assignment solution, a task offloading solution can be achieved by deciding the processing order on each computing node where multiple tasks are assigned. The ordering algorithm, i.e., task scheduling, on a computing node has been studied since the invention of the operating system, and there are several mature heuristic solutions. This paper focuses on the scheduling of tasks across computing nodes for E2C. Therefore, this paper just applies one of the simplest methods, First Fit (FF), for ordering the task processing on every computing node. In the future, we will try to design a more efficient task-ordering algorithm for better performance.

4.3 Imbalanced Mutation

In general, the mutation operator used by evolutionary algorithms is a “balanced” mutation, where the value of every dimension is mutated to possible values with an identical probability. Such as, for a task, there are n candidate computing nodes, i.e., n possible positions in the corresponding dimension. Then, the corresponding dimension is mutated to all possible positions each with a probability of 1/n, when the mutation operator is performed on it. Thus, the application of the balanced mutation operator is not concerning the resource heterogeneity in that computing nodes have different capacities, which may lead to resource inefficiency.

Therefore, PIMR exploits an imbalanced mutation, which set the probability of each value that a dimension is mutated to is positively associated with the corresponding computing node’s capacity. The capacity is evaluated by the ratio of the slack time to the finish time for each computing node and each task, where the slack time is the time distance of the finish time to the deadline. If the finish time is later than the deadline, then the computing node has zero probability of processing the task. Then, the probability (ρi,k) that the kth task is assigned to the ith candidate computing node is calculated by Eq. (16), when the imbalance mutation is performed on the dimension.

ρi,k=max{0,dk−fi,k}/fi,k∑i(max{0,dk−fi,k}/fi,k)(16)

4.4 Task Rescheduling

As illustrated above subsections, PIMR randomly assigns tasks to their candidate computing node in each offloading solution of particles, and thus, there can be a load imbalance between computing nodes, leading to many tasks that are rejected due to dissatisfaction with their requirements. Therefore, PIMR reschedules these rejected tasks to improve the acceptance ratio and resource efficiency. Given the task offloading solution derived from a particle position, for each rejected task, PIMR schedules it to the first computing node having available resources to meet its deadline constraint.

5  Performance Evaluation

In this section, this paper illustrates simulated experiments and discusses the experiment results.

5.1 Simulated Experimental Environment

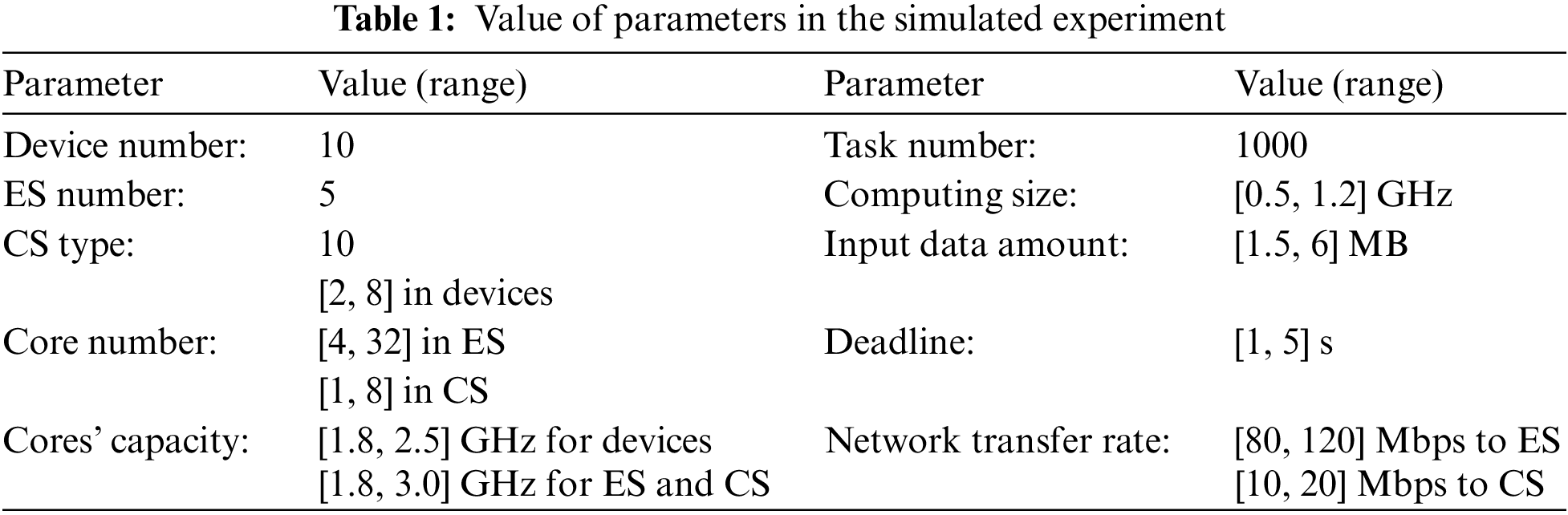
The simulated environments are established by referring to related works and reality [26], where the values of parameters are shown in Table 1.

PIMR is compared with the following classical and up-to-date task offloading algorithms.

•   First Fit (FF) is one of the most classical and simplest scheduling algorithms for various computing environments. FF is to assign the first task to the first computing node that can meet the deadline constraint.

•   First Fit Decreasing (FFD) is the same as FF, except that it assigns the task with the biggest computing size at first.

•   Earliest Deadline First (EDF) is the same as FF, except that it schedules the task with the earliest deadline every time.

•   Short Job First (SJF) schedules the task with minimal computing size each time.

•   Random (RAND) randomly generates a population with multiple individuals and provides the task offloading solution that corresponds to the individual with the best fitness.

•   Genetic Algorithm (GA) uses the crossover, mutation, and selection operators for population evolution [11,12].

•   GA with Replacement (GAR) is the same as GA, except that it replaces each chromosome with its best offspring after performing the crossover operator, and doesn’t perform selection [16].

•   Particle Swarm Optimization (PSO) only uses Eqs. (13) and (14) for moving particles [9].

•   PSO with mutation (PSOM) adds a mutation operator on each particle’s position at the end of each iteration [17].

•   The combination of GA and PSO (GAPSO) sequentially uses GA and PSO for evolution [18].

The metrics used for measuring the performance of each task offloading algorithm include the following aspects.

•    The number of accepted tasks is identical to the acceptance ratio, which is one of the commonly used metrics for quantifying service quality or user satisfaction.

•    Overall computing resource utilization is one of the most popular approaches for the quantification of resource efficiency.

•    The task processing rate is to evaluate processing efficiency. Two metrics are used in this paper, the finished computing size per time unit, and the processed data amount per time unit.

The experiments are conducted as following steps. (1) A simulated E2C environment is generated with random parameters. (2) Every metric of each algorithm is measured in the simulated E2C. (3) For each metric, its value is normalized by dividing it into that of FF for every algorithm, to highlight the performance differences between different algorithms. (4) The previous three steps are repeated more than one hundred times, and in the following, the box plots for each metric are presented. Experiment results show that PIMR is statistically different from any other for each metric.

5.2 Experiment Results

5.2.1 Service Quality

Fig. 3 gives the normalized number of accepted tasks when applying different task offloading algorithms. As shown in this figure, PIMR can accept 8.93%–37.0% more task numbers than others, on average. In addition, PIMR has a stable performance in maximizing the accepted task number, as it has no outlier as shown in the box plot of Fig. 3. This confirms the performance superiority of our proposed algorithm, mainly benefiting from the imbalanced mutation and the task rescheduling approaches. The mutation operator can improve the population diversity, which increases the ability of PSO to break away from the local optimum, and thus PSOM has slightly better performance than PSO in the accepted task number optimization, as shown in Fig. 3, PIMR improves the mutation operator for PSOM by unbalancing the probabilities of positions mutated, where there is a positive correlation between the capacity of computing nodes and the probabilities that tasks are assigned to the nodes. This can result in particles being denser at the possible best positions, and thus there is more likely to make the algorithm converge to an optimal position. In addition, PIMR performs rescheduling for rejected tasks. This can not only increase the number of accepted tasks but also improve the efficiency of resource usage. These two improvement approaches bring PIMR a competitive advantage over other algorithms.

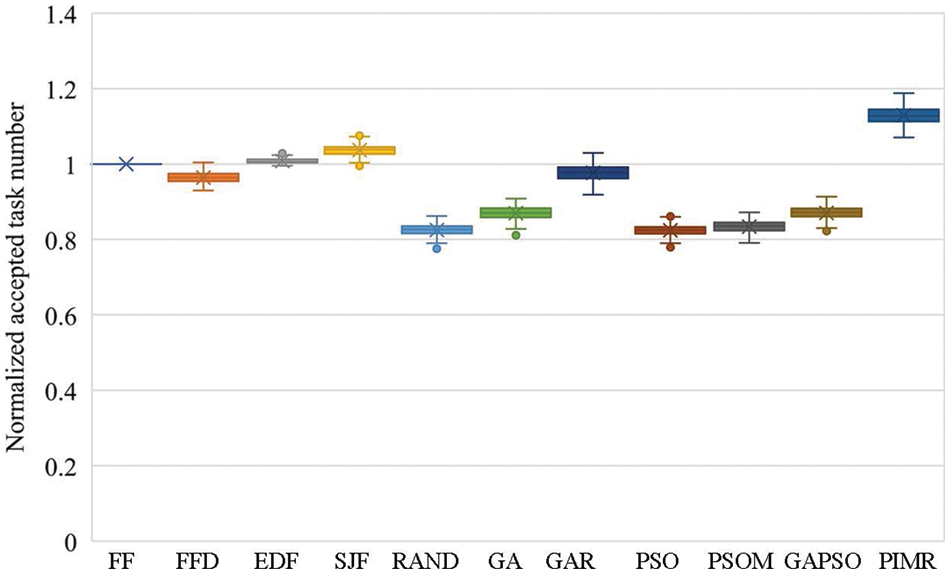
Figure 3: Normalized accepted task numbers achieved by different algorithms

From Fig. 3, it can be also seen that some meta-heuristic-based algorithms have poor performance than heuristic-based algorithms, even though meta-heuristics have global search abilities. The main reasons may be as followings. GA has a good global search ability due to its crossover and mutation operators. But GA has low convergence velocity, especially in large-scale search spaces including most cases of the task offloading problem in E2C. Therefore, GAR uses the replacement to take the place of the mutation operator, as done by the position updates of PSO, and achieves better performance than GA. PSO has a fast convergence rate, but easily falls into the local optimum. Therefore, in the offloading problem with a large-scale solution space, PSO has only slightly better performance than RAND. GAPSO only sequentially exploits GA and PSO, which is an inefficient combination approach and thus achieves comparable performance to GA or PSO.

5.2.2 Resource Efficiency

Fig. 4 shows the resource utilizations achieved by various offloading algorithms. This figure shows that heuristics have higher resource utilization than meta-heuristics. This is because heuristics prefer to process tasks locally and offload tasks to ES when local devices have full overloads. Only when there is no available local or edge resource, tasks are considered to be offloaded to CS by heuristics. This can lead to some delay-insensitive tasks being processed locally at first, and thus fewer tasks being offloaded to ES and CS, when applying heuristics, compared with meta-heuristics, resulting in less time consumed by data transfers. PIMR has a similar utilization to other meta-heuristics. Concerning the much better performance of PIMR in the acceptance ratio optimization, PIMR performs better than other meta-heuristics overall. Compared with heuristics, PIMR accepts more tasks at the cost of computing resource utilization. It's worth it because the acceptance ratio impacts not only the profit but also the reputation of service providers.

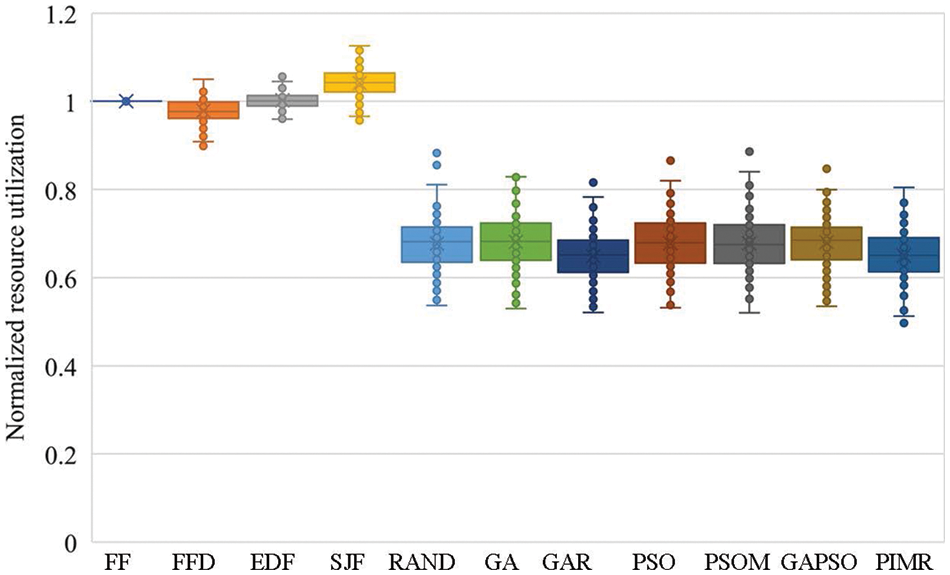
Figure 4: Normalized resource utilizations achieved by different algorithms

5.2.3 Processing Rate

Figs. 5 and 6 present the processing rates in computing and data processing, respectively. PIMR achieves fast computing and data processing rates, which are 12.2%–37.1% and 11.0%–39.7%, compared with other algorithms. These results confirm the high task processing efficiency of PIMR. This is because PIMR accepts much more tasks, i.e., processes more computing and data, than other offloading algorithms, as illustrated in Section 5.2.1. And all offloading algorithms have comparable makespan (the latest finish time of all accepted tasks) in our experiments.

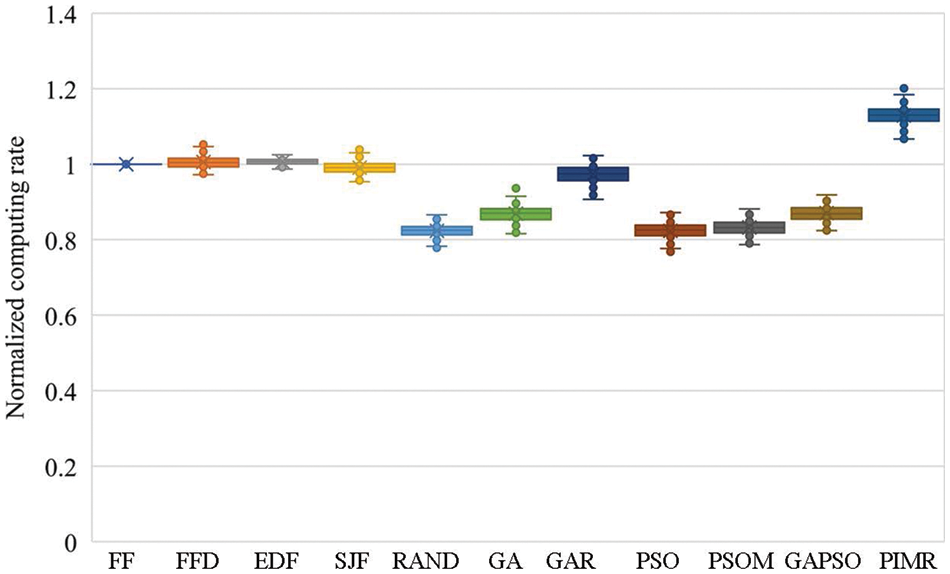
Figure 5: Normalized computing rates of various algorithms

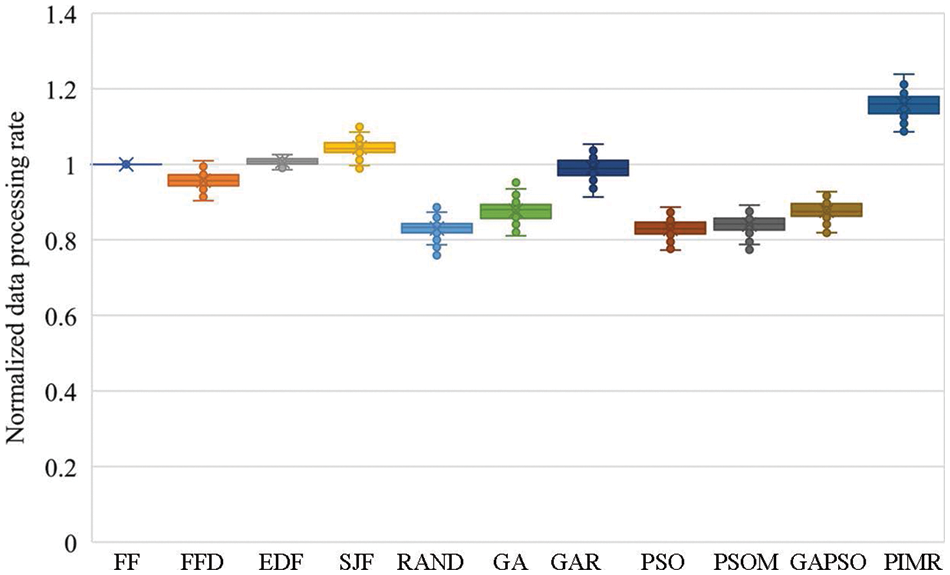
Figure 6: Normalized data processing rates of various algorithms

5.2.4 Performance of Imbalanced Mutation and Rescheduling

In this section, the impacts of the imbalanced mutation operator and the task rescheduling approaches on offloading algorithms are evaluated. Results are shown in Figs. 7 and 8. Where X_IM is the algorithm X exploiting the imbalanced mutation, respectively, in Fig. 6. X_RS is the offloading algorithm X integrated with the task rescheduling, in Fig. 8.

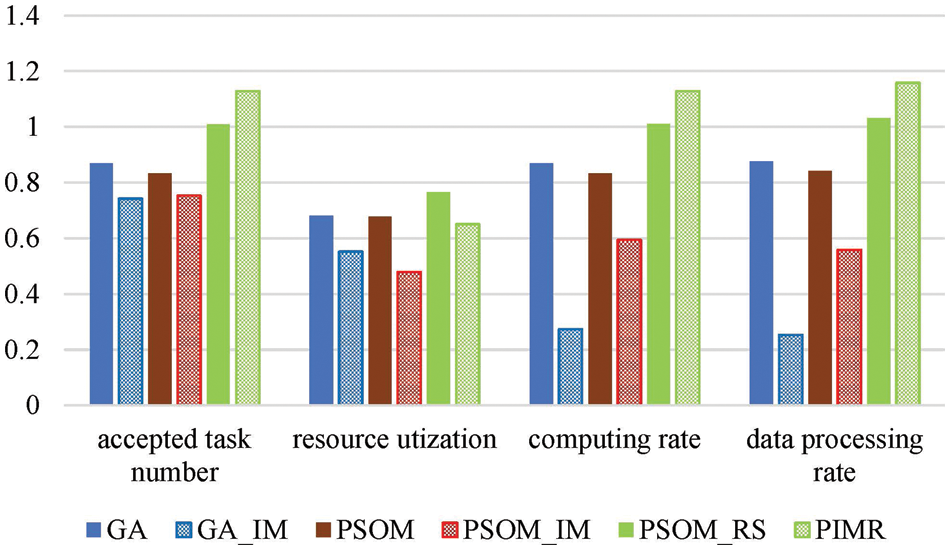
Figure 7: The impacts of the imbalanced mutation on offloading algorithms

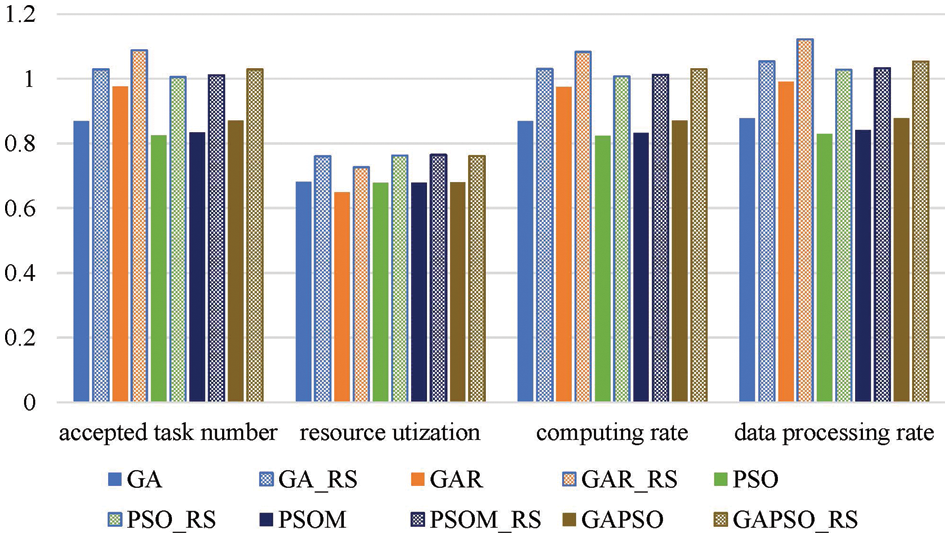
Figure 8: The improvement of the task rescheduling approach on various offloading algorithms

From Fig. 7, it can be seen that the imbalanced mutation degrades the performance of GA and PSOM, which is contrary to our original purpose of aiming at increasing the probability that algorithms converge to the global optimum for the offloading problem. The reason for the adverse effects on the performance improvement of the imbalanced mutation may be that the solution space is so huge that it’s very rare that an individual is updated into a region including an optimal solution. In addition, the imbalanced mutation can speed up the convergence rate, and thus make it easy that offloading algorithms to be trapped into local optima when no individual is moved into a global best region. But the imbalanced mutation has a good complementarity with the task rescheduling approach, as shown in Fig. 7, PIMR has better performance than PSOM_RS in both service quality and processing rate. This gives us an inspiration that some designed improvement schemes may have reverse effects, but they may be complementary to others, and their joint application can perform much better than their application alone. Fig. 8 shows that the rescheduling approach can improve offloading algorithms by 11.2%–23.8% in various performance metrics.

6  Conclusion

This paper studies the task offloading problem in E2C environments. This paper first formulates the problem into a BNLP, where the objective is maximizing the accepted task number, which is one of the commonly used metrics for quantifying service quality and user satisfaction. To solve the problem with polynomial time complexity, this paper proposes a task offloading algorithm, PIMR, based on PSO. And to improve the performance, PIMR integrates two improvement approaches in PSO, the imbalanced mutation and the task rescheduling. At last, this paper evaluates the performance of PIMR through extensive experiments, and the results confirm the performance superiority of the proposed algorithm in various aspects. Experiment results show that PIMR has an 8.93%-37.0% higher acceptance ratio and 11.0%–39.7% processing rate, compared with ten classical and up-to-date algorithms, and the imbalanced mutation and the task rescheduling jointly do have an improvement in PIMR. In this paper, we only focus on independent tasks, which are common in e.g., data processing and Web applications. In the future, we will extend our work to support the offloading of interdependent in E2C, to expand the application scope.

Funding Statement: The research was supported by the key scientific and technological projects of Henan Province with Grant No. 232102211084, the Natural Science Foundation of Henan with Grant No. 222300420582, the Key Scientific Research Projects of Henan Higher School with Grant No. 22A520033, Zhengzhou Basic Research and Applied Research Project with Grant No. ZZSZX202107, and China Logistics Society with Grant No. 2022CSLKT3-334.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Zhang, F. Lyu, P. Yang, W. Wu and J. Gao, “IoT intelligence empowered by end-edge-cloud orchestration,” China Communications, vol. 19, no. 7, pp. 152–156, 2022. [Google Scholar]

2. F. Saeik, M. Avgeris, D. Spatharakis, N. Santi, D. Dechouniotis et al., “Task offloading in edge and cloud computing: A survey on mathematical, artificial intelligence and control theory solutions,” Computer Networks, vol. 195, pp. 108177, 2021. [Google Scholar]

3. B. Wang, Y. Song, Y. Sun and J. Liu, “Analysis model for server consolidation of virtualized heterogeneous data centers providing internet services,” Cluster Computing, vol. 22, no. 3, pp. 911–928, 2019. [Google Scholar]

4. X. Wang, J. Li, Z. Ning, Q. Song, L. Guo et al., “Wireless powered mobile edge computing networks: A survey,” ACM Computing Survey, In Press, 2023. https://doi.org/10.1145/3579992 [Google Scholar] [CrossRef]

5. B. Wang, C. Wang, W. Huang, Y. Song and X. Qin, “A survey and taxonomy on task offloading for edge-cloud computing,” IEEE Access, vol. 8, pp. 186080–186101, 2020. https://doi.org/10.1109/ACCESS.2020.3029649 [Google Scholar] [CrossRef]

6. M. Y. Akhlaqi and Z. B. Mohd Hanapi, “Task offloading paradigm in mobile edge computing-current issues, adopted approaches, and future directions,” Journal of Network and Computer Applications, vol. 212, no. 10, pp. 103568, 2023. [Google Scholar]

7. Y. Sang, J. Cheng, B. Wang and M. Chen, “A three-stage heuristic task scheduling for optimizing the service level agreement satisfaction in device-edge-cloud cooperative computing,” PeerJ Computer Science, vol. 8, no. 3, pp. e851, 2022. [Google Scholar] [PubMed]

8. C. Wang, R. Guo, H. Yu, Y. Hu, C. Liu et al., “Task offloading in cloud-edge collaboration-based cyber physical machine tool,” Robotics and Computer-Integrated Manufacturing, vol. 79, no. 8, pp. 102439, 2023. [Google Scholar]

9. B. Wang, J. Cheng, J. Cao, C. Wang and W. Huang, “Integer particle swarm optimization based task scheduling for device-edge-cloud cooperative computing to improve SLA satisfaction,” PeerJ Computer Science, vol. 8, no. 5, pp. e893, 2022. [Google Scholar] [PubMed]

10. T. Gao, Q. Tang, J. Li, Y. Zhang, Y. Li et al., “A particle swarm optimization with Lévy flight for service caching and task offloading in edge-cloud computing,” IEEE Access, vol. 10, pp. 76636–76647, 2022. [Google Scholar]

11. B. Wang, B. Lv and Y. Song, “A hybrid genetic algorithm with integer coding for task offloading in edge-cloud cooperative computing,” IAENG International Journal of Computer Science, vol. 49, no. 2, pp. 503–510, 2022. [Google Scholar]

12. S. Chakraborty and K. Mazumdar, “Sustainable task offloading decision using genetic algorithm in sensor mobile edge computing,” Journal of King Saud University—Computer and Information Sciences, vol. 34, no. 4, pp. 1552–1568, 2022. [Google Scholar]

13. J. Yadav and Suman, “E-MOGWO algorithm for computation offloading in fog computing,” Intelligent Automation & Soft Computing, vol. 36, no. 1, pp. 1063–1078, 2023. https://doi.org/10.32604/iasc.2023.032883 [Google Scholar] [CrossRef]

14. Q. Xu, G. Zhang and J. Wang, “Research on cloud-edge-end collaborative computing offloading strategy in the internet of vehicles based on the M-TSA algorithm,” Sensors, vol. 23, no. 10, pp. 4682, 2023. [Google Scholar] [PubMed]

15. M. S. Bali, K. Gupta, D. Gupta, G. Srivastava, S. Juneja et al., “An effective technique to schedule priority aware tasks to offload data on edge and cloud servers,” Measurement: Sensors, vol. 26, pp. 100670, 2023. [Google Scholar]

16. A. A. Hussain and F. Al-Turjman, “Hybrid genetic algorithm for IOMT-cloud task scheduling,” Wireless Communications and Mobile Computing, vol. 2022, no. 5, pp. 6604286, 2022. [Google Scholar]

17. N. E. Nwogbaga, R. Latip, L. S. Affendey and A. R. Abdul Rahiman, “Attribute reduction based scheduling algorithm with enhanced hybrid genetic algorithm and particle swarm optimization for optimal device selection,” Journal of Cloud Computing, vol. 11, pp. 15, 2022. [Google Scholar]

18. A. Farsi, S. Ali Torabi and M. Mokhtarzadeh, “Integrated surgery scheduling by constraint programming and meta-heuristics,” International Journal of Management Science and Engineering Management, In Press, 2022. [Online]. Available: https://doi.org/10.1080/17509653.2022.2093289 [Google Scholar] [CrossRef]

19. J. Zhang, Z. Ning, R. H. Ali, M. Waqas, S. Tu et al., “A many-objective ensemble optimization algorithm for the edge cloud resource scheduling problem,” IEEE Transactions on Mobile Computing, In Press, 2023. [Online]. Available: https://doi.org/10.1109/TMC.2023.3235064 [Google Scholar] [CrossRef]

20. X. Xu, B. Shen, S. Ding, G. Srivastava, M. Bilal et al., “Service offloading with deep Q-network for digital twinning-empowered internet of vehicles in edge computing,” IEEE Transactions on Industrial Informatics, vol. 18, no. 2, pp. 1414–1423, 2020. [Google Scholar]

21. M. Berkelaar, K. Eikland and P. Notebaert, “lp_solve 5.5, open source (mixed-integer) linear programming system,” 2004. [Online]. Available: http://lpsolve.sourceforge.net/5.5/ [Google Scholar]

22. MathWorks, Inc., “Optimization toolbox: Solve linear, quadratic, conic, integer, and nonlinear optimization problems,” 2022. [Online]. Available: https://ww2.mathworks.cn/en/products/optimization.html [Google Scholar]

23. C. Huang, X. Zhou, X. Ran, J. Wang, H. Chen et al., “Adaptive cylinder vector particle swarm optimization with differential evolution for UAV path planning,” Engineering Applications of Artificial Intelligence, vol. 121, no. 3, pp. 105942, 2023. [Google Scholar]

24. S. Tiwari and A. Kumar, “Advances and bibliographic analysis of particle swarm optimization applications in electrical power system: Concepts and variants,” Evolutionary Intelligence, vol. 16, no. 1, pp. 23–47, 2023. [Google Scholar]

25. Y. Xue, Q. Zhang and A. Slowik, “Automatic topology optimization of echo state network based on particle swarm optimization,” Engineering Applications of Artificial Intelligence, vol. 117, pp. 105574, 2023. [Google Scholar]

26. Amazon Web Services, Inc., “Cloud computing services—Amazon Web Services (AWS),” 2023. [Online]. Available: https://aws.amazon.com/ [Google Scholar]