 Open Access
Open Access
ARTICLE
Numerical Comparison of Stagnation Point Casson Fluid Stream over Flat and Cylindrical Surfaces with Joule Heating and Chemical Reaction Impacts
1
Department of Engineering Mathematics, Koneru Lakshmaiah Education Foundation, Vaddeswaram, Guntur, 522302, India
2
Department of Mathematics, Dhanekula Institute of Engineering & Technology, Ganguru, Vijayawada, 521139, India
* Corresponding Author: Sridhar Wuriti. Email:
Frontiers in Heat and Mass Transfer 2023, 21, 407-426. https://doi.org/10.32604/fhmt.2023.043305
Received 28 June 2023; Accepted 28 July 2023; Issue published 30 November 2023
Abstract
In this particular study, we have considered the flow of Casson fluid over inclined flat and cylindrical surfaces, and have conducted a numerical analysis taking into account various physical factors such as mixed convection, stagnation point flow, MHD, thermal radiation, viscous dissipation, heat generation, Joule heating effect, variable thermal conductivity and chemical reaction. Flow over flat plate phenomena is observed aerospace industry, and airflow over solar panels, etc. Cylindrical surfaces are commonly used in several applications interacting with fluids, such as bridges, cables, and buildings, so the study of fluid flow over cylindrical surfaces is more important. Due to the motivation of these applications, in this paper, a comparative study of fluid flow over these two surfaces is considered. By applying appropriate similarity transformations, the governing PDEs of the problem have been transformed into non-linear ODEs, which are solved by utilizing the Keller box technique. We have examined the impact of distinct parameters by plotting velocity and thermal concentration graphs. All the profiles are plotted in both cases of cylindrical and inclined flat surface. It has been observed that for higher Casson and Magnetic parameter values, a decreasing velocity profile is noted for progressive values of the Eckert Number, thermal conductivity parameter, Joule heating parameter, heat generation, and growth in temperature profiles are witnessed. While the Prandtl number shows the opposite trend. Further, it has been observed that the concentration profile declines for incremental observations of Schmidt number and chemical reaction parameters. Computed Local parameters like the coefficient of skin friction for various values of Casson parameter and Curvature parameter, Skin friction value increases for increasing observations of Curvature parameter the phenomena agree with existing literature. Also, Nusselt number is calculated for various observations of curvature and variable thermal conductivity parameters. Nusselt number decreases in magnitude with rising observations of varying thermal conductivity argument at both flat and cylindrical surfaces. The values are matched with prevailing results and noted a good agreement.Keywords
Nomenclature
| x, r | Cylindric coordinates |
| u, v | Components of velocity |
| Angle of inclination | |
| Β | Casson argument |
| Kinematic viscosity coefficient ( | |
| Acceleration due to gravity ( | |
| Solutal expansion coefficient | |
| Thermal expansion coefficient (per ° | |
| Magnetic constraint | |
| Pr | Prandtl number |
| Sc | Schmidt number |
| Free stream temperature | |
| T | Fluid temperature |
| B0 | Magnetic field constant |
| C | Fluid Concentration (mol/m3) |
| Free stream concentration | |
| Free stream velocity | |
| Electrical conductivity (s/m) | |
| Specific heat (J/Kg.K) | |
| Q | Heat flux (W/m2) |
| K | Thermal conductivity (W/mk) |
| Chemical reaction parameter | |
| Variable thermal conductivity parameter | |
| A | Velocity ratio parameter |
| Rd | Thermal radiation parameter |
| Concentration Grashof number | |
| Thermal Grashof number | |
| Mass diffusivity parameter | |
| Ec | Eckert number |
| Curvature parameter | |
| Γ | Chemical reaction parameter |
The widespread occurrence of non-Newtonian fluid behaviour in various applications, including natural and technological ones. After introducing the concept of non-Newtonian fluids, a brief overview of their distinct features is mentioned [1]. Under convective boundary conditions, an incompressible mixed convection immobility point flow non-Newtonian fluid over an elongating sheet is analyzed by Hayat et al. [2]. Mukhopadhyay et al. [3] investigated the turbulent non-Newtonian 2-dimensional fluid stream over an extending surface with a predetermined surface temperature using the shooting method. Swathi Mukhopadhyay conducted a numerical analysis of non-Newtonian fluid flow and heat transfer over a non-linearly stretched surface using the shooting method [4]. An incompressible three-dimensional Casson fluid Porous boundary layer flow is examined under the influence of MHD by Hayat et al. [5]. Non-Newtonian boundary layer flow was numerically explored by suction or blowing heat transfer fluid at the surface towards an exponentially increasing surface by Pramanik [6]. Bhattacharya [7] studied the stagnation point flow of Casson fluid flow with the influence of thermal radiation and concluded that the heat transfer rate increases for enhanced values of the magnetic parameter. Medikare et al. [8] explored the immobility point flow of Casson fluid flow over a nonlinear extending sheet and concluded that the rate of heat transfer and wall friction drag enhances progressive amounts of the Casson argument. Unsteady free convective MHD boundary layer analytical expression, thermal radiation and chemical reaction are achieved from the Casson fluid flow past an oscillating vertical plate numerically analyzed by Kataria et al. [9]. Rauf et al. [10] studied 3-dimensional Casson Nanofluid stream using the RK Fehlberg technique and observed that the level of mass transfer enhances for progressive observations of the Biot number and Brownian movement argument. Ajayi et al. [11] studied the issue of non-Newtonian fluid flow past an object’s upper surface that is neither perfectly horizontal/vertical is taken into consideration. In this problem, energy dissipation is convected to temperature-dependent plastic dynamic viscosity. Siddiq et al. [12] studied the stagnation point flow of micropolar Nanofluid over a shrinking sheet and concluded that decrement in concentration profiles is witnessed for progressive values of the Schmidt number and Brownian motion parameter. Later, Anantha Kumar et al. [13] investigated thermal radiation influence on Casson fluid course across a curved elongating sheet using the RK shooting technique and concluded that the velocity of the fluid declines in both cases of increasing observations of magnetic and Casson parameter values. Raza [14] investigated the combined velocity slip and thermal radiation effects on a stretched sheet that has been convective. Another fact taken into account is the Magnetohydrodynamics (MHD) effect close to the stagnation point. In an electrically conducting Casson fluid stream via a slanted permeable micro channel, the combined impacts of the magnetic field, suction/injection, and convective exterior conditions were analyzed by Gireesha et al. [15]. Study of the impact of thermal diffusion and heat production on MHD, the chemical reaction is obtained by allowing Casson fluid to flow past an oscillating vertical plate inserted through porous material analyzed by Patel et al. [16]. Nusselt number enhances progressive observations of Magnetic and volume fraction parameters discussed by Khan et al. [17] in the analysis of hybrid nanofluid flow over stretching surface. Bejan number and entropy generation have similar impacts on electric field influence concluded by Hayat et al. [18]. The basics of various thermophysical characteristics of higher-order chemical reactions, including the viscous dissipation on nanofluid, and continuously extending porous sheet are considered and analyzed by Gopal et al. [19]. After that, Khan et al. [20–24] studied entropy exploration with melting heat effect, radiation, and porosity and concluded that the impact of heat conductivity on ternary Nanofluid and concludes that for enhanced observation of radiation temperature of fluid enhances and consequently rise in entropy is observed. Temperature losses for augmented amounts of Prandtl number in the case of Reiner Rivlin fluid flow over a stretching sheet. Velocity profiles decline for porosity in both cases of nanoparticles, whereas the opposite effect is witnessed in the case of entropy generation. Radiation influence for higher values of magnetic parameter temperature and entropy enhancement is noted in an analysis of entropy exploration study on Prandtl fluid flow. The heat source and MHD blended convection fluid course across a slanted flat plate in Casson theory numerically using the shooting method analyzed by Ramzan et al. [25]. Ganesh et al. [26] observed entropy exploration on Casson Nanofluid flow with the influence of higher order chemical reaction and concludes for higher amounts of the order of chemical reaction constraint Nusselt number enhances and the Sherwood number declines. Reddy et al. [27] considered Casson fluid flow with Soret, Joule heating, and viscous dissipation influences utilizing Homotopy analysis technique. Satya narayana et al. [28] concluded in their study that temperature enhances with an increase in the Eckert number and variable thermal conductivity parameter. Hayat et al. [29] examined the Casson fluid flow approaches a stretching surface near its stagnation point and conclude that Nusselt number decreases for progressive values of the Eckert number. Abbas et al. [30] explored heat and mass relocation in an unstable exterior layer Casson fluid course over an extending/shrinking sheet with radiation influence with the Spectral collocation quasi-linearization method. Ramesh et al. [31] analyzed Casson fluid flow across a stretching sheet with adaptive thickness and radiation. Sridhar et al. [32] examined the hydromagnetic Williamson Nanofluid over an absorbent media past an extending sheet with constant and erratic thickness. Also, Ganesh et al. [33] examined the heat transmission of a Casson nanofluid through an absorbent medium over a movable plate with changeable heat conductivity, adjustable thickness and chemical reaction. Waqas et al. [34] investigated heat transmission of radiative Nanofluid flow across a cylinder and concluded that temperature distribution enhances progressive values of the magnitude of nanoparticles. Bilal et al. [35] examined Williamson Nanofluid flow over a cylinder with adaptive thermal conductivity and observed that the Nanofluid’s velocity reduces for higher Weissenberg number values. Islam et al. [36] analyzed the thermal influence on mixed convection flow of Maxwell nanofluid over a bidirectional stretching cylinder and concluded that concentration increases for the thermal diffusion and reduces for the Brownian motion argument. Later Rehman et al. [37] investigated the immobility point Casson fluid stream upon slanted flat and cylindric surfaces and found that the Nusselt number decreases with enhanced values of the thermal conductivity. The velocity of Casson fluid decreases in all cases of a flat and cylindrical surfaces. A Casson fluid is the most appropriate flow model for non-Newtonian fluids. Casson fluids exhibit yield stress and have numerous applications. If shear stress is less than the elastic limit, Casson fluid acts similar to an elastic solid and no flow occurs. On the other hand, if shear stress is greater than yield stress it ensures the flow of Casson fluid. Few specific examples of Casson fluid are emulsions, slurries, and artificial fibres. The contribution of Casson fluid can be witnessed in the preparation of multiple products such as synthetic lubricants, pharmaceutical chemicals, paints, etc.
As heat transfer involves transferring and converting energy, it is important to define the specified level of heat exchange at a specified temperature modification. It is imperative for some components, such as turbine blades, electrical machines, electronic gadgets, transformers, bearings, etc, to remove thermal energy at a quick rate to prevent overheating. Therefore, it is essential to understand how heat transfers and the governing laws of heat transfer. By mass transfer, we mean the transfer of matter based on a concentration difference between species in a system. It has several applications in the fields of science, engineering and technology. As a result of its importance in a wide variety of industrial and scientific applications, stagnation point flow continues to be an interesting area of research for scientists and investigators. Stagnation flow is useful for designing thrust bearings and radial diffusers, reducing drag, and cooling by transpiration. Radiation is the heat transfer process that happens using electromagnetic waves. The transmission of heat by radiation comprises the drift of heat energy from the origin to the space surrounded by it. The movement of energy can be carried out by using electromagnetic waves. Energy is transferred by thermal radiation in combustion chambers, furnaces, and nuclear explosions. The Joule heating effect is the process of creating heat when a current passes through an electrical conductor. Joule heating is used in many heating devices, such as electric stoves, electric heaters, soldering irons, cartridge heaters, and food processing equipment. Flow over flat plate phenomena is observed aerospace industry, and airflow over solar panels, etc. Cylindrical surfaces are commonly used in several applications interacting with fluids, such as bridges, cables, buildings, so the study of fluid flow over cylindrical surface has a greater importance.
Due to the motivation of these applications, In this paper, a comparative study of Casson fluid flow over these two surfaces is taken into consideration. In the present study, Casson fluid’s two-dimensional stagnation point flow is analyzed on both flat and cylindrical surfaces with the influences of radiation, mixed convection, MHD, heat source, Joule heating, viscous dissipation and chemical reaction. Here a magnetic field is applied externally to fluid flow. The governing equations are explained by Keller Box numerical technique.
We considered the two-dimensional Casson fluid stream, Inclined at an angle α at both flat and cylindric surfaces. Here u and v are components of velocity towards the r-axis and x-axis Flow over surface is affected by MHD, Chemical reaction, viscous dissipation, radiation, Joule heating, variable thermal conductivity and mixed convection. The geometry of the problem is mentioned in Fig. 1. The basic equations of continuity and momentum, and energy in vector form are taken as
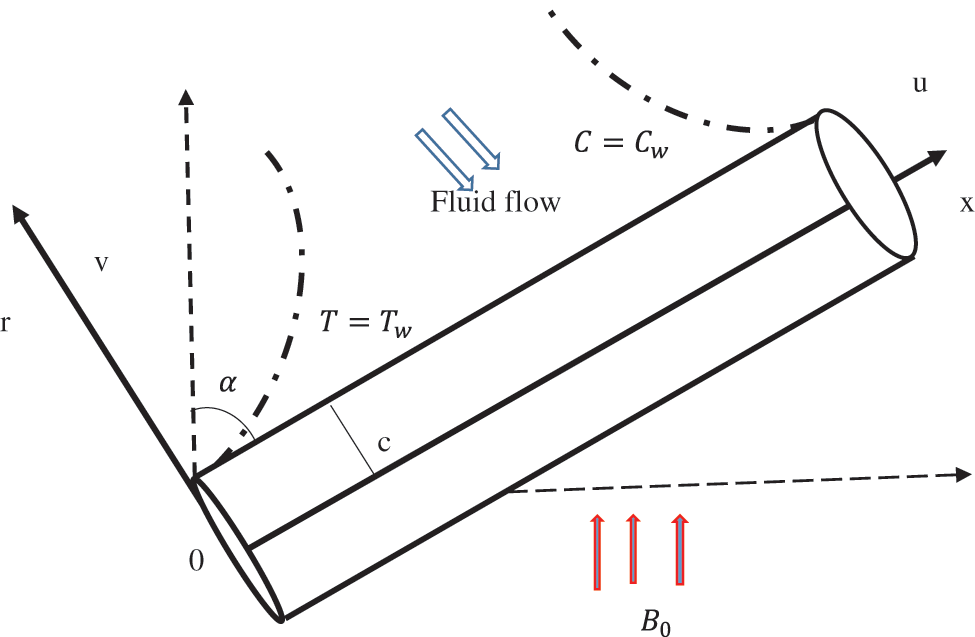
Figure 1: Problem’s flow model
Based on these suppositions, the leading partial differential equations [34–36] are
In this case, the boundary conditions are as follows:
Corresponding similarity transformations [36] are
By utilizing the similarity transforms, the governing Eqs. (2)–(4) are converted to
and the converted boundary conditions
Using,
Using the concept of finite differences, convert the equations to difference equations and linearize them using Newton’s method.
The system of linear equations are
where,
Further, the resultant system of linear equations is solved using Block tri-diagonal elimination technique and solved using LU decomposition method.
The matrix form of equations [15] is
where,
To validate the method, the current outcomes are matched with old literature.
The influence of distinct parameters is analyzed by plotting graphs for both cases of a flat plate (G = 0), Cylindrical surface (G = 0.4) with MATLAB.
Here for all the graphs, we considered curvature parameter G = 0.0 for flat plate and G = 0.4 for cylindrical surfaces. Fig. 2 shows the velocity graphs of the Casson argument. For enhanced values of the Casson parameter, the velocity is found to be decreasing in both cases of flat plate and cylindrical surface. For higher values of the Casson parameter, the viscosity of the fluid increases, which causes the thickness of the momentum boundary layer to decrease so a decrement in velocity profiles is witnessed. Fig. 3 portrays the velocity profiles of the Magnetic constraint. A decrement in velocity graphs is noted for progressive observations of the Magnetic parameter. With augmented amounts of magnetic parameters, a force called Lorentz force will be produced due to this flow speed of fluid reduction observed. The same phenomena are observed in both cases of flat and cylindrical surfaces. Fig. 4 displays velocity profiles for increasing observations of the velocity ratio parameter. We observed that Casson fluid velocity is straightaway influenced by the velocity ratio argument, with higher observations of the argument leading to higher magnitudes of the velocity of the fluid. Prandtl number is the ratio of momentum diffusivity to thermal diffusivity. It is particularly useful in controlling the relative thickness of momentum and thermal boundary layers. For smaller values of the Prandtl number, heat diffuses quickly. Fig. 5 depicts temperature profiles of enhanced observations of Prandtl number. Increasing the Prandtl number, a decrease in heat conductivity is noted. So the temperature declination happens. The same phenomenon is observed in both cases of flat and cylindrical surfaces. Fig. 6 discloses temperature profiles of heat generation argument. For enhanced values of heat generation parameter, temperature growth is noted in both cases of flat and cylindrical surfaces. Thermal conductivity is the property of a material to transfer heat from a region of high temperature to a low temperature. Fig. 7 portrays temperature graphs of the thermal conductivity constraint. For increasing observations of thermal conductivity parameter temperature distribution enhances in both cases of flat and cylindrical surfaces. Fig. 8 shows temperature outlines of Eckert number. For enhanced observations of Eckert number, The driving force of the fluid is converted to internal energy, so temperature enhancement is observed in profiles. The Joule heating effect enhances the heat transfer process. Fig. 9 depicts the temperature graphs of Joule heating. For enhanced observations of the Joule heating parameter, it produces electricity in the conductor consequently it raises the temperature distribution in both cases of Flat and cylindrical surfaces. Schmidt number is the ratio of momentum spreading to mass spreading. Fig. 10 displays concentration sketches of Schmidt number. For increasing units of Schmidt number, mass transfer enhancement is witnessed so concentration profiles decrease in both cases. Fig. 11 depicts the concentration graphs of the Chemical reaction argument. For higher values of the chemical reaction argument, chemical molecular diffusivity decreases, so the fluid concentration decreases. This phenomenon we can observe in both cases of flat and cylindrical surfaces.
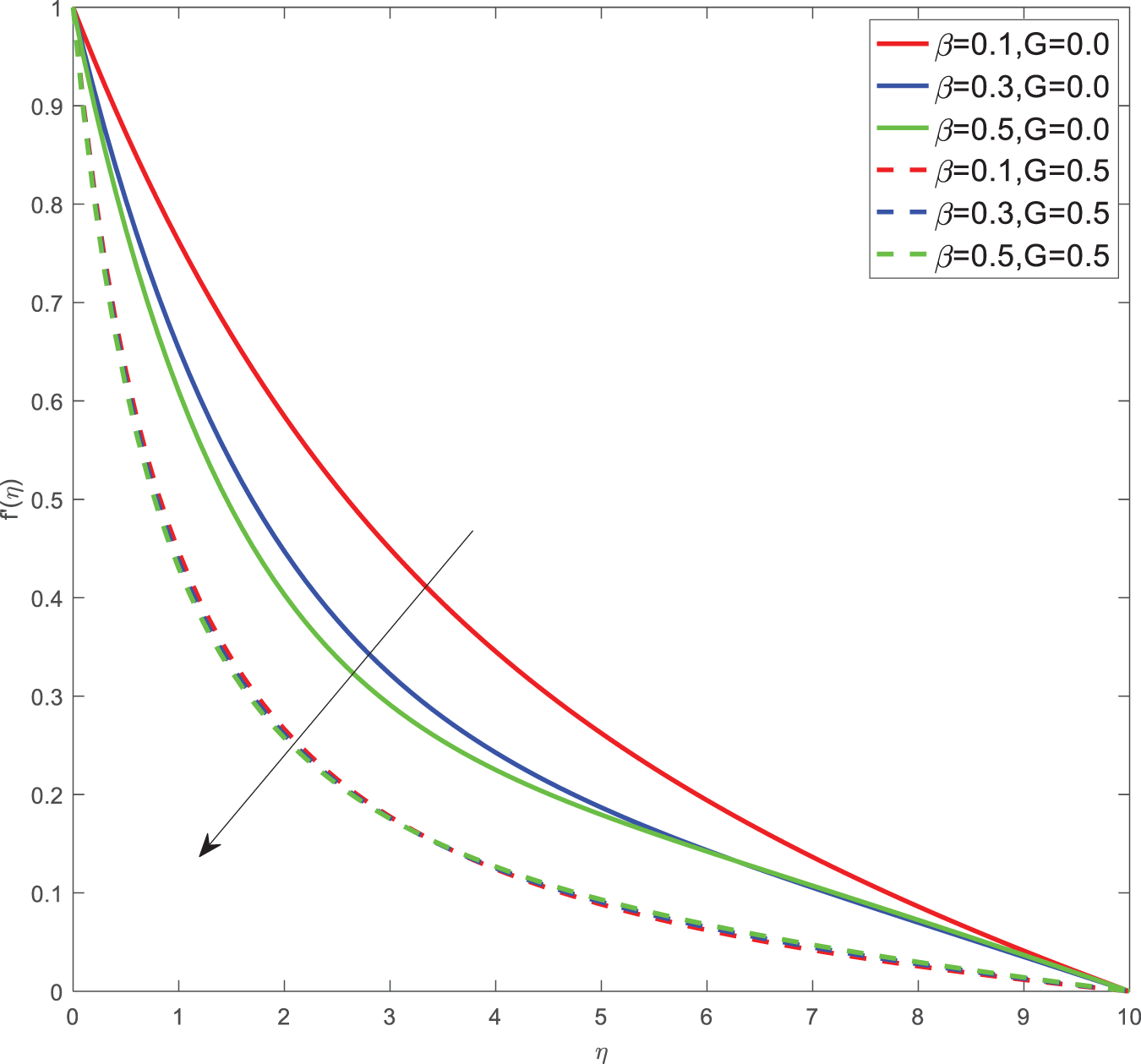
Figure 2: Velocity profiles for

Figure 3: Velocity profiles of M, G
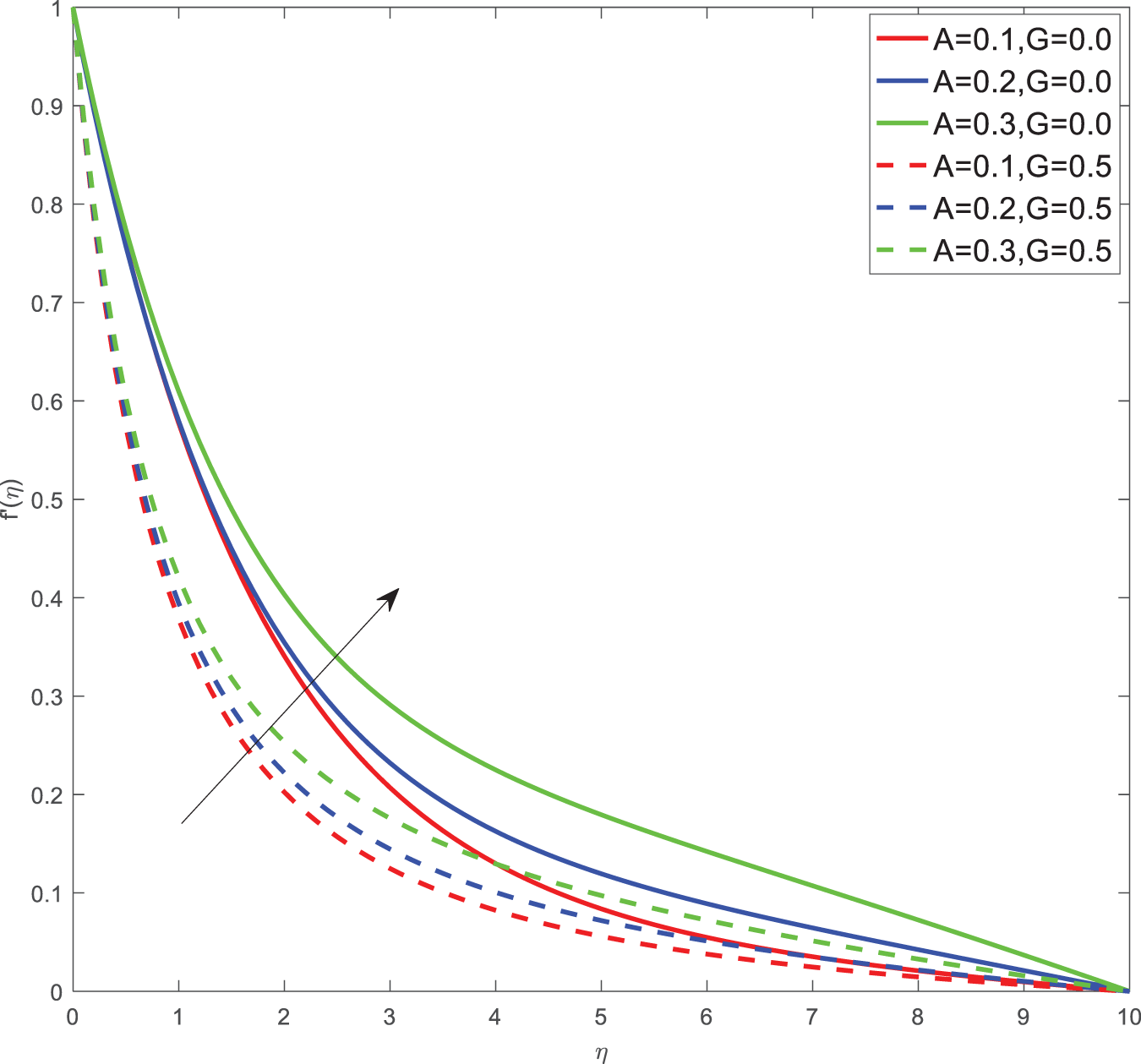
Figure 4: Velocity profiles of A, G
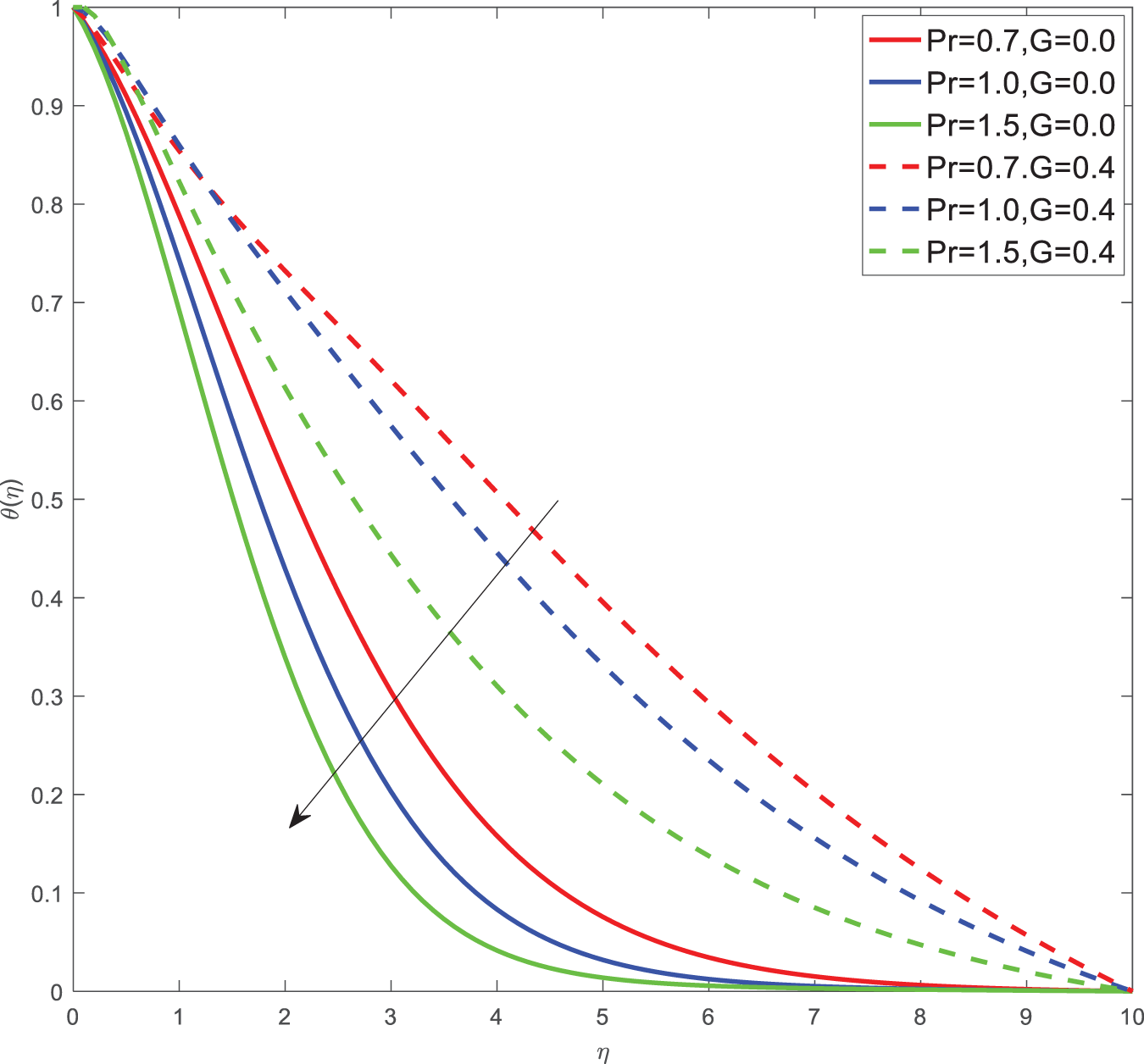
Figure 5: Temperature outlines of Pr, G
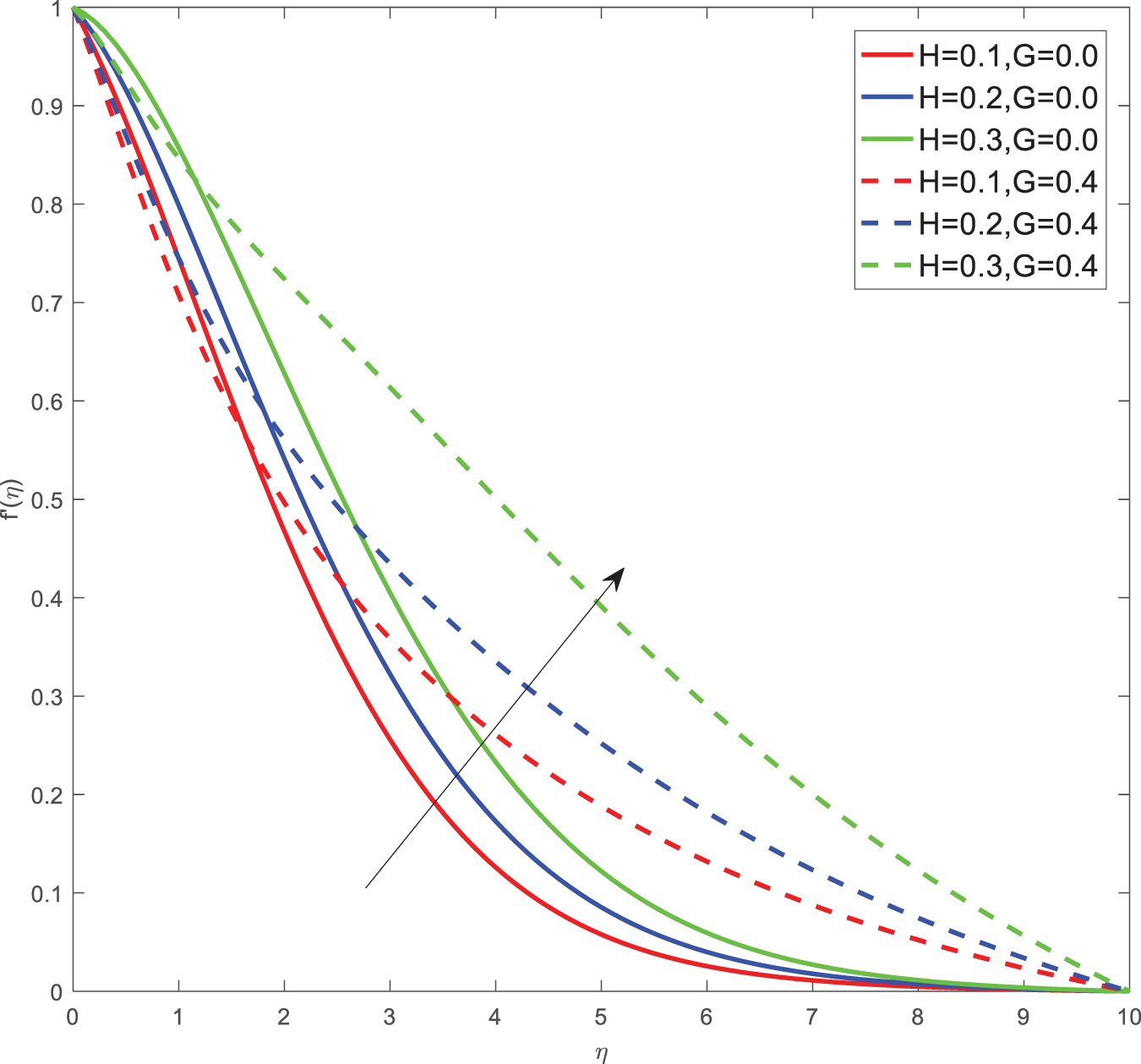
Figure 6: Temperature outlines of H, G
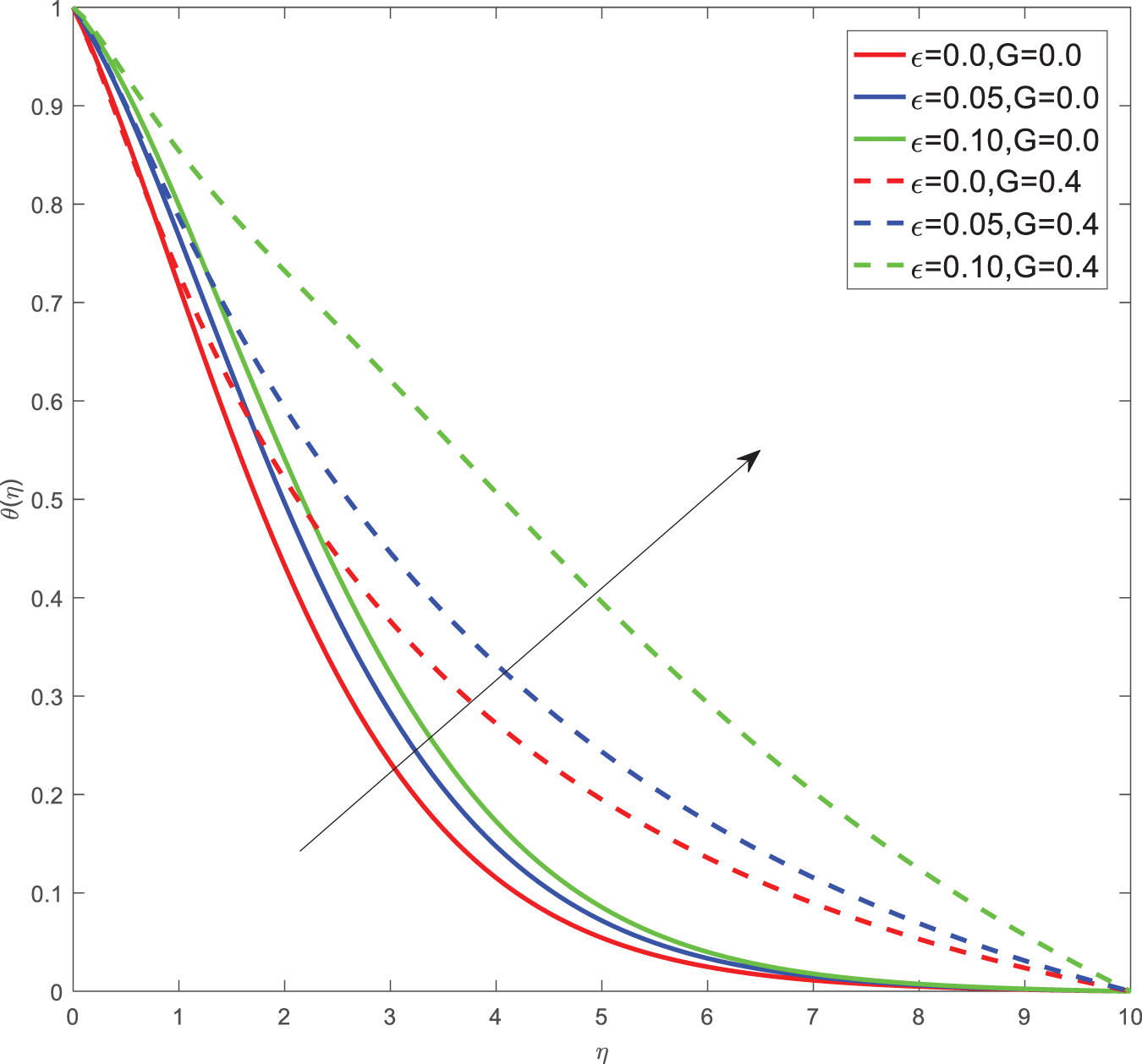
Figure 7: Temperature outlines of
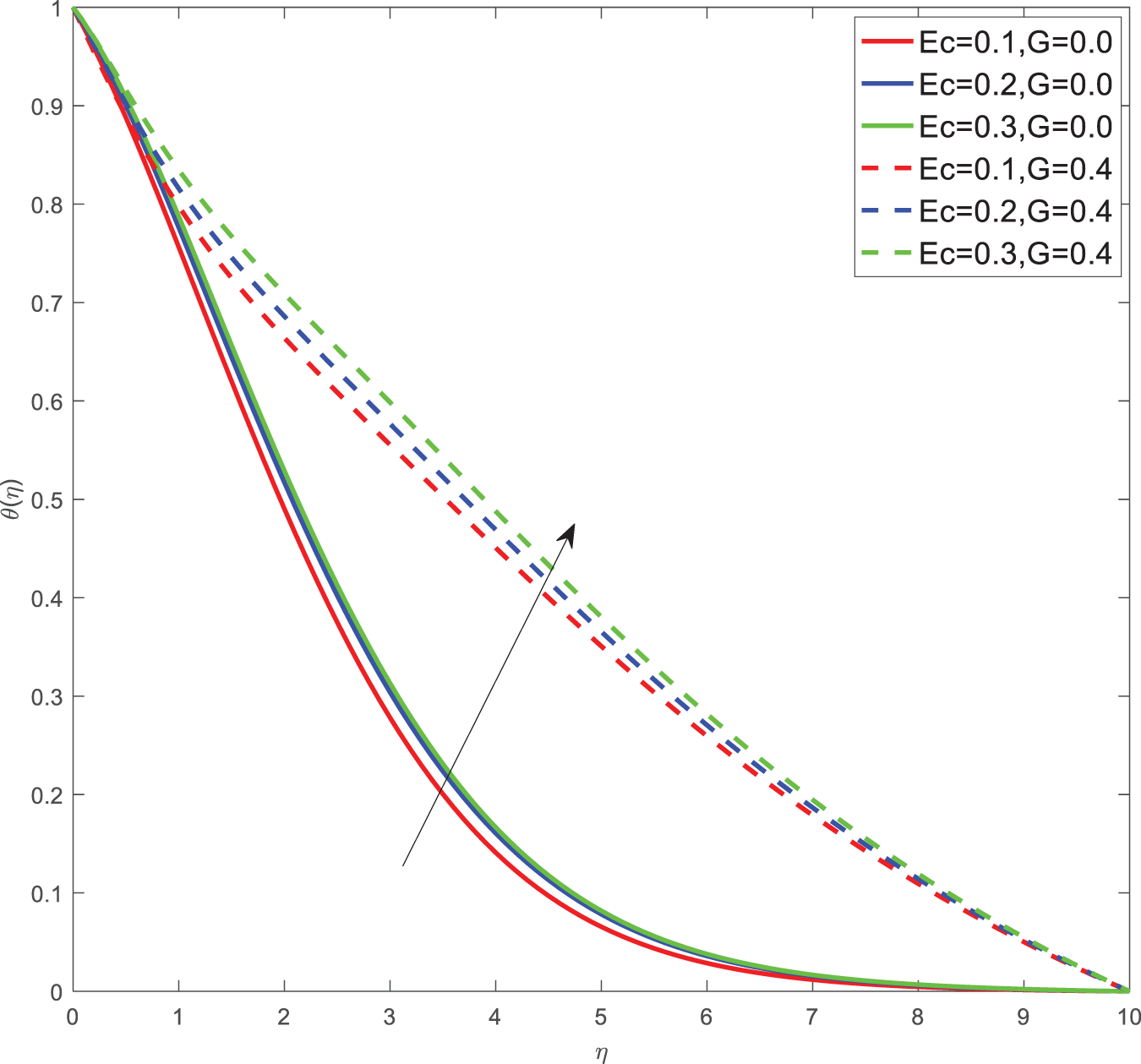
Figure 8: Temperature outlines of Ec, G
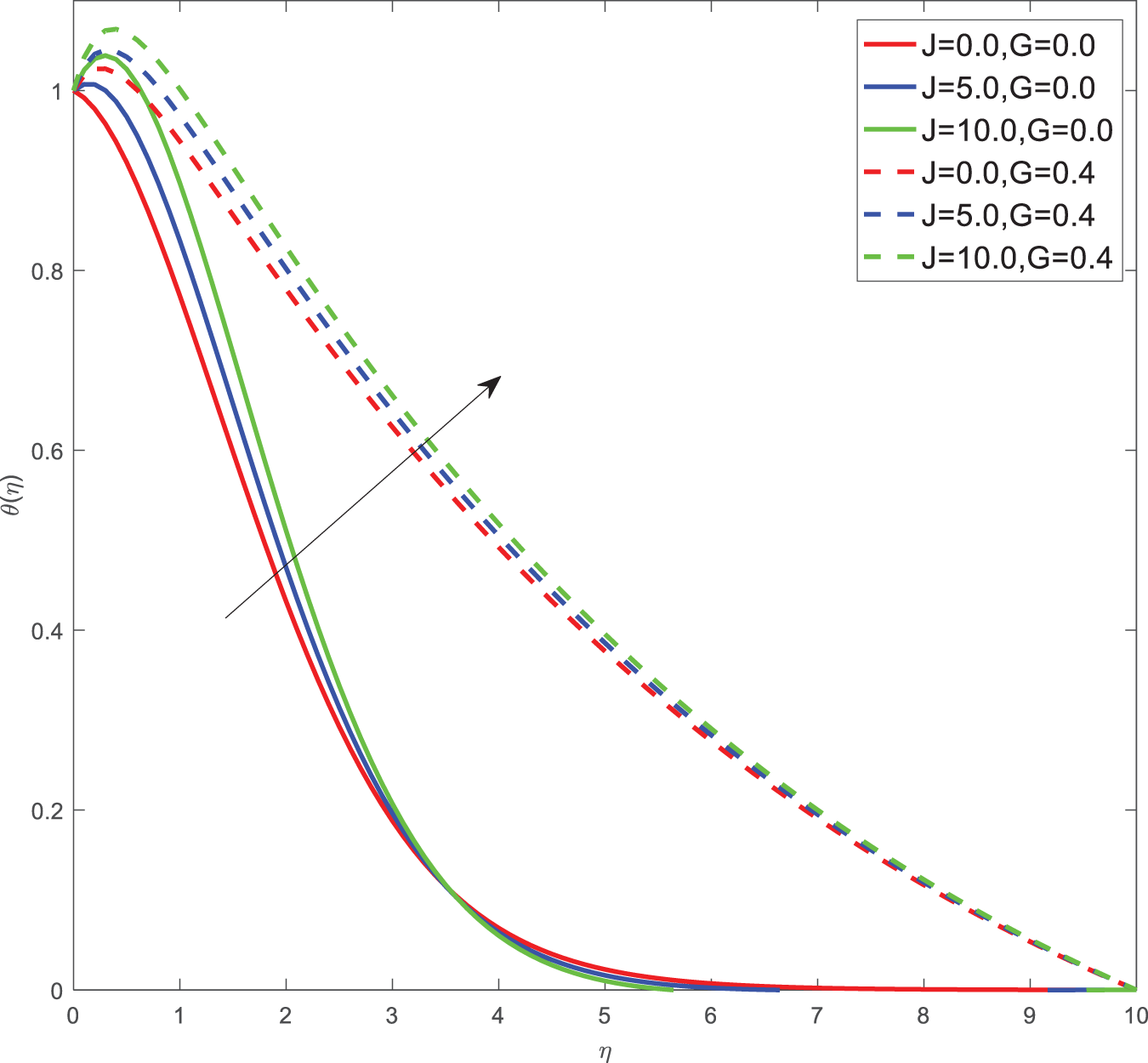
Figure 9: Temperature profiles of J, G
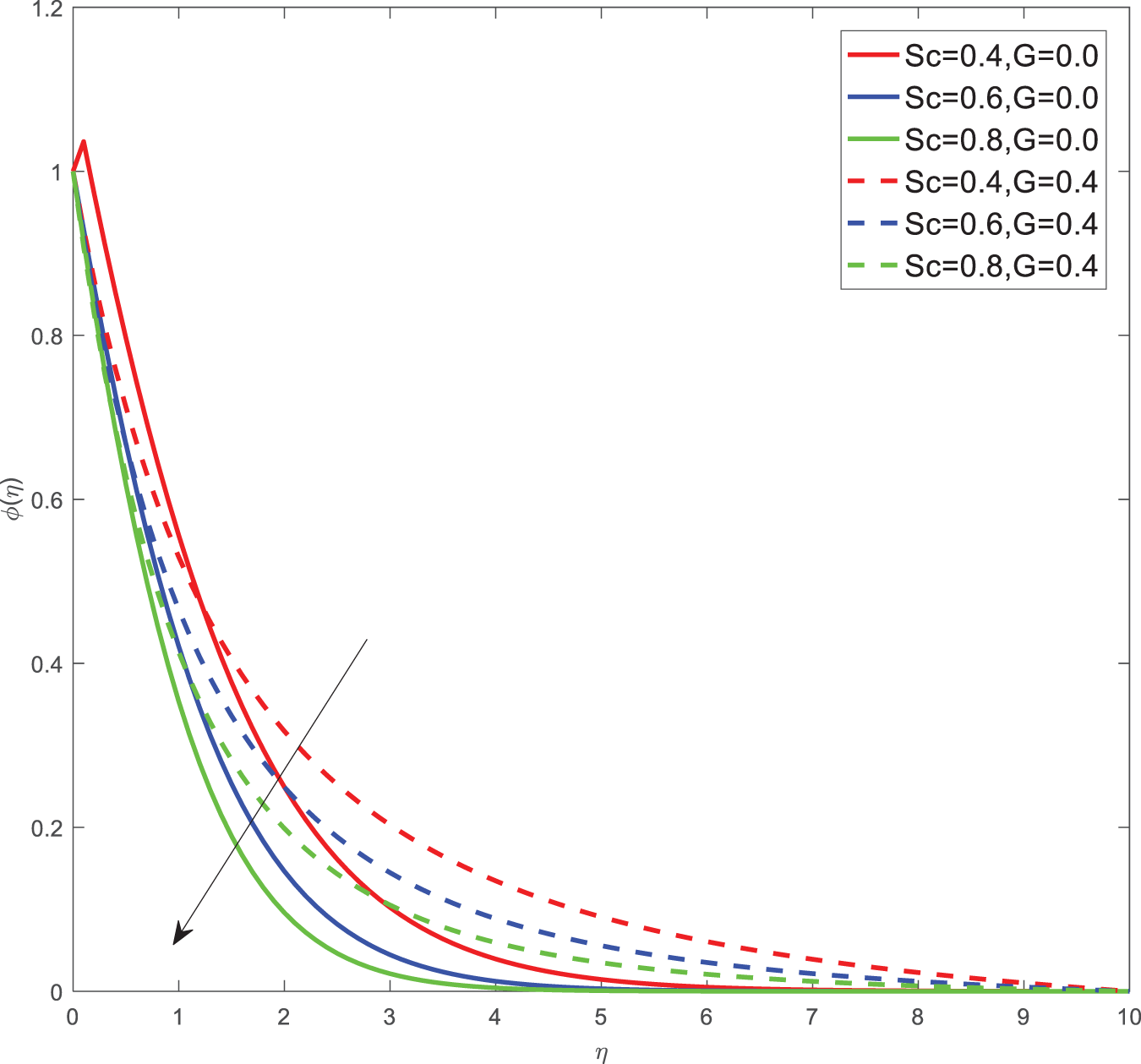
Figure 10: Concentration profiles of Sc, G
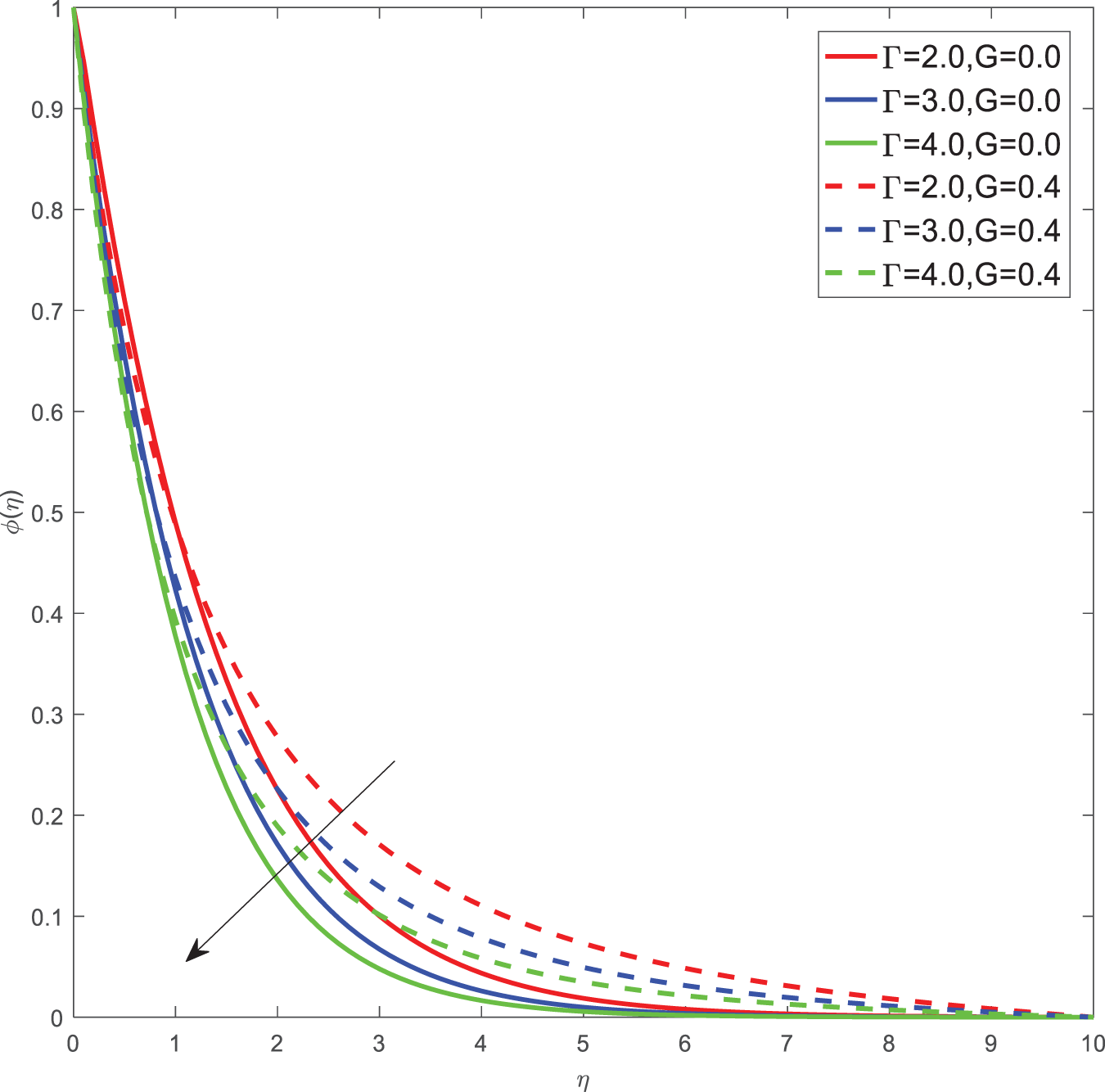
Figure 11: Concentration profiles of
The measure of skin friction rises as the curvature argument increases and decreases with the Casson parameter’s progressive values. This phenomenon agrees with the previous study mentioned in Table 1. Also, the Nusselt number decreases in magnitude with increasing observations of curvature parameter and variable thermal conductivity parameter and these values are in accordance with previous studies presented in Table 2.
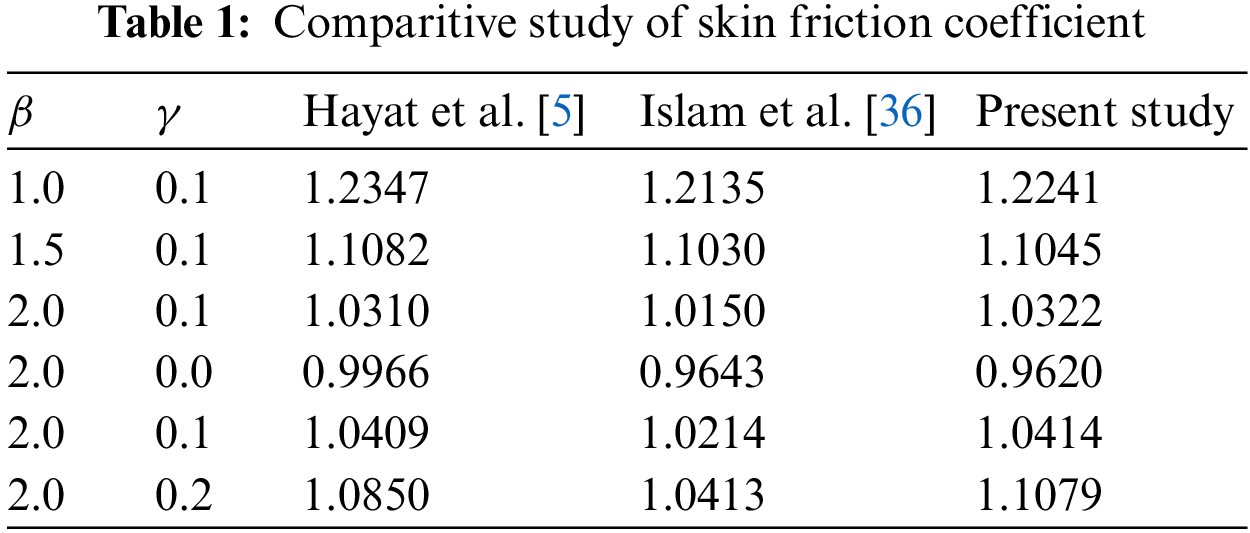
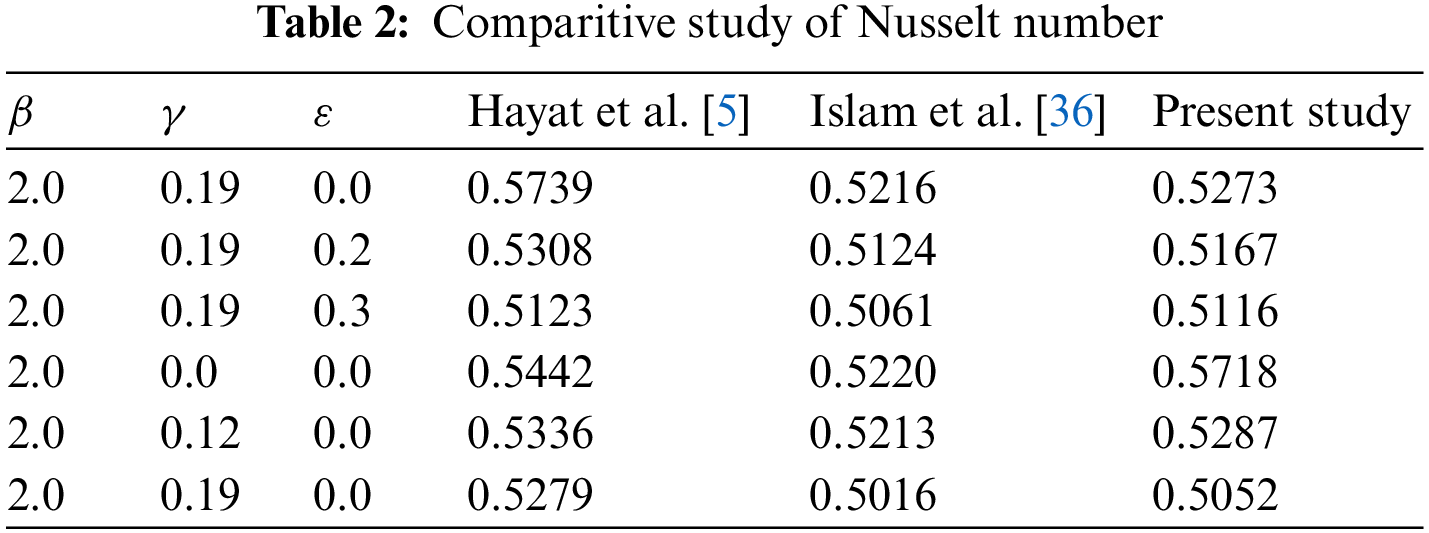
In this paper, a two-dimensional Casson fluid flow at both inclined flat and cylindrical surfaces, a comparative study of heat and mass transfer characteristics in a Casson immobility point flow is investigated. Flow is influenced by MHD, thermal radiation, Joule heating, variable thermal conductivity, mixed convection, viscous dissipation and chemical reaction. The corresponding equations are resolved by employing Keller Box method. Numerical calculations are analyzed, and the following observations are noted:
• A decrement in velocity graphs was witnessed for progressive estimates of Casson, Magnetic parameters and the reverse trend is observed for higher observations of velocity ratio parameter.
• Increment in temperature graphs witnessed for incremental estimates of the Eckert number, Joule heating, thermal conductivity parameter, and heat generating parameter. The opposite trend is noted for the Prandtl number.
• Concentration graphs decline for the Schmidt number, Chemical reaction.
• The magnitude of friction drag rises as the curvature argument increases.
• Nusselt number reduces in magnitude with enhanced observations of changeable thermal conductivity parameter.
• In the present investigation, a comparative study is carried out between two surfaces flat and cylindrical, by considering Casson fluid flow and this work can be expanded for other non-Newtonian fluids.
Acknowledgement: The authors are thankful to Koneru Lakshmaiah Education Foundation for providing research facilities to carry out this study.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: Sridhar Wuriti: Supervision, Conceptualization, Validation, Software; Shaik Jafarullah: Writing–original draft, Methodology, Data curation, Visualization, Project administration; Raghavendra Ganesh Ganugapai: Visualization, Writing review & editing; Srinivasa Rao Talagadadevi: Conceptualization, Data curation.
Availability of Data and Materials: Data will be made available on request.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. Chhabra, R. P. (2010). Non-newtonian fluids: An introduction. In: Krishnan, J., Deshpande, A., Kumar, P. (Eds.Rheology of complex fluids. New York, NY: Springer. https://doi.org/10.1007/978-1-4419-6494-6_1 [Google Scholar] [CrossRef]
2. Hayat, T., Shehzad, S. A., Alsaedi, A., Alhothuali, M. S. (2012). Mixed convection stagnation point flow of Casson fluid with convective boundary conditions. Chinese Physics Letters, 29(11), 114704. [Google Scholar]
3. Mukhopadhyay, S., De, P. R., Bhattacharyya, K., Layek, G. C. (2013). Casson fluid flow over an unsteady stretching surface. Ain Shams Engineering Journal, 4(4), 933–938. [Google Scholar]
4. Mukhopadhyay, S. (2013). Casson fluid flow and heat transfer over a nonlinearly stretching surface. Chinese Physics B, 22(7), 074701. [Google Scholar]
5. Hayat, T., Asad, S., Alsaedi, A. (2014). Flow of variable thermal conductivity fluid due to inclined stretching cylinder with viscous dissipation and thermal radiation. Applied Mathematics and Mechanics, 35(6), 717–728. [Google Scholar]
6. Pramanik, S. (2014). Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation. Ain Shams Engineering Journal, 5(1), 205–212. [Google Scholar]
7. Bhattacharyya, K. (2013). MHD stagnation-point flow of Casson fluid and heat transfer over a stretching sheet with thermal radiation. Journal of Thermodynamics, 2013, 1–9. [Google Scholar]
8. Medikare, M., Joga, S., Chidem, K. K. (2016). MHD stagnation point flow of a Casson fluid over a nonlinearly stretching sheet with viscous dissipation. American Journal of Computational Mathematics, 6(1), 37–48. [Google Scholar]
9. Kataria, H. R., Patel, H. R. (2016). Soret and heat generation effects on MHD Casson fluid flow past an oscillating vertical plate embedded through porous medium. Alexandria Engineering Journal, 55(3), 2125–2137. [Google Scholar]
10. Rauf, A., Siddiq, M. K., Abbasi, F. M., Meraj, M. A., Ashraf, M. et al. (2016). Influence of convective conditions on three dimensional mixed convective hydromagnetic boundary layer flow of Casson nanofluid. Journal of Magnetism and Magnetic Materials, 416, 200–207. [Google Scholar]
11. Ajayi, T. M., Omowaye, A. J., Animasaun, I. L. (2017). Viscous dissipation effects on the motion of Casson fluid over an upper horizontal thermally stratified melting surface of a paraboloid of revolution: Boundary layer analysis. Journal of Applied Mathematics, 2017, 1697135, 1–13. [Google Scholar]
12. Siddiq, M. K., Rauf, A., Shehzad, S. A., Abbasi, F. M., Meraj, M. A. (2018). Thermally and solutally convective radiation in MHD stagnation point flow of micropolar nanofluid over a shrinking sheet. Alexandria Engineering Journal, 57(2), 963–971. [Google Scholar]
13. Anantha Kumar, K., Sugunamma, V., Sandeep, N. (2019). Effect of thermal radiation on MHD Casson fluid flow over an exponentially stretching curved sheet. Journal of Thermal Analysis and Calorimetry, 140(5), 2377–2385. [Google Scholar]
14. Raza, J. (2019). Thermal radiation and slip effects on magnetohydrodynamic (MHD) stagnation point flow of Casson fluid over a convective stretching sheet. Propulsion and Power Research, 8(2), 138–146. [Google Scholar]
15. Gireesha, B., Srinivasa, C., Shashikumar, N., Macha, M., Singh, J. et al. (2019). Entropy generation and heat transport analysis of Casson fluid flow with viscous and Joule heating in an inclined porous microchannel. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 233(5), 1173–1184. https://doi.org/10.1177/0954408919849987 [Google Scholar] [CrossRef]
16. Patel, H. R. (2019). Effects of heat generation, thermal radiation, and hall current on MHD Casson fluid flow past an oscillating plate in porous medium. Multiphase Science and Technology, 31(1), 87–107. [Google Scholar]
17. Khan, M. I., Ahmad Khan, S., Hayat, T., Waqas, M., Alsaedi, A. (2019). Modeling and numerical simulation for flow of hybrid nanofluid (SiO2/C3H8O2) and (MoS2/C3H8O2) with entropy optimization and variable viscosity. International Journal of Numerical Methods for Heat & Fluid Flow, 30(8), 3939–3955. [Google Scholar]
18. Hayat, T., Khan, S. A., Alsaedi, A., Fardoun, H. M. (2020). Heat transportation in electro-magnetohydrodynamic flow of Darcy-Forchheimer viscous fluid with irreversibility analysis. Physica Scripta, 95(10), 105214. [Google Scholar]
19. Gopal, D., Saleem, S., Jagadha, S., Ahmad, F., Othman Almatroud, A. et al. (2021). Numerical analysis of higher order chemical reaction on electrically MHD nanofluid under influence of viscous dissipation. Alexandria Engineering Journal, 60(1), 1861–1871. [Google Scholar]
20. Khan, S. A., Hayat, T., Alsaedi, A., Ahmad, B. (2021). Melting heat transportation in radiative flow of nanomaterials with irreversibility analysis. Renewable and Sustainable Energy Reviews, 140, 110739. [Google Scholar]
21. Khan, S. A., Hayat, T., Alsaedi, A. (2022). Numerical study for entropy optimized radiative unsteady flow of Prandtl liquid. Fuel, 319, 123601. [Google Scholar]
22. Khan, S. A., Hayat, T., Alsaedi, A. (2022). Simultaneous features of soret and dufour in entropy optimized flow of reiner-rivlin fluid considering thermal radiation. International Communications in Heat and Mass Transfer, 137, 106297. [Google Scholar]
23. Khan, S. A., Hayat, T., Alsaedi, A. (2022). Entropy optimization for nanofluid flow with radiation subject to a porous medium. Journal of Petroleum Science and Engineering, 217, 110864. [Google Scholar]
24. Khan, S. A., Hayat, T., Alsaedi, A. (2022). Thermal conductivity performance for ternary hybrid nanomaterial subject to entropy generation. Energy Reports, 8, 9997–10005. [Google Scholar]
25. Ramzan, M., Saeed, A., Kumam, P., Ahmad, Z., Junaid, M. S. et al. (2022). Influences of Soret and Dufour numbers on mixed convective and chemically reactive Casson fluids flow towards an inclined flat plate. Heat Transfer, 51, 4393–4433. Portico. [Google Scholar]
26. Ganesh, G. R., Sridhar, W., Al-Farhany, K., Ahmed, S. E. (2022). Electrically MHD Casson nanofluid flow and entropy exploration under the influence of the viscous dissipation, radiation, and higher-order chemical reaction. Physica Scripta, 97(6), 065208. [Google Scholar]
27. Reddy, C. R., Rao, C. V., Surender, O. (2015). Soret, Joule heating and hall effects on free convection in a Casson fluid saturated porous medium in a vertical channel in the presence of viscous dissipation. Procedia Engineering, 127, 1219–1226. [Google Scholar]
28. Venkateswarlu, B., Satya Narayana, P. V. (2016). Influence of variable thermal conductivity on mhd Casson fluid flow over a stretching sheet with viscous dissipation, soret and dufour effects. Frontiers in Heat and Mass Transfer, 7(1), 1–9. https://doi.org/10.5098/hmt.7.16 [Google Scholar] [CrossRef]
29. Hayat, T., Zahid Iqbal, F. (2013). Stretched flow of Casson fluid with variable thermal conductivity. Walailak Journal of Science and Technology, 10(2), 181–190. [Google Scholar]
30. Abbas, Z., Sheikh, M., Motsa, S. S. (2016). Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation. Energy, 95, 12–20. [Google Scholar]
31. Ramesh, G. K., Prasannakumara, B. C., Gireesha, B. J., Rashidi, M. M. (2016). Casson fluid flow near the stagnation point over a stretching sheet with variable thickness and radiation. Journal of Applied Fluid Mechanics, 9(3), 1115–1122. [Google Scholar]
32. Sridhar, W., Vijaya Lakshmi, G., AlFarhany, K., Ganesh, G. R. (2021). MHD Williamson nanofluid across a permeable medium past an extended sheet with constant and irregular thickness. Heat Transfer, 50(8), 8134–8154. [Google Scholar]
33. Ganesh, G. R., Sridhar, W. (2022). Effect of chemical reaction towards MHD marginal layer movement of Casson nanofluid through porous media above a moving plate with an adaptable thickness. Pertanika Journal of Science and Technology, 30(1), 477–495. [Google Scholar]
34. Waqas, H., Yasmin, S., Muhammad, T., Imran, M. (2021). Flow and heat transfer of nanofluid over a permeable cylinder with nonlinear thermal radiation. Journal of Materials Research and Technology, 14, 2579–2585. [Google Scholar]
35. Bilal, M., Siddique, I., Borawski, A., Raza, A., Nadeem, M. et al. (2022). Williamson magneto nanofluid flow over partially slip and convective cylinder with thermal radiation and variable conductivity. Scientific Reports, 12(1), 12727. [Google Scholar] [PubMed]
36. Islam, S., Khan, A., Kumam, P., Alrabaiah, H., Shah, Z. et al. (2020). Radiative mixed convection flow of maxwell nanofluid over a stretching cylinder with joule heating and heat source/sink effects. Scientific Reports, 10(1), 17823. https://doi.org/10.1038/s41598-020-74393-2 [Google Scholar] [PubMed] [CrossRef]
37. Rehman, K. U., Shatanawi, W., Yaseen, S. (2023). A comparative numerical study of heat and mass transfer individualities in Casson stagnation point fluid flow past a flat and cylindrical surfaces. Mathematics, 11(2), 470. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools