Energy-Efficient Clustering Using Optimization with Locust Game Theory

1  Introduction

Wireless Sensor Networks (WSNs) are a collection of cost-effective, multipurpose Sensor Nodes (SNs) which work together to detect a specific area as an Area of Interest (AoI). The system collects the data from the AoI and sends it to a Base Station (BS) for processing. WSNs have made it simpler to monitor remote places. They are particularly successful in gathering information in a variety of remote locations, including rescue teams, forests, war-prone regions, undersea research, and weather patterns. WSNs have numerous SNs that are connected to a BS. However, it is difficult to power and replace SNs in remote places [1].

SNs in WSNs help to detect communication and gather data collaboratively. A certain quantity of energy is consumed during this procedure. However, SNs are powered by a rechargeable battery and have a finite quantity of energy in case the batteries die. Also, they do not need to change the battery pack or update it promptly. The communication of the data collected will be hampered to some extent, and the entire sensor network may become incapacitated [2]. Consequently, extending the lifespan of the complete sensor network is energy-efficient and has become a major challenge in real-world remote sensing applications.

In real-world applications, wireless SNs are powered by limited-capacity batteries and WSNs.This node is placed unprotected or in unsafe places in a challenging way. They are powered by batteries, and the surveillance region is unregulated. This makes it difficult to store energy supplies and rechargeable batteries. Thus, decreasing the energy consumption of the network seems to be the most effective method to extend the lifespan of the sensor network [3] and ensure the continuous operation of WSNs. Many professionals and academicians have undertaken various types of research to optimize network energy consumption to a certain extent [4–9].

Cluster-based or hierarchical routing is a common mode of communication with appealing qualities such as efficiency and flexibility. The general concepts of routing protocol have been combined with most of the energy-saving approaches in WSNs. Nodes with lots of energy are evaluated for their abilities to analyze and communicate the data in the framework of a hierarchical technique [10]. Low-energy terminals on either side are utilized to gather data in areas close to the objective. Hierarchical navigation is an effective method to reduce power usage within clustered architectures by aggregating the data. Hierarchical routing approaches combine operations to minimize the number of transmitted packets for delivery to a specific sink [11].

In these circumstances, assigning special roles to nodes can considerably extend the lifespan of the network and the flexibility of design. Cluster Heads (CHs) are special nodes that serve as anchors in the hierarchy or cluster-based systems. Scaling is a key attribute in WSNs. Owing to the limits given by the original assumption, this idea is still a challenge that hasn’t been solved in most of the routing approaches. Cluster-based methods find single sinks and a few CHs in a general WSN to increase the influence of their coverage spaces [12].

The assignment of unique purposes to nodes in such circumstances can considerably extend the lifetime of the system and the adaptability of technology. CHs are the special nodes that serve as referrals in hierarchical or clustered systems. The Locust Search (LS-II) method [13] is a meta-heuristic optimization technique derived from the modeling of desert locust biological behavior. A locust acts in two ways; alone and in groups. The solitary method prevents the components from interacting with other entities to discover new sources of food. The sociological perspective, on either hand, takes into account the large proportion of entities in locations with ample food supplies.

The locust concentrating process includes the movement of an entity in lowland areas to all those components in locations with the greatest food supplies. The LS-II technique combines both tendencies to produce highly powerful global and regional searching capabilities.

These properties have led to the application of LS-II in a wide range of challenging optimization formulas, including parameterization in chaotic systems [14], image processing [15,16], and pattern recognition [17].

The main contributions of the proposed method are given below:

•   Identify the CHs effectively and minimize energy consumption using the LS-II algorithm

•   Multi-Swarm Optimization (MSO) helps to find the optimal routing path, and the SN energy is stored feasibly.

•   A penalty technique is designed to motivate SNs to embrace collaborative tactics in operational plans to prevent their destructive behavior if they go to sleep.

•   For sensor networks exhibiting selfish behavior, the optimum amount of penalty sessions are established to efficiently improve the lifetime of the network.

The remaining sections of this paper are structured as follows; Section 2 discusses the related research. Section 3 describes the WSNs and optimization methods for minimizing energy consumption. Section 4 discusses the experimental results and comparison. Section 5 concludes the proposed optimization method with future work.

2  Related Work

Whenever an unbalanced situation occurs in information transfer across the transmission network, an energetic vacuum is generated, causing the sink nodes to die prematurely and reducing the lifespan of the network [18,19]. Researchers [20,21] offered a strategy wherein the communication range was changed depending on the proximity between the CHs and their users. The use of the firefly optimization technique also extended the longevity of the program. The method was applied against the standardized methods in a variety of scenarios. According to the findings of their research, the proposed method produced good outcomes in terms of network life. The author, on the other hand, made no mention of the energy maximization of SNs while preserving the optimal CH range.

The researcher [22] proposed the particle swarm optimization-based unequal fault-tolerant clustering (PSO-UFC) technology. Unbalanced grouping and fault-tolerant difficulties of the present energy-balanced unequal clustering technique were solved effectively in the method for the long-term network. An absence of inequity in the clustering method was used to equalize intra-cluster and inter-cluster power use among the master CHs (MCHs) to find a remedy for the unbalanced in the clustering algorithm. Moreover, with the PSO-UFC method, the internet connection was restored by selecting an additional CH, termed substitute CH, in the event of an impetuous MCH breakdown. The lifespan maximization of SNs, on the other hand, has appeared to be dependent on an optimized clustering method that reduces end-to-end delay.

In [23], the author proposed regional energy-aware clustering with isolated nodes (REAC-IN) for grouping. The CH was chosen in REAC-IN based on the weight, and the value was calculated using the residual energy of each sensor and the average overall energy of all sensors in each cluster. In the end, the proposed approach had good results when compared to the other WSN protocols, although numerous difficulties had been overlooked. A fresh, enhanced method was developed to overcome those limitations. Grouping and task selection were used to demonstrate the suggested technique which could transcend the limits of the REAC-IN routing algorithm. Their suggested methodology surpassed other methodological approaches.

The researchers [24] used an upgraded harmony search (HS)-based routing to transport the incoming packets between CHs and the sinks from another study. The efficiency of the combined grouping and forwarding system was assessed using energy cost, the proportion of live and dead components, and system longevity. In comparison with the existing methods, the novel cuckoo–HS-based combined navigation and grouping method provided more results. When constructing the state-of-the-art meta-heuristic algorithms with merged forwarding and clustering, the researcher disregarded incorporating the lifespan and end-to-end latency elements.

3  Proposed MSGE-LS Methodology

The proposed multi-swarm with energy-efficient game theory on locust search(MSGE-LS)method consists of two models; the energy model and the network model. The proposed method efficiently selects the CH and optimally chooses the route for routing. It effectively minimizes energy consumption and improves the life span of the network. Fig. 1 shows the architecture of the proposed method. MSO with game theory optimally chooses the routing path, and LS-II helps to select the CH successfully.

Figure 1: Architecture of the proposed method

3.1 Network Model

A WSN is a network made up of a randomized number of nodes that form various groups, each with a CH node and many cluster members (CMs). Every CM has a detection range through which each node can receive information from the observed item and transmit it to the appropriate CH, who subsequently sends it to the sink node.

The functioning phases of an SN (exit phase) occur when the node has to transmit and receive information, and the inactive monitoring phase occurs when a network has no information to transmit and receive. To save power, all functionalities on the SN are switched off when it is in silent mode. The energy usage of the SN can be regarded as zero in this state. In this work, the SNs are considered to be appropriate and the energy in severe conditions is restricted and divided. As an advantage, the SN will be feasible to fulfill the goal of maximizing life span.

Therefore, to save power usage, maximize the lifespan of the network, and ensure the performance of the network, the SN must reach a latent state as much as feasible when it is in the inactive monitoring phase.

3.2 Energy Model

The energy consumption of the SN is influenced by a variety of variables. The primary elements that have a direct impact on the energy consumption of the SN are listed below. Different energy consumption aspects of SNs throughout the process of information need to be investigated to compute the power leftovers of the SN.

3.3 Locust Search II

The LS-II approach is a metaheuristic method developed by studying the social behavior of locust swarms. The methods in LS-II prevent individuals from congregating in favorable locations and promoting the search area by redistributing the agents [25]. The LS-II technique combines both the tendencies to produce highly efficient domestic and global search capabilities. These properties have led to its application in solving difficult problems [26–43].

LS-II is a follow-up of the initial LS. Unlike the original LS, LS-II includes additional controllers and processes to boost its performance and reduce the accumulation of agents. Whenever the procedure arrives with multiple locally optimal solutions, such methods allow for a more accurate balance between exploratory and exploitative in identifying the global solution.

A population (PO) of N locusts constitutes a group of N possible solutions in LS-II, that is, PO = {x1,…, xN}. The parts of PO communicate with one another as they explore an n-dimensional area. Every solution xi = [xi,1,…, xi,n] is located within the limited space UN = {xi Rn|ld xi, d ud (where ld and ud represent the minimum and maximum values for the d-th choice variables, respectively). LS-II, like any other metaheuristic technique, is based on an iterative development wherein the optimal solutions change their position with every repetition. The position of each candidate solution is changed by using several methods after the two behavioral patterns seen in the locust insects, namely, isolated and social activities.

3.3.1 Solitary Process

Candidate solutions in the solo phase follow different paths in evaluating potential sources of food (good solutions). The search agents avoid focusing on the other elements during this procedure. This process is based on the concept of attractions and repulsion forces that are experienced by the answers in the PO populations. The ensuring attractiveness and repulsive pressures (called social force) are experienced by a given search agent xi under such parameters, which are explicitly described by the following formulation at each iteration t.

SPit=∑j=1i≠jN⁡spi,jt (1)

Here spi,jt denotes the paired attraction-repulsion among the candidate answers xi and xj, which are expressed by the representations.

spi,jt=ρ(xi, xj)M(ri,j)hi,j+rand(−1, 1) (2)

opens ρ(xi, xj) signifies the dominant level among xi and xj. The fact is represented by the capable value as  M(ri,j) , whereas ri,j represents the Euclidian distance ||xi−xj||. The unit vector from xi to xj is the vector.

hi,j=xi−xj||xi−xj|| (3)

The below connection defines the social component M(ri,j):

M(ri,j)=Ae−rijB−e−rij (4)

Components A and B correspondingly denote the attraction-repulsion proportion and the influencing quantity. ρ(xi, xj)  is the function that represents the relative dominance of the candidate solutions of every search agent. It is evaluated with such a value inside the range [0, N−1] to execute  ρ(xi, xj) . The strongest candidate option has the rank of 0, whereas the poorest component has the ranking of N−1. Concerning the generated fitness value, the ideas of the best and the worst are explored. The score of dominance is modeled as follows once the rankings for every candidate solution have been delegated:

ρ(xi, xj)={e−(rank(xi)N) if rank (xi)≤rank(xj)e−(rank(xj)N)if rank (xi)>rank(xj) (5)

As a result of the huge social power Sti affects every search agent xi which has a distinct inclination to be attracted or rejected by the other components within the population’s SP. In such cases, the new position xi∗ estimated by the searching agent xi is due to the effect of the total force that calculated as follows:

xi∗=xi+Sit (6)

3.3.2 Social Process

Even during the solitary phase, the social process is used to enhance the precision of the best candidate solution provided by SP*. Even during the social practice, a subgroup of searching agents B = {b1,…, bq} is produced, which includes the finest q parts of the population, SP*. Next, within a constrained subspace Ciof  ∈ U, a set Mi of new random solutions (Mi = {mi1,…, mia}) is produced for every candidate solution x*I ∈ B. The boundaries of the subdomain Ci wherein the alternative solutions are formed around x*i = [xi1,…, xin] are shown as follows:

Ci,dlower=xi,d∗−r (7)

Ci,dUpper=xi,d∗−r (8)

The upper and the lower boundaries of every subcategory Ci for the d decision variable (d ∈ [1,…, n]) are Ci,dlower and Ci,dUpper , respectively. The perturbation r on the other side is computed using the standard formula,

r=∑d=1n⁡(ud−ld)n.β (9)

The lower and the upper bounds for the d-choice variables are denoted by ld and ud, respectively. n is the total number of dimensions, and it correlates to a scaling component that controls the maximum size of Ci. The number of falls between the beta ranges is [0, 1].

Eventually, the best component of the set incorporated by the value of x*i with all its corresponding random solutions {mi1,…, mia} is acquired as the new role of the searching agent xt + 1i. The following terminology can be used to describe this assignment.

xit+1=best(xi∗, m1i, …., mai) (10)

3.4 Multi Swarm Optimization with Game Theory

The multi-PSO swarms discussed in this paper do not generalize instantaneously because the swarms do not communicate. If the time is appropriate to acquire another swarm, there may be communication; nevertheless, one swarm diminishes as a result of a variety of information exchange topologies. Therefore, two multi-swarm approaches are proposed. Multi-charged particle swarm optimization (CPSO) is a multi-population form of CPSO. As a substitute for standard atom targets, multi-quantum swarm optimization uses quantum swarms based on quantization.

Blackwell founded CPSO on the orbit concept of an atom’s nucleus, which orbits the earth by electrons. In CPSO, a certain number of atoms receive a charge that repels the other charged particles. The charged particles are those that have been assigned a value, while neutral particles are those that have not been given a charge. Particle speeds are updated using a standard updating formula with an additional option dependent on their closeness to the other electrons.

parentve→i(t+1)=ωv→i(t)+c1r→1(t)(pbest→−x→i(t)+c2r→2(t)(gbest→−x→i(t)) (11)

In formula (11), vei is the speed of the particle, xi is the location of the particle, pbest is the individual perfect location of the particle, and gbest is the best-found position of the swarm given a star neighborhood architecture.

The CPSO speed updating formula is as follows:

parentve→i(t+1)=ωv→i(t)+c1r→1(t)(pbest→−x→i(t)+c2r→2(t)(gbest→−x→i(t))+∑∀j≠i⁡aij (12)

Eq. (13) gives the velocity among the particles i and j:

aij={QpiQpj||x→i−x→j||0otherwise(x→i−x→j)if ρcore<||x→i−x→j||≤p  (13)

Here, Qpi are the charges of particle where i, p, and pcore are the radii of influence of the accelerating component.

In vanilla PSO, neutral particles behave because they will. However, CPSO will show a convergence of neutral particles around gbest. As a result, CPSO provides a greater amount of variance throughout the loop and overcomes the linear collapsing issue that vanilla PSO has. Despite CPSO’s excellent management of the diversity problem, an outside method to deal with the obsolete storage is required.

To explore the multiple potential peaks in parallel, a swarm is partitioned into sub-swarms. In concluding the research on the local optimum, diversity is raised but the probability is diminished. Furthermore, such swarms consist of two sorts of particles; (i) PSO particles closely approximate the PSO method but aim to obtain a greater location and (ii) quantum particles orbit all around the sub swarm location in a radius cloud has to maintain diversity in addition to the optimization technique. The issue of diversity loss is addressed by quantum particles. The location of quantum particles is calculated using Eq. (14):

p→i∈Bn(rcloud) (14)

The goal of MQSQ is to find a peak in every swarm, which is then monitored by the proposed method. A swarm interaction is performed in an eliminating process to ensure that the two swarms do not use the same peaks. The exclusion process among the swarms that are close together (distance smaller) employs a simple competitive strategy. The swarm with the best fitness value for its swarm attractor is declared as the winner, whereas for the loser, the swarming is dispatched and re-initialized in the search area.

Gaming Model Establishment

SNs can move between awake and asleep states reasonably to extend the lifespan of WSN. Consequently, SN dynamic switching can be considered as a game issue. The following is an example of the concept:

GT={NP, K, {ui}} (15)

The players in WSN are represented by NP. The reason is that all the sensor network nodes are active in receiving and delivering the sensor data. All sensor network nodes are included in the game participants. To put it in another way, the game player is sensor Si, with i = {1, 2, and n}.

The operational area of players is denoted by the letter K. In this paper, the sensor network evaluates the strategic space of the game player by evaluating the power usage. Specifically, the sensor network needs to enter the relaxed state from the active state but does not join the sleep state from the active state due to the sensible choice of SNs. The functional form of a player is represented by the UI.

ui(si, s−i)=Ui(si, s−i)−COi(si, s−i) (16)

Here si denotes the approach of the SN. Apart from the SNs, si is the approach used by the nodes. The income value of SN Si is Ui (si, −si), whereas the cost value of SNSi is COi (si, −si).

In Fig. 2 flowchart of the proposed method is shown for optimal CH selection and routing path. In the starting stage, it initializes the nodes, BS location and energy. Clusters are formed by calculating the distance between the networks that match the ground station and the energy levels of the nodes. MSO should be used to confirm the best local position. The LS-II completes the search method (ongoing process) that begins with the population’s SP(k), that is, being randomly initialized during the first repetition (k = 0). The solo operator is then applied to the present population SP (k). As an outcome, an SP population (temporary population) is created. Lastly, the new population SP(k + 1) is generated using social operations. This cycle is repeated several times until it reaches a point.

Figure 2: Flowchart of MSGE-LS

4  Analysis of Results

The suggested MSGE-LS method is tested in this part by evaluating its efficiency with that of GA, LS, and MSO-based clustering. The statistical tests are run on a Dell OptiplexTM 3020 PC featuring an Intel Core i7-4770 3.4 GHz processor, 8 MB cache, inbuilt Intel graphics, 16 GB RAM, 1 TB HDD, and Windows 10 operating system. For the simulations, Matlab R2019a is employed. Table 1 lists the network parameters that were employed during the process.

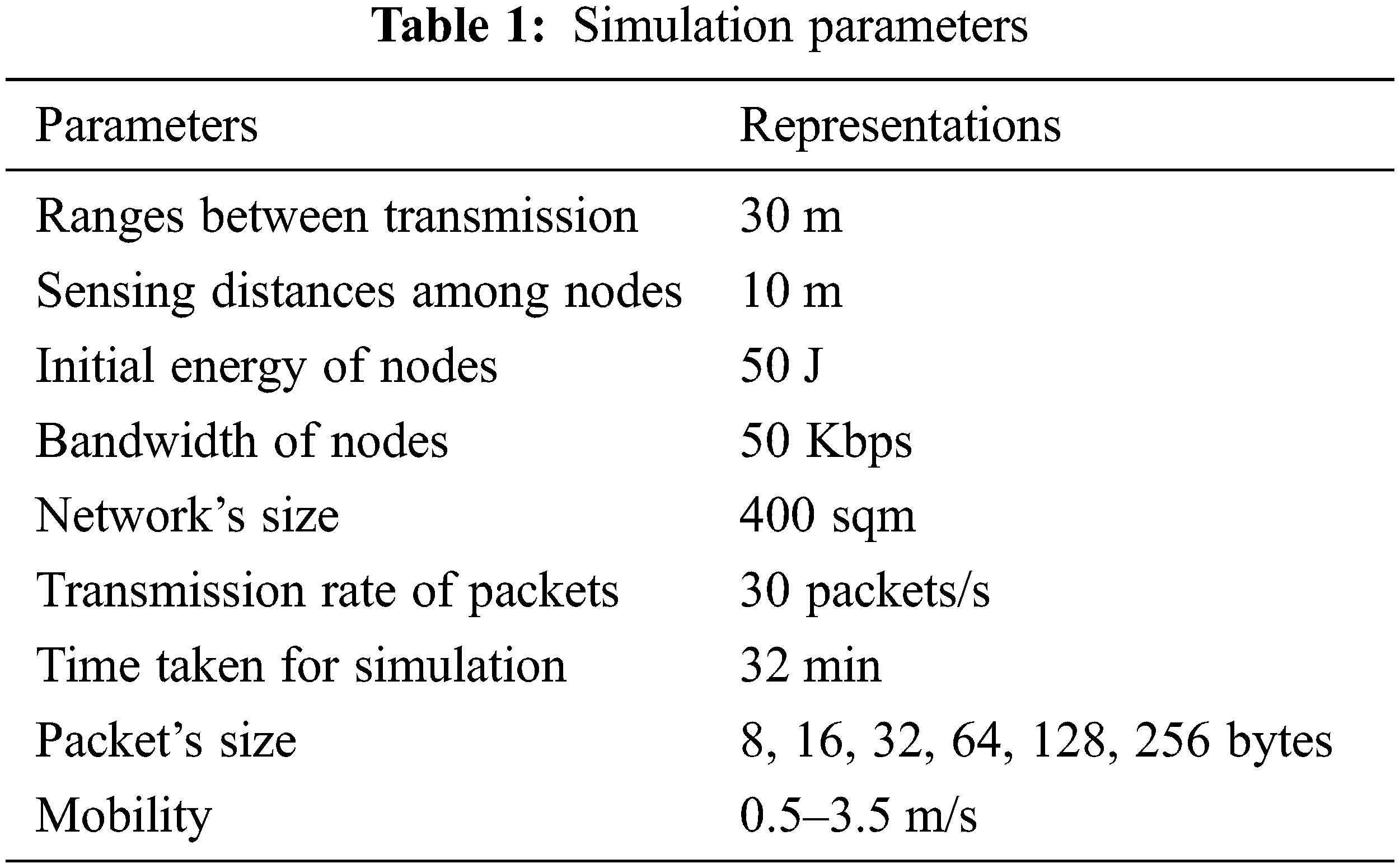
The experiment of the proposed method is calculated using 200–1400 nodes and 0–800 rounds. The criteria that were taken into account are stated; number of clusters that generated the overall end-to-end delay in seconds, mean packet loss rates, lifespan computations, throughput, and total power dissipated in joules. The experimental calculations are shown in Table 2.

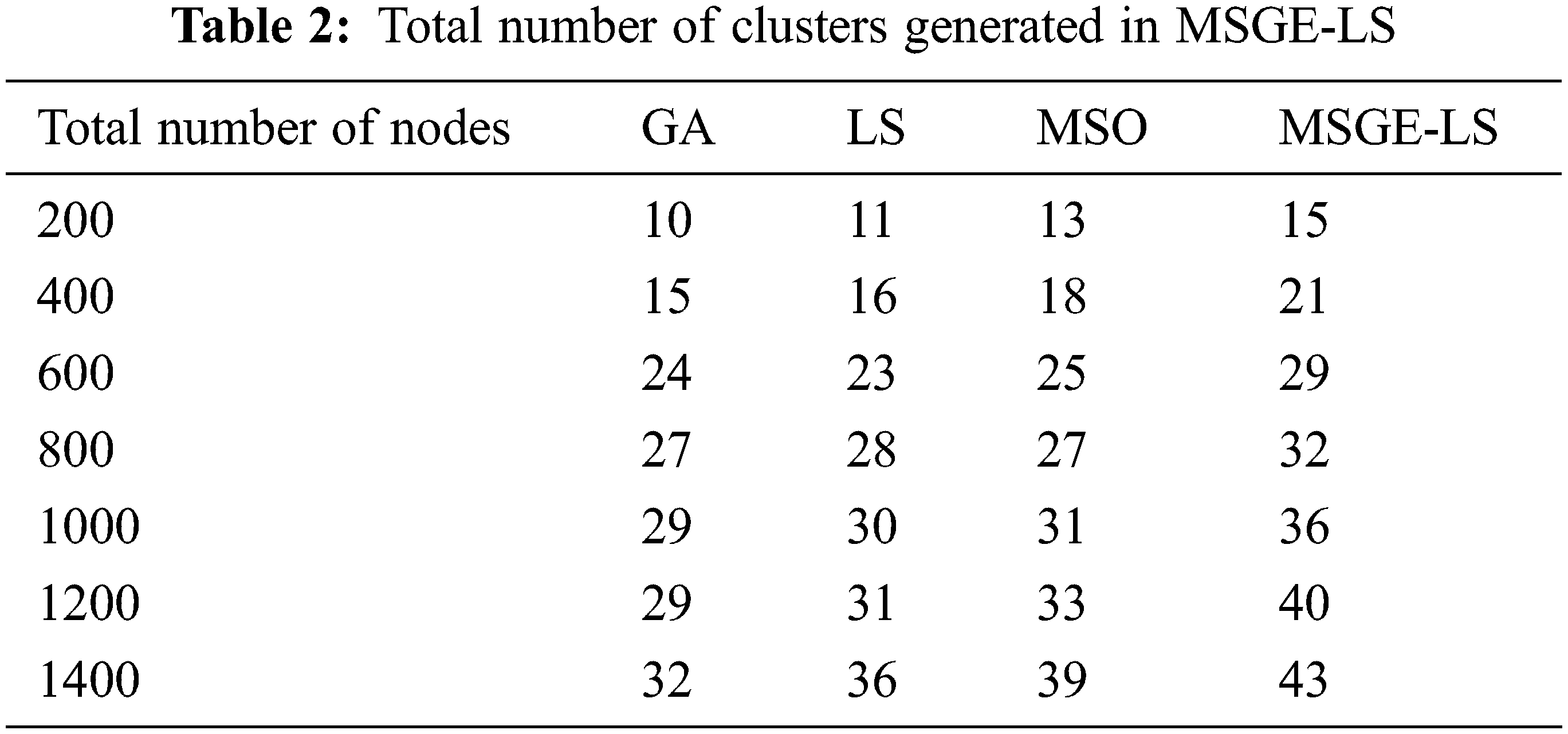
The proposed MSGE-LS method forms 4% of clusters higher than the other methods in 1400 rounds. The existing GA method forms 32 clusters, LS forms 36 clusters, and MSO forms 39 clusters in 1400 rounds. For 200, 400, 600, 800, 1000, 1200, and 1400 nodes, MSGE-LS improves approximately by 32%, 15%, 10%, 9%, 16%, and 13%, respectively, while compared with GA. MSGE-LS also outperforms LS by 9%, 14%, 7%, 5%, 6% and 0%. Fig. 3 shows the number of clusters formed during 1400 nodes.

Figure 3: Formations of clusters

The proposed MSGE-LS method achieves 65.31% of the minimum packet loss rate compared to the existing methods. In the existing methods, GA achieves 84.56%, LS achieves 80.35%, and MSO achieves 88.45% in average packet loss rates for 1400 rounds. For 200, 400, 600, 800, 1000, 1200, and 1400 nodes, the MSGE-LS has a reduced loss rate of 20%, 22%, 24%, 19%, 8%, and 20% when compared with GA and 12%, 11%, 18%, 17%, 11%, 9%, and 19% when compared to LS. MSGE-LS is also found to be more effective than MSO-based clustering by 6%, 5%, 5%, 7%, 4%, and 3% for 200, 400, 600, 800, 1000, and 1200 nodes, correspondingly. The experimental calculations are shown in Table 3. Fig. 4 shows the average packet loss rate.

Figure 4: Average packet loss rate

The proposed method has a minimum average end-to-end delay compared with GA, MSO, and LS. MSGE-LS achieve 0.057001 s of end-to-end delay. Fig. 5 shows the average end-to-end delay rates. When compared with GA, MSGE-LS has a reduced average of end-to-end delay benefit of 19%, 20%, 11%, 9%, and 5% for 200, 400, 600, 1000, and 1200 nodes, respectively, but a greater delay benefit of 9% for 800 nodes. When compared to MSO, MSGE-LS has a median end-to-end delay benefit of 0%, 3%, 7%, 4%, 0%, and 0%.

Figure 5: End-to-end delay

The number of packets sent out to the ground station is measured by the throughput. It is preferable to transmit the greatest number of packages possible all through the lifespan of the network. Fig. 6 shows how to take this metric. The throughput is proportional to the number of active SNs sending the packets of data in each round, implying that the amount of data collected is greater. The suggested protocol provides the highest throughput, as shown in Fig. 6.

Figure 6: Throughput

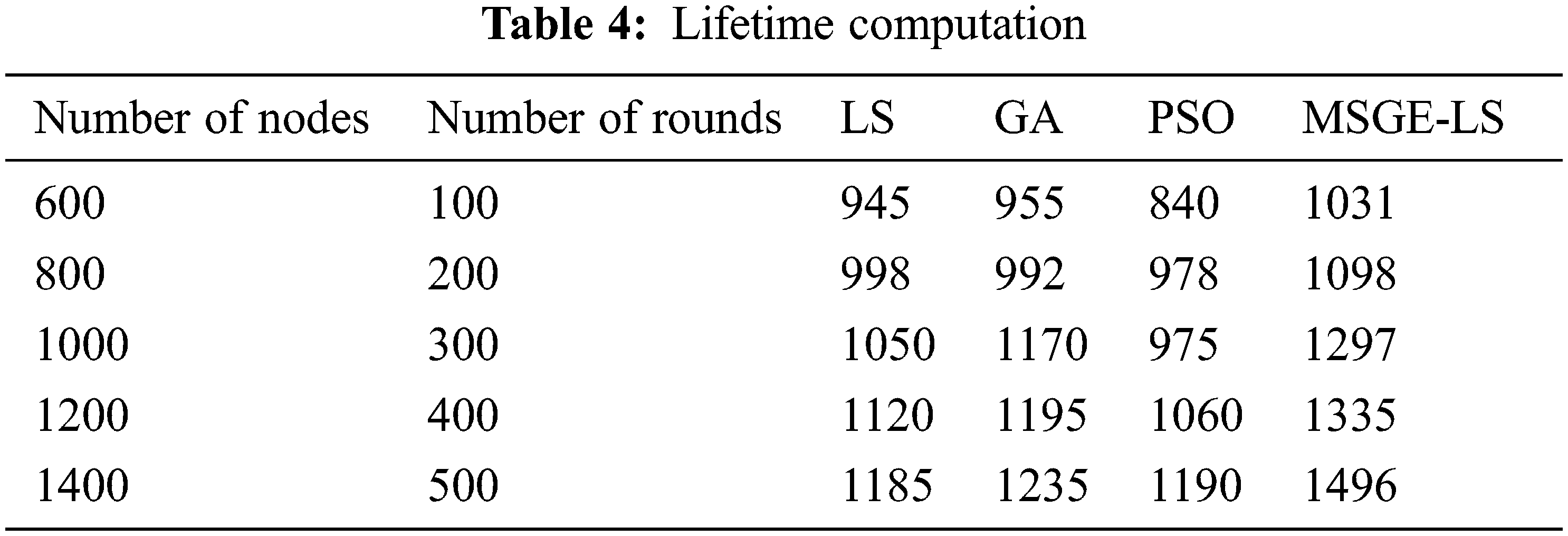
When compared to the existing techniques such as GA, LS, and MSO, MSGE-LS has a higher lifetime computation Fig. 7. The lifetime computation of the proposed method is provided in Table 4.

Figure 7: Lifetime computation

The cost of computation is directly proportional to time. If the minimum nodes take more time to cluster, they will consume more energy and have a high storage cost. In this proposed research, the computation time is of high concern, and the cost of computation is reduced. This helps in improving the lifetime of the network with less component loss in terms of battery life, storage space and so on.

5  Conclusion

Two of the most essential criteria for operating WSNs successfully and consistently are energy conservation and energy consumption. At present, more importance is given to technical issues and resource management. The main goal of this research is to use the LS-II method to improve WSN CH selection. Therefore, a method that relies on MSO and game theory has been developed to improve WSN and CH selection routing. The solution generated was based on both energy efficiency and network responsiveness. The suggested method optimizes routing and extends the lifetime of the network by selecting the effective CHs in reaction to the networks. According to the findings, the suggested scheme outperforms the comparative methods in simulations. The suggested protocol is evaluated using several parameters, such as the lifetime of the network, energy usage, energy divergence, number of packets transmitted, and system stability duration. The research has shown that the suggested methodology performs well in terms of increasing the lifespan of the network and providing a good energy load.

The limitation of this research is the lack of energy efficiency across the network. In such a situation, the challenging due nodes are considered as players. If one node acts as a player, the whole algorithm takes responsibility only for that player’s node. In the future, a better optimization model can be used for node optimization.

Funding Statement: This work was suppoted by Korea Institute for Advancement of Technology (KIAT) grant funded by the Korea Government (MOTIE) (P0012724, The Competency Development Program for Industry Specialist) and the Soonchunhyang University Research Fund.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Suganthi, N. Umapathi, M. Mahdal and M. Ramachandran, “Multi swarm optimization based clustering with tabu search in wireless sensor network,” Sensors, vol. 22, no. 5, pp. 1736–1745, 2022. [Google Scholar] [PubMed]

2. A. Rodríguez, M. P. Cisneros, J. C. R. Caro, C. D. V. Soto, J. Gálvez et al., “Robust clustering routing method for wireless sensor networks considering the locust search scheme,” Energies, vol. 14, no. 11, pp. 3019–3025, 2021. [Google Scholar]

3. X. Yan, C. Huang, J. Gan and X. Wu, “Game theory based energy-efficient clustering algorithm for wireless sensor networks,” Sensors, vol. 22, no. 2, pp. 478–485, 2022. [Google Scholar] [PubMed]

4. X. Huan, K. S. Kim, S. Lee, E. G. Lim and A. Marshall, “A beaconless asymmetric energy-efficient time synchronization scheme for resource-constrained multi-hop wireless sensor networks,” IEEE Transactions on Communications, vol. 68, no. 3, pp. 1716–1730, 2019. [Google Scholar]

5. S. Chamanian, S. Baghaee, H. Uluşan, O. Zorlu, E. U. Biyikoglu et al., “Implementation of energy-neutral operation on vibration energy harvesting WSN,” IEEE Sensors Journal, vol. 19, no. 8, pp. 3092–3099, 2019. [Google Scholar]

6. R. Ashween, B. Ramakrishnanand and M. M. Joe, “Energy efficient data gathering technique based on optimal mobile sink node selection for improved network lifetime in wireless sensor network (WSN),” Wireless Personal Communications, vol. 113, no. 4, pp. 2107–2126, 2020. [Google Scholar]

7. S. Q. Zhang, Y. Tao and J. J. Dai, “Multi-hop clustering routing protocol for energy harvesting wireless sensor networks,” Computer Engineering Design, vol. 40, no. 4, pp. 611–616, 2019. [Google Scholar]

8. N. Saxena, A. Roy and J. Shin, “Dynamic duty cycle and adaptive contention window based QoS-MAC protocol for wireless multimedia sensor networks,” Computer Networks, vol. 52, no. 13, pp. 2532–2542, 2018. [Google Scholar]

9. M. B. Dowlatshahi, M. K. Rafsanjani and B. B. Gupta, “An energy-aware grouping memetic algorithm to schedule the sensing activity in WSNs-based IoT for smart cities,” Applied Soft Computing, vol. 108, no. 2, pp. 107473, 2021. [Google Scholar]

10. S. Kassan, J. Gaber and P. Lorenz, “Game theory based distributed clustering approach to maximize wireless sensors network lifetime,” Journal of Network and Computer Applications, vol. 123, no. 11, pp. 80–88, 2018. [Google Scholar]

11. S. Shen, H. Ma, E. Fan, K. Hu, S. Yu et al., “A non-cooperative non-zero-sum game-based dependability assessment of heterogeneous WSNs with malware diffusion,” Journal of Network and Computer Applications, vol. 91, no. 3, pp. 26–35, 2017. [Google Scholar]

12. A. González, E. Cuevas, F. Fausto, A. Valdivia and R. Rojas, “A template matching approach based on the behavior of swarms of locust,” Applied Intelligence, vol. 47, no. 4, pp. 1087–1098, 2017. [Google Scholar]

13. X. Fu, P. Pace, L. Aloi Yang and G. Fortino, “Topology optimization against cascading failures on wireless sensor networks using a memetic algorithm,” Computer Networks, vol. 177, no. 3, pp. 107327, 2020. [Google Scholar]

14. X. Cheng, D. Ciuonzo and P. S. Rossi, “Multibit decentralized detection through fusing smart and dumb sensors based on Rao test,” IEEE Transactions on Aerospace and Electronic Systems, vol. 56, no. 2, pp. 1391–1405, 2019. [Google Scholar]

15. D. Ciuonzo, P. S. Rossi and P. K. Varshney, “Distributed detection in wireless sensor networks under multiplicative fading via generalized score tests,” IEEE Internet of Things, vol. 8, no. 11, pp. 9059–9071, 2021. [Google Scholar]

16. A. Shahraki, A. Taherkordi, O. Haugen and F. Eliassen, “Clustering objectives in wireless sensor networks: A survey and research direction analysis,” Computer Networks, vol. 180, no. 4, pp. 107376, 2020. [Google Scholar]

17. M. Krishnan, S. Yun and Y. M. Jung, “Improved clustering with firefly-optimization-based mobile data collector for wireless sensor networks,” AEU-International Journal of Electronics and Communications, vol. 97, no. 3, pp. 242–251, 2018. [Google Scholar]

18. M. Krishnan, Y. M. Jung and S. Yun, “An improved clustering with particle swarm optimization-based mobile sink for wireless sensor networks,” in Proc. 2nd Int. Conf. on Trends in Electronics and Informatics (ICOEI), Tirunelveli, India, pp. 11–12, 2018. [Google Scholar]

19. Y. Xu, O. Ding, R. Qu and K. Li, “Hybrid multi-objective evolutionary algorithms based on decomposition for wireless sensor network coverage optimization,” Applied Soft Computing, vol. 68, no. 4, pp. 268–282, 2018. [Google Scholar]

20. T. Kaur and D. Kumar, “Particle swarm optimization-based unequal and fault tolerant clustering protocol for wireless sensor networks,” IEEE Sensors Journal, vol. 18, no. 11, pp. 4614–4622, 2018. [Google Scholar]

21. V. Varsha, J. Singh and M. Bala, “Tabu search based energy efficient clustering protocol for wireless sensor networks,” Global Journal of Computers & Technology, vol. 5, no. 2, pp. 302–309, 2017. [Google Scholar]

22. G. P. Gupta, “Improved cuckoo search-based clustering protocol for wireless sensor networks,” Procedia Computer Science, vol. 125, no. 6, pp. 234–240, 2018. [Google Scholar]

23. L. Kong, J. S. Pan, V. Snášel, P. W. Tsai and T. W. Sung, “An energy-aware routing protocol for wireless sensor network based on genetic algorithm,” Telecommunication Systems, vol. 67, no. 3, pp. 451–463, 2018. [Google Scholar]

24. J. Wang, Y. Gao, W. Liu, A. K. Sangaiah and H. J. Kim, “An improved routing schema with special clustering using PSO algorithm for heterogeneous wireless sensor network,” Sensors, vol. 19, no. 3, pp. 671–684, 2019. [Google Scholar] [PubMed]

25. M. Abouhawwash and K. Deb, “Karush-Kuhn-tucker proximity measure for multi-objective optimization based on numerical gradients,” in Proc. 2016 on Genetic and Evolutionary Computation Conf. Companion, ACM, Denver Colorado USA, pp. 525–532, 2016. [Google Scholar]

26. A. H. E. Bassiouny, M. Abouhawwash and H. S. Shahen, “New generalized extreme value distribution and its bivariate extension,” International Journal of Computer Applications, vol. 173, no. 3, pp. 1–10, 2017. [Google Scholar]

27. A. H. E. Bassiouny, M. Abouhawwash and H. S. Shahen, “Inverted exponentiated gamma and it’s a bivariate extension,” International Journal of Computer Application, vol. 3, no. 8, pp. 13–39, 2018. [Google Scholar]

28. A. H. E. Bassiouny, H. S. Shahen and M. Abouhawwash, “A new bivariate modified weibull distribution and its extended distribution,” Journal of Statistics Applications & Probability, vol. 7, no. 2, pp. 217–231, 2018. [Google Scholar]

29. M. Abouhawwash and M. A. Jameel, “KKT proximity measure versus augmented achievement scalarization function,” International Journal of Computer Applications, vol. 182, no. 24, pp. 1–7, 2018. [Google Scholar]

30. H. S. Shahen, A. H. E. Bassiouny and M. Abouhawwash, “Bivariate exponentiated modified Weibull distribution,” Journal of Statistics Applications & Probability, vol. 8, no. 1, pp. 27–39, 2019. [Google Scholar]

31. M. Abouhawwash and M. A. Jameel, “Evolutionary multi-objective optimization using Benson’s Kush-Kuhn-tucker proximity measure,” in Proc. Int. Conf. on Evolutionary Multi-Criterion Optimization, East Lansing, Michigan, USA, pp. 27–38, 2019. [Google Scholar]

32. M. Abouhawwash, M. A. Jameel and K. Deb, “A smooth proximity measure for optimality in multi-objective optimization using Benson’s method,” Computers & Operations Research, vol. 117, no. 2, pp. 104900, 2020. [Google Scholar]

33. M. Abouhawwash, K. Deb and A. Alessio, “Exploration of multi-objective optimization with genetic algorithms for PET image reconstruction,” Journal of Nuclear Medicine, vol. 61, no. 1, pp. 572–572, 2020. [Google Scholar]

34. M. AbdelBasset, R. Mohamed, M. Elhoseny, M. Abouhawwash, Y. Nam et al., “Efficient MCDM model for evaluating the performance of commercial banks: A case study,” Computers, Materials & Continua, vol. 67, no. 3, pp. 2729–2746, 2021. [Google Scholar]

35. B. Gomathi, S. Balaji, V. K. Kumar, M. Abouhawwash, S. Aljahdali et al., “Multi-objective optimization of energy aware virtual machine placement in the cloud data center,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1771–1785, 2022. [Google Scholar]

36. M. Kumar, K. Venkatachalam, M. Masud and M. Abouhawwash, “Novel dynamic scaling algorithm for energy-efficient cloud computing,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1547–1559, 2022. [Google Scholar]

37. R. S. Ram, K. Venkatachalam, M. Masud and M. Abouhawwash, “Air pollution prediction using dual graph convolution LSTM technique,” Intelligent Automation & Soft Computing, vol. 33, no. 3, pp. 1639–1652, 2022. [Google Scholar]

38. A. J. Basha, N. Rajkumar, M. A. AlZain, M. Masud and M. Abouhawwash, “Fog based self-sovereign identity with RSA in securing IoMT data,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1693–1706, 2022. [Google Scholar]

39. G. Ravikumar, K. Venkatachalam, M. A. AlZain, M. Masud and M. Abouhawwash, “Neural cryptography with fog computing network for health monitoring using IoMT,” Computer Systems Science and Engineering, vol. 44, no. 1, pp. 945–959, 2023. [Google Scholar]

40. R. Rajdevi, K. Venkatachalam, M. Masud, M. A. AlZain and M. Abouhawwash, “Proof of activity protocol for IoMT data security,” Computer Systems Science and Engineering, vol. 44, no. 1, pp. 339–350, 2023. [Google Scholar]

41. G. Ravikumar, K. Venkatachalam, M. Masud and M. Abouhawwash, “Cost-efficient scheduling using smart contract cognizant ethereum for IoMT,” Intelligent Automation & Soft Computing, vol. 33, no. 2, pp. 865–877, 2022. [Google Scholar]

42. N. Mittal, H. Singh, V. Mittal, S. Mahajan, A. K. Pandit et al., “Optimization of cognitive radio system using self-learning salp swarm algorithm,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3821–3835, 2022. [Google Scholar]

43. A. Garg, A. Parashar, D. Barman, S. Jain, D. Singhal et al., “Autism spectrum disorder prediction by an explainable deep learning approach,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1459–1471, 2022. [Google Scholar]