 Open Access
Open Access
ARTICLE
Hyperparameter Optimization for Capsule Network Based Modified Hybrid Rice Optimization Algorithm
1 School of Computer Science and Technology, Hubei University of Technology, Wuhan, 430068, China
2 State Key Laboratory of Information Engineering in Surveying, Mapping and Remote Sensing, Wuhan University, Wuhan, 430079, China
* Corresponding Author: Zhina Song. Email:
Intelligent Automation & Soft Computing 2023, 37(2), 2019-2035. https://doi.org/10.32604/iasc.2023.039949
Received 25 February 2023; Accepted 02 April 2023; Issue published 21 June 2023
Abstract
Hyperparameters play a vital impact in the performance of most machine learning algorithms. It is a challenge for traditional methods to configure hyperparameters of the capsule network to obtain high-performance manually. Some swarm intelligence or evolutionary computation algorithms have been effectively employed to seek optimal hyperparameters as a combinatorial optimization problem. However, these algorithms are prone to get trapped in the local optimal solution as random search strategies are adopted. The inspiration for the hybrid rice optimization (HRO) algorithm is from the breeding technology of three-line hybrid rice in China, which has the advantages of easy implementation, less parameters and fast convergence. In the paper, genetic search is combined with the hybrid rice optimization algorithm (GHRO) and employed to obtain the optimal hyperparameter of the capsule network automatically, that is, a probability search technique and a hybridization strategy belong with the primary HRO. Thirteen benchmark functions are used to evaluate the performance of GHRO. Furthermore, the MNIST, Chest X-Ray (pneumonia), and Chest X-Ray (COVID-19 & pneumonia) datasets are also utilized to evaluate the capsule network learnt by GHRO. The experimental results show that GHRO is an effective method for optimizing the hyperparameters of the capsule network, which is able to boost the performance of the capsule network on image classification.Keywords
Internet and information technology have rapidly developed in the big data era. Images have become a crucial production factor [1–3]. Since machine learning algorithms can intelligently process massive amounts of data to extract valuable potential information, they have been applied in image classification tasks. Image classification is the task of assigning corresponding labels to images from the provided set of categories.
The primary methods for image classification are divided into traditional machine learning and deep learning algorithms. One of the most typical classification methods is support vector machine (SVM) [4] in traditional machine learning algorithms. Up to now, deep learning algorithms have gradually become popular methods for image classification, including convolutional neural network (CNN) [5,6], transformer [7], and capsule network (CapsNet) [8,9]. In recent years, ConvNeXt [10], a pure convolutional neural network, has outperformed the famous Swin-transformer. Moreover, CapsNet, with a good hyperparameter configuration, is also a good solution for image classification [11,12]. CapsNet is a novel neural network based on the capsule structure and combined with convolution to have superior performance on some tasks [13–15]. Because the output of CapsNet consists of vectors, it contains more information than CNN, such as the orientation of features. This also leads to the complex structural hyperparameters of CapsNet. The optimized CapsNet can effectively balance the speed of convergence and accuracy of the model and reduce the training time and computational cost.
In essence, hyperparameter optimization is a combinatorial optimization problem. Swarm intelligence or evolutionary computation algorithms are effective means for hyperparameter optimization problem. With the development of optimization algorithms, some novel hyperparameter optimization methods have gradually emerged for hyperparameter optimization of CNN. These methods could be applied to optimize the hyperparameters of CapsNet. Only if a good combination of hyperparameters is selected, we can obtain a high-performance CapsNet. Since CapsNet requires a long training period for image classification tasks, it is necessary to choose a swarm intelligence or evolutionary computation algorithm with a faster convergence speed and excellent search capability for the hyperparameter optimization of CapsNet. Hybrid rice optimization (HRO) algorithm [16] has a faster convergence speed and can preserve population diversity with reduced computation cost than other algorithms, which have applications in several fields. For example, Jin et al. [17] proposed an improved fuzzy C-means (HROFCM) method based on HRO to select the better feature. HROFCM overcomes the defect which is multiple local optima. Thus the classifier obtained good performance in network intrusion detection. Shu et al. [18] proposed the parallel model and serial model combined HRO and the binary ant colony optimization (BACO) algorithm. The two models enhance the efficiency and robustness of HRO in solving the 0–1 knapsack problem.
Because of the good performance of HRO in the areas mentioned above, HRO is considered for finding hyperparameters of CapsNet in this paper. However, HRO is still essentially a random search algorithm and also suffers from the problem of easily falling into the local optima. Therefore, this paper improves the primary HRO by genetic search and further applies the genetic hybrid rice optimization (GHRO) algorithm for the hyperparameter optimization of CapsNet. The main contributions of this paper are summarized as follows:
• For the maintainer line, we proposed a genetic search strategy and mutation rate to enhance the global search capability of HRO.
• For the restorer line, a hybridization probability was introduced to accept some inferior solution to maintain the population diversity.
• For CapsNet, the kernel size, the stride, the number of the kernel of convolution, the optimizer, the routing times, the dimension of capsules, the activation function, and so on, can be reasonably adjusted by GHRO. GHRO is able to optimize the hyperparameters to help us build a high-performance CapsNet model.
The organization of this paper is as follows: Section 2 reviews the related work in recent years. Section 3 describes the fundamentals of HRO and CapsNet. Section 4 elaborates GHRO and the process of the hyperparameter optimization problem in CapsNet. Section 5 presents and analyses the experimental results. Finally, Section 6 is the conclusions and future works.
2.1 Hyperparameter Optimization Based on Swarm Intelligence or Evolutionary Computation Algorithms
Traditional hyperparameter optimization methods are hard to solve combinatorial optimization problems in high-dimensional space. Fortunately, swarm intelligence or evolutionary computation algorithms can find the optimum efficiently in high-dimensional space. For instance, Guo et al. [19] combined genetic algorithm (GA) and taboo search (TS) for the hyperparameter optimization problem. The hybrid optimization algorithm shows excellent search capability with faster convergence and found the hyperparameter combination with better performance than RS and BO in the experiment. Mahareek et al. [20] designed a student performance prediction model based on a simulated annealing (SA) algorithm, which showed better performance than the original model. The hyperparameter optimization of CNN based on particle swarm optimization (PSO) algorithm has obtained excellent performance on both hydraulic pistons pump intelligent fault diagnosis [21] and speech recognition tasks [22]. Xiao et al. [23] proposed a variable-length GA to automate the optimization of CNN hyperparameters and improve the image classification accuracy. Elgeldawi et al. [24] combined the advantages of PSO with GA to fine-tune the hyperparameters and successfully applied the resulting improved model for the Arabic sentiment analysis problem. Lee et al. [25] optimized the deep learning model hyperparameters based on GA, and the model performance on the Alzheimer’s diagnosis brain dataset improved by 11.73% compared with the CNN before optimization. Meng et al. [26] optimized the backpropagation neural network for milling tool wear prediction by gravitational search algorithm (GSA). Differential evolution (DE) [27] and the Cuckoo search algorithm (CS) [28] have also achieved satisfactory results in the application of hyperparameter optimization.
Even though these methods obtained good results in optimizing the hyperparameters of machine learning models, there are still some shortcomings in these algorithms. SA and DE are slow to converge and sensitive to the initial parameter settings of the algorithms. GA, TS, and CS are susceptible to the local optima, while PSO and GSA are fast to converge but cannot jump out of the local optima to find the global optima. In all, there is room for investigating more efficient optimization algorithms to optimize the hyperparameters for machine learning models. In view of the converge speed and the searching ability of HRO, it is suitable for handling the hyperparameter optimization problem.
CapsNet provides a new way to extract the main features of images different from convolution. Compared to CNN, CapsNet achieves better classification results in image classification tasks with MNIST, Fashion-MNIST, SVHN dataset [29], and smallNORB dataset [30]. These studies and improved the dynamic routing algorithm and convolution layer of CapsNet to design a more effective CapsNet. Meanwhile, several modified models of CapsNet are applied in image segmentation [31], disease diagnosis [32], and sentiment analysis [33]. One of the most significant reasons for these researchers is the reasonable hyperparameter combinations. However, researchers configured these hyperparameters of CapsNet with a lot of effort. It is difficult to establish CapsNet with an excellent hyperparameter combination, which requires enormous energy and patience. Therefore, it is necessary to seek an efficient optimization method for the hyperparameter combination in CapsNet.
3.1 The Fundamentals of Hybrid Rice Optimization Algorithm
The three-line breeding technology of Chinese hybrid rice provides some novel ideas for designing algorithms. Ye et al. proposed the HRO in 2016. The three-line breeding technology divides rice individuals into three categories. The rice individuals produce the better genes by hybridization and self-crossing. It means that the theory uses a maintainer line to maintain male sterility and achieve seed multiplication of sterile lines and a restorer line to restore fertility and obtain a robust dominant hybrid combination for application. In HRO, the gene string of rice is encoded in the feasible solution. These feasible solutions evolve toward the optimum in the search space according to several specific evolutionary rules. The correspondence between the hybrid breeding evolution process and the algorithm is shown in Fig. 1.
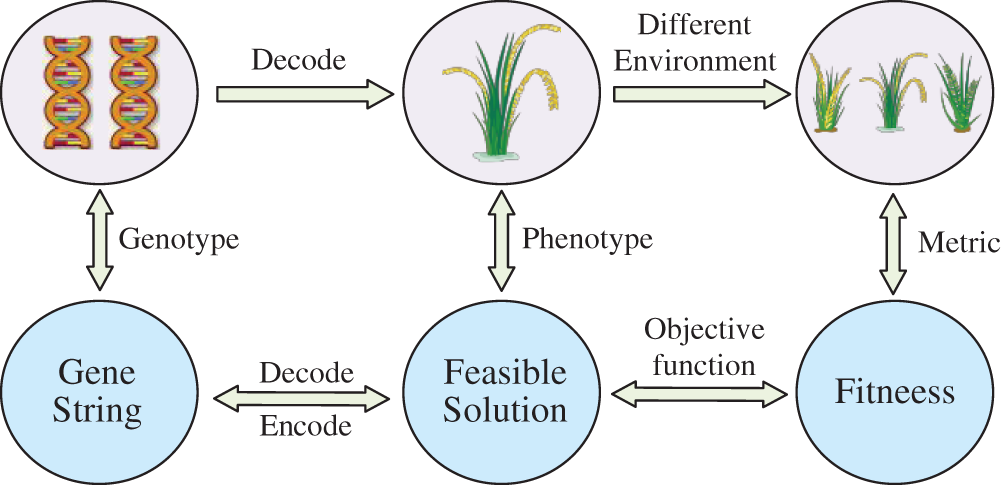
Figure 1: Mapping relationship between hybrid breeding evolution and swarm intelligence algorithm
First, HRO sorts individuals of the population
3.2 The Basic Structure of CapsNet
CapsNet is a neural network composed of multiple capsules, and its input and output are vectors. In addition, the dynamic routing algorithm updates CapsNet between two layers of vectors. Compared to CNN, the scalar features in CNN are replaced by the vector features in CapsNet because the vector features contain abundant image features. In the output, the length of the vector represents the probability of detected features. The direction of the vector represents the geometric state of detected features, such as direction, position, line thickness, and other information. These instantiated parameters extracted by capsules are equivariant. When the observed objects move or the visual conditions change, the values in the vectors change accordingly, but their lengths remain unchanged. Consequently, CapsNet compensates for the shortcomings of CNN, which is highly sensitive to the slight feature transformation of images.
A typical CapsNet is composed of an input layer, two convolutional layers, a primary capsule layer (Primary-Caps), a digitization capsule layer (Digit-Caps), and an output layer. Fig. 2 shows a typical structure of the CapsNet. The MNIST dataset is used to illustrate the training process of CapsNet, and the MNIST dataset has 10 classes from 0 to 9. The input layer of CapsNet is a
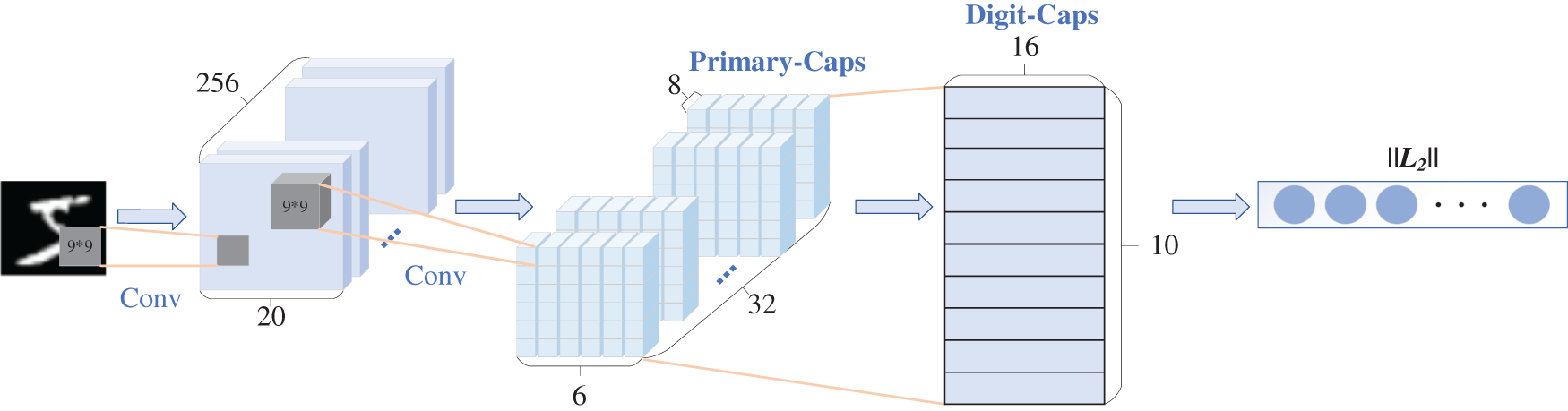
Figure 2: The typical CapsNet structure
Although CapsNet had successful applications in several different areas, some hyperparameters need to be optimized in CapsNet. These hyperparameters often rely on manual settings. An automatic hyperparameter optimization method for CapsNet based on GHRO is proposed to overcome this dilemma of manual setting. HRO combined with the genetic search and the hybridization strategy are expounded in Section 4.1. Section 4.2 describes in detail the process of the improved HRO to solve the hyperparameter optimization problem of CapsNet.
The most significant characteristic of GA is that its selection operator, crossover operator, and variation operator, which simulates the process of biological evolution. The genetic mechanism makes the search process very flexible, effectively ensuring that GA has a powerful global search capability. Nonetheless, the randomness of GA in the evolutionary process causes the algorithm lose the ability to perform valuable exploration in the vicinity of reasonable solutions. Therefore, the standard GA has the defects of poor local search capability, which can result in it falling into the local optimum.
HRO sorts and divides the population into maintainer, restorer, and sterile lines according to their fitness. In the process of population evolution, the maintainer line remains unchanged. The sterile line is intercrossed with them to produce the next generation of sterile individuals. The self-crossing, including the renewal, is belonging to swarm intelligence that enables individuals with intermediate fitness to approach the current optimum at a certain rate while avoiding the local optimum. However, the maintainer line without any operator weakens the global search capability of HRO in the later period. Additionally, the self-crossing operator of the restorer line limits population diversity, which results in the premature convergence of HRO because of falling into the local optimum. This phenomenon is named premature in evolutionary computation.
To overcome the above problems, GHRO is designed by profoundly integrating the advantages of GA and HRO. The core of GHRO is to introduce the idea of a genetic search and hybridization strategy into HRO, which can effectively eliminate the defect of premature and preserve population diversity. Fig. 3 shows the main process of GHRO.
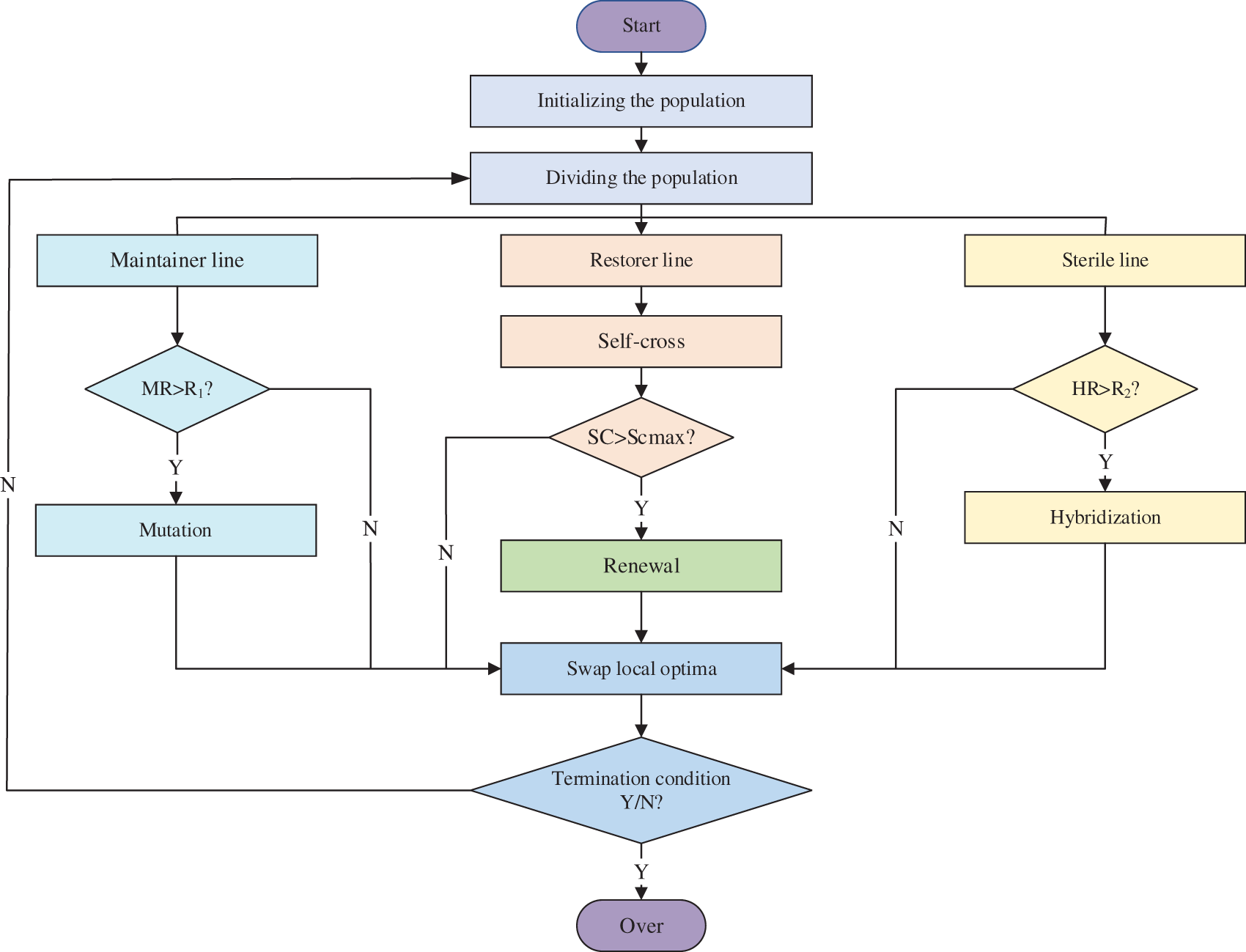
Figure 3: The main process of GHRO
Individuals in the maintainer line mutate according to the mutation rate (MR). The genetic search mechanism can enhance the ability of HRO to jump out of the local optimum and improve the global exploitation of the algorithm. The genetic search mechanism is described as Eq. (1):
where
In addition to mutation, GHRO also introduces the hybridization rate (HR) to accept inferior solutions in the sterile line with a certain probability, increasing the diversity of population. The main process is generating a number between zero and one before the population individuals mutate and hybridize. If this random number is less than MR, it performs mutation, less than HR, and it performs hybridization.
4.2 Hyperparameter Optimization of CapsNet Based on GHRO
To address the problem of manually configuring hyperparameters in CapsNet, GHRO is applied to automatically search the optimal hyperparameters of CapsNet, which is named GHRO-CapsNet.
The classical CapsNet generally is composed of three different components: convolution layers, capsule structure, and reconfiguration network. The depth of CapsNet deepens as the number of capsule and convolution layers increase. In this way, the learning capability of CapsNet increases. Unfortunately, the time and space complexity of the network also increases. In addition, these parameters which need to be adjusted are model training parameters during training, including weight, bias, and coupling coefficient. The other parameters that need to be set in advance are collectively referred to as the model hyperparameters. For example, the common model hyperparameters of CapsNet include the relevant parameters of convolution, the channel of the capsule layer, and the routing iterations.
The structure of CapsNet changes with these model hyperparameters. And the prediction accuracy for image classification is determined by the structure of CapsNet. Therefore, the hyperparameter configuration problem of CapsNet must be optimized. Existing research show that these model hyperparameters directly determine the performance of CapsNet, such as the batch size, number of convolutional kernels, and activation function. The batch size is a critical parameter that influences the performance of the network. For instance, the larger the training batch size is, the faster the computation speeds. However, the accuracy rate may decrease. The convolutional kernels determine the structure of capsules in CapsNet. And the convolutional kernels perform feature extraction by sliding over the image in a certain number of strides. The more the feature maps are contained, the better the prediction result of the network will be, but the computing cost of the network will increase. What’s more, the choice of activation function in the convolutional layer is also significant. Different activation functions have different characteristics, and the improper choice of activation function might lead to slow convergence, increased computational expenses, or gradient disappearance.
It is well known that shallow convolution exhibits poor performance in extracting complex image features. These fuzzy features which are updated by the dynamic routing algorithm will lead to poor classification performance. ResNet-50 is an excellent backbone for extracting image features in CNN. Therefore, it is reasonable to apply ResNet-50 with excellent feature extraction ability as the backbone of CapsNet. For GHRO, the maximum iteration is 30, the population size is 12, and the individual dimension is 14. Each algorithm runs ten times independently. In other words, a total of 12 × 30 × 10 CapsNet need to be validated. Meanwhile, the maximum number of self-crossings in GHRO-CapsNet is 20. Table 1 describes the hyperparameters required to be optimized. The values of these hyperparameters are were selected based on prior experience and experimentation. C is the first convolution layer, P is the Primary-Caps, and F is the FC layer. Fig. 4 shows the structure of GHRO-CapsNet. Each individual organized by these hyperparameters represents a unique CapsNet structure, and these individuals search freely in the solution space, dramatically increasing the diversity of CapsNet structures and the possibility of finding a new network structure with excellent performance. The pseudo-code for the genetic hybrid rice optimizing capsule network is described in Algorithm 1.

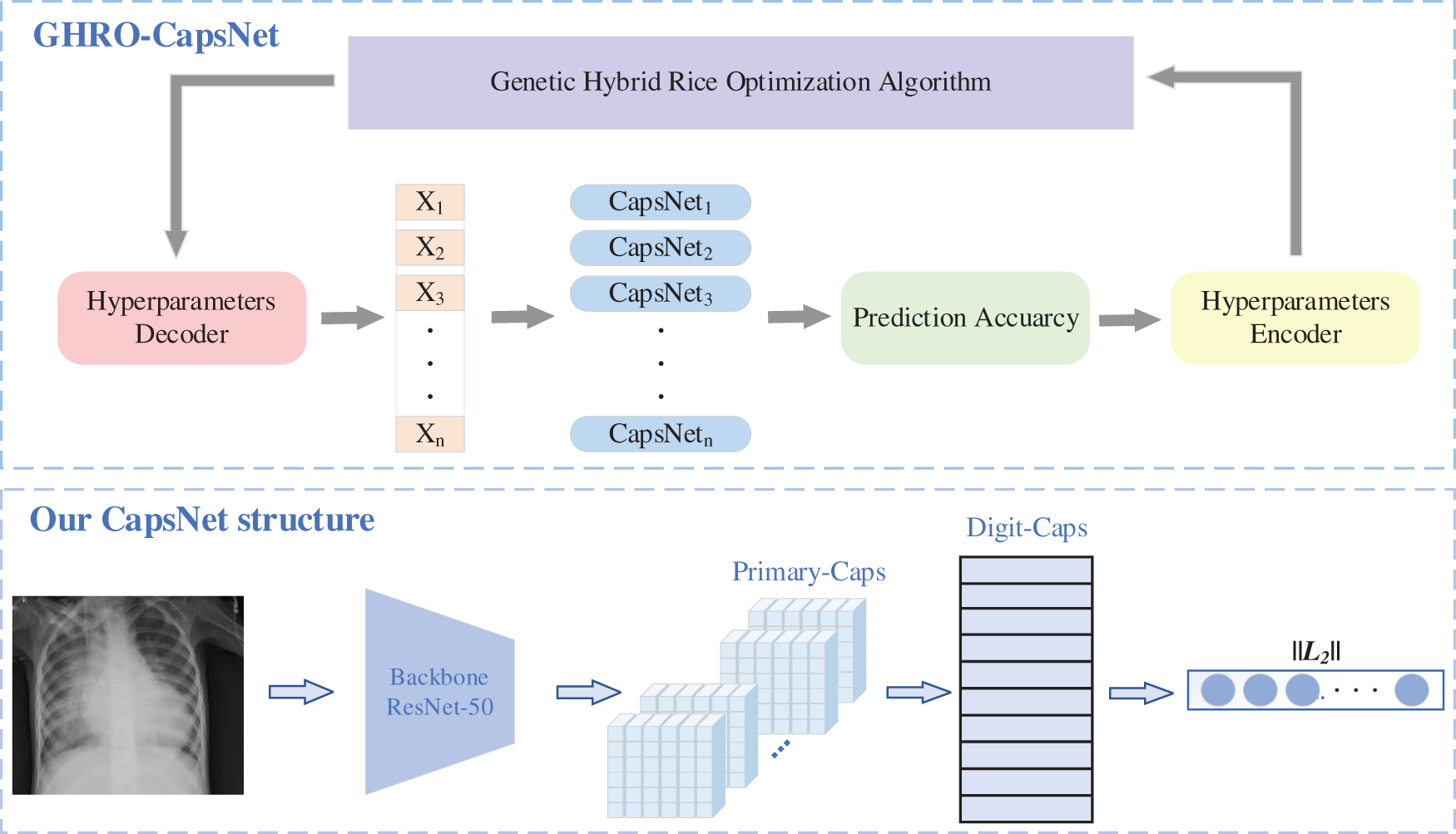
Figure 4: The architecture of GHRO-CapsNet

5 Experiment Result and Analysis
In this section, the experiment is divided into two components. The first component (Section 5.1) is to evaluate the performance of GHRO. The second component (Section 5.2) applies the GHRO for hyperparameter optimization of CapsNet to the MNIST dataset, Chest X-Ray (Pneumonia) [35], and Chest X-ray (COVID-19 & Pneumonia) datasets [36] collected from Guangzhou Women and Children’s Medical Centre.
5.1 Evaluation for Genetic Hybrid Rice Optimization on Function Benchmarks
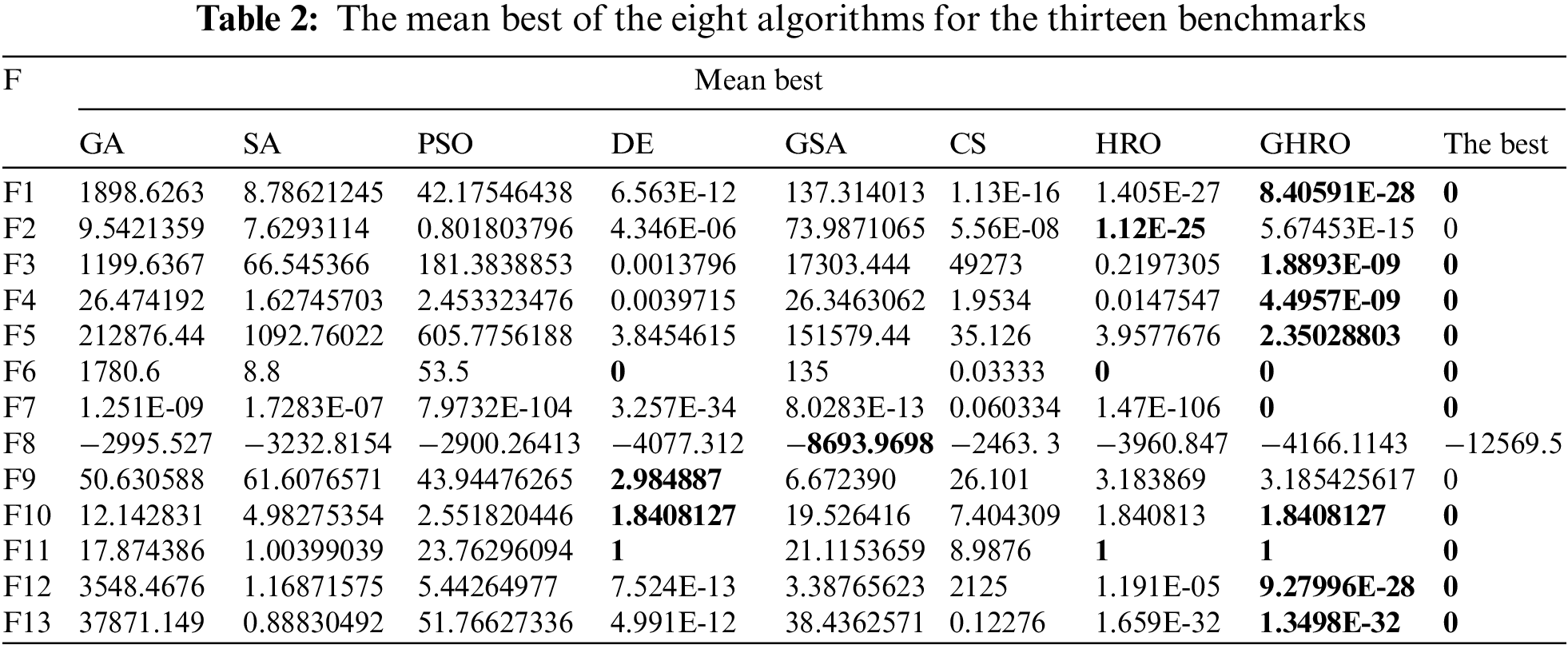
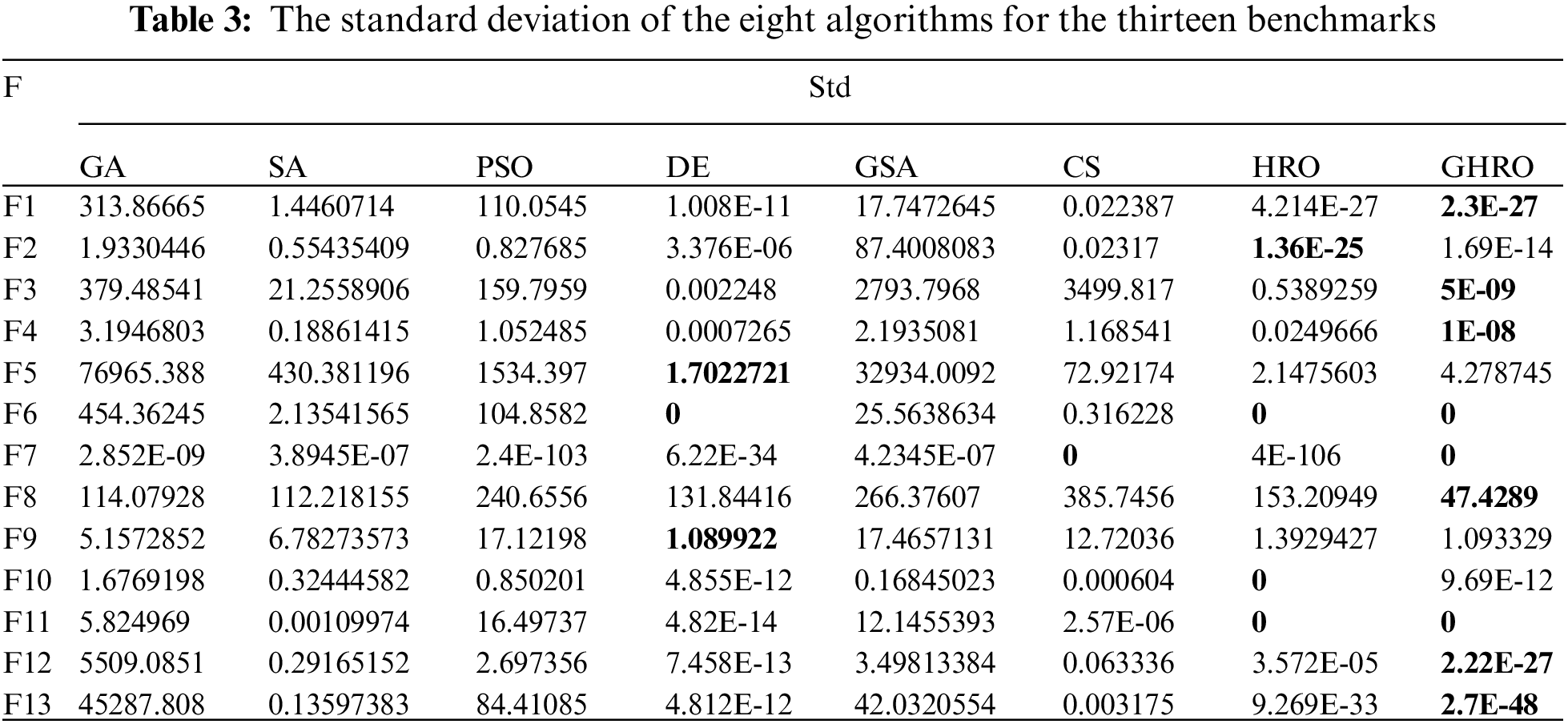
For GHRO, we compared it with GA, SA, PSO, DE, GSA, CS, and HRO on 13 benchmark functions [37], which contain two major classes of unimodal and multimodal functions, respectively. Among them, the benchmark functions from F1 to F7 are unimodal test functions with only one best solution and variable dimensions, and they can effectively evaluate the local exploration capability of GHRO. These benchmark functions from F8 to F13 are ordinary multimodal benchmark functions, which means that the benchmark functions have more than one local optimum. These local optima grow rapidly with the variables dimension. The best solutions of multimodal benchmark functions increase by components, and they focus on the balance of local exploration and global exploration ability. There are 14 hyperparameters to be optimized in CapsNet. The margin of these hyperparameters is rounded down to 10. Therefore, the dimension of the individual component is set to 10.
The bold entries in the above table indicate the optimal result among all algorithms. To avoid randomness in the experiment, each algorithm runs 30 times independently. Mean best and “std” are used as the metrics. Mean best is the mean of the results of thirty experiments. And the standard deviation is used to evaluate the effect of randomness on these algorithms.
As shown in Table 2, the mean best of GHRO is better than the other algorithms, except for F2 and F9. At the same time, it is obvious that GHRO is superior in F1, F3-F6, and F10-F13, resulting in the values of 8.40591E-28, 1.8893E-09, 4.4957E-09, 2.35028803, 0, 0, 1.8408127, 1, 9.27996E-28, and 1.3498E-32, respectively. Table 3 shows the standard deviation of the eight algorithms. GHRO is strength in F1, F3, F4, F6, F7, F8, F11, F12, and F13, accounting for 69% of all benchmark functions. In particular, the standard deviation of GHRO is 0 on F6, F7, and F11. Therefore, GHRO is more stable than the other algorithms. In short, the experimental results indicate that the HR and MR balance the search capability of HRO. Meanwhile, the two strategies retain the characteristics of stable and fast convergence of HRO. Compared to the other algorithms, GHRO is probably an excellent solution for solving the hyperparameter optimization problem of CapsNet. Therefore, HRO and GHRO are applied to search for the hyperparameter configuration of CapsNet.
5.2 Assessment for Hyperparameter Optimization of GHRO-CapsNet
5.2.1 Description of Experimental Environment and Data
The working environment is as follows: Windows 10 operating system, Intel(R) Xeon(R) Silver 4210R CPU@2.40 GHz Hexa-core processor, 64G running memory, and Tesla M40 24 GB graphics card configuration. The development environment is Anaconda 3.4, Pytorch-GPU version 1.11.0, Python version 3.7, and some third-party libraries, such as Matplotlib, Tqdm, Pandas, and Numpy.
The MNIST, Chest X-ray (pneumonia), and Chest X-ray (COVID-19 & Pneumonia) datasets are described in Tables 4–6. They are divided into training and testing sets with a ratio of 6:1, 8:2, and 8:2. The image resolution of MNIST is 28, and the image size of the other two datasets is resized to 224.
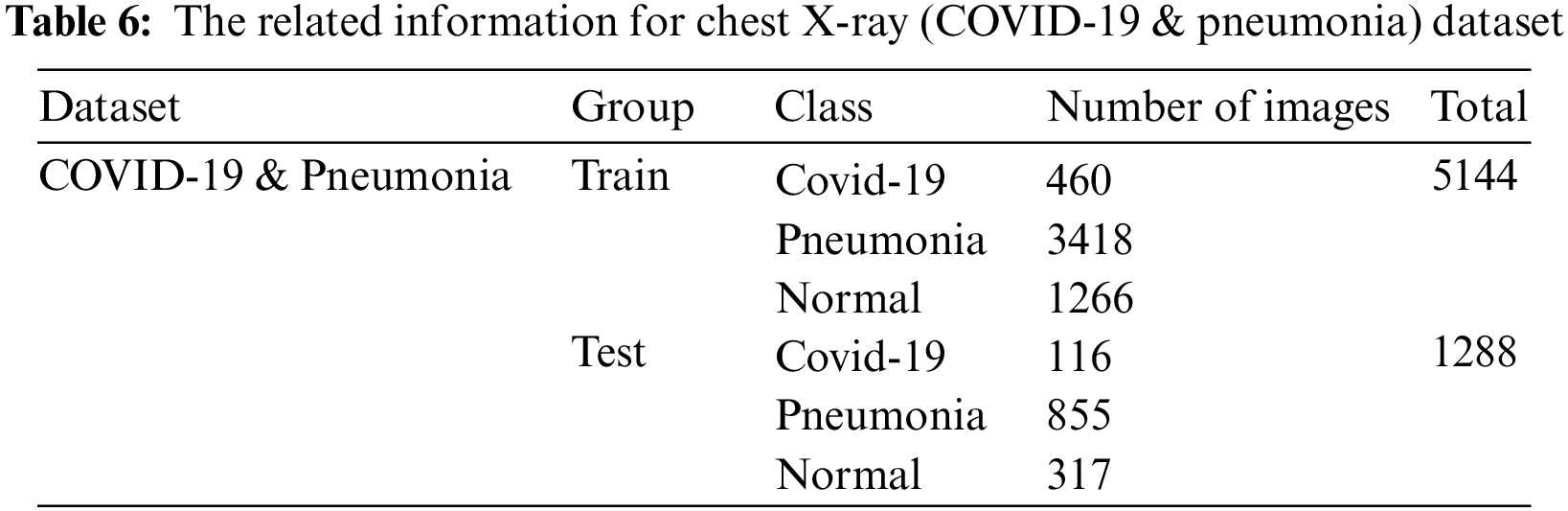
5.2.2 Experimental Result for GHRO-CapsNet
By statistics and analysis of the experimental data, the average of the correct rates of the ten groups of experiments is calculated. The best hyperparameter combinations of HRO-CapsNet and GHRO-CapsNet searched establish high-performance CapsNet on MNIST, Chest X-ray (Pneumonia) and Chest X-ray (COVID-19 & Pneumonia) datasets, respectively. MNIST is a simple dataset, thus classification accuracy is always used as its performance metric. The confusion matrix, average classification accuracy, precision, recall, and F1-Score are utilized to performance metrics for the other two datasets. Fig. 5 shows the confusion matrixes for the Pneumonia and Pneumonia & COVID-19 datasets.
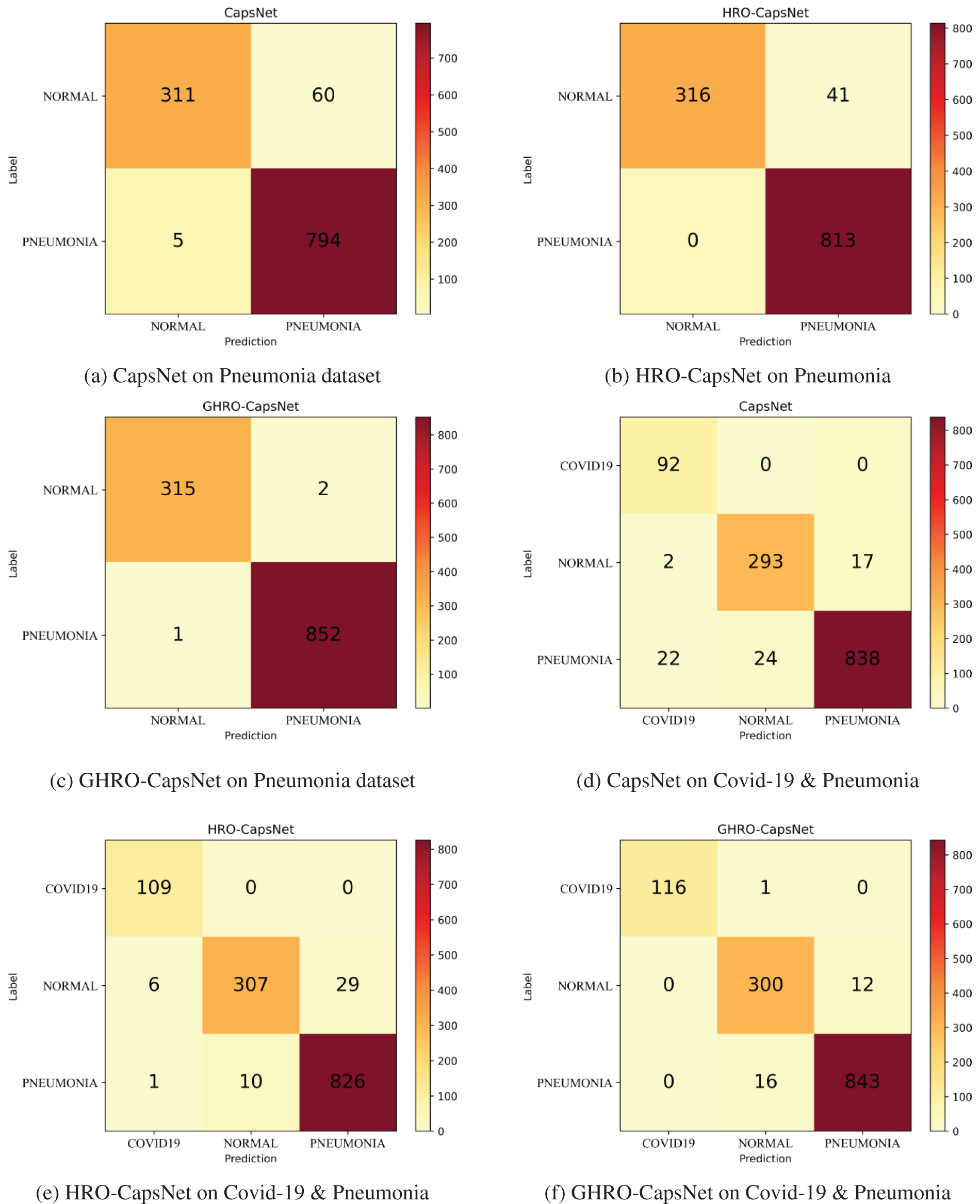
Figure 5: Confusion matrix of models on pneumonia and Covid-19 & pneumonia dataset
The performance of CapsNet, HRO-CapsNet, and GHRO-CapsNet is compared in Table 7. Based on GHRO, the precision of CapsNet has improved from 95.17% to 99.74% for Pneumonia dataset, and from 95.04% to 97.73% for COVID-19 & Pneumonia dataset. Similarly, GHRO optimization has raised the recall of CapsNet from 94.44% to 99.74% for Pneumonia dataset and from 94.95% to 97.74% for COVID-19 & Pneumonia dataset. Finally, GHRO has also boosted the F1-Score of CapsNet from 94.80% to 99.74% for Pneumonia dataset and from 94.99% to 97.73% for COVID-19 & Pneumonia dataset. The improvement of these performance metrics has demonstrated the superior classification performance of GHRO-CapsNet.
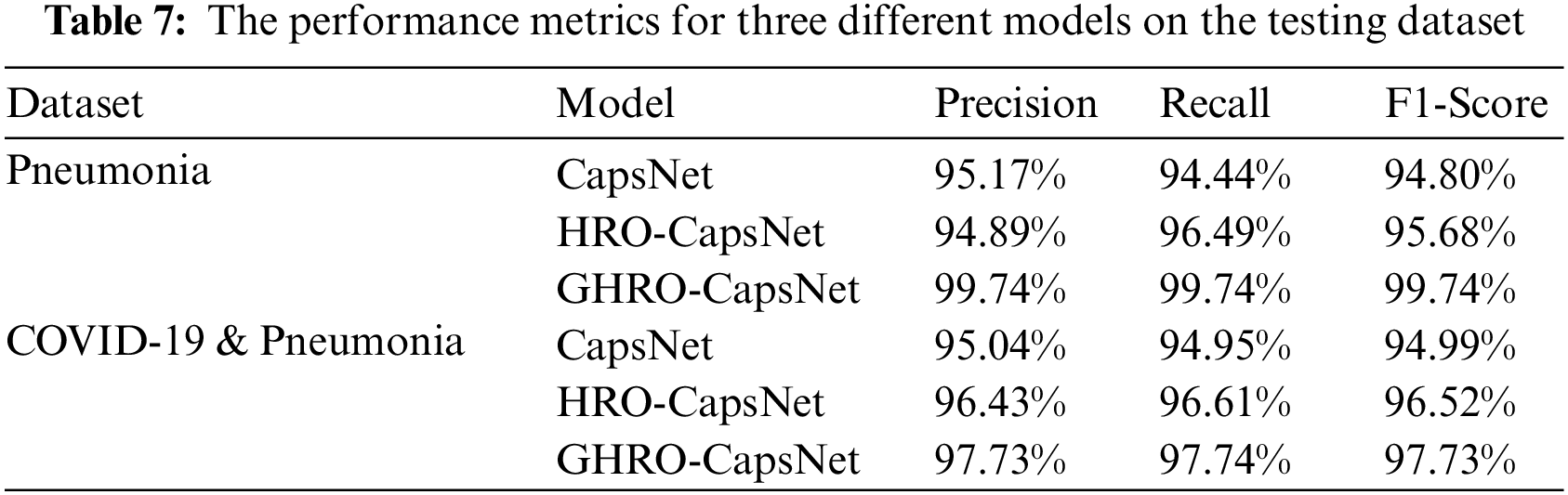
Table 8 presents the average classification accuracies of various models. GHRO-CapsNet achieved the best average classification accuracy of 99.73% on the MNIST dataset, 99.74% on the Pneumonia dataset, and 97.75% on the COVID-19 & Pneumonia dataset, respectively. Compared to CapsNet, GHRO-CapsNet increased the classification accuracy by 0.53% on the MNIST dataset, 5.3% on the Pneumonia data, and 2.8% on the Chest X-Ray (pneumonia) dataset. Additionally, GHRO-CapsNet has advantages over HRO-CapsNet and other recent methods in the three datasets. The experiment aims to demonstrate that GHRO can obtain a better hyperparameters combination of CapsNet. It is encouraging that our proposed genetic search strategy and hybridization factor enhance the later search capability of HRO so that the derived hyperparameter combination constitutes a new CapsNet with better classification results. Furthermore, GHRO-CapsNet performs better than HRO-CapsNet and CapsNet on MNIST, Chest X-Ray (pneumonia), and Chest X-ray (COVID-19 & Pneumonia) datasets, which verifies the effectiveness and practicality of GHRO-CapsNet.
In this paper, we propose a modified HRO to search the optimal hyperparameters of CapsNet to build a CapsNet model with excellent image classification performance. Specifically, the hyperparameter combinations of CapsNet are encoded to numerical parameters, which is viewed as a combinatorial optimization problem and handled by GHRO. During the evolution process of the algorithm, a genetic search strategy makes the algorithm less susceptible to local optimal solutions. On the other hand, the genetic search strategy also balances the local exploration and global search capability of the algorithm. Moreover, the hybridization factor maintains the population diversity of hyperparameter combinations in the hybridization process. Facilitated by these two improved strategies, the algorithm searches for better hyperparameter combinations of CapsNet more efficiently, resulting in better performance of CapsNet for image classification tasks.
The experimental results of 13 benchmark functions show that GHRO has an excellent ability to find the better solution in complex space. Three optimal CapsNet models are searched on the MNIST, Chest X-Ray (pneumonia), and Chest X-ray (COVID-19 & Pneumonia) datasets. These three GHRO-CapsNet models attained high accuracy rates on three distinct datasets: MNIST, Chest X-Ray (pneumonia), and Chest X-Ray (COVID-19 & Pneumonia). Specifically, the models achieved 99.73%, 99.74%, and 97.75% accuracy on the respective datasets. These new CapsNet structures all have excellent performance than the original CapsNet in the three datasets. Therefore, the experimental results demonstrated that GHRO-CapsNet could be an effective and automatic method for the hyperparameter optimization of CapsNet. In the future, the research will focus on further improving the CapsNet with other optimization algorithms. Moreover, it makes sense to use GHRO to optimize the hyperparameters of other networks in machine learning.
Funding Statement: This work was supported by National Natural Science Foundation of China (Grant: 41901296, 62202147).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. S. Sen, S. Agarwal, P. Chakraborty and K. P. Singh, “Astronomical big data processing using machine learning: A comprehensive review,” Experimental Astronomy, vol. 53, no. 1, pp. 1–43, 2022. [Google Scholar]
2. K. Bowe, G. Lightbody, A. Staines and D. M. Murray, “Big data, machine learning, and population health: Predicting cognitive outcomes in childhood,” Pediatric Research, vol. 93, pp. 300–307, 2023. [Google Scholar] [PubMed]
3. K. A. Brown, S. Brittman, N. Maccaferri, D. Jariwala and U. Celano, “Machine learning in nanoscience: Big data at small scales,” Nano Letters, vol. 20, no. 1, pp. 2–10, 2019. [Google Scholar] [PubMed]
4. W. Doorsamy and V. Rameshar, “Investigation of PCA as a compression pre-processing tool for X-ray image classification,” Neural Computing and Applications, vol. 35, pp. 1099–1109, 2023. [Google Scholar]
5. S. Poornima, N. Sripriya, A. F. Alrasheedi, S. S. Askar and M. Abouhawwash, “Hybrid convolutional neural network for plant diseases prediction,” Intelligent Automation & Soft Computing, vol. 36, no. 2, pp. 2393–2409, 2023. [Google Scholar]
6. A. Kumar, A. R. Tripathi, S. C. Satapathy and Y. D. Zhang, “SARS-Net: COVID-19 detection from chest x-rays by combining graph convolutional network and convolutional neural network,” Pattern Recognition, vol. 122, pp. 108255, 2022. [Google Scholar] [PubMed]
7. Y. E. Almalki, M. Zaffar, M. Irfan, M. A. Abbas, M. Khalid et al., “A Novel-based swin transfer based diagnosis of COVID-19 patients,” Intelligent Automation & Soft Computing, vol. 35, no. 1, pp. 163–180, 2023. [Google Scholar]
8. R. Pucci, C. Micheloni, G. L. Foresti and N. Martinel, “Deep interactive encoding with capsule networks for image classification,” Multimedia Tools and Applications, vol. 79, pp. 32243–32258, 2020. [Google Scholar]
9. X. Ai, J. Zhuang, Y. Wang, P. Wan and Y. Fu, “ResCaps: An improved capsule network and its application in ultrasonic image classification of thyroid papillary carcinoma,” Complex and Intelligent Systems, vol. 8, pp. 1865–1873, 2021. [Google Scholar]
10. Z. Liu, H. Mao, C. -Y. Wu, C. Feichtenhofer, T. Darrell et al., “A convnet for the 2020s,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New Orleans, LA, USA, pp. 11976–11986, 2022. [Google Scholar]
11. G. Sun, S. Ding, T. Sun, C. Zhang and W. Du, “A novel dense capsule network based on dense capsule layers,” Applied Intelligence, vol. 52, no. 3, pp. 3066–3076, 2022. [Google Scholar]
12. J. Li, Q. Zhao, N. Li, L. Ma, X. Xia et al., “A survey on capsule networks: Evolution, application, and future development,” in Proc. 2021 Int. Conf. on High Performance Big Data and Intelligent Systems (HPBD&IS), Macau, China, pp. 177–185, 2021. [Google Scholar]
13. V. Mazzia, F. Salvetti and M. Chiaberge, “Efficient-capsnet: Capsule network with self-attention routing,” Scientific Reports, vol. 11, no. 1, pp. 14634, 2021. [Google Scholar] [PubMed]
14. S. Rajagopal, T. Ramakrishnan and S. Vairaprakash, “Anatomical region detection scheme using deep learning model in video capsule endoscope,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1927–1941, 2022. [Google Scholar]
15. D. Peng, D. Zhang, C. Liu and J. Lu, “BG-SAC: Entity relationship classification model based on self-attention supported capsule networks,” Applied Soft Computing, vol. 91, pp. 106186, 2020. [Google Scholar]
16. Z. Ye, L. Ma and H. Chen, “A hybrid rice optimization algorithm,” in Proc. 2016 11th Int. Conf. on Computer Science & Education (ICCSE), Nagoya, Japan, pp. 169–174, 2016. [Google Scholar]
17. C. Jin, Z. Ye, C. Wang, L. Yan and R. Wang, “A network intrusion detection method based on hybrid rice optimization algorithm improved fuzzy C-means,” in Proc. 2018 IEEE 4th Int. Symp. on Wireless Systems Within the Int. Conf. on Intelligent Data Acquisition and Advanced Computing Systems (IDAACS-SWS), Lviv, Ukraine, pp. 47–52, 2018. [Google Scholar]
18. Z. Shu, Z. Ye, X. Zong, S. Liu, D. Zhang et al., “A modified hybrid rice optimization algorithm for solving 0–1 knapsack problem,” Applied Intelligence, vol. 52, no. 5, pp. 5751–5769, 2022. [Google Scholar]
19. B. Guo, J. Hu, W. Wu, Q. Peng and F. Wu, “The Tabu_genetic algorithm: A novel method for hyper-parameter optimization of learning algorithms,” Electronics, vol. 8, no. 5, pp. 579, 2019. [Google Scholar]
20. E. A. Mahareek, A. S. Desuky and H. A. El-Zhni, “Simulated annealing for SVM parameters optimization in student’s performance prediction,” Bulletin of Electrical Engineering Informatics, vol. 10, no. 3, pp. 1211–1219, 2021. [Google Scholar]
21. Y. Zhu, G. Li, R. Wang, S. Tang, H. Su et al., “Intelligent fault diagnosis of hydraulic piston pump combining improved LeNet-5 and PSO hyperparameter optimization,” Applied Acoustics, vol. 183, pp. 108336, 2021. [Google Scholar]
22. V. Passricha and R. K. Aggarwal, “PSO-Based optimized CNN for hindi ASR,” International Journal of Speech Technology, vol. 22, pp. 1123–1133, 2019. [Google Scholar]
23. X. Xiao, M. Yan, S. Basodi, C. Ji and Y. Pan, “Efficient hyperparameter optimization in deep learning using a variable length genetic algorithm,” arXiv preprint arXiv: 2006.12703, 2020. [Google Scholar]
24. E. Elgeldawi, A. Sayed, A. R. Galal and A. M. Zaki, “Hyperparameter tuning for machine learning algorithms used for arabic sentiment analysis,” Informatics, vol. 8, no. 4, pp. 79, 2021. [Google Scholar]
25. S. Lee, J. Kim, H. Kang, D. Y. Kang and J. Park, “Genetic algorithm based deep learning neural network structure and hyperparameter optimization,” Applied Sciences, vol. 11, no. 2, pp. 744, 2021. [Google Scholar]
26. X. Meng, J. Zhang, G. Xiao, Z. Chen, M. Yi et al., “Tool wear prediction in milling based on a GSA-BP model with a multisensor fusion method,” The International Journal of Advanced Manufacturing Technology, vol. 114, pp. 3793–3802, 2021. [Google Scholar]
27. C. E. da Silva Santos, R. C. Sampaio, L. dos Santos Coelho, G. A. Bestard and C. H. Ilanos, “Multi-objective adaptive differential evolution for SVM/SVR hyperparameters selection,” Pattern Recognition, vol. 110, pp. 107649, 2021. [Google Scholar]
28. X. N. Bui, H. Nguyen, Q. H. Tran, D. A. Nguyen and H. B. Bui, “Predicting ground vibrations due to mine blasting using a novel artificial neural network-based cuckoo search optimization,” Natural Resources Research, vol. 30, pp. 2663–2685, 2021. [Google Scholar]
29. J. Rajasegaran, V. Jayasundara, S. Jayasekara, H. Jayasekara, S. Seneviratne et al., “Deepcaps: Going deeper with capsule networks,” in In Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 10725–10733, 2019. [Google Scholar]
30. G. E. Hinton, S. Sabour and N. Frosst, “Matrix capsules with EM routing,” in Proc. Int. Conf. on Learning Representations (ICLR), Vancouver, BC, Canada, 2018. [Google Scholar]
31. F. J. Garcia-Espinosa, D. Concha, J. J. Pantrigo and A. Cuesta-Infante, “Visual classification of dumpsters with capsule networks,” Multimedia Tools and Applications, vol. 81, no. 21, pp. 31129–31143, 2022. [Google Scholar]
32. R. Maurya, V. K. Pathak and M. K. Dutta, “Computer-aided diagnosis of auto-immune disease using capsule neural network,” Multimedia Tools and Applications, vol. 81, pp. 13611–13632, 2022. [Google Scholar]
33. P. Demotte, K. Wijegunarathna, D. Meedeniya and I. Perera, “Enhanced sentiment extraction architecture for social media content analysis using capsule networks,” Multimedia Tools and Applications, vol. 82, pp. 8665–8690, 2023. [Google Scholar] [PubMed]
34. Z. Ye, W. Cai, S. Liu, K. Liu, M. Wang et al., “A band selection approach for hyperspectral image based on a modified hybrid rice optimization algorithm,” Symmetry, vol. 14, no. 7, pp. 1293, 2022. [Google Scholar]
35. “Chest X-ray images (Pneumonia),” Kaggle.com, 2022. [Online]. Available: https://www.kaggle.com/datasets/paultimothymooney/chest-xray-pneumonia [Google Scholar]
36. P. Patel, “Chest X-ray (COVID-19 & pneumonia),” Kaggle.com, 2020. [Online]. Available: https://www.kaggle.com/prashant268/chest-xray-covid19-pneumonia [Google Scholar]
37. X. Yao, Y. Liu and G. Lin, “Evolutionary programming made faster,” IEEE Transactions on Evolutionary Computation, vol. 3, no. 2, pp. 82–102, 1999. [Google Scholar]
38. P. Gavrikov and J. Keuper, “Cnn filter DB: An empirical investigation of trained convolutional filters,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, New Orleans, LA, USA, pp. 19066–19076, 2022. [Google Scholar]
39. M. Shaikh, I. F. Siddiqui, Q. Arain, J. Koo, M. A. Unar et al., “MDEV model: A novel ensemble-based transfer learning approach for pneumonia classification using CXR images,” Computer Systems Science and Engineering, vol. 46, no. 1, pp. 287–302, 2023. [Google Scholar]
40. M. S. Islam, S. J. Das, M. R. A. Khan, S. Momen and N. Mohammed, “Detection of COVID-19 and pneumonia using deep convolutional neural network,” Computer Systems Science and Engineering, vol. 44, no. 1, pp. 519–534, 2023. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF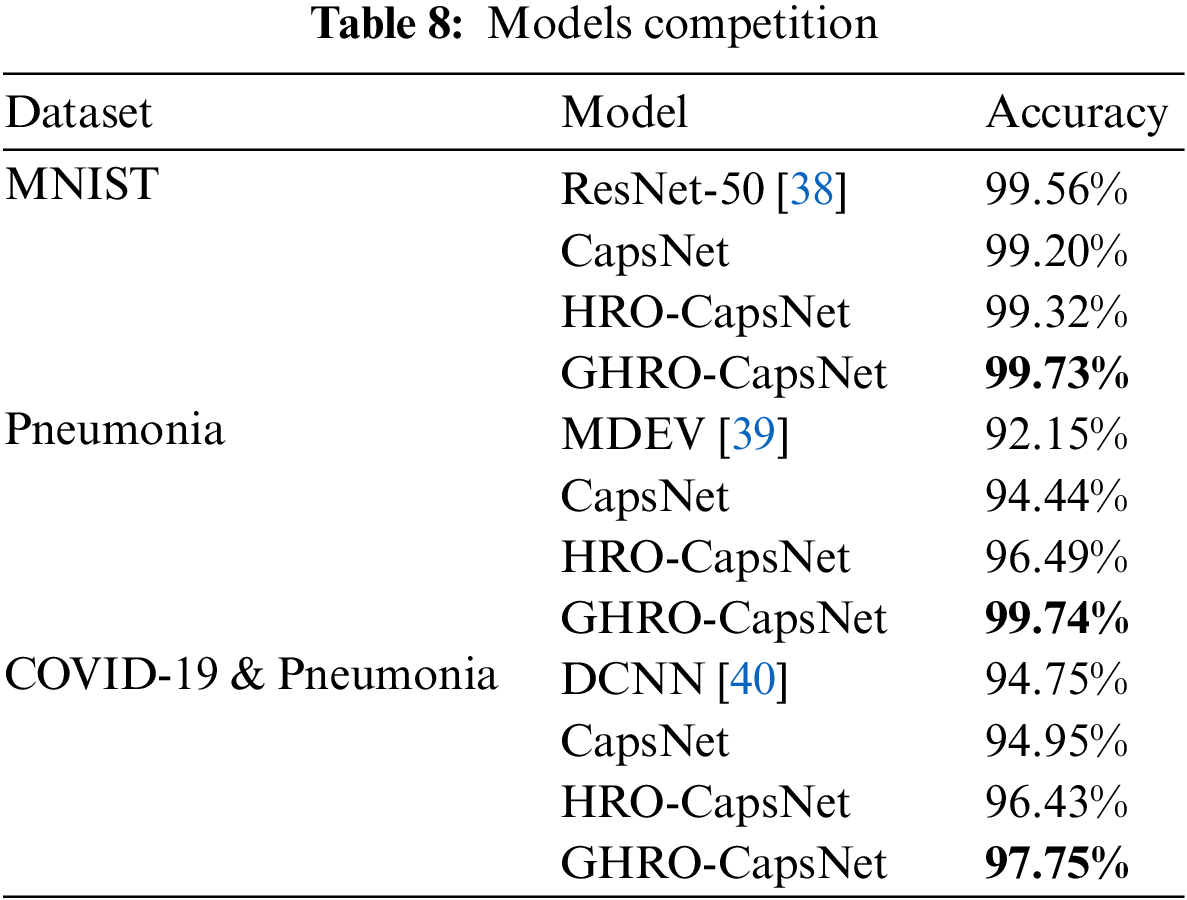
 Downloads
Downloads
 Citation Tools
Citation Tools