Effective Return Rate Prediction of Blockchain Financial Products Using Machine Learning

1  Introduction

The advancement of artificial intelligence (AI) experiences massive variations for years in which numerous effective applications have been provided to the general public to offer a very comfortable life at present [1]. One such significant research branch of AI technologies is known as machine learning (ML), the 3 demonstrative learning technologies: semi-supervised, supervised, and unsupervised. All these 3 technologies are utilized solely in an intellectual system and obviously, they could be further integrated when it becomes necessary to solve a problematic matter in question collectively [2,3]. The underlying ideology of ML is using unlabelled or labelled input data for finding suitable regulations to categorize the yet strange data or to predict events in the upcoming years. In recent times, economic globalization was speedily developed, and along with that, distinct prospects restricting industrial growth were overcome with the rapid enhancing sources [4]. Speedy development in socio-economic markets was monitored. The media of socio-economic advancement decides socio-economic markets. It controls or manages the allotment of the whole economic and public scheme and therefore turns into a crucial portion of socio-economic advancement [5,6]. The worldwide internet growth has resulted in the development of multiple internet related financial products like Yu’EBao, Baidu Economic Management, and this evolution definitely has significant effects on community.

Currently, a brand-new internet economics structure established by world impacts namely digital currency, peer-to-peer (P2P), blockchain (BC), and crowdfunding, might act as a majority portion in the expansion of the global monetary markets [7]. BC systems can be fixed as orderly developments in which the intrusion has huge influences by transferring the function of industries from centralized to decentralized arrangements. Every time it alters the unreliable agent without demanding entity related systems [8,9]. Adding to the progressive growth, the interference of BC finance generates a strong influence on orthodox financial goals [10]. These influences effectively gained the attention of researchers who study BC financial products. Owing to the shortfalls stated in literature works that regularly utilized the speedy placement of AI approaches, a quantity of authors implied arithmetic systems for computing and examining the quantifiable financial data.

Ji et al. [11] discussed several recent DL techniques like deep residual network, deep neural network (DNN), convolutional neural network (CNN), long short-term memory (LSTM), and its group for Bitcoin price prediction. Salb et al. [12] offer optimized techniques such as enhancing the support vector machine (SVM) technique by utilizing an enhanced version of technique sine cosine for anticipating cryptocurrency values. The fundamental of sine cosine algorithm (SCA) is improved with easy exploration process and then estimated by related to other approaches run on matching sets of data. Snihovyi et al. [13] create the 3 application elements into single robo-advisor that integrates their structure and modern financial instrument–cryptocurrency for the first time. The primary component is LSTM-NN that predicts the cryptocurrency prices daily. The secondary component utilizes robo-advising technique for building an investment plan for novice cryptocurrency investors with distinct risk attitudes in investment decisions. The tertiary component has been ETL (Extract-Transform-Load) to a statistics data set and NNs methods. Kim et al. [14] examine the connection amongst inherent Ethereum BC data and Ethereum prices. Moreover, it can be explored that BC data regarding other publicly accessible coins on the market has been connected with Ethereum prices. Metawa et al. [15] progress the intelligent return rate prediction method utilizing DL to BC financial products (RRP-DLBFP). The presented RRP-DLBFP algorithm contains planning an LSTM technique for prediction analysis of return rate. Also, the Adam optimization was executed to optimum alter the LSTM technique hyperparameters, therefore improving the prediction efficiency. Some other models are also available in the literature [16–18].

This study introduces a novel Jellyfish search optimization based extreme learning machine with autoencoder (JSO-ELMAE) for return rate prediction of BC financial products. The presented JSO-ELMAE model designs a new ELMAE model to predict the return rate of financial products. Besides, the JSO algorithm is exploited to tune the parameters related to the ELMAE model which in turn boosts the classification results. The application of JSO technique assists in optimal parameter adjustment of the ELMAE model to predict the bitcoin return rates. The experimental validation of the JSO-ELMAE approach was executed and the results are inspected in many aspects. In short, the key contribution of the study is listed as follows.

•   Design a new ELMAE model to predict the return rate of financial products.

•   Apply JSO algorithm is exploited to tune the parameters related to the ELMAE model.

•   Employ JSO technique for optimal parameter adjustment of the ELMAE model to predict the bitcoin return rates.

•   Validate the performance of the proposed model on Ethereum (ETH) return rate and investigate the results under several measures.

2  The Proposed Model

In this study, a new JSO-ELMAE algorithm was introduced for return rate prediction of BC financial products. The presented JSO-ELMAE model designs a new ELMAE model to predict the return rate of financial products. Besides, the JSO algorithm is exploited to tune the parameters related to the ELMAE model which in turn boosts the classification results.

2.1 Process Involved in ELMAE Model

Primarily, the presented JSO-ELMAE model designs a new ELMAE model to predict the return rate of financial products. At this time, ELMAE was regarded as a classifier method. It executes attained features and evaluates the probability for objects present in the image. Mostly, the activation function and dropout layer are utilized to establish non-linearity and decrease over-fitting problems correspondingly. The ELM has been determined as single hidden-layer feed-forward neural network (SLFN). It can be obvious that hidden layer is non-linear because of the occurrence of nonlinear activation function [19]. Thus, the resultant layer is linear without activation function. It has been collected in 3 layers such as input, hidden, as well as output layers. Consider that x is a trained sample and f(x) denotes the simulation result of NN. The SLFN together with k hidden node is executed by provided function:

fELM(x)=BT.G(w,b,x),(1)

whereas G(w,b,x) stands for the hidden layer activation function, w determines the input weighted matrix that connects input as well as hidden layers, b signifies the bias weighted of hidden layer, and B=[β1β2…βm] refers the weighted in hidden as well as output layers. In event of ELM, utilizing n trained samples, d input neuron, k hidden neuron, and m resultant neurons (that is, m classes), Eq. (1) was formulated as:

tj=BT⋅g(⟨wj,xi⟩+bj),i=1,2,⋯n,(2)

whereas ti denotes the m-dimension needed resultant vector for ith trained sample xi, the d dimension wj refers the jth weighted vector in the input layer to jth hidden neuron, and bj defines the bias of jth hidden neuron. During this method, ⟨wj,xi⟩ stands for the interior product of wj and xi. The sigmoid function g was utilized as activation function, so the outcome of jth hidden neuron is determined as [20]:

g(⟨wj,xi⟩+bj)=1/(1+exp(−wjTxi+bj2e2)),(3)

In which exp(.) denotes the exponent arithmetic, and e2 stands for the steepness attributes. In matrix format, technique (2) has been restructured as:

HB=T,(4)

whereas T∈Rn×m demonstrates the target outcome, B∈Rk×m. H=[h(x1)⋮h(xn)] is meant that hidden layer resultant matrix of ELM that is the size of (n,k) that is expressed as:

H=g(W.X+b)=[g(⟨w1,x1⟩+b1)⋯g(⟨wk,x1⟩+bk)⋮⋯⋮g(⟨w1,xn⟩+b1)⋯g(⟨wk,xn⟩+bk)]n×k(5)

Afterward, B is defined by minimal norm least-squares solution:

B=H†T=HT(IC+HHT)−1T,(6)

whereas C signifies the regularization variable and ELM is demonstrated as:

fELM(x)=h(x)HT(IC+HHT)−1T,(7)

The ELM has been upgraded as kernel-based ELM (KELM) with kernel trick. Assume

Ω=HHT,(8)

Whereas

Ωi,j=k(xj,xj),(9)

whereas xi and xj defines the ith and jth trained samples correspondingly. Then, replacing HHT by Ω, the suggestions of KELM are expressed as:

fKELM(x)=h(x)HT(IC+Ω)−1T,(10)

In which fKELM(x) implies the simulation result of KELM technique, as well as h(x)HT=[k(x′x1)k(x,xn)]. The ELM-AE technique depicts the features based on singular measures. MELM has been determined as a multilayer neural network (MNN) by stacking several ELMAEs. Let X(i)=[x1(i),⋯,xn(i)], whereas xk(i) signifies the ith data illustration for input xk,k=1 to n. Consider Λ(i)=[λ1(i),⋯,λn(i)] defines the ith transformation matrix, whereas λk(i) signifies the transformation vector executed to representation learning with respect to xk(i).

According to Eq. (10), B is exchanged by Λ(i) and T is changed by X(i) correspondingly from MELM. Fig. 1 depicts the framework of ELMAE technique.

H(i)Λ(i)=X(i),(11)

whereas H(i) demonstrates the outcome matrix of ith hidden layer by represents of X(i), and Λ(i) that is determined as:

Λ(i)=(H(i))T(IC+H(i)(H(i))T)−1X(i).(12)

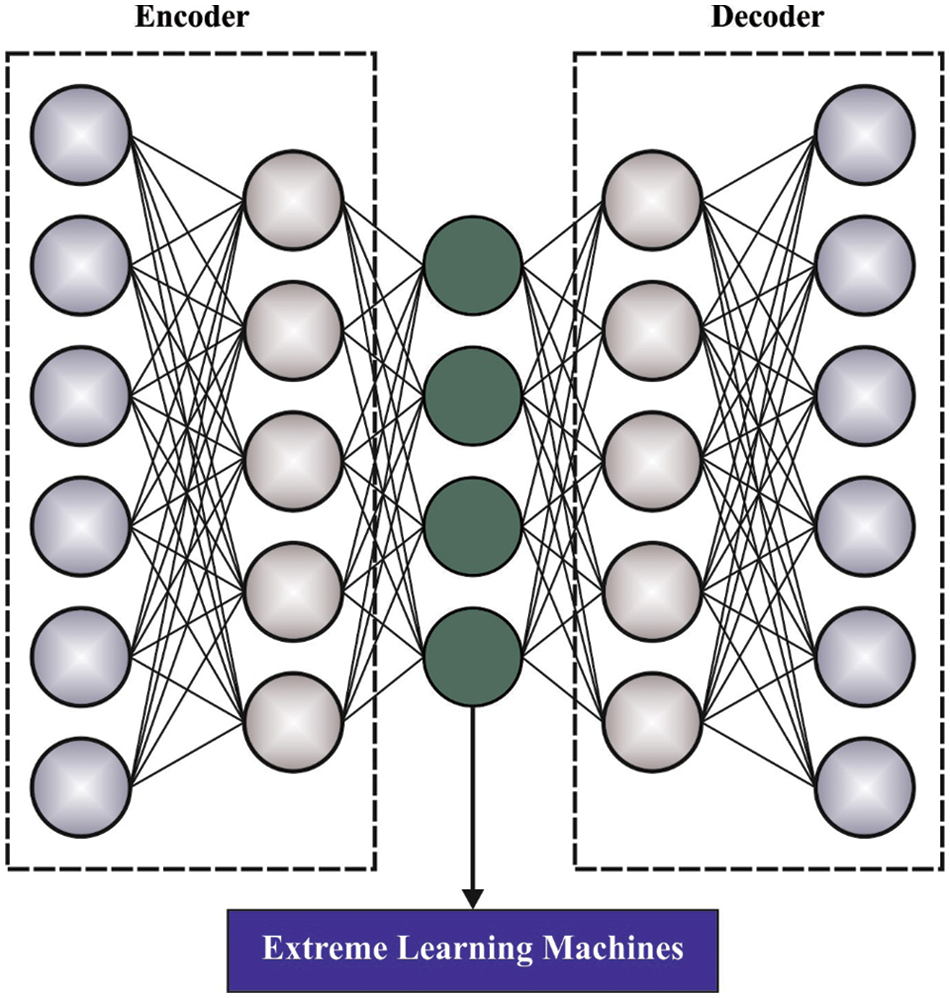
Figure 1: Architecture of ELMAE

Also,

X∗=g(X(i)(Λ(i))T),(13)

where X∗ implies the last implication of X(1). X∗ represents the executed as hidden layer outcome to evaluate the last weighted β∗ and it can be rewritten as:

β∗=(X∗)†T=(X∗)T(IC+X∗(X∗)T)−1T.(14)

2.2 Parameter Optimization Process

In this work, the JSO algorithm is exploited to tune the parameters related to the ELMAE model which in turn boosts the classification results [21–23]. In JSO, the initialized population of the jellyfish is seeded in a different form by projecting chaotic logistics as follows [24]:

Xi(t+1)=4v0(1−Xi),0≤v0≤1(15)

In Eq. (15), Xi refers to the ith jellyfish chaotic counterparts, and vo a randomly generated value of v0∈(0,1),v0∉{0.0,0.25,0.75,0.5,1.0}. The JSO is governed and modeled using three rules in the following:

•   The jellyfish moves inside the swarm or towards the ocean current. The transitions between them are guided through a timing control system (TCS) [25].

•   Next, when the food supply is sufficient, the jellyfish is attracted to the corresponding position.

•   Then, the objective values display the food quantity. A time regulation parameter (t), as described in the following expression is utilized to represent the TCS.

c(t)=|(1−tMaxiter)×(2×rand(0,1)−1)|(16)

In Eq. (16), t indicates the present iteration, Maxiter represent the entire iterations. The TCS randomly ranges from [0, 1]. The jellyfish could adapt the ocean current wherever the direction (trend) is evaluated by utilizing the mean of jellyfish (μ) and the optimal individual amongst themselves (X∗). Accordingly, the new jellyfish location can be defined by the following expression:

Xi(t+1)=R×(X∗−3×R×μ)+Xi(t)(17)

In Eq. (17), R indicates the random integer ranges from [0, 1]. When the jellyfish does not follow the current of the ocean, it travels inside the swarm that takes the active or passive movement behavior. In the passive movement, most jellyfish move all over the particular site where the location is adjusted by [26]:

Xi(t+1)=0.1×R×(Ub−Lb)+Xi(t)(18)

In Eq. (18), Ub and Lb correspondingly represents the high and low limits of design parameters. In the active type, once the food quantity at the location of the jellyfish (j) exceeds the counterpart at (i), it starts moving towards the first as given below:

Xi(t+1)={Xi(t)R(×Xj(t)Xi(t))iff(Xi)f(Xj)Xi(t)R(×Xi(t)Xj(t))iff(X0)<f(Xj)(19)

In Eq. (19), f indicates the food volume with respect to the objective valuation associated with jellyfish location. The TCS is utilized for performing the selection condition of active and passive types. With that regard, a random number is generated within the interval of [0-1]. When the number is large when compared to the term (1−c(t)), jellyfish determines the passive movement. Otherwise, it determines the active movement. Since the TCS values decline from [0, 1] over time, passive movement was firstly selected, and active movement is selected as time passes. A jellyfish returns to the reverse bounds when the venture preceding the bounding search field. The re-entry process is denoted by the following equation:

{Xi,d′=(Xi,d−Ub,d)+L(d)ifXi,d>Ub,dXi,d′=(Xi,d−Lb,d)+U(d)ifXi,d<Lb,d(20)

In Eq. (20), Xi,d characterizes the ith location of jellyfish in dth dimension to be adjusted afterward the limits are inspected. Fig. 2 demonstrates the process involved in jellyfish. In addition, the JSO algorithm derives a fitness function to effectively choose the hyperparameters involved in the ELMAE model. The fitness function involves the minimization of error rate, i.e., the difference between the actual and forecasted values obtained by the proposed model should be as low as possible. The candidate solution attaining minimal error values during the return rate prediction values of BC financial products should be considered as optimal solution and vice versa. Therefore, the use of the metaheuristic JSO algorithm helps in accomplishing enhanced predictive performance.

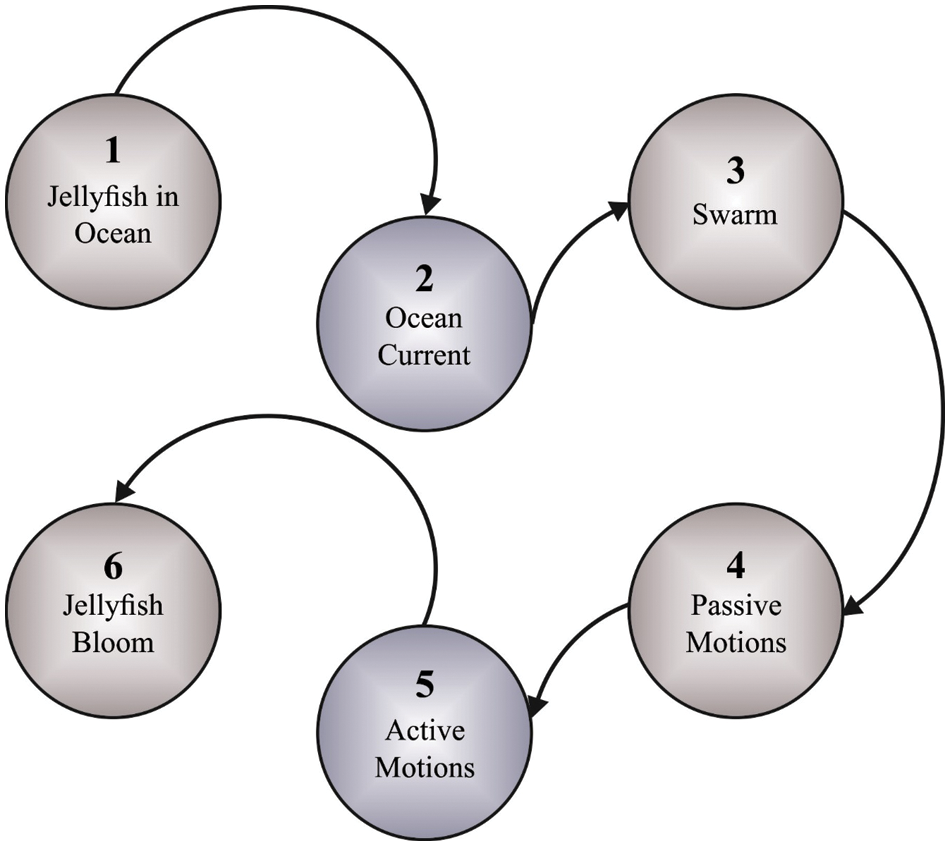
Figure 2: Process in jellyfish

3  Results and Discussion

For verifying the goodness of the presented JSO-ELMAE method, the Ethereum (ETH) return rate is selected as target and the experimental analysis is executed on it for verifying the predictive outcomes on the time series. The comparative study is made with recent models under several measures.

Tab. 1 provides a detailed predictive result analysis of the JSO-ELMAE model under three test runs. The results inferred that the JSO-ELMAE model has obtained effective predictive outcomes. Fig. 3 offers a comprehensive predictive outcome of the JSO-ELMAE model under run-1. The figure represented that the JSO-ELMAE model has predicted the bitcoin return rate values closer to original value. For instance, on test sample 1 and actual value of 2.718, the JSO-ELMAE model has predicted the value of 2.838. Besides, on test sample 50 and actual value of 2.818, the JSO-ELMAE approach has predicted the value of 2.898. Additionally, on test sample 60 and actual value of 3.177, the JSO-ELMAE algorithm has predicted the value of 3.317. Then, on test sample 70 and actual value of 3.175, the JSO-ELMAE algorithm has predicted the value of 3.265. On the other hand, on test sample 80 and actual value of 3.072, the JSO-ELMAE algorithm has predicted the value of 2.872. In line with, on test sample 90 and actual value of 2.616, the JSO-ELMAE algorithm has predicted the value of 2.566. In addition, on test sample 100 and actual value of 2.953, the JSO-ELMAE methodology has predicted the value of 3.103. Thus, it is apparent that the JSO-ELMAE model has obtained closer predictive outcomes over other models.

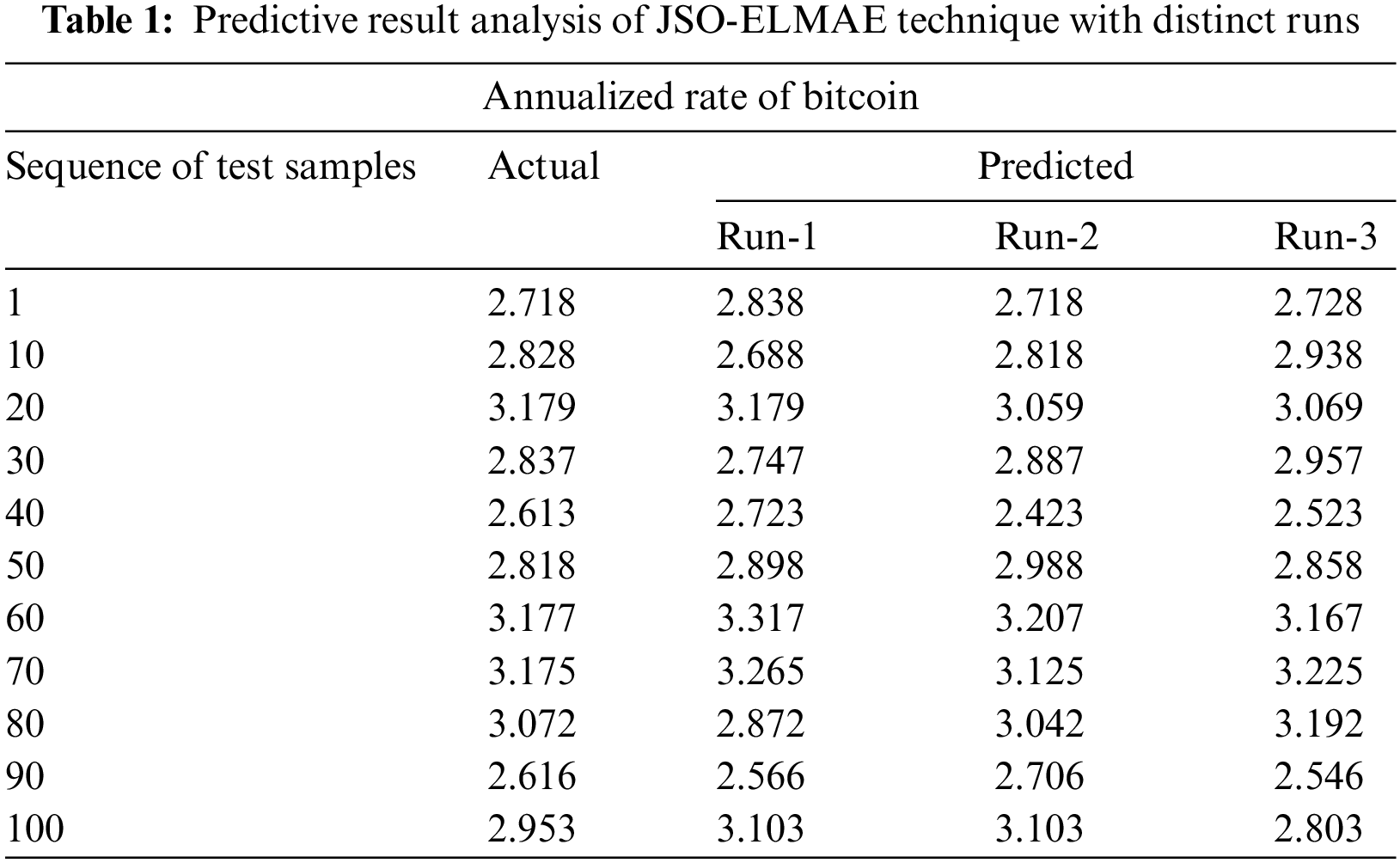
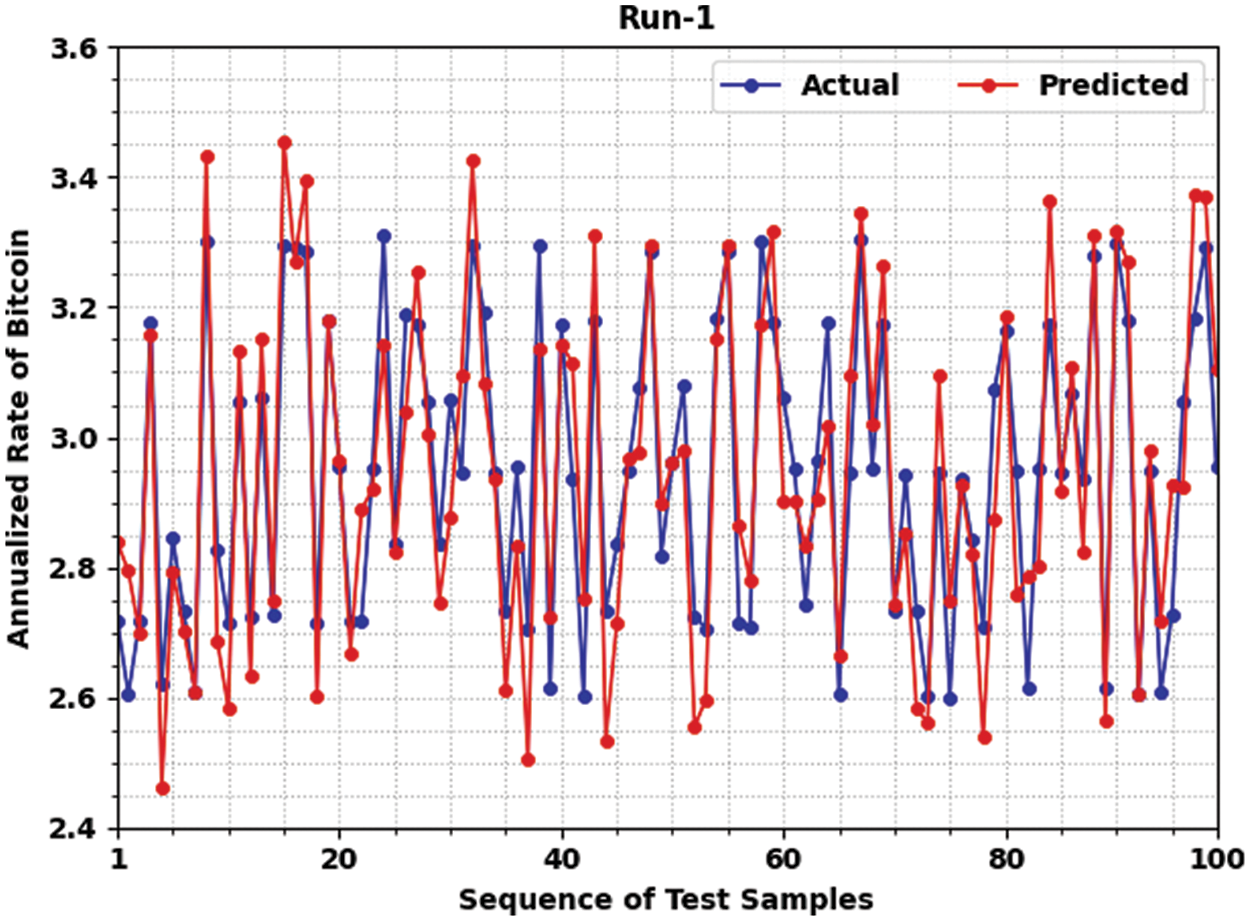
Figure 3: Predictive result analysis of JSO-ELMAE technique under run-1

Fig. 4 provides a comprehensive predictive outcome of the JSO-ELMAE algorithm under run-2. The figure signified that the JSO-ELMAE methodology has predicted the bitcoin return rate values closer to original value. For instance, on test sample 1 and actual value of 2.718, the JSO-ELMAE approach has predicted the value of 2.718. Moreover, on test sample 50 and actual value of 2.818, the JSO-ELMAE system has predicted the value of 2.988. Additionally, on test sample 60 and actual value of 3.177, the JSO-ELMAE algorithm has predicted the value of 3.207. Then, on test sample 70 and actual value of 3.175, the JSO-ELMAE algorithm has predicted the value of 3.125. On the other hand, on test sample 80 and actual value of 3.072, the JSO-ELMAE algorithm has predicted the value of 3.042. In line with, on test sample 90 and actual value of 2.616, the JSO-ELMAE algorithm has predicted the value of 2.706. At last, on test sample 100 and actual value of 2.953, the JSO-ELMAE algorithm has predicted the value of 3.103. Thus, it is apparent that the JSO-ELMAE model has obtained closer predictive outcomes over other models.

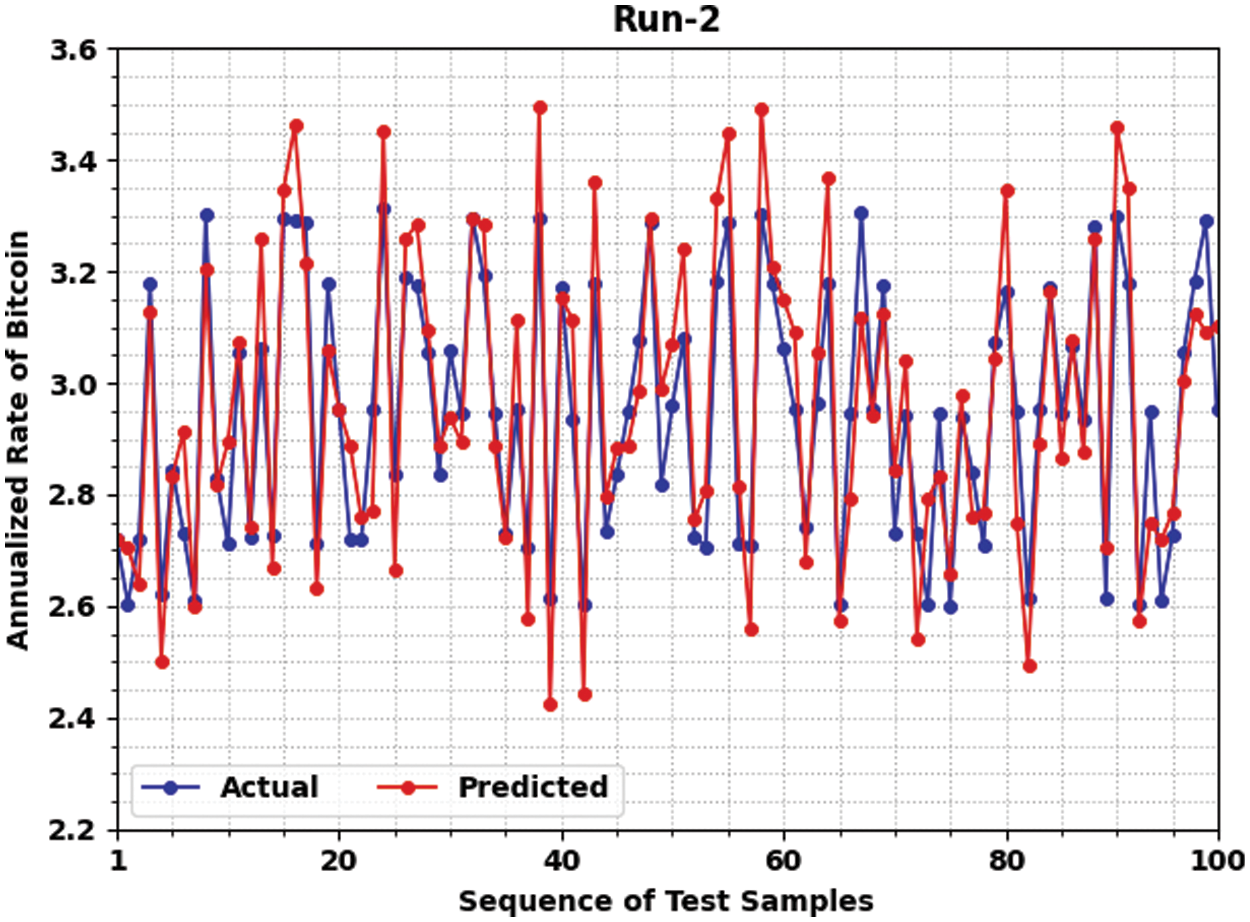
Figure 4: Predictive result analysis of JSO-ELMAE technique under run-2

Fig. 5 depicts a comprehensive predictive outcome of the JSO-ELMAE algorithm under run-3. The figure demonstrated that the JSO-ELMAE approach has predicted the bitcoin return rate values closer to original value. For instance, on test sample 1 and actual value of 2.728, the JSO-ELMAE system has predicted the value of 2.838. Besides, on test sample 50 and actual value of 2.818, the JSO-ELMAE method has predicted the value of 2.858.

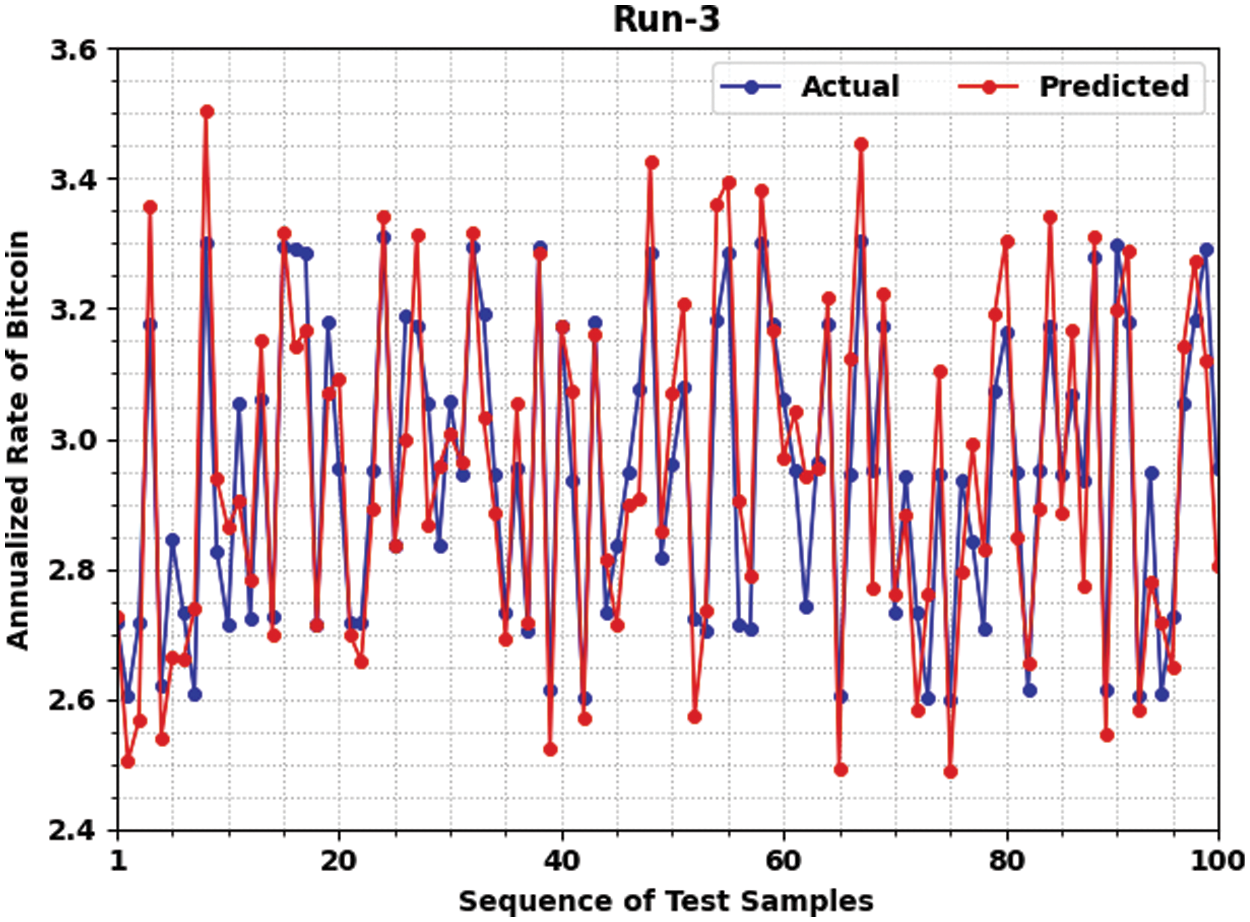
Figure 5: Predictive result analysis of JSO-ELMAE technique under run-3

Additionally, on test sample 60 and actual value of 3.177, the JSO-ELMAE algorithm has predicted the value of 3.167. Then, on test sample 70 and actual value of 3.175, the JSO-ELMAE algorithm has predicted the value of 3.225. On the other hand, on test sample 80 and actual value of 3.072, the JSO-ELMAE algorithm has predicted the value of 3.192. In line with, on test sample 90 and actual value of 2.616, the JSO-ELMAE algorithm has predicted the value of 2.546. Eventually, on test sample 100 and actual value of 2.953, the JSO-ELMAE system predicted the value of 2.803. Thus, it is apparent that the JSO-ELMAE model has obtained closer predictive outcomes over other models.

Tab. 2 provides a comprehensive comparison study of the JSO-ELMAE model with other models [27]. Fig. 6 provides a brief MSE examination of the JSO-ELMAE model with existing models on both TR and TS sets. The experimental results implied that the JSO-ELMAE model has shown effectual results with minimal values of MSE. For instance, on TR data, the JSO-ELMAE model has offered reduced MSE of 0.0129 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN models have obtained increased MSE of 0.0655, 0.0601, 0.1181, 0.0752, 0.0955, and 0.1068. Also, on TS data, the JSO-ELMAE algorithm has obtainable decreased MSE of 0.0244 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN methods have obtained improved MSE of 0.0802, 0.0903, 0.1172, 0.1021, 0.1012, and 0.1006.

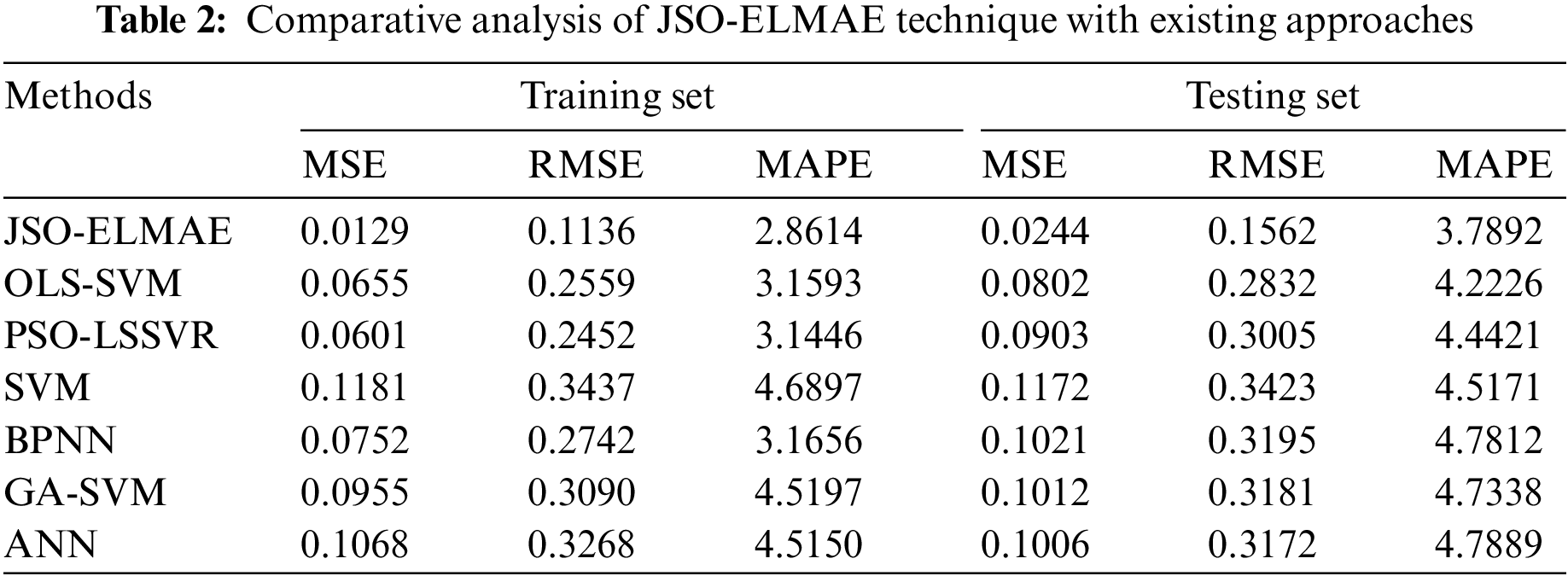
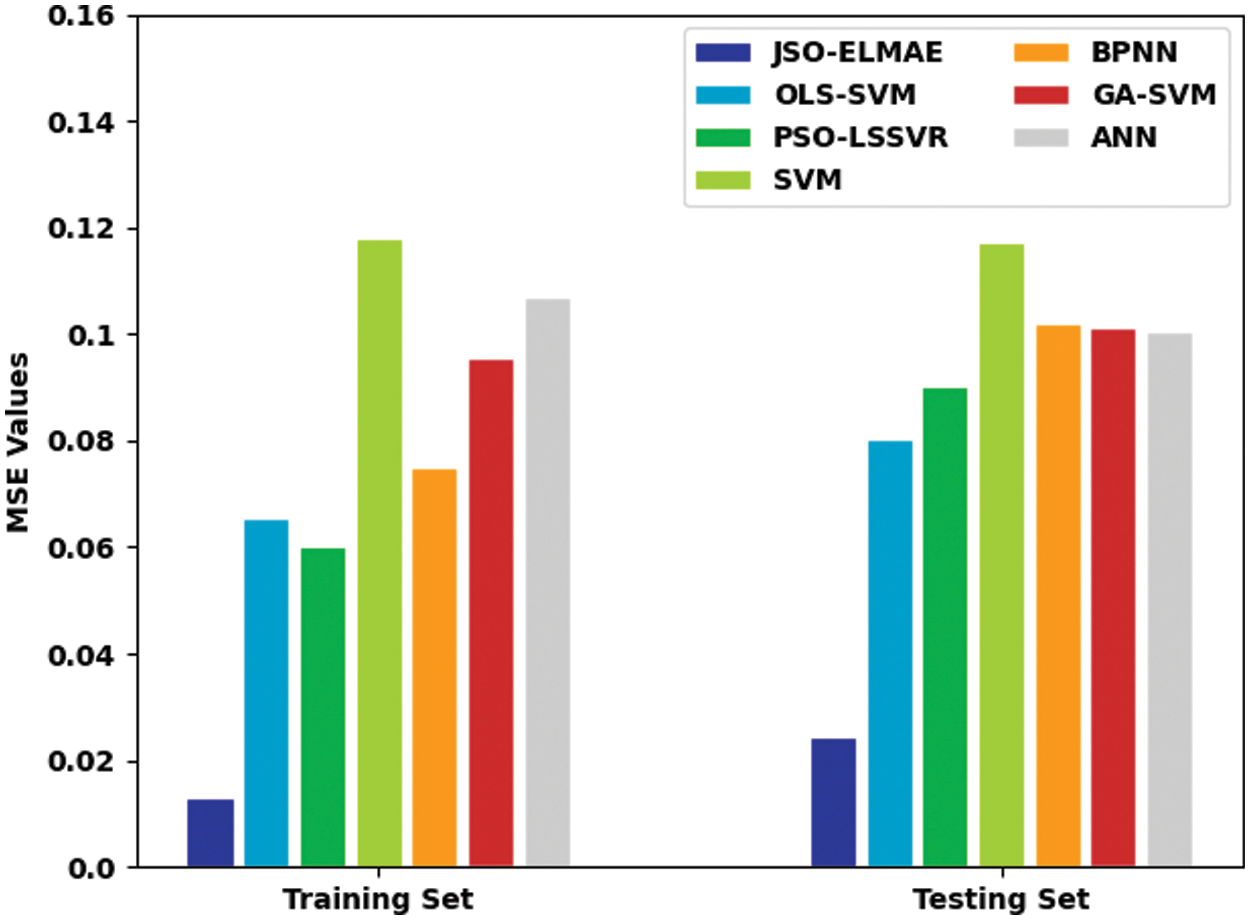
Figure 6: MSE analysis of JSO-ELMAE technique with existing approaches

Fig. 7 offers a brief RMSE analysis of the JSO-ELMAE model with existing approaches on both TR and TS sets. The experimental outcomes implied that the JSO-ELMAE model has demonstrated effectual results with minimal values of RMSE. For instance, on TR data, the JSO-ELMAE model has offered reduced RMSE of 0.1136 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN algorithms have obtained higher RMSE of 0.2559, 0.2452, 0.3437, 0.2752, 0.3090, and 0.3268. Also, on TS data, the JSO-ELMAE approach has accessible minimal RMSE of 0.1562 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN techniques have reached improved RMSE of 0.2832, 0.3005, 0.3423, 0.3195, 0.3181, and 0.3172.

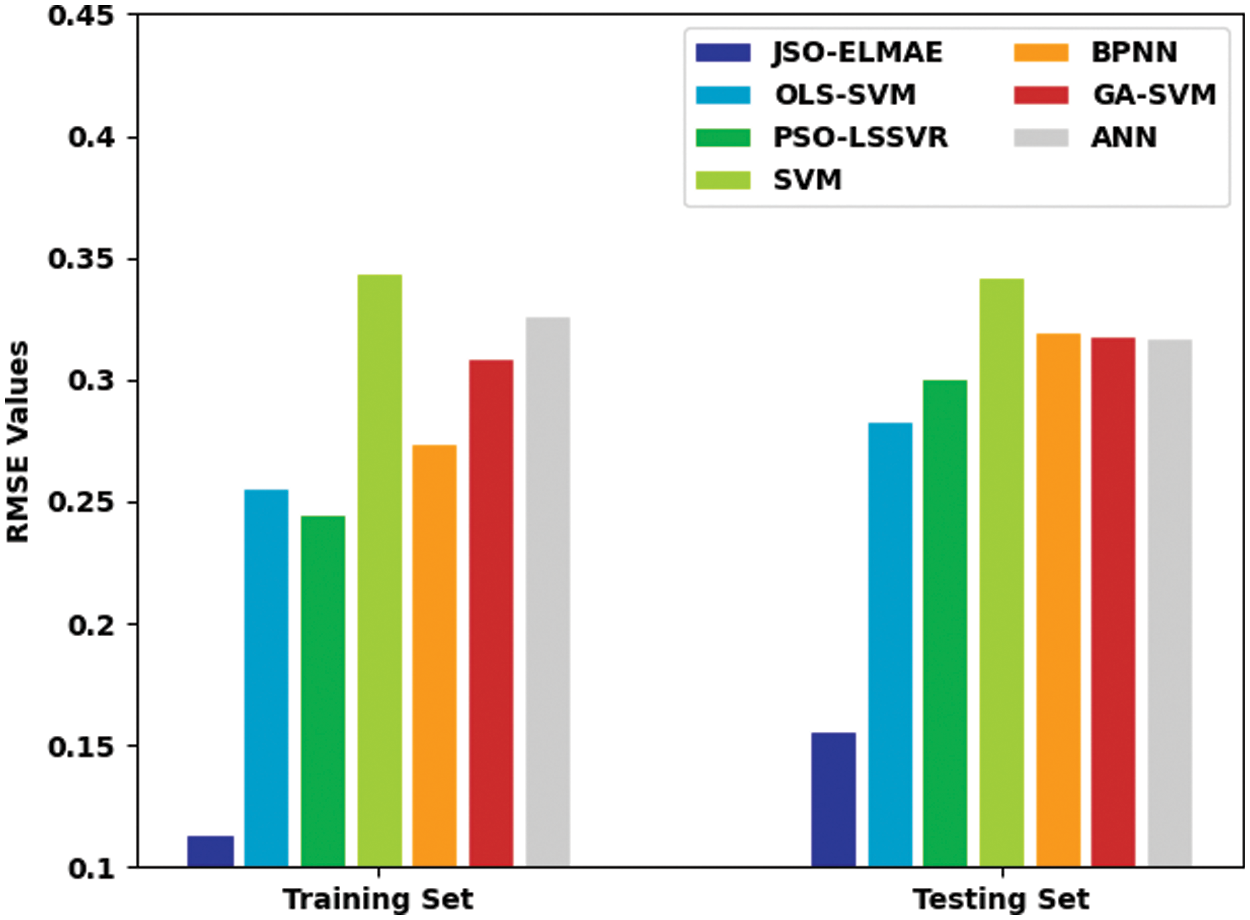
Figure 7: RMSE analysis of JSO-ELMAE technique with existing approaches

Fig. 8 determines a brief MAPE investigation of the JSO-ELMAE algorithm with existing techniques on both TR and TS sets. The experimental outcomes exposed that the JSO-ELMAE algorithm has demonstrated effectual results with minimal values of MAPE. For sample, on TR data, the JSO-ELMAE approach has obtainable decreased MAPE of 2.8614 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN algorithms have gained increased MAPE of 3.1593, 3.1446, 4.6897, 0.3.1656, 4.5197, and 4.5150. At last, on TS data, the JSO-ELMAE algorithm has obtainable minimal MAPE of 3.7892 whereas the OLS-SVM, PSO-LSSVR, SVM, BPNN, GA-SVM, and ANN techniques have gained improved MAPE of 4.2226, 4.4421, 4.5171, 4.7812, 4.7338, and 4.7889.

Figure 8: MAPE analysis of JSO-ELMAE technique with existing approaches

Therefore, the experimental results assured the supremacy of the JSO-ELMAE model over recent models. It can be employed for reliable and robust forecasting the return rate of BC financial products in real time environments.

4  Conclusion

In this study, a novel JSO-ELMAE algorithm was introduced for return rate prediction of BC financial products. The presented JSO-ELMAE model designs a new ELMAE model for predicting the return rate of financial products. Besides, the JSO algorithm is exploited to tune the parameters related to the ELMAE model which in turn boosts the classification results. The application of JSO technique assists in optimal parameter adjustment of the ELMAE model to predict the bitcoin return rates. The experimental validation of the JSO-ELMAE algorithm was executed and the results are inspected in many aspects. The experimental values demonstrated the enhanced performance of the JSO-ELMAE model over recent state of art approaches. In future, DL models are included to raise the predictive outcomes of the ELMAE algorithm.

Funding Statement: This research was supported in part by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (NRF-2021R1A6A1A03039493) and in part by the NRF grant funded by the Korea government (MSIT) (NRF-2022R1A2C1004401).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  F. Chen, H. Wan, H. Cai and G. Cheng, “Machine learning in/for blockchain: Future and challenges,” Canadian Journal of Statistics, vol. 49, no. 4, pp. 1364–1382, 2021. [Google Scholar]

 2.  A. Ozbayoglu, M. Gudelek and O. Sezer, “Deep learning for financial applications: A survey,” Applied Soft Computing, vol. 93, pp. 106384, 2020. [Google Scholar]

 3.  J. Vergne, “Decentralized vs. distributed organization: Blockchain, machine learning and the future of the digital platform,” Organization Theory, vol. 1, no. 4, pp. 263178772097705, 2020. [Google Scholar]

 4.  B. Yong, J. Shen, X. Liu, F. Li, H. Chen et al., “An intelligent blockchain-based system for safe vaccine supply and supervision,” International Journal of Information Management, vol. 52, pp. 102024, 2020. [Google Scholar]

 5.  E. Grant, “Big data-driven innovation, deep learning-assisted smart process planning, and product decision-making information systems in sustainable industry 4.0,” Economics, Management, and Financial Markets, vol. 16, no. 1, pp. 9, 2021. [Google Scholar]

 6.  Z. Wang, M. Li, J. Lu and X. Cheng, “Business innovation based on artificial intelligence and blockchain technology,” Information Processing & Management, vol. 59, no. 1, pp. 102759, 2022. [Google Scholar]

 7.  W. Gao and C. Su, “Analysis on block chain financial transaction under artificial neural network of deep learning,” Journal of Computational and Applied Mathematics, vol. 380, pp. 112991, 2020. [Google Scholar]

 8.  Y. Zhang, F. Xiong, Y. Xie, X. Fan and H. Gu, “The impact of artificial intelligence and blockchain on the accounting profession,” IEEE Access, vol. 8, pp. 110461–110477, 2020. [Google Scholar]

 9.  J. Sun, Y. Zhou and J. Lin, “Using machine learning for cryptocurrency trading,” in 2019 IEEE Int. Conf. on Industrial Cyber Physical Systems (ICPS), Taipei, Taiwan, pp. 647–652, 2019. [Google Scholar]

10. A. Dutta, S. Kumar and M. Basu, “A gated recurrent unit approach to bitcoin price prediction,” SSRN Journal, vol. 13, pp. 1–16, 2019, https://doi.org/10.2139/ssrn.3514069. [Google Scholar]

11. S. Ji, J. Kim and H. Im, “A comparative study of bitcoin price prediction using deep learning,” Mathematics, vol. 7, no. 10, pp. 898, 2019. [Google Scholar]

12. M. Salb, M. Zivkovic, N. Bacanin, A. Chhabra and M. Suresh, “Support vector machine performance improvements for cryptocurrency value forecasting by enhanced sine cosine algorithm,” in Computer Vision and Robotics, Algorithms for Intelligent Systems Book Series, Singapore: Springer, pp. 527–536, 2022. [Google Scholar]

13. O. Snihovyi, V. Kobets and O. Ivanov, “Implementation of robo-advisor services for different risk attitude investment decisions using machine learning techniques,” in Int. Conf. on Information and Communication Technologies in Education, Research, and Industrial Applications, Cham: Springer, vol. 1007, pp. 298–321, 2018. [Google Scholar]

14. H. M. Kim, G. W. Bock and G. Lee, “Predicting ethereum prices with machine learning based on blockchain information,” Expert Systems with Applications, vol. 184, pp. 115480, 2021. [Google Scholar]

15. N. Metawa, M. Alghamdi, I. E. Hasnony and M. Elhoseny, “Return rate prediction in blockchain financial products using deep learning,” Sustainability, vol. 13, no. 21, pp. 11901, 2021. [Google Scholar]

16. V. D’Amato, S. Levantesi and G. Piscopo, “Deep learning in predicting cryptocurrency volatility,” Physica A: Statistical Mechanics and Its Applications, vol. 596, pp. 127158, 2022. [Google Scholar]

17. J. M. Kim, C. Cho and C. Jun, “Forecasting the price of the cryptocurrency using linear and nonlinear error correction model,” Journal of Risk and Financial Management, vol. 15, no. 2, pp. 74, 2022. [Google Scholar]

18. I. Nasirtafreshi, “Forecasting cryptocurrency prices using recurrent neural network and long short-term memory,” Data & Knowledge Engineering, vol. 139, pp. 102009, 2022. [Google Scholar]

19. A. Vasantharaj, P. S. Rani, S. Huque, K. S. Raghuram, R. Ganeshkumar et al., “Automated brain imaging diagnosis and classification model using rat swarm optimization with deep learning based capsule network,” International Journal of Image and Graphics, Article in press, 2021, https://doi.org/10.1142/S0219467822400010. [Google Scholar]

20. J. Xia, D. Yang, H. Zhou, Y. Chen, H. Zhang et al., “Evolving kernel extreme learning machine for medical diagnosis via a disperse foraging sine cosine algorithm,” Computers in Biology and Medicine, vol. 141, pp. 105137, 2022. [Google Scholar]

21. O. A. Alzubi, J. A. Alzubi, K. Shankar and D. Gupta, “Blockchain and artificial intelligence enabled privacy-preserving medical data transmission in internet of things,” Transactions on Emerging Telecommunications Technologies, vol. 32, pp. 1–14, 2021. https://doi.org/10.1002/ett.4360. [Google Scholar]

22. G. N. Nguyen, N. H. L. Viet, M. Elhoseny, K. Shankar, B. B. Gupta et al., “Secure blockchain enabled cyber-physical systems in healthcare using deep belief network with ResNet model,” Journal of Parallel and Distributed Computing, vol. 153, pp. 150–160, 2021. [Google Scholar]

23. B. L. Nguyen, E. L. Lydia, M. Elhoseny, I. V. Pustokhina, D. A. Pustokhin et al., “Privacy preserving blockchain technique to achieve secure and reliable sharing of IoT data,” Computers, Materials & Continua, vol. 65, no. 1, pp. 87–107, 2020. [Google Scholar]

24. M. Farhat, S. Kamel, A. M. Atallah and B. Khan, “Optimal power flow solution based on jellyfish search optimization considering uncertainty of renewable energy sources,” IEEE Access, vol. 9, pp. 100911–100933, 2021. [Google Scholar]

25. J. S. Chou and D. N. Truong, “Multiobjective optimization inspired by behavior of jellyfish for solving structural design problems,” Chaos, Solitons & Fractals, vol. 135, pp. 109738, 2020. [Google Scholar]

26. J. S. Chou and D. N. Truong, “A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean,” Applied Mathematics and Computation, vol. 389, pp. 125535, 2021. [Google Scholar]

27. M. Sivaram, E. L. Lydia, I. V. Pustokhina, D. A. Pustokhin, M. Elhoseny et al., “An optimal least square support vector machine based earnings prediction of blockchain financial products,” IEEE Access, vol. 8, pp. 120321–120330, 2020. [Google Scholar]