 Open Access
Open Access
ARTICLE
Thermal Performance Analysis of Shell and Tube Heat Exchanger Using Hybrid Nanofluids Based on Al2O3, TiO2, and ZnO Nanoparticles
1 Department of Mechanical Engineering, Mehran University of Engineering and Technology, Jamshoro, 76080, Pakistan
2 Department of Mechanical & Industrial Engineering, College of Engineering, Qatar University, Doha, P.O. Box 2713, Qatar
* Corresponding Author: Laveet Kumar. Email:
(This article belongs to the Special Issue: Innovative Heat Transfer Fluids for Enhanced Energy Sustainability in Thermal Systems)
Frontiers in Heat and Mass Transfer 2025, 23(3), 833-856. https://doi.org/10.32604/fhmt.2025.064805
Received 24 February 2025; Accepted 17 April 2025; Issue published 30 June 2025
Abstract
Climate change, rising fuel prices, and fuel security are some challenges that have emerged and have grown worldwide. Therefore, to overcome these obstacles, highly efficient thermodynamic devices and heat recovery systems must be introduced. According to reports, much industrial waste heat is lost as flue gas from boilers, heating plants, etc. The primary objective of this study is to investigate and compare unary (Al2O3) thermodynamically, binary with three different combinations of nanoparticles namely (Al2O3 + TiO2, TiO2 + ZnO, Al2O3 + ZnO) and ternary (Al2O3 + TiO2 + ZnO) as a heat transfer fluid. Initially, three different types of binary nanofluids were prepared by dispersing two types of nanoparticles in individual trails, such as aluminum oxide, zinc oxide, and titanium dioxide in various combined concentrations (e.g., 2%, 4%, and 6%) into the water as the base fluid, using an ultrasonicator to ensure uniform suspension. The operating parameters such as nanoparticle concentration and flow rate are varied to evaluate the performance of various hybrid nanofluids under counterflow configuration. The findings of this research indicate that the binary nanofluid Al2O3 + ZnO exhibits the highest thermal performance factor (2.83), followed by the ternary nanofluid Al2O3 + TiO2 + ZnO (0.828), with the lowest performance observed for the unary nanofluid Al2O3 (0.799). This research highlights the need for advancement into novel nanomaterial combinations, optimization of required fluid properties, stability enhancement, and thermal performance to strengthen the utilization of hybrid nanofluids in heat exchangers.Graphic Abstract
Keywords
Several challenging issues such as fuel prices and energy affordability highlight the need for efficient and cost-effective mechanical components in heat recovery systems for energy utilization. With the global decline in fossil fuel supplies and the surge in energy consumption, there is an urgent demand for energy-efficient and sustainable equipment to support economic and societal progress [1,2]. Heat exchangers, being critical components in numerous industrial and technological processes such as power generation, chemical processing, water desalination, refrigeration, and air conditioning, play a vital role in reducing energy consumption through effective heat transfer [3]. Among the different kinds of heat exchangers shell and tube heat exchangers are frequently utilized in industrial applications due to their robust design and adaptability [4]. While significant advancements have been made to increase the thermal performance of heat exchangers, the potential of hybrid nanofluid fluids with multiple nanoparticles in combination remains under explored.
The performance of heat exchangers can be improved by using active or the passive methods. The active method requires an external power source while passive excludes external power requirements. The passive techniques involve increasing the heat transfer surface by adding fins, artificial roughness, coiled wires, blocks, or twisted tapes to create turbulence in the flow. This raises the thermal boundary layer, which in turn increases the rate of heat transmission [5]. The thermal characteristics of the flowing fluid can be easily improved by adding nanoparticles to the base fluid, which would increase HX’s overall efficiency without causing a significant pressure decrease [6]. However, using hybrid nanofluids in heat exchangers instead of basic nanofluids and conventional fluids like oil, water, and ethylene glycol is a more efficient technique. A hybrid nanofluid is a novel fluid that is prepared by mixing multiple types of nanoparticles such as metal, metal oxides, and carbon nanostructured materials into base fluids. As a result, the fluid’s thermal conductivity increases, raising the heat transfer coefficient (HTC). This could contribute to heat exchangers becoming more compact and efficient by reducing their size and weight [7]. Balakrishnan et al. [8] analyzed the performance of AlO3-W and Cu-W nanofluids in a shell and tube heat exchanger experimentally. Analysis was done on how the concentration of nanoparticles affected the thermal conductivity, Nusselt number, viscosity, and heat transfer coefficient. The findings of the study indicate that Cu-W and AlO3-W nanofluids increased their thermal conductivity by 29% and 39%, respectively, at 0.12 weight percent. Because of their higher viscosity, nanofluids increased friction even as they enhanced convective heat transfer. Because of its improved thermophysical characteristics, the AlO3-W nanofluid demonstrated greater pressure drop performance. Abid et al. [9] analyzed the use of hybrid nanofluids in evacuated tube solar collectors to improve heat transfer in solar thermal applications. Among the four absorption cycles, the quadruple effect shows the highest performance, achieving a COP of 2.287. Hybrid nanofluids improve collector efficiency but have the highest exergy destruction rate at 114.93 kW. Increased weak solution percentages enhance COP, while higher generator temperatures reduce it. Mezrakchi [10] study investigates flow characteristics and heat transfer of several hybrid nanofluids (like Al2O3-EG-Water and CuO-ZnO-Water) as coolants in a shell and tube heat exchanger across the eight-inlet flow velocities. CuO-ZnO-Water showed the maximum heat transfer, with an exceeding 9% temperature reduction, especially at lower velocities. Large Reynolds numbers improved Nusselt numbers while lowering friction factors, with a 43% friction factor drop between Reynolds numbers 10 to 40 K. Findings highlight the need to optimize nanoparticle types for enhanced coolant performance in industrial heat exchangers. Rao et al. [11] revealed that alumina nanoparticles (22 nm) are used to investigate the heat transfer rate of alumina nanofluids in a shell and tube heat exchanger under turbulent flow utilizing forced convection. Under parallel and counterflow settings, nanofluids with different alumina contents (0.13%, 0.27%, 0.4%, and 0.53%) were investigated while keeping mass flow rates and inlet temperatures constant. The computed characteristics and non-dimensional numbers show enhanced heat transfer rates in comparison to traditional fluids. AbuGhanem et al. [12] investigate the use of alumina nanofluids in turbulent flow to improve heat transfer in a shell and tube heat exchanger. The findings indicate that, in comparison to traditional fluids, heat transfer rates are considerably enhanced by raising the percentage of alumina and decreasing the size of the nanoparticles. Improved performance in parallel and counterflow circumstances is confirmed by the experiment. Peyghambarzadeh et al. [13] examined the Al2O3/water nanofluid in automobile radiators and discovered half heat augmentation in comparison to pure water. Nguyen et al. [14] experimented with a radiator-type heat exchanger with a 6.8% volume nanoparticle concentration of Al2O3/water and discovered a 40% improvement in the heat transfer coefficient. The performance of AlO3 + TiO2 + SiO2/water ternary nanofluids in heat transfer is examined by Ramadhan et al. [15] work using wire coil inserts in plain tubes. At a 3.0% volume concentration, the ternary nanofluids exhibit a maximum thermal conductivity boost of 24.8%, improving heat transfer by up to 199.23%. The thermal performance is further improved by the addition of wire coil inserts, and when the volume concentration rises, the thermal performance factor (TPF) also improves.
The literature review presented in this section indicates that hybrid nanofluids hold significant potential for enhancing heat transfer efficiency due to their superior thermal conductivity and heat transfer rates. Studies have shown that key factors such as particle size, nanoparticle concentration, and flow configuration greatly influence their performance, making them ideal for advanced applications like heat exchangers and solar thermal systems, where optimized thermal properties are crucial for improved efficiency.
The current study primarily focuses on unary, binary, and ternary nanofluids’ performance under varying operating conditions. This creates a critical knowledge gap in leveraging the synergistic effects of multiple nanoparticles to improve heat transfer performance.
The primary objective of this study is to bridge the gap in the existing literature by thermodynamically investigating and comparing the thermal performance of unary, binary, and ternary hybrid nanofluids and highlighting their suitability for industrial applications. The findings of this research contribute to the development of energy-efficient and sustainable heat exchanger technologies, addressing the growing need for improved thermal management systems.
This paper outlines several vital innovations and contributions:
• The innovative combination of nanoparticles for the development of hybrid nanofluids for performance enhancement of heat exchangers.
• The optimized combination of nanoparticles, pH levels, and surfactants for enhanced stability of nanofluids in thermal applications.
• Comprehensive performance analysis of heat exchangers based on unary, binary, and ternary nanofluids.
• Conducting a parametric study to analyze thermal performance factors for prepared hybrid fluids.
• The remaining section of the paper is organized as follows: Section 2 the materials, methods, modeling assumptions, input parameters, and mathematical model. Section 3 presents the results and discussion of the study. The study concludes with Section 5, consisting of the conclusions of the study.
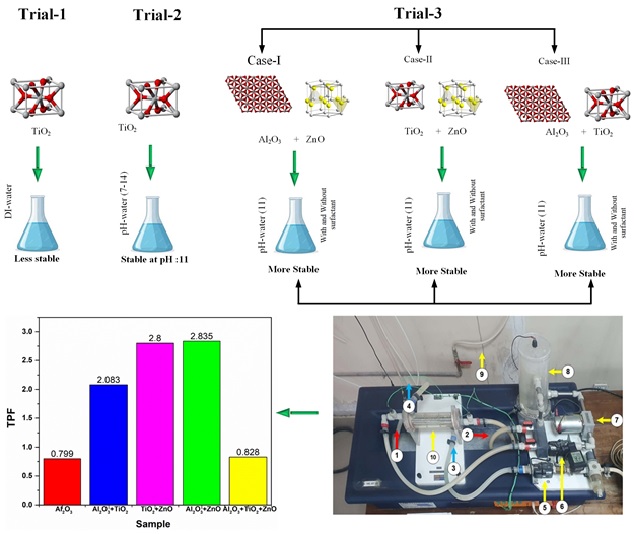
In this study three types of nanoparticles were used namely Al2O3, TiO2 and ZnO which were purchased from Sigma-Aldrich, Petaling Jaya, Malaysia. The physical and chemical properties of these nanoparticles are summarized in Table 1 [16]. The selection of these nanoparticles was based on criteria such as favorable thermal characteristics, cost-effectiveness, and non-toxicity. To investigate the effects of various nanoparticle combinations, binary and ternary nanofluids were formulated in six distinct combinations, as detailed in Table 2. The primary objective of these combinations was to enhance the stability of the nanofluids. To achieve this, multiple trials were conducted, both with and without the presence of surfactants, using pH-adjusted water. Sodium dodecyl sulfate (SDS) was employed as the surfactant in this study, as it is commonly used to improve the stability of nanofluids.

2.2 Preparation and Characterization of NFs
The hybrid NFs were prepared by a wo-step method by dispersing various volume fractions, i.e., 2%, 4% and 6% into the base fluid. The main problem with two step method is the coagulation of nanoparticles in base fluid. To prevent this ultrasonication, addition of surfactants and pH control techniques are used to avoid agglomeration effect [16,19].
Fig. 1 represents the experimental setup used for the validation purpose of this research, employing the Armfield HT30XC shell and tube heat exchanger model. The setup comprises counter flow arranged heat exchanger, pumps, a storage tank, flow controller, temperature sensors, control panel, and heater. This setup also illustrates the detailed working mechanism of the shell and tube heat exchanger, with each component numbered to represent its specific function in the system’s operation. The hot fluid enters the tube side through the hot fluid inlet (1), flows through the tubes, and exits via the hot fluid outlet (2) after transferring its heat. Simultaneously, the cold fluid enters the shell side through the cold fluid inlet (2), flows across the shell, absorbs heat from the hot fluid, and exits through the cold fluid outlet (3). The circulation of both fluids is maintained using dedicated pumps and flow controller (5 and 6), while a reservoir (8) stores the fluid under controlled conditions to ensure continuous operation. The main heat exchange occurs in the shell and tube section (10), where thermal energy is transferred from the hot fluid to the cold fluid across the tube walls, ensuring the fluids remain separated to prevent any mixing. Table 3 shows the specifications and operating conditions of shell and tube heat exchanger.
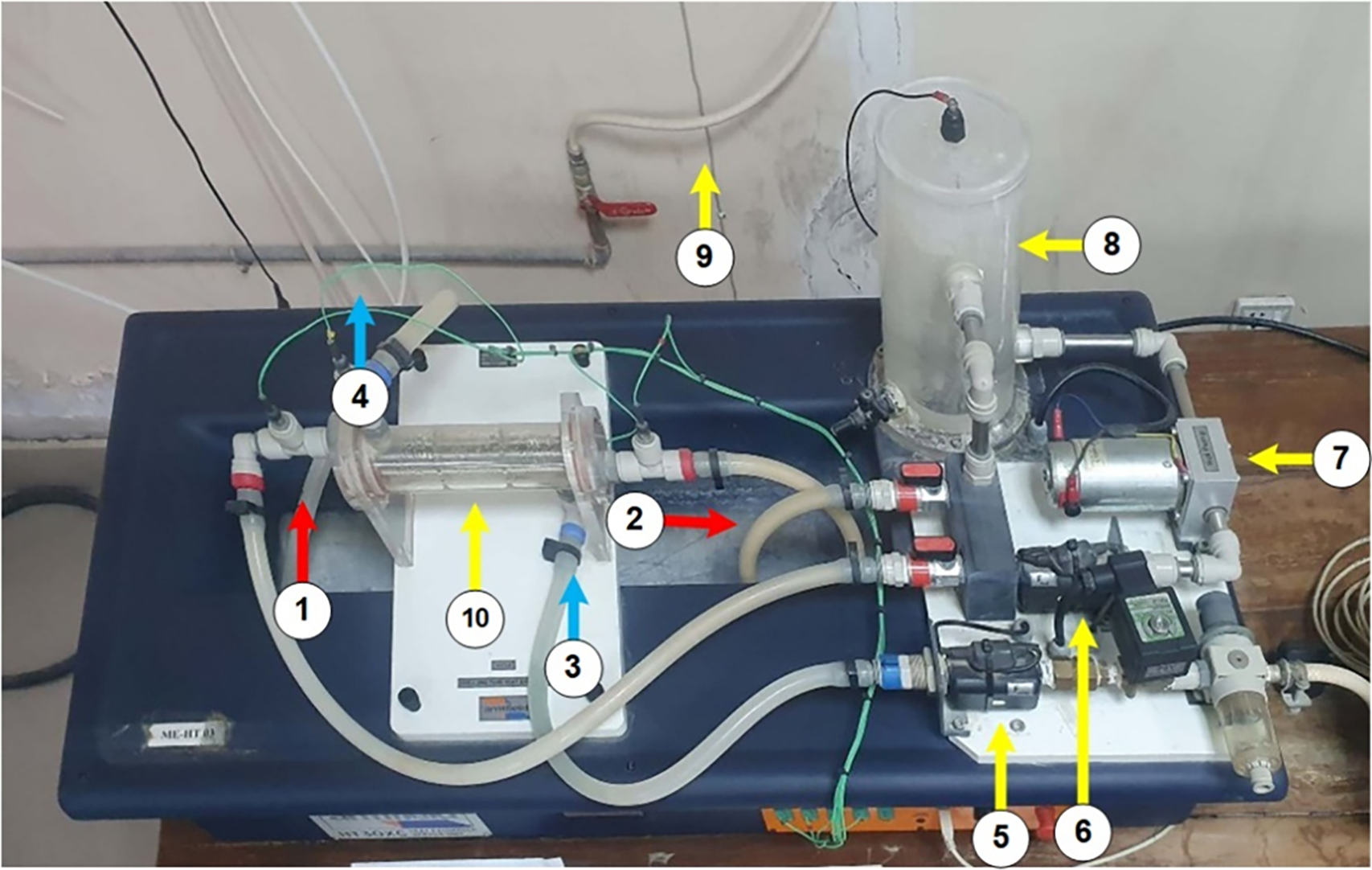
Figure 1: Experimental setup of shell and tube heat exchanger. (1) Hot fluid inlet; (2) Hot fluid outlet; (3) Cold fluid inlet; (4) Cold fluid outlet; (5) Cold fluid flow controller; (6) Hot fluid flow controller; (7) Hot fluid pump; (8) Hot fluid storage tank; (9) Cold fluid supply from overheat tank; (10) Effective heat transfer area

2.3.1 Modelling Assumptions and System Input Parameters
Mathematical modeling of the shell and tube heat exchanger driven by hybrid nanofluid is presented in this section. To solve the various system models, an engineering equation solver (EES) is used. Table 3 lists the input parameters for the shell and tube heat exchanger, as depicted in Fig. 1 of the reference model [20]. Considering the following assumptions, the mathematical models of the proposed systems which include unary, binary, and ternary nanofluids are analyzed:
• The process is assumed to be steady state.
• The potential and kinetic energy changes are negligible.
• Pressure losses in pipes are ignored.
• Fluids (hybrid fluid and water) are assumed to be incompressible
• System is assumed to be adiabatic.
Thermophysical properties, including density (
The volume fraction of different configurations of hybrid nanofluids can be determined by using Eq. (1).
where φ, mnp, ρnp and Vbasefluid are volume fraction, mass of nanoparticles, density of the nanoparticles and volume of base fluid, respectively.
Density of nanofluid with different particle concentrations can be determined using Eq. (2).
Specific heat of nanofluid can be determined by using Pak and Cho model as shown in Eq. (3). Where, the subscripts bf and nf represent the base fluid and nanofluid, respectively.
Thermal conductivity of nanofluid for each type of nanoparticle can be determined by using Maxwell model as shown in Eqs. (4)–(6).
The effective thermal conductivity for a nanofluid with multiple types of nanoparticles can be calculated using Eq. (7).
The dynamic viscosity of a hybrid nanofluid can be determined using Batchelor model as shown in Eq. (8) [23].
The heat transfer rate (Q) can be calculated using Eq. (9) [24].
Log mean temperature difference (LMTD) for counter flow can be determined using Eq. (10).
Tube side flow area, A can be determined by Eq. (11) [25].
The Reynolds number (
The effectiveness (ε) of a heat exchanger can be determined using Eq. (13).
The Prandtl number of nanofluid can be determined using Eq. (14).
The Nusselt number (
Friction factor (F) for nanofluid flow in heat exchanger can be calculated by:
If, flow situation is laminar:
If the flow is turbulent, then Reynolds number can be calculated by Blasius correlation using Eq. (17).
Mean velocity of nanofluid Um can be determined by using Eq. (18).
Pressure drop, ΔP of nanofluid can be determined by using Eq. (19).
Pumping power, P can be determined by using Eq. (20).
Thermal performance factor (TPF) of nanofluids can be determined by using Eq. (21).
where Nubf, Nunf, Fbf and Fnf are Nusselt number of base fluid, Nusselt number of nanofluid, friction factor of base fluid and friction factor nanofluid, respectively.
The thermodynamic model of the shell and tube heat exchanger using nanofluids in this study is compared and validated against findings from existing literature, for different range of volume fraction, density is illustrated in Fig. 2a. Density of the present study is closely align with [23,26] at all the concentrations, with minimal average difference error 2.23%.
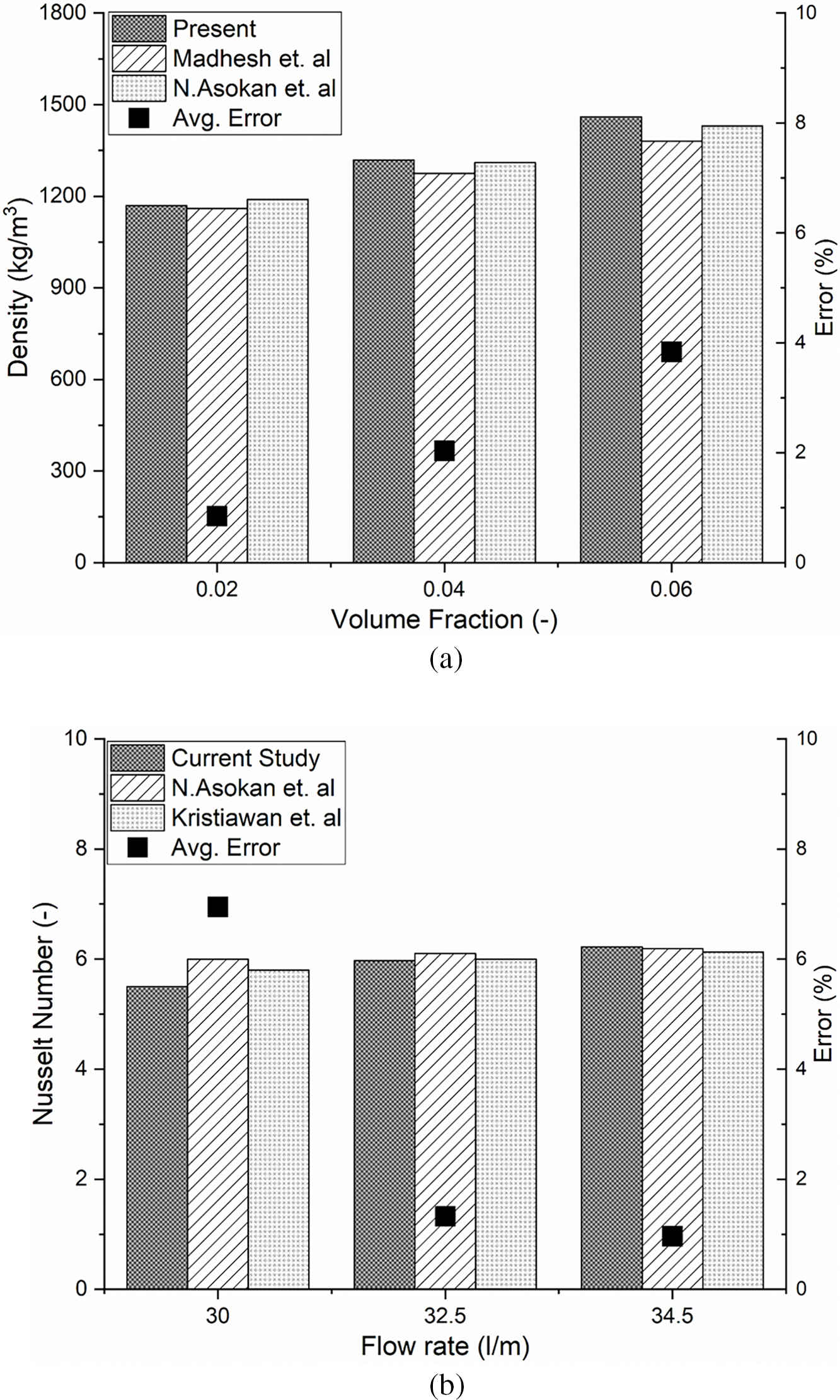
Figure 2: (a) Model validation by comparison of density of nanofluid with reference models [23,26]. (b) Model validation by comparison of Nusselt number of nanofluid with reference models [23,27]
Similarly, Fig. 2b represents comparison of Nusselt number of nanofluid with reference models [23,27]. The results of the current study show a close alignment with references literatures across all flow rates, with a minimal average difference error of 6.8% at reference designed conditions, confirming the accuracy of the proposed model.
The stability of nanofluids (NFs) and the behavior of nanoparticles in the base fluid remain unresolved challenge, as each type of nanoparticle interacts differently with various base fluids. Nanoparticle agglomeration not only leads to agglomeration and clogging but also reduces thermal conductivity. Surfactants and pH are commonly used to stabilize nanofluids. surfactants addition reduces the surface tension of the base fluids, enhancing the dispersion of nanoparticles [22]. The stability of the hybrid nanofluids was determined by evaluating the zeta potential (ζ) of the nanofluid. In this study, zeta potential was measured by using Malvern Zeta sizer to assess their stability. Zeta potential is determined by the electrophoretic movement of charged particles in response to an electric field. Strong repulsive forces are indicated by higher absolute zeta potential values (ζ > ±30 mV), which hinder aggregation and ensures long-term dispersion stability.
Fig. 3 presents the zeta potential curves for a binary nanofluid sample (TiO2 + ZnO) with and without the presence of a surfactant. The presence of the surfactant enhances nanofluid stability, as indicated by the higher-intensity zeta potential peak. Experimental results show that the zeta potential increases from −44.2 to −47.8 mV with the inclusion of the surfactant.
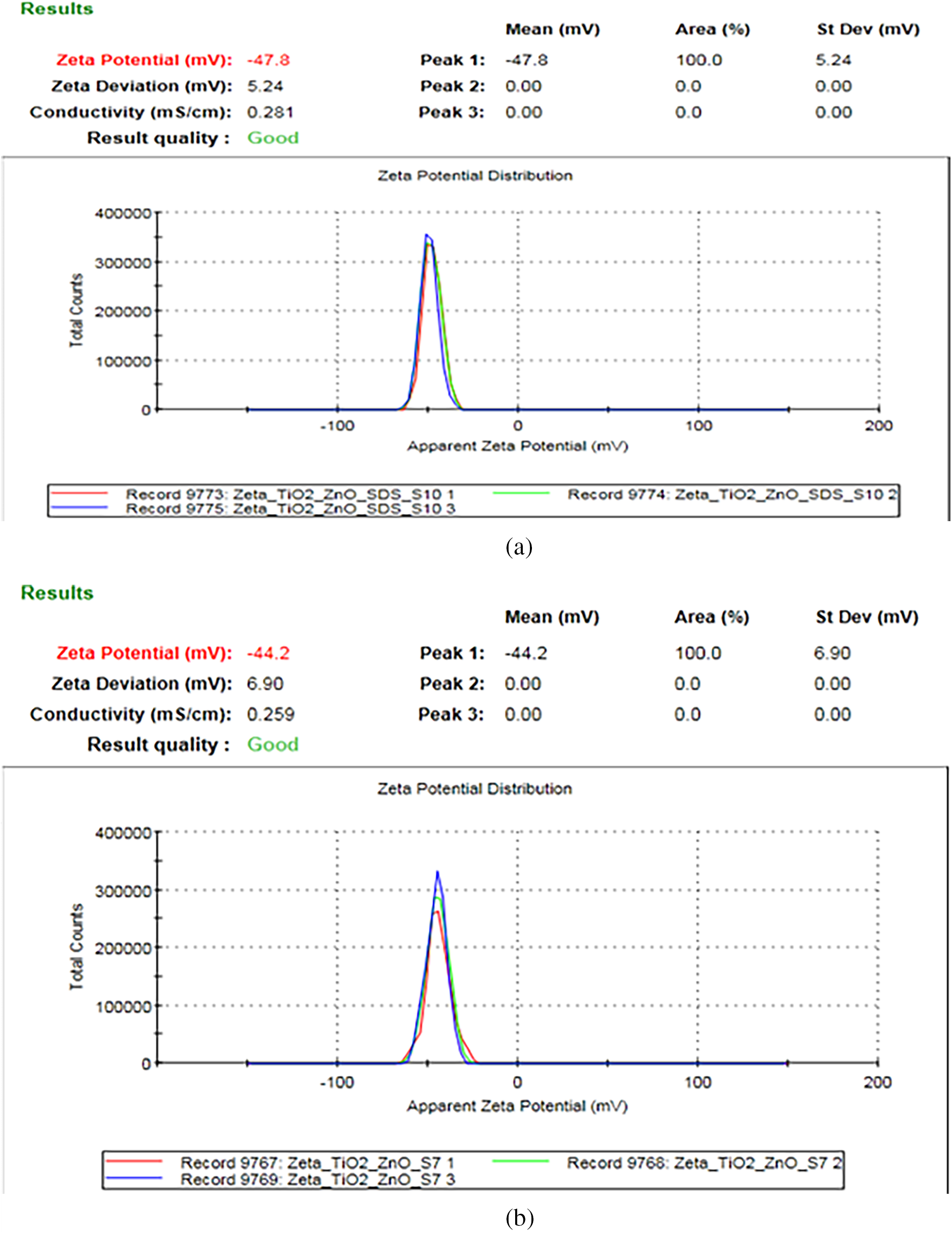
Figure 3: Zeta potential curves for binary TiO2 + ZnO nanoparticles (a) with surfactant (b) without surfactant
Fig. 4 displays the zeta potential curves for a binary nanofluid sample (Al2O3 + ZnO) with and without the presence of a surfactant. The addition of the surfactant improves stability, as evidenced by the higher-intensity zeta potential peak. Experimental results indicate an increase in zeta potential from −42.4 to −44.1 mV with the surfactant addition.
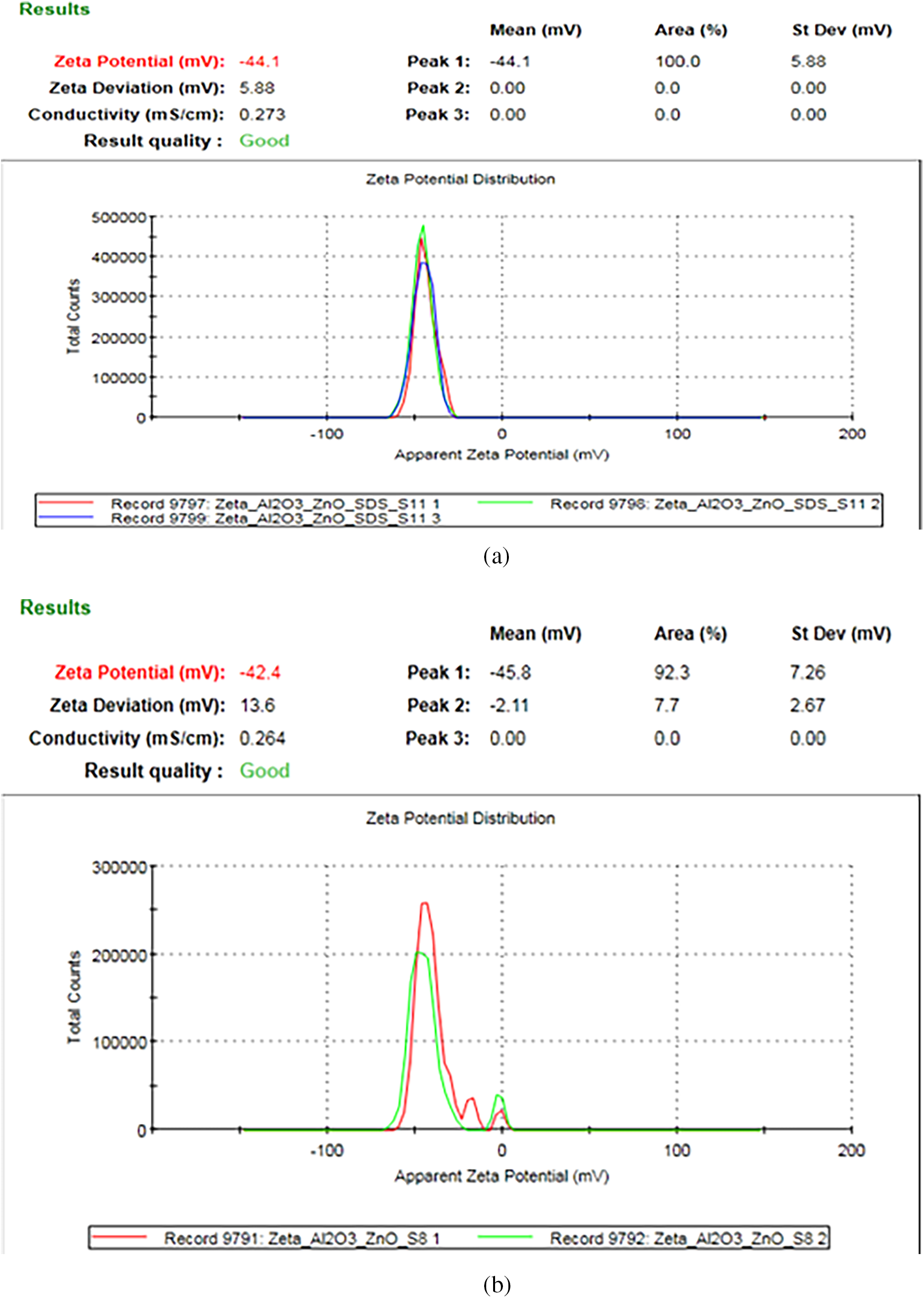
Figure 4: Zeta potential curves for binary Al2O3 + ZnO nanoparticles (a) with surfactant (b) without surfactant
Fig. 5 highlights the zeta potential curves for binary nanofluid sample (Al2O3 + TiO2) with and without presence of surfactant. Based on experimental results the zeta potential decreases slightly from −47.7 to −44.9 mV with the addition of surfactant. Moreover, the selected binary nanofluid (Al2O3 + TiO2) without any addition of surfactant illustration good dispersion, this is due to phenomena that, in polar liquids Al2O3 is able to improve a substantial amount of surface charge that can increase dispersion stability by electrostatic repulsion [16,28].
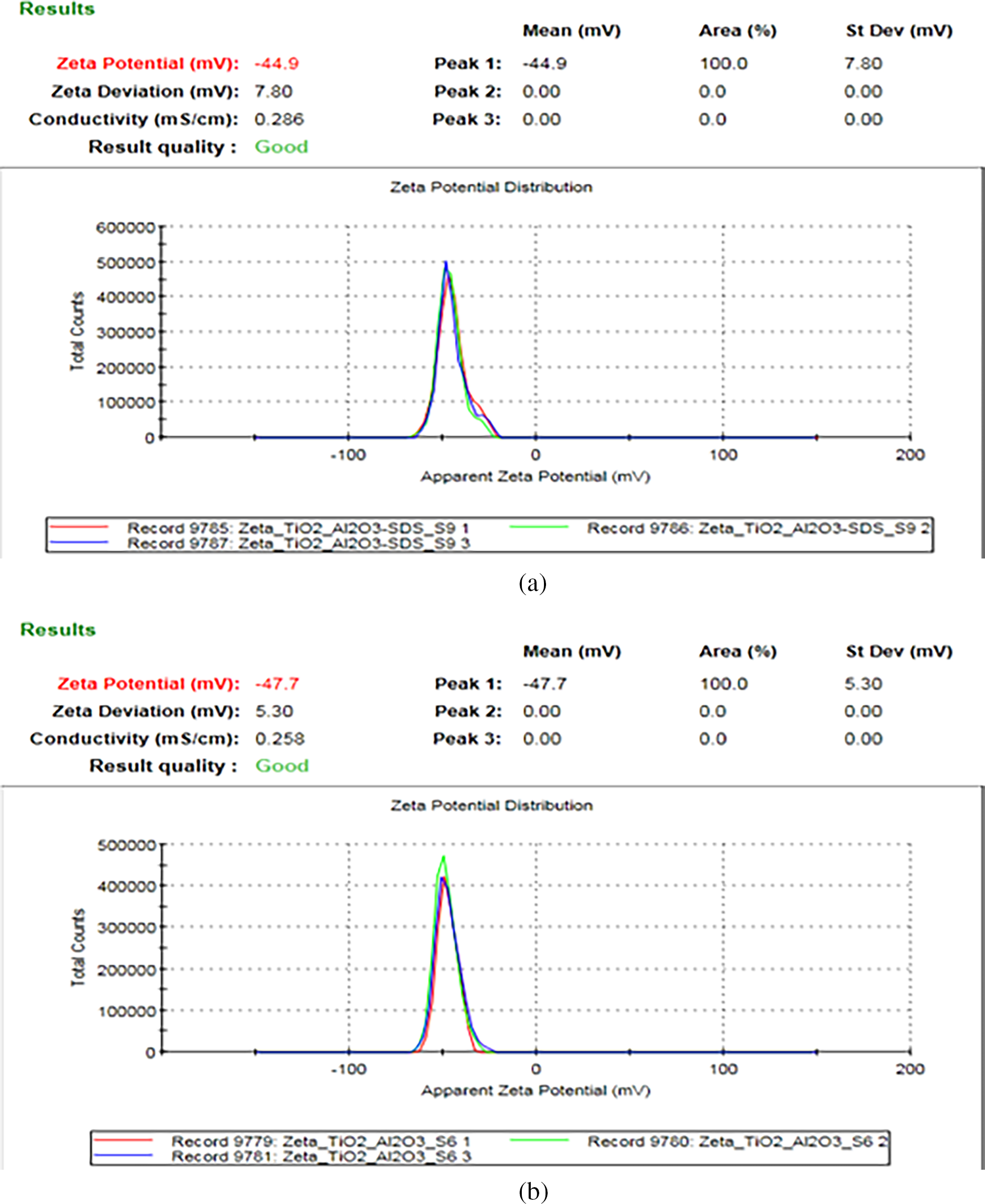
Figure 5: Zeta potential curves for binary Al2O3 + TiO2 nanoparticles (a) with surfactant (b) without surfactant
Fig. 6 shows the zeta potential curves for the ternary nanofluid sample (Al2O3 + TiO2 + ZnO), both with and without the addition of a surfactant. The stability improves with the addition of the surfactant, indicated by a higher-intensity zeta potential peak. Experimental results reveal that the zeta potential increases from −34.3 to −40.9 mV with the addition of surfactant.
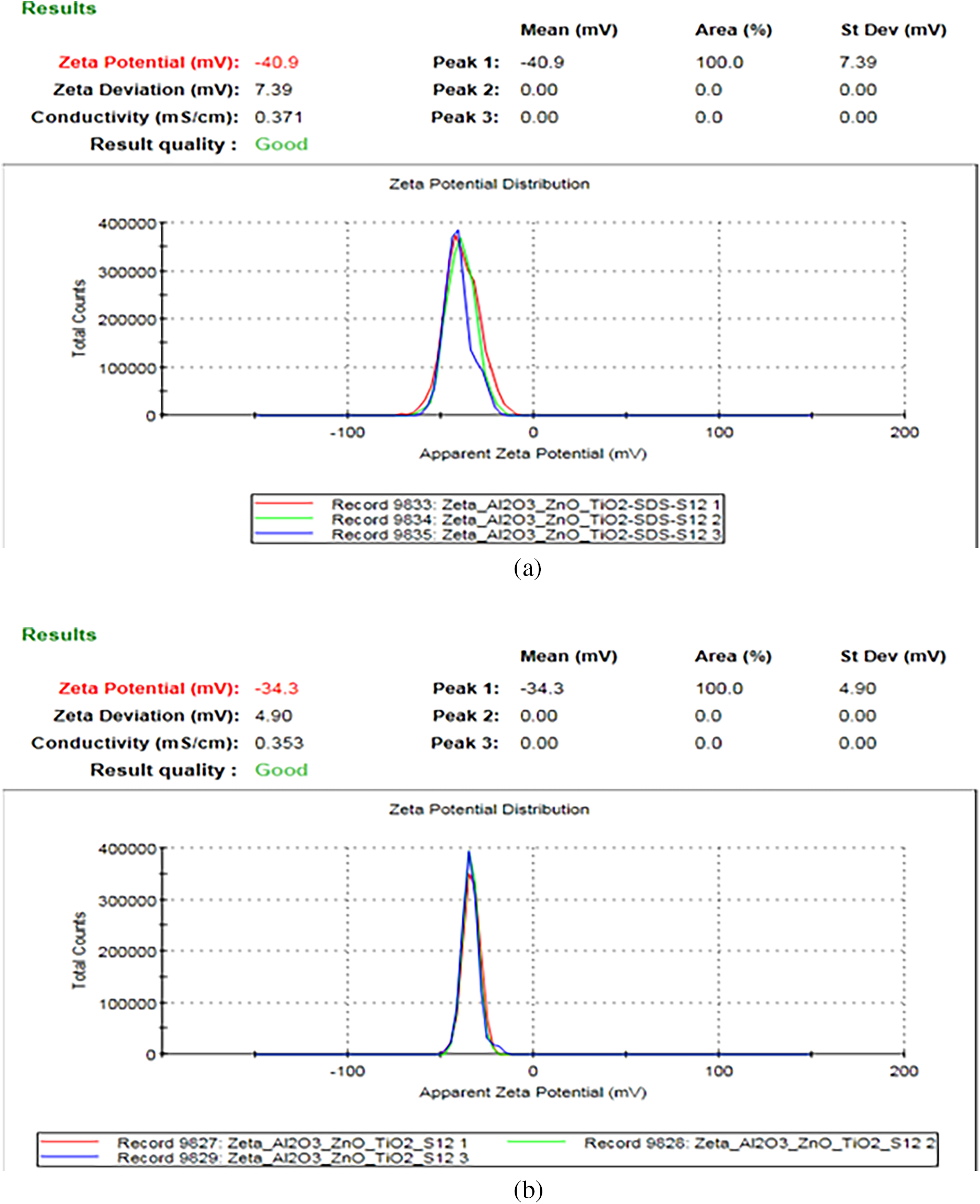
Figure 6: Zeta potential curves for ternary Al2O3 + TiO2 + ZnO nanoparticles (a) with surfactant (b) without surfactant
According to the zeta potential study, surfactant addition typically improves the stability of binary and ternary nanofluids, as evidenced by higher zeta potential values. The improved stability of binary nanofluids is particularly noticeable in the situations of TiO2 + ZnO and Al2O3 + ZnO, where the zeta potential values reached −47.8 and −44.1 mV, respectively. The ternary nanofluid (Al2O3 + TiO2 + ZnO) also showed slightly good stability, with its zeta potential increasing from −34.3 to −40.9 mV when surfactant was added.
3.3 Effect of Concentration of Nanoparticle on Density of Nanofluid
The study examines the impact of nanoparticle concentration on the density of various nanofluids as shown in Fig. 7, demonstrating a clear trend where density increases with higher nanoparticle fractions, ranging from 0.01 to 0.09. This is because the quantity of nanoparticles dispersed in the base fluid has increased. Deionized (DI) water serves as a base fluid with a density of 1000 kg/m3, while the density of Al2O3 nanofluid rises from 1027 to 1261 kg/m3 as concentration increases. Notably, among the three binary combinations, the TiO2 + ZnO nanofluid demonstrates the most substantial increase in density, with values ranging from 1076 to 1706 kg/m3 as the nanoparticle concentration increases. The ternary nanofluid composed of Al2O3, TiO2, and ZnO achieves the highest density, ranging from 1106 to 1972 kg/m3, highlighting the cumulative effect of multiple nanoparticles.
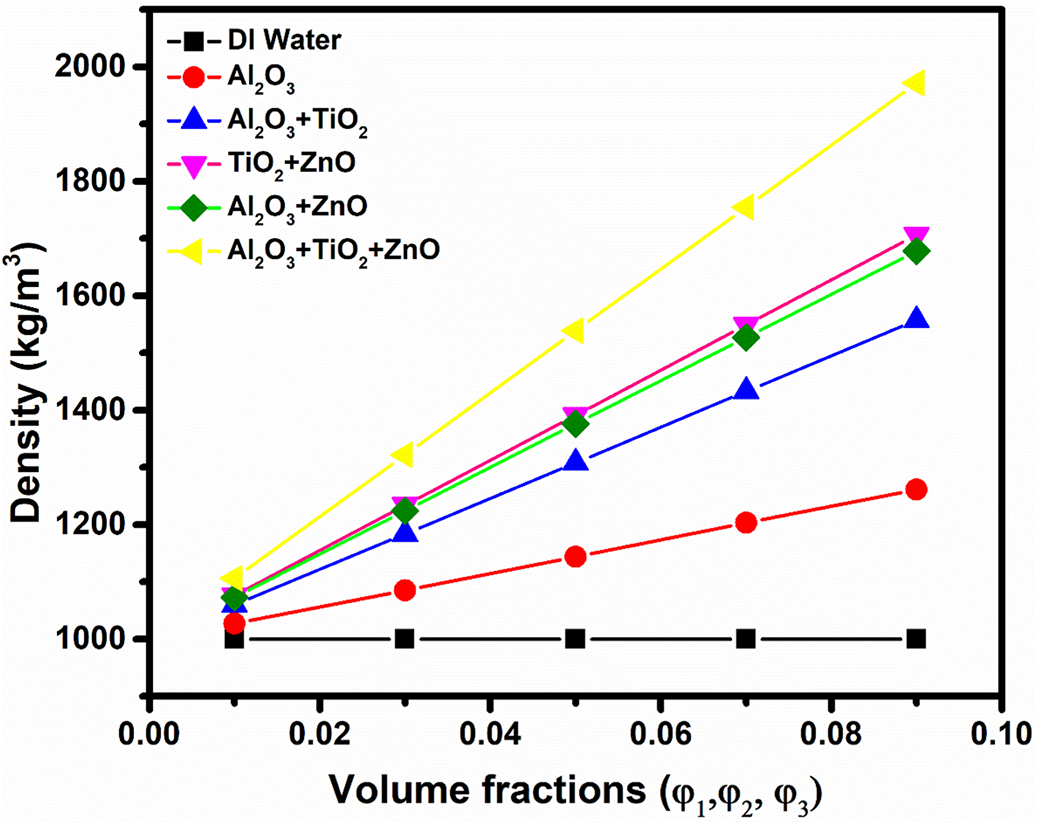
Figure 7: Effect of volume fraction of nanoparticles on density of different nanofluids
3.4 Effect of Concentration of Nanoparticle on Reynolds Number of Nanofluid
Fig. 8 demonstrates the variation of volume fraction on Reynolds number for DI water, unary, binary and ternary nanofluids. The results demonstrate a clear decrease in Reynolds number as nanoparticle concentration increases across all nanofluid. This is because the addition of nanoparticles increases the dynamic viscosity (μ) of the fluid, which reduces the Reynolds number as given by the Eq. (12). While DI water maintains a constant Reynolds number of 82 at all concentrations due to absence of nanoparticles, thereby preserving its flow properties.
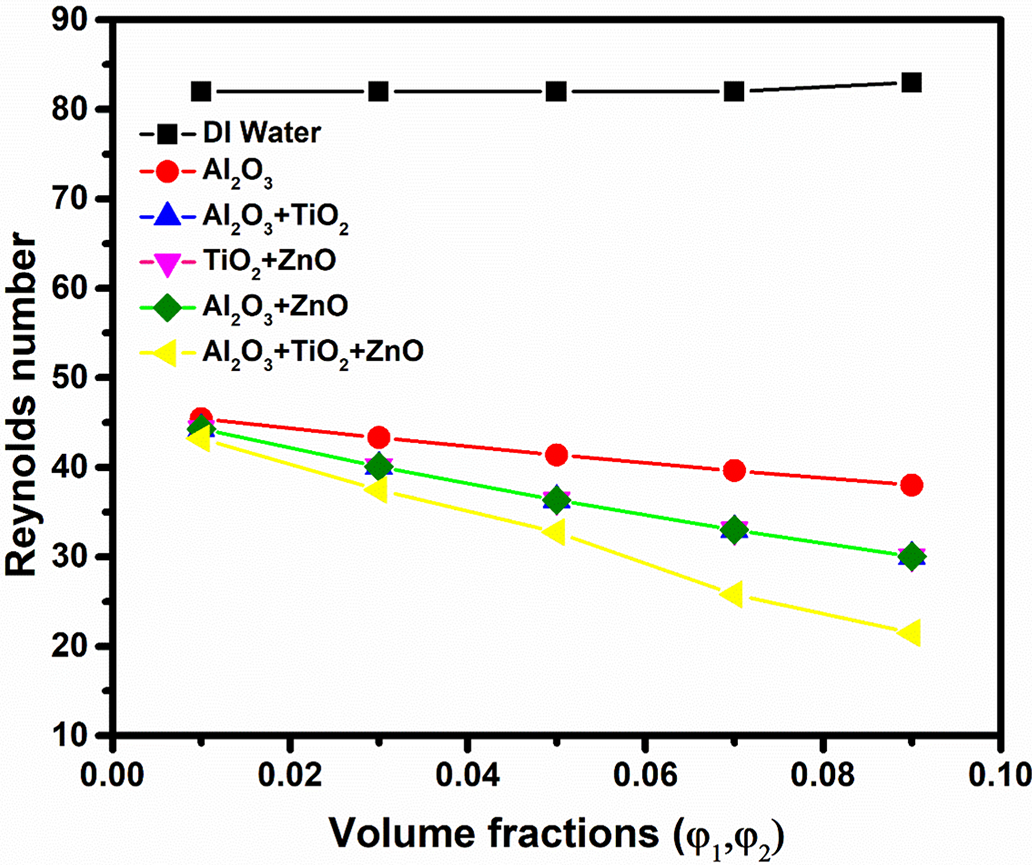
Figure 8: Effect of volume fraction on Reynolds number of different nanofluids
In contrast, unary, binary, and ternary nanofluids display progressively lower Reynolds numbers as the nanoparticle concentration rises from 0.01 to 0.09. The unary Al2O3 nanofluid has a modest decline, while the binary nanofluids (Al2O3 + TiO2, TiO2 + ZnO, and Al2O3 + ZnO) exhibit a similar trend with slightly greater reductions, showing more impact of the added particles on flow characteristics. The ternary Al2O3 + TiO2 + ZnO combination sees the steepest drop, with Reynolds numbers falling from 43.23 at a 0.01 concentration to 21.5 at 0.09. These findings suggest that higher nanoparticle concentrations generally increase viscosity and reduce flow velocity, resulting in lower Reynolds numbers. The binary nanofluids, particularly Al2O3 + TiO2, TiO2 + ZnO, and Al2O3 + ZnO, also exhibit significant improvements in heat transfer rates. For instance, the heat transfer rate for Al2O3 + TiO2 nanofluid progresses from 1180 W at 0.01 concentration to 6840 W at 0.09 concentration, while TiO2 + ZnO shows a similar trend, starting at 1190 W and reaching 6402 W. Al2O3 + ZnO slightly outperforms TiO2 + ZnO with values ranging from 1225 to 6695 W.
3.5 Effect of Concentration of Nanoparticles on Viscosity of Nanofluid
Fig. 9 demonstrates the variation of volume fraction on viscosity for DI water, unary, binary and ternary nanofluids. The results indicate that viscosity increases with rising volume fraction in all hybrid fluid cases, while DI water shows no change due to the absence of nanoparticles. This increase in viscosity of nanofluids increases with nanoparticle concentration due to enhanced interparticle interactions, increased solid volume fraction, and greater resistance to fluid motion.
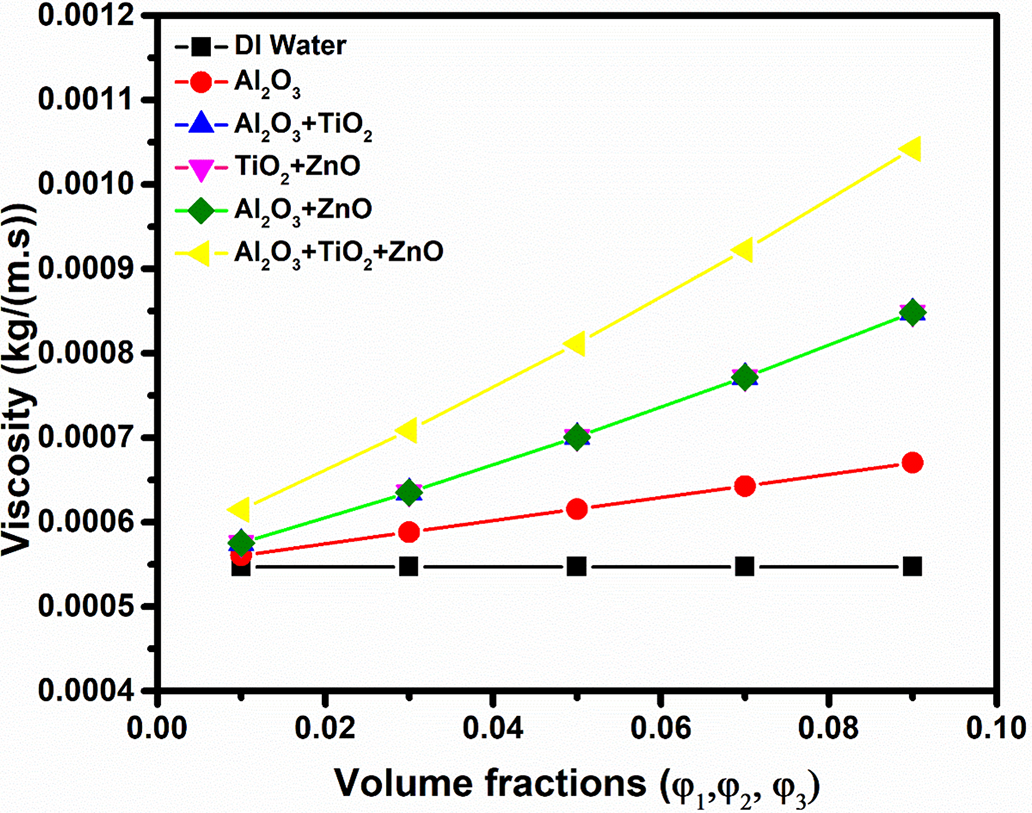
Figure 9: Effect of volume fraction of nanoparticles on viscosity of different nanofluids
In comparison, the unary nanofluid (Al2O3) shows an initial increase in viscosity due to single particle fluid interactions. Binary nanofluids further amplify viscosity compared to unary nanofluids, likely due to two particle interactions. The ternary nanofluid (Al2O3 + TiO2 + ZnO) displays the highest viscosity at all volume fractions, suggesting more complex interactions among three nanoparticle types. This rise in viscosity with added nanoparticle types and concentrations implies improvement in thermal properties but also indicates increased flow resistance, which may impact pumping power and system design in practical applications.
3.6 Effect of Concentration of Nanoparticles on Heat Transfer Rate
Fig. 10 demonstrates how the heat transfer rate varies with volume fraction for deionized (DI) water, unary, binary, and ternary nanofluids. The results indicate a significant increase in heat transfer rate as the concentration of nanoparticles increases across all cases of nanofluids, this is due to enhancement of thermal conductivity of the fluid, improving heat transfer efficiency. Additionally, increased nanoparticle interactions and Brownian motion enhance convective heat transfer, leading to higher energy transport.
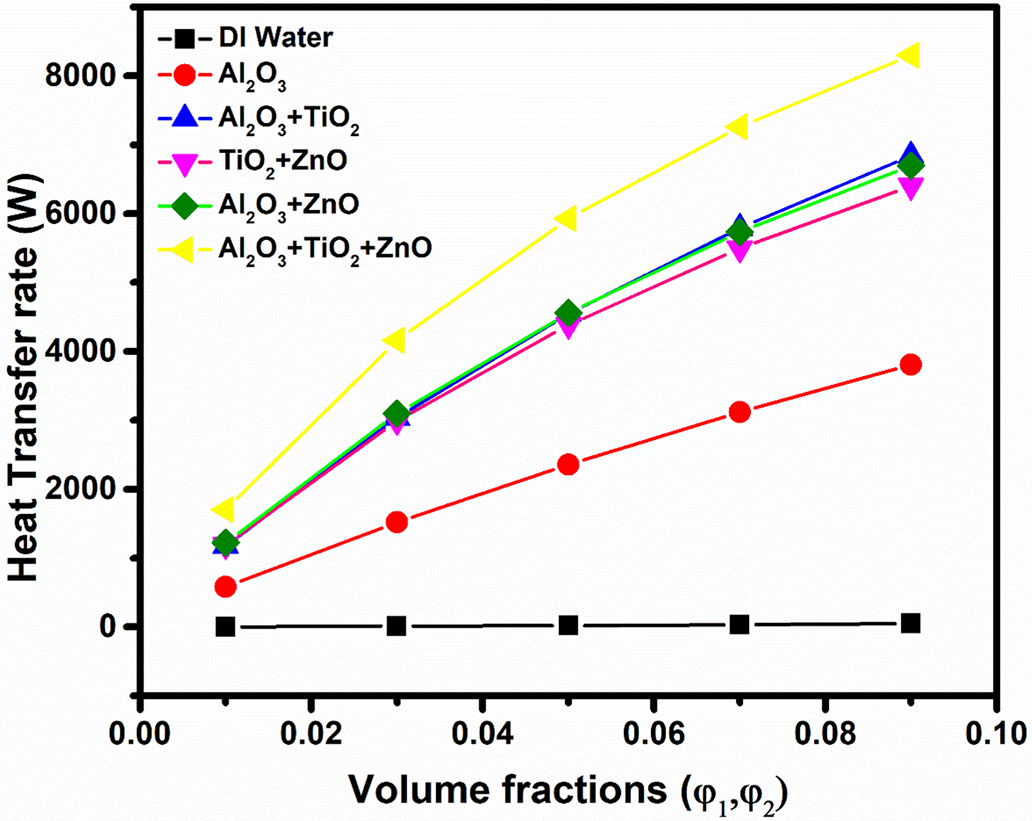
Figure 10: Effect of volume fraction of nanoparticles on Heat transfer rate for different nanofluids
For deionized (DI) water, the heat transfer rate increases gradually reaches to its highest value 52 W at 0.09 concentration, highlighting its limited thermal performance as a base fluid. In contrast, the unary Al2O3 nanofluid demonstrates much higher heat transfer rates, starting at 584.2 W at 0.01 concentration and reaching 3806 W at 0.09 concentration. This dramatic enhancement showcases the effective thermal conductivity of Al2O3 nanoparticles. The binary nanofluids, exhibit significant improvements in heat transfer rates. For instance, the heat transfer rate for Al2O3 + TiO2 nanofluid progresses from 1180 W at 0.01 concentration to 6840 W at 0.09 concentration, while TiO2 + ZnO shows a similar trend, starting at 1190 W and reaching 6402 W. Al2O3 + ZnO slightly outperforms TiO2 + ZnO with values ranging from 1225 to 6695 W.
Notably, the ternary nanofluid Al2O3 + TiO2 + ZnO exhibits the highest heat transfer rates among all cases, with a remarkable increase from 1705 W at 0.01 concentration to 8300 W at 0.09 concentration. This indicates that combining multiple nanoparticles results in enhanced thermal performance, underscoring the advantages of using multi-component nanofluids in heat transfer applications. Overall, the data suggest that increasing nanoparticle concentration significantly boosts heat transfer rates, with ternary combinations providing the most effective thermal performance.
3.7 Effect of Flow Rate on Heat Transfer Coefficient
The Fig. 11 represents the heat transfer coefficient (U) as a function of volume flow rate for DI water, unary, binary and ternary nanofluids at three different nanoparticle concentrations: 2%, 4%, and 6%. The results illustrate that, in all subgraphs (a), (b) and (c), increasing the flow rate and nanoparticle concentration enhances heat transfer performance. This improvement is attributed to increased turbulence, better nanoparticle dispersion, and reduced thermal boundary layer thickness, resulting in a higher heat transfer coefficient for nanofluids compared to DI water. In contrast, the introduction of unary Al2O3 nanoparticles leads to a significant rise in the heat transfer coefficient, demonstrating the positive impact of nanofluids on convective heat transfer and thermal conductivity.
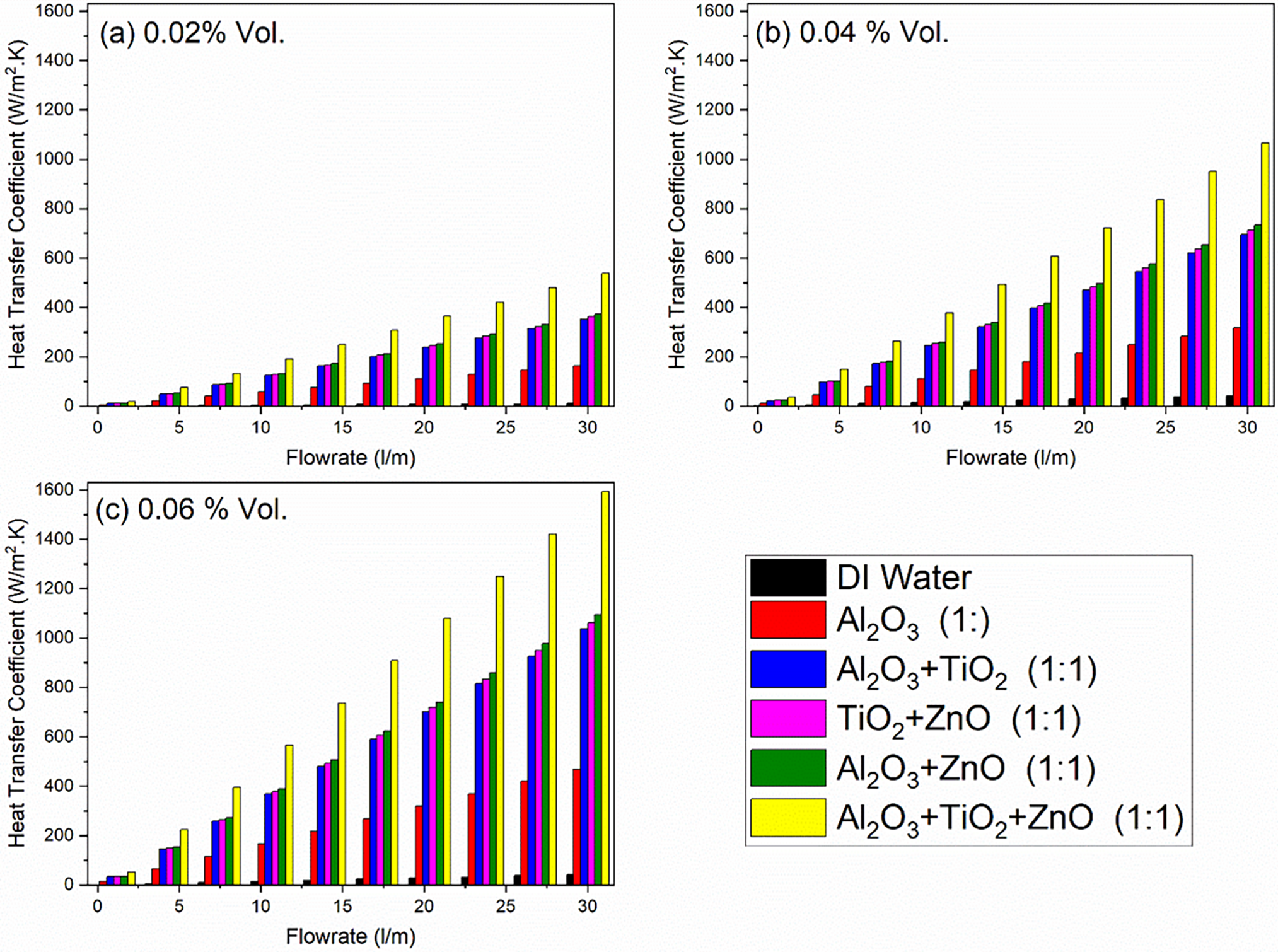
Figure 11: Effect of concentration of nanoparticles on Heat transfer coefficient against volume flow rates for different nanofluids. In all subgraphs (a–c), increasing the flow rate and nanoparticle concentration enhances heat transfer performance
When investigating binary nanofluids, the combinations of Al2O3 + TiO2, TiO2 + ZnO, and Al2O3 + ZnO show even higher heat transfer coefficients than unary Al2O3, suggesting that the interactions between different nanoparticles can result in enhanced thermal performance. The heat transfer coefficients for these binary mixtures indicate improved thermal behavior due to the combined effects of multiple nanoparticles, which may enhance particle dispersion and reduce thermal resistance.
The ternary nanofluid (Al2O3 + TiO2 + ZnO) achieves the highest heat transfer coefficients among all cases, reaching up to 537.8, 1065 and 1592 at 2%, 4% and 6% vol. concentration, respectively. This is attributed to the blending different nanoparticles can lead to synergistic effects that further improve thermal performance. This suggests that utilizing a combination of multiple nanoparticles not only enhances the thermal conductivity but also facilitates superior convective heat transfer compared to unary and binary combinations.
It is clear indication from graphs that with the increment of concentration of nanoparticles the heat transfer coefficient increases.
3.8 Effect of Flow Rate on Nusselt Number
The Fig. 12 represents the Nusselt number (Nu) as a function of volume flow rate for DI water, unary, binary and ternary nanofluids at three different nanoparticle concentrations: 2%, 4%, and 6%. The results clearly demonstrate that that as the flowrate increases along with concentration of nanoparticles, the Nusselt number of the prepared nanofluid samples also increases as shown in subgraphs (a), (b) and (c). This is due to the fact that an increase in flowrate causes the Reynolds number to rise, which is proportional to the fluid’s Nusselt number according to the correlation in Eq. (15). DI Water serves as the baseline and exhibits the lowest Nusselt numbers, indicating relatively poor heat transfer capabilities compared to nanofluids.
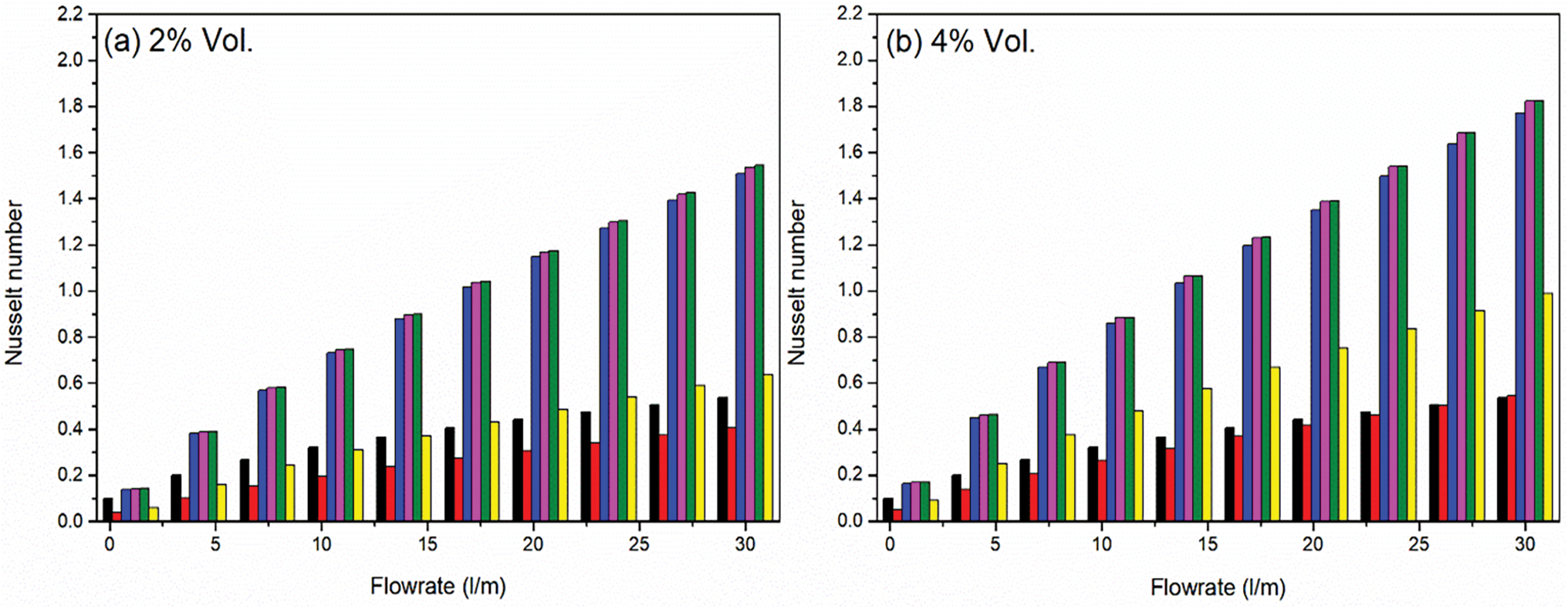
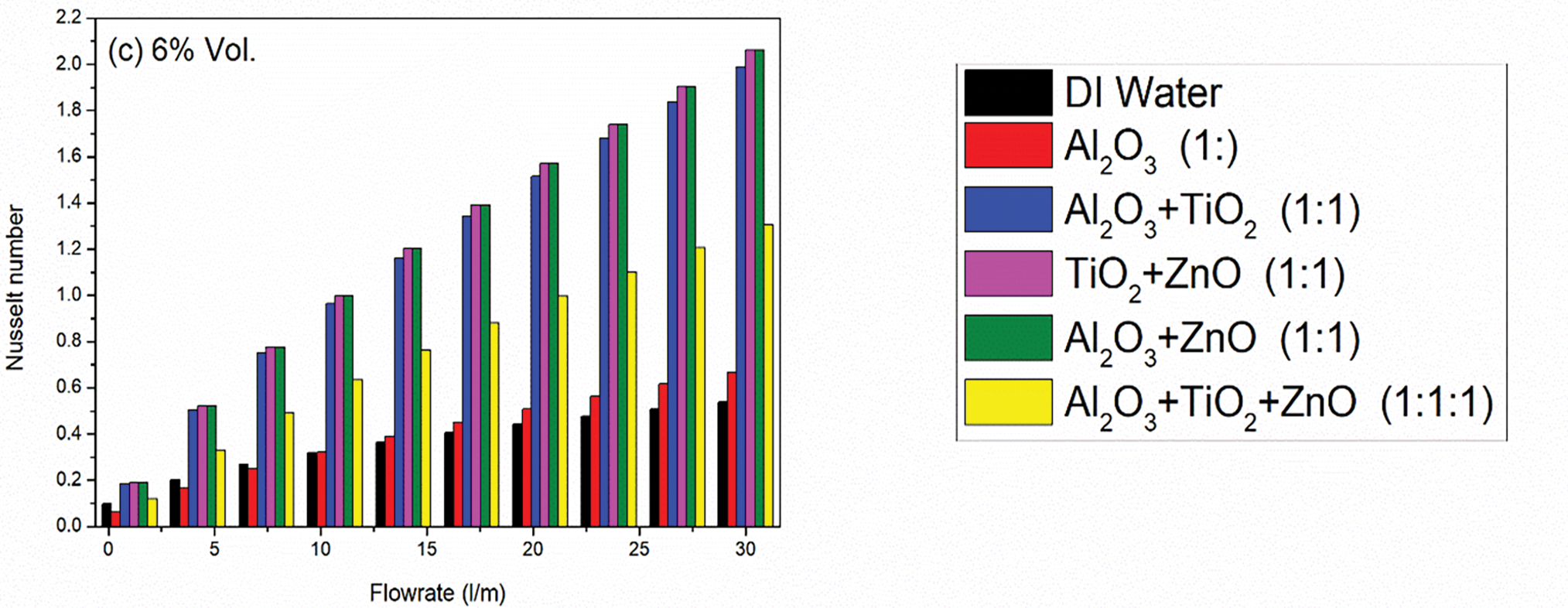
Figure 12: Effect of concentration of nanoparticles on Nusselt Number against volume flow rates for different nanofluids. As the flowrate increases along with concentration of nanoparticles, the Nusselt number of the prepared nanofluid samples also increases as shown in subgraphs (a–c)
In contrast, the binary nanofluids, specifically Al2O3 + TiO2, TiO2 + ZnO, and Al2O3 + ZnO exhibit considerably higher Nusselt numbers, indicating a marked improvement in convective heat transfer performance. The Nusselt numbers out of these three cases, Al2O3 + ZnO reaches to its highest value (2.061) at 6% vol. concentration due to synergistic effects that enhance thermal conductivity and flow characteristics, optimized particle size and distribution that improve dispersion and stability and favorable interactions between the nanoparticles and the base fluid that enhance convective heat transfer efficiency.
The ternary nanofluid (Al2O3 + TiO2 + ZnO) yields a mixed performance with Nusselt numbers reaches to its value (1.306) at 6% vol. concentration. While this is an improvement over unary Al2O3 but weakness over binary, it does not reach the levels seen in the binary combinations, suggesting that the combination of three nanoparticles may lead to increased interaction and viscosity that could hinder optimal convective heat transfer performance. The behavior of the ternary nanofluid indicates that while the combination of Al2O3, TiO2, and ZnO may provide some benefits, the complexities of multiple particle interactions and potential increases in viscosity can limit its effectiveness compared to binary nanofluids. It highlights the need for careful consideration of the nanoparticle types and concentrations used in ternary combinations to optimize their convective thermal performance in practical applications.
3.9 Evaluation of Thermal Performance Factor (TPF)
Fig. 13 highlights the thermal performance factor for hybrid nanofluids selected in this study. The thermal performance factor (TPF) of binary nanofluids is higher than ternary nanofluids because binary nanofluids provide a better balance between thermal conductivity enhancement and low to moderate viscosity. In contrast, ternary nanofluids tend to have higher viscosity due to increased nanoparticle interactions, leading to greater flow resistance and reduced convective heat transfer efficiency.
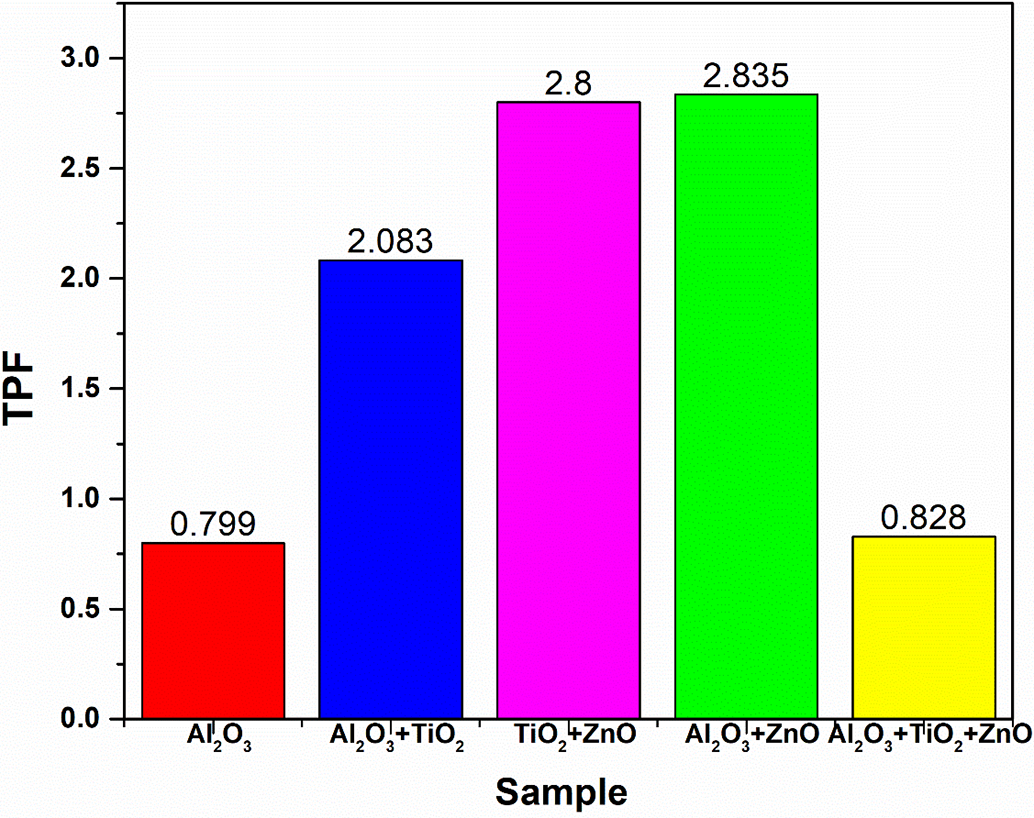
Figure 13: Thermal performance factor for different nanofluids
The thermal performance factor (TPF) analysis for various nanofluids indicates distinct differences in heat transfer efficiency across unary, binary, and ternary combinations. The unary Al2O3 nanofluid, with a TPF of 0.799, shows limited improvement over deionized (DI) water, suggesting modest heat transfer enhancement. Binary nanofluids, however, display substantial gains in thermal performance: Al2O3 + TiO2 reaches a TPF of 2.083, TiO2 + ZnO achieves 2.8, and Al2O3 + ZnO slightly surpasses this with a TPF of 2.835, this is due to fact that, ZnO and AlO3 both have higher thermal conductivities than TiO2, their combination probably improves heat transmission by increasing effective thermal conductivity more than other mixes. In contrast, the ternary nanofluid (Al2O3 + TiO2 + ZnO) yields a TPF of 0.828, indicating that while the addition of a third nanoparticle does not enhance performance as compared to the case of binary. Ternary nanofluids can sometimes exhibit diminished TPF due to complex inter particle dynamics, viscosity-related drawbacks, and reduced synergistic effects, suggesting that binary combinations may often provide an optimal balance for thermal enhancement.
4 Uncertainty Analysis of the Experimental Setup
In this section, an uncertainty analysis of the thermal parameters of the experimental setup has been performed. The total uncertainty
If U is the function of n independent linear parameters as U = U of
where
Hence, fractional uncertainty of the U (given that uncertainties in
Using Eq. (24), fractional uncertainties can be estimated. By using the aforementioned approach, the greatest absolute uncertainty for every parameter is computed and, for every experiment, it is less than 5%. Uncertainty values quantifies within this limit confirm the reliability of the measured data [29]. The uncertainties related to the experimental setup’s measuring devices are listed in Table 4.

The objective of this study is to improve the stability of hybrid nanofluids and thermodynamic comparative analysis of various hybrid nanofluid used as heat transfer fluids. This includes unary nanofluid (Al2O3), three binary combinations (Al2O3 + TiO2, TiO2 + ZnO, Al2O3 + ZnO), and a ternary blend (Al2O3 + TiO2 + ZnO). Following are the major findings of this study:
• The stability of nanofluid was found to improve in pH-adjusted water compared to deionized (DI) water, with optimal stability observed at a pH of 11, with additional enhancement observed upon the use of a surfactant.
• Increasing nanoparticle concentration results in a decline in Reynolds number across all cases, excluding DI water, which remains constant. This decrease in Reynolds number with higher volume fractions is likely due to the higher density and viscosity imparted by the nanoparticles, which can hinder flow velocity.
• In a comparison of hybrid nanofluids, binary nanofluids, especially Al2O3 + ZnO exhibited the highest TPF (2.835), indicating superior thermal performance.
• Despite of higher heat transfer rate and specific heat, the ternary nanofluid exhibits a modest TPF (0.828) due to increased density and viscosity. These properties can raise the fluid’s resistance to flow, thereby increasing the required pumping power and diminishing overall energy efficiency gains.
The results reveal that binary nanofluids, particularly Al2O3 + ZnO, offer an optimal balance of thermal enhancement and flow stability, outperforming unary and ternary combinations. The findings highlight the importance of careful selection of nanoparticle types and concentrations to optimize heat transfer applications, as well as considering the trade-offs associated with viscosity and flow properties. The findings of this study can be easily scaled up and applied to shell and tube heat exchangers for enhanced thermal performance. Furthermore, this work suggests future directions for engineers to incorporate pressure drop analysis due to addition of multiple particles in the base fluid and computational fluid dynamics (CFD) simulations approach alongside experimental approaches.
Acknowledgement: Authors acknowledge the Mehran University of Engineering and Technology, Jamshoro for providing the necessary experimental facilities. The findings herein reflect the work, and are solely the responsibility, of the authors.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: Conceptualization, Ans Ahmed Memon and Laveet Kumar; methodology, Ans Ahmed Memon and Laveet Kumar; software, Ans Ahmed Memon and Laveet Kumar; validation, Ans Ahmed Memon and Laveet Kumar; formal analysis, Laveet Kumar; resources, Ans Ahmed Memon and Laveet Kumar; data curation, Ans Ahmed Memon and Laveet Kumar; writing—original draft preparation, Ans Ahmed Memon; writing—review and editing, Laveet Kumar, Abdul Ghafoor Memon, Khanji Harijan and Ahmad K. Sleiti; supervision, Laveet Kumar, Abdul Ghafoor Memon, Khanji Harijan and Ahmad K. Sleiti. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data that support the findings of this study are available from the corresponding author upon reasonable request.
Ethics Approval: Not applicable.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
Nomenclature
| Variables | |
| A | Area of heat exchanger (m2) |
| Cp | Specific heat (J · kg−1 · K) |
| D | Diameter (m) |
| F | Friction Factor |
| H | Heat transfer coefficient (W · m−2 · K) |
| K | Thermal-Conductivity of nanoparticles (W · m−1 · K−1) |
| L | Length of tube (m) |
| ·m | Mass flow rate (L · min−1) |
| Nu | Nusselt numbers (−) |
| NTU | Number of heat transfer units |
| P | Pumping power (W) |
| Pr | Prandtl number (−) |
| Re | Reynolds number |
| Q | Heat transfer rate (W) |
| T | Temperature (°C) |
| U | Overall heat transfer coefficient (W · m2 · K−1) |
| U | Velocity (m · s−1) |
| V | Volumetric flow rate (m3 · s−1) |
| Greek Symbols | |
| Density (kg · m−3) | |
| Volumetric fraction (%) | |
| ε | Effectiveness of heat exchanger (−) |
| µ | Dynamic viscosity of nanofluid (Pa·s) |
| ΔTLMTD | Logarithmic mean temperature difference (°C) |
| ΔP | Pressure drop (Pa) |
| Subscripts | |
| B | Baffle |
| bf | Base fluid |
| h | Height |
| i | Inner |
| In | Inlet |
| Nanoparticle | |
| nf | Nanofluids |
| o | Outer |
| t | Tube |
| Acronym | |
| Al2O3 | Aluminum oxide |
| EES | Engineering equation solver |
| DI | Deionized water |
| HTF | Heat Transfer Fluid |
| TPF | Thermal performance factor |
| HTC | Heat transfer coefficient |
| SDS | Sodium dodecyl sulfate |
| TiO2 | Titanium oxide |
| ZnO | Zink oxide |
References
1. Ali K, Ahmad S, Tayebi T, Ashraf M, Jamshed W, Abd-Elmonem A, et al. Thermal attributes of hybrid (MWCNT-NiZnFe2O4) nanofluid flow having motile microbes and activation energy: a computational approach. Case Stud Therm Eng. 2023;47(1):103088. doi:10.1016/j.csite.2023.103088. [Google Scholar] [CrossRef]
2. Al-Obaidi MA, Rashid FL, Rasheed MK, Aljibori HSS, Mohammed HI, Mahdi AJ, et al. Recent achievements in heat transfer enhancement with hybrid nanofluid in heat exchangers: a comprehensive review. Int J Thermophys. 2024;45(9):133. doi:10.1007/s10765-024-03428-x. [Google Scholar] [CrossRef]
3. Skheel OR, Yasin NJ, Al-abbas AH, Soomro SA. Experimental study of the wickless heat pipe heat exchanger by using nano fluid. J Tech. 2023;5(4):115–30. doi:10.51173/jt.v5i4.1278. [Google Scholar] [CrossRef]
4. Niamsuwan S, Kittisupakorn P, Mujtaba IM. Control of milk pasteurization process using model predictive approach. Comput Chem Eng. 2014;66:2–11. doi:10.1016/j.compchemeng.2014.01.018. [Google Scholar] [CrossRef]
5. Zhang J, Zhu XW, Mondejar ME, Haglind F. A review of heat transfer enhancement techniques in plate heat exchangers. Renew Sustain Energy Rev. 2019;101:305–28. doi:10.1016/j.rser.2018.11.017. [Google Scholar] [CrossRef]
6. Radhika GB, Malika M, Sonawane SS, Uslu H, Mohammed HA. Experimental investigation of industrial hybrid nanofluids in heat exchangers. Hybrid Nanofluids Appl Chem Pet Ind. 2025;2025(12):149–68. doi:10.1016/B978-0-443-21451-6.00009-7. [Google Scholar] [CrossRef]
7. Borode AO, Ahmed NA, Olubambi PA. A review of heat transfer application of carbon-based nanofluid in heat exchangers. Nano-Struct Nano-Objects. 2019;20(1):100394. doi:10.1016/j.nanoso.2019.100394. [Google Scholar] [CrossRef]
8. Balakrishnan S, Suriya M, Tamilarasan P, Thanigaivel S. Impact of nanoparticle concentration on thermal properties of nanofluids in heat exchangers. E3S Web Conf. 2025;619(18):05008. doi:10.1051/e3sconf/202561905008. [Google Scholar] [CrossRef]
9. Abid M, Khan MS, Ratlamwala TAH, Malik MN, Ali HM, Cheok Q. Thermodynamic analysis and comparison of different absorption cycles driven by evacuated tube solar collector utilizing hybrid nanofluids. Energy Convers Manag. 2021;246(3):114673. doi:10.1016/j.enconman.2021.114673. [Google Scholar] [CrossRef]
10. Al Mezrakchi R. Investigation of various hybrid nanofluids to enhance the performance of a shell and tube heat exchanger. AIMS Energy. 2024;12(1):235–55. doi:10.3934/energy.2024011. [Google Scholar] [CrossRef]
11. Rao MSE, Sreeramulu D. Experimental investigation of heat transfer rate of nano fluids using a shell and tube heat exchanger. IOP Conf Ser Mater Sci Eng. 2016;149(1):012204. doi:10.1088/1757-899X/149/1/012204. [Google Scholar] [CrossRef]
12. AbuGhanem M, Raafat PB, Ibrahim FN. An in-depth comparative analysis of entropy generation and heat transfer in micropolar-williamson, micropolar-Maxwell, and micropolar-Casson binary nanofluids within PTSCs. ZAMM-J Appl Math Mech Z Für Angew Math Und Mech. 2024;104(10):e202300912. doi:10.1002/zamm.202300912. [Google Scholar] [CrossRef]
13. Peyghambarzadeh S, Hashemabadi SH, Jamnani MS, Hoseini SM. Improving the cooling performance of automobile radiator with Al2O3/water nanofluid. Appl Therm Eng. 2011;31(10):1833–8. doi:10.1016/j.applthermaleng.2011.02.029. [Google Scholar] [CrossRef]
14. Nguyen CT, Roy G, Gauthier C, Galanis N. Heat transfer enhancement using Al2O3–water nanofluid for an electronic liquid cooling system. Appl Therm Eng. 2007;27(8–9):1501–6. doi:10.1016/j.applthermaleng.2006.09.028. [Google Scholar] [CrossRef]
15. Ramadhan AI, Umar E, Azmi WH, Sari AM. Heat transfer performance of Al2O3-TiO2-SiO2 ternary nanofluids in plain tube with wire coil inserts. Mech Eng Soc Ind. 2024;4(1):50–67. doi:10.31603/mesi.10996. [Google Scholar] [CrossRef]
16. Memon AA, Kumar L, Memon AG, Harijan K, Said Z. Stability enhancement of Al2O3, ZnO, and TiO2 binary nanofluids for heat transfer applications. Open Phys. 2024;22(1):20230199. doi:10.1515/phys-2023-0199. [Google Scholar] [CrossRef]
17. Said Z, Assad MEH, Hachicha AA, Bellos E, Abdelkareem MA, Alazaizeh DZ, et al. Enhancing the performance of automotive radiators using nanofluids. Renew Sustain Energy Rev. 2019;112:183–94. doi:10.1016/j.rser.2019.05.052. [Google Scholar] [CrossRef]
18. Wu X, Lee J, Varshney V, Wohlwend JL, Roy AK, Luo T. Thermal conductivity of wurtzite zinc-oxide from first-principles lattice dynamics-a comparative study with gallium nitride. Sci Rep. 2016;6(1):1–10. [Google Scholar]
19. Kumar L, Walvekar R, Khalid M. An overview of recent advancements and applications of hybrid nanofluids. Mater Today Proc. 2023. doi:10.1016/j.matpr.2023.02.060. [Google Scholar] [CrossRef]
20. Ans Ahmed Memon LK, Harijan K, Memon AG. Heat transfer enhancement using TiO2 based nano fluid in shell and tube heat exchanger. In: Proceedings of the 2nd World Energy Storage Conference: WESC-2022; 2022 Dec 18–21; Istanbul, Türkiye. [Google Scholar]
21. Zheng D, Wang J, Chen Z, Baleta J, Sundén B. Performance analysis of a plate heat exchanger using various nanofluids. Int J Heat Mass Transf. 2020;158:119993. doi:10.1016/j.ijheatmasstransfer.2020.119993. [Google Scholar] [CrossRef]
22. Prasanna ASB, Ramji K. Effect of surface modification on the thermophysical properties of ethylene glycol dispersed with Al2O3 nanoparticles for solar thermal applications. Proc Inst Mech Eng Part N J Nanomater Nanoeng Nanosyst. 2024;231:23977914241259084. doi:10.1177/23977914241259084. [Google Scholar] [CrossRef]
23. Asokan N, Gunnasegaran P, Wanatasanappan VV. Experimental investigation on the thermal performance of compact heat exchanger and the rheological properties of low concentration mono and hybrid nanofluids containing Al2O3 and CuO nanoparticles. Therm Sci Eng Prog. 2020;20:100727. doi:10.1016/j.tsep.2020.100727. [Google Scholar] [CrossRef]
24. Chandio MW, Kumar L, Memon AG, Awad MM. Thermodynamic, economic, and environmental evaluation of internal combustion engine exhaust gas-driven Organic Rankine cycles for power generation and desalination. Int J Thermofluids. 2025;25:101046. doi:10.1016/j.ijft.2024.101046. [Google Scholar] [CrossRef]
25. Kumar L, Hasanuzzaman M, Rahim N. Real-time experimental performance assessment of a photovoltaic thermal system cascaded with flat plate and heat pipe evacuated tube collector. J Sol Energy Eng. 2022;144(1):011004. doi:10.1115/1.4051861. [Google Scholar] [CrossRef]
26. Madhesh D, Kalaiselvam S. Experimental analysis of hybrid nanofluid as a coolant. Procedia Eng. 2014;97:1667–75. doi:10.1016/j.proeng.2014.12.317. [Google Scholar] [CrossRef]
27. Kristiawan B, Santoso B, Juwana WE, Ramadhan RM, Riandana I. Numerical investigation of laminar convective heat transfer for TiO2/water nanofluids using two-phase mixture model (Eulerian approach). AIP Conf Proc. 2017;1788(1):030002. doi:10.1063/1.4968255. [Google Scholar] [CrossRef]
28. Somasundaran P, Mehta SC, Yu X, Krishnakumar S. Colloid systems and interfaces stability of dispersions through polymer and surfactant adsorption. In: Birdi KS, editor. Handbook of surface and colloid chemistry. 3rd ed. Boca Raton, FL, USA: CRC Press; 2008. p. 388–433. [Google Scholar]
29. Sardarabadi M, Passandideh-Fard M, Heris SZ. Experimental investigation of the effects of silica/water nanofluid on PV/T (photovoltaic thermal units). Energy. 2014;66(S1):264–72. doi:10.1016/j.energy.2014.01.102. [Google Scholar] [CrossRef]
30. Kline SJ. Describing uncertainties in single-sample experiments. Mech Eng. 1963;75:3–8. [Google Scholar]
31. Taylor J. Introduction to error analysis, the study of uncertainties in physical measurements. 2nd ed. New York, NY, USA: University Science Books; 1997. 344 p. [Google Scholar]
Cite This Article
 Copyright © 2025 The Author(s). Published by Tech Science Press.
Copyright © 2025 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools