Carrageenan (CA) is a kind of hydrophilic polysaccharide extracted from red algae. In this paper, a very small amount of Ba2+ was added to carrageenan spinning...

Guided by the theoretical processes of mindfulness and psychological well-being, this study examined serenity as a mediator between mindfulness facets and psychological...

La démocratie en santé met en avant le respect des droits individuels et des droits collectifs des usagers du système de santé. Elle connaît un essor depuis une...
It is with our great pleasure to announce Prof. Manchun Li, Nanjing University, China, as the new Editor-in-Chief for Revue Internationale de Géomatique (RIG, the International Journal...
In line with our ongoing business development, Tech Science Press has relocated to a new office address in Henderson. Please note the updated details below: Change DetailsBeforeAfterHenderson...

The collocation method is a widely used numerical method for science and engineering problems governed by partial differential equations. This paper provides...

The safety and stability of high-speed maglev trains traveling on viaducts in crosswinds critically depend on their aerodynamic characteristics. Therefore,...
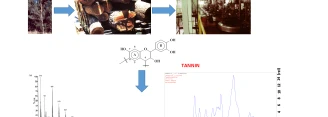
Condensed and hydrolysable tannins are non-toxic natural polyphenols that are a commercial commodity industrialized for tanning hides to obtain leather...
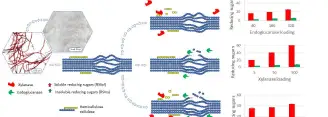
This study was conducted to evaluate the effectiveness of enzymes in purifying and reducing the degree of polymerization of cellulose for the production...
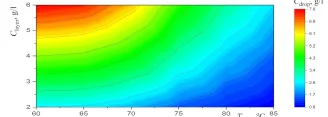
New experimental results, which are important for the potential use of small levitating droplets as biochemical microreactors, are reported. It is shown...
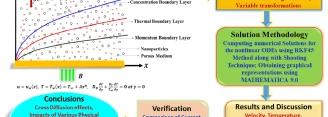
The primary aim of this research endeavor is to examine the characteristics of magnetohydrodynamic Williamson nanofluid flow past a nonlinear stretching...
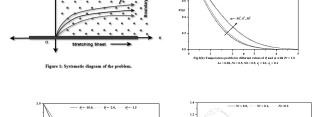
This investigation aims to analyze the effects of heat transport characteristics in the unsteady flow of nanofluids over a moving plate caused by a moving...

The escalating need for reliability analysis (RA) and reliability-based design optimization (RBDO) within engineering challenges has prompted the advancement...
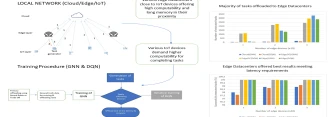
In a network environment composed of different types of computing centers that can be divided into different layers (clod, edge layer, and others), the...
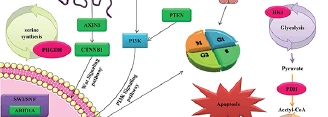
Noncoding RNAs instruct the Cas9 nuclease to site-specifically cleave DNA in the CRISPR/Cas9 system. Despite the high incidence of hepatocellular carcinoma...
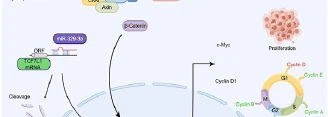
An important factor in the emergence and progression of osteosarcoma (OS) is the dysregulated expression of microRNAs (miRNAs). Transcription factor 7-like...
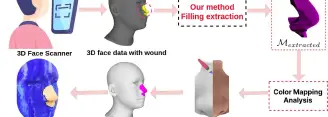
Facial wound segmentation plays a crucial role in preoperative planning and optimizing patient outcomes in various medical applications. In this paper,...

This article reviews the theory of fairness in AI–from machine learning to federated learning, where the constraints on precision AI fairness and perspective...

The study focuses on the development of biocompatible and stable FA-functionalized nanocrystalline cellulose (NCC) as a potential drug delivery system...
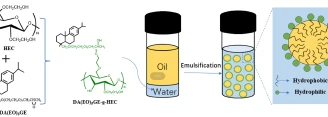
Dehydroabietyl polyethylene glycol glycidyl ether-grafted hydroxyethyl cellulose (HEC) polymer surfactant (DA(EO)5GE-g-HEC) was prepared using ring-opening...

The second edition of the expert consensus on pediatric nutrition was formed based on a global update of pediatric nutrition guidelines or consensus worldwide,...
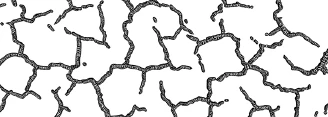
The peridynamics proposed by Silling [1] is a non-local theory of solid mechanics. It redefines the problems by using integral equations rather than partial...

In modern time, experts started to use interdisciplinary properties with the developing of technology and science. Thus, these disciplines provide more...

More than half of the world population is living in cities. It requires extended infrastructure and various services to support the densely concentrated...

In the last two decades, the topic of computational intelligence (CI) has undergone several definitions. Adaptation and self-organization algorithms and...

The interface between computer science and statistics has developed considerably in recent years, with exponential progress in the fields of data analysis,...

Swarm intelligence (SI) is the collective behavior of decentralized, self-organized systems, natural or artificial. In SI, an individual has a simple...

Precise resources and energy forecasting is important to facilitate the decision-making process in order to achieve higher efficiency and reliability...

Heuristic and computing techniques are technologies that are poised to transform the way humans will interact with machines, and the role that machines...

The collocation method is a widely used numerical method for science and engineering problems governed by partial differential equations. This paper provides...

The safety and stability of high-speed maglev trains traveling on viaducts in crosswinds critically depend on their aerodynamic characteristics. Therefore,...

Condensed and hydrolysable tannins are non-toxic natural polyphenols that are a commercial commodity industrialized for tanning hides to obtain leather...

This study was conducted to evaluate the effectiveness of enzymes in purifying and reducing the degree of polymerization of cellulose for the production...

New experimental results, which are important for the potential use of small levitating droplets as biochemical microreactors, are reported. It is shown...

The primary aim of this research endeavor is to examine the characteristics of magnetohydrodynamic Williamson nanofluid flow past a nonlinear stretching...

This investigation aims to analyze the effects of heat transport characteristics in the unsteady flow of nanofluids over a moving plate caused by a moving...

The escalating need for reliability analysis (RA) and reliability-based design optimization (RBDO) within engineering challenges has prompted the advancement...

In a network environment composed of different types of computing centers that can be divided into different layers (clod, edge layer, and others), the...

Noncoding RNAs instruct the Cas9 nuclease to site-specifically cleave DNA in the CRISPR/Cas9 system. Despite the high incidence of hepatocellular carcinoma...

An important factor in the emergence and progression of osteosarcoma (OS) is the dysregulated expression of microRNAs (miRNAs). Transcription factor 7-like...

Facial wound segmentation plays a crucial role in preoperative planning and optimizing patient outcomes in various medical applications. In this paper,...

This article reviews the theory of fairness in AI–from machine learning to federated learning, where the constraints on precision AI fairness and perspective...

The study focuses on the development of biocompatible and stable FA-functionalized nanocrystalline cellulose (NCC) as a potential drug delivery system...

Dehydroabietyl polyethylene glycol glycidyl ether-grafted hydroxyethyl cellulose (HEC) polymer surfactant (DA(EO)5GE-g-HEC) was prepared using ring-opening...

The second edition of the expert consensus on pediatric nutrition was formed based on a global update of pediatric nutrition guidelines or consensus worldwide,...

The peridynamics proposed by Silling [1] is a non-local theory of solid mechanics. It redefines the problems by using integral equations rather than partial...

In modern time, experts started to use interdisciplinary properties with the developing of technology and science. Thus, these disciplines provide more...

More than half of the world population is living in cities. It requires extended infrastructure and various services to support the densely concentrated...

In the last two decades, the topic of computational intelligence (CI) has undergone several definitions. Adaptation and self-organization algorithms and...

The interface between computer science and statistics has developed considerably in recent years, with exponential progress in the fields of data analysis,...

Swarm intelligence (SI) is the collective behavior of decentralized, self-organized systems, natural or artificial. In SI, an individual has a simple...

Precise resources and energy forecasting is important to facilitate the decision-making process in order to achieve higher efficiency and reliability...

Heuristic and computing techniques are technologies that are poised to transform the way humans will interact with machines, and the role that machines...

Guest Editors: Massimo Ficco; Marek R. Ogiela Deadline: 30 March 2025

Guest Editors: J. Paulo Davim; Ankit D. Oza Deadline: 25 February 2025

Guest Editors: Rui Araújo; Jiafu Su Deadline: 31 January 2025

Guest Editors: Yuan Ren; Hwa Kian Chai; Ziyuan Fan; Xiaoling Liu; Xiang Xu Deadline: 31 December 2024

Guest Editors: Yunpeng Wu; Zhenkun Li; Chuang He; Li Ai Deadline: 31 December 2024

Guest Editors: Maosen Cao; Dayang Li Deadline: 31 December 2024

Guest Editors: Enrico Mini; Guido Bocci; Antonello Di Paolo; Stefania Nobili Deadline: 31 December 2024

Guest Editors: Haitao Yu; Eva Binder; Qiushi Chen; Hui Wang; Xizhuo Chen Deadline: 31 December 2024

Guest Editors: Mohammad Shokouhifar; Frank Werner Deadline: 31 December 2024

Guest Editors: Azhar Imran; Jianqiang Li; Khursheed Aurangzeb Deadline: 31 December 2024

Guest Editors: Pattabhi Ramaiah Budarapu; Timon Rabczuk Deadline: 31 December 2024

Guest Editors: Zhengxuan Liu; Zhenya Zhang Deadline: 30 December 2024

Guest Editors: Lin Qiu; Hanying Zou; Yanhui Feng; Huansheng Ning; Cheng Chen Deadline: 10 December 2024

Guest Editors: Fateh Mebarek-Oudina; Ioannis E. Sarris Deadline: 07 December 2024

Guest Editors: Quanwang Wu; Yishui Zhu; Jialei Liu; Jabar Mahmood Deadline: 30 November 2024

Guest Editors: Manuel J. Cabral S. Reis; Carlos Manuel José Alves Serôdio;... Deadline: 15 November 2024






